Abstract
Time-modulated arrays (TMAs) are electromagnetic systems whose radiated power pattern is controlled by the application of variable-width periodical pulses to the individual elements. The nonlinear nature of the array operation causes the appearance of radiation patterns at the harmonic frequencies of such periodic pulses. The technique can be used for improving the side-lobe level (SLL) topology of the radiation pattern at the central frequency and/or to profitably exploit the harmonic patterns in order to supply smart antenna capabilities. Among the latter features, the TMA harmonic beamforming takes on special importance due to its attractive trade-off performance-hardware complexity. From this perspective, TMAs are sensors capable of transforming the spatial diversity of a communication channel into frequency diversity, thus improving the performance of a wireless communication. In addition to a walk through the origins of the concept, and a brief analysis of the mathematical fundamentals, this paper organizes the prolific state of the art of TMAs in two major thematic blocks: (1) TMA design from an antenna perspective; and (2) TMA design from a signal processing perspective.
1. Introduction
Wireless services demanding more mobility, capacity, and robustness have placed wireless communications as the fastest growing sector of the telecommunication industry nowadays. As a result, the increasingly limited wireless medium has to be smartly exploited and antennas are called to play an important role to achieve such a goal. A proper combination of antenna features and signal processing allows us to jointly and efficiently act in the space, frequency, and time domains in order to provide suitable alternatives to the complex task of faithfully receiving the desired signals and efficiently mitigating the unwanted ones.
One of the primary objectives of an intelligent system supported by a sensor network is its sustainability. The investigation of new technologies allowing for reducing the power consumption of sensor networks is aimed towards the design of smart antennas with low loss, muting and adaptive beamforming features. Additionally, such a smart antenna technology has to consider the hardware complexity, making the solution feasible in the context of sensors. Moreover, antenna devices pertaining to sensor networks must be capable of sensing the external electromagnetic environment, thus properly reconfiguring the radiation characteristics of the generated field to guarantee both the required quality of service of the communication link and a reduced power consumption.
However, some technical challenges remain in order to develop the adequate antenna technologies capable of supporting the aforementioned features in a limited physical space that the mobility demand dictates. In fact, today’s wireless standards consider multiple-antenna techniques [1,2,3] in order to exploit space diversity, spatial multiplexing and beamforming to achieve better levels of reliability and capacity. Such advantages, however, are obtained at the expense of increased system complexity, which may be unaffordable in small-size and low-cost sensor devices with a required low-power consumption.
The concept of TMA is a feasible multi-antenna technique that provides a significant hardware simplification. Furthermore, TMA, typified as unconventional phased arrays architectures, have been intensively researched during the last few years at an increasing pace [4].
1.1. What is a TMA?
TMA, in their simplest configuration, are antenna arrays whose radiated power patterns are controlled by periodically enabling and disabling the excitations of the individual array elements, as illustrated in Figure 1. Hardware implementations of TMA simplify considerably since they can be done with switches rather than the complex weight multiplications of conventional arrays.
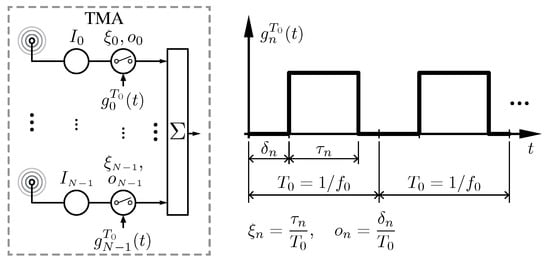
Figure 1.
On the left hand side, the block diagram of a linear time-modulated array (TMA) with N elements implemented with radio-frequency (RF) switches, with being the static excitation of the n-th element of the array. On the right hand side, the periodic () pulse train that governs the n-th switch, , which is characterized by the normalized pulse duration and the normalized switch-on instant .
The TMA radiated field with N isotropic elements distributed along the z-axis is given by [5]
where is a periodic function with a fundamental period , which governs the n-th array element, with ; and represent the n-th antenna element complex static current excitation in its polar form ( is its modulus and is its phase) and the position on the z-axis, respectively; is the carrier frequency of the incoming signal; θ is the angle with respect to the array main axis; and is the wave number for a wavelength .
Since is a periodic signal, it can be represented by the following exponential Fourier series:
where, in a conventional TMA, is a periodic rectangular pulse train with duration and delay (see Figure 1). In such a case, is given by [6]
where denotes the function, are the normalized pulse durations, and are the normalized pulse delays. In some cases, and according to the properties of the pulses, , the dependency on can be avoided, yielding , but, in this work, we consider the general form. Note that for we have . Substituting Equation (2) into Equation (1) allows for rewriting the TMA radiated field as
Observe that the first term in Equation (4) is the array factor at the fundamental mode () frequency , which shows that, by means of the normalized pulse durations , we are able to reconfigure exclusively the magnitude of the excitations and thus control the radiation pattern. On the other hand, the second term in Equation (4) reveals the existence of sideband radiation (SR) at frequencies (harmonics). Note that by modifying and/or we can also control the radiation pattern at each sideband harmonic, in this case being able to simultaneously reconfigure the magnitude and the phase of the excitations. The SR can be either minimized or, as explained in the forthcoming sections, profitably exploited.
1.2. TMA Features
As shown above, the periodic modulation of a TMA is a nonlinear operation that generates sideband signals radiated at frequencies shifted from the carrier frequency at multiples of the time-modulation rate . The time parameters which govern the TMA (specifically, the switch-on durations and the switch-on delays [7,8]) can be optimized to:
- exploit the fundamental pattern only —at the carrier frequency — with the aim of achieving ultra-low side-lobe level (SLL) while minimizing the SR, or
- profitably exploit the harmonic patterns, endowing the TMA with smart antenna capabilities.
Hence, and according to the second point, by adapting the harmonic patterns to the wireless channel, and by combining its corresponding outputs, TMA are able to perform adaptive beamforming with the benefit of using a single RF front-end. In this regard, the fact of avoiding the utilization of as many RF chains as the number of multipath components to be exploited, offers a series of key advantages:
- Hardware simplicity, with the subsequent impact on the size and the cost of the system.
- Power consumption, as it has been remarked and properly quantified in recent papers like (Table I, [2]) and (Tables I and II, [3]), which have also proposed hybrid analog–digital architectures for beamforming. Indeed, in a fully digital implementation of an linear beamforming network (LBFN), the number of required RF chains, L, must be equal to the number of antenna elements N. In practice, however, a relationship is often preferable due to a number of reasons, the power consumption per RF being the front-end one of the most important ones.
- Nonexistence of issues related to synchronization, phase coherence or coupling between different RF chains.
In summary, the application of periodic pulses at the antenna level has the effect of converting space diversity into frequency diversity and, thus, a single RF front-end is enough to exploit such a space diversity.
2. State of the Art
2.1. The Origin of the TMA Concept
The pioneering idea of using the time as an additional degree of freedom to control the radiation pattern of an antenna was proposed by Shanks and Bickmore, from the Microwave Laboratory at the Hughes Aircraft Company, Glendale, CA, USA in 1959 [9]. The authors introduced theoretically this entirely new idea in antenna design and suggested several possible physical antenna configurations, such as a square wave switched linear array. However, they employed a common parabolic dish antenna in their first experimental tests and applied a nutation movement to the primary horn with a frequency of 133 Hz. With this technique, they achieved a multi-pattern operation obtaining simultaneously a sum diagram at the fundamental frequency and a difference diagram at the first sideband harmonic.
In 1963, Kummer et al. —also from Hughes Aircraft Company— experimentally extended the concept of “time-modulated antenna” to antenna arrays [5], thus coining the term TMA. They obtained ultra-low side lobe patterns by inserting a set of RF switches —programmed according to a predetermined periodic time sequence— in the feed network of an 8-element waveguide slotted linear array working at the X-band. Kummer et al. stated that the higher the SLL improvement by applying time modulation, the higher the cost in the system gain. The source of this gain cost is the nonlinear nature of the periodic modulation, which inherently generates sideband radiated loss signals. Consequently, SR had been primarily identified as a phenomenon that severely degrades the TMA gain. As a matter of fact, Kummer et al. focused on two representative examples. On the one hand, they selected an initial static Dolph–Tschebyshev pattern with −30 dB SLL improved down to about −40 dB —by applying time modulation implemented by means of RF switches —at the expense of a modest loss in the antenna gain (0.3 dB). On the other hand, they considered a uniform static aperture distribution —with an SLL of −13 dB— improved down to −40 dB through time modulation with a much higher price to be paid (2.4 dB) in terms of the antenna gain. In this way, Kummer et al. have implicitly opened the door to future research that would be focused on minimizing the SR while improving the SLL through the application of the TMA technique.
2.2. TMA Design under an (Exclusive) Antenna Perspective
Most of the research works involving TMA have been developed under an antenna designer point of view. More specifically, they focus on the synthesis of an appropriate shape of the radiation pattern. We therefore classify such works depending on the patterns that are synthesized, i.e., fundamental or harmonics.
2.2.1. Fundamental Mode Pattern
Although it represents a natural and immediate area worth of investigation, the development of methods to minimize the SR did not start until the early 2000s when the first optimization algorithms emerged. The reason is that the sophisticated methods necessary to carry out this kind of optimization arrived simultaneously with the development of more powerful computers. In this sense, Yang et al. introduced in 2002 the TMA synthesis supported by systematic algorithms, capable of optimizing the SLL and the SR simultaneously by using differential evolution algorithms [10]. In subsequent works, and with the same optimization objectives, other algorithms were considered: genetic algorithms [11], simulating annealing [12,13], particle swarm optimization [14], and artificial bee colony [15]. Further works involved additional parameters in the multi-objective optimization, like the half power beam width [16]. Other innovative —and structurally different— techniques have been recently proposed to minimize the SR based on modulating the RF switches with non-uniform [17] or multiple [18] time modulation periods.
Later on, an additional degree of freedom was introduced in the synthesis process by considering the switch-on instants of the periodic rectangular pulses —in addition to the pulse durations— applied to the antenna excitations [7,19]. In [20], the time modulation period was split into several time steps with variable lengths and, for each time step, the switch-on and switch-off times were optimized via the differential evolution algorithm to improve the SR radiation. In a further development, the impact of the periodic pulses time shift on the SR was theoretically analyzed [8]. Likewise, hardware solutions based on sub-arraying techniques [21] or the use of fixed bandwidth elements [22], as well as the impact of pulse shaping [23], were also investigated to reduce the SR.
In addition to linear geometrical configurations, planar and even conformal TMA were also analyzed and optimized in terms of SLL and SR [19,24,25,26], as well as planar adaptive absorbers for radar based on phase-switched screen, whose design was modeled by means of the time-switched array theory [26].
Another key aspect in the TMA technique is the antenna gain and how it is affected by both the SR and the switching network. In [27], Yang et al. characterized the TMA gain and quantified the TMA efficiency. More specifically, they separated the switching network efficiency (which accounts for the time fraction that the switches are off) and the TMA power efficiency (the ratio between the fundamental mode mean radiated power and the total mean radiated power, i.e., the useful radiated power divided by total radiated power) being the total efficiency of the TMA the product of both. In order to improve the switching efficiency. In [28], the utilization of single-pole double-throw (SPDT) switches was proposed in such a way that a single RF switch governs two adjacent elements of the array, so that, whenever complementary time sequences are synthesized, the off time is reduced to zero, and consequently the switching efficiency is set to an almost ideal value. More sophisticated structures based on the use of a reconfigurable power divider/combiner have been evaluated in [29] in order to improve the switching network efficiency of the array.
On the other hand, since the fluctuations of the antenna gain —due to the application of a periodic on–off modulation to the static excitations— may severely affect the behavior of a received signal, some research works focused on the switching sequence, primarily to keep the instantaneous directivity of the main beam constant [30,31]. TMA were also analyzed —exclusively from the radiation properties point of view— so as to be exploited in different applications, e.g., for the suppression of interferences and undesired signals impinging on the antenna aperture. Such a capability of adaptive nulling in time-varying scenarios was evaluated in [32] by Poli et al., and completed in [33]. Further examples are the synthesis of the so-called power-patterns for wide coverage purposes [34,35], or radar applications [36,37].
Apart from all of these applications, tools for a more accurate analysis of TMA were also developed. In this sense, and in order to evaluate rigorously some nonlinear performance aspects of TMA as a radiating system (e.g., the effects of mutual coupling between elements), a full-wave computation of the radiated far field was addressed by Masotti et al. in [38] by properly developing a multi-domain computer aided design platform. Aligned with this research topic, a full-wave analysis of the instantaneous and average behaviors of TMA is available in [39].
2.2.2. Harmonic Patterns
As already pointed out, the SR is not necessarily a damaging phenomenon and can be profitably exploited to improve the performance of a TMA. As a matter of fact, the exploitation of the harmonic patterns endows TMA with smart-antenna capabilities. In this sense, the seminal work by Shanks [40] theoretically introduced the beam-scanning capabilities of TMA and, as an example, such features have been efficiently applied to an experimental prototype in [41].
Adaptive beamforming was originally studied from a practical and simplified point of view by Li et al. [42], focusing on the harmonic patterns synthesis in [6], and even taking advantage of time redundancy in [43]. Another strategy for beamforming through pulse splitting techniques was investigated in [44]. In such a technique, based on particle swarm optimization, two patterns were simultaneously generated: the first one at the central frequency and the second one at a preselected harmonic with an arbitrary order, keeping the SR below a given level. An example of how harmonic beamforming with TMA can be profitably applied, in this case to blanking in spectrometry and radar, was proposed in [45].
Beam steering with TMA was also introduced by Li et al. [46], and a more elaborated version, with control of the side-lobe level, was addressed in [47]. Applications of beam steering like direction finding or direction of arrival (DOA) estimation were analyzed in [48,49,50].
Reflector arrays were also considered for being implemented using time modulation. Wang et al. introduced the concept of time-modulated reflector array (TMRA) in [51], which was analyzed more deeply in [52]. A TMRA makes use of the topology of a conventional reflector array, i.e., consists of a matrix of scattering elements which are illuminated by a feed horn but, instead of phase shifters, it uses discrete time switching to achieve beam steering or beamforming functions. As a result, the radiation pattern is controlled by adjusting the time-domain scattering. It was also proven that, by employing double-layer designs [53], it is possible to increase the energy efficiency of TMRA.
Another interesting field for TMA applications is wireless power transmission, introduced by Masotti et al. in [54]. In this case, the real-time beamforming features of TMA are properly exploited following a two-step procedure: firstly, to precisely localize the tag to be powered and, subsequently, to perform the directive wireless power transmission.
In recent investigations, the TMA philosophy was involved in more complex hybrid solutions contributing to improve the performance of the overall antenna system. In this way, time modulation was applied —together with in-phase and quadrature (I/Q) modulation— to phased arrays in order to generate a scanning beam at the single positive sideband [55]. Time modulation was considered, jointly with retrodirective techniques, to synthesize coaperture antenna arrays [56] and also to obtain time-invariant spatial-fine-focusing beampatterns in frequency diverse arrays [57].
2.3. TMA Design under a Signal Processing Perspective
This section is divided into two parts. First, the initial approaches that have jointly considered TMA and wireless communications are introduced. Second, the models involving TMA together with linear digital transmitter and receivers are addressed. Multipath fading wireless channels together with diversity exploitation at the receiver are also considered. Finally, the efficiency of the TMA as well as how to improve it are taken into account, leading to the so-called enhanced time-modulated array (ETMA).
2.3.1. Interaction of TMAs with Information Signals: First Approaches
Most of the above-referenced investigations exclusively focus on the synthesis of the antenna patterns. The fundamental and/or the harmonic components are manipulated in some way, without considering the interaction between the TMA technique and the signals sent or received by such an antenna. This subsection is devoted to those works that apply TMA to wireless communications.
As a starting point, it is necessary to find the signal frequency restrictions, i.e., the relationship between the time modulation frequency, the signal bandwidth, and the carrier frequency that must be satisfied in order to keep the integrity of the signals transmitted/received over the TMA. Those restrictions were initially stated by Shanks and Bickmore [9], and completed by Brégains et al. [58], where additional closed-form expressions for the total mean SR power and for the TMA power efficiency were properly derived.
The transmission of narrowband amplitude-modulation (AM) and frequency-modulation (FM) signals was theoretically analyzed by Li et al. [59] and, for the case of AM, experimentally proved in [60]. Other specific cases were also investigated like a dual-channel AM receiver [61], the transmission of linearly frequency modulated (LFM) signals [62], or the feasibility of implementing a dual function of radar and communication [63,64].
The TMA technology was also proposed—originally by Zhu et al.—to transmit direction-dependent signals in the context of secure communications [65,66,67]. The idea is based on generating a null level of SR in some desired directions and a high level of SR on other directions in order to distort the signal. Conditions of frequency overlapping between the signal replicas placed in adjacent harmonic frequencies must be satisfied, paradoxically contrary to those ones established in [9].
A first study on the signal-to-noise ratio (SNR) in a system with a receiver TMA was presented in [68] by Zhu et al. This work describes a specific case exploiting the fundamental pattern and the first positive harmonic to receive two different binary phase shift-keying (BPSK) signals over additive white Gaussian noise (AWGN) channels. The multibeam characteristics of TMA were also proposed for spatial multiplexing by He et al. [69], although the performance with broadband signals was not analyzed. More recent works focus on the hardware design of TMA applied to spatial filtering of signals [70], and even for interference suppression in mm-Wave communications [71].
Note that, although the TMA topic has been mainly considered from a theoretical point of view, several prototypes have already been described in the literature [41,42,46,49,50,56,60,69,70].
2.3.2. Towards Using TMAs in Wireless Communication Systems
None of the above-referenced works analyze in depth, and in a theoretical way, the influence of TMA on digital communication wireless systems. In this sense, the feasibility of TMA for digital communications has been investigated in [72]. This first insight towards the study of the impact of the TMA technique on the transmission of digital signals has focused on a particular family: linear modulations (Chapter 5, [73]). The main reason for this choice is that these signals exhibit the simplest schemes to be considered in any analysis pertaining to digital signal transmission systems. On the other hand, a TMA by itself imposes a nonlinear transformation—derived from the application of periodic pulses to the antenna excitations, as mentioned above—and, therefore, linear modulations avoid the introduction of additional nonlinearities in the communication system. The block diagram in Figure 2 illustrates the continuous-time version of the system under study, in which a linearly modulated digital signal is first generated by means of an in-phase and quadrature modulator at carrier , and, next, is radiated through a TMA that exploits its fundamental pattern assuming a fast decay of the harmonics. Note that we restrict ourselves to the continuous-time model (thus the digital-to-analog converter (DAC) is not included) and that the digital information symbols are generated at a symbol period . Accordingly, the restrictions to safeguard the integrity of the signal and the radiated power (useful and SR) under those conditions have been mathematically analyzed and quantified, both in the time and frequency domains.
- The referred restrictions are the following:
- , with being the TMA fundamental frequency and the carrier frequency of the TMA input signal (see Figure 2).
- , where is the bandwidth of the TMA input signal , is the symbol period and is the so-called roll-off factor when the transmit filter corresponds to the well known raised cosine filter [74].
- The radiated power through the TMA is given by:where (expressed in watts) represents the power radiated by an isotropic antenna transmitting a linearly modulated equivalent baseband digital signal with a power density (it is possible to consider , with being the average transmit symbol energy and ρ the roll-off factor of the raised cosine filter), whereas represents the TMA power transfer function (dimensionless) accounting for both the array geometry and the time-modulated elements radiating a carrier signal. The expression coincides with the array total power in (Equation (30), [58]) and is employed to separate the useful power for () from the harmonic SR losses for ().
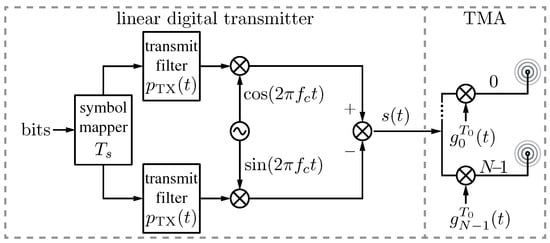
Figure 2.
Transmitter block diagram considering a linearly modulated digital signal radiated through a time-modulated array (TMA) exploiting its fundamental pattern: is the transmit filter, is the carrier frequency, is the TMA input signal, and are the periodic () functions governing the N array elements.
Once the conditions for faithfully transmitting digital signals over a TMA have been stated, as well as the SR losses characterized, the next step consists in investigating the impact of a TMA on the performance of a digital communication system. Aligned with this idea, the performance —or quality— of the communication link in which the TMA is involved was studied in [75]. In such a work, the TMA exclusively exploits its fundamental pattern (a pencil beam pattern in this case). The block diagram of the corresponding digital communication system under study is shown in Figure 3. Such a study characterized, for the first time and from a theoretical point of view, the bit error rate (BER) (Chapter 6, p. 171, [73]) of a linearly modulated digital communication system with a TMA at the receiver for the simplest case of an AWGN channel model (Chapter 1, p. 33, [76]).
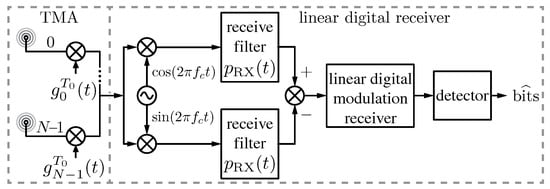
Figure 3.
Receiver block diagram based on a linear digital modulation scheme incorporating a TMA. The notation is the same as in Figure 2 except , which denotes the receive filter.
However, the major potentialities of TMA for wireless communications are unavoidably related to the exploitation of their harmonic patterns. In this sense, most works available in the literature address the harmonic beamforming capability exhibited by TMA focusing exclusively on a radiation point of view. Accordingly, different scenarios of harmonic beamforming have been properly investigated, e.g., the conversion of spatial diversity into frequency diversity [6,42,43,44,45], the mitigation of interfering signals [6,42], the orthogonality between patterns [66,69], and the advantages of time redundancy [43]. However, all of those works have neglected a crucial aspect in the system performance when communications signals are involved: the TMA efficiency. Therefore, a more ambitious extension of the analysis in [75] had to be undertaken, by involving the TMA in a multipath fading communication where the antenna efficiency played a key role. Hence, the true challenge at this point is the synthesis of an efficient harmonic beamforming where it is not enough to satisfy certain conditions in terms of locations of maxima and nulls, but to safeguard the TMA efficiency and, consequently, the average SNR at the receiver (recall that the gain per beam path is proportional to the TMA efficiency [27]). The pioneering work involving the efficiency in the TMA beamforming design is [77], which is devoted to the performance analysis of TMA for the angle diversity reception of digital communication signals. Figure 4 shows the system block diagram whose performance is analyzed in [77]: a narrowband wireless communication system using a conventional M-ary linear digital modulation assuming an omnidirectional antenna at the transmitter, and a TMA, together with a maximum ratio combining (MRC) at the receiver, to exploit the channel diversity through the beamforming with the first positive TMA harmonic patterns.
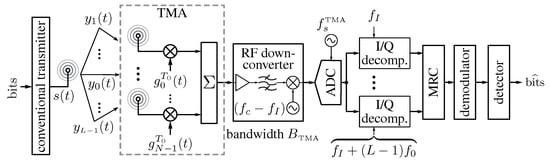
Figure 4.
Block diagram of a system consisting of a conventional linear digital transmitter equipped with an omni-directional antenna and a receiver with a TMA designed for exploiting channel diversity at the receiver through maximum ratio combining (MRC).
According to Figure 4, once the transmitted signal arrives through a multipath channel at the receiver, we obtain L different replicas constituting the TMA input. Each of the L replicas at the TMA output appears at a different (harmonic) frequency , with . Assuming that has been correctly selected according to the bandwidth of , the TMA output signal occupies a total bandwidth . After the RF down-conversion at a frequency (being the lowest intermediate frequency), the obtained signal is sampled at a frequency (fulfilling the Nyquist criterion) and each of the resulting L digital signals is I/Q decomposed (including the corresponding receive filter) at a different intermediate frequency , with . Finally, the obtained L complex-valued signals are combined in an MRC and the resulting signal is demodulated to obtain the received bits. Notice that, for the sake of simplicity, channel estimation and equalization are assumed to be perfect. Note also that the non-linear operation carried out by the TMA allows for employing a single RF branch (with increasing bandwidth) followed by a single analog-to-digital converter (ADC) (with a higher sampling rate) to exploit L signal replicas impinging at the TMA. Consequently, the complexity of the receiver structure is simplified and, above all, its power consumption is reduced.
The investigations in [77] also lead to the detection of certain limitations of rectangular pulses when the aim is to achieve a flexible and efficient beamforming with TMA. Such vulnerabilities are directly related to the frequency response of rectangular pulses (Chapter 3, p89, [78]): a minimum main-lobe width and a modest side-lobe level (−13 dB), together with a slow (first order) asymptotic side-lobe decay. In fact, taking as the starting point the weaknesses of rectangular pulses when applied to harmonic beamforming, the following two contributions were introduced in [79]:
- A type of pulses that are more suitable for harmonic beamforming with TMA: the so-called sum-of-weighted-cosine (SWC) pulses [80].
- Based on the previous pulses, a new family of beamforming TMA, termed ETMA, is characterized and evaluated in terms of efficiency by properly comparing it to conventional beamforming TMA based on rectangular pulses.
Figure 5 shows the block diagram of an ETMA where the static excitations of the array are time-modulated by more sophisticated periodical waveforms parametrized by (normalized pulse durations), (normalized pulse time shifts), and (pulse weights), , , and , where N is the number of antenna elements, L is the order of the highest exploited harmonic, and K is the order of the pulse. A common denominator of these recent investigations [72,75,77,79] is that TMA are analyzed and evaluated not only from an antenna outlook, but also from a signal processing perspective.
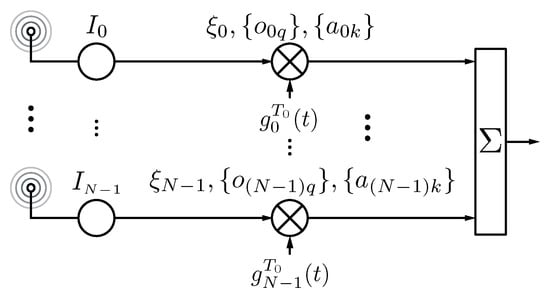
Figure 5.
Block diagram of a TMA governed by periodical sum-of-weighted-cosine (SWC) pulses .
3. Challenges and Future Research Lines
The interplay between TMA and digital communications still faces a number of challenges. Among them, we highlight the following ones:
- The exploitation of TMA at transmission. Up to now, the applications of TMA in the area of digital communications mainly focus on receiving TMA. Hence, the performance of transmitting TMA from a signal processing outlook, and in different scenarios, is still an unexplored research field. We propose two areas which certainly deserve further exploration: (1) the performance analysis of transmitting TMA in multiuser scenarios; and (2) the feasibility of diversity transmission techniques with TMA.
- Performance with broadband signals. The TMA state of the art exclusively focuses on narrowband signals. However, communications nowadays must unavoidably deal with broadband signals. The higher the bandwidth, the higher the switching frequency in the TMA, the wider the bandwidth at the RF stage, and the higher the sampling rate at the ADC. On the other hand, an analysis of TMA behavior under frequency-selective fading still remains to be done.
- Beamforming design through the preprocessing of periodic pulses. More specifically, we propose a more accurate design of the periodic pulses in the frequency domain. The Fourier transform of a periodic pulse is a discrete spectrum with impulses at multiples of the time-modulation frequency and whose corresponding areas are times the associated exponential Fourier series coefficients. Therefore, a simpler design, by applying the Fourier series coefficients properties to preprocess conventional rectangular pulses before they are applied to the antenna elements, is possible.
4. Conclusions
The state of the art of TMA is organized in this work from two perspectives depending on the antenna synthesis criteria: (1) designs from an antenna perspective (exclusively) or (2) designs from a signal processing perspective. Most of the research works about TMA belong to the first group and are characterized by studying the TMA in an isolated manner, or, in other words, exclusively under the antenna designer point of view. The second group consists of those investigations that consider, in addition, the interaction between the TMA technique and the nature of the signals sent or received by such an antenna, i.e., those works with a strong component of array signal processing and, therefore, constituting the hybrid discipline antennas-signal processing. The most recent works belong to the latter group and definitely are marking the future lines of investigation in this promising topic.
Acknowledgments
Financial support from the Xunta de Galicia (ED431C 2016-045, ED341D R2016/012, ED431G/01), the Agencia Estatal de Investigación of Spain (TEC2013-47141-C4-1-R, TEC2015-69648-REDC, TEC2016-75067-C4-1-R) and the European Union (European Regional Development Fund - ERDF), is gratefully acknowledged.
Author Contributions
Roberto Maneiro-Catoira, Julio Brégains, José A. García-Naya, and Luis Castedo carried out the literature research; Roberto Maneiro-Catoira, Julio Brégains, José A. García-Naya, and Luis Castedo wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ADC | analog-to-digital converter |
| AM | amplitude modulation |
| AWGN | additive white Gaussian noise |
| BER | bit error rate |
| BPSK | binary phase shift-keying |
| DAC | digital-to-analog converter |
| DOA | direction of arrival |
| ETMA | enhanced time-modulated array |
| FM | frequency modulation |
| LBFN | linear beamforming network |
| LFM | linearly frequency modulated |
| MRC | maximum ratio combining |
| RF | radio frequency |
| SLL | side-lobe level |
| SNR | signal-to-noise ratio |
| SPDT | single-pole double-throw |
| SR | sideband radiation |
| SWC | sum-of-weighted-cosine |
| TMA | time-modulated array |
| TMRA | time-modulated reflector array |
References
- Renzo, M.D.; Haas, H.; Ghrayeb, A.; Sugiura, S.; Hanzo, L. Spatial Modulation for Generalized MIMO: Challenges, Opportunities, and Implementation. Proc. IEEE 2014, 102, 56–103. [Google Scholar] [CrossRef]
- Heath, R.W.; González-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A.M. An Overview of Signal Processing Techniques for Millimeter Wave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Méndez-Rial, R.; Rusu, C.; González-Prelcic, N.; Alkhateeb, A.; Heath, R.W. Hybrid MIMO Architectures for Millimeter Wave Communications: Phase Shifters or Switches? IEEE Access 2016, 4, 247–267. [Google Scholar] [CrossRef]
- Rocca, P.; Oliveri, G.; Mailloux, R.J.; Massa, A. Unconventional Phased Array Architectures and Design Methodologies—A Review. Proc. IEEE 2016, 104, 544–560. [Google Scholar] [CrossRef]
- Kummer, W.H.; Villeneuve, A.T.; Fong, T.; Terrio, F. Ultra-low sidelobes from time-modulated arrays. IEEE Trans. Antennas Propag. 1963, 11, 633–639. [Google Scholar] [CrossRef]
- Poli, L.; Rocca, P.; Oliveri, G.; Massa, A. Harmonic Beamforming in Time-Modulated Linear Arrays. IEEE Trans. Antennas Propag. 2011, 59, 2538–2545. [Google Scholar] [CrossRef]
- Tennant, A.; Chambers, B. Control of the harmonic radiation patterns of time-modulated antenna arrays. In Proceedings of the 2008 IEEE Antennas and Propagation Society International Symposium, San Diego, CA, USA, 5–11 July 2008; pp. 1–4.
- Aksoy, E.; Afacan, E. Calculation of Sideband Power Radiation in Time-Modulated Arrays With Asymmetrically Positioned Pulses. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 133–136. [Google Scholar] [CrossRef]
- Shanks, H.; Bickmore, R. Four-Dimensional Electromagnetic Radiators. Can. J. Phys. 1959, 37, 263–275. [Google Scholar] [CrossRef]
- Yang, S.; Gan, Y.B.; Qing, A. Sideband suppression in time-modulated linear arrays by the differential evolution algorithm. IEEE Antennas Wirel. Propag. Lett. 2002, 1, 173–175. [Google Scholar] [CrossRef]
- Yang, S.; Gan, Y.B.; Qing, A.; Tan, P.K. Design of a uniform amplitude time modulated linear array with optimized time sequences. IEEE Trans. Antennas Propag. 2005, 53, 2337–2339. [Google Scholar] [CrossRef]
- Fondevila, J.; Brégains, J.C.; Ares, F.; Moreno, E. Optimizing uniformly excited linear arrays through time modulation. IEEE Antennas Wirel. Propag. Lett. 2004, 3, 298–301. [Google Scholar] [CrossRef]
- Fondevila, J.; Brégains, J.C.; Ares, F.; Moreno, E. Application of time modulation in the synthesis of sum and difference patterns by using linear arrays. Microw. Opt. Technol. Lett. 2006, 48, 829–832. [Google Scholar] [CrossRef]
- Poli, L.; Rocca, P.; Manica, L.; Massa, A. Handling Sideband Radiations in Time-Modulated Arrays Through Particle Swarm Optimization. IEEE Trans. Antennas Propag. 2010, 58, 1408–1411. [Google Scholar] [CrossRef]
- Mandal, S.K.; Ghatak, R.; Mahanti, G.K. Minimization of side lobe level and side band radiation of a uniformly excited time modulated linear antenna array by using Artificial Bee Colony algorithm. In Proceedings of the 2011 IEEE Symposium on Industrial Electronics and Applications (ISIEA), Langkawi, Malaysia, 25–28 September 2011; pp. 247–250.
- Mandal, S.K.; Mahanti, G.K.; Ghatak, R. Differential evolution algorithm for optimizing the conflicting parameters in time-modulated linear array antennas. Prog. Electromagn. Res. B 2013, 51, 101–118. [Google Scholar] [CrossRef]
- He, C.; Yu, H.; Liang, X.; Geng, J.; Jin, R. Sideband Radiation Level Suppression in Time-Modulated Array by Nonuniform Period Modulation. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 606–609. [Google Scholar] [CrossRef]
- Guo, J.; Yang, S.; Chen, Y. Efficient Sideband Suppression in 4D Antenna Arrays with Multiple Time Modulation Frequencies. In Proceedings of the Antennas and Propagation Society International Symposium (APSURSI), 2016 IEEE, Fajardo, Puerto Rico, 26 June–1 July 2016; pp. 699–700.
- Poli, L.; Rocca, P.; Manica, L.; Massa, A. Pattern synthesis in time-modulated linear arrays through pulse shifting. IET Microw. Antennas Propag. 2010, 4, 1157–1164. [Google Scholar] [CrossRef]
- Zhu, Q.; Yang, S.; Zheng, L.; Nie, Z. Design of a Low Sidelobe Time Modulated Linear Array With Uniform Amplitude and Sub-Sectional Optimized Time Steps. IEEE Trans. Antennas Propag. 2012, 60, 4436–4439. [Google Scholar] [CrossRef]
- Tong, Y.; Tennant, A. Reduced Sideband Levels in Time-Modulated Arrays Using Half-Power Sub-Arraying Techniques. IEEE Trans. Antennas Propag. 2011, 59, 301–303. [Google Scholar] [CrossRef]
- Tong, Y.; Tennant, A. Sideband level suppression in time-modulated linear arrays using modified switching sequences and fixed bandwidth elements. Electron. Lett. 2012, 48, 10–11. [Google Scholar] [CrossRef]
- Bekele, E.T.; Poli, L.; Rocca, P.; D’Urso, M.; Massa, A. Pulse-Shaping Strategy for Time Modulated Arrays –Analysis and Design. IEEE Trans. Antennas Propag. 2013, 61, 3525–3537. [Google Scholar] [CrossRef]
- Yang, S.; Nie, Z.; Yang, F. Synthesis of low sidelobe planar antenna arrays with time modulation. In Proceedings of the 2005 Asia-Pacific Microwave Conference, Suzhou, China, 4–7 December 2005; Volume 3, pp. 1–3.
- Aksoy, E.; Afacan, E. An Inequality for the Calculation of Relative Maximum Sideband Level in Time-Modulated Linear and Planar Arrays. IEEE Trans. Antennas Propag. 2014, 62, 3392–3397. [Google Scholar] [CrossRef]
- Tennant, A.; Chambers, B. Time-Switched Array Analysis of Phase-Switched Screens. IEEE Trans. Antennas Propag. 2009, 57, 808–812. [Google Scholar] [CrossRef]
- Yang, S.; Gan, Y.; Tan, P. Evaluation of directivity and gain for time-modulated linear antenna arrays. Microw. Opt. Technol. Lett. 2004, 42, 167–171. [Google Scholar] [CrossRef]
- Zhu, Q.; Yang, S.; Yao, R.; Nie, Z. Gain Improvement in Time-Modulated Linear Arrays Using SPDT Switches. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 994–997. [Google Scholar]
- Chen, J.; Liang, X.; Jin, R.; Geng, J.; He, C.; Li, P. Efficiency Improvement For Time Modulated Antenna Arrays. In Proceedings of the 2016 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (2016 IEEE AP-S & USNC-URSI), Fajardo, Puerto Rico, 26 June–1 July 2016.
- Manica, L.; Rocca, P.; Poli, L.; Massa, A. Almost Time-Independent Performance in Time-Modulated Linear Arrays. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 843–846. [Google Scholar] [CrossRef]
- Rocca, P.; Poli, L.; Massa, A. Instantaneous directivity optimisation in time-modulated array receivers. IET Microw. Antennas Propag. 2012, 6, 1590–1597. [Google Scholar] [CrossRef]
- Poli, L.; Rocca, P.; Oliveri, G.; Massa, A. Adaptive nulling in time-modulated linear arrays with minimum power losses. IET Microw. Antennas Propag. 2011, 5, 157–166. [Google Scholar] [CrossRef]
- Rocca, P.; Poli, L.; Oliveri, G.; Massa, A. Adaptive Nulling in Time-Varying Scenarios Through Time-Modulated Linear Arrays. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 101–104. [Google Scholar] [CrossRef]
- Yang, S.; Gan, Y.B.; Khiang, T.P. A new technique for power-pattern synthesis in time-modulated linear arrays. IEEE Antennas Wirel. Propag. Lett. 2003, 2, 285–287. [Google Scholar] [CrossRef]
- Balderas, L.I.; Reyna, A.; Panduro, M.A. Time-Modulated Concentric Ring Antenna Array for a Wide Coverage Pattern. In Proceedings of the 2016 IEEE Antennas and Propagation Society International Symposium (APSURSI), Fajardo, Puerto Rico, 26 June–1 July 2016; pp. 709–710.
- Li, G.; Yang, S.; Nie, Z. A Study on the Application of Time Modulated Antenna Arrays to Airborne Pulsed Doppler Radar. IEEE Trans. Antennas Propag. 2009, 57, 1579–1583. [Google Scholar] [CrossRef]
- Euzière, J.; Guinvarc’h, R.; Uguen, B.; Gillard, R. Optimization of Sparse Time-Modulated Array by Genetic Algorithm for Radar Applications. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 161–164. [Google Scholar] [CrossRef]
- Masotti, D.; Francia, P.; Costanzo, A.; Rizzoli, V. Rigorous Electromagnetic/Circuit-Level Analysis of Time-Modulated Linear Arrays. IEEE Trans. Antennas Propag. 2013, 61, 5465–5474. [Google Scholar] [CrossRef]
- Yao, A.M.; Wu, W.; Fang, D.G. Efficient and Effective Full-Wave Analysis of the Instantaneous and Average Behaviors of Time-Modulated Arrays. IEEE Trans. Antennas Propag. 2015, 63, 2902–2913. [Google Scholar] [CrossRef]
- Shanks, H. A new technique for electronic scanning. IRE Trans Antennas Propag. 1961, 9, 162–166. [Google Scholar] [CrossRef]
- Bogdan, G.; Yashchyshyn, Y.; Jarzynka, M. Time-Modulated Antenna Array with Lossless Switching Network. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1827–1830. [Google Scholar] [CrossRef]
- Li, G.; Yang, S.; Chen, Y.; Nie, Z. A Hybrid Analog-Digital Adaptive Beamforming in Time-Modulated Linear Arrays. Electromagnetics 2010, 30, 356–364. [Google Scholar] [CrossRef]
- Tong, Y.; Tennant, A. A Two-Channel Time Modulated Linear Array With Adaptive Beamforming. IEEE Trans. Antennas Propag. 2012, 60, 141–147. [Google Scholar] [CrossRef]
- Poli, L.; Moriyama, T.; Rocca, P. Pulse splitting for harmonic beamforming in time- modulated linear arrays. Int. J. Antennas Propag. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Barott, W.C.; Himed, B. Time-Modulated Array Pattern for Sidelobe Blanking in Spectrometry and Radar. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1015–1018. [Google Scholar] [CrossRef]
- Li, G.; Yang, S.; Chen, Y.; Nie, Z.P. A novel electronic beam steering technique in time modulated antenna array. Prog. Electromagn. Res. 2009, 97, 391–405. [Google Scholar] [CrossRef]
- Tong, Y.; Tennant, A. Simultaneous control of sidelobe level and harmonic beam steering in time-modulated linear arrays. Electron. Lett. 2010, 46, 201–202. [Google Scholar] [CrossRef]
- Li, G.; Yang, S.; Nie, Z. Direction of Arrival Estimation in Time Modulated Linear Arrays With Unidirectional Phase Center Motion. IEEE Trans. Antennas Propag. 2010, 58, 1105–1111. [Google Scholar]
- Tennant, A. Experimental Two-Element Time-Modulated Direction Finding Array. IEEE Trans. Antennas Propag. 2010, 58, 986–988. [Google Scholar] [CrossRef]
- He, C.; Liang, X.; Li, Z.; Geng, J.; Jin, R. Direction Finding by Time-Modulated Array With Harmonic Characteristic Analysis. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 642–645. [Google Scholar] [CrossRef]
- Wang, Y.; Tennant, A. Time-modulated reflector array. Electron. Lett. 2012, 48, 972–974. [Google Scholar] [CrossRef]
- Wang, Y.; Tennant, A. Experimental Time-Modulated Reflector Array. IEEE Trans. Antennas Propag. 2014, 62, 6533–6536. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, F.; Tennant, A. Increasing the energy efficiency of time-modulated reflector-arrays using double layer designs. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–5.
- Masotti, D.; Costanzo, A.; Prete, M.D.; Rizzoli, V. Time-Modulation of Linear Arrays for Real-Time Reconfigurable Wireless Power Transmission. IEEE Trans. Microw. Theory Tech. 2016, 64, 331–342. [Google Scholar] [CrossRef]
- Yao, A.M.; Wu, W.; Fang, D.G. Single-Sideband Time-Modulated Phased Array. IEEE Trans. Antennas Propag. 2015, 63, 1957–1968. [Google Scholar] [CrossRef]
- Yao, A.M.; Wu, W.; Fang, D.G. Study on Reconfigurable Coaperture Antenna Arrays Based on Time-Modulation and Retrodirective Techniques. IEEE Trans. Antennas Propag. 2016, 64, 1713–1724. [Google Scholar] [CrossRef]
- Yao, A.M.; Wu, W.; Fang, D.G. Frequency Diverse Array Antenna Using Time-Modulated Optimized Frequency Offset to Obtain Time-Invariant Spatial Fine Focusing Beampattern. IEEE Trans. Antennas Propag. 2016, 64, 4434–4446. [Google Scholar] [CrossRef]
- Brégains, J.C.; Fondevila-Gómez, J.; Franceschetti, G.; Ares, F. Signal Radiation and Power Losses of Time-Modulated Arrays. IEEE Trans. Antennas Propag. 2008, 56, 1799–1804. [Google Scholar] [CrossRef]
- Li, G.; Yang, S.; Zhao, Z.; Nie, Z.P. A study of AM and FM signal reception of time modulated linear antenna arrays. Prog. Electromagn. Res. Lett. 2009, 7, 171–181. [Google Scholar] [CrossRef]
- Zhu, Q.; Yang, S.; Yao, R.; Huang, M.; Nie, Z.P. Unified Time- and Frequency-Domain Study on Time-Modulated Arrays. IEEE Trans. Antennas Propag. 2013, 61, 3069–3076. [Google Scholar] [CrossRef]
- Yavuz, Y.; Karahan, M.; Aksoy, E. A dual channel AM receiver structure in 4D arrays. In Proceedings of the 2015 IEEE International Symposium on Antennas and Propagation USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 19–25 July 2015; pp. 804–805.
- Guo, J.; Yang, S.; Zhu, Q.; Nie, Z.P. 4D antenna arrays for LFM signal transmission. In Proceedings of the 2015 IEEE International Symposium on Antennas and Propagation USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 19–25 July 2015; pp. 820–821.
- Euzière, J.; Guinvar’h, R.; Hinostroza, I.; Uguen, B.; Gillard, R. Time Modulated Array for dual function radar and communication. In Proceedings of the 2015 IEEE International Symposium on Antennas and Propagation USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 19–25 July 2015; pp. 806–807.
- Euzière, J.; Guinvar’h, R.; Hinostroza, I.; Uguen, B.; Gillard, R. Optimizing communication in TMA for radar. In Proceedings of the 2016 IEEE International Symposium on Antennas and Propagation USNC/URSI National Radio Science Meeting, Fajardo, Puerto Rico, 26 June–1 July 2016; pp. 705–706.
- Zhu, Q.; Yang, S.; Yao, R.; Nie, Z. Directional Modulation Based on 4-D Antenna Arrays. IEEE Trans. Antennas Propag. 2014, 62, 621–628. [Google Scholar] [CrossRef]
- Rocca, P.; Zhu, Q.; Bekele, E.T.; Yang, S.; Massa, A. 4-D Arrays as Enabling Technology for Cognitive Radio Systems. IEEE Trans. Antennas Propag. 2014, 62, 1102–1116. [Google Scholar] [CrossRef]
- Hannan, M.A.; Poli, L.; Rocca, P.; Massa, A. Pulse Sequence Optimization in Time-Modulated Arrays for Secure Communications. In Proceedings of the 2016 IEEE Antennas and Propagation Society International Symposium (APSURSI), Fajardo, Puerto Rico, 26 June–1 July 2016; pp. 695–696.
- Zhu, Q.; Yang, S.; Rocca, P.; Nie, Z. Signal-to-noise ratio and time-modulated signal spectrum in four-dimensional antenna arrays. IET Microw. Antennas Propag. 2015, 9, 264–270. [Google Scholar] [CrossRef]
- He, C.; Liang, X.; Zhou, B.; Geng, J.; Jin, R. Space-Division Multiple Access Based on Time-Modulated Array. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 610–613. [Google Scholar] [CrossRef]
- Bogdan, G.; Jarzynka, M.; Yashchyshyn, Y. Experimental study of signal reception by means of time-modulated antenna array. In Proceedings of the 2016 21st International Conference on Microwave, Radar and Wireless Communications (MIKON), Krakow, Poland, 9–11 May 2016; pp. 1–4.
- Yashchyshyn, Y.; Derzakowski, K.; Bajurko, P.R.; Marczewski, J.; Kozłowski, S. Time-Modulated Reconfigurable Antenna Based on Integrated S-PIN Diodes for mm-Wave Communication Systems. IEEE Trans. Antennas Propag. 2015, 63, 4121–4131. [Google Scholar] [CrossRef]
- Maneiro-Catoira, R.; Brégains, J.; García-Naya, J.A.; Castedo, L. On the Feasibility of Time-Modulated Arrays for Digital Linear Modulations: A Theoretical Analysis. IEEE Trans. Antennas Propag. 2014, 62, 6114–6122. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Proakis, J.G. Digital Communications, 5th ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Maneiro-Catoira, R.; Brégains, J.; García-Naya, J.A.; Castedo, L. Impact of Time-Modulated Arrays on the BER of Linear Digital Modulations. J. Electromagn. Waves Appl. 2015, 29, 2147–2154. [Google Scholar] [CrossRef]
- Sklar, B. Digital Communications, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Maneiro-Catoira, R.; Brégains, J.; García-Naya, J.A.; Castedo, L.; Rocca, P.; Poli, L. Performance Analysis of Time-Modulated Arrays for the Angle Diversity Reception of Digital Linear Modulated Signals. IEEE J. Sel. Top. Signal Process. 2017, 11, 247–258. [Google Scholar] [CrossRef]
- Prabhu, K.M.M. Window Functions and their Applications in Signal Processing, 1st ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2014. [Google Scholar]
- Maneiro-Catoira, R.; Brégains, J.; García-Naya, J.A.; Castedo, L. Enhanced Time-Modulated Arrays for Harmonic Beamforming. IEEE J. Sel. Top. Signal Process. 2017, 11, 259–270. [Google Scholar] [CrossRef]
- Nuttall, A. Some windows with very good sidelobe behavior. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 84–91. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).