Novel Approach for the Recognition and Prediction of Multi-Function Radar Behaviours Based on Predictive State Representations
Abstract
:1. Introduction
2. PSR-Based Framework of MFR
2.1. PSR and System-Dynamics Matrix
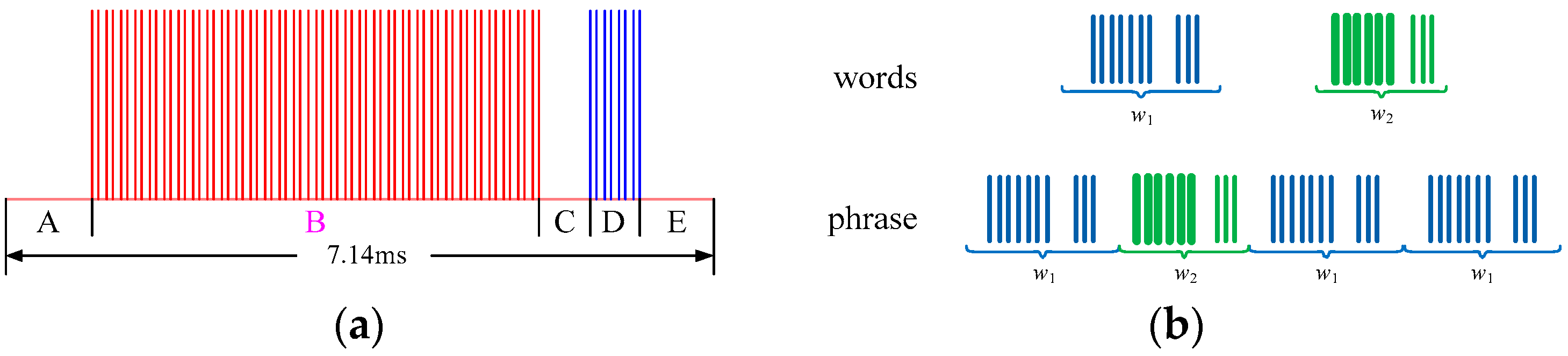
- o—observation, and the finite discrete set constituted by all observations is called the observation space, denoted as o ∈ O;
- h—history, which is an observation sequence from the initial time to the current time, h = o1o2…ot;
- e—event, which is an observation following the history, e = ot+1ot+2…. For linear PSR, if any event probability can be expressed by a linear combination of the probabilities of events in a set, the elements in the set are called core events, Q = {q1, q2, …, q|Q|};
- p(e|h)—the probability of event e under the condition of a given history h.
2.2. PSR Model for MFR Hierarchical Structure
2.3. Process for MFR Behaviours
- (1)
- Modelling and training for the PSR-based MFR models. The system-dynamics matrix for each operating mode will be obtained via suffix-history algorithm [33], discovering the sets of core events Q, and yielding the model parameters, such as mo|λ and Mo|λ.
- (2)
- Posteriori probability distribution estimation for MFR operating modes. The modes in the input test sequence are identified, and the distribution is calculated via the grid-filter estimator.
- (3)
- Multi-step prediction for MFR signal sequence. With the fusion of prediction results for each mode, the prediction probability distribution for all observations is calculated, from which the prediction results are estimated under the MAP criterion.
3. Novel Algorithms for MFR Behaviour Recognition and Prediction
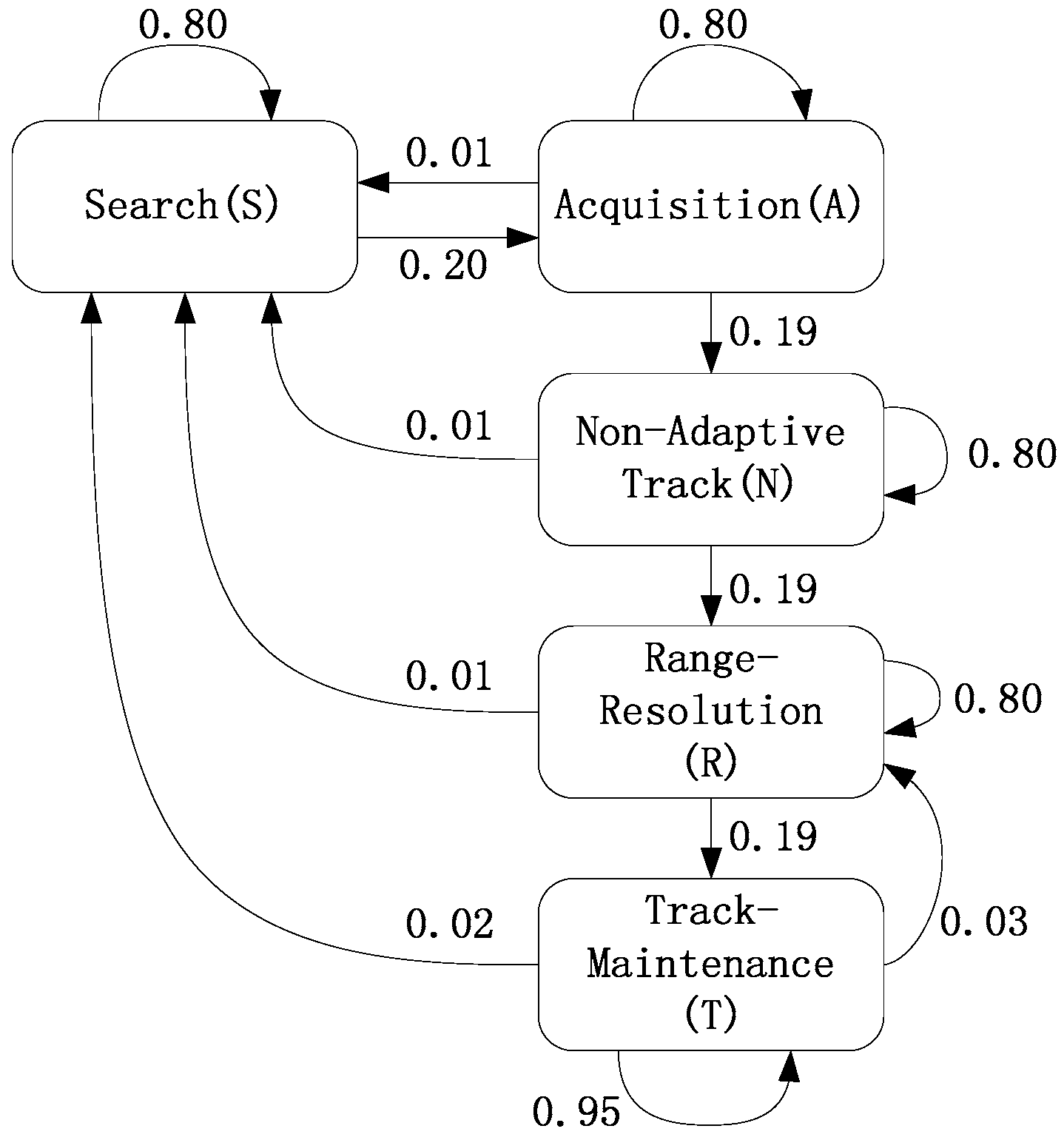
3.1. Recognition for Operating Modes
3.2. Fast Prediction for MFR Signals
4. Simulations
4.1. Simulation Settings
4.2. Results
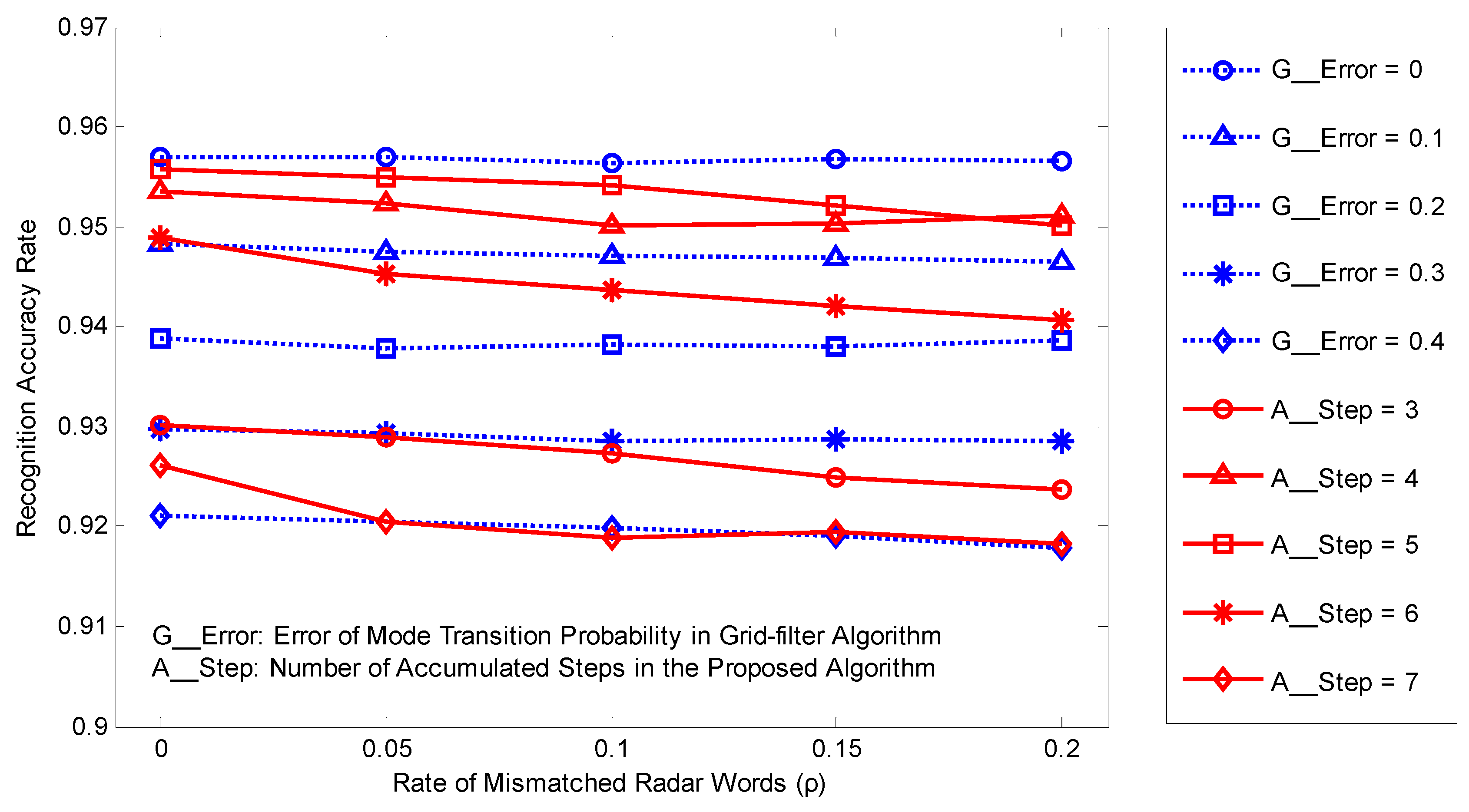
4.2.1. Simulations of Operating Mode Recognition
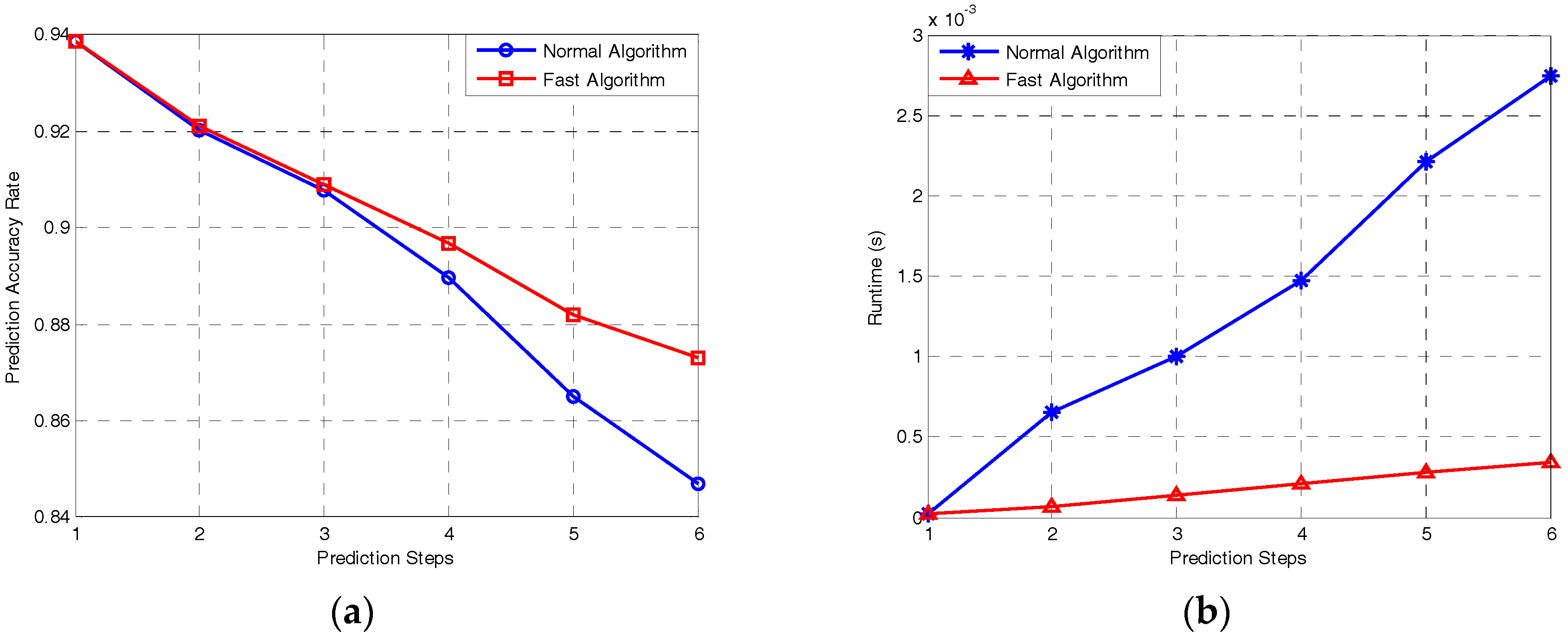
4.2.2. Simulations of Multi-Step Prediction
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Butler, J. Tracking and Control in Multi-Function Radar. Ph.D. Thesis, University of London, London, UK, 1998. [Google Scholar]
- Charlish, A. Autonomous Agents for Multi-Function Radar Resource Management. Ph.D. Thesis, University of London, London, UK, 2011. [Google Scholar]
- Behar, V.; Kabakchiev, C.; Li, X.R. Signal processing for a benchmark for radar resource allocation in the presence of ECM. Signal Process. 2005, 85, 767–780. [Google Scholar] [CrossRef]
- Olivier, K.; Cilliers, J.E.; Plessis, M.D. Design and performance of wideband DRFM for radar test and evaluation. Electron. Lett. 2011, 47, 824–825. [Google Scholar] [CrossRef]
- Ciuonzo, D.; De Maio, A.; Orlando, D. A unifying framework for adaptive radar detection in homogeneous plus structured interference—Part I: On the maximal invariant statistic. IEEE Trans. Signal Process. 2016, 64, 2894–2906. [Google Scholar] [CrossRef]
- Ciuonzo, D.; De Maio, A.; Orlando, D. A unifying framework for adaptive radar detection in homogeneous plus structured interference—Part II: Detectors design. IEEE Trans. Signal Process. 2016, 64, 2907–2919. [Google Scholar] [CrossRef]
- Bandiera, F.; Besson, O.; Ricci, G. Direction detector for distributed targets in unknown noise and interference. Electron. Lett. 2013, 49, 68–69. [Google Scholar] [CrossRef] [Green Version]
- Ciuonzo, D.; De Maio, A.; Orlando, D. On the statistical invariance for adaptive radar detection in partially homogeneous disturbance plus structured interference. IEEE Trans. Signal Process. 2016, 65, 1222–1234. [Google Scholar] [CrossRef]
- Haykin, S. Cognitive radar: A way of the future. IEEE Signal Process. Mag. 2006, 23, 30–40. [Google Scholar] [CrossRef]
- Manz, B. Cognition: EW gets brainy. J. Electron. Def. 2012, 35, 32–39. [Google Scholar]
- Wei, Y.M.; Meng, H.D.; Liu, Y.M.; Wang, X.Q. Extended target recognition in cognitive radar networks. Sensors 2010, 10, 10181–10197. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.T.; Wu, Z.L.; Yin, Z.D.; Quan, T.F.; Sun, H.J. Hybrid radar emitter recognition based on rough k-Means Classifier and Relevance Vector Machine. Sensors 2013, 13, 848–864. [Google Scholar] [CrossRef] [PubMed]
- Dudczyk, J. Radar emission sources identification based on hierarchical agglomerative clustering for large data sets. J. Sens. 2016, 2016, 1879327. [Google Scholar] [CrossRef]
- Dudczyk, J.; Kawalec, A. Specific emitter identification based on graphical representation of the distribution of radar signal parameters. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 391–396. [Google Scholar] [CrossRef]
- Dudczyk, J.; Kawalec, A. Fast-decision identification algorithm of emission source pattern in database. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 385–389. [Google Scholar] [CrossRef]
- Yang, Z.T.; Qiu, W.; Sun, H.J.; Nallanathan, A. Robust radar emitter recognition based on the three-dimensional distribution feature and transfer learning. Sensors 2016, 16, 289. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, M.; Liu, L.; Diao, M. LPI radar waveform recognition based on time-frequency distribution. Sensors 2016, 16, 1682. [Google Scholar] [CrossRef] [PubMed]
- Visnevski, N.; Krishnamurthy, V.; Haykin, S.; Currie, B.; Dilkes, F.; Lavoie, P. Multi-function radar emitter modelling: A stochastic discrete event system approach. In Proceedings of the 2003 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; pp. 6295–6300.
- Bhat, S.S.; Narayanan, R.M.; Rangaswamy, M. Performance and optimization for multimodal radar operation. Sensors 2012, 12, 12673–12693. [Google Scholar] [CrossRef]
- Yue, W.Z.; Zhang, Y.; Liu, Y.M.; Xie, J.W. Radar constant-modulus waveform design with prior information of the extended target and clutter. Sensors 2016, 16, 889. [Google Scholar] [CrossRef] [PubMed]
- Visnevski, N. Syntactic Modelling of Multi-Function Radars. Ph.D. Thesis, McMaster University, Hamilton, ON, Canada, 2005. [Google Scholar]
- Visnevski, N.; Haykin, S.; Krishnamurthy, V.; Dilkes, F.; Lavoie, P. Hidden Markov models for radar pulse train analysis in electronic warfare. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 19–23 March 2005; Volume 5, pp. 597–600.
- Norouzi, T.; Norouzi, Y. Scheduling the usage of radar and jammer during peace and war time. IET Radar Sonar Navig. 2012, 6, 929–936. [Google Scholar] [CrossRef]
- Efendioglu, H.S.; Yildirim, T.; Fidanboylu, K. Prediction of force measurements of a microbend sensor based on an artificial neural network. Sensors 2009, 9, 7167–7176. [Google Scholar] [CrossRef] [PubMed]
- Niu, G.; Yang, B.S. Dempster–Shafer regression for multi-step-ahead time-series prediction towards data-driven machinery prognosis. Mech. Syst. Signal Process. 2009, 23, 740–751. [Google Scholar] [CrossRef]
- Hu, C.; Youn, B.D.; Kim, T.; Wang, P. A co-training-based approach for prediction of remaining useful life utilizing both failure and suspension data. Mech. Syst. Signal Process. 2015, 63, 75–90. [Google Scholar] [CrossRef]
- Pardo, J.; Zamoramartinez, F.; Botellarocamora, B. Online learning algorithm for time series forecasting suitable for low cost wireless sensor networks nodes. Sensors 2015, 15, 9277–9304. [Google Scholar] [CrossRef] [PubMed]
- Littman, M.; Sutton, R.; Singh, S. Predictive Representations of State. In Advances in Neural Information Processing Systems 14; MIT Press: Vancouver, BC, Canada, 2002; pp. 1555–1561. [Google Scholar]
- Wolfe, B.; James, M.R.; Singh, S. Modeling multiple-mode systems with Predictive State Representations. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, San Diego, CA, USA, 21–24 June 2010; pp. 1747–1752.
- Singh, S.; James, M.R.; Rudary, M. Predictive state representations: A new theory for modeling dynamical systems. In Proceedings of the 20th Conference on Uncertainty in Artificial Intelligence, Banff, AB, Canada, 7–11 July 2004; pp. 512–519.
- Ou, J.; Chen, Y.G.; Zhao, F.; Liu, J.; Xiao, S.P. Method for operating mode identification of multi-function radars based on Predictive State Representations. IET Radar Sonar Navig. 2016, 11, 426–433. [Google Scholar] [CrossRef]
- Thon, M.; Jaeger, H. Links between multiplicity automata, observable operator models and Predictive State Representations: A unified learning framework. J. Mach. Learn. Res. 2015, 16, 103–147. [Google Scholar]
- Wolfe, B.; James, M.R.; Singh, S. Learning Predictive State Representations in dynamical systems without reset. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 985–992.
- Arasaratnam, I.; Haykin, S.; Kirubarajan, T.; Dilkes, F. Tracking the mode of operation of multi-function radars. In Proceedings of the 2006 IEEE Conference on Radar, New York, NY, USA, 24–27 April 2006; pp. 233–238.
- Liu, Y.L.; Li, R.H. Discovery and learning of models with predictive state representations for dynamical systems without reset. Knowl. Based Syst. 2009, 22, 557–561. [Google Scholar]
- Arora, S.; Barak, B. Computational Complexity: A Modern Approach; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]


| Mode | Phrases | Mode | Phrases | |
|---|---|---|---|---|
| Search (S) | 4-Word Search | [w1w2w4w5] | Track-Maintenance (T) | [w1w7w7w7] |
| [w2w4w5w1] | [w2w7w7w7] | |||
| [w4w5w1w2] | [w3w7w7w7] | |||
| [w5w1w2w4] | [w4w7w7w7] | |||
| 3-Word Search | [w1w3w5w1] | [w5w7w7w7] | ||
| [w3w5w1w3] | [w6w7w7w7] | |||
| [w5w1w3w5] | [w1w8w8w8] | |||
| Acquisition (A) | [w1w1w1w1] | [w2w8w8w8] | ||
| [w2w2w2w2] | [w3w8w8w8] | |||
| [w3w3w3w3] | [w4w8w8w8] | |||
| [w4w4w4w4] | [w5w8w8w8] | |||
| [w5w5w5w5] | [w6w8w8w8] | |||
| Non-Adaptive Track (N) or Track-Maintenance (T) | [w1w6w6w6] | [w1w9w9w9] | ||
| [w2w6w6w6] | [w2w9w9w9] | |||
| [w3w6w6w6] | [w3w9w9w9] | |||
| [w4w6w6w6] | [w4w9w9w9] | |||
| [w5w6w6w6] | [w5w9w9w9] | |||
| Range-Resolution (R) | [w7w6w6w6] | [w6w9w9w9] | ||
| [w8w6w6w6] | [w7w7w7w7] | |||
| [w9w6w6w6] | [w8w8w8w8] | |||
| A or N or T | [w6w6w6w6] | [w9w9w9w9] | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, J.; Chen, Y.; Zhao, F.; Liu, J.; Xiao, S.
Novel Approach for the Recognition and Prediction of Multi-Function Radar Behaviours Based on Predictive State Representations
. Sensors 2017, 17, 632.
https://doi.org/10.3390/s17030632
Ou J, Chen Y, Zhao F, Liu J, Xiao S.
Novel Approach for the Recognition and Prediction of Multi-Function Radar Behaviours Based on Predictive State Representations
. Sensors. 2017; 17(3):632.
https://doi.org/10.3390/s17030632
Ou, Jian, Yongguang Chen, Feng Zhao, Jin Liu, and Shunping Xiao.
2017. "Novel Approach for the Recognition and Prediction of Multi-Function Radar Behaviours Based on Predictive State Representations
" Sensors 17, no. 3: 632.
https://doi.org/10.3390/s17030632
Ou, J., Chen, Y., Zhao, F., Liu, J., & Xiao, S.
(2017). Novel Approach for the Recognition and Prediction of Multi-Function Radar Behaviours Based on Predictive State Representations
. Sensors, 17(3), 632.
https://doi.org/10.3390/s17030632




