Performance Analysis of BDS Medium-Long Baseline RTK Positioning Using an Empirical Troposphere Model
Abstract
:1. Introduction
2. Methodology
2.1. Traditional Observation Model for Medium-Long Baseline RTK
2.2. RZTD-Constrained RTK Model
3. Experiment and Result Analysis
3.1. Data Collection and Processing Strategy
3.2. Performance Analysis of Traditional Medium-Long Baseline RTK
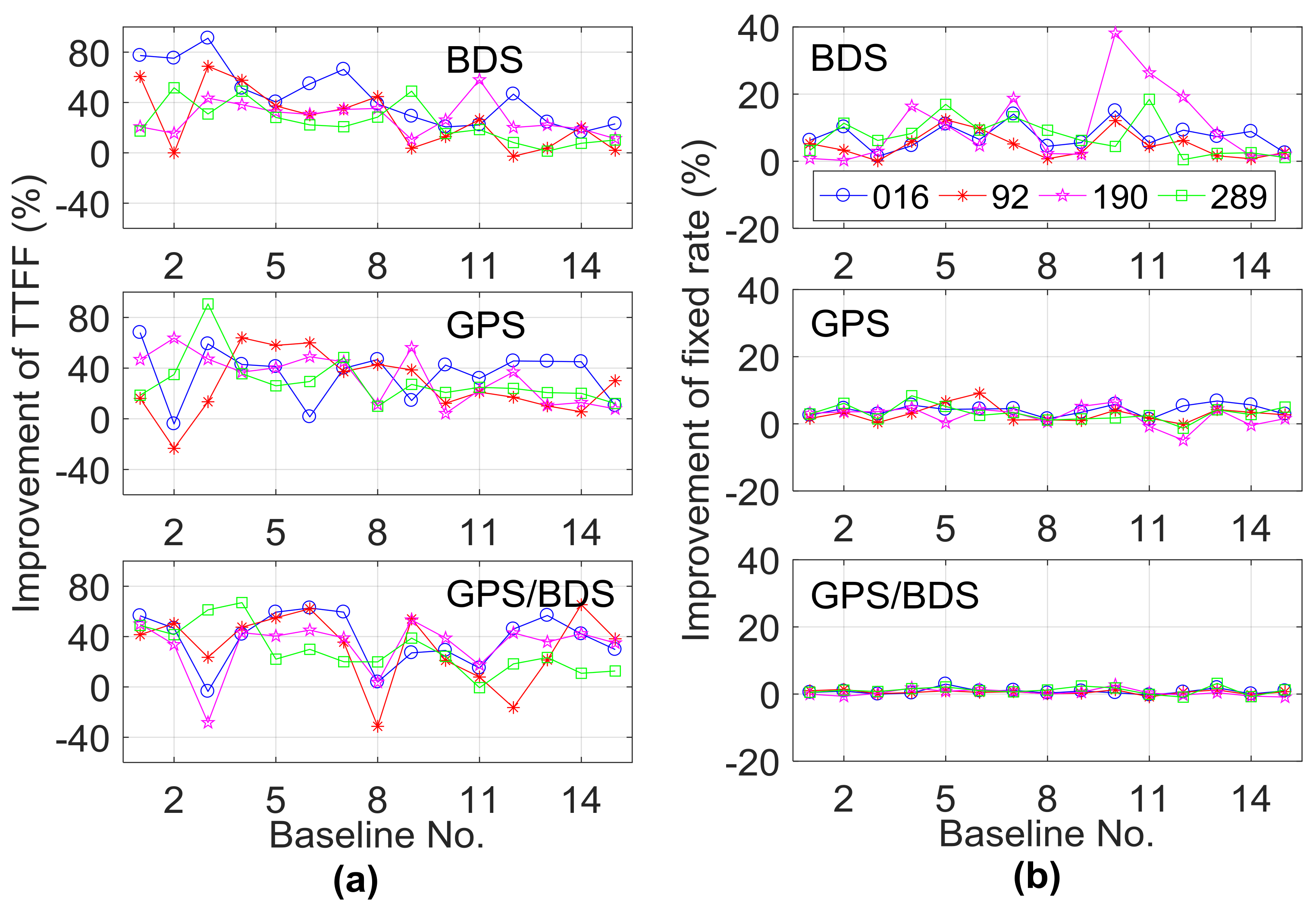
3.3. Performance Analysis of RZTD-Constrained Medium-Long Baseline RTK
4. Discussion
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bock, Y.; Gourevitch, S.A.; Counselman, C.C.I.; King, R.W.; Abbot, R.I. Interferometric analysis of GPS phase observations. Manuscr. Geod. 1986, 11, 282–288. [Google Scholar]
- Hu, G.R.; Khoo, H.S.; Goh, P.C.; Law, C.L. Development and assessment of GPS virtual reference stations for RTK positioning. J. Geod. 2003, 77, 292–302. [Google Scholar] [CrossRef]
- Odijk, D. Stochastic modelling of the ionosphere for fast GPS ambiguity resolution. In Proceedings of the Geodesy Beyond 2000-the Challenges of the First Decade, IAG General Assembly, Birmingham, UK, 19–30 July 2000; pp. 387–392. [Google Scholar]
- Wielgosz, P.; Kashani, I.; Grejner-Brzezinska, D. Analysis of long-range network RTK during a severe ionospheric storm. J. Geod. 2005, 79, 524–531. [Google Scholar] [CrossRef]
- Hu, G.; Abbey, D.A.; Castleden, N.; Featherstone, W.E.; Earls, C.; Ovstedal, O.; Weihing, D. An approach for instantaneous ambiguity resolution for medium-to long-range multiple reference station networks. GPS Solut. 2005, 9, 1–11. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Feng, Y.; Gao, W.; Yang, L. GNSS ambiguity resolution with controllable failure rate for long baseline network RTK. J. Geod. 2014, 88, 99–112. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, H.; Bai, Z.; Qian, C.; Fan, C.; Zhou, P.; Shu, B. Fast ambiguity resolution for long-range reference station networks with ionospheric model constraint method. GPS Solut. 2017, 2, 617–626. [Google Scholar] [CrossRef]
- Wanninger, L. Improved ambiguity resolution by regional differential modelling of the ionosphere. In Proceedings of the ION GPS 1995, Palm Springs, CA, USA, 12–15 September 1995; pp. 55–62. [Google Scholar]
- Han, S.; Rizos, C. GPS network design and error mitigation for real-time continuous array monitoring system. In Proceedings of the ION GPS 1996, Kansas City, MO, USA, 17–20 September 1996; pp. 1827–1836. [Google Scholar]
- Takasu, T.; Yasuda, A. Kalman-filter-based integer ambiguity resolution strategy for long-baseline RTK with ionospheric and troposphere estimation. In Proceedings of the ION GNSS 2010, Portland, OR, USA, 21–24 September 2010; pp. 161–171. [Google Scholar]
- Parkins, A. Increasing GNSS RTK availability with a new single-epoch batch partial ambiguity resolution algorithm. GPS Solut. 2011, 15, 391–402. [Google Scholar] [CrossRef]
- Dai, L.; Eslinger, D.; Sharpe, T. Innovative algorithms to improve long range RTK reliability and availability. In Proceedings of the ION NTM 2007, San Diego, CA, USA, 22–24 January 2007; pp. 860–872. [Google Scholar]
- Li, J.; Yang, Y.; Xu, J.; He, H.; Guo, H. GNSS multi-carrier fast partial ambiguity resolution strategy tested with real BDS/GPS dual-and triple-frequency observations. GPS Solut. 2015, 19, 5–13. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Odolinski, R.; Odijk, D. Instantaneous BeiDou+ GPS RTK positioning with high cut-off elevation angles. J. Geod. 2014, 88, 335–350. [Google Scholar] [CrossRef]
- Feng, Y.; Li, B. Wide area real time kinematic decimetre positioning with multiple carrier GNSS signals. Sci. China Ser. D 2010, 53, 731–740. [Google Scholar] [CrossRef]
- Guo, H.; He, H.; Li, J.; Wang, A. Estimation and mitigation of the main errors for centimetre-level COMPASS RTK solutions over medium-long baselines. J. Navig. 2011, 64, 113–126. [Google Scholar] [CrossRef]
- Gong, X.; Lou, Y.; Liu, W.; Zheng, F.; Gu, S.; Wang, H. Rapid ambiguity resolution over medium-to-long baselines based on GPS/BDS multi-frequency observables. Adv. Space Res. 2017, 59, 794–803. [Google Scholar] [CrossRef]
- Li, B.; Feng, Y.; Shen, Y.; Wang, C. Geometry-specified troposphere decorrelation for subcentimeter real-time kinematic solutions over long baselines. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Ahn, Y.W.; Kim, D.; Dare, P.; Park, J. Estimation of troposphere decorrelation using the combined zenith-dependent parameter. In Proceedings of the ION GNSS 2008, Savannah, GA, USA, 16–19 September 2008; pp. 261–270. [Google Scholar]
- Dodson, A.H.; Shardlow, P.J.; Hubbard, L.C.M.; Elgered, G.; Jarlemark, P.O.J. Wet tropospheric effects on precise relative GPS height determination. J. Geod. 1996, 70, 188–202. [Google Scholar] [CrossRef]
- Kim, D.; Langley, R.B. Long-range single-baseline RTK for complementing network-based RTK. In Proceedings of the ION GNSS 2007, Fort Worth, TX, USA, 25–28 September 2007; pp. 639–650. [Google Scholar]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Hugentobler, U.; Teunissen, P.; Nakamura, S. Initial assessment of the COMPASS/BeiDou2 regional navigation satellite system. GPS Solut. 2013, 17, 211–222. [Google Scholar] [CrossRef]
- Shi, C.; Zhao, Q.; Hu, Z.; Liu, J. Precise relative positioning using real tracking data from COMPASS GEO and IGSO satellites. GPS Solut. 2013, 17, 103–119. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Wang, A.; Xu, J.; He, H.; Guo, H.; Dai, X. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system. Sci. China Ser. D 2014, 57, 144–152. [Google Scholar] [CrossRef]
- Deng, C.; Tang, W.; Liu, J.; Shi, C. Reliable single-epoch ambiguity resolution for short baselines using combined GPS/BeiDou system. GPS Solut. 2014, 18, 375–386. [Google Scholar] [CrossRef]
- He, H.; Li, J.; Yang, Y.; Xu, J.; Guo, H.; Wang, A. Performance assessment of single-and dual-frequency BeiDou/GPS single-epoch kinematic positioning. GPS Solut. 2014, 18, 393–403. [Google Scholar] [CrossRef]
- Leandro, R.; Santos, M.C.; Langley, R.B. UNB neutral atmospheric models: Development and performance. In Proceedings of the ION NTM 2006, Monterey, CA, USA, 18–20 January 2006; pp. 564–573. [Google Scholar]
- Böhm, J.; Heinkelmann, R.; Schuh, H. Short note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Hu, C.Y.Y. A new method to accelerate ppp convergence time by using a global zenith troposphere delay estimate model. J. Navig. 2014, 67, 899–910. [Google Scholar] [CrossRef]
- Ibrahim, H.; El-Rabbany, A. Performance analysis of NOAA tropospheric signal delay model. Meas. Sci. Technol. 2011, 22, 115107–115113. [Google Scholar] [CrossRef]
- Chen, W.; Gao, C.; Pan, S. Assessment of GPT2 empirical troposphere model and application analysis in precise point positioning. In Proceedings of the China Satellite Navigation Conference (CSNC) 2014, Nanjing, China, 21–23 May 2014; pp. 451–463. [Google Scholar]
- Lu, C.; Li, X.; Zus, F.; Heinkelmann, R.; Dick, G.; Ge, M.; Schuh, H. Improving BeiDou real-time precise point positioning with numerical weather models. J. Geod. 2017, 91, 1019–1029. [Google Scholar] [CrossRef]
- Zhang, J.; Lachapelle, G. Precise estimation of residual tropospheric delays using a regional GPS network for real-time kinematic applications. J. Geod. 2001, 75, 255–266. [Google Scholar] [CrossRef]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef]
- Teunissen, P.J. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Verhagen, S.; Teunissen, P. The ratio test for future GNSS ambiguity resolution. GPS Solut. 2013, 17, 535–548. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contribution to the theory of atmospheric refraction. Bull. Geod. 1973, 107, 13–34. [Google Scholar] [CrossRef]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to Gamit/Globk; Massachusetts Institute of Technology: Cambridge, MA, USA, 2008. [Google Scholar]












| Baseline | No. | Length (km) | Elevation Difference (m) | Baseline | No. | Length (km) | Elevation Difference (m) |
|---|---|---|---|---|---|---|---|
| DXWY-DXZX | 1 | 38.3 | 214 | DXWY-LXHZ | 9 | 85.5 | 66 |
| DXWY-DXLT | 2 | 41.2 | 160 | GNAX-GNYL | 10 | 112.9 | 311 |
| DXLT-LXHZ | 3 | 47.7 | 271 | DXZX-LXHZ | 11 | 119.8 | 280 |
| GNYL-DXLT | 4 | 48.3 | 310 | GNAX-DXZX | 12 | 121.4 | 8 |
| GNYL-DXWY | 5 | 53.6 | 105 | GNAX-DXWY | 13 | 138.9 | 206 |
| GNYL-LXHZ | 6 | 58.4 | 39 | GNAX-DXLT | 14 | 158.0 | 1 |
| GNYL-DXZX | 7 | 74.0 | 319 | GNAX-LXHZ | 15 | 166.9 | 272 |
| DXZX-DXLT | 8 | 78.9 | 9 | - | - | - |
| Traditional RTK | RZTD-constrained RTK | |
| Observations (variance) | Uncombined DD pseudorange (m) | Uncombined DD pseudorange (m) |
| Uncombined DD carrier phase (m) | Uncombined DD carrier phase (m) | |
| Pseudo-observations (variance) | - | RZTD derived from GPT2 model (m) |
| Troposphere mapping function | GMF | GMF |
| Initial troposphere RZTD (variance) | 0.0 m (0.152 m2) | 0.0 m (0.152 m2) |
| Initial ambiguity (variance) | derived from pseudorange (302 cycle2) | derived from pseudorange (302 cycle2) |
| Initial slant ionosphere delay (variance) | 0.0 m (m2) | 0.0 m (m2) |
| Process noise of troposphere RZTD | m/ | m/ |
| Estimator | Kalman filter | Kalman filter |
| Improvement Rate (%) | BDS | GPS | GPS/BDS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 016 | 092 | 190 | 289 | 016 | 092 | 190 | 289 | 016 | 092 | 190 | 289 | |
| TTFF | 45.2 | 26.7 | 27.9 | 23.9 | 35.4 | 26.8 | 32.7 | 29.5 | 38.2 | 31.7 | 32.8 | 29.2 |
| Fixed rate | 7.5 | 4.8 | 10.3 | 7.5 | 4.1 | 2.9 | 2.3 | 3.2 | 0.8 | 0.5 | 0.4 | 1.1 |
| STD | 54.0 | 50.3 | 47.7 | 57.7 | 24.8 | 28.1 | 28.4 | 24.6 | 41.3 | 34.7 | 24.0 | 36.0 |
| RMS error | 44.2 | 39.5 | 36.3 | 40.2 | 22.9 | 17.3 | 15.7 | 17.8 | 33.1 | 14.7 | 12.1 | 19.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, B.; Liu, H.; Xu, L.; Qian, C.; Gong, X.; An, X. Performance Analysis of BDS Medium-Long Baseline RTK Positioning Using an Empirical Troposphere Model. Sensors 2018, 18, 1199. https://doi.org/10.3390/s18041199
Shu B, Liu H, Xu L, Qian C, Gong X, An X. Performance Analysis of BDS Medium-Long Baseline RTK Positioning Using an Empirical Troposphere Model. Sensors. 2018; 18(4):1199. https://doi.org/10.3390/s18041199
Chicago/Turabian StyleShu, Bao, Hui Liu, Longwei Xu, Chuang Qian, Xiaopeng Gong, and Xiangdong An. 2018. "Performance Analysis of BDS Medium-Long Baseline RTK Positioning Using an Empirical Troposphere Model" Sensors 18, no. 4: 1199. https://doi.org/10.3390/s18041199
APA StyleShu, B., Liu, H., Xu, L., Qian, C., Gong, X., & An, X. (2018). Performance Analysis of BDS Medium-Long Baseline RTK Positioning Using an Empirical Troposphere Model. Sensors, 18(4), 1199. https://doi.org/10.3390/s18041199






