Maglev Train Signal Processing Architecture Based on Nonlinear Discrete Tracking Differentiator
Abstract
:1. Introduction
- (1)
- Since there exist inevitable electromagnetic disturbances, which exert an influence on the working condition of the gap sensor, the gap sensor generates not only real signals that reflect the real gap information, but also noise that may influence the normal functioning of the controller if this noised gap sensor is utilized directly as the feedback without preprocessing. To minimize the influence caused by this kind of noise disturbance, a gap sensor signal must be filtered before it is used by the controller. At present, most commonly used filters for gap signals are simple first-order low-pass filters, for which the filtering performance and the real-time requirement contradict each other. To enhance the filter’s performance, a big filtering coefficient is required, whereas a big filtering coefficient usually causes a large phase lag that undermines the stabilities of the levitation system [3]. A new filtering strategy with higher filtering performance and smaller phase lag is needed.
- (2)
- Train-track coupled vibration is a special phenomenon for a maglev system due to the elastic property of the steel track [4]. It is found that if the information of the movement of the track is obtained for computation of the control output, this vibration can be effectively suppressed [5,6]. Since the differential of gap is the relative velocity between the electromagnet and the track, this information is effective for suppression of this kind of vibration. However, the acquisition of differential for a discrete signal is a difficult task. The differential of a given discrete signal can amplify the noise, especially the high frequency noise. Sometimes, the real differential result can be overwhelmed by this amplified noise. Therefore, a differentiator that can acquire the differential for signals within the given frequency region without amplifying the high frequency noise is needed.
- (3)
- Model based signal processing strategy is effective in filtering and obtaining derivative signals under the condition that the object model is time invariant and precisely known a priori; however, the maglev model is sometimes not precise and is always time varying due to the changing passenger amount and the varying relative position between the electromagnet and the track [7]. For this reason, the signal processing method with less dependence on the system model is more suitable for the maglev train levitation system.
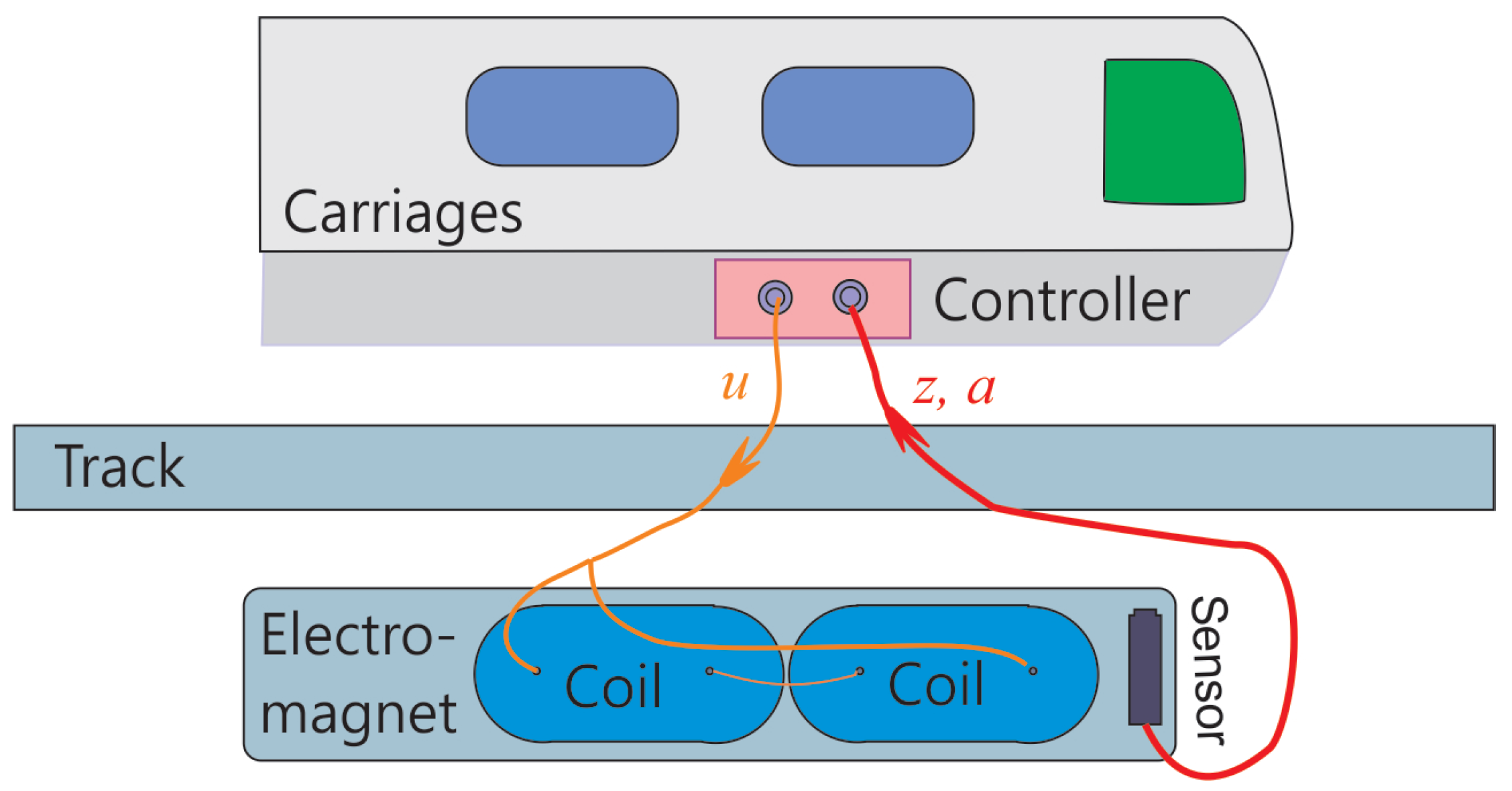
2. Signal Processing Architecture Based on Tracking Differentiator
- there is no magnetic flux leakage,
- there is no external disturbance force,
- there is only the vertical movement of the electromagnet,
- the track is rigid,
3. Nonlinear Second Order Discrete Tracking Differentiator Based on Boundary Characteristics
3.1. Preliminaries of the Discrete Tracking Differentiator
3.2. Procedure to Calculate the Control Comprehensive Function
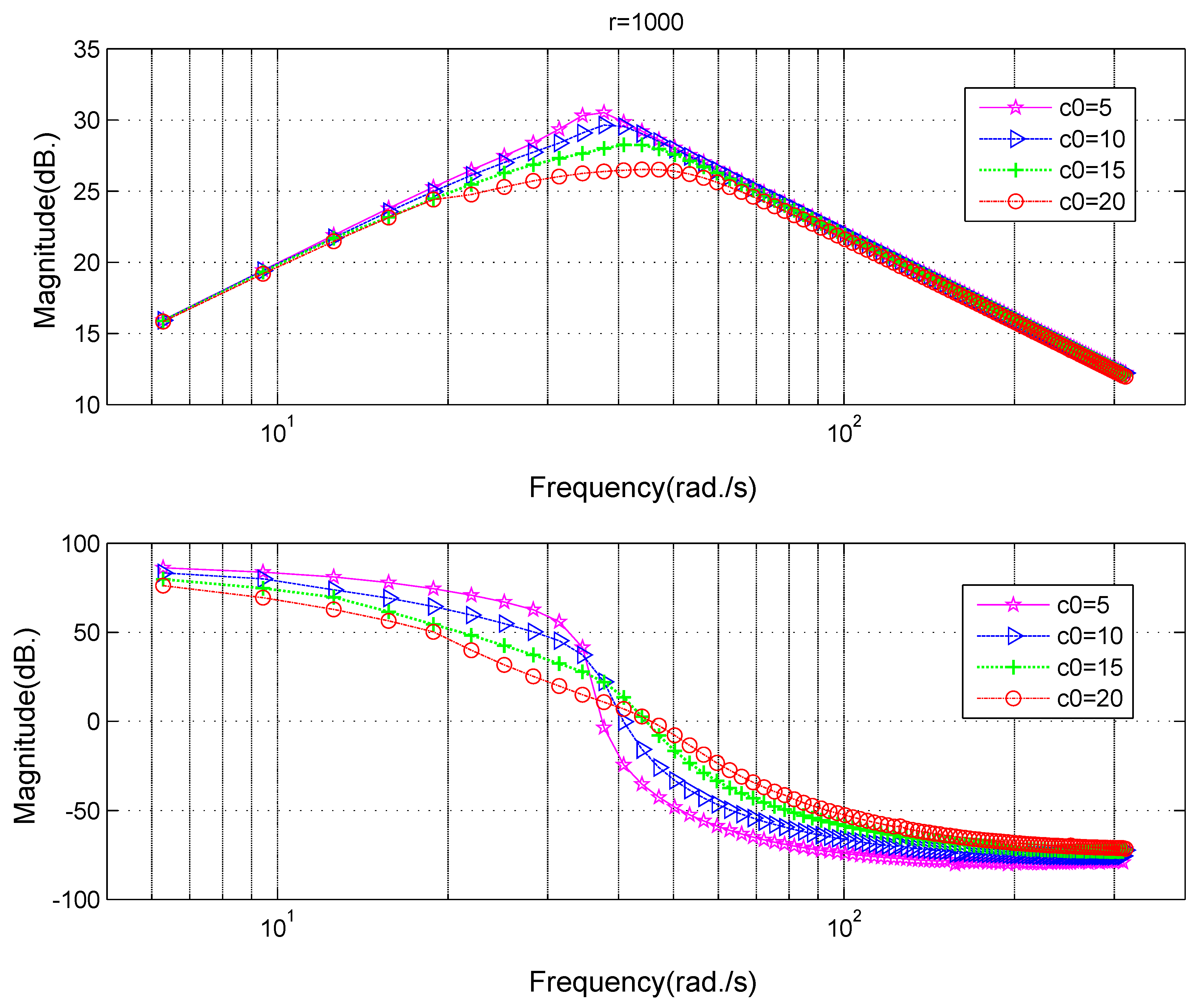
3.3. Influence of the Parameters
4. Simulation and Experiment Analysis
4.1. Simulation of TD Based Signal Processing Architecture in MATLAB-Simulink
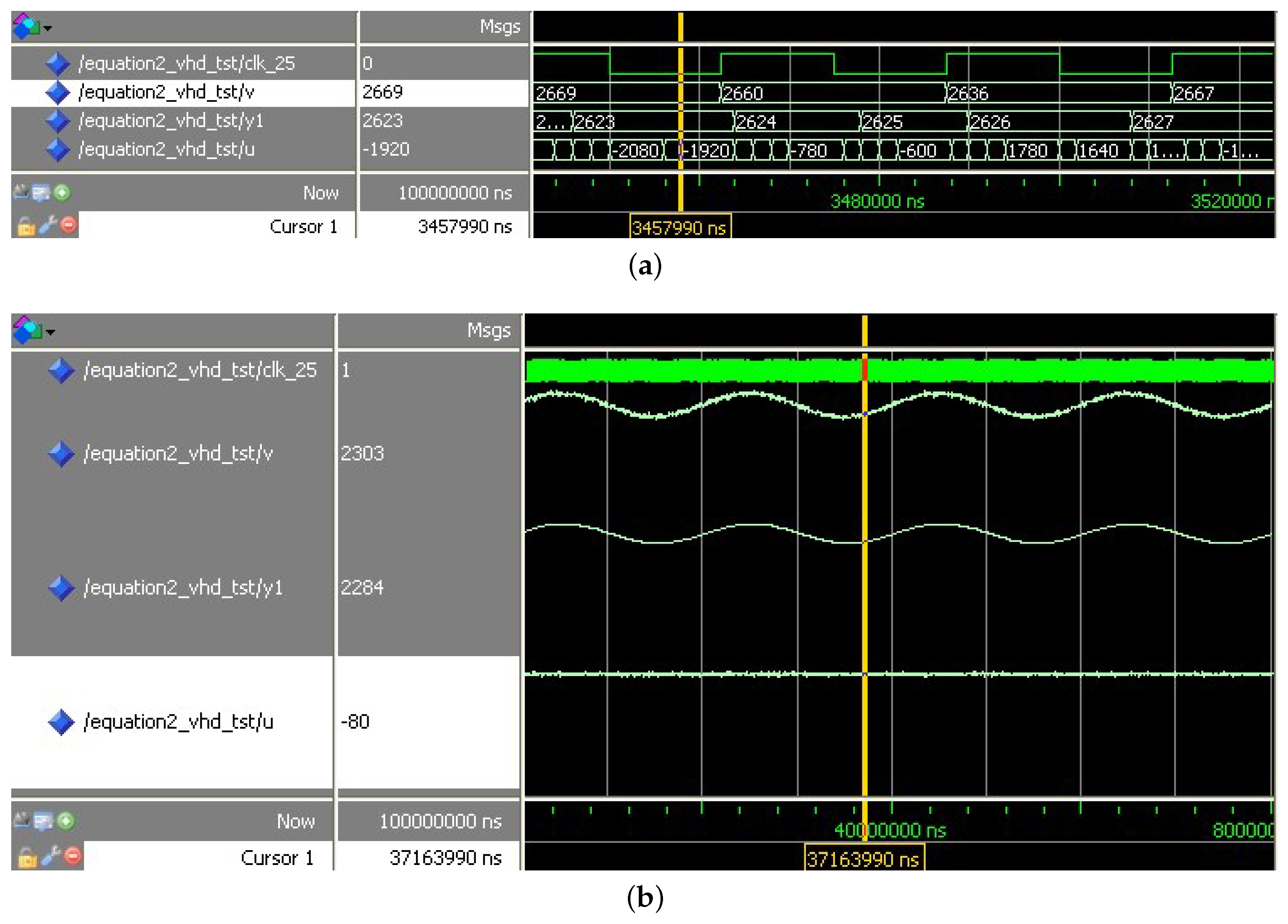
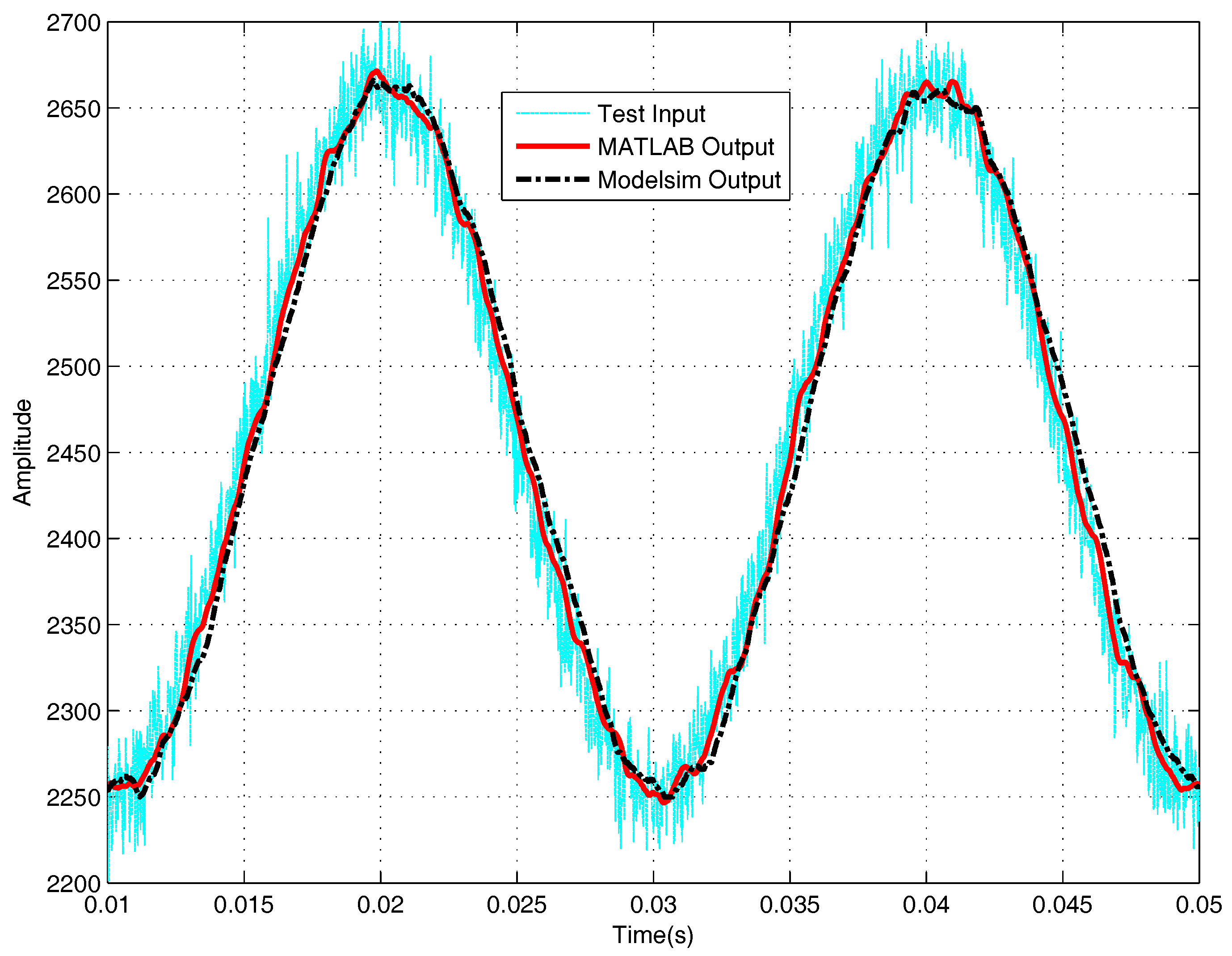
4.2. VHDL Implementation and MATLAB-Modelsim Simulation for TD
- (1)
- Generate the desired input signal in a MATLAB file and store the signal data into a text document. In this process, signals with almost any properties can be generated easily.
- (2)
- Import of the input signal. In this step, Modelsim reads the text document generated in step (1), and import the stored data as the input data for the tracking differentiator.
- (3)
- Operation of tracking differentiator. This is the core step of this entire simulation.
- (4)
- Storage of the output data. All data are stored in a text file.
- (5)
- Reading of the output data and make some necessary signal processing via MATLAB’s signal processing tools.
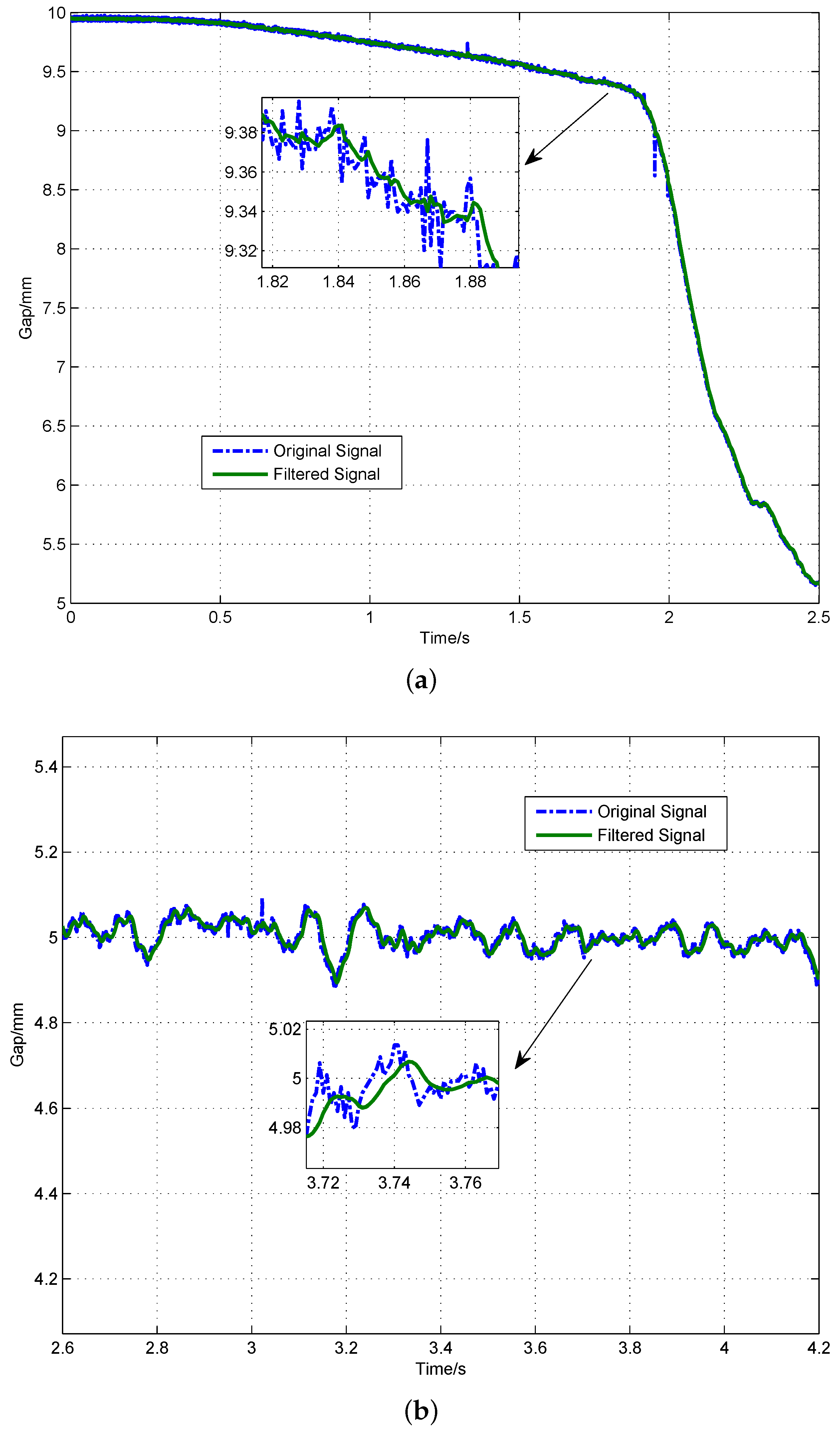
4.3. Experiment Analysis of the Proposed Signal Processing Architecture
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, H.W.; Kim, K.C.; Lee, J. Review of maglev train technologies. IEEE Trans. Magn. 2006, 42, 1917–1925. [Google Scholar]
- Liu, Z.; Long, Z.; Li, X. Maglev Train Overview. In Maglev Trains; Springer: Berlin, Germany, 2015; pp. 1–28. [Google Scholar]
- Heng-kun, L.; Wen-sen, C.; A-Ming, H. Influence of Signal Delay on Stability of Magnetic Suspension System. Inf. Control 2009, 4, 022. [Google Scholar]
- Zhou, D.F.; Hansen, C.H.; Li, J.; Chang, W.S. Review of Coupled Vibration Problems in EMS Maglev Vehicles. Int. J. Acoust. Vib. 2010, 15, 10–23. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Zhou, D.; Cui, P.; Wang, L.; Yu, P. The active control of maglev stationary self-excited vibration with a virtual energy harvester. IEEE Trans. Ind. Electron. 2015, 62, 2942–2951. [Google Scholar] [CrossRef]
- Wang, L.; Li, J.; Zhou, D.; Li, J. An Experimental Validated Control Strategy of Maglev Vehicle-Bridge Self-Excited Vibration. Appl. Sci. 2017, 7, 38. [Google Scholar] [CrossRef]
- Cui, P.; Li, J.; Liu, D. Carrying capacity for the electromagnetic suspension low-speed maglev train on the horizontal curve. Sci. China Technol. Sci. 2010, 53, 1082–1087. [Google Scholar] [CrossRef]
- Kumar, B.; Roy, S.D. Design of digital differentiators for low frequencies. Proc. IEEE 1988, 76, 287–289. [Google Scholar] [CrossRef]
- Pei, S.C.; Shyu, J.J. Design of FIR Hilbert transformers and differentiators by eigenfilter. IEEE Trans. Circ. Syst. 1988, 35, 1457–1461. [Google Scholar]
- Zhang, H.; Xie, Y.; Xiao, G.; Zhai, C.; Kang, H.; Tang, J. Tracking Differentiator via Time Criterion. In Proceedings of the American Control Conference, Milwaukee, WI, USA, 27–29 June 2018. [Google Scholar]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Levant, A. Robust exact differentiation via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Nunes, E.V.L.; Hsu, L.; Lizarralde, F. Global exact tracking for uncertain systems using output-feedback sliding mode control. IEEE Trans. Autom. Control 2009, 54, 1141–1147. [Google Scholar] [CrossRef]
- Oliveira, T.; Peixoto, A.; Nunes, E.; Hsu, L. Control of uncertain nonlinear systems with arbitrary relative degree and unknown control direction using sliding modes. Int. J. Adapt. Control Signal Process 2007, 21, 692–707. [Google Scholar] [CrossRef]
- Wang, X.; Lin, H. Design and analysis of a continuous hybrid differentiator. IET Control Theory Appl. 2011, 5, 1321–1334. [Google Scholar] [CrossRef]
- Angulo, M.T.; Moreno, J.A.; Fridman, L. Robust exact uniformly convergent arbitrary order differentiator. Automatica 2013, 49, 2489–2495. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2009; Volume 34. [Google Scholar]
- Utkin, V.I.; Poznyak, A.S. Adaptive sliding mode control with application to super-twist algorithm: Equivalent control method. Automatica 2013, 49, 39–47. [Google Scholar] [CrossRef]
- Jinqing, H.; Lulin, Y. The Discrete Form of Tracking-Differentiator. J. Syst. Sci. Math. Sci. 1999, 3. [Google Scholar]
- Zhang, H.; Xie, Y.; Xiao, G.; Zhai, C. Closed-form solution of discrete-time optimal control and its convergence. IET Control Theory Appl. 2017, 12, 413–418. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, W.; Tang, K. A new inertial aid method for high dynamic compass signal tracking based on a nonlinear tracking differentiator. Sensors 2012, 12, 7634–7647. [Google Scholar] [CrossRef] [PubMed]
- Chunhui, D.; Zhiqiang, L.; Yunde, X.; Song, X. Research on the filtering algorithm in speed and position detection of maglev trains. Sensors 2011, 11, 7204–7218. [Google Scholar]
- Song, X.; Zhiqiang, L.; Ning, H.; Wensen, C. A high precision position sensor design and its signal processing algorithm for Maglev train. Sensors 2012, 12, 5. [Google Scholar]
- Zhang, D.P.; Zheng, W.; Wang, Y.D.; Zhang, L. X-Ray Pulsar Profile Recovery Based on Tracking-Differentiator. Math. Probl. Eng. 2016, 2016, 1563–5147. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, H.; Zou, J.; Zheng, G. Tracking differentiator-based dynamic surface control for the power control of the wind generation system in the wind farm. Proc. Instit. Mech. Eng. I J. Syst. Control Eng. 2013, 227, 275–285. [Google Scholar] [CrossRef]
- Dou, F.S.; Dai, C.H. Filtering algorithm and direction identification in relative position estimation based on induction loop-cable. J. Cent. South Univ. 2016, 23, 112–121. [Google Scholar] [CrossRef]
- Ibraheem, I.K.; Abdul-Adheem, W.R. On the Improved Nonlinear Tracking Differentiator based Nonlinear PID Controller Design. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 234–241. [Google Scholar]
- Shen, J.; Xin, B.; Cui, H.; Gao, W. Speed Control of Single-axis Rotation INS By Tracking Differentiator Based Fuzzy PID. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2976–2986. [Google Scholar] [CrossRef]
- Shao, X.; Wang, H. Back-stepping robust trajectory linearization control for hypersonic reentry vehicle via novel tracking differentiator. J. Frankl. Inst. 2016, 353, 1957–1984. [Google Scholar] [CrossRef]
- Tian, D.; Shen, H.; Dai, M. Improving the rapidity of nonlinear tracking differentiator via feedforward. IEEE Trans. Ind. Electron. 2014, 61, 3736–3743. [Google Scholar] [CrossRef]
- Hongwei, W.; Heping, W. A Comparison Study of Advanced Tracking Differentiator Design Techniques. Procedia Eng. 2015, 99, 1005–1013. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Evans, L.C. An Introduction to Mathematical Optimal Control Theory Version 0.2. Available online: https://math.berkeley.edu/evans/control.course.pdf (accessed on 20 May 2018).
- Arora, J. Introduction to Optimum Design; Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Meyer-Baese, U.; Meyer-Baese, U. Digital Signal Processing with Field Programmable Gate Arrays; Springer: Berlin, Germany, 2007; Volume 65. [Google Scholar]
- Taylor, F. Digital Filters: Principles and Applications with MATLAB; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 30. [Google Scholar]
















© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Li, X.; Xie, Y.; Long, Z. Maglev Train Signal Processing Architecture Based on Nonlinear Discrete Tracking Differentiator. Sensors 2018, 18, 1697. https://doi.org/10.3390/s18061697
Wang Z, Li X, Xie Y, Long Z. Maglev Train Signal Processing Architecture Based on Nonlinear Discrete Tracking Differentiator. Sensors. 2018; 18(6):1697. https://doi.org/10.3390/s18061697
Chicago/Turabian StyleWang, Zhiqiang, Xiaolong Li, Yunde Xie, and Zhiqiang Long. 2018. "Maglev Train Signal Processing Architecture Based on Nonlinear Discrete Tracking Differentiator" Sensors 18, no. 6: 1697. https://doi.org/10.3390/s18061697
APA StyleWang, Z., Li, X., Xie, Y., & Long, Z. (2018). Maglev Train Signal Processing Architecture Based on Nonlinear Discrete Tracking Differentiator. Sensors, 18(6), 1697. https://doi.org/10.3390/s18061697




