Vibration-Induced Errors in MEMS Tuning Fork Gyroscopes with Imbalance
Abstract
:1. Introduction
2. Theoretical Study on the Vibration Response of the Ideal TFG
- for the left gyro:
- for the right gyro:
- for the left gyro:
- for the right gyro:
3. Sense Capacitance Nonlinearity
4. Theoretical Study of the Vibration Response of a Non-Ideal TFG
- coupled gyros:
- uncoupled gyros:
4.1. Stiffness Imbalance
4.2. Mass Imbalance
4.3. Damping Imbalance
4.4. Summary
5. Models and Parameters
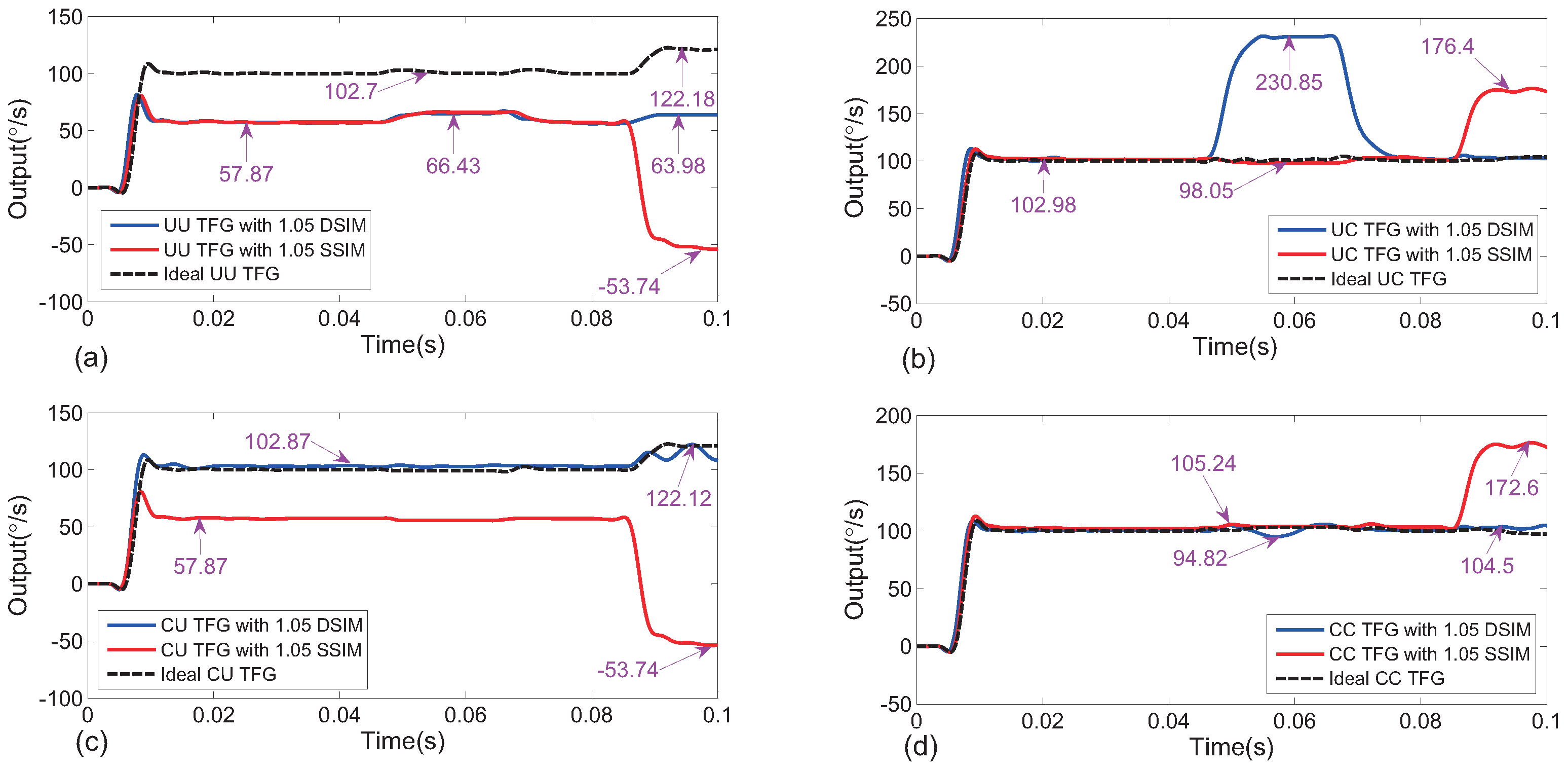
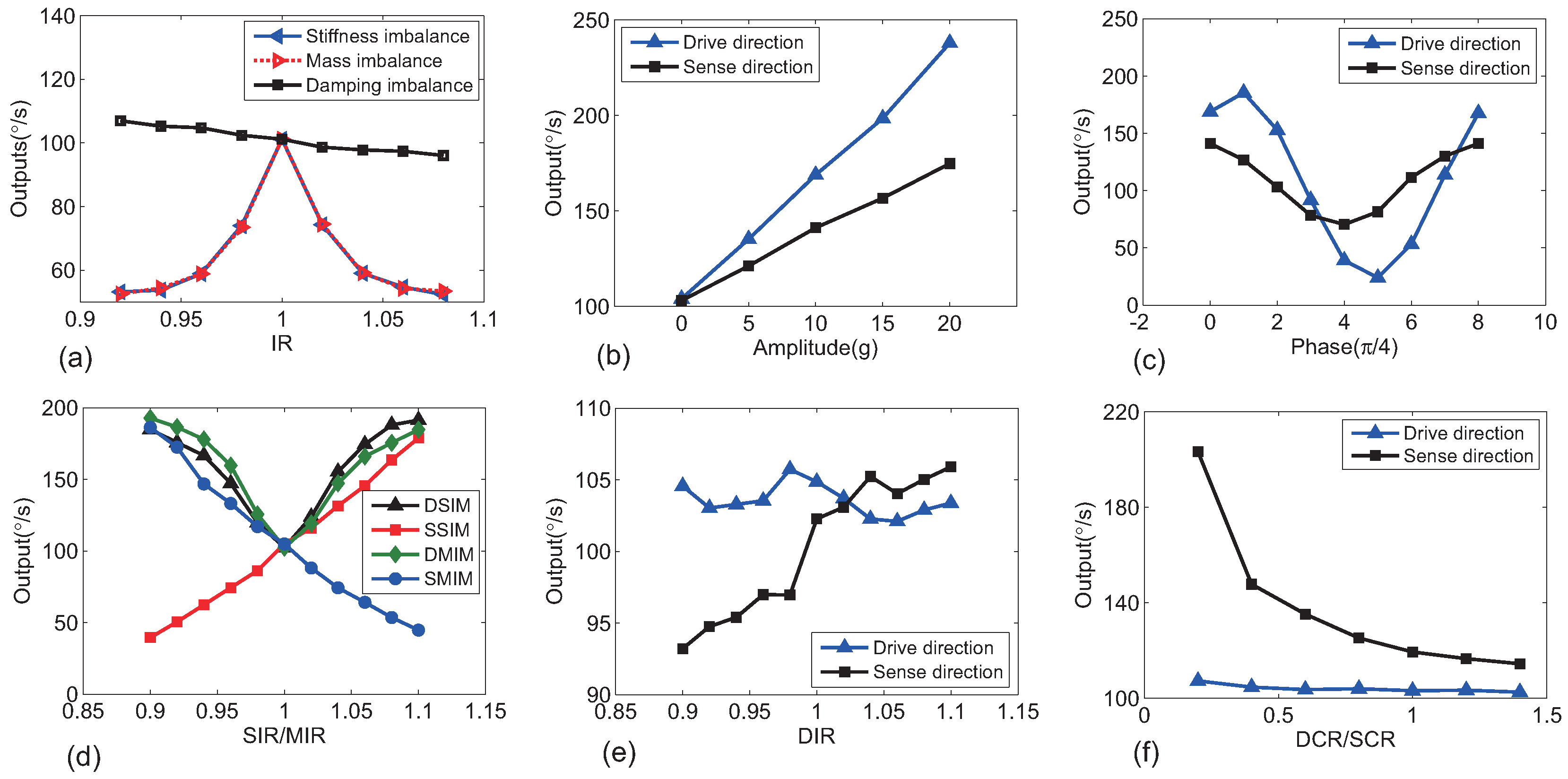
6. Simulation and Discussion
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
Appendix E
- driving forces:
- Coriolis forces:
- driving forces:
- Coriolis forceswhere the phase angle is the damping ratio. Ideal displacements difference / and error displacements difference ratio is given by . Therefore, Equations (23) and (24) are achieved.
Appendix F
Appendix G
References
- Yazdi, N.; Ayazi, F.; Najafi, K. Micromachined inertial sensors. Proc. IEEE 1998, 86, 1640–1659. [Google Scholar] [CrossRef]
- Prikhodko, I.P.; Zotov, S.A.; Trusov, A.A.; Shkel, A.M. Sub-degree-per-hour silicon MEMS rate sensor with 1 million Q-factor. In Proceedings of the International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Beijing, China, 5–9 June 2011; pp. 2809–2812. [Google Scholar]
- Cho, J.; Gregory, J.A.; Najafi, K. High-Q, 3kHz single-crystal-silicon cylindrical rate-integrating gyro (CING). In Proceedings of the IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Paris, France, 29 January–2 February 2012; pp. 172–175. [Google Scholar]
- Zotov, S.A.; Trusov, A.A.; Shkel, A.M. High-range angular rate sensor based on mechanical frequency modulation. J. Microelectromech. Syst. 2012, 21, 1640–1659. [Google Scholar] [CrossRef]
- Wang, W.; Lv, X.Y.; Sun, F. Design of a novel MEMS gyroscope array. Sensors 2013, 13, 1651–1663. [Google Scholar] [CrossRef] [PubMed]
- Xia, D.; Yu, C.; Kong, L. The development of micromachined gyroscope structure and circuitry technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef] [PubMed]
- Shkel, A.M. Type I and type II micromachined vibratory gyroscopes. In Proceedings of the IEEE PLANS, Position Location and Navigation Symposium, San Diego, CA, USA, 25–27 April 2006; pp. 586–593. [Google Scholar]
- Geen, J.A.; Sherman, S.J.; Chang, J.F.; Lewis, S.R. Single-chip surface micromachined integrated gyroscope with 50/spl deg//h Allan deviation. IEEE J. Solid-State Circuits 2002, 37, 1860–1866. [Google Scholar] [CrossRef]
- Zaman, M.F.; Sharma, A.; Ayazi, F. High performance matched-mode tuning fork gyroscope. In Proceedings of the IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Istanbul, Turkey, 22–26 January 2006; pp. 66–69. [Google Scholar]
- Giacci, F.; Dellea, S.; Langfelder, G. Signal integrity in capacitive and piezoresistive single-and multi-axis MEMS gyroscopes under vibrations. Microelectron. Reliab. 2017, 75, 59–68. [Google Scholar] [CrossRef]
- Ding, X.; Li, H.; Ni, Y.; Sang, P. Analysis of frequency response and scale-factor of tuning fork micro-gyroscope operating at atmospheric pressure. Sensors 2015, 15, 2453–2472. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Fedder, G.K. Integrated microelectromechanical gyroscopes. J. Aerosp. Eng. 2003, 16, 65–75. [Google Scholar] [CrossRef]
- Schofield, A.R.; Trusov, A.A.; Acar, C.; Shkel, A.M. Anti-phase driven rate gyroscope with multi-degree of freedom sense mode. In Proceedings of the International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Lyon, France, 10–14 June 2007; pp. 1199–1202. [Google Scholar]
- Yoon, S.W.; Lee, S.W.; Perkins, N.C.; Najafi, K. Vibration sensitivity of MEMS tuning fork gyroscopes. In Proceedings of the IEEE Conference on Sensors, San Diego, CA, USA, 28–31 October 2007; pp. 115–119. [Google Scholar]
- Schofield, A.R.; Trusov, A.A.; Shkel, A.M. Multi-degree of freedom tuning fork gyroscope demonstrating shock rejection. In Proceedings of the IEEE Conference on Sensors, Atlanta, GA, USA, 28–31 October 2007; pp. 120–123. [Google Scholar]
- Yoon, S.W.; Lee, S.; Najafi, K. Vibration-induced errors in MEMS tuning fork gyroscopes. Sens. Actuators A Phys. 2012, 180, 32–44. [Google Scholar] [CrossRef]
- Sharma, A.; Zaman, M.F.; Ayazi, F. A Sub-0.2∘/hr Bias Drift Micromechanical Silicon Gyroscope with Automatic CMOS Mode-Matching. IEEE J. Solid-State Circuits 2009, 44, 1593–1608. [Google Scholar] [CrossRef]
- Phani, A.S.; Seshia, A.A.; Palaniapan, M.; Howe, R.T.; Yasaitis, J. Modal coupling in micromechanical vibratory rate gyroscopes. IEEE Sens. J. 2006, 6, 1144–1152. [Google Scholar] [CrossRef]
- Singh, T.P.; Sugano, K.; Tsuchiya, T.; Tabata, O. Frequency response of in-plane coupled resonators for investigating the acceleration sensitivity of MEMS tuning fork gyroscopes. Microsyst. Technol. 2012, 18, 797–803. [Google Scholar] [CrossRef]
- Guan, Y.; Gao, S.; Liu, H.; Niu, S. Acceleration sensitivity of tuning fork gyroscopes: Theoretical model, simulation and experimental verification. Microsyst. Technol. 2015, 21, 1313–1323. [Google Scholar] [CrossRef]
- Chen, Y.; Jiao, J.; Xiong, B.; Che, L.; Li, X.; Wang, Y. A novel tuning fork gyroscope with high Q-factors working at atmospheric pressure. Microsyst. Technol. 2005, 11, 111–116. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, S.; Wang, C.; Yang, B. Structure-decoupled dual-mass MEMS gyroscope with self-adaptive closed-loop detection. Nano/Micro Engineered and Molecular Systems (NEMS). In Proceedings of the IEEE International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Xiamen, China, 20–23 January 2010; pp. 624–627. [Google Scholar]
- Yang, B.; Wang, X.; Deng, Y.; Hu, D. Mechanical Coupling Error Suppression Technology for an Improved Decoupled Dual-Mass Micro-Gyroscope. Sensors 2016, 16, 503. [Google Scholar] [CrossRef] [PubMed]
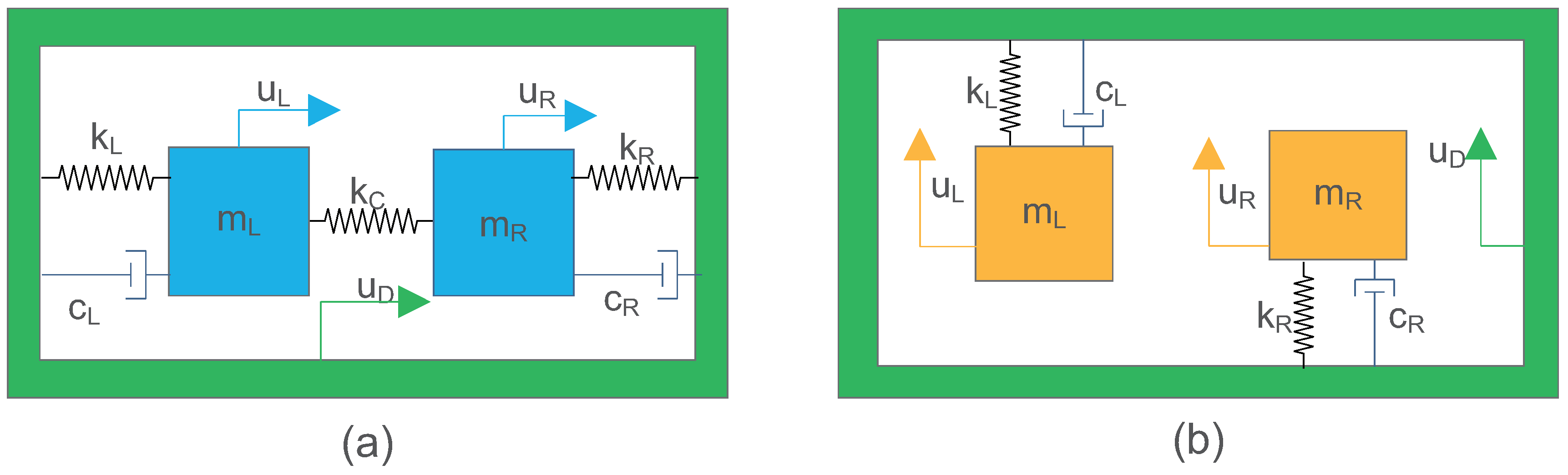
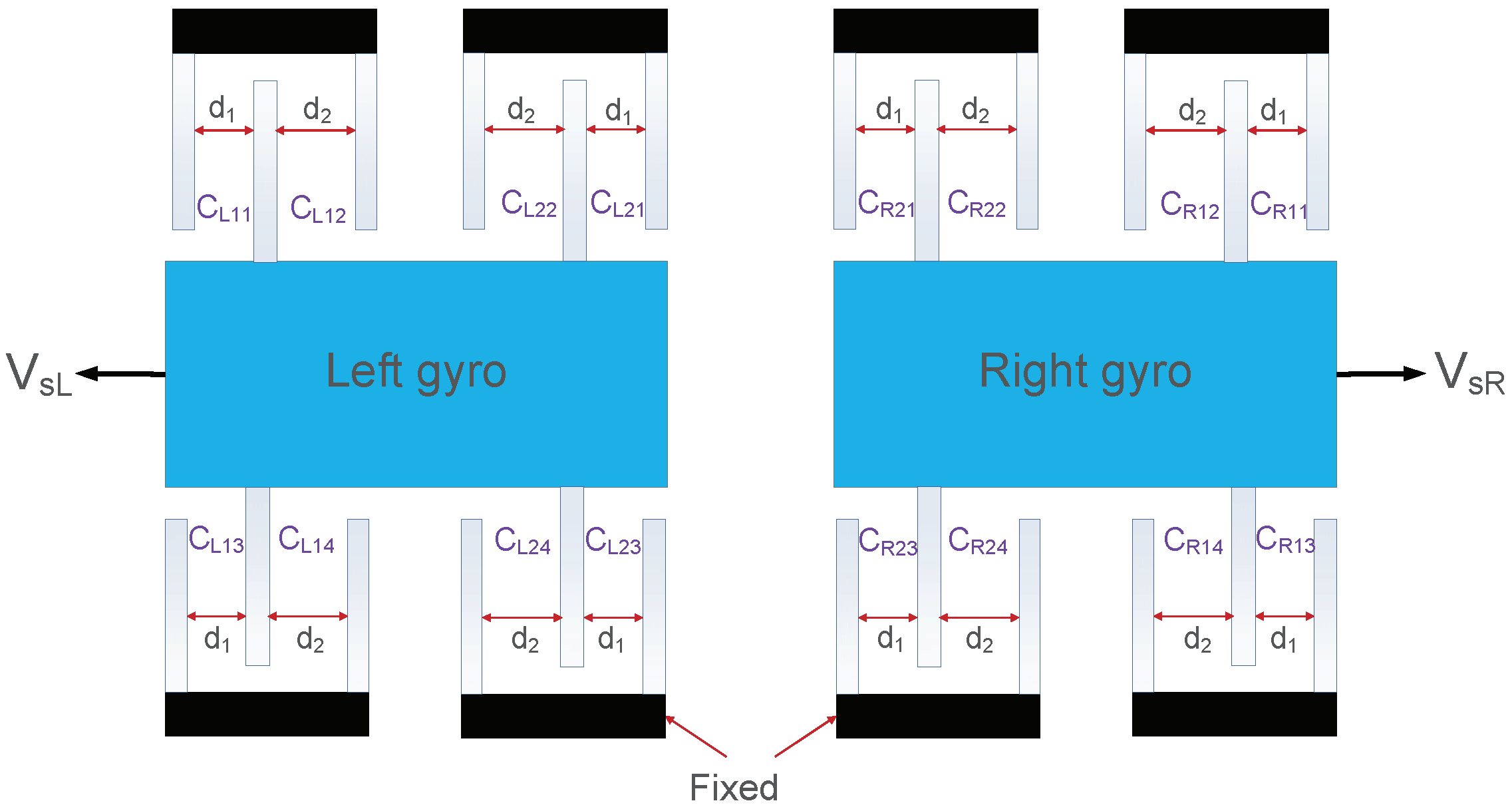

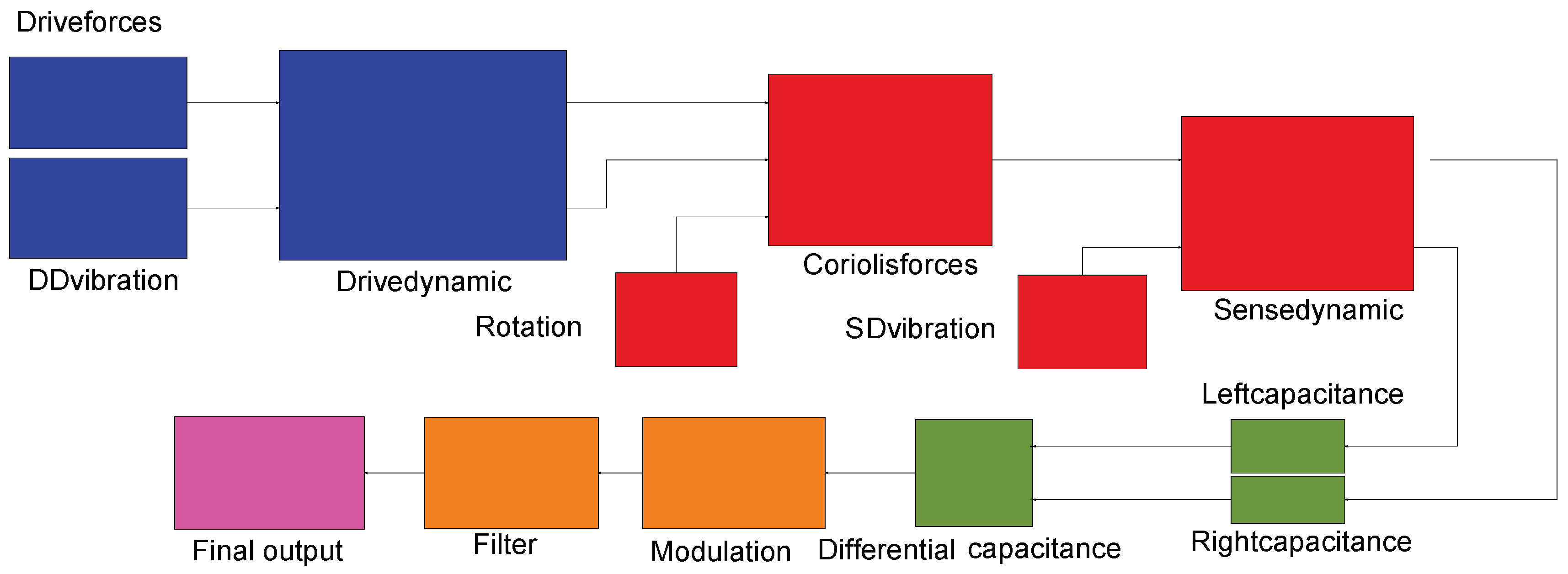

| Force-related | |
| Operating force (driving or Coriolis force) of the left/right gyro of a TFG | |
| External vibration acceleration | |
| Coriolis acceleration amplitude: response of TFG to rotation in normal direction | |
| Driving force amplitude | |
| Amplitude of and in ideal TFG/Amplitude of | |
| Operating angular frequency | |
| Vibration angular frequency | |
| First/second resonant angular frequency of 2-DOFs model | |
| Phase of the external vibration acceleration | |
| Displacement-related | |
| Total absolute displacement of the left/right gyro of a TFG | |
| Total displacement of the left/right gyro of a TFG relative to the device | |
| Total absolute displacement of the device | |
| Displacement caused by operating force / external vibration | |
| v | |
| Error/ideal displacements difference | |
| TFG structure-related | |
| Mass of left gyro/right gyro/left or right gyro of ideal TFG | |
| Stiffness of left gyro mass/right gyro mass/left or right gyro mass of ideal TFG | |
| Coupling stiffness between left and right gyro mass | |
| Damping of left gyro mass/right gyro mass/left or right gyro mass of ideal TFG | |
| Stiffness/mass/damping imbalance ratio (IR)/ | |
| b | Coupling stiffness ratio (CR) |
| Capacitance-related | |
| Total capacitance value of the left/right gyro | |
| Value of and of ideal TFG not in operation | |
| Sense capacitance overlapping area | |
| Initial sense capacitance gaps | |
| , | Capacitance value of each capacitor of left gyro shown in Figure 2 |
| , | Capacitance value of each capacitor of right gyro shown in Figure 2 |
| Given by / | |
| Given by / | |
| Differential capacitive readouts of the left/right gyro, given by / | |
| Final capacitance output of a TFG, given by | |
| Final capacitance output caused by external vibration/rotation | |
| Permittivity | |
| Other subscripts | |
| Subscripts indicating drive/sense mode or direction | |
| Subscripts indicating stiffness/mass/damping-related | |
| First/second resonant frequency-related displacement or coefficient | |
| Calculation-related | |
| In-phase/anti-phase modal factor of coupled gyros system with stiffness imbalance | |
| In-phase/anti-phase modal factor of coupled gyros system with mass imbalance | |
| Force ratio given by or | |
| Error displacements difference ratio, given by , with stiffness/mass/damping imbalance |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Resonant frequency | 10 kHz | Q-factor | 50 |
| Drive mass | 2 g | Sense mass | 0.8 g |
| Driving force amplitude | 0.2 N | Drive damping coefficient | Ns/m |
| Sense damping coefficient | Ns/m | Drive-mode siffness | 3.95 N/m |
| Sense-mode stiffness | 2.26 N/m | Sense capacitance overlapping area | m |
| Initial total sense capacitance | F | Sense comb number | 80 |
| Sense capacitance gaps | 1, 2 m | Low-pass filter cut-off frequency | 100 Hz |
| TFG Type | Simulated Output of TFGs (∘/s) | |||||
|---|---|---|---|---|---|---|
| DSIM | DMIM | DDIM | SSIM | SMIM | SDIM | |
| UU-Type | 57.13 | 56.55 | 96.28 | 56.70 | 57.55 | 95.68 |
| UC-Type | 103.95 | 98.73 | 102.27 | 102.98 | 95.99 | 101.48 |
| CU-Type | 105.06 | 93.36 | 102.44 | 56.70 | 57.48 | 95.69 |
| CC-Type | 101.02 | 103.01 | 102.42 | 102.98 | 95.98 | 101.82 |
| TFG Type | Simulated Output of TFGs (∘/s) | |||||
|---|---|---|---|---|---|---|
| DSIM | DMIM | DDIM | SSIM | SMIM | SDIM | |
| UU-Type | 106.01 | 104.09 | 104.02 | −54.56 | −50.44 | 112.04 |
| UC-Type | 168.82 | 156.94 | 107.07 | 141.12 | 68.29 | 102.86 |
| CU-Type | 106.44 | 92.92 | 104.49 | −54.46 | −50.44 | 112.04 |
| CC-Type | 102.41 | 107.24 | 102.58 | 141.12 | 68.29 | 102.86 |
| CR | In-Phase Sense Axis Resonant Frequency (Hz) | |||||
|---|---|---|---|---|---|---|
| SIR | 0.2 | 0.5 | 0.8 | 1.1 | 1.4 | |
| 1.05 | 8556.5 | 7158.9 | 6278.8 | 5659.6 | 5193.6 | |
| 1 | 8451.5 | 7071.1 | 6201.7 | 5590.2 | 5129.9 | |
| 0.95 | 8345.2 | 6982.1 | 6123.7 | 5519.9 | 5065.4 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Dong, L.; Zhao, W.-S.; Yan, H.; Teh, K.S.; Wang, G. Vibration-Induced Errors in MEMS Tuning Fork Gyroscopes with Imbalance. Sensors 2018, 18, 1755. https://doi.org/10.3390/s18061755
Fang X, Dong L, Zhao W-S, Yan H, Teh KS, Wang G. Vibration-Induced Errors in MEMS Tuning Fork Gyroscopes with Imbalance. Sensors. 2018; 18(6):1755. https://doi.org/10.3390/s18061755
Chicago/Turabian StyleFang, Xiang, Linxi Dong, Wen-Sheng Zhao, Haixia Yan, Kwok Siong Teh, and Gaofeng Wang. 2018. "Vibration-Induced Errors in MEMS Tuning Fork Gyroscopes with Imbalance" Sensors 18, no. 6: 1755. https://doi.org/10.3390/s18061755
APA StyleFang, X., Dong, L., Zhao, W.-S., Yan, H., Teh, K. S., & Wang, G. (2018). Vibration-Induced Errors in MEMS Tuning Fork Gyroscopes with Imbalance. Sensors, 18(6), 1755. https://doi.org/10.3390/s18061755







