A Fiber Bragg Grating Based Torsional Vibration Sensor for Rotating Machinery
Abstract
1. Introduction
2. Sensor Principles and Model
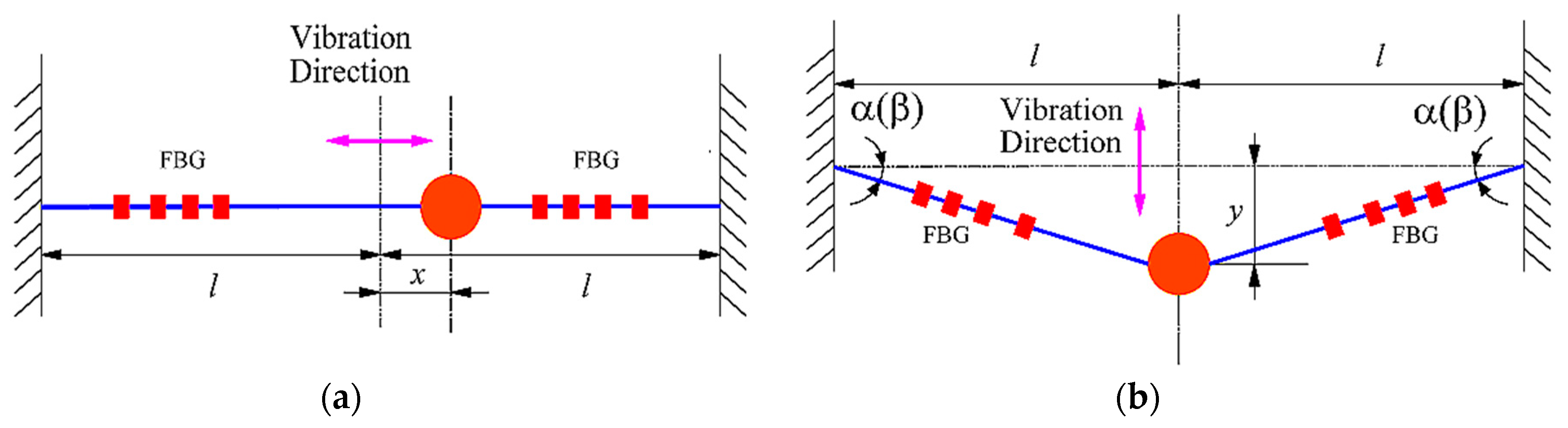
2.1. Principle of the Sensor
2.2. Mathmatical Model of the Sensor
3. Numerical Analysis and Structural Parameter Design
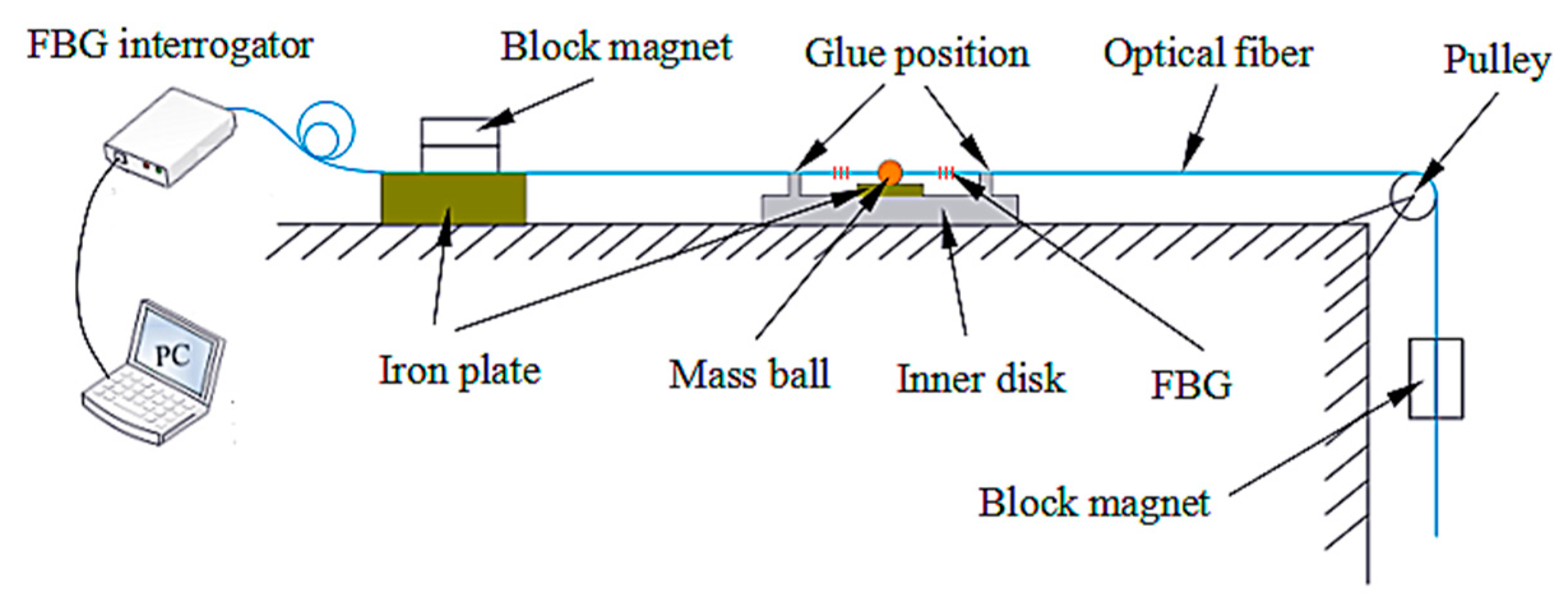
4. Experiments and Discussion
4.1. Amplitude-Frequency Property Experiments
4.1.1. Exciter Excitation Experiments
4.1.2. Hammering Excitation Experiments
4.2. Sensitivity Experiments
4.3. Anti-Interference Characteristic Experiments
4.4. Temperature Effects Experiments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ye, J.; Li, T.; Zeng, Z.L. Review of Research on Shafts’ Torsional Vibration Measurement. Ship Eng. 2014, 36, 6–9. [Google Scholar]
- Ji, T.G.; Ding, L.B.; Zhang, H. Wireless sensor data acquisition system of rotating component. J. Transducer Technol. 2003, 22, 46–48. [Google Scholar]
- Yang, Z.J.; Liao, M.F. Measurement of Torsional Vibration using Acceleration Sensors. Noise Vib. Control 2008, 5, 044. [Google Scholar]
- Liao, M.F.; Duan, S.G.; Li, Y.F. New Method to Measure the Torsional Vibration of Rotor. Acta Aeronaut. 2006, 27, 525–530. [Google Scholar]
- Lv, B.L.; Ouyang, H.J.; Li, W.Y.; Shuai, Z.; Wang, G. An indirect torsional vibration receptance measurement method for shaft structures. J. Sound Vib. 2016, 372, 11–30. [Google Scholar] [CrossRef]
- Jiang, Y.; Liao, M.; Wang, S. New measuring method for torsional vibration of aeroengine rotor. J. Vib. Meas. Diagn. 2013, 33, 410–415. [Google Scholar]
- He, Q.; Du, D. Study on intelligent measurement system of torsional vibration for turbine-generator shafts. Chin. J. Sci. Instrum. 2007, 28, 483–487. [Google Scholar]
- Zhao, W.S.; Xiong, S.B. Application of Hilbert Transform for Measurement of Torsional Vibration. J. Taiyuan Univ. Technol. 2006, 16, 1–189. [Google Scholar]
- Zhang, M.J.; Guo, D.A. Method of Torsional Vibration Measurement Based on Electromagnetic Induction. J. Exp. Mech. 2009, 24, 233–238. [Google Scholar]
- Xiang, L.; Yang, S.; Gan, C. Torsional vibration measurements on rotating shaft system using laser doppler vibrometer. Opt. Lasers Eng. 2012, 50, 1596–1601. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, B.; Dong, Q. Research on the torsional vibration measurement based on laser doppler technique. Acta Opt. Sin. 2006, 26, 389–392. [Google Scholar]
- Liu, T.Y.; Berwick, M.; Jackson, D.A. Novel fiber-optic torsional vibrometers. Rev. Sci. Instrum. 1992, 63, 2164–2169. [Google Scholar] [CrossRef]
- Miles, T.J.; Lucas, M.; Halliwell, N.A.; Rothberg, S. Torsional And Bending Vibration Measurement On Rotors Using Laser Technology. J. Sound Vib. 1999, 226, 441–467. [Google Scholar] [CrossRef]
- Shi, X.J.; Shao, J.P.; Si, J.S.; Li, B.N. Experiment and simulation of rotor’s torsional vibration based on sensorless detection technology. In Proceedings of the IEEE International Conference on Automation and Logistics, Qingdao, China, 1–3 September 2008; pp. 2673–2678. [Google Scholar]
- Sheng, H.J.; Tsai, P.T.; Lee, W.Y.; Lin, G.R.; Sun, H.T. Random rotary position sensor based on fiber Bragg gratings. IEEE Sens. J. 2012, 12, 1436–1441. [Google Scholar] [CrossRef]
- Sheng, H.J.; Lin, G.R.; Tsai, P.T.; Yang, C.A.; Kuo, M.H.; Sun, H.T.; Fu, M.Y.; Liu, M.F. Random-rotational angle sensor based on fiber Bragg gratings. In Proceedings of the 17th Opto-Electronics and Communications Conference, Busan, Korea, 2–6 July 2012; pp. 192–193. [Google Scholar]
- Yu, H.; Yang, X.; Tong, Z.; Cao, Y.; Zhang, A. Temperature independent rotational angle sensor based on fiber Bragg grating. IEEE Sens. J. 2011, 11, 1233–1235. [Google Scholar] [CrossRef]
- Kruger, L.; Swart, P.L.; Chtcherbakov, A.A.; van Wyk, A.J. Non-contact torsion sensor using fibre Bragg gratings. Meas. Sci. Technol. 2004, 15, 1448. [Google Scholar] [CrossRef]
- Li, T.L.; Shi, C.Y.; Tan, Y.G.; Zhong, Z.D. Fiber Bragg Grating Sensing-Based Online Torque Detection on Coupled Bending and Torsional Vibration of Rotating Shaft. IEEE Sens. J. 2007, 17, 1999–2007. [Google Scholar] [CrossRef]
- Hill, K.O.; Meltz, G. Fiber bragg grating technology fundamentals and overview. J. Light. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]














| Number of FBGs | #1FBG | #2FBG | #3FBG | #4FBG |
|---|---|---|---|---|
| Initial center wavelength (nm) | 1539.688 | 1542.635 | 1549.608 | 1551.632 |
| Wavelength after prestress (nm) | 1541.682 | 1544.638 | 1551.639 | 1553.665 |
| Wavelength shift after prestress (nm) | 1.994 | 2.003 | 2.031 | 2.033 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wei, L.; Li, R.; Liu, Q.; Yu, L. A Fiber Bragg Grating Based Torsional Vibration Sensor for Rotating Machinery. Sensors 2018, 18, 2669. https://doi.org/10.3390/s18082669
Wang J, Wei L, Li R, Liu Q, Yu L. A Fiber Bragg Grating Based Torsional Vibration Sensor for Rotating Machinery. Sensors. 2018; 18(8):2669. https://doi.org/10.3390/s18082669
Chicago/Turabian StyleWang, Jingjing, Li Wei, Ruiya Li, Qin Liu, and Lingling Yu. 2018. "A Fiber Bragg Grating Based Torsional Vibration Sensor for Rotating Machinery" Sensors 18, no. 8: 2669. https://doi.org/10.3390/s18082669
APA StyleWang, J., Wei, L., Li, R., Liu, Q., & Yu, L. (2018). A Fiber Bragg Grating Based Torsional Vibration Sensor for Rotating Machinery. Sensors, 18(8), 2669. https://doi.org/10.3390/s18082669






