A Submillimeter-Level Relative Navigation Technology for Spacecraft Formation Flying in Highly Elliptical Orbit
Abstract
:1. Introduction
- In addition to optical metrology, (a) MWR can provide precise ranging results as backup equipment, during the science observation period around apogee; and (b) can avoid sunlight disturbance which occurs in the optical spectrum, for specific space science missions such as solar corona observation.
- Microwave ranging relies on a carefully designed transceiver antenna with relatively wider main lobe angle of a few degrees, which greatly reduces the burden of the high-precision pointing mechanism used for optical metrology. At the same time, microwave ranging can operate in pseudo-code mode or carrier mode for coarse/precise ranging if necessary, as required by mission control, providing flexible solutions to the GNC system.
- We have inherited a great deal of microwave ranging technology from existing space experience. MWR has been developed and tested previously, and successfully verified in one LEO formation mission [15].
- As an essential supplement to the MWR system, BeiDou III B1C/B2a dual-frequency new-generation navigation signal receive and process technology can be fully tested and verified in HEO formation missions. The B1C/B2a dual-frequency receiver on-board can provide highly precise time synchronization solutions with nanosecond precision, which serves as a time-scale benchmark between formation spacecrafts. Moreover, the receiver can provide precise stand-alone navigation solutions while using a precise orbit determination algorithm.
- Microwave can also be used for real-time data transmission between spacecraft for original scientific data exchange, differential GPS measurement data transmission for relative navigation, etc.
2. Submillimeter-Level Microwave Ranging
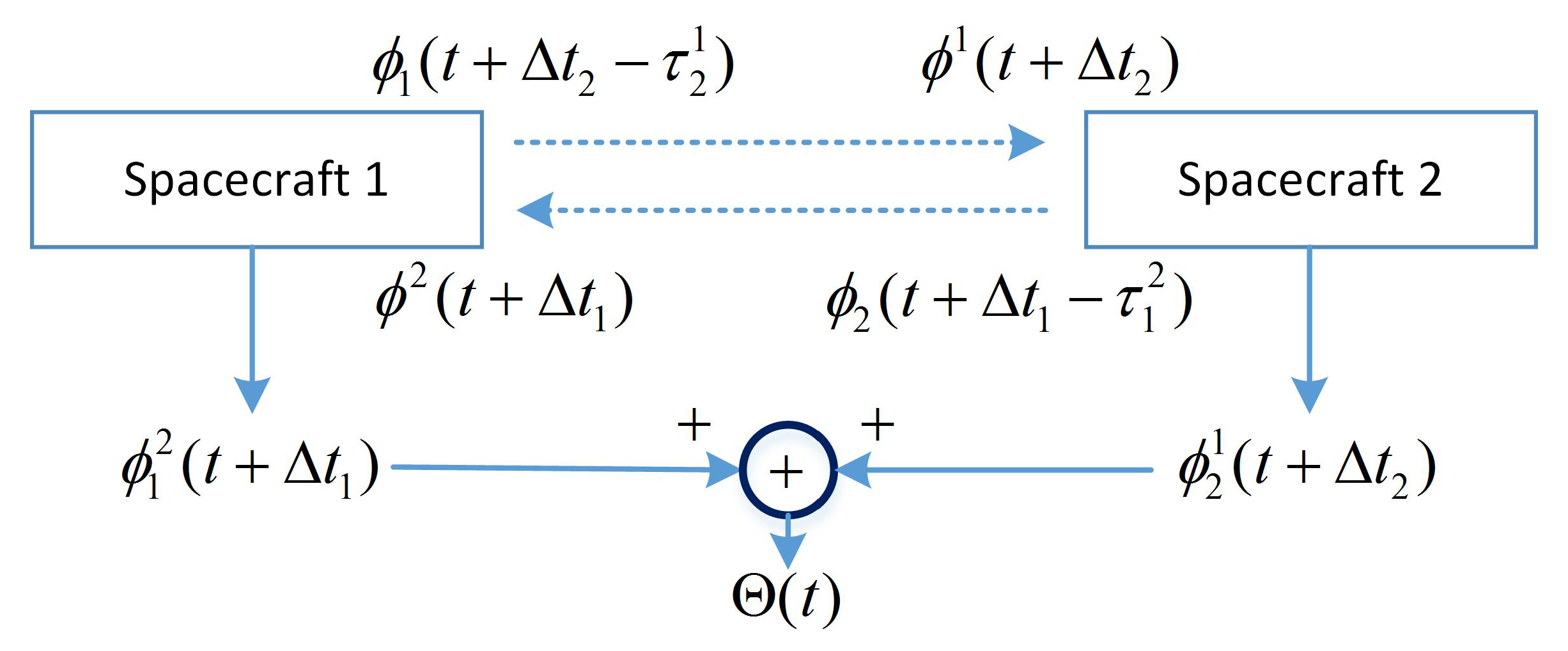
2.1. MWR Measurement Modeling
- Correction of ionospheric influence by dual-frequency measurement during space flight around perigee;
- Synchronous bidirectional ranging comparison that cancels the long-term instability of the oscillator source; and,
- Carrier phase measurement by frequency difference to improve the accuracy.
2.2. Ranging Error Sources Analysis
- Carrier phase measurement error due to system noiseThe carrier phase measurement error due to system noise can be given as ():where Hz, the noise bandwidth of the phase-locked loop (PLL); is the length of the carrier wave (K band m, Ka band m); s, the PLL pre-detection integration time; and is the carrier-to-noise ratio ( dB-Hz).With calculation, the measurement errors due to system noise are m, m.
- Carrier phase measurement error caused by phase noise of local oscillatorThe carrier phase measurement error (for the third-order tracking loop) introduced by the local oscillator’s Allan variance can be given by the following empirical formula:where Hz, the bandwidth of the PLL; s, the short-term stability length of the Allan variance; , the Allan variance; is the carrier frequency; K = 24.5 GHz; and Ka = 32.7 GHz.With calculation, the phase measurement errors due to local oscillator Allan variance are m for the K band and m for the Ka band.
- Phase measurement error due to dynamic stressDynamic stress error is closely related to the tracking loop order. For three-order PLL, the dynamic stress is given as:where is the line of sight (LOS) acceleration rate (m/s). For the PLL bandwidth Hz, the LOS acceleration rate is 10 m/s, and the dynamic error m.
- Summary of phase measurement errorThe total measurement error while using three-order PLL can be modeled as:K band: (m)Ka band: (m)
2.3. MWR Payload Development
2.3.1. Antenna Scheme Design
2.3.2. Frequency Reference Unit
2.3.3. Microwave Channel
2.3.4. Signal Processing Hardware Platform
3. Relative Dynamics for Spacecraft Formation
4. Mission Orbit and Relative Navigation Filter
4.1. Real Formation Mission Orbit
4.2. Relative Navigation Using Adaptive Kalman Filter
5. Test and Simulation
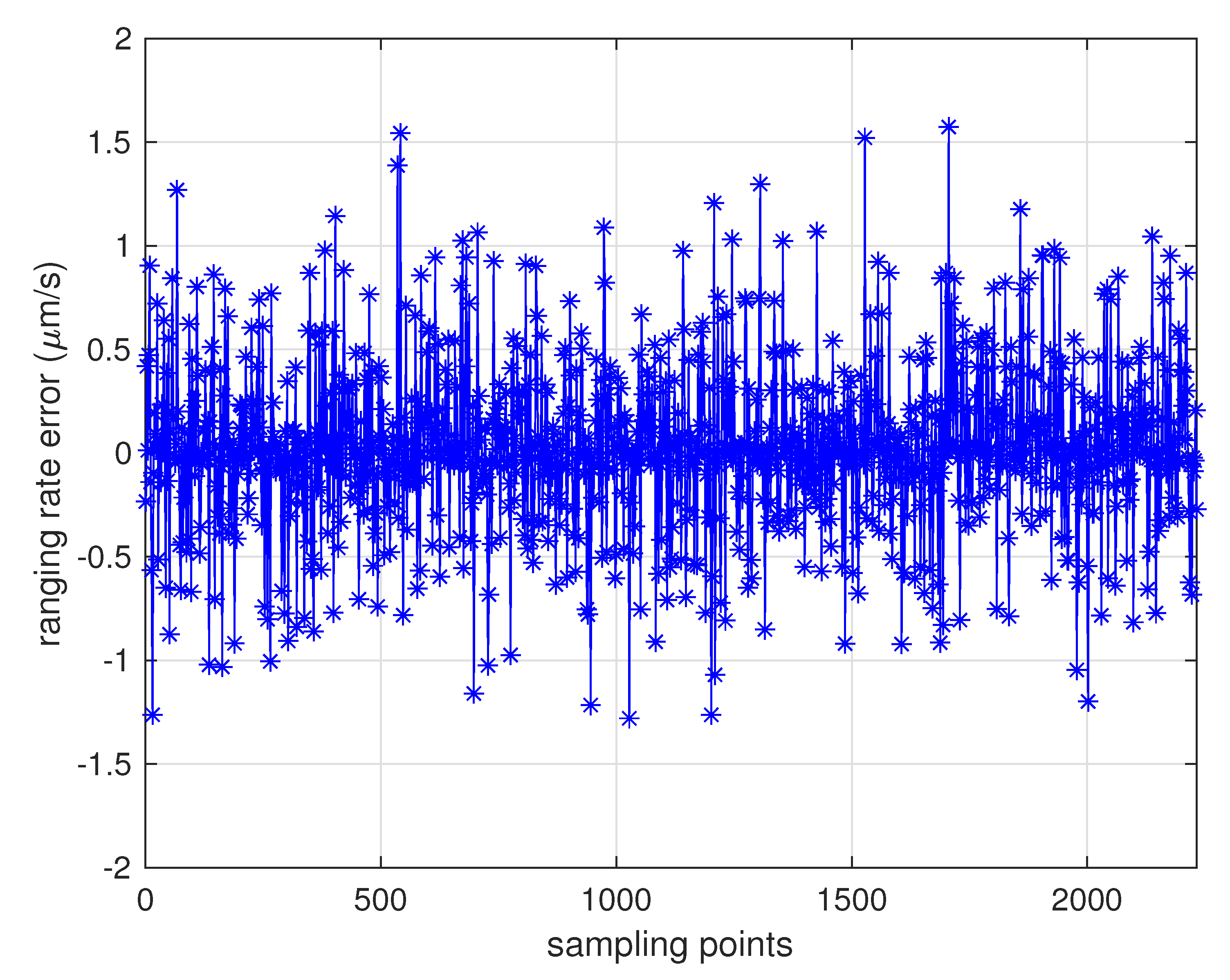
5.1. Assessment of MWR Ranging Accuracy
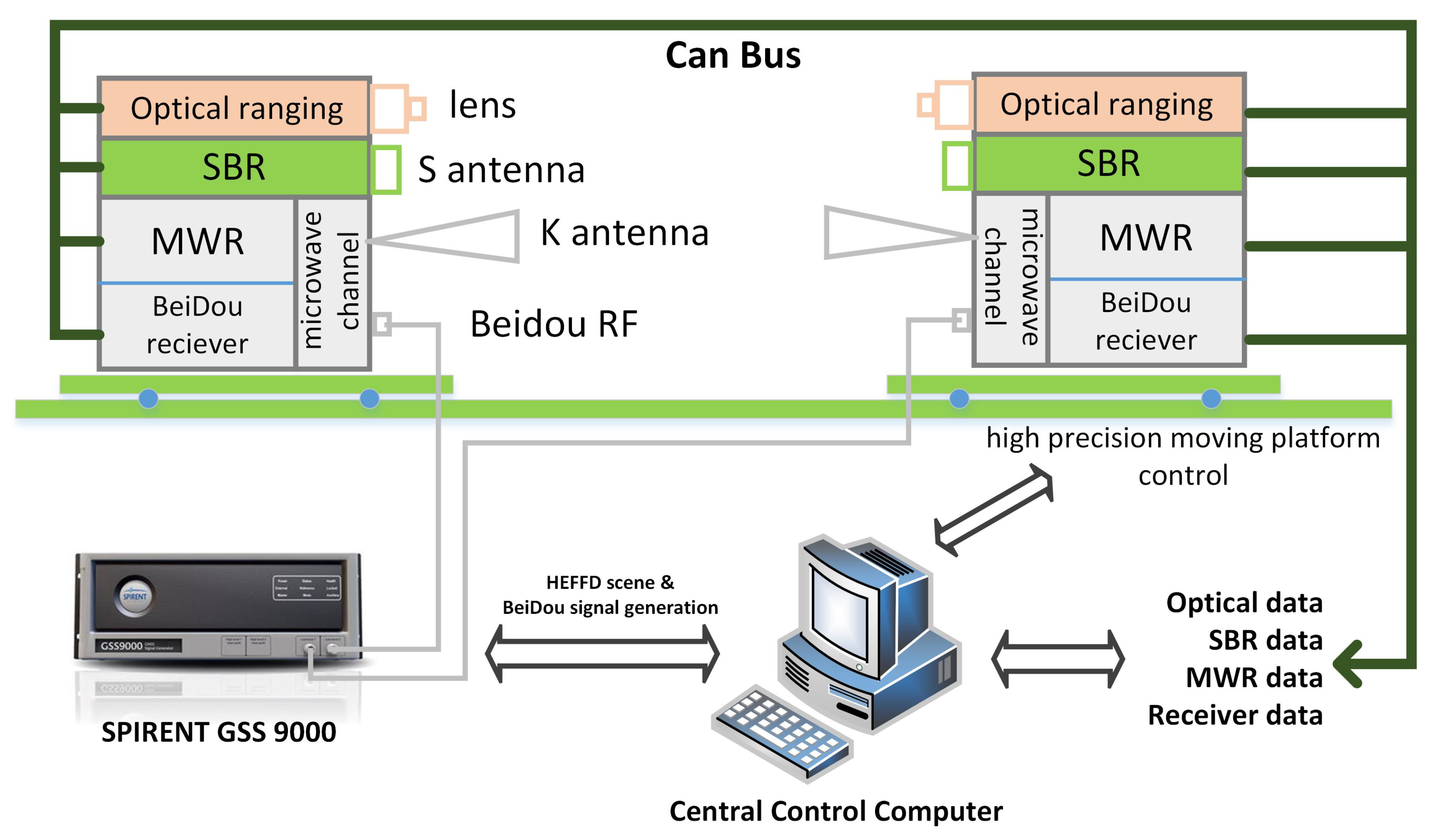
5.2. Hardware-in-the-Loop Simulation for SFF Relative Navigation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Busse, F.D. Precise Formation-State Estimation in Low Earth Orbit Using Carrier Differential GPS. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2003. [Google Scholar]
- Tapley, B.D. Flechtner, F. Bettadpur, S.V. Watkins, M.M. The Status and Future Prospect for GRACE after the First Decade. AGUFM 2013, 2013, G32A-01. [Google Scholar]
- Bryant, R.; Moran, M.S.; McElroy, S.A.; Holifield, C.; Thome, K.J.; Miura, T.; Biggar, S.F. Data continuity of Earth observing 1 (EO-1) Advanced Land I satellite image (ALI) and Landsat TM and ETM+. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1204–1214. [Google Scholar] [CrossRef]
- Congratulations, TanDEM-X - 10 years of 3D mapping from space. 2020. Available online: https://www.dlr.de/content/en/articles/news/2020/02/20200625_congratulations-tandem-x-ten-years-of-3d-mapping-from-space.html (accessed on 25 June 2020).
- Hawker, L.; Neal, J.; Bates, P. Accuracy assessment of the TanDEM-X 90 Digital Elevation Model for selected floodplain sites. Remote Sens. Environ. 2019, 232, 111319. [Google Scholar] [CrossRef]
- Persson, S.; Veldman, S.; Bodin, P. PRISMA—A formation flying project in implementation phase. Acta Astronaut. 2009, 65, 1360–1374. [Google Scholar] [CrossRef]
- Winternitz, L.B.; Bamford, W.A.; Price, S.R.; Carpenter, J.R.; Long, A.C.; Farahmand, M. Global positioning system navigation above 76,000 km for NASA’s magnetospheric multiscale mission. Navig. J. Inst. Navig. 2017, 64, 289–300. [Google Scholar] [CrossRef] [Green Version]
- Escoubet, C.P.; Fehringer, M.; Goldstein, M. Introduction the cluster mission. Ann. Geophys. 2001, 19, 1197–1200. [Google Scholar] [CrossRef] [Green Version]
- Bavdaz, M.; Peacock, A.; Parmar, A.; Beijersbergen, M. XEUS mission and instruments. In Proceedings of the International Symposium on Optical Science and Technology, San Diego, CA, USA, 29 July–3 August 2001. [Google Scholar] [CrossRef] [Green Version]
- XEUS Formation Flight. Available online: https://sci.esa.int/web/sci-ft/-/38535-xeus-formation-flight (accessed on 1 September 2019).
- Fridlund, C.V.M. The Darwin mission. Adv. Space Res. 2004, 34, 613–617. [Google Scholar] [CrossRef]
- Kaltenegger, L.; Fridlund, M. The Darwin mission: Search for extra-solar planets. Adv. Space Res. 2005, 3, 1114–1122. [Google Scholar] [CrossRef]
- Etienne, R.; Andres, A.; Alessandro, B.; Joseph, B.; Cristina, B.; Steve, B.; Gerardo, C.; Ileana, C.; Vladimir, D.; Radoslav, D.; et al. Design Status of ASPIICS, an Externally Occulted Coronagraph for PROBA-3. In Proceedings of the Solar Physics and Space Weather Instrumentation VI, San Diego, CA, USA, 9–13 August 2015; Volume 9604, p. 15. [Google Scholar] [CrossRef]
- Peters, T.V.; Branco, J.; Escorial, D.; Castellani, L.T.; Cropp, A. Mission Analysis for PROBA-3 Nominal Operations. Acta Astronaut. 2014, 102, 296–310. [Google Scholar] [CrossRef]
- Shao, F. Long March 2C rocket “one rocket three satellites” launched successfully. China Equip. Eng. 2017, 20, 4. [Google Scholar]
- Kim, J.; Lee, S.W. Flight performance analysis of GRACE K-band ranging instrument with simulation data. Acta Astronaut. 2009, 65, 1571–1581. [Google Scholar] [CrossRef]
- Clohessy, W.H.; Wiltshire, R. Terminal guidance system for satellite rendezvous. J. Aerosp. Sci. 1960, 27, 653–658. [Google Scholar]
- Schaub, H.; Junkins, J.L. Analytical Mechanics of Aerospace Systems; American Institute of Aeronautics and Astronautics, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Eggleston, J.M.; Dunning, R.S. Analytical evaluation of a method of midcourse guidance for rendezvous with Earth satellites. In NASA TD-883; NASA Technical Reports Server: Washington, DC, USA, June 1961. [Google Scholar]
- Karlgaard, C.D. Robust rendezvous navigation in elliptical orbit. J. Guid. Control Dyn. 2006, 29, 495–499. [Google Scholar] [CrossRef]
- Ardaens, J.S.; D’Amico, S.; Cropp, A. GPS-based relative navigation for the Proba-3 formation flying mission. Acta Astronaut. 2013, 91, 341–355. [Google Scholar] [CrossRef]
- Loreggia, D.; Fineschi, S.; Capobianco, G.; Bemporad, A.; Casti, M.; Landini, F.; Nicolini, G.; Zangrilli, L.; Massone, G.; Noce, V.; et al. PROBA-3 mission and the Shadow Position Sensors: Metrology measurement concept and budget. Adv. Space Res. 2020, in press. [Google Scholar] [CrossRef]
- Whitaker, H.P. An adaptive system for control of the dynamics performance of aircraft and spacecraft. Inst. Aeronaut. Sci. Pap. 1959, 59–100. [Google Scholar]
- Whitaker, H.P.; Oshurn, P.V.; Kezer, A. New Developments in the Design of Model Reference Adaptive Control Systems; Institute of Aeronautical Sciences: Reston, VA, USA, 1961; pp. 61–69. [Google Scholar]
- Wang, X. Improved adaptive filter with application to relative navigation. GPS Solut 2011, 15, 121–128. [Google Scholar] [CrossRef]










| Items | Model |
|---|---|
| GA—the geopotential effect of the Earth | 20th order and degree |
| GA—Sun and Moon gravities | high-precision DE405/LE405 planetary ephemerides model |
| GA—solid Earth tides | IERS Conventions 1996 |
| GA—ocean tides | Center for Space Research 3.0 model |
| NGA—the atmospheric drag | NRLMSISE-00 empirical model |
| NGA—the solar radiation pressure | IERS Standards 1992 |
| Parameter | Value | Unit |
|---|---|---|
| Apogee altitude | 60,530 | km |
| Perigee altitude | 600 | km |
| Inclination | 59 | deg |
| Argument of perigee | 42 | deg |
| RAAN | 25 | deg |
| True anomaly | 0 | deg |
| Items | Symbol | Unit | K Band | Ka Band |
|---|---|---|---|---|
| Frequency | f | GHz | 24.517002 | 32.692746 |
| Transmitting power | W | 10 | 10 | |
| Transmitting power | dBW | 10 | 10 | |
| Transmitting feed loss | dB | 0.5 | 0.5 | |
| Transmit antenna gain | dBi | 16 | 16 | |
| Effective isotropic radiated power | dBW | 25.5 | 25.5 | |
| Space distance | d | km | 100 | 100 |
| Flux density | dBW/m | −85.49209857 | −85.49209857 | |
| Space propagationloss | dB | −160.2311193 | −162.7308 | |
| Power level of receiving antenna | dBW | −134.7311193 | −137.2308 | |
| Receiving antenna gain | dBi | 15 | 15 | |
| Polarization mismatch loss | dB | 1 | 1 | |
| Antenna gain of receiving system port | dBi | 14 | 14 | |
| Receiving feed loss | dB | 0.5 | 0.5 | |
| Power level of receiver input port | dBm | −91.23111929 | −93.73080004 | |
| Noise temperature of receiving antenna | K | 150 | 150 | |
| Temperature of receiving feeder | K | 290 | 290 | |
| Receiver noise factor | dB | 10 | 10 | |
| Receiver noise temperature | K | 228 | 228 | |
| Receiver noise temperature | dBK | 23.57934847 | 23.57934847 | |
| ENT of Receiver port | K | 393.2248687 | 393.2248687 | |
| ENT of Receiver port | dBK | 25.94640976 | 25.94640976 | |
| G/T value of Receiver port | dB/K | −12.44640976 | −12.44640976 | |
| ENT at the receiver system port | K | 441.2055593 | 441.2055593 | |
| ENT at the receiver system port | dBK | 26.44640976 | 26.44640976 | |
| G/T value of receiver system port | dB/K | −12.44640976 | −12.44640976 | |
| Carrier-to-noise ratio | dB-Hz | 80.82247095 | 78.3227902 |
| Parameter | Unit | KF-BeiDou/SBR* | AF-BeiDou/SBR* | AF-MWR | ||||
|---|---|---|---|---|---|---|---|---|
| Perigee | Apogee | Perigee | Apogee | Perigee | Apogee | |||
| range | m | ME* | / | |||||
| RMS | / | 9.50 | ||||||
| range rate | m/s | ME | / | 8.5 | ||||
| RMS | 9.8 | / | 2.6 | |||||
| elevation angle | deg | ME | / | |||||
| RMS | / | |||||||
| elevation rate | deg/s | ME | / | |||||
| RMS | / | |||||||
| azimuth angle | deg | ME | / | |||||
| RMS | / | |||||||
| azimuth rate | deg/s | ME | / | |||||
| RMS | / | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Gong, D.; Jiang, Y.; Mo, Q.; Kang, Z.; Shen, Q.; Wu, S.; Wang, D. A Submillimeter-Level Relative Navigation Technology for Spacecraft Formation Flying in Highly Elliptical Orbit. Sensors 2020, 20, 6524. https://doi.org/10.3390/s20226524
Wang X, Gong D, Jiang Y, Mo Q, Kang Z, Shen Q, Wu S, Wang D. A Submillimeter-Level Relative Navigation Technology for Spacecraft Formation Flying in Highly Elliptical Orbit. Sensors. 2020; 20(22):6524. https://doi.org/10.3390/s20226524
Chicago/Turabian StyleWang, Xiaoliang, Deren Gong, Yifei Jiang, Qiankun Mo, Zeyu Kang, Qiang Shen, Shufan Wu, and Dengfeng Wang. 2020. "A Submillimeter-Level Relative Navigation Technology for Spacecraft Formation Flying in Highly Elliptical Orbit" Sensors 20, no. 22: 6524. https://doi.org/10.3390/s20226524






