Trajectory Identification for Moving Loads by Multicriterial Optimization
Abstract
:1. Introduction
- A large number of potential excitation points, that is, the degrees of freedom (DOFs) in which the excitation force can be applied and should be thus identified.
- A limited number of sensors that can be employed to measure the structural response to the unknown excitation and provide information for the identification process.
2. Moving Load and Nonparametric Structural Model
2.1. Moving Load
2.2. Measured and Modeled Response
3. Trajectory Identification
3.1. Measurement-Based Objective Function
3.2. Geometric Regularity of the Trajectory
3.3. Multicriterial Optimization and Pareto Front
4. Numerical Optimization
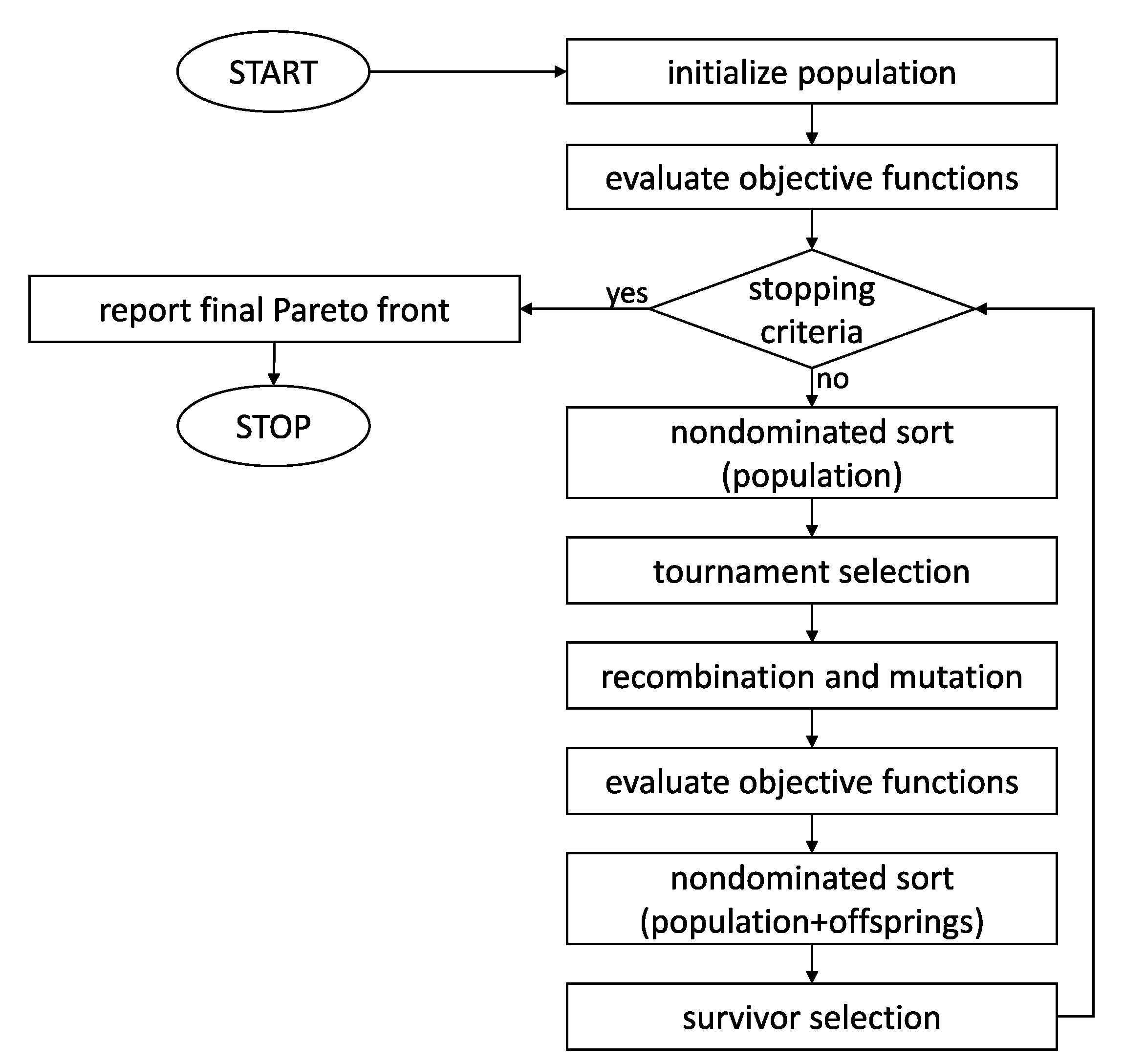
4.1. Optimization Algorithm
4.2. Trajectory Representation and Encoding
4.3. Genetic Operators and Initial Population
4.4. Objective Functions
5. Experimental Verification
5.1. Experimental Test Stand
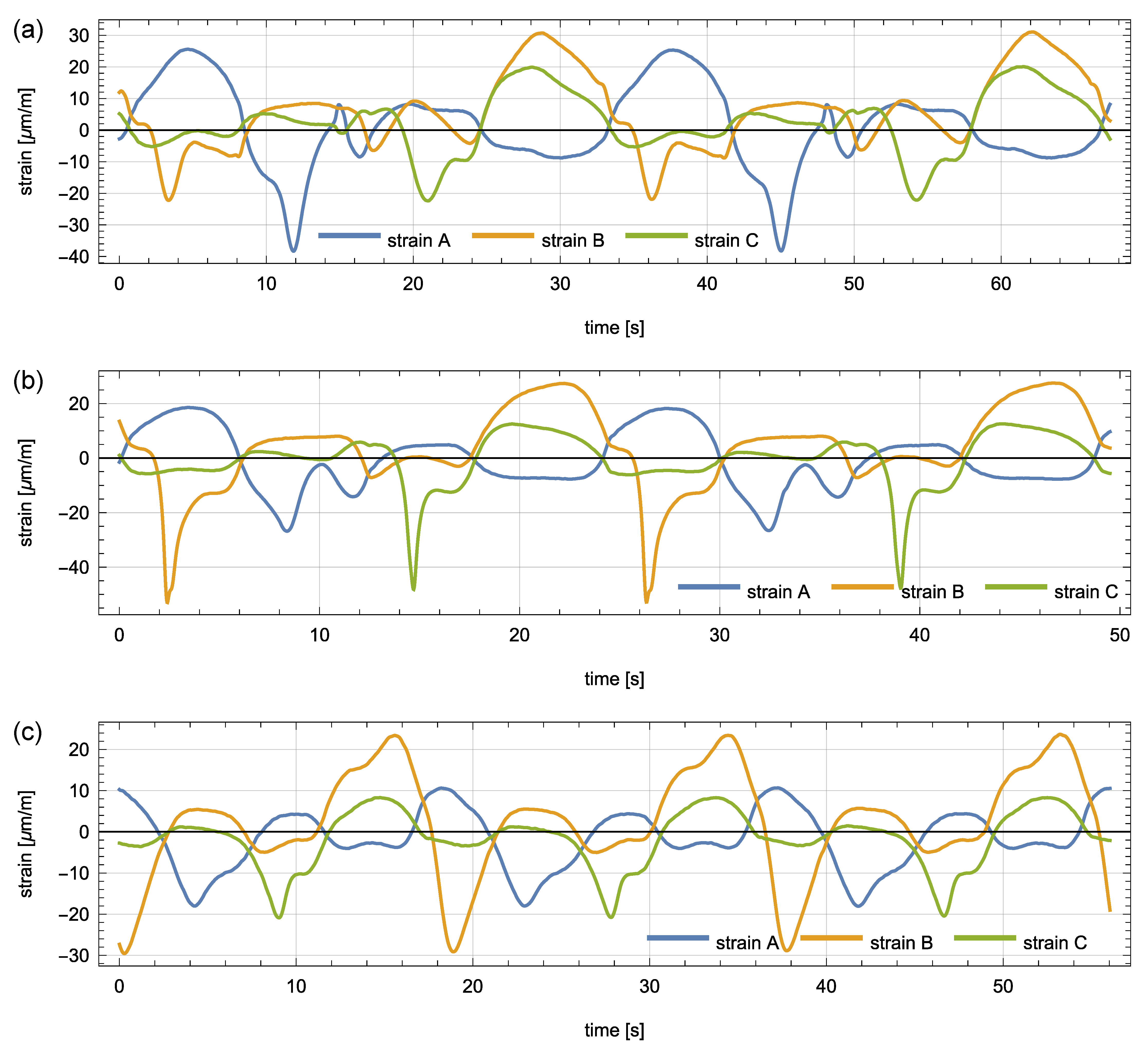
5.2. Responses to Test Trajectories and Nonparametric Model of the Plate
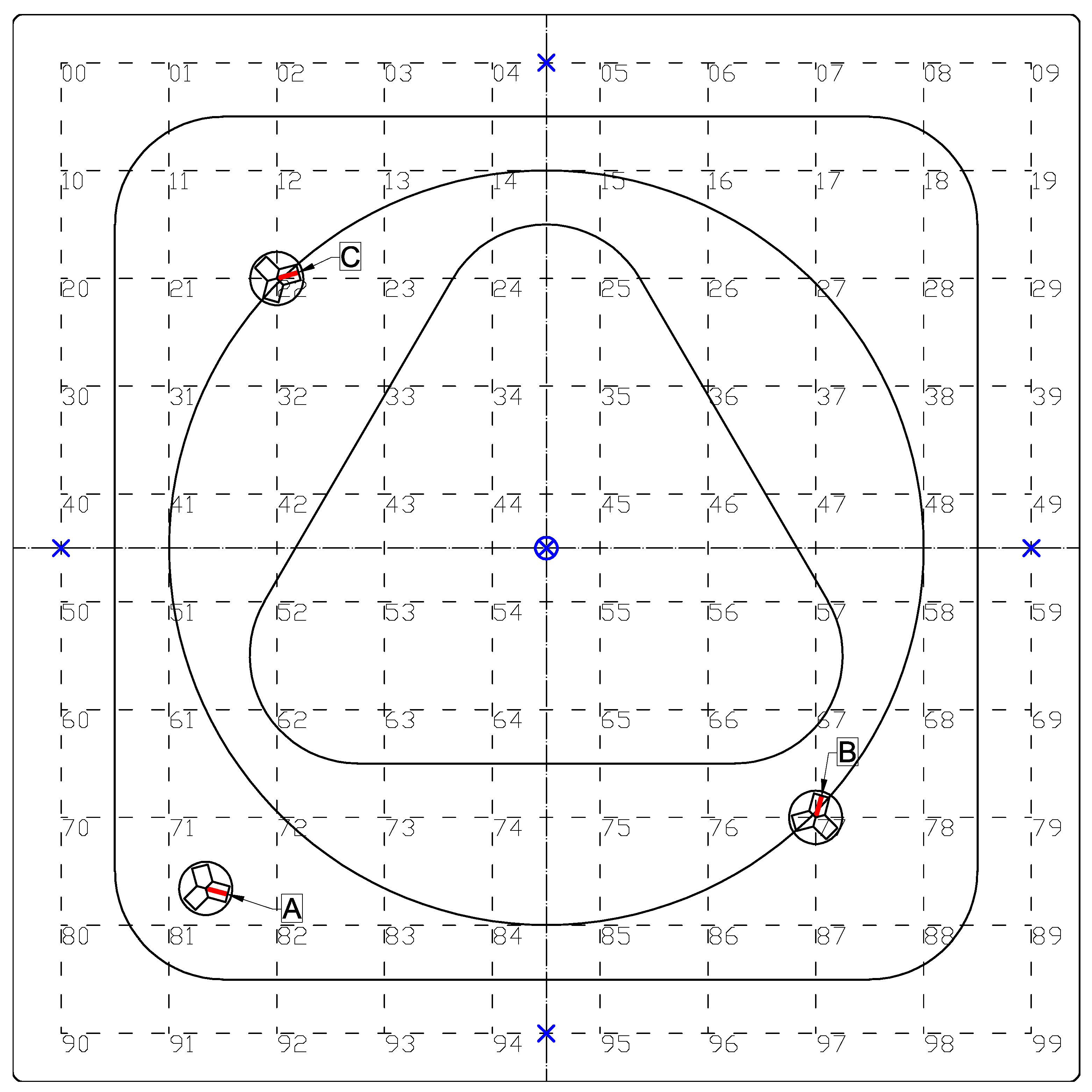
- The plate was discretized into a 10 × 10 point grid with 10 cm × 10 cm cells, as shown in Figure 3.
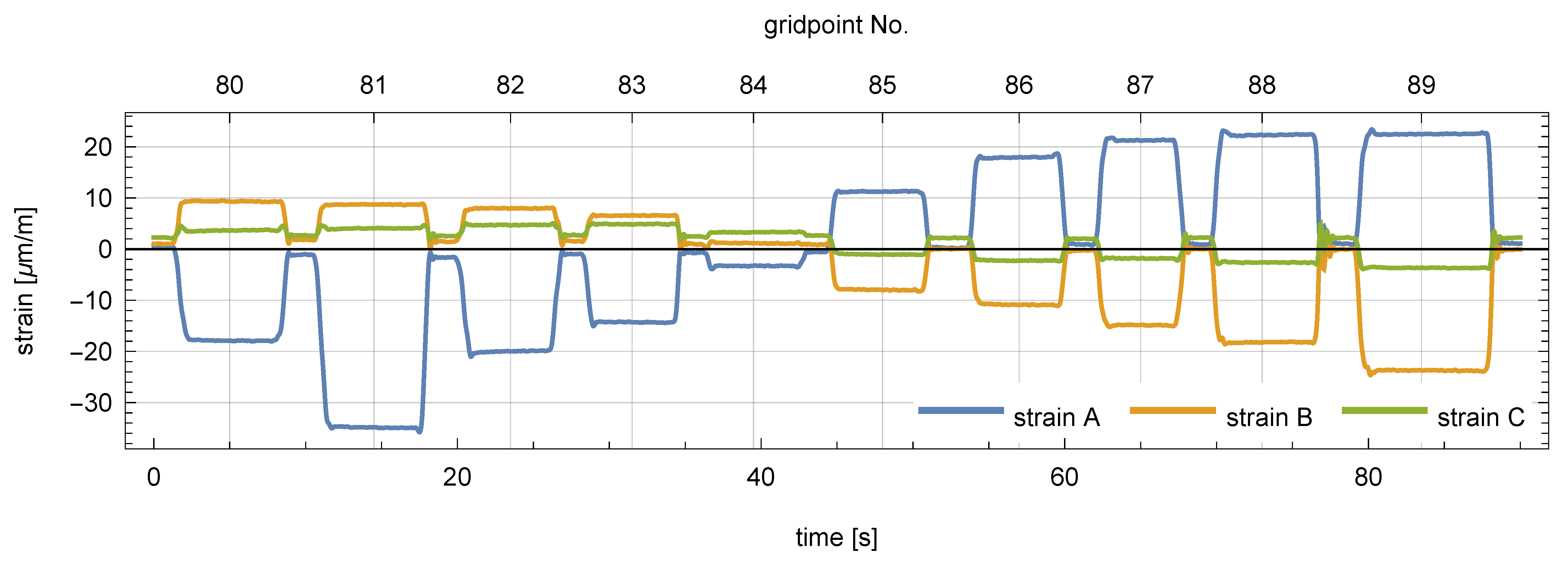
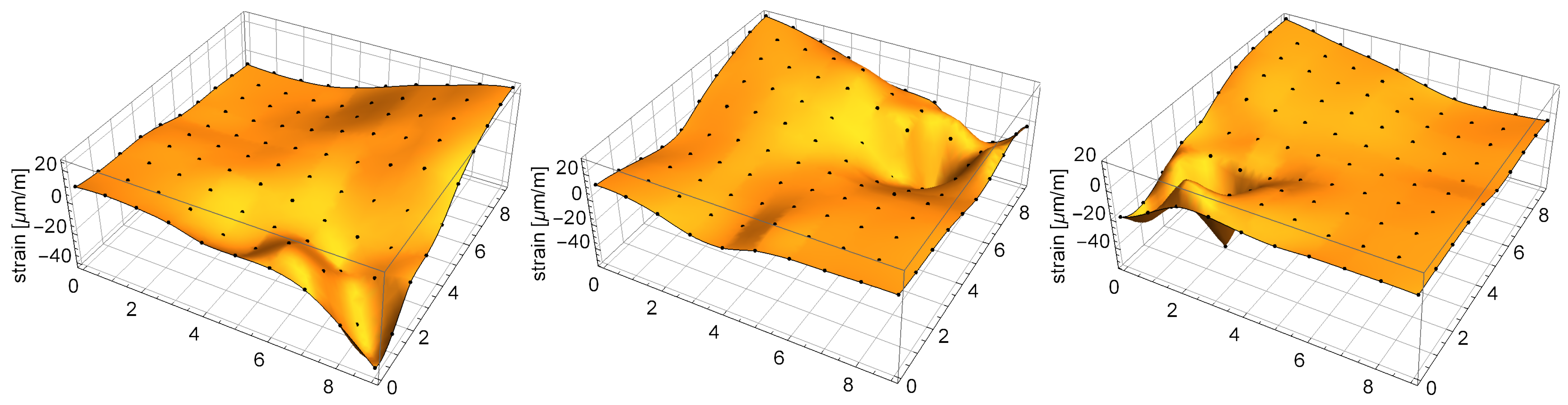
- The constant gravity load of a 0.265 kg mass was applied successively in all 100 points of the grid, and the responses of the sensors were recorded. A fragment of the measurement signal (load in points No. 80 to 89) is shown in Figure 5. A limited degree of nonlinearity can be observed in the responses of the sensors: a small drift of the readings in the unloaded state (bias drift) and a small relaxation-like behavior, which can be probably linked to the sensor–plate adhesive layer. Such effects increase the measurement error, and although they are undesirable in applications, they helped here to test the robustness of the proposed method.
- Finally, the response vectors corresponding to the 100 grid points were extracted and spline-interpolated in 2D to form the continuous response surfaces and the nonparametric model . The three interpolated response surfaces are shown in Figure 6.
5.3. The Trivial -Optimum Trajectories
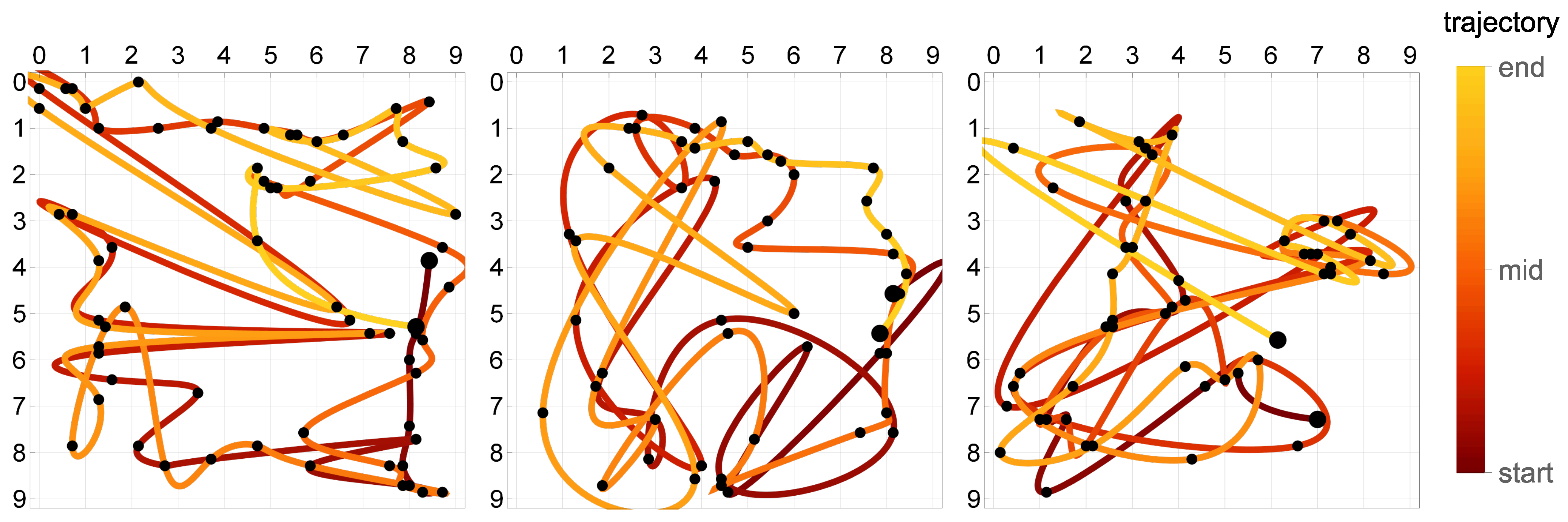
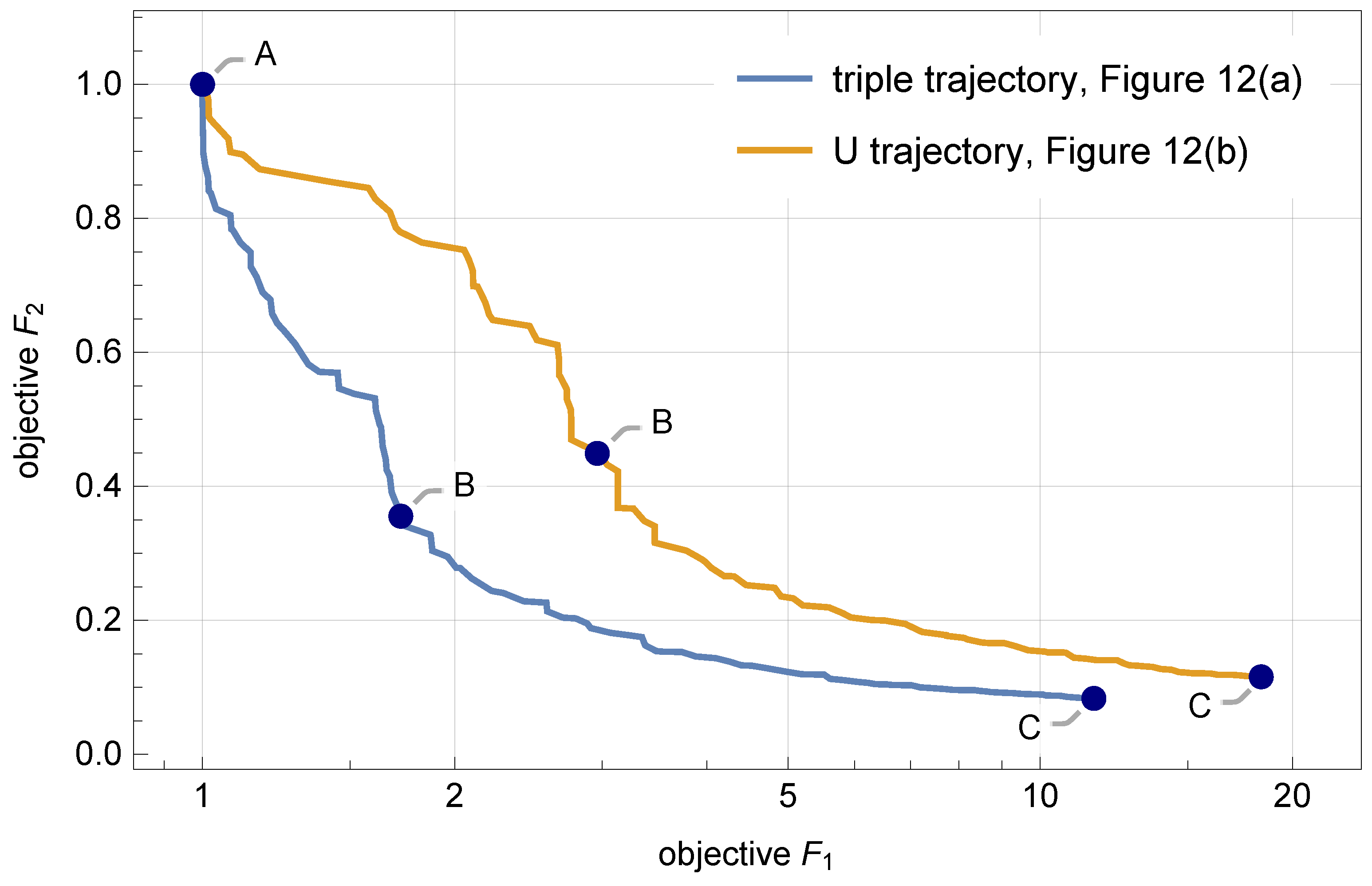
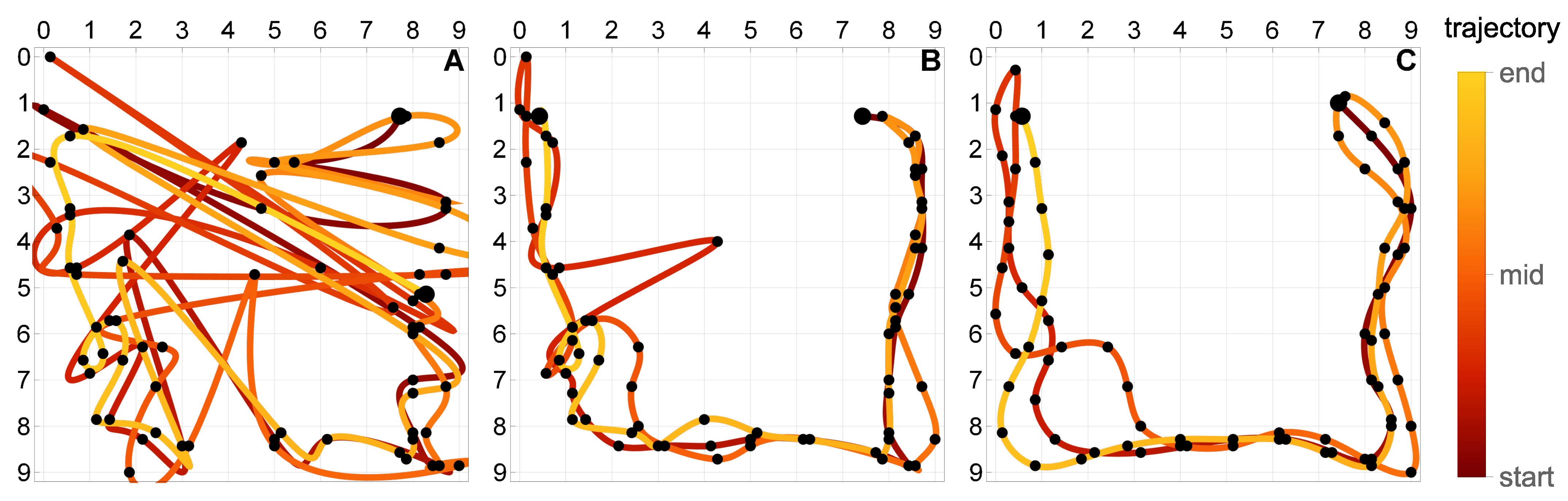
5.4. Multicriterial Identification of Test Trajectories
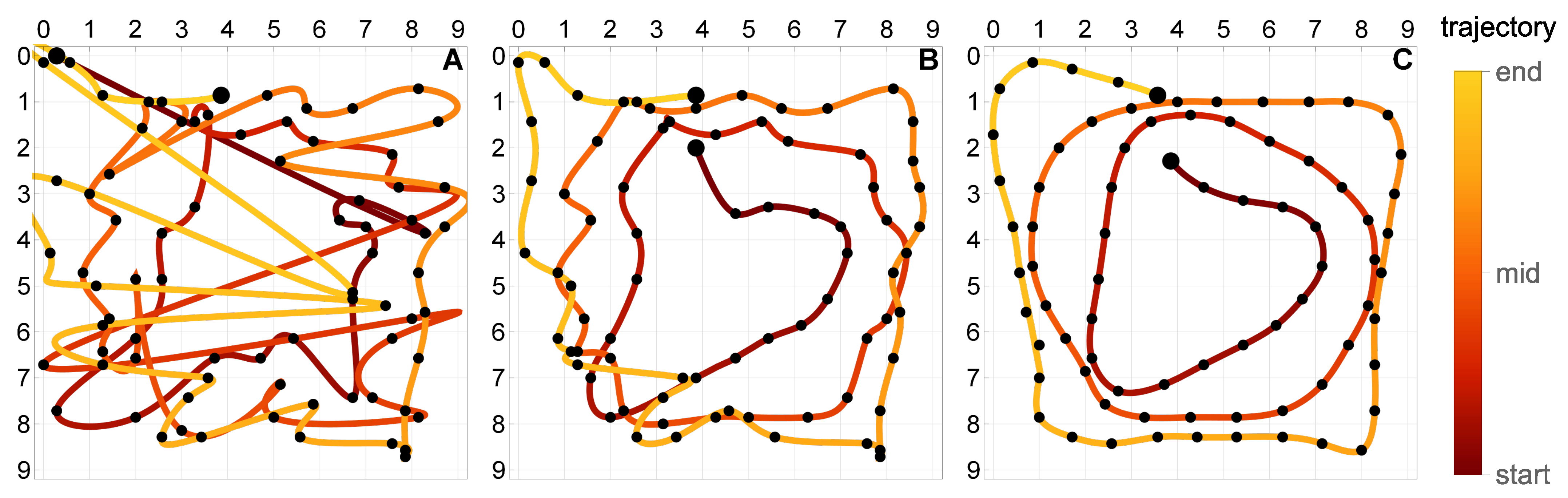
5.5. Compound Trajectories
- Figure 12a: the moving load starts at the top of the plate and follows clockwise the triangle, circle, and the square trajectory, each of them once. This trajectory has two small discontinuities at the top of the plate which occur when the load switches the basic trajectory.
- Figure 12b: the moving load starts at the upper right corner of the plate and follows a U-shaped trajectory, which is composed of three segments of the basic square trajectory. The path is followed three times, along the points w–x–y–z–y–x–w–x–y–z, with two sharp U-turns at the points w and z.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Farrar, C.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Brownjohn, J. Structural health monitoring of civil infrastructure. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2007, 365, 589–622. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tibaduiza Burgos, D.; Gomez Vargas, R.; Pedraza, C.; Agis, D.; Pozo, F. Damage identification in structural health monitoring: A brief review from its implementation to the use of data-driven applications. Sensors 2020, 20, 733. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, Z.; Chen, Z.; Bao, Y.; Li, H. Convolutional neural network-based data anomaly detection method using multiple information for structural health monitoring. Struct. Control Health Monit. 2019, 26, e2296. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Beck, J.; Li, H. Multitask sparse bayesian learning with applications in structural health monitoring. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 732–754. [Google Scholar] [CrossRef]
- Sony, S.; Laventure, S.; Sadhu, A. A literature review of next-generation smart sensing technology in structural health monitoring. Struct. Control Health Monit. 2019, 26, e2321. [Google Scholar] [CrossRef]
- Annamdas, V.; Bhalla, S.; Soh, C. Applications of structural health monitoring technology in Asia. Struct. Health Monit. 2017, 16, 324–346. [Google Scholar] [CrossRef]
- Miśkiewicz, M.; Pyrzowski, Ł.; Wilde, K.; Mitrosz, O. Technical Monitoring System for a New Part of Gdańsk Deepwater Container Terminal. Pol. Marit. Res. 2017, 24, 149–155. [Google Scholar] [CrossRef] [Green Version]
- Gr ebowski, K.; Rucka, M.; Wilde, K. Non-destructive testing of a sport tribune under synchronized crowd-induced excitation using vibration analysis. Materials 2019, 12, 2148. [Google Scholar] [CrossRef] [Green Version]
- Hou, J.; An, Y.; Wang, S.; Wang, Z.; Jankowski, L.; Ou, J. Structural damage localization and quantification based on additional virtual masses and Bayesian theory. J. Eng. Mech. 2018, 144, 04018097. [Google Scholar] [CrossRef]
- Miśkiewicz, M.; Sobczyk, B.; Tysiac, P. Non-destructive testing of the longest span soil-steel bridge in Europe-field measurements and FEM calculations. Materials 2020, 13, 3652. [Google Scholar] [CrossRef] [PubMed]
- Rustighi, E.; Elliott, S. Force transmissibility of structures traversed by a moving system. J. Sound Vib. 2008, 311, 97–108. [Google Scholar] [CrossRef]
- Zhu, X.; Law, S. Recent developments in inverse problems of vehicle–bridge interaction dynamics. J. Civ. Struct. Health Monit. 2016, 6, 107–128. [Google Scholar] [CrossRef]
- Yu, L.; Chan, T. Recent research on identification of moving loads on bridges. J. Sound Vib. 2007, 305, 3–21. [Google Scholar] [CrossRef]
- Klinkov, M.; Fritzen, C.P. An updated comparison of the force reconstruction methods. Key Eng. Mater. 2007, 347, 461–466. [Google Scholar] [CrossRef]
- Hadamard, J. Sur les problèmes aux dérivées partielles et leur signification physique. Princet. Univ. Bull. 1902, 13, 49–52. [Google Scholar]
- Lourens, E.; Reynders, E.; De Roeck, G.; Degrande, G.; Lombaert, G. An augmented Kalman filter for force identification in structural dynamics. Mech. Syst. Signal Process. 2012, 27, 446–460. [Google Scholar] [CrossRef]
- Jacquelin, E.; Bennani, A.; Hamelin, P. Force reconstruction: Analysis and regularization of a deconvolution problem. J. Sound Vib. 2003, 265, 81–107. [Google Scholar] [CrossRef]
- Hansen, P. Discrete Inverse Problems: Insight and Algorithms; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Qiao, B.; Zhang, X.; Wang, C.; Zhang, H.; Chen, X. Sparse regularization for force identification using dictionaries. J. Sound Vib. 2016, 368, 71–86. [Google Scholar] [CrossRef]
- Pan, C.D.; Yu, L.; Liu, H.L.; Chen, Z.P.; Luo, W.F. Moving force identification based on redundant concatenated dictionary and weighted l1-norm regularization. Mech. Syst. Signal Process. 2018, 98, 32–49. [Google Scholar] [CrossRef]
- Zhong, J.; Liu, H.; Yu, L. Sparse regularization for traffic load monitoring using bridge response measurements. Measurement 2019, 131, 173–182. [Google Scholar] [CrossRef]
- Liu, H.; Yu, L.; Luo, Z.; Pan, C. Compressed sensing for moving force identification using redundant dictionaries. Mech. Syst. Signal Process. 2020, 138, 106535. [Google Scholar] [CrossRef]
- Sun, Y.; Luo, L.; Chen, K.; Qin, X.; Zhang, Q. A time-domain method for load identification using moving weighted least square technique. Comput. Struct. 2020, 234, 106254. [Google Scholar] [CrossRef]
- Yu, L.; Chan, T. Moving force identification from bridge dynamic responses. Struct. Eng. Mech. 2005, 21, 369–374. [Google Scholar] [CrossRef]
- Zhang, Q.; Jankowski, Ł.; Duan, Z. Simultaneous identification of moving masses and structural damage. Struct. Multidiscip. Optim. 2010, 42, 907–922. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Jankowski, Ł.; Duan, Z. Simultaneous identification of moving vehicles and bridge damages considering road rough surface. Math. Probl. Eng. 2013, 2013, 963424. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Lu, Q. Force localization and reconstruction using a two-step iterative approach. J. Vib. Control 2018, 24, 3830–3841. [Google Scholar] [CrossRef]
- Feng, W.; Li, Q.; Lu, Q. Force localization and reconstruction based on a novel sparse Kalman filter. Mech. Syst. Signal Process. 2020, 144, 106890. [Google Scholar] [CrossRef]
- Rezayat, A.; Nassiri, V.; De Pauw, B.; Ertveldt, J.; Vanlanduit, S.; Guillaume, P. Identification of dynamic forces using group-sparsity in frequency domain. Mech. Syst. Signal Process. 2016, 70–71, 756–768. [Google Scholar] [CrossRef]
- Wambacq, J.; Maes, K.; Rezayat, A.; Guillaume, P.; Lombaert, G. Localization of dynamic forces on structures with an interior point method using group sparsity. Mech. Syst. Signal Process. 2019, 115, 593–606. [Google Scholar] [CrossRef]
- Aucejo, M.; De Smet, O. A space-frequency multiplicative regularization for force reconstruction problems. Mech. Syst. Signal Process. 2018, 104, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Samagassi, S.; Jacquelin, E.; Khamlichi, A.; Sylla, M. Bayesian sparse regularization for multiple force identification and location in time domain. Inverse Probl. Sci. Eng. 2019, 27, 1221–1262. [Google Scholar] [CrossRef] [Green Version]
- Bao, Y.; Li, H.; Chen, Z.; Zhang, F.; Guo, A. Sparse l1 optimization-based identification approach for the distribution of moving heavy vehicle loads on cable-stayed bridges. Struct. Control Health Monit. 2016, 23, 144–155. [Google Scholar] [CrossRef]
- Gawlicki, M.; Jankowski, Ł. Identification of moving loads using the l1 norm minimization. AIP Conf. Proc. 2018, 1922, 100007. [Google Scholar] [CrossRef] [Green Version]
- Zawidzki, M.; Jankowski, Ł. Multiobjective optimization of modular structures: Weight versus geometric versatility in a Truss-Z system. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 1026–1040. [Google Scholar] [CrossRef]
- Milan, A.; Schindler, K.; Roth, S. Multi-Target Tracking by Discrete-Continuous Energy Minimization. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2054–2068. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Zhou, A.; Qu, B.Y.; Li, H.; Zhao, S.Z.; Suganthan, P.N.; Zhang, Q. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Ehrgott, M. Multicriteria Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef] [Green Version]
- Caruana, R.A.; Schaffer, J.D. Representation and Hidden Bias: Gray vs. Binary Coding for Genetic Algorithms. In Machine Learning Proceedings 1988; Laird, J., Ed.; Morgan Kaufmann: San Francisco, CA, USA, 1988; pp. 153–161. [Google Scholar] [CrossRef]
- Casciati, F.; Casciati, S.; Faravelli, L. A contribution to the modelling of human induced excitation on pedestrian bridges. Struct. Saf. 2017, 66, 51–61. [Google Scholar] [CrossRef]
- Mirshekari, M.; Pan, S.; Fagert, J.; Schooler, E.; Zhang, P.; Noh, H. Occupant localization using footstep-induced structural vibration. Mech. Syst. Signal Process. 2018, 112, 77–97. [Google Scholar] [CrossRef]
- Samet, A.; Ben Souf, M.; Bareille, O.; Ichchou, M.; Fakhfakh, T.; Haddar, M. Vibration sources identification in coupled thin plates through an inverse energy method. Appl. Acoust. 2017, 128, 83–93. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Soman, R.; Malinowski, P. Optimization of sensor placement for structural health monitoring: A review. Struct. Health Monit. 2019, 18, 963–988. [Google Scholar] [CrossRef]
- Błachowski, B.; Świercz, A.; Ostrowski, M.; Tauzowski, P.; Olaszek, P.; Jankowski, Ł. Convex relaxation for efficient sensor layout optimization in large-scale structures subjected to moving loads. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 1085–1100. [Google Scholar] [CrossRef]
- Zhu, X.; Law, S. Structural health monitoring based on vehicle-bridge interaction: Accomplishments and challenges. Adv. Struct. Eng. 2015, 18, 1999–2015. [Google Scholar] [CrossRef]
- Hou, J.; Li, Z.; Jankowski, Ł.; Wang, S. Estimation of virtual masses for structural damage identification. Struct. Control Health Monit. 2020, 27, e2585. [Google Scholar] [CrossRef]
- Pisarski, D.; Myśliński, A. Online adaptive algorithm for optimal control of structures subjected to travelling loads. Optim. Control. Appl. Methods 2017, 38, 1168–1186. [Google Scholar] [CrossRef]
- Hou, J.; Jankowski, Ł.; Ou, J. Frequency-domain substructure isolation for local damage identification. Adv. Struct. Eng. 2015, 18, 137–153. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gawlicki, M.; Jankowski, Ł. Trajectory Identification for Moving Loads by Multicriterial Optimization. Sensors 2021, 21, 304. https://doi.org/10.3390/s21010304
Gawlicki M, Jankowski Ł. Trajectory Identification for Moving Loads by Multicriterial Optimization. Sensors. 2021; 21(1):304. https://doi.org/10.3390/s21010304
Chicago/Turabian StyleGawlicki, Michał, and Łukasz Jankowski. 2021. "Trajectory Identification for Moving Loads by Multicriterial Optimization" Sensors 21, no. 1: 304. https://doi.org/10.3390/s21010304






