Energy Harvesting in a System with a Two-Stage Flexible Cantilever Beam
Abstract
:1. Introduction
2. Mathematical Model Formulation
3. Research Results
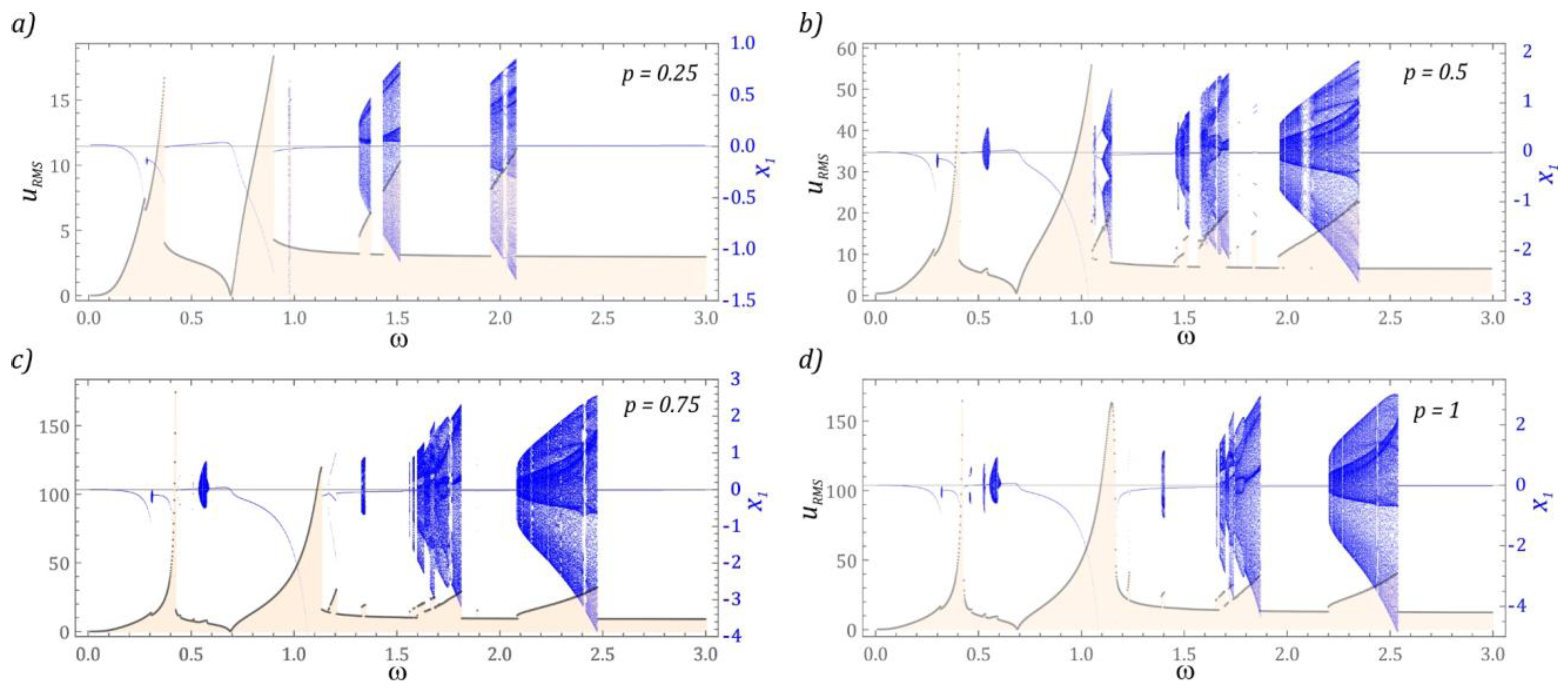
3.1. Periodic Solutions
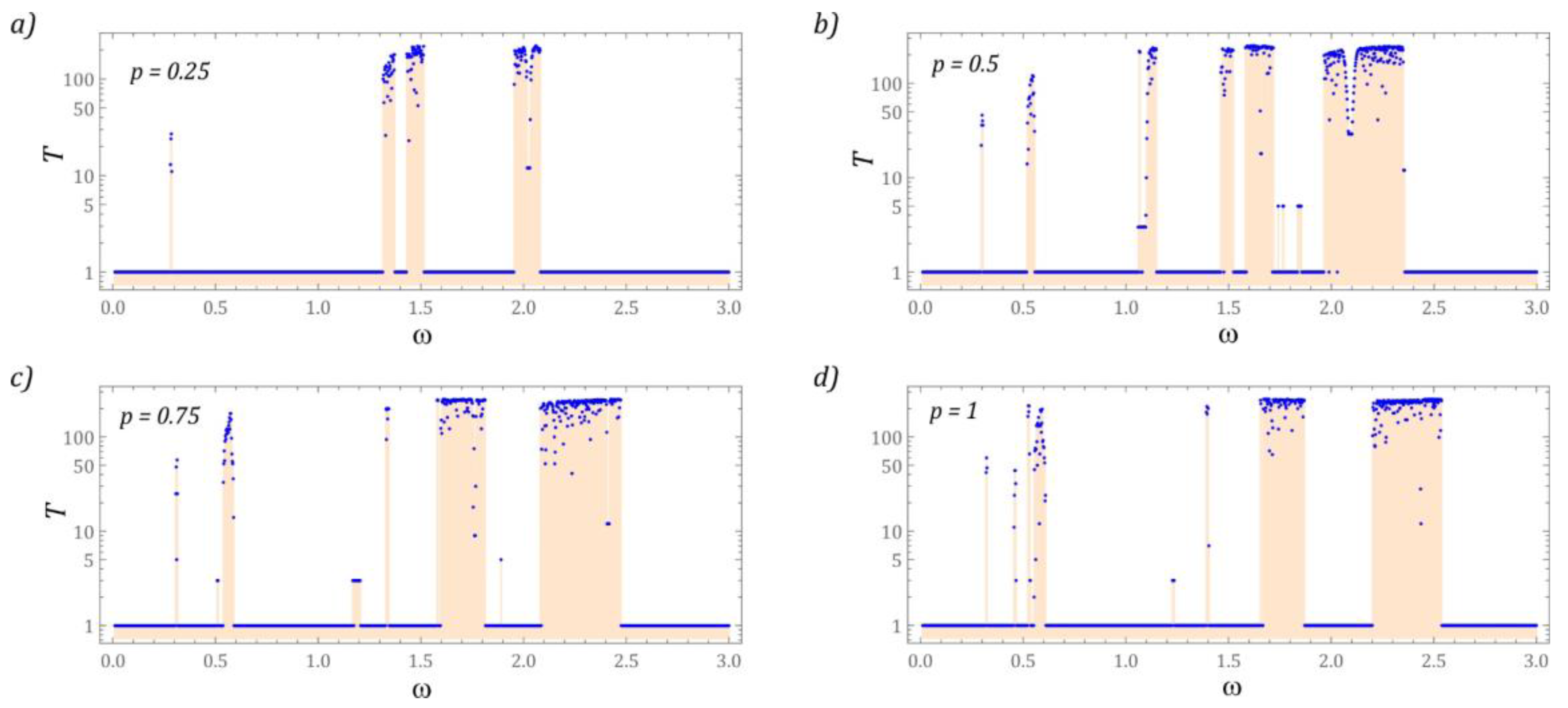
3.2. Chaotic and Quasiperiodic Solutions
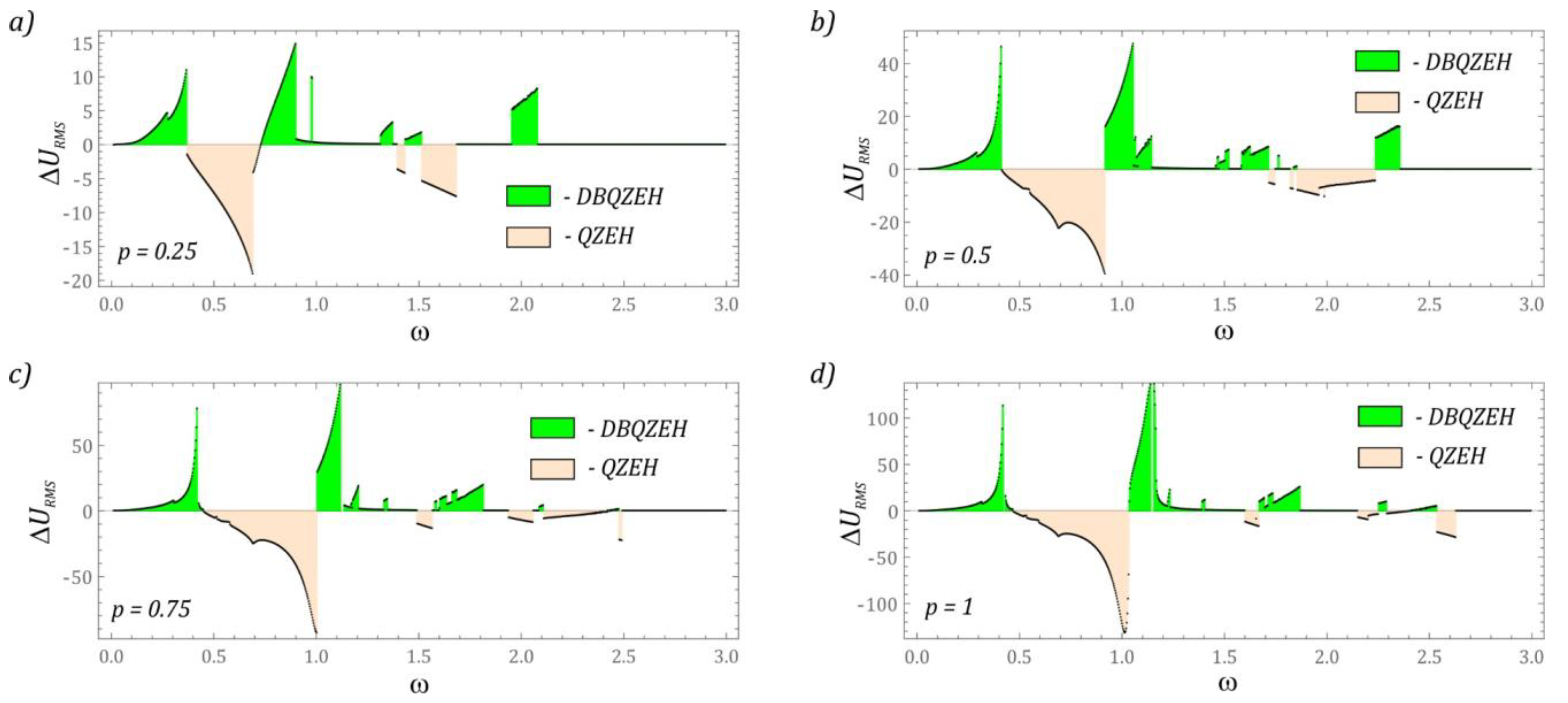
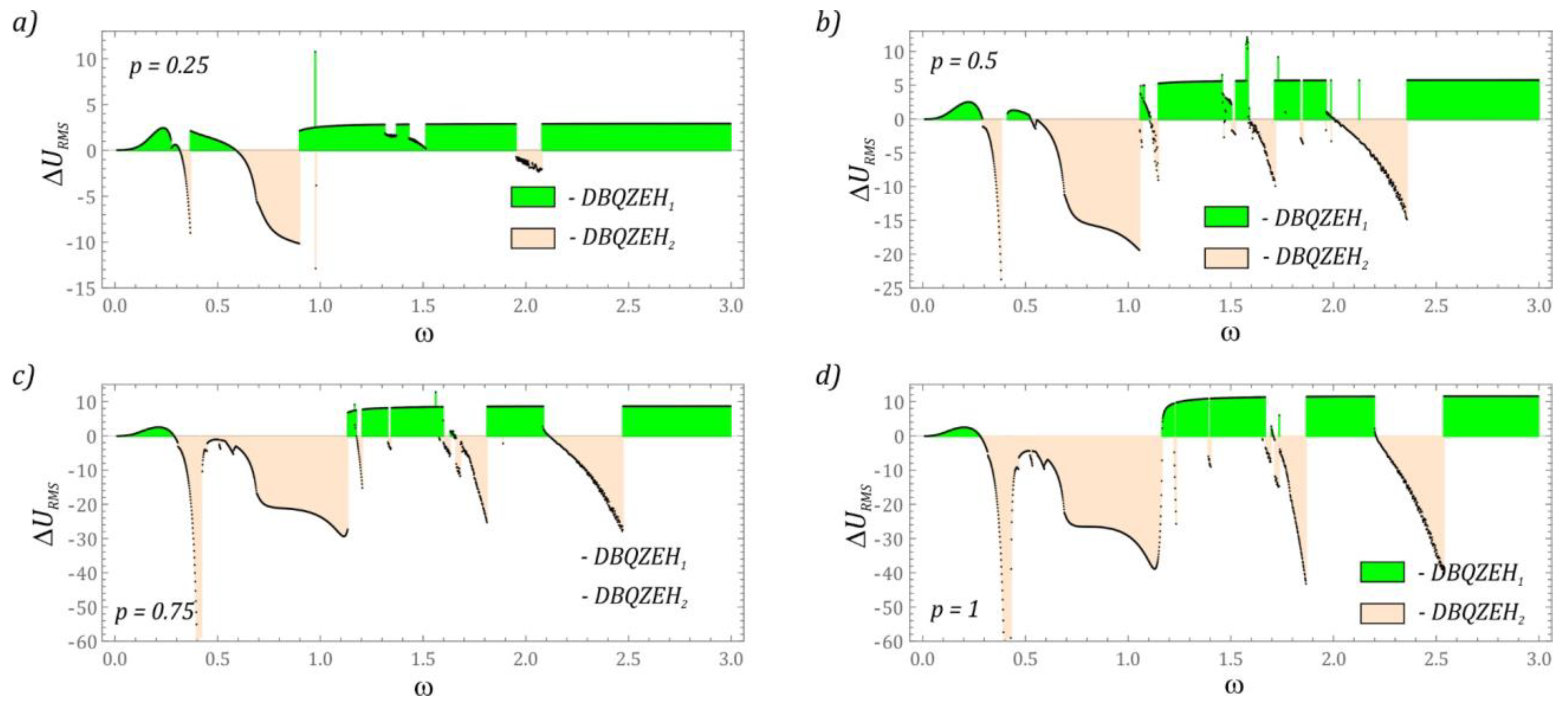
3.3. Efficiency of Energy Harvesting
4. Final Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy harvesting from human and machine motion for wireless electronic devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef]
- Karami, M.A.; Inman, D.J. Powering pacemakers from heartbeat vibrations using linear and nonlinear energy harvesters. Appl. Phys. Lett. 2022, 100, 042901. [Google Scholar] [CrossRef]
- Zhou, S.; Lallart, M.; Erturk, A. Multistable vibration energy harvesters: Principle, progress, and perspectives. J. Sound Vib. 2022, 528, 116886. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley and Sons: Chichester, UK, 2011. [Google Scholar] [CrossRef]
- Lan, C.; Qin, W. Enhancing ability of harvesting energy from random vibration by decreasing the potential barrier of bistable harvester. Mech. Syst. Signal Process. 2017, 85, 71–81. [Google Scholar] [CrossRef]
- Zhou, Z.; Qin, W.; Yang, Y.; Zhu, P. Improving efficiency of energy harvesting by a novel penta-stable configuration. Sens. Actuators A Phys. 2017, 265, 297–305. [Google Scholar] [CrossRef]
- Erturk, A.; Hoffmann, J.; Inman, D.J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102. [Google Scholar] [CrossRef]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear energy harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef]
- Cunha, A., Jr.; Litak, G.; Wolszczak, P. Effect of stochastic excitation on sub-harmonic solutions in a bistable energy harvester. AIP Conf. Proc. 2022, 2425, 410003. [Google Scholar] [CrossRef]
- Yang, G.; Stark, B.; Hollis, S.; Burrow, S.G. Challenges for Energy Harvesting Systems Under Intermittent Excitation. IEEE J. Emerg. Sel. Top. Circuits Syst. 2014, 4, 364–374. [Google Scholar] [CrossRef]
- Brennan, M.J.; Gatti, G. Harvesting Energy from Time-Limited Harmonic Vibrations: Mechanical Considerations. J. Vib. Acoust. 2017, 139, 051019. [Google Scholar] [CrossRef]
- Rodrigues, C.; Ramosa, M.; Esteves, R.; Correia, J.; Clemente, D.; Gonçalves, F.; Mathias, N.; Gomes, M.; Silva, J.; Duarte, C.; et al. Integrated study of triboelectric nanogenerator for ocean wave energy harvesting: Performance assessment in realistic sea conditions. Nano Energy 2021, 84, 105890. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, C.; Zhao, P.; Chen, W. Research on Piezoelectric Energy harvesting from Multi-Direction Wind-Induced Vibrations. IOP Conf. Ser. Earth Environ. Sci. 2020, 617, 012014. [Google Scholar] [CrossRef]
- Cleante, V.G.; Brennan, M.J.; Gatti, G.; Thompson, D.J. Energy harvesting from the vibrations of a passing train: Effect of speed variability. J. Phys. Conf. Ser. 2016, 744, 012080. [Google Scholar] [CrossRef]
- Qiana, F.; Xu, T.-B.; Zuo, L. Piezoelectric energy harvesting from human walking using a two-stage amplification mechanism. Energy 2019, 189, 116140. [Google Scholar] [CrossRef]
- Lallart, M.; Zhou, S.; Yang, Z.; Yan, L.; Li, K.; Chen, Y. Coupling mechanical and electrical nonlinearities: The effect of synchronized discharging on tristable energy harvesters. Appl. Energy 2020, 266, 114516. [Google Scholar] [CrossRef]
- Iqbal, M.; Nauman, M.M.; Khan, F.U.; Abas, P.E.; Cheok, Q.; Iqbal, A.; Aissa, B. Vibration-based piezoelectric, electromagnetic, and hybrid energy harvesters for microsystems applications: A contributed review. Int. J. Energy Res. 2021, 45, 65–102. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, W.; Su, M. Response of a stochastic multiple attractors wind-induced vibration energy harvesting system with impacts. Int. J. Non-Linear Mech. 2021, 138, 103853. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, S.; Han, Q.; Litak, G. Response analysis of the nonlinear vibration energy harvester with an uncertain parameter. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2020, 234, 393–407. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, S.; Litak, G. Uncertainty analysis of excitation conditions on performance of nonlinear mono-stable energy harvesters. Int. J. Struct. Stab. Dyn. 2019, 19, 1950052. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, S.; Litak, G. Theoretical analysis of multi-stable energy harvesters with high-order stiffness terms. Commun. Nonlinear Sci. Numer. Simul. 2019, 69, 270–286. [Google Scholar] [CrossRef]
- Gaidys, R.; Stasytis, E.; Daniulaitis, V.; Narijauskaitė, B. Vibration energy harvester (veh) for a free body moving in space at vibro shock mode. Mechanika 2022, 28, 222–229. [Google Scholar] [CrossRef]
- Yang, T.; Cao, Q. Novel multi-stable energy harvester by exploring the benefits of geometric nonlinearity. J. Stat. Mech. Theory Exp. 2019, 2019, 033405. [Google Scholar] [CrossRef]
- Liu, Q.; Qin, W.; Yang, Y.; Zhou, Z. Promote performance of vibration energy harvesting by amplified inertial force and clamped piezoelectric beams. Mech. Syst. Signal Process. 2022, 178, 109291. [Google Scholar] [CrossRef]
- Wolszczak, P.; Lygas, K.; Litak, G. Dynamics identification of a piezoelectric vibrational energy harvester by image analysis with a high speed camera. Mech. Syst. Signal Process. 2018, 107, 43–52. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Quinn, D.D. On the role of nonlinearities in vibratory energy harvesting: A critical review and discussion. Appl. Mech. Rev. 2014, 66, 040801. [Google Scholar] [CrossRef]
- Huguet, T.; Badel, A.; Druet, O.; Lallart, M. Drastic bandwidth enhancement of bistable energy harvesters: Study of subharmonic behaviors and their stability robustness. Appl. Energy 2018, 226, 607–617. [Google Scholar] [CrossRef]
- Litak, G.; Ambrożkiewicz, B.; Wolszczak, P. Dynamics of a nonlinear energy harvester with subharmonic responses. J. Phys. Conf. Ser. 2021, 1736, 012032. [Google Scholar] [CrossRef]
- Toroń, B.; Mistewicz, K.; Jesionek, M.; Kozioł, M.; Zubko, M.; Stróż, D. A new hybrid piezo/triboelectric SbSeI nanogenerator. Energy 2022, 238, 122048. [Google Scholar] [CrossRef]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A review of energy harvesting using piezoelectric materials: State-of-the-art a decade later (2008–2018). Smart Mater. Struct. 2019, 28, 113001. [Google Scholar] [CrossRef]
- Keshmiri, A.; Deng, X.; Wu, N. New energy harvester with embedded piezoelectric stacks. Compos. Part B Eng. 2019, 163, 303–313. [Google Scholar] [CrossRef]
- Liang, H.; Hao, G.; Olszewski, O.Z. A review on vibration-based piezoelectric energy harvesting from the aspect of compliant mechanisms. Sens. Actuators A Phys. 2021, 331, 112743. [Google Scholar] [CrossRef]
- Sun, X.; Jing, X. Analysis and design of a nonlinear stiffness and damping system with a scissor-like structure. Mech. Syst. Signal Process. 2016, 66-67, 723–742. [Google Scholar] [CrossRef]
- Gatti, G. Optimizing elastic potential energy via geometric nonlinear stiffness. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 106035. [Google Scholar] [CrossRef]
- Yan, G.; Zou, H.-X.; Wang, S.; Zhao, L.-C.; Wu, Z.-Y.; Zhang, W.-M. Bio-inspired vibration isolation: Methodology and design. Appl. Mech. Rev. 2021, 73, 020801. [Google Scholar] [CrossRef]
- Qian, F.; Hajj, M.R.; Zuo, L. Bio-inspired bi-stable piezoelectric harvester for broadband vibration energy harvesting. Energy Convers. Manag. 2020, 222, 113174. [Google Scholar] [CrossRef]
- Litak, G.; Margielewicz, J.; Gaska, D.; Rysak, A.; Trigona, C. On Theoretical and numerical aspects of bifurcations and hysteresis effects in kinetic energy harvesters. Sensors 2022, 22, 381. [Google Scholar] [CrossRef]
- Zhu, Y.-P.; Lang, Z.Q. Beneficial effects of antisymmetric nonlinear damping with application to energy harvesting and vibration isolation under general inputs. Nonlinear Dyn. 2022, 108, 2917–2933. [Google Scholar] [CrossRef]
- Rubes, O.; Chalupa, J.; Ksica, F.; Hadas, Z. Development and experimental validation of self-powered wireless vibration sensor node using vibration energy harvester. Mech. Syst. Signal Process. 2021, 160, 107890. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, F.; Qin, Z.; Han, Q.; Wang, T.; Chu, F. Piezoelectric energy harvester for rolling bearings with capability of self-powered condition monitoring. Energy 2022, 238, 121770. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Li, R.; Dai, L.; Wang, W.; Yang, K. Dynamic responses of a two-degree-of-freedom bistable electromagnetic energy harvester under filtered band-limited stochastic excitation. J. Sound Vib. 2021, 511, 116334. [Google Scholar] [CrossRef]
- Lopes, V.G.; Peterson, J.V.L.L.; Cunha, A.J. Nonlinear Characterization of a Bistable Energy Harvester Dynamical System. Springer Proc. Phys. 2019, 228, 71–88. [Google Scholar] [CrossRef]
- Chen, L.; Liao, X.; Sun, B.; Zhang, N.; Wu, J. A numerical-experimental dynamic analysis of high-efficiency and broadband bistable energy harvester with self-decreasing potential barrier effect. Appl. Energy 2022, 317, 119161. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tristable energy harvester: Modeling and experiment verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Zhou, S.; Zuo, L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 271–284. [Google Scholar] [CrossRef]
- Yang, X.; Wang, C.; Lai, S.K. A magnetic levitation-based tristable hybrid energy harvester for scavenging energy from low-frequency structural vibration. Eng. Struct. 2020, 221, 110789. [Google Scholar] [CrossRef]
- Yang, T.; Cao, Q. Dynamics and performance evaluation of a novel tristable hybrid energy harvester for ultra-low level vibration resources. Int. J. Mech. Sci. 2019, 156, 123–136. [Google Scholar] [CrossRef]
- Zayed, A.A.A.; Assal, S.F.M.; Nakano, K.; Kaizuka, T.; El-Bab, A.M.R.F. Design procedure and experimental verification of a broadband quad-stable 2-DOF vibration energy harvester. Sensors 2019, 19, 2893. [Google Scholar] [CrossRef]
- Qian, Y.; Chen, Y. Research on multi-valued response and bursting oscillation of series multi-stable piezoelectric energy harvester. Eur. Phys. J. Plus 2022, 137, 588. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.; Wang, W.; Feng, J. A low-frequency, wideband quad-stable energy harvester using combined nonlinearity and frequency up-conversion by cantilever-surface contact. Mech. Syst. Signal Process. 2018, 112, 305–318. [Google Scholar] [CrossRef]
- Martens, W.; von Wagner, U.; Litak, G. Stationary response of nonlinear magneto-piezoelectric energy harvester systems under stochastic excitation. Eur. Phys. J. Spéc. Top. 2013, 222, 1665–1673. [Google Scholar] [CrossRef]
- Margielewicz, J.; Gąska, D.; Litak, G.; Wolszczak, P.; Trigona, C. Nonlinear dynamics of a star-shaped structure and variable configuration of elastic elements for energy harvesting applications. Sensors 2022, 22, 2518. [Google Scholar] [CrossRef]
- Margielewicz, J.; Gąska, D.; Litak, G.; Wolszczak, P.; Yurchenko, D. Nonlinear dynamics of a new energy harvesting system with quasi-zero stiffness. Appl. Energy 2022, 307, 118159. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, L.; Chang, Y.; Cong, C. Design and characteristic analysis of magnetostrictive bistable vibration harvester with displacement amplification mechanism. Energy Convers. Manag. 2021, 243, 114361. [Google Scholar] [CrossRef]
- Poddaeva, O.; Fedosova, A. Damping capacity of materials and its effect on the dynamic behavior of structures. Review. Energy Rep. 2021, 7, 299–307. [Google Scholar] [CrossRef]
- Litak, G.; Margielewicz, J.; Gąska, D.; Wolszczak, P.; Zhou, S. Multiple solutions of the tristable energy harvester. Energies 2021, 14, 1284. [Google Scholar] [CrossRef]





| Name | Symbol | Beam I | Beam II |
|---|---|---|---|
| Length | Li | 0.13 m | 0.06 m |
| Width | 0.025 m | 0.018 m | |
| Height | hi | 0.0003 m | 0.0002 m |
| Material | E | 210 GPa | |
| Load mass | mi | 0.025 kg | 0.026 kg |
| Stiffness | ki | 16 Nm−1 | 35 Nm−1 |
| Energy dissipation | ci | 0.00013 Nsm−1 | 0.00019 Nsm−1 |
| Length of the compensation springs | a0 | 0.03 m | |
| Stiffness of the compensation springs | kCi | 72 Nm−1 | |
| Total resistance | RZ | 1.1 × 106 Ω | |
| Piezoelectric capacity | CP | 72 nF | |
| Electromechanical constant of piezoelectric converter | kP | 3.985 × 10−5 m/V | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Margielewicz, J.; Gąska, D.; Litak, G.; Wolszczak, P.; Zhou, S. Energy Harvesting in a System with a Two-Stage Flexible Cantilever Beam. Sensors 2022, 22, 7399. https://doi.org/10.3390/s22197399
Margielewicz J, Gąska D, Litak G, Wolszczak P, Zhou S. Energy Harvesting in a System with a Two-Stage Flexible Cantilever Beam. Sensors. 2022; 22(19):7399. https://doi.org/10.3390/s22197399
Chicago/Turabian StyleMargielewicz, Jerzy, Damian Gąska, Grzegorz Litak, Piotr Wolszczak, and Shengxi Zhou. 2022. "Energy Harvesting in a System with a Two-Stage Flexible Cantilever Beam" Sensors 22, no. 19: 7399. https://doi.org/10.3390/s22197399
APA StyleMargielewicz, J., Gąska, D., Litak, G., Wolszczak, P., & Zhou, S. (2022). Energy Harvesting in a System with a Two-Stage Flexible Cantilever Beam. Sensors, 22(19), 7399. https://doi.org/10.3390/s22197399










