State of Charge Estimation of Lithium-Ion Batteries Based on an Adaptive Iterative Extended Kalman Filter for AUVs
Abstract
:1. Introduction
2. Lithium-Ion Battery Modeling
2.1. Equivalent Circuit Model
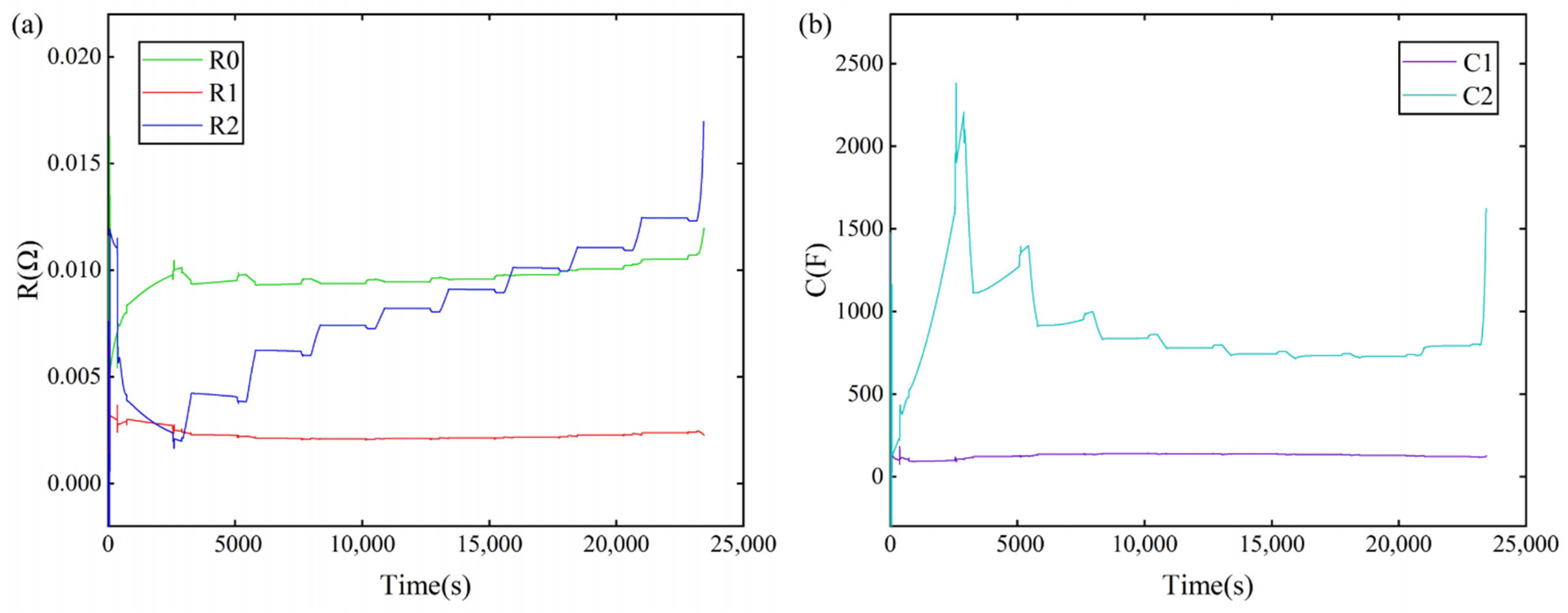
2.2. Parameter Identification of the Battery Model
3. SOC Estimation Based on AIEKF
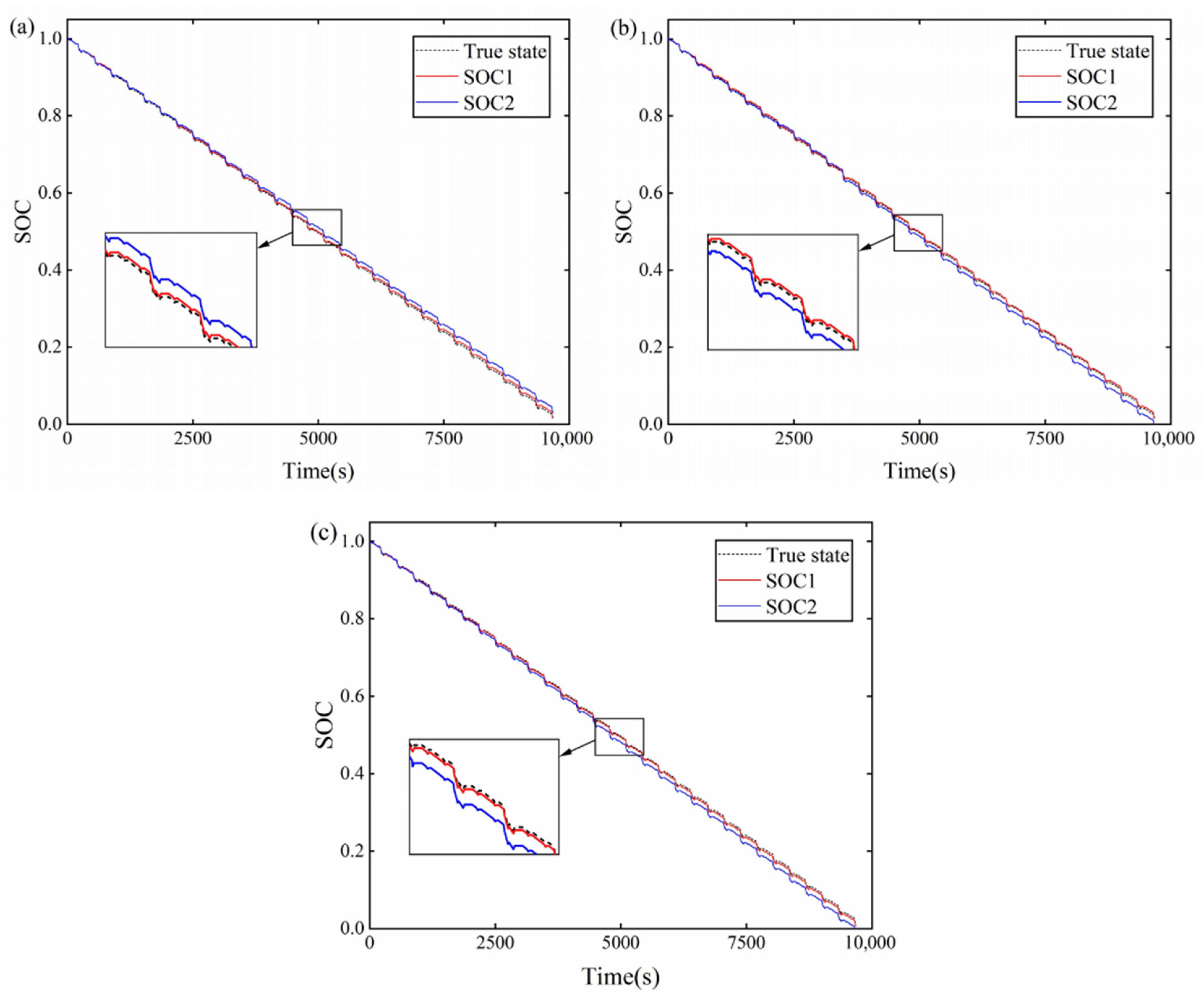
4. Experimental Results and Discussion
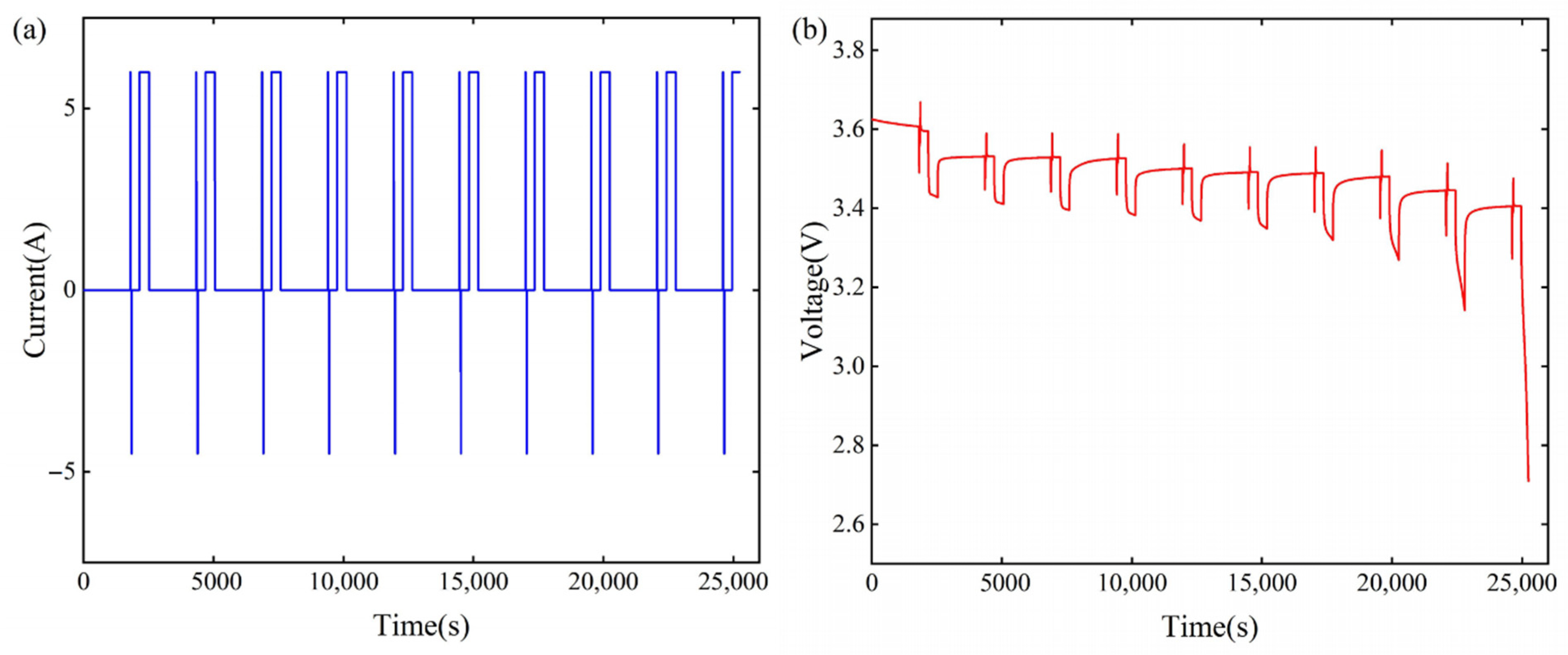
4.1. Battery Test Platform
4.2. SOC–OCV–T Test
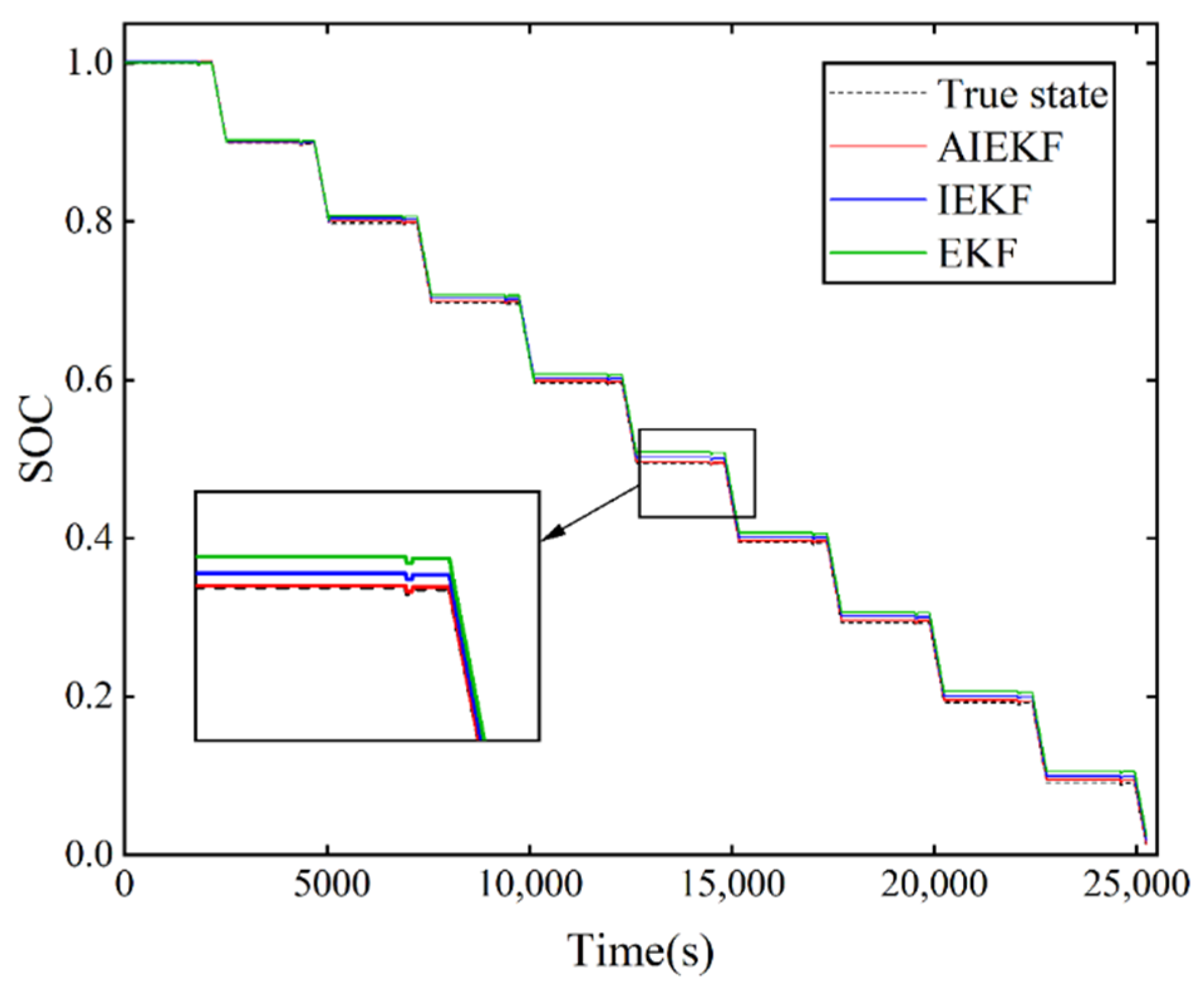
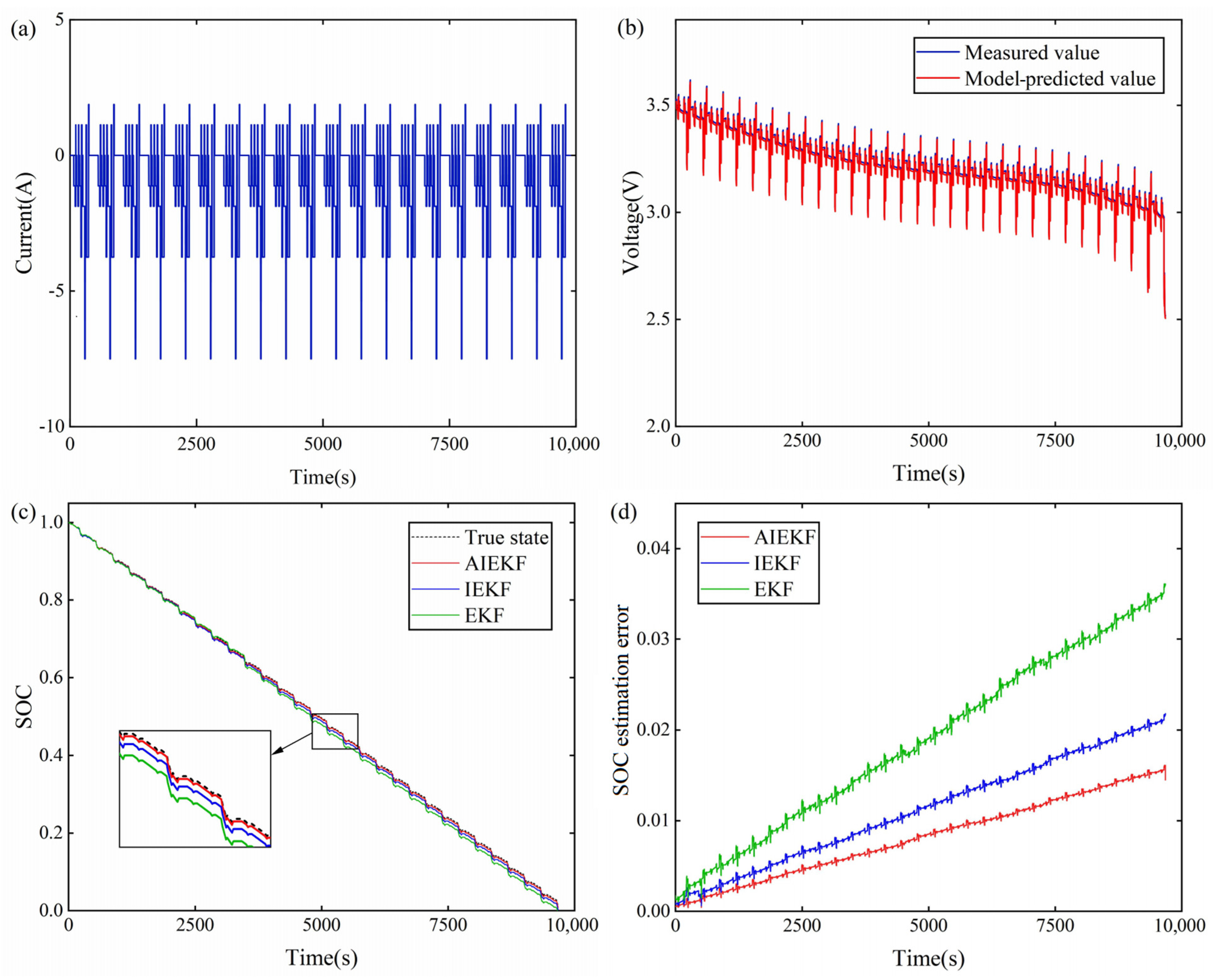
4.3. Analysis of Simulation and Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Scrosati, B.; Hassoun, J.; Sun, Y.K. Lithium-ion batteries. A look into the future. Energy Environ. Sci. 2011, 4, 3287–3295. [Google Scholar] [CrossRef]
- Campestrini, C.; Horsche, M.F.; Zilberman, I.; Heil, T.; Zimmermann, T.; Jossen, A. Validation and benchmark methods for battery management system functionalities: State of charge estimation algorithms. J. Energy Storage 2016, 7, 38–51. [Google Scholar] [CrossRef]
- Szumanowski, A.; Chang, Y. Battery management system based on battery nonlinear dynamics modeling. IEEE Trans. Veh. Technol. 2008, 57, 1425–1432. [Google Scholar] [CrossRef]
- Li, Z.; Huang, J.; Liaw, B.Y.; Zhang, J. On state-of-charge determination for lithium-ion batteries. J. Power Sources 2017, 348, 281–301. [Google Scholar] [CrossRef] [Green Version]
- Zheng, F.; Xing, Y.; Jiang, J.; Sun, B.; Kim, J.; Pecht, M. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries. Appl. Energy 2016, 183, 513–525. [Google Scholar] [CrossRef]
- Meng, J.; Yue, M.; Diallo, D. A degradation empirical-model-free battery end-of-life prediction framework based on gaussian process regression and Kalman filter. IEEE Trans. Transp. Electrif. 2022, 8, 1–11. [Google Scholar] [CrossRef]
- Feng, F.; Lu, R.; Zhu, C. A combined state of charge estimation method for lithium-ion batteries used in a wide ambient temperature range. Energies 2014, 7, 3004–3032. [Google Scholar] [CrossRef] [Green Version]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural network approach for estimating state of charge of lithium-ion battery using backtracking search algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Hu, J.; Hu, J.; Lin, H.; Li, X.; Jiang, C.; Qiu, X.; Li, W. State-of-charge estimation for battery management system using optimized support vector machine for regression. J. Power Sources 2014, 269, 682–693. [Google Scholar] [CrossRef]
- Sepasi, S.; Roose, L.R.; Matsuura, M.M. Extended Kalman filter with a fuzzy method for accurate battery pack state of charge estimation. Energies 2015, 8, 5217–5233. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The co-estimation of state of charge, state of health, and state of function for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2017, 67, 92–103. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Lai, X.; Zheng, Y.; Sun, T. A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries. Electrochim. Acta 2018, 259, 566–577. [Google Scholar] [CrossRef]
- Meng, J.; Boukhnifer, M.; Diallo, D. Lithium-ion battery monitoring and observability analysis with extended equivalent circuit model. In Proceedings of the 2020 28th Mediterranean Conference on Control and Automation (MED), Saint-Raphaël, France, 15–18 September 2020; pp. 764–769. [Google Scholar]
- Charkhgard, M.; Farrokhi, M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF. IEEE Trans. Ind. Electron. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- Wang, T.; Chen, S.; Ren, H.; Zhao, Y. Model-based unscented Kalman filter observer design for lithium-ion battery state of charge estimation. Int. J. Energy Res. 2018, 42, 1603–1614. [Google Scholar] [CrossRef]
- Peng, J.; Luo, J.; He, H.; Lu, B. An improved state of charge estimation method based on cubature Kalman filter for lithium-ion batteries. Appl. Energy 2019, 253, 113520. [Google Scholar] [CrossRef]
- Charkhgard, M.; Zarif, M.H. Design of adaptive H∞ filter for implementing on state-of-charge estimation based on battery state-of-charge-varying modelling. IET Power Electron. 2015, 8, 1825–1833. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, J.; Wang, G.; Lu, D.D.C.; He, T. Differential voltage analysis based state of charge estimation methods for lithium-ion batteries using extended Kalman filter and particle filter. Energy 2018, 158, 1028–1037. [Google Scholar] [CrossRef]
- Misyris, G.S.; Doukas, D.I.; Papadopoulos, T.A.; Labridis, D.P.; Agelidis, V.G. State-of-charge estimation for li-ion batteries: A more accurate hybrid approach. IEEE Trans. Energy Convers. 2018, 34, 109–119. [Google Scholar] [CrossRef]
- Wang, S.; Fernandez, C.; Yu, C.; Fan, Y.; Cao, W.; Stroe, D. A novel charged state prediction method of the lithium ion battery packs based on the composite equivalent modeling and improved splice Kalman filtering algorithm. J. Power Sources 2020, 471, 228450. [Google Scholar] [CrossRef]
- Lao, Z.; Xia, B.; Wang, W.; Lai, Y.; Wang, M. A novel method for lithium-ion battery online parameter identification based on variable forgetting factor recursive least squares. Energies 2018, 11, 1358. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Chen, J.; Lan, F. Enhanced online model identification and state of charge estimation for lithium-ion battery under noise corrupted measurements by bias compensation recursive least squares. J. Power Sources 2020, 456, 227984. [Google Scholar] [CrossRef]
- Roscher, M.A.; Bohlen, O.S.; Sauer, D.U. Reliable state estimation of multicell lithium-ion battery systems. IEEE Trans. Energy Convers. 2011, 26, 737–743. [Google Scholar] [CrossRef]
- Zhu, Q.; Xu, M.; Liu, W.; Zheng, M. A state of charge estimation method for lithium-ion batteries based on fractional order adaptive extended Kalman filter. Energy 2019, 187, 115880. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, D.; Cheng, J.; Wang, B.; Luk, P.C.K. An improved Thevenin model of lithium-ion battery with high accuracy for electric vehicles. Appl. Energy 2019, 254, 113615. [Google Scholar] [CrossRef]
- Lai, X.; Gao, W.; Zheng, Y.; Ouyang, M.; Li, J.; Han, X.; Zhou, L. A comparative study of global optimization methods for parameter identification of different equivalent circuit models for li-ion batteries. Electrochim. Acta 2019, 295, 1057–1066. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, D.; He, H.; Cao, W.; Dong, G. A noise-tolerant model parameterization method for lithium-ion battery management system. Appl. Energy 2020, 268, 114932. [Google Scholar] [CrossRef]
- Wei, Z.; Dong, G.; Zhang, X.; Pou, J. Noise-immune model identification and state-of-charge estimation for lithium-ion battery using bilinear parameterization. IEEE Trans. Ind. Electron. 2020, 68, 312–323. [Google Scholar] [CrossRef]
- Mastali, M.; Vazquez-Arenas, J.; Fraser, R.; Fowler, M.; Afshar, S.; Stevens, M. Battery state of the charge estimation using Kalman filtering. J. Power Sources 2013, 239, 294–307. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-charge estimation of the lithium-ion battery using an adaptive extended Kalman filter based on an improved Thevenin model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- El Din, M.S.; Hussein, A.A.; Abdel-Hafez, M.F. Improved battery SOC estimation accuracy using a modified UKF with an adaptive cell model under real EV operating conditions. IEEE Trans. Transp. Electrif. 2018, 4, 408–417. [Google Scholar] [CrossRef]
- Peng, S.; Chen, C.; Shi, H.; Yao, Z. State of charge estimation of battery energy storage systems based on adaptive unscented Kalman filter with a noise statistics estimator. IEEE Access 2017, 5, 13202–13212. [Google Scholar] [CrossRef]





| Method | HPPC | DST | ||
|---|---|---|---|---|
| MAE (%) | RMSE (%) | MAE (%) | RMSE (%) | |
| EKF | 1.2648 | 1.1783 | 1.4357 | 1.2518 |
| IEKF | 1.1450 | 0.9256 | 1.3274 | 1.0392 |
| AEKF | 0.9715 | 0.7482 | 1.1509 | 0.8253 |
| AIEKF | 0.6582 | 0.2549 | 0.8326 | 0.3471 |
| Reference | Method | Model | MAE (%) |
|---|---|---|---|
| [32] | EKF | Rint | <4 |
| [33] | AEKF | 2RC | <2 |
| [34] | UKF | 1RC | <1.7 |
| [35] | AUKF | 2RC | <1.5 |
| Method | Computational Time (s) |
|---|---|
| EKF | 0.6418 |
| IEKF | 1.1273 |
| AEKF | 1.0849 |
| AIEKF | 0.9524 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Zhai, B.; Shi, Z.; Liang, J.; Peng, Z. State of Charge Estimation of Lithium-Ion Batteries Based on an Adaptive Iterative Extended Kalman Filter for AUVs. Sensors 2022, 22, 9277. https://doi.org/10.3390/s22239277
Fu Y, Zhai B, Shi Z, Liang J, Peng Z. State of Charge Estimation of Lithium-Ion Batteries Based on an Adaptive Iterative Extended Kalman Filter for AUVs. Sensors. 2022; 22(23):9277. https://doi.org/10.3390/s22239277
Chicago/Turabian StyleFu, You, Binhao Zhai, Zhuoqun Shi, Jun Liang, and Zhouhua Peng. 2022. "State of Charge Estimation of Lithium-Ion Batteries Based on an Adaptive Iterative Extended Kalman Filter for AUVs" Sensors 22, no. 23: 9277. https://doi.org/10.3390/s22239277






