A Novel Traffic Prediction Method Using Machine Learning for Energy Efficiency in Service Provider Networks
Abstract
1. Introduction
- 1.
- A novel method is proposed and developed to compare different types of neural networks in terms of their ability to process time series data, specifically in real-time traffic analysis. This methodology aimed to evaluate the performance of various neural network models and identify the most suitable option for the task.
- 2.
- A novel bundle Ethernet energy efficiency methodology was designed. This algorithm was based on the expected traffic and used the best-performing neural network, selected by the methodology outlined in point 1.
- 3.
- The proposed traffic prediction method and energy-saving Ethernet bundle methodology were evaluated. The performance of the traffic prediction methodology was compared between neural networks. The energy-saving Ethernet bundle was evaluated in terms of energy savings by comparing the performance algorithms proposed in point 2. The results were analyzed to determine the feasibility and effectiveness of the proposed solution.
2. Related Works
2.1. Works Related to Methods of Traffic Prediction Based on Machine Learning and Neural Networks
2.2. Works Related to Energy Efficiency in Link Aggregation Groups or Bundle Ethernet
3. Traffic Prediction Methodology
3.1. Data Collection
3.2. Structure of RNN, LSTM, GRU, and OS-ELM
3.3. Data Processing for RNN, LSTM, GRU, and OS-ELM
3.3.1. Data Processing for RNN, LSTM, and GRU
- 1.
- Transform the data into a supervised learning problem. In the time series problem, the data are modified as follows: The observation at the last time step as the input and the observation at the current time step as the output. This represents the single-step sliding window. It is mainly the only variable to compare, so it is a univariate problem [41].
- 2.
- Time-dependent time series data. The trend can be removed from the observations and then returned to the original prediction scale. A standard way to remove a trend is to differentiate the data.
- 3.
- Normalize the observations. The default activation function of the RNN, LSTM, and GRU models is the hyperbolic tangent , which has values between −1 and 1. The observations will be normalized in the same way, that is, between −1 and 1. This regularization helps to avoid corrupting the experimental set with information from the test dataset.
3.3.2. Data Processing for OS-ELM
- 1.
- Transform the data into a supervised learning problem. In preparing the data, the model is instructed in the same way as recurrent neural networks, that is, the sliding window or prediction step will be one step.
- 2.
- 3.
- Normalize the observations. In the OS-ELM model, the recommended scale is to normalize the data by subtracting the mean and dividing by the standard deviation.
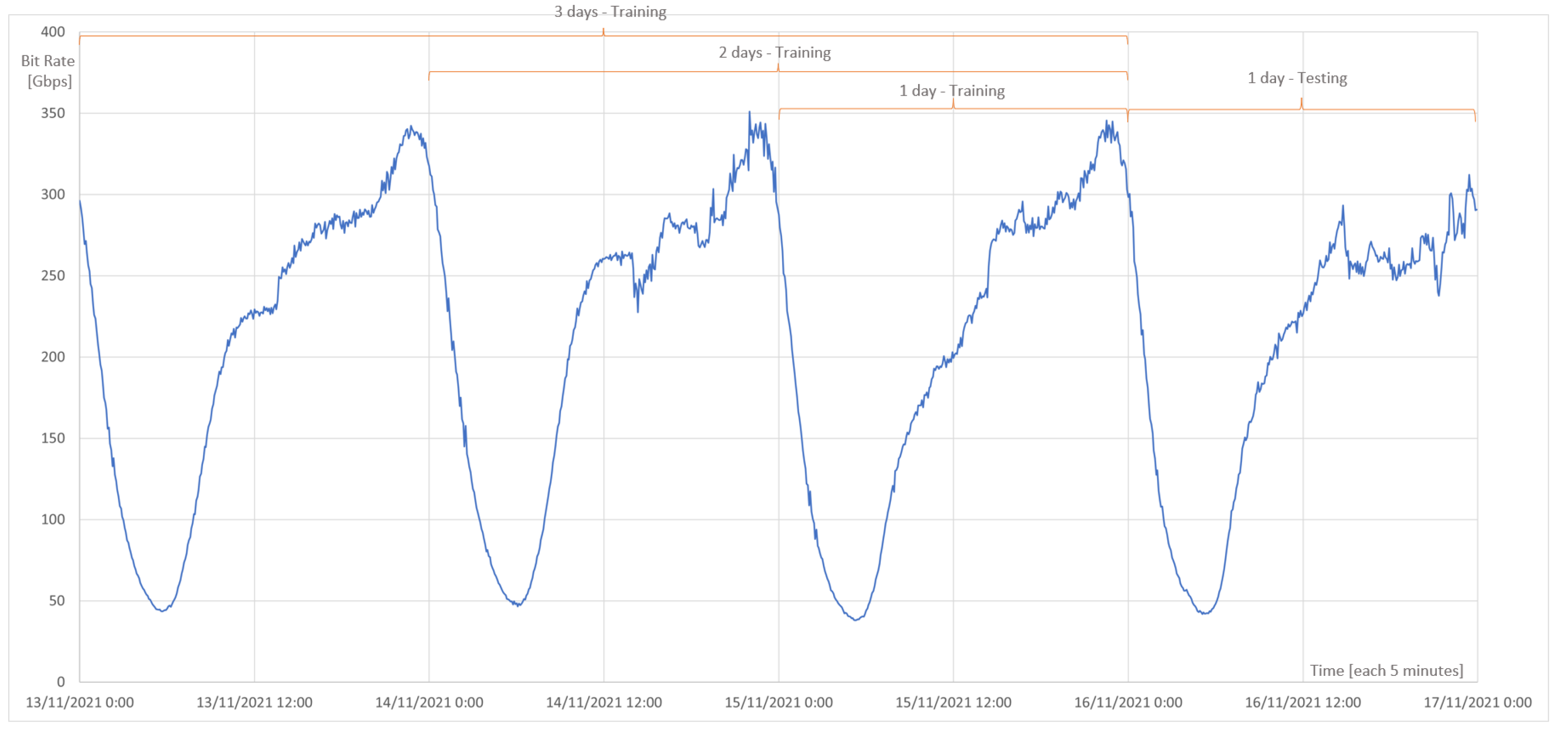
3.4. Training and Testing Data
3.5. Hyperparameters of RNN, LSTM, GRU, and OS-ELM
3.5.1. RNN, LSTM, and GRU Hyperparameters
- 1.
- Number of neurons: It is the number of hidden layers added to the RNN, LSTM, and GRU cell.
- 2.
- Epochs: It is the number of times each training dataset will pass through the neural network.
- 3.
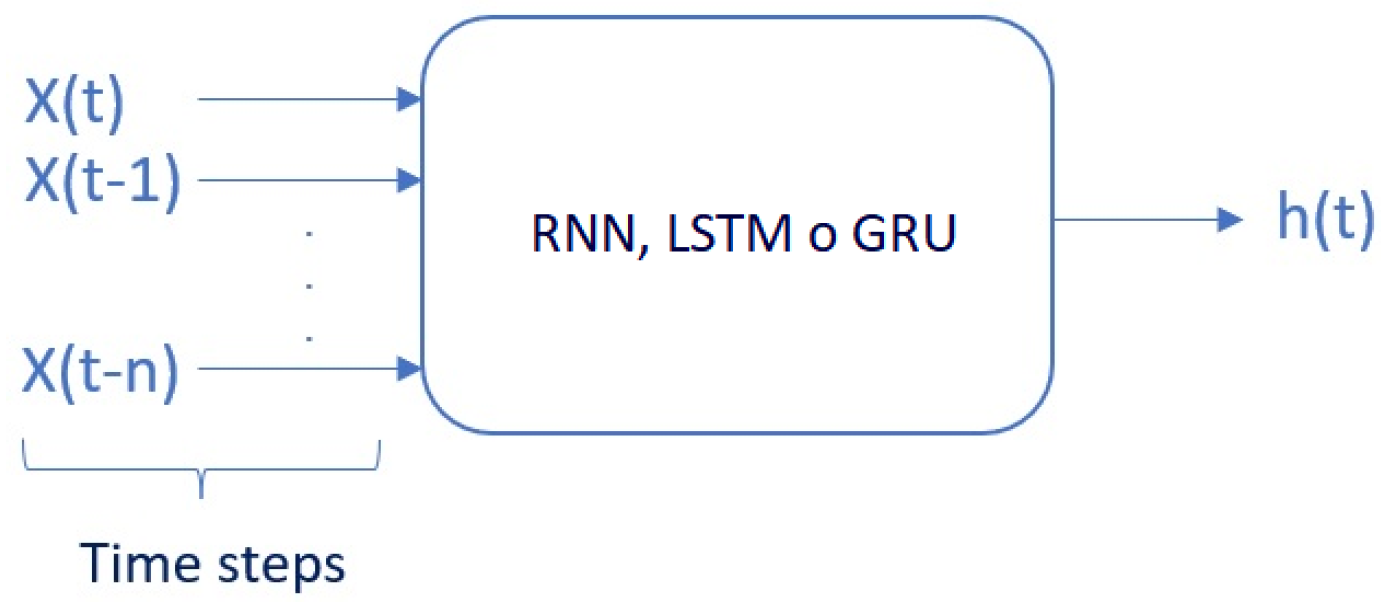
- Time steps: The number of time steps specified determines the number of input variables x used to predict the next time step h, as shown in Figure 3. In recurrent neural networks, time steps (also known as lags) refer to the number of previous time steps that are used as input to predict the next time step. For example, if the time steps are set to 3, the network will use the previous 3 time steps of the data as input to predict the next time step. The number of time steps can have a significant impact on the performance of the network, as it determines the amount of context that the network has access to when making predictions.
- 4.
- Adam optimizer: The Adam algorithm [67] is one that combines RMSProp with momentum. To date, there is no algorithm that has superior performance over others in different scenarios [68], so it is recommended to use the optimization algorithm with which the user feels the most comfortable when adjusting the hyperparameters. For running the simulations, the Adam-based optimization algorithm will be configured for RNN, LSTM, and GRU. Ref. [69] indicates that the Adam optimization algorithm has been a very popular optimizer in deep learning networks in recent years.
3.5.2. OS-ELM Hyperparameters
- 1.
- Number of neurons: It is the number of hidden layers added to the OS-ELM cell.
- 2.
- Forgetting factor: The forgetting factor allows the OS-ELM neural network to continuously forget obsolete input data in the training process, in order to reduce its negative effect on subsequent learning. If the forgetting factor equals 1, it means that the OS-ELM neural network does not forget anything. If the forgetting factor is less than 1, it starts to forget data.
3.6. Metrics
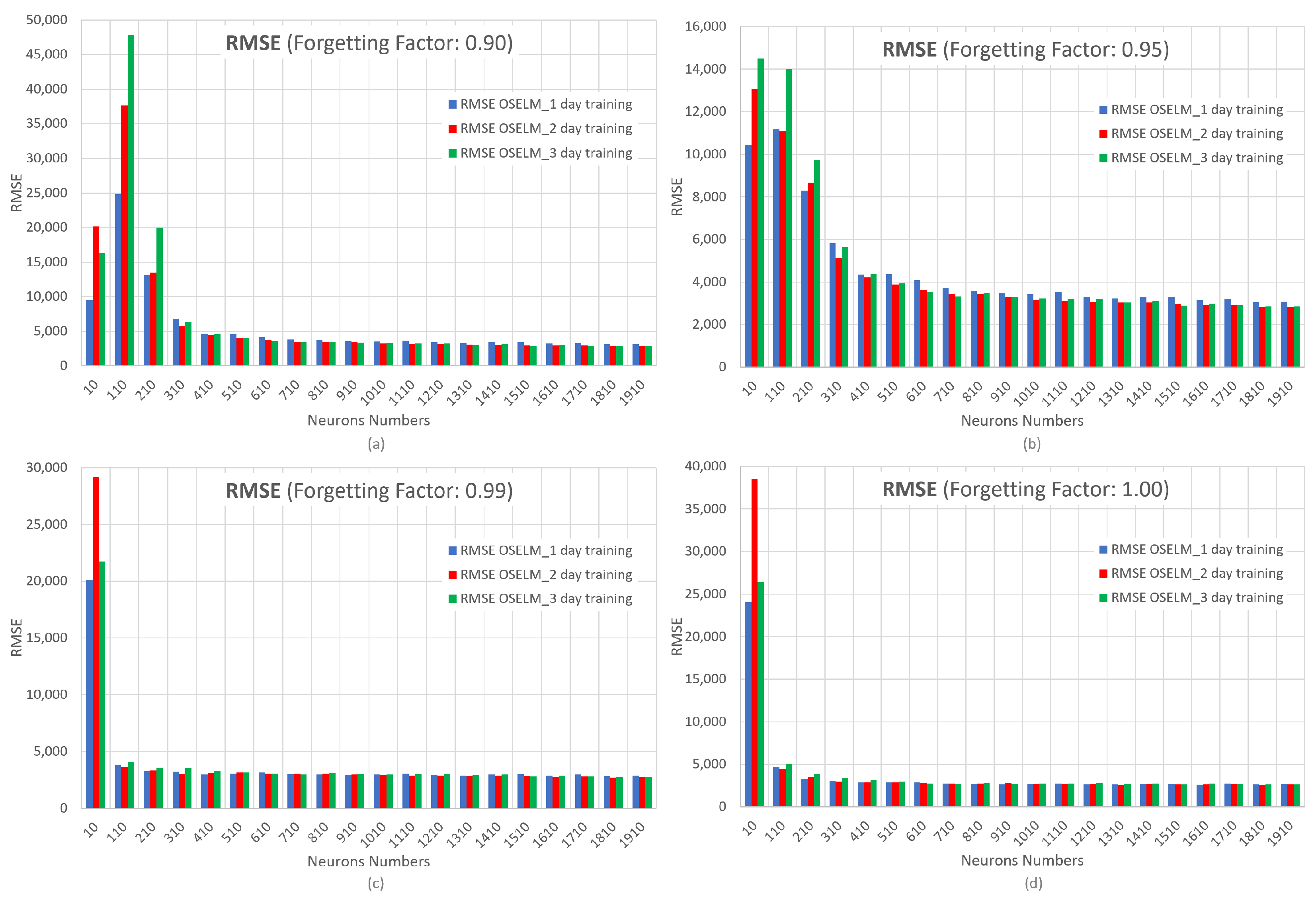
3.6.1. Root Mean Squared Error (RMSE)
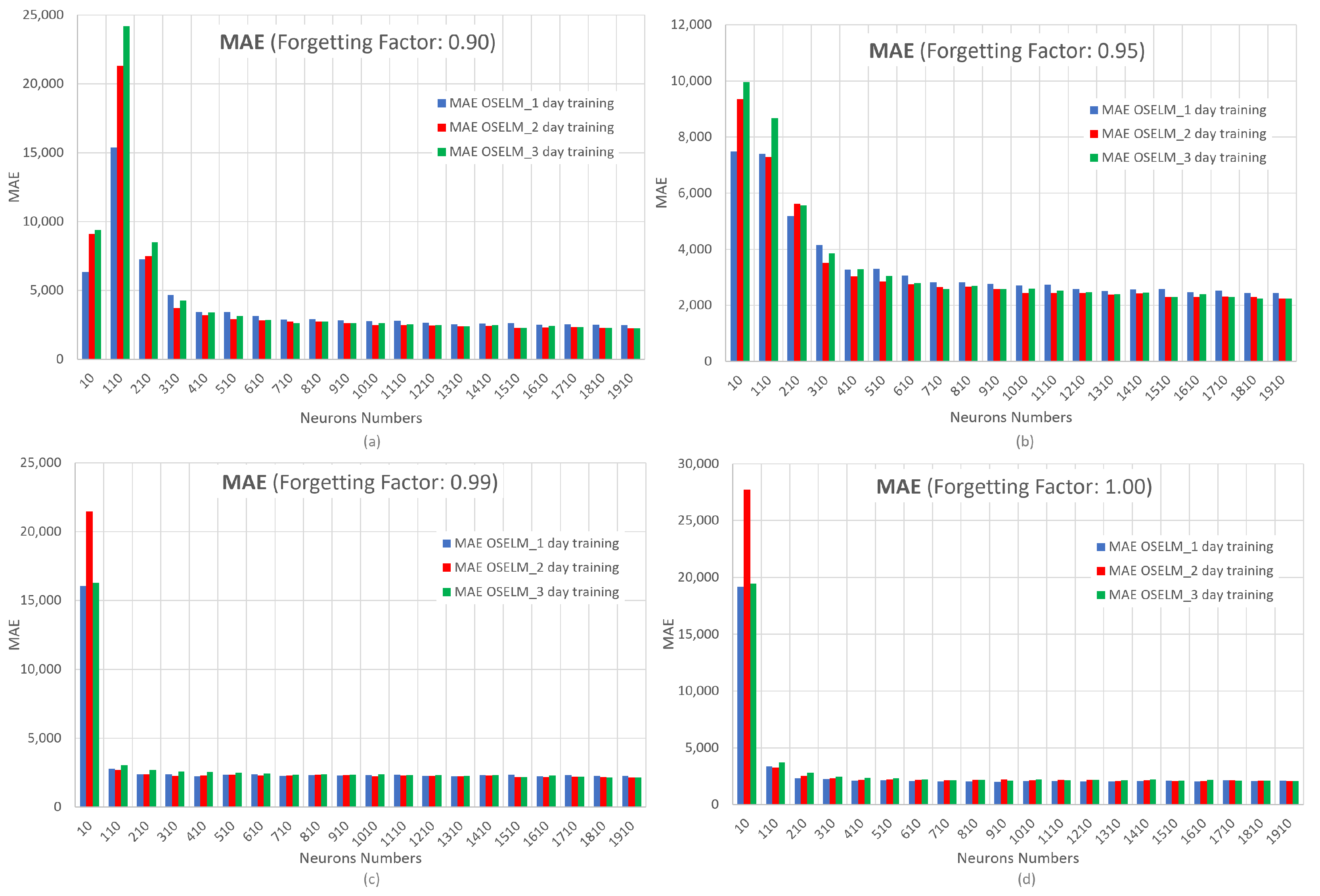
3.6.2. Mean Absolute Error (MAE)
3.6.3. Mean Absolute Percentage Error (MAPE)
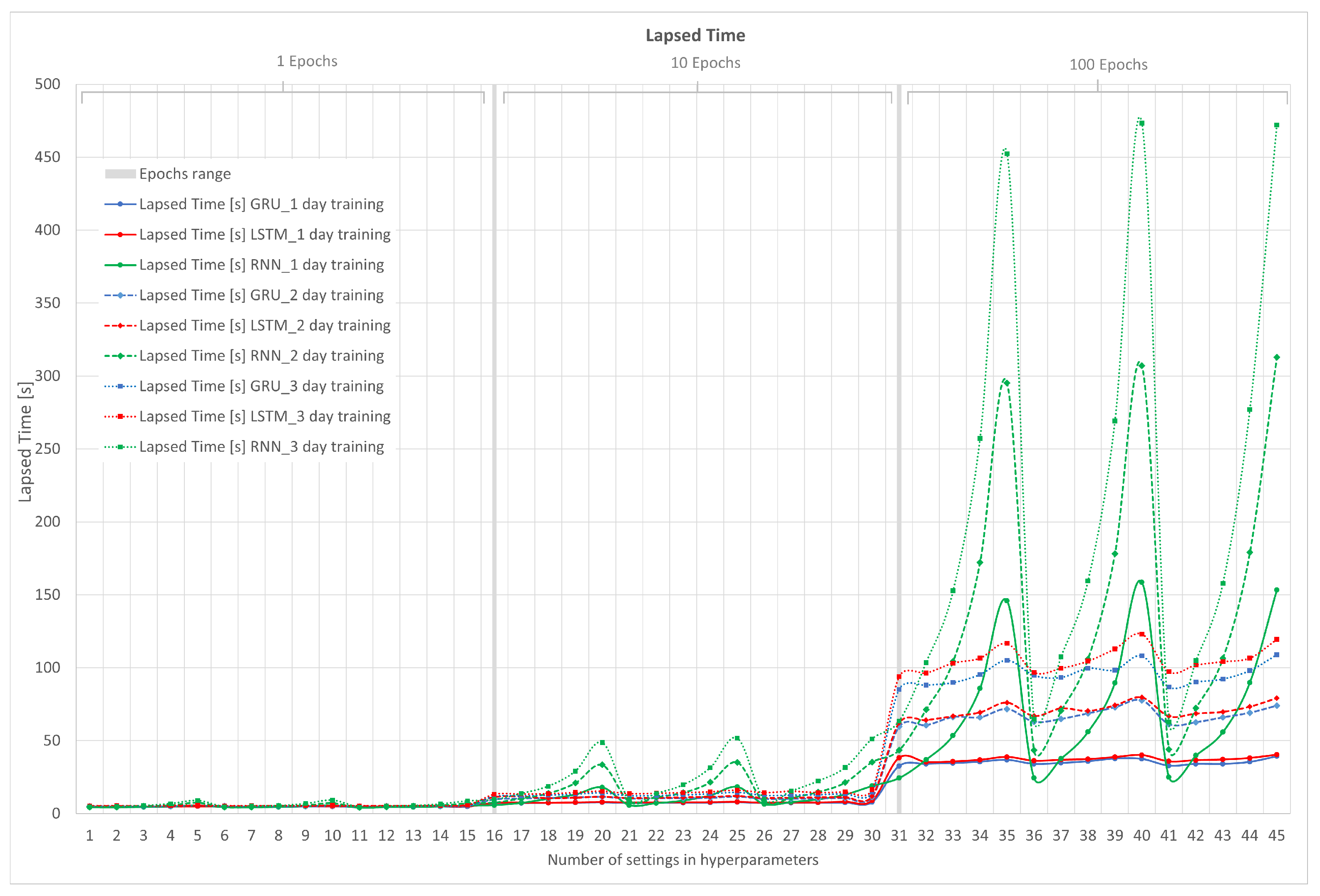
3.6.4. Computational Time
4. Bundle Ethernet Energy Efficiency Methodology
4.1. Threshold-Based and Prediction-Based Algorithms
4.1.1. Threshold-Based Algorithm
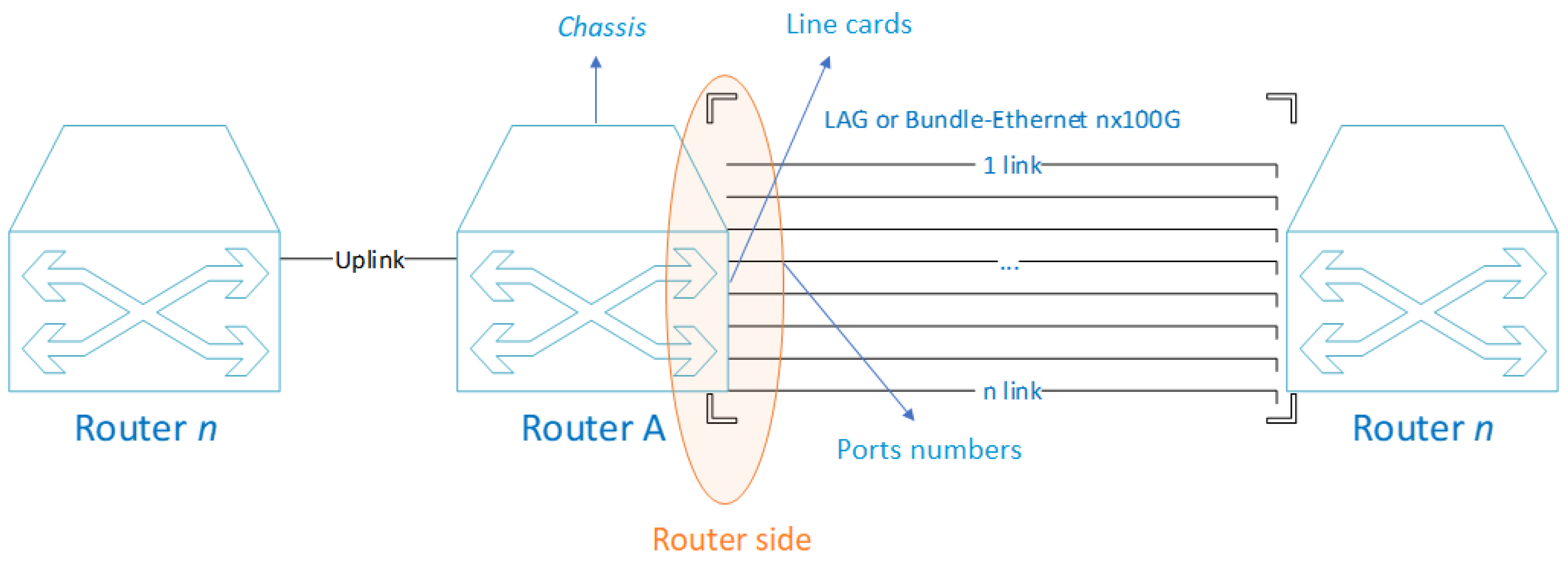
- : Raw value of the link speed in Gbps at a previous timestamp, i.e., ( ). This value is obtained from the Network Performance Monitor platform and is a continuous variable.
- : Number of links initially possessed by the LAG or BE; it is a discrete integer variable and dimensionless.
- : Port bandwidth measured in Gbps, and it is a continuous variable.
| Algorithm 1 Threshold-based Algorithm with raw value in |
| Require: raw value in t−1: ; numbers of links in LAG: ; port bandwidth: ▹ x is defined as a ratio variable ▹ is defined as ports active ▹ is defined as ports deactivate if then ▹ is defined as ports active update if then activate ports ▹ set in router activate ports deactivate ports ▹ set in router deactivate ports else activate ports ▹ set in router activate ports deactivate ports ▹ set in router deactivate ports end if end if |
4.1.2. Prediction-Based Algorithm
| Algorithm 2 Prediction-based algorithm |
| Require: prediction value: ; numbers of links in LAG: ; port bandwidth: ▹ x is defined as a ratio variable ▹ is defined as ports active ▹ is defined as ports deactivate if then ▹ is defined as ports active update if then activate ports ▹ set in router activate ports deactivate ports ▹ set in router deactivate ports else activate ports ▹ set in router activate ports deactivate ports ▹ set in router deactivate ports end if end if |
4.2. Metrics
5. Case Study
5.1. Network Topology
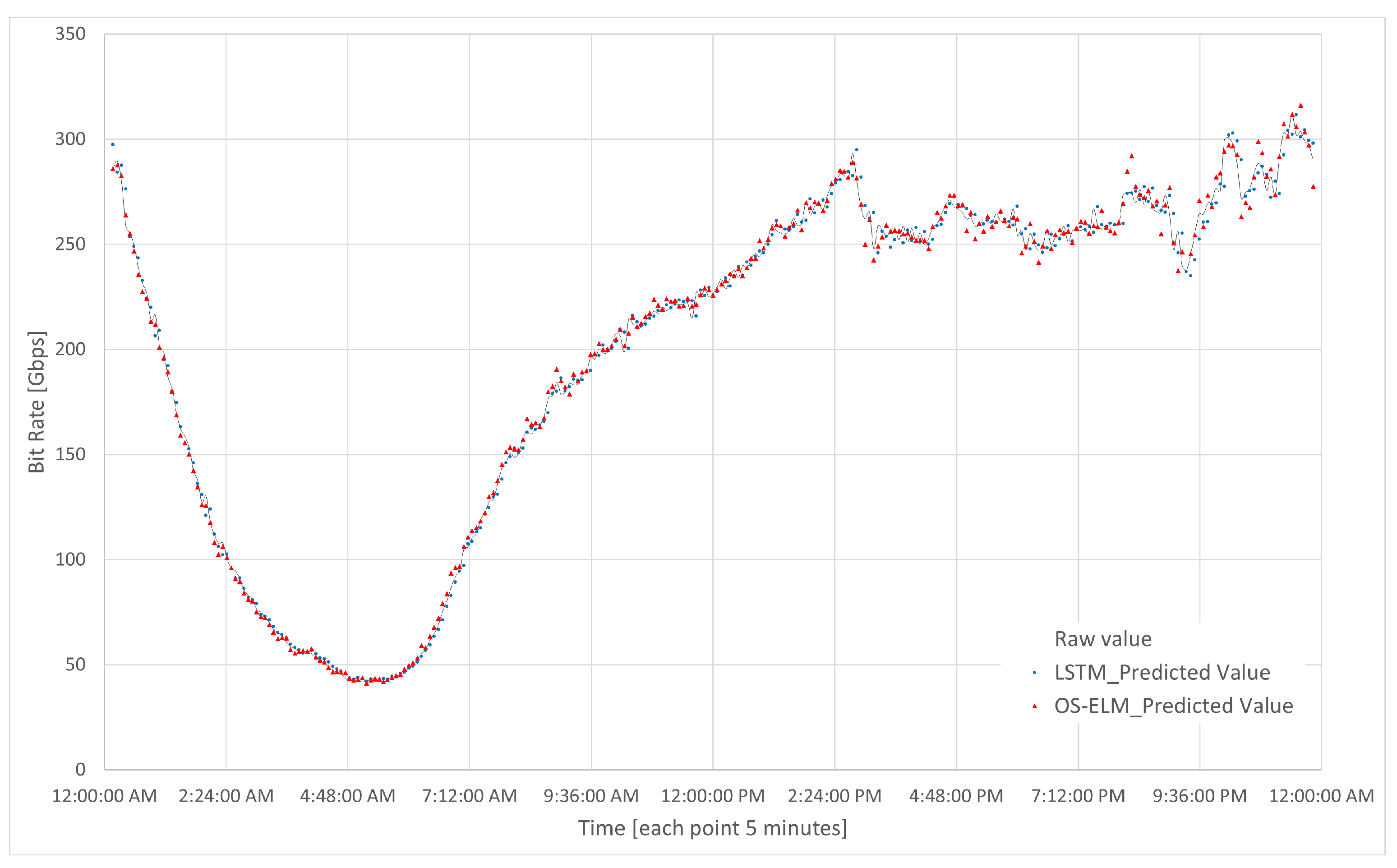
5.2. Traffic Description
- First set: 576 observations:
- -
- Training observations: 288;
- -
- Testing observations: 288.
- Second set: 864 observations:
- -
- Training observations: 576;
- -
- Testing observations: 288.
- Third set: 1152 observations:
- -
- Training observations: 864;
- -
- Testing observations: 288.
5.3. Equipment Characteristics
6. Traffic Forecasting Results in Case Study
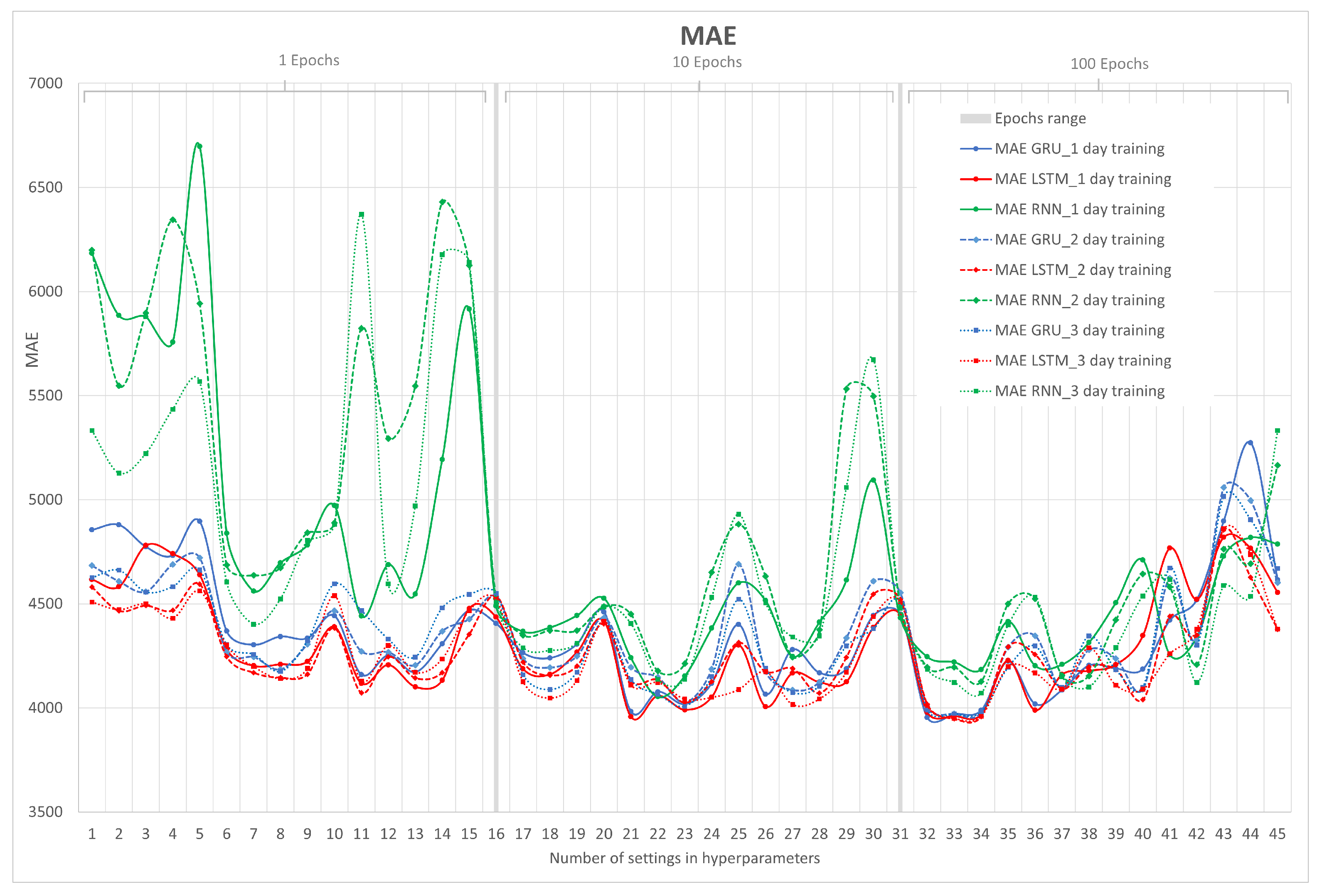
6.1. Simulation Results of RNN, LSTM, and GRU
- -
- Time steps (lags): 1, 4, 8, 16, and 32.
- -
- Number of neurons: 1, 10, and 50.
- -
- Epochs: 1, 10, and 100.
6.2. Simulation Results of the OS-ELM Neural Network
- -
- Number of neurons: 10, 110, 210, 310, 410, 510, 610, 710, 810, 910, 1010, 1110, 1210, 1310, 1410, 1510, 1610, 1710, 1810, and 1910.
- -
- Forgetting factor: 0.9, 0.95, 0.99, and 1.00.
6.3. Final Neural Network Selection
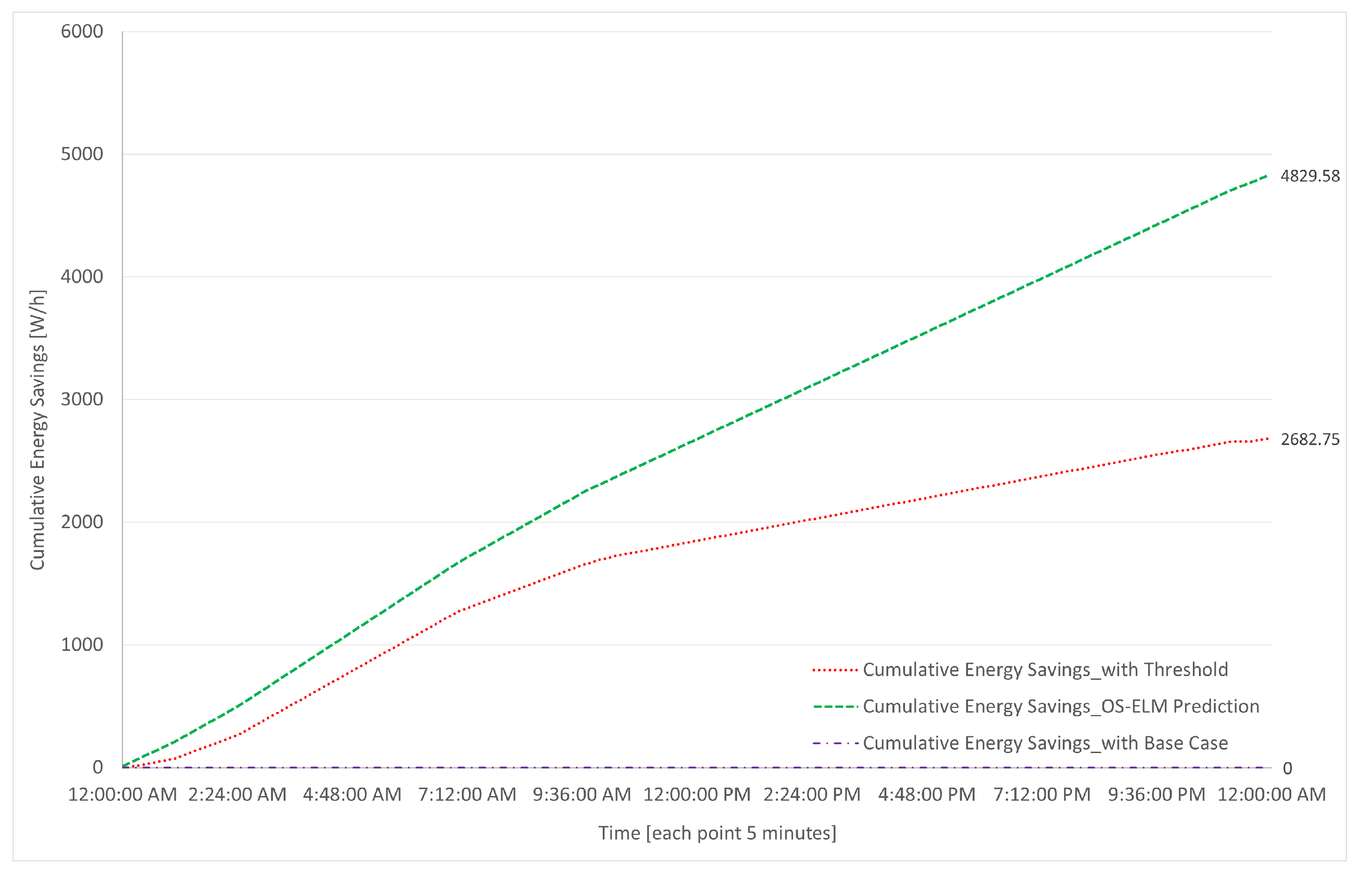
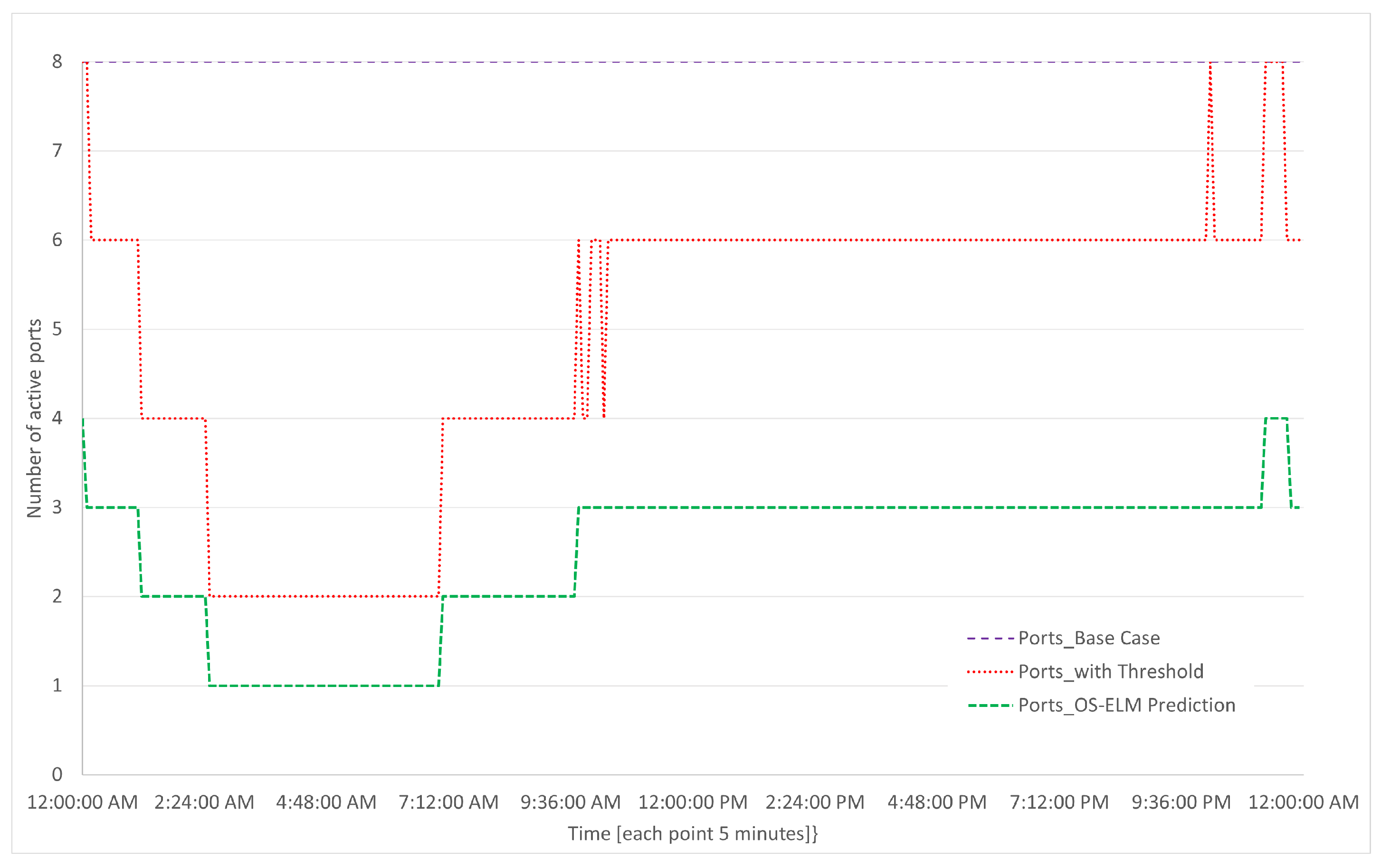
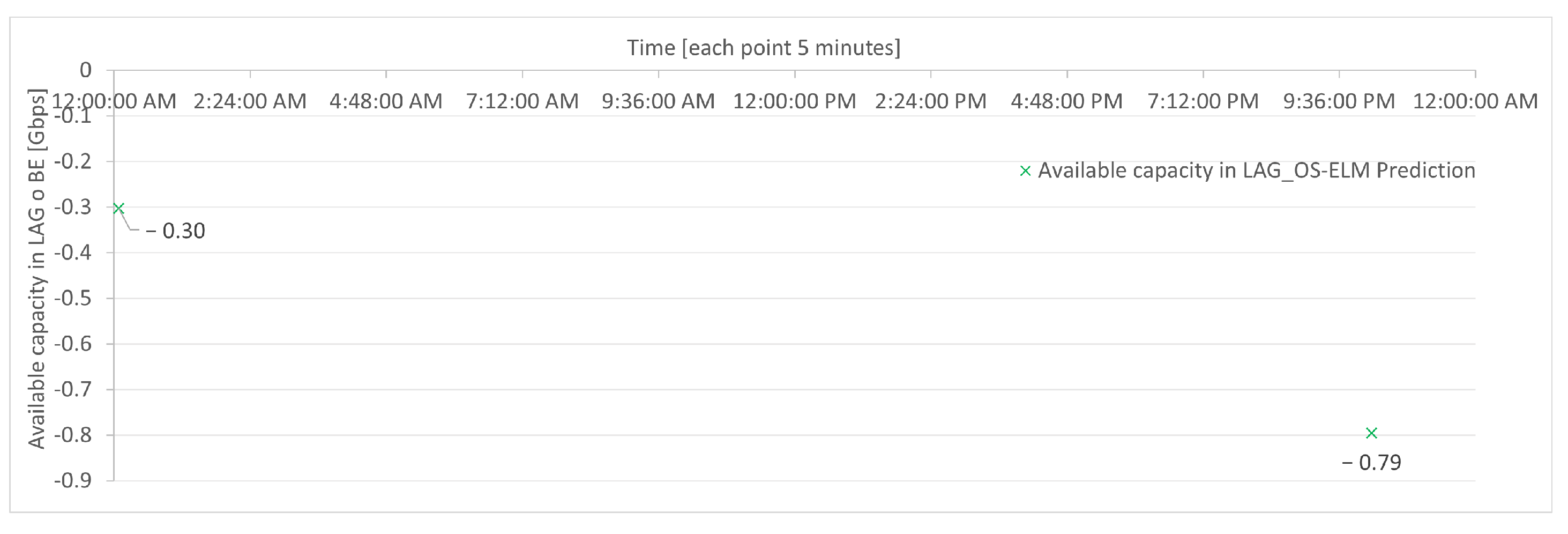
7. Results of Energy Efficiency Algorithms in the Case Study
8. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ARIMA | Autoregressive Integrated Moving Average |
| BE | Bundle Ethernet |
| BLSTM | Bidirectional Long Short-Term Memory |
| CDN | Content Delivery Network |
| CNN | Convolutional Neural Networks |
| DLHT | Dynamic Local Heuristic Threshold |
| DNN | Deep Neural Network |
| DRCN | Design of Reliable Communication Networks |
| DT | Decision Tree |
| EEE | Energy Efficient Ethernet |
| ELM | Extreme Learning Machine |
| EPC | Evolved Packet Core |
| FLHT | Fixed Local Heuristic Threshold |
| GPU | Graphics Processing Unit |
| GRU | Gated Recurrent Units |
| IEEE | Institute of Electrical and Electronics Engineers |
| IGR | Internet Gateway Router |
| ILP | Integer Linear Programming |
| IOT | Internet of Things |
| IP | Internet Protocol |
| LACP | Link Aggregation Control Protocol |
| LAG | Link Aggregation Groups |
| LP | Linear Programming |
| LPI | Low Power Idle |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MAPD | Mean Absolute Percentage Deviation |
| MAPE | Mean Absolute Percentage Error |
| MILP | Mixed-Integer Linear Problem |
| OS-ELM | Online Sequential Extreme Learning Machine |
| OTN | Optical Transport Network |
| PHY | Physical Layer |
| RF | Random Forest |
| RMSE | Root Mean Squared Error |
| RNN | Recurrent Neural Network |
| SARIMA | Seasonal Autoregressive Integrated Moving Average |
| SDN | Software-Defined Network |
| SMA | Simple Moving Average |
| SNMP | Simple Network Management Protocol |
| SPA | Standby Port Algorithm |
| SVM | Support Vector Machine |
| TQA | Two-Queuing Algorithm |
| TSO | Telecom Service Operator |
| WDM | Wavelength Division Multiplexing |
Appendix A
References
- Ahmed, K.M.U.; Bollen, M.H.J.; Alvarez, M. A Review of Data Centers Energy Consumption and Reliability Modeling. IEEE Access 2021, 9, 152536–152563. [Google Scholar] [CrossRef]
- Andrae, A.; Edler, T. On Global Electricity Usage of Communication Technology: Trends to 2030. Challenges 2015, 6, 117–157. [Google Scholar] [CrossRef]
- Junior, R.R.R.; Vieira, M.A.M.; Vieira, L.F.M.; Loureiro, A.A.F. Intra and inter-flow link aggregation in SDN. Telecommun. Syst. 2022, 79, 95–107. [Google Scholar] [CrossRef]
- Addis, B.; Capone, A.; Carello, G.; Gianoli, L.G.; Sanso, B. Energy Management Through Optimized Routing and Device Powering for Greener Communication Networks. IEEE/ACM Trans. Netw. 2014, 22, 313–325. [Google Scholar] [CrossRef]
- Mahadevan, P.; Sharma, P.; Banerjee, S.; Ranganathan, P. A power benchmarking framework for network devices. In Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Proceedings of the 8th International IFIP-TC 6 Networking Conference, Aachen, Germany, 11–15 May 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 795–808. [Google Scholar] [CrossRef]
- Fisher, W.; Suchara, M.; Rexford, J. Greening backbone networks. In Proceedings of the first ACM SIGCOMM Workshop on Green Networking; ACM: New York, NY, USA, 2010; pp. 29–34. [Google Scholar] [CrossRef]
- IEEE Standards Association. IEEE Std 802.1AX-2020 (Revision of IEEE Std 802.1AS-2014); IEEE Std 802.1AX™-2020, IEEE Standard for Local and Metropolitan Area Networks—Link Aggregation. IEEE Standards Association: Piscataway, NJ, USA, 2020; Volume 2020, pp. 1–421.
- Bianzino, A.P.; Chaudet, C.; Rossi, D.; Rougier, J.L. A Survey of Green Networking Research. IEEE Commun. Surv. Tutor. 2012, 14, 3–20. [Google Scholar] [CrossRef]
- IEEE 802.3az-2010; Energy Efficient Ethernet. IEEE: Piscataway, NJ, USA, 2010.
- Reviriego, P.; Christensen, K.; Bennett, M.; Nordman, B.; Maestro, J.A. Energy Efficiency in Ethernet. In Green Communications; John Wiley & Sons, Ltd.: Chichester, UK, 2015; pp. 277–290. [Google Scholar] [CrossRef]
- Liu, L.; Ramamurthy, B. A dynamic local method for bandwidth adaptation in bundle links to conserve energy in core networks. Opt. Switch. Netw. 2013, 10, 481–490. [Google Scholar] [CrossRef]
- Fondo-Ferreiro, P.; Rodríguez-Pérez, M.; Fernández-Veiga, M.; Herrería-Alonso, S. Matching SDN and Legacy Networking Hardware for Energy Efficiency and Bounded Delay. Sensors 2018, 18, 3915. [Google Scholar] [CrossRef]
- Imaizumi, H.; Nagata, T.; Kunito, G.; Yamazaki, K.; Morikawa, H. Power Saving Mechanism Based on Simple Moving Average for 802. In 3ad Link Aggregation. In Proceedings of the 2009 IEEE Globecom Workshops, Honolulu, HI, USA, 30 November–4 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Nihale, S.; Sharma, S.; Parashar, L.; Singh, U. Network Traffic Prediction Using Long Short-Term Memory. In Proceedings of the 2020 International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 2–4 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 338–343. [Google Scholar] [CrossRef]
- Rau, F.; Soto, I.; Zabala-Blanco, D. Forescating Mobile Network Traffic based on Deep Learning Networks. In Proceedings of the 2021 IEEE Latin-American Conference on Communications (LATINCOM), Santo Domingo, Dominican Republic, 17–19 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Andreoletti, D.; Troia, S.; Musumeci, F.; Giordano, S.; Maier, G.; Tornatore, M. Network Traffic Prediction based on Diffusion Convolutional recurrent neural networks. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Paris, France, 29 April–2 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 246–251. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, C.; He, H.; Wu, W.; Zhuang, W.; Shen, X. Cellular Traffic Load Prediction with LSTM and Gaussian Process Regression. In Proceedings of the ICC 2020–2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Liang, N.-Y.; Huang, G.-B.; Saratchandran, P.; Sundararajan, N. A Fast and Accurate Online Sequential Learning Algorithm for Feedforward Networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef]
- Rau, F.; Soto, I.; Adasme, P.; Zabala-Blanco, D.; Azurdia-Meza, C.A. Network Traffic Prediction Using Online-Sequential Extreme Learning Machine. In Proceedings of the 2021 Third South American Colloquium on Visible Light Communications (SACVLC), Toledo, Brazil, 11–12 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, H.; Singla, R. An intrusion detection system using network traffic profiling and online sequential extreme learning machine. Expert Syst. Appl. 2015, 42, 8609–8624. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, Z.; Gao, J.; Xu, C. Forecast Methods for Time Series Data: A Survey. IEEE Access 2021, 9, 91896–91912. [Google Scholar] [CrossRef]
- Wu, J.; He, Y. Prediction of GDP in Time Series Data Based on Neural Network Model. In Proceedings of the 2021 IEEE International Conference on Artificial Intelligence and Industrial Design (AIID), Guangzhou, China, 28–30 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 20–23. [Google Scholar] [CrossRef]
- Do, Q.H.; Doan, T.T.H.; Nguyen, T.V.A.; Duong, N.T.; Linh, V.V. Prediction of Data Traffic in Telecom Networks based on Deep Neural Networks. J. Comput. Sci. 2020, 16, 1268–1277. [Google Scholar] [CrossRef]
- Mao, Q.; Hu, F.; Hao, Q. Deep Learning for Intelligent Wireless Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2018, 20, 2595–2621. [Google Scholar] [CrossRef]
- Hou, Y.; Zheng, X.; Han, C.; Wei, W.; Scherer, R.; Połap, D. Deep Learning Methods in Short-Term Traffic Prediction: A Survey. Inf. Technol. Control 2022, 51, 139–157. [Google Scholar] [CrossRef]
- Huang, S.C.; Wu, C.F. Energy Commodity Price Forecasting with Deep Multiple Kernel Learning. Energies 2018, 11, 3029. [Google Scholar] [CrossRef]
- Xiao, C.; Choi, E.; Sun, J. Opportunities and challenges in developing deep learning models using electronic health records data: A systematic review. J. Am. Med. Inform. Assoc. 2018, 25, 1419–1428. [Google Scholar] [CrossRef] [PubMed]
- Lepot, M.; Aubin, J.B.; Clemens, F. Interpolation in Time Series: An Introductive Overview of Existing Methods, Their Performance Criteria and Uncertainty Assessment. Water 2017, 9, 796. [Google Scholar] [CrossRef]
- Zhang, X.; Kuehnelt, H.; De Roeck, W. Traffic Noise Prediction Applying Multivariate Bi-Directional Recurrent Neural Network. Appl. Sci. 2021, 11, 2714. [Google Scholar] [CrossRef]
- Shin, J.; Yeon, K.; Kim, S.; Sunwoo, M.; Han, M. Comparative Study of Markov Chain With Recurrent Neural Network for Short Term Velocity Prediction Implemented on an Embedded System. IEEE Access 2021, 9, 24755–24767. [Google Scholar] [CrossRef]
- Impedovo, D.; Dentamaro, V.; Pirlo, G.; Sarcinella, L. TrafficWave: Generative Deep Learning Architecture for Vehicular Traffic Flow Prediction. Appl. Sci. 2019, 9, 5504. [Google Scholar] [CrossRef]
- Sha, S.; Li, J.; Zhang, K.; Yang, Z.; Wei, Z.; Li, X.; Zhu, X. RNN-Based Subway Passenger Flow Rolling Prediction. IEEE Access 2020, 8, 15232–15240. [Google Scholar] [CrossRef]
- Zeng, C.; Ma, C.; Wang, K.; Cui, Z. Parking Occupancy Prediction Method Based on Multi Factors and Stacked GRU-LSTM. IEEE Access 2022, 10, 47361–47370. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, S.M.; Dey, K.; Chowdhury, M. Development and Evaluation of Recurrent Neural Network-Based Models for Hourly Traffic Volume and Annual Average Daily Traffic Prediction. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 489–503. [Google Scholar] [CrossRef]
- Chui, K.T.; Gupta, B.B.; Liu, R.W.; Zhang, X.; Vasant, P.; Thomas, J.J. Extended-Range Prediction Model Using NSGA-III Optimized RNN-GRU-LSTM for Driver Stress and Drowsiness. Sensors 2021, 21, 6412. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, M.; Sun, N.; Alexander, D.C.; Feng, J.; Yeo, B.T. Modeling Alzheimer’s disease progression using deep recurrent neural networks. In Proceedings of the 2018 International Workshop on Pattern Recognition in Neuroimaging (PRNI), Singapore, 12–14 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Li, P.; Shi, Y.; Xing, Y.; Liao, C.; Yu, M.; Guo, C.; Feng, L. Intra-Cluster Federated Learning-Based Model Transfer Framework for Traffic Prediction in Core Network. Electronics 2022, 11, 3793. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Yuan, D.; Zhang, M. Citywide Cellular Traffic Prediction Based on Densely Connected Convolutional Neural Networks. IEEE Commun. Lett. 2018, 22, 1656–1659. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, S.; Wang, C.X.; Hong, X.; McLaughlin, S. Artificial Intelligence to Manage Network Traffic of 5G Wireless Networks. IEEE Netw. 2018, 32, 58–64. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, L.; Xie, C.; Yang, B.; Liu, Q. Citywide Cellular Traffic Prediction Based on a Hybrid Spatiotemporal Network. Algorithms 2020, 13, 20. [Google Scholar] [CrossRef]
- Kao, C.C.; Chang, C.W.; Cho, C.P.; Shun, J.Y. Deep Learning and Ensemble Learning for Traffic Load Prediction in Real Network. In Proceedings of the 2020 IEEE Eurasia Conference on IOT, Communication and Engineering (ECICE), Yunlin, Taiwan, 23–25 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 36–39. [Google Scholar] [CrossRef]
- Santos, G.L.; Rosati, P.; Lynn, T.; Kelner, J.; Sadok, D.; Endo, P.T. Predicting short-term mobile Internet traffic from Internet activity using recurrent neural networks. Int. J. Netw. Manag. 2022, 32, e2191. [Google Scholar] [CrossRef]
- Nejadettehad, A.; Mahini, H.; Bahrak, B. Short-term Demand Forecasting for Online Car-hailing Services Using recurrent neural networks. Appl. Artif. Intell. 2020, 34, 674–689. [Google Scholar] [CrossRef]
- Kumar, B.P.; Hariharan, K.; Shanmugam, R.; Shriram, S.; Sridhar, J. Enabling internet of things in road traffic forecasting with deep learning models. J. Intell. Fuzzy Syst. 2022, 43, 6265–6276. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Park, J.M.; Kim, J.H. Online recurrent extreme learning machine and its application to time-series prediction. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: Piscataway, NJ, USA, 2017; Volume 2017-May, pp. 1983–1990. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, K.; Li, J.; Lin, X.; Yang, B. LSTM-based traffic flow prediction with missing data. Neurocomputing 2018, 318, 297–305. [Google Scholar] [CrossRef]
- Baytas, I.M.; Xiao, C.; Zhang, X.; Wang, F.; Jain, A.K.; Zhou, J. Patient Subtyping via Time-Aware LSTM Networks. In KDD ’17, Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; ACM: New York, NY, USA, 2017; pp. 65–74. [Google Scholar] [CrossRef]
- Rubanova, Y.; Chen, R.T.; Duvenaud, D. Latent odes for irregularly-sampled time series. arXiv 2019, arXiv:1907.03907. [Google Scholar]
- Vecoven, N.; Ernst, D.; Drion, G. A bio-inspired bistable recurrent cell allows for long-lasting memory. PLoS ONE 2021, 16, e0252676. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, Z. Recover missing sensor data with iterative imputing network. In Proceedings of the Workshops at the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar] [CrossRef]
- Weerakody, P.B.; Wong, K.W.; Wang, G.; Ela, W. A review of irregular time series data handling with gated recurrent neural networks. Neurocomputing 2021, 441, 161–178. [Google Scholar] [CrossRef]
- Mahmood, A.; Mat Kiah, M.L.; Reza Z’Aba, M.; Qureshi, A.N.; Kassim, M.S.S.; Azizul Hasan, Z.H.; Kakarla, J.; Sadegh Amiri, I.; Azzuhri, S.R. Capacity and Frequency Optimization of Wireless Backhaul Network Using Traffic Forecasting. IEEE Access 2020, 8, 23264–23276. [Google Scholar] [CrossRef]
- Ba, S.; Ouédraogo, I.A.; Oki, E. A power consumption reduction scheme in hose-model networks with bundled links. In Proceedings of the 2013 IEEE International Conference on Green Computing and Communications and IEEE Internet of Things and IEEE Cyber, Physical and Social Computing, GreenCom-iThings-CPSCom 2013, Beijing, China, 20–23 August 2013; pp. 40–45. [Google Scholar] [CrossRef]
- Galán-Jiménez, J.; Gazo-Cervero, A. Designing energy-efficient link aggregation groups. Ad. Hoc. Netw. 2015, 25, 595–605. [Google Scholar] [CrossRef]
- Rodriguez-Perez, M.; Fernandez-Veiga, M.; Herreria-Alonso, S.; Hmila, M.; Lopez-Garcia, C. Optimum Traffic Allocation in Bundled Energy-Efficient Ethernet Links. IEEE Syst. J. 2018, 12, 593–603. [Google Scholar] [CrossRef]
- Fondo-Ferreiro, P.; Rodriguez-Perez, M.; Fernandez-Veiga, M. Implementing energy saving algorithms for ethernet link aggregates with ONOS. In Proceedings of the 2018 5th International Conference on Software Defined Systems, SDS 2018, Barcelona, Spain, 23–26 April 2018; pp. 118–125. [Google Scholar] [CrossRef]
- Ramakrishnan, N.; Soni, T. Network Traffic Prediction Using recurrent neural networks. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 187–193. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated recurrent neural networks on Sequence Modeling. In Proceedings of the NIPS 2014 Deep Learning and Representation Learning Workshop, Montreal, QC, Canada, 12 December 2014. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, W.; Li, Y.; Zhang, S. Residual compensation extreme learning machine for regression. Neurocomputing 2018, 311, 126–136. [Google Scholar] [CrossRef]
- Lim, J.-s.; Lee, S.; Pang, H.S. Low complexity adaptive forgetting factor for online sequential extreme learning machine (OS-ELM) for application to nonstationary system estimations. Neural Comput. Appl. 2013, 22, 569–576. [Google Scholar] [CrossRef]
- Jian, L.; Gao, F.; Ren, P.; Song, Y.; Luo, S. A Noise-Resilient Online Learning Algorithm for Scene Classification. Remote Sens. 2018, 10, 1836. [Google Scholar] [CrossRef]
- Shrivastava, S. Cross Validation in Time Series, 2020. Available online: https://medium.com/@soumyachess1496 (accessed on 17 May 2023).
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Tashman, L.J. Out of Sample Tests of Forecasting Accuracy: An Analysis and Review. Int. J. Forecast. 2000, 16, 437–450. [Google Scholar] [CrossRef]
- Varma, S.; Simon, R. Bias in error estimation when using cross-validation for model selection. BMC Bioinform. 2006, 7, 91. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar] [CrossRef]
- Schaul, T.; Antonoglou, I.; Silver, D. Unit Tests for Stochastic Optimization. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar] [CrossRef]
- Bock, S.; Goppold, J.; Weiß, M. An improvement of the convergence proof of the ADAM-Optimizer. In Proceedings of the OTH CLUSTERKONFERENZ, Weiden, Germany, 13 April 2018. [Google Scholar] [CrossRef]
- Carling, K.; Meng, X. Confidence in Heuristic Solutions. J. Glob. Optim. 2015, 63, 381–399. [Google Scholar] [CrossRef]
- Yue, Y.; Wang, Q.; Yao, J.; O’Neil, J.; Pudvay, D.; Anderson, J. 400GbE Technology Demonstration Using CFP8 Pluggable Modules. Appl. Sci. 2018, 8, 2055. [Google Scholar] [CrossRef]
- Zhang, W.; Bathula, B.G.; Sinha, R.K.; Doverspike, R.; Magill, P.; Raghuram, A.; Choudhury, G. Cost Comparison of Alternative Architectures for IP-over-Optical Core Networks. J. Netw. Syst. Manag. 2016, 24, 607–628. [Google Scholar] [CrossRef]
- IEEE Standards Association. IEEE Std 802.3ad-2000; IEEE Standard for Information Technology—Local and Metropolitan Area Networks—Part 3: Carrier Sense Multiple Access with Collision Detection (CSMA/CD) Access Method and Physical Layer Specifications-Aggregation of Multiple Link Segments. IEEE Standards Association: Piscataway, NJ, USA, 2000; pp. 1–184. [CrossRef]
- Braun, R.P. 100Gbit/s IP-Router and DWDM Transmission Interoperability Field Tests. In Proceedings of the Photonic Networks, 12. ITG Symposium, Leipzig, Germany, 2–3 May 2011; pp. 1–3. [Google Scholar]
- IEEE. IEEE Std 802.3-2015; IEEE Std 802.3-2015 (Revision of IEEE Std 802.3-2012). IEEE Standards Association: Piscataway, NJ, USA, 2016; pp. 1–4017. [CrossRef]
- IEEE Standards Association. IEEE Std 802.3bm-2015; IEEE Standard for Ethernet Amendment 3: Physical Layer Specifications and Management Parameters for 40 Gb/s and 100 Gb/s Operation over Fiber Optic Cables. IEEE: Piscataway, NJ, USA, 2015.
- Reviriego, P.; Hernadez, J.A.; Larrabeiti, D.; Maestro, J.A. Burst Transmission in Energy Efficient Ethernet. IEEE Internet Comput. 2010, 14, 50–57. [Google Scholar] [CrossRef]










| Hardware | |
|---|---|
| CPU | Intel(R) Core(TM) 8600 K at 5.1 Ghz |
| RAM | 32 Gb |
| Graphics card | NVIDIA GeForce(R) RTX 2080. |
| Software | |
| Python | 3.7.10 |
| Tensorflow | 2.2.0 |
| Keras | 2.3.0 |
| Pandas | 1.2.4 |
| Scikit-Learn | 0.24.1 |
| Slot | Board Info | Typical Power at 25 °C (W) |
|---|---|---|
| Slot1 | LPUF-480-E | 290 |
| Slot1-PIC0 | PIC-2*100GBase-QSFP28 | 73 |
| Slot1-PIC1 | PIC-2*100GBase-QSFP28 | 73 |
| Slot2 | LPUF-480-E | 290 |
| Slot2-PIC0 | PIC-2*100GBase-QSFP28 | 73 |
| Slot2-PIC1 | PIC-2*100GBase-QSFP28 | 73 |
| Number | Hyperparameters Setting | Number | Hyperparameters Setting | Number | Hyperparameters Setting |
|---|---|---|---|---|---|
| 1 | 1,1,1 | 16 | 1,1,10 | 31 | 1,1,100 |
| 2 | 4,1,1 | 17 | 4,1,10 | 32 | 4,1,100 |
| 3 | 8,1,1 | 18 | 8,1,10 | 33 | 8,1,100 |
| 4 | 16,1,1 | 19 | 16,1,10 | 34 | 16,1,100 |
| 5 | 32,1,1 | 20 | 32,1,10 | 35 | 32,1,100 |
| 6 | 1,10,1 | 21 | 1,10,10 | 36 | 1,10,100 |
| 7 | 4,10,1 | 22 | 4,10,10 | 37 | 4,10,100 |
| 8 | 8,10,1 | 23 | 8,10,10 | 38 | 8,10,100 |
| 9 | 16,10,1 | 24 | 16,10,10 | 39 | 16,10,100 |
| 10 | 32,10,1 | 25 | 32,10,10 | 40 | 32,10,100 |
| 11 | 1,50,1 | 26 | 1,50,10 | 41 | 1,50,100 |
| 12 | 4,50,1 | 27 | 4,50,10 | 42 | 4,50,100 |
| 13 | 8,50,1 | 28 | 8,50,10 | 43 | 8,50,100 |
| 14 | 16,50,1 | 29 | 16,50,10 | 44 | 16,50,100 |
| 15 | 32,50,1 | 30 | 32,50,10 | 45 | 32,50,100 |
| Type | Group | Training | Time Step (Lags) | Number Neurons | Epochs | RMSE | MAE | MAPE | Lapsed Time [s] |
|---|---|---|---|---|---|---|---|---|---|
| RNN | First | 1 day | 4 | 10 | 10 | 5711.161 | 4054.292 | 0.02137 | 7.177 |
| RNN | Second | 2 days | 16 | 1 | 100 | 5728.889 | 4126.839 | 0.02184 | 172.208 |
| RNN | Third | 3 days | 16 | 1 | 100 | 5679.286 | 4070.981 | 0.02126 | 257.146 |
| LSTM | First | 1 day | 8 | 1 | 100 | 5573.399 | 3961.516 | 0.01959 | 35.745 |
| LSTM | Second | 2 days | 8 | 1 | 100 | 5581.399 | 3947.681 | 0.01998 | 66.765 |
| LSTM | Third | 3 days | 8 | 1 | 100 | 5585.884 | 3950.845 | 0.01958 | 103.195 |
| GRU | First | 1 day | 4 | 1 | 100 | 5612.749 | 3953.799 | 0.01970 | 34.093 |
| GRU | Second | 2 days | 8 | 1 | 100 | 5600.504 | 3972.234 | 0.01962 | 66.179 |
| GRU | Third | 3 days | 8 | 1 | 100 | 5600.595 | 3971.039 | 0.01962 | 89.822 |
| Type | Group | Training | Forgetting Factor | Number Neurons | RMSE | MAE | MAPE | Lapsed Time [s] |
|---|---|---|---|---|---|---|---|---|
| OS-ELM | First | 1 day | 0.95 | 410 | 4336.068 | 3273.084 | 0.01761 | 1.128 |
| OS-ELM | Second | 2 days | 0.95 | 410 | 4221.912 | 3037.816 | 0.01642 | 1.182 |
| OS-ELM | Third | 3 days | 0.95 | 410 | 4384.103 | 3276.136 | 0.01778 | 1.113 |
| Type | Training | RMSE | % RMSE | MAE | % MAE | MAPE | % MAPE | Lapsed Time [s] | Times |
|---|---|---|---|---|---|---|---|---|---|
| OS-ELM | 2 days | 4221.912 | 26% | 3037.816 | 25% | 0.01642 | 23% | 1.182 | 217.6x |
| LSTM | 1 day | 5573.399 | 2% | 3961.516 | 3% | 0.01999 | 6% | 35.745 | 7.2x |
| GRU | 2 days | 5600.504 | 1% | 3972.234 | 2% | 0.01962 | 8% | 66.179 | 3.9x |
| RNN | 3 days | 5679.286 | - | 4070.981 | - | 0.02126 | - | 257.146 | - |
| Type | Training | RMSE | % RMSE | MAE | % MAE | MAPE | % MAPE | Lapsed Time [s] | Times |
|---|---|---|---|---|---|---|---|---|---|
| OS-ELM | 2 days | 4221.912 | 24% | 3037.816 | 23% | 0.01642 | 18% | 1.182 | 30.2x |
| LSTM | 1 day | 5573.399 | - | 3961.516 | - | 0.01999 | - | 35.745 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rau, F.; Soto, I.; Zabala-Blanco, D.; Azurdia-Meza, C.; Ijaz, M.; Ekpo, S.; Gutierrez, S. A Novel Traffic Prediction Method Using Machine Learning for Energy Efficiency in Service Provider Networks. Sensors 2023, 23, 4997. https://doi.org/10.3390/s23114997
Rau F, Soto I, Zabala-Blanco D, Azurdia-Meza C, Ijaz M, Ekpo S, Gutierrez S. A Novel Traffic Prediction Method Using Machine Learning for Energy Efficiency in Service Provider Networks. Sensors. 2023; 23(11):4997. https://doi.org/10.3390/s23114997
Chicago/Turabian StyleRau, Francisco, Ismael Soto, David Zabala-Blanco, Cesar Azurdia-Meza, Muhammad Ijaz, Sunday Ekpo, and Sebastian Gutierrez. 2023. "A Novel Traffic Prediction Method Using Machine Learning for Energy Efficiency in Service Provider Networks" Sensors 23, no. 11: 4997. https://doi.org/10.3390/s23114997
APA StyleRau, F., Soto, I., Zabala-Blanco, D., Azurdia-Meza, C., Ijaz, M., Ekpo, S., & Gutierrez, S. (2023). A Novel Traffic Prediction Method Using Machine Learning for Energy Efficiency in Service Provider Networks. Sensors, 23(11), 4997. https://doi.org/10.3390/s23114997










