Impedance Variation in a Coaxial Coil Encircling a Metal Tube Adapter
Abstract
:1. Introduction
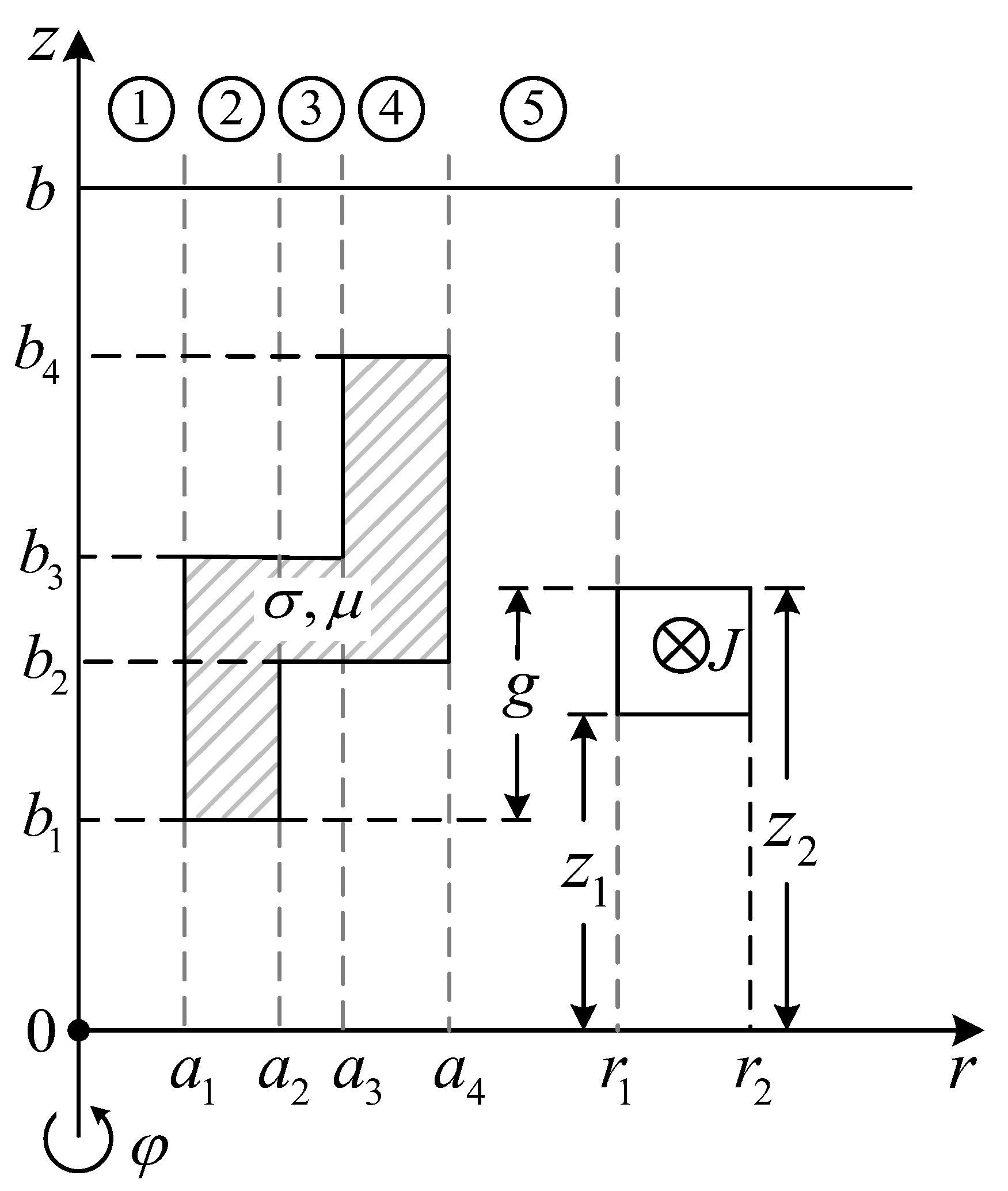
2. Formulation
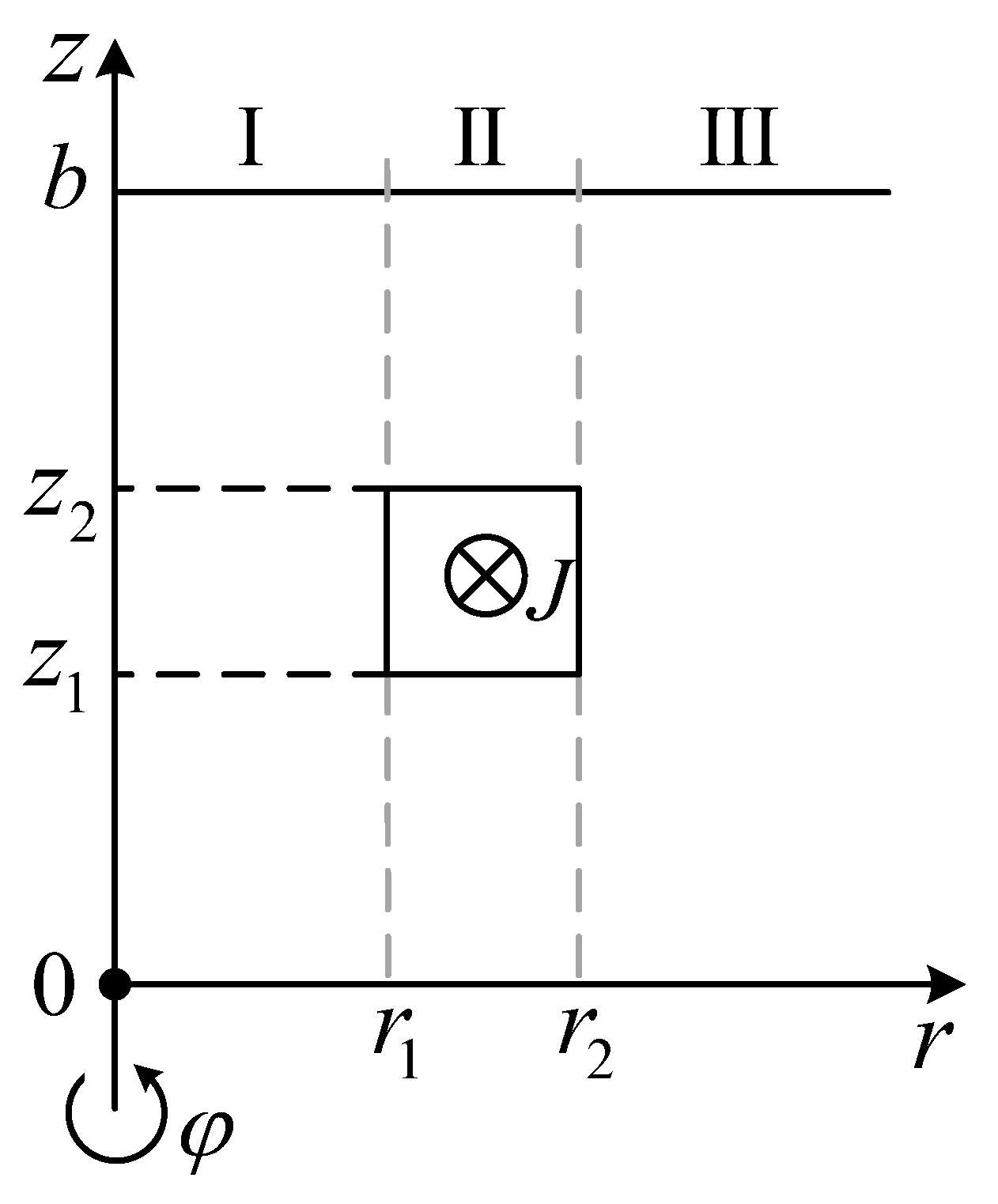
2.1. Vector Potential of the Source Coil
2.2. Impedance Change in the Coil Encircling the Metal Tube Adapter
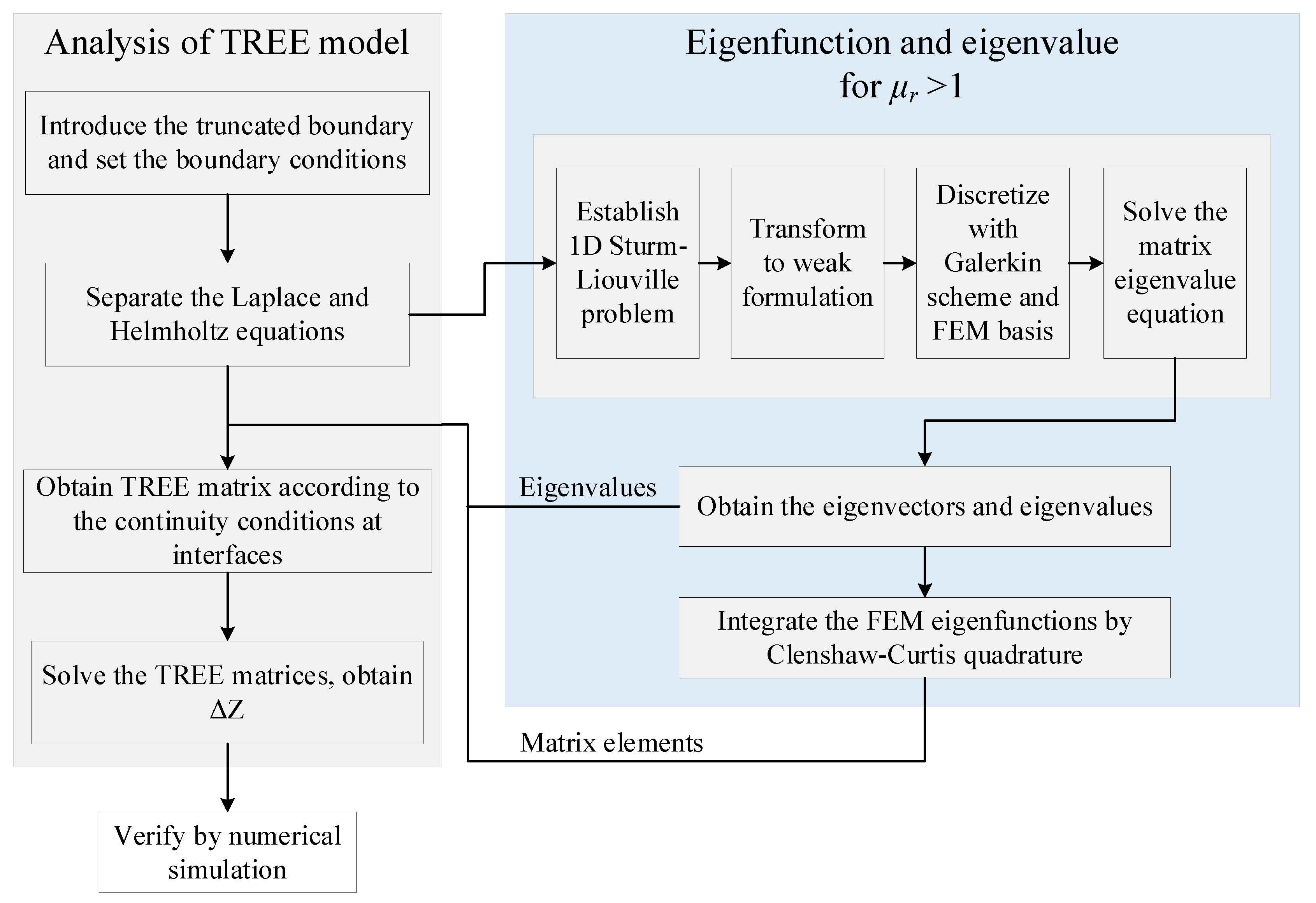
3. Eigenfunctions and the Associated Integrals of the Multi-Subdomain Regions
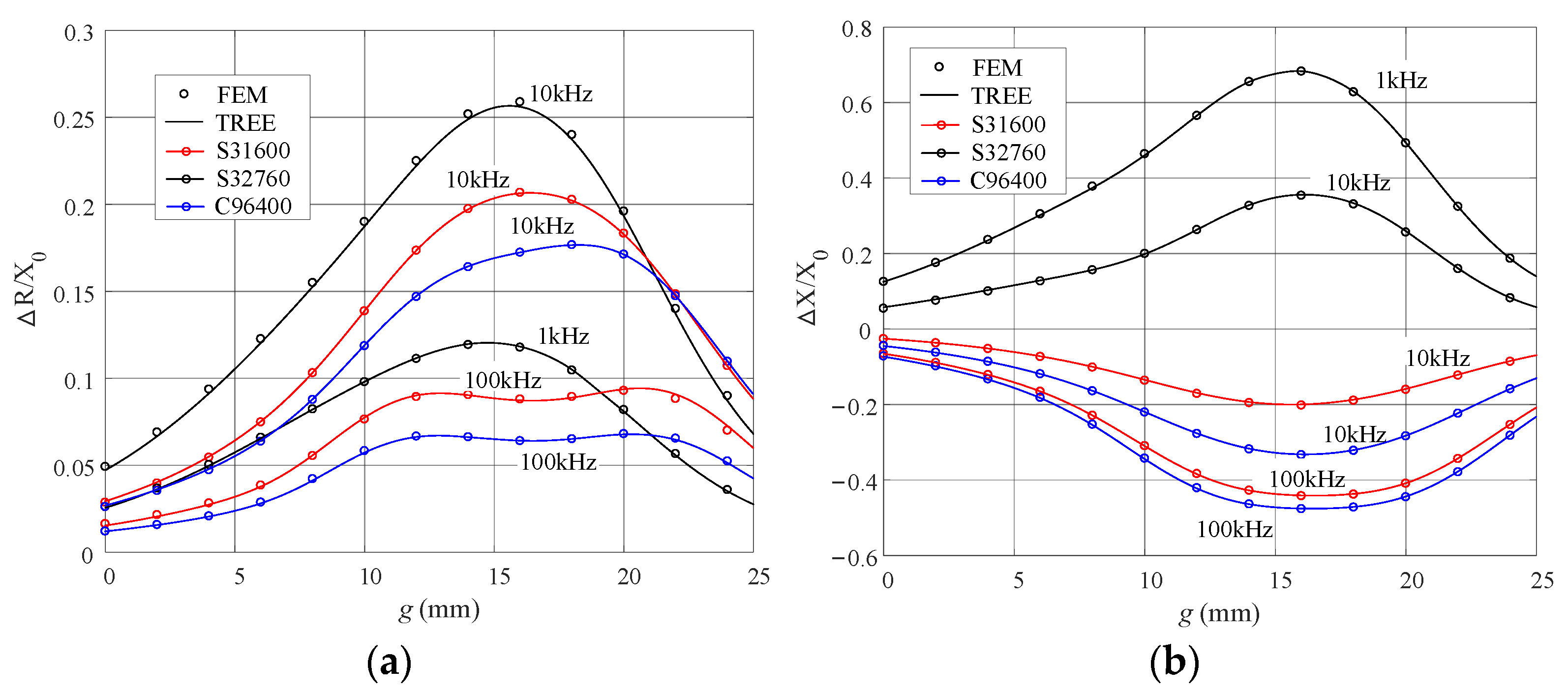
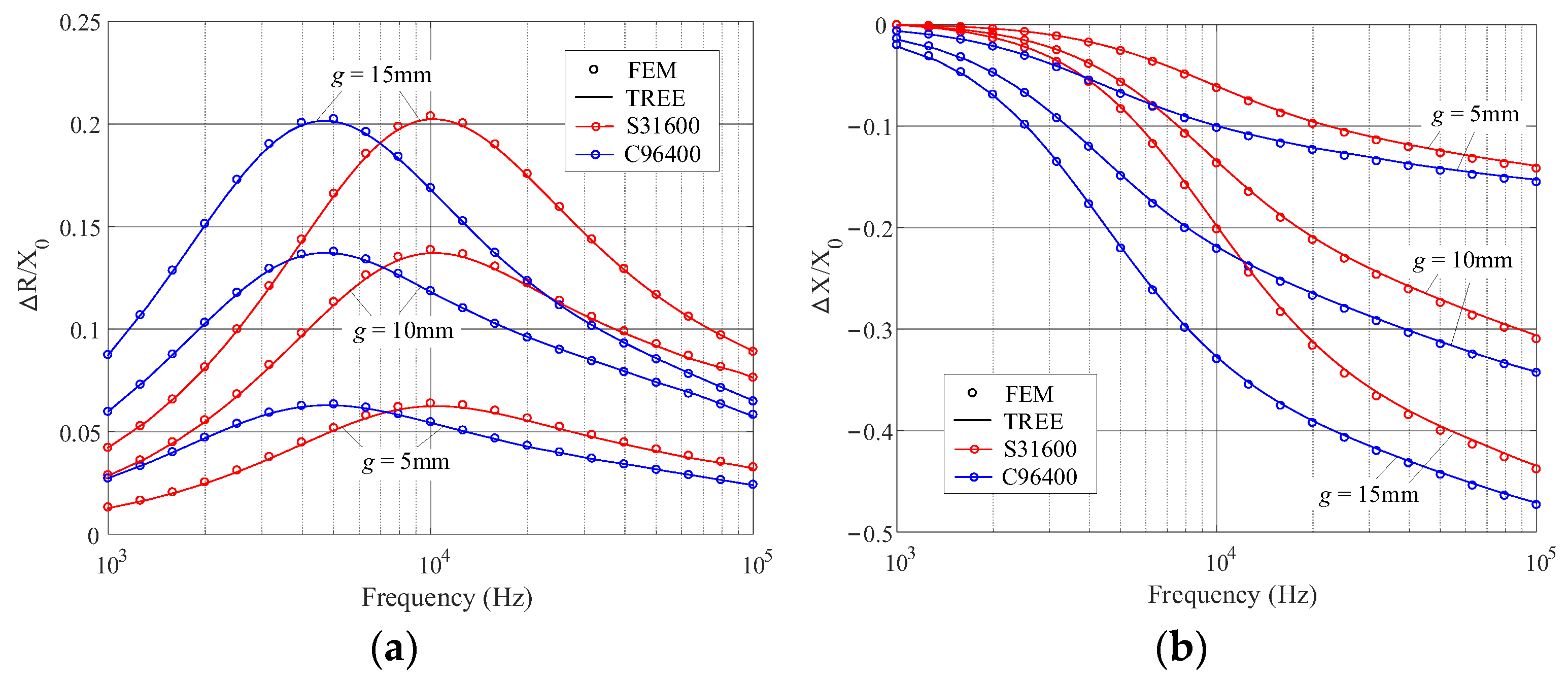
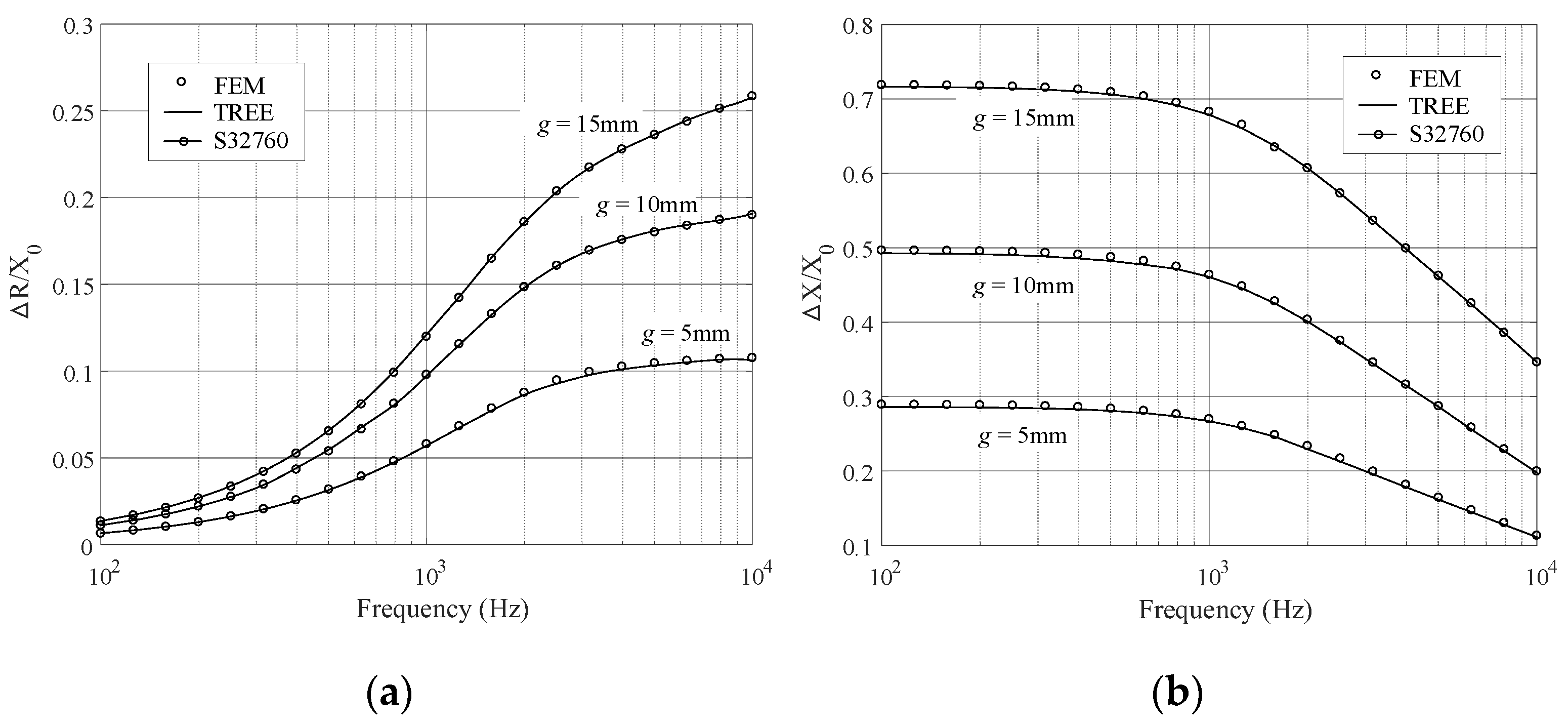
4. Numerical Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dodd, C.V.; Deeds, W.E. Analytical solutions to eddy current probe-coil problems. J. Appl. Phys. 1968, 39, 2829–2838. [Google Scholar] [CrossRef]
- Hannakam, L.; Tepe, R. Feldschwächung durch leitende Rechteckzylinder im Luftspalt. Arch. Elektrotechnik 1979, 61, 137–144. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Kriezis, E. Eddy Current Canonical Problems (with Applications to Nondestructive Evaluation); Tech Science Press: Forsyth, GA, USA, 2006. [Google Scholar]
- Theodoulidis, T. Model of ferrite-cored probes for eddy current nondestructive evaluation. J. Appl. Phys. 2003, 93, 3071–3078. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Bowler, J. Eddy current coil interaction with a right-angled conductive wedge. Proc. R. Soc. A 2005, 461, 3123–3139. [Google Scholar] [CrossRef]
- Bowler, J.; Theodoulidis, T. Eddy currents induced in a conducting rod of finite length by a coaxial encircling coil. J. Phys. D Appl. Phys. 2005, 38, 2861–2868. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Kriezis, E. Series expansions in eddy current nondestructive evaluation models. J. Mater. Process. Technol. 2005, 161, 343–347. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Bowler, J. Eddy-current interaction of a long coil with a slot in a conductive plate. IEEE Trans. Magn. 2005, 41, 1238–1247. [Google Scholar] [CrossRef]
- Bowler, J.; Theodoulidis, T. Coil impedance variation due to induced current at the edge of a conductive plate. J. Phys. D Appl. Phys. 2006, 39, 2862–2868. [Google Scholar] [CrossRef]
- Hannakam, L.; Kost, A. Leitender Rechteckkeil im Felde einer Doppelleitung. Arch. Elektrotechnik 1982, 65, 363–368. [Google Scholar] [CrossRef]
- Hannakam, L.; Orglmeister, R. Induzierte Wirbelstrombelag an ausgeprägten Massivpolen hoher Permeabilität bei Wanderfelderregung. Arch. Elektrotechnik 1984, 67, 49–55. [Google Scholar] [CrossRef]
- Filtz, M.; Nethe, A. Bemerkung zur Lösung des dreidimensionalen Wirbelstromproblems in Kreiszylindern endlicher Länge. Arch. Elektrotechnik 1993, 76, 195–200. [Google Scholar] [CrossRef]
- Filtz, M.; Nethe, A. Anregung dreidimensionaler Wirbelströme in massiven Kreizylindern endlicher Länge durch ein homogenes magnetisches Wechselfeld beliebiger Ausrichtung. Arch. Elektrotechnik 1990, 73, 227–237. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Bowler, J. Interaction of an eddy-current coil with a right-angled conductive wedge. IEEE Trans. Magn. 2010, 46, 1034–1042. [Google Scholar] [CrossRef]
- Delves, L.; Lyness, J. A numerical method for locating the zeros of an analytic function. Math. Comput. 1967, 21, 543–560. [Google Scholar] [CrossRef]
- Tytko, G.; Dawidowski, L. Locating complex eigenvalues for analytical eddy-current models used to detect flaws. Compel 2019, 36, 1800–1809. [Google Scholar] [CrossRef]
- Vasic, D.; Ambrus, D.; Bilas, V. Computation of the eigenvalues for bounded domain. IEEE Trans. Magn. 2016, 52, 7004310. [Google Scholar] [CrossRef]
- Yang, X.; Luo, Y.; Kyrgiazoglou, A.; Zhou, X.; Theodoulidis, T.; Tytko, G. Impedance variation of a reflection probe near the edge of a magnetic metal plate. IEEE Sens. J. 2023, 23, 15479–15488. [Google Scholar] [CrossRef]
- Yang, X.; Luo, Y.; Kyrgiazoglou, A.; Tytko, G.; Theodoulidis, T. An analytical model of an eddy-current coil near the edge of a conductive plate. IET Electr. Power Appl. 2022, 16, 1017–1029. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Skarlatos, A.; Tytko, G. Computation of eigenvalues and eigenfunctions in the solution of eddy current problems. Sensors 2023, 23, 3055. [Google Scholar] [CrossRef]
- Stahlmann, H.D. Der Differentialtransformator als induktiver Stellungsmelder. Arch. Elektrotechnik 1983, 66, 277–281. [Google Scholar] [CrossRef]
- Sun, H.; Bowler, J.; Theodoulidis, T. Eddy currents induced in a finite length layered rod by a coaxial coil. IEEE Trans. Magn. 2005, 41, 2455–2461. [Google Scholar]
- Skarlatos, A.; Theodoulidis, T. Calculation of the eddy-current flow around a cylindrical through-hole in a finite-thickness plate. IEEE Trans. Magn. 2015, 15, 6201507. [Google Scholar] [CrossRef]
- Luo, Y. Field and inductance calculations for coaxial circular coils with magnetic cores of finite length and constant permeability. IET Electr. Power Appl. 2017, 11, 1254–1264. [Google Scholar] [CrossRef]
- Courant, R.; Hilbert, D. Methoden der Mathematischen Physik I; Springer: New York, NY, USA, 1968. [Google Scholar]
- Abramowitz, M.; Stegun, A. Handbook of Mathematical Functions; US Government Printing Office: Washington, DC, USA, 1972.
- Arnoldi, W.E. The principle of minimized iterations in the solution of the matrix eigenvalue problem. Q. Appl. Math. 1951, 9, 17–29. [Google Scholar] [CrossRef]
- Olver, F.; Lozier, D.; Boisvert, R.; Clark, C. NIST Handbook of Mathematical Functions; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Clenshaw, C.; Curtis, A. A method for numerical integration on an automatic computer. Numer. Math. 1960, 2, 197–205. [Google Scholar] [CrossRef]
- Hildebrand, F.B. Introduction to Numerical Analysis; Dover Publications: Mineola, NY, USA, 1987. [Google Scholar]
- Boniardi, M.; Casaroli, A. Rostfreie Edelstähle. Available online: http://www.fa-fe.com/files/pdf/libri_articoli/de/1-Rostfreie_Edelstahle.pdf (accessed on 15 August 2023).
- Conway, T. Inductance calculations for circular coils of rectangular cross section and parallel axes using Bessel and Struve functions. IEEE Trans. Magn. 2010, 46, 75–81. [Google Scholar] [CrossRef]

| Metal (UNS) | Conductivity σ (MS/m) | Relative Permeability μr |
|---|---|---|
| C96400 | 2.9 | 1 |
| S31600 | 1.33 | 1.02 |
| S32760 | 1.25 | 29 |
| Parameter | Parameter | ||
|---|---|---|---|
| a1 (mm) | 5 | b1 (mm) | 40 |
| a2 (mm) | 8 | b2 (mm) | 48 |
| a3 (mm) | 11 | b3 (mm) | 51 |
| a4 (mm) | 14 | b4 (mm) | 59 |
| b (mm) | 100 |
| Parameter | |
|---|---|
| Inner radius r1 (mm) | 15 |
| Outer radius r2 (mm) | 18 |
| Axial length z2 − z1 (mm) | 6 |
| Number of turns | 300 |
| Metal (UNS) | Frequency | Summation Terms | Quadrature Nodes | Mesh Elements | Execution Time of Eigenvalue and Eigenfunction Computation | Total Execution Time |
|---|---|---|---|---|---|---|
| S31600 | 10 kHz | 30 | 80 | 510 | 0.19 s | 0.55 s |
| 100 kHz | 40 | 80 | 510 | 0.26 s | 0.73 s | |
| S32760 | 1 kHz | 55 | 80 | 510 | 0.36 s | 1.00 s |
| 10 kHz | 70 | 90 | 510 | 0.54 s | 1.30 s | |
| C96400 | 10 kHz | 30 | 80 | 510 | 0.19 s | 0.56 s |
| 100 kHz | 50 | 80 | 510 | 0.34 s | 0.90 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Yang, X. Impedance Variation in a Coaxial Coil Encircling a Metal Tube Adapter. Sensors 2023, 23, 8302. https://doi.org/10.3390/s23198302
Luo Y, Yang X. Impedance Variation in a Coaxial Coil Encircling a Metal Tube Adapter. Sensors. 2023; 23(19):8302. https://doi.org/10.3390/s23198302
Chicago/Turabian StyleLuo, Yao, and Xinyi Yang. 2023. "Impedance Variation in a Coaxial Coil Encircling a Metal Tube Adapter" Sensors 23, no. 19: 8302. https://doi.org/10.3390/s23198302





