Vehicle–Bridge Interaction Modelling Using Precise 3D Road Surface Analysis
Abstract
:1. Introduction
2. Methodologies
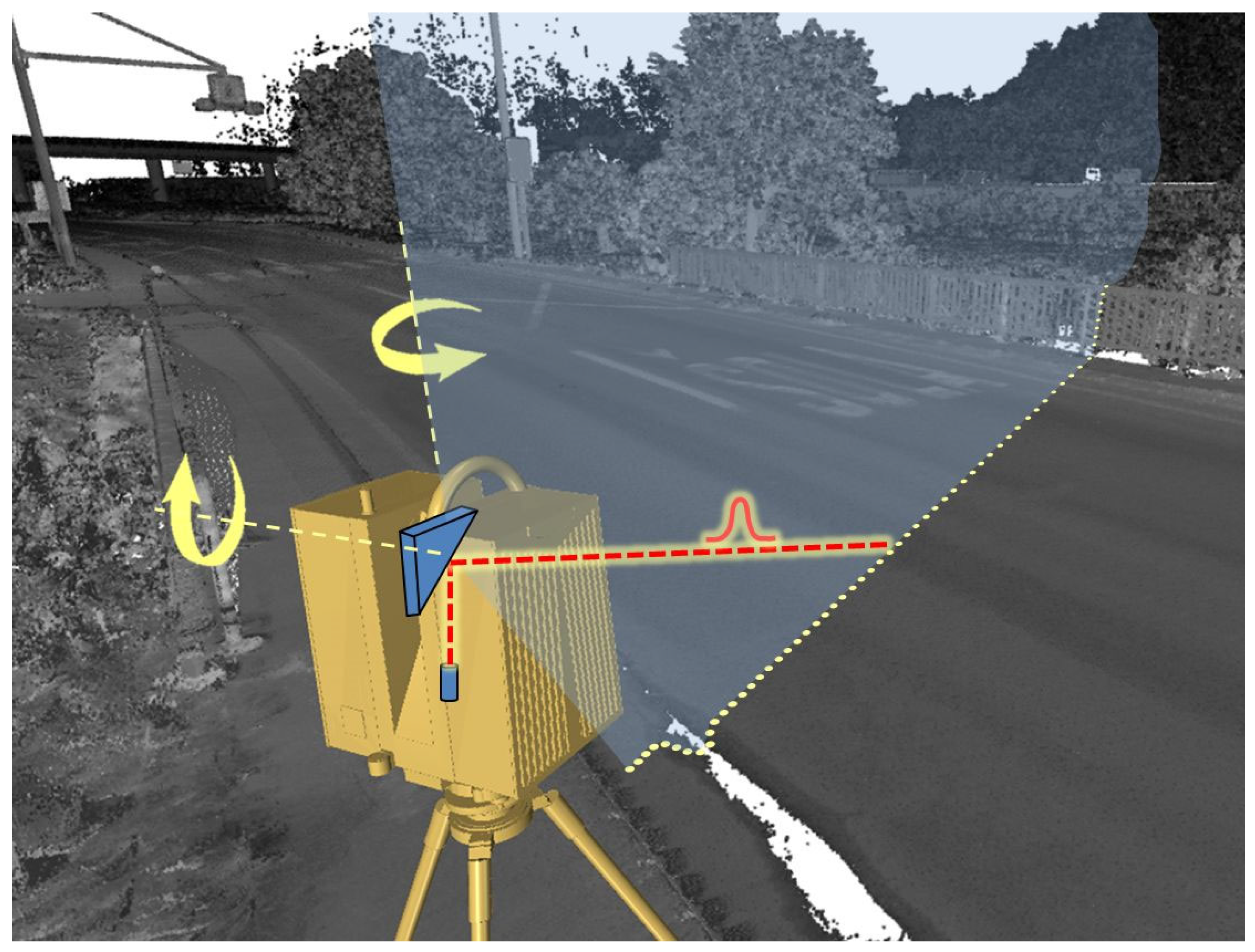
2.1. Road Surface Modelling
- Positioning within the reference coordinate system,
- Filtering of the point cloud,
- Point-to-surface transformation,
- Surface optimisation (e.g., decimation and smoothing).
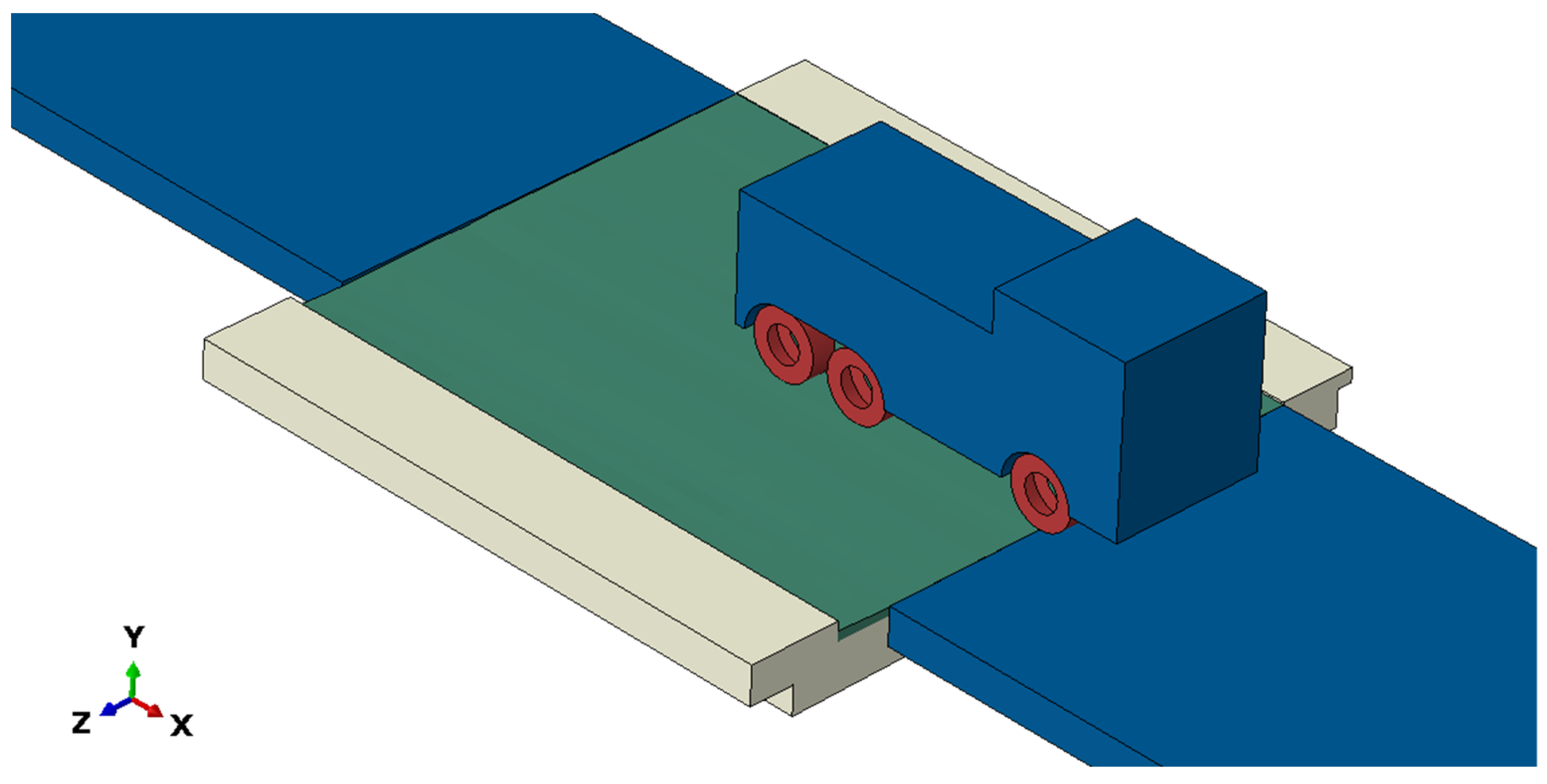
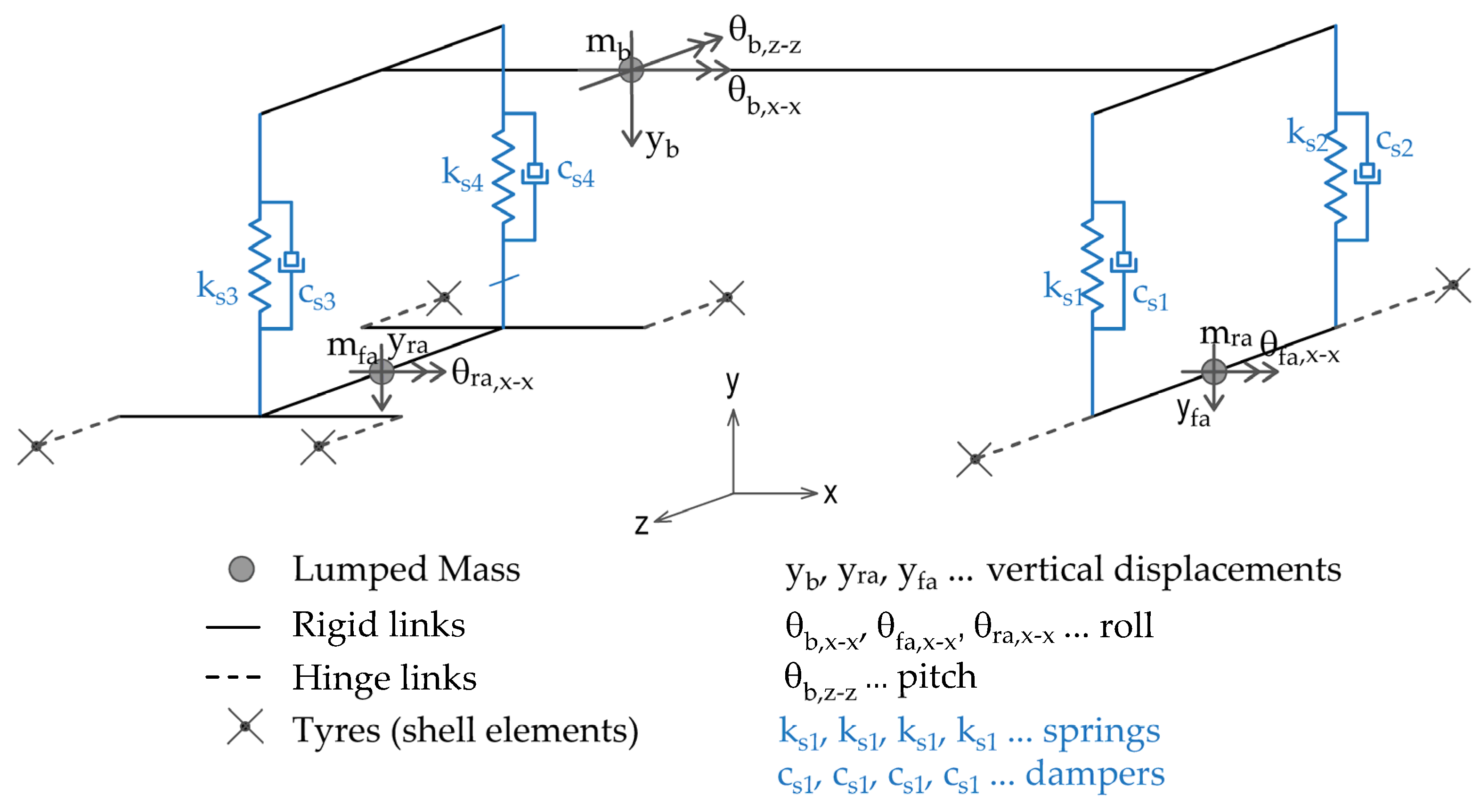
2.2. Modelling the Vehicle–Bridge Interaction Considering the Measured Road Surface Unevenness
3. Field Measurements
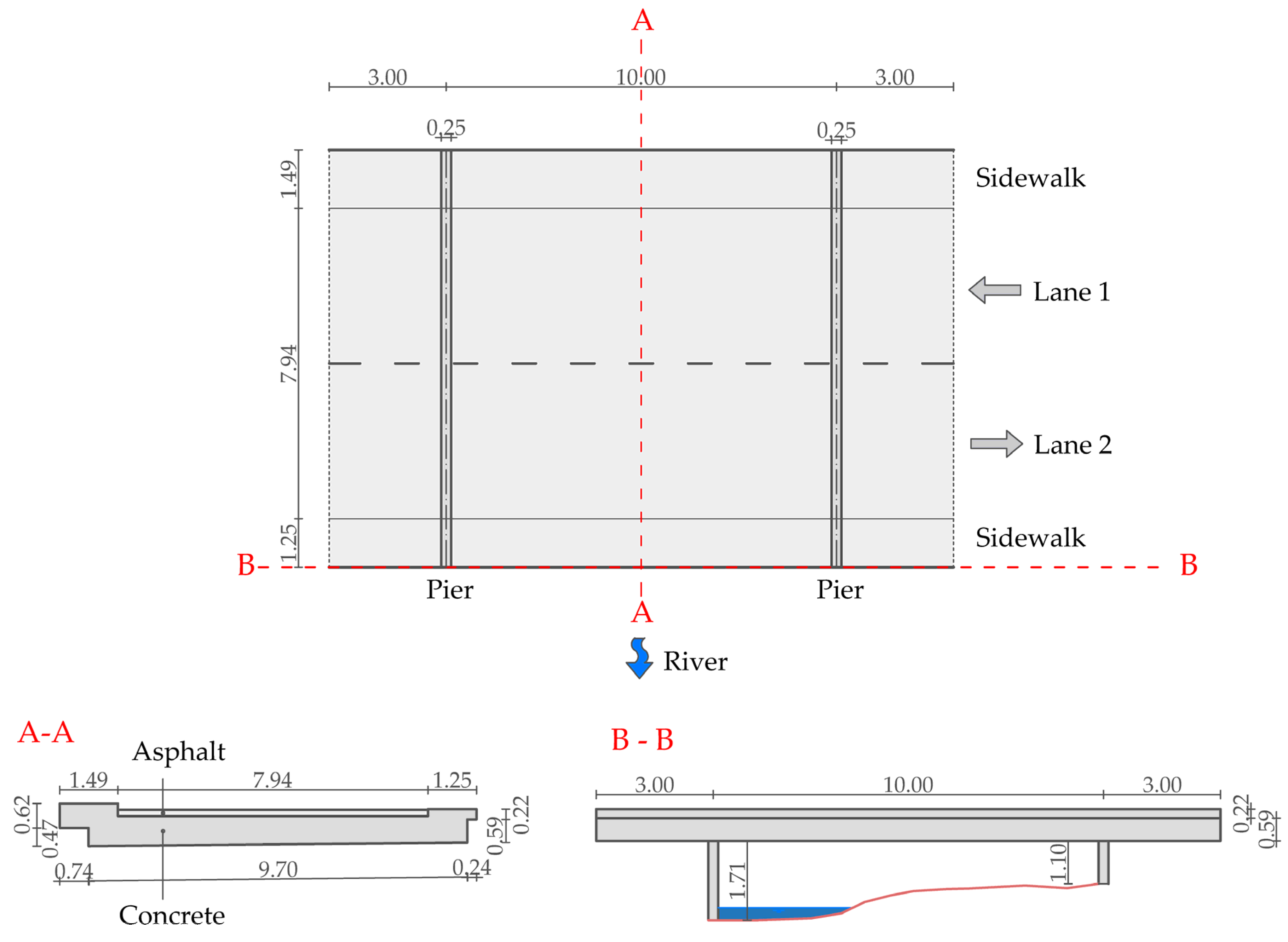
3.1. Test Bridge Geometry
3.2. Dynamic Properties of the Bridge and Vehicle
3.3. Bridge Response to the Crossing Vehicle
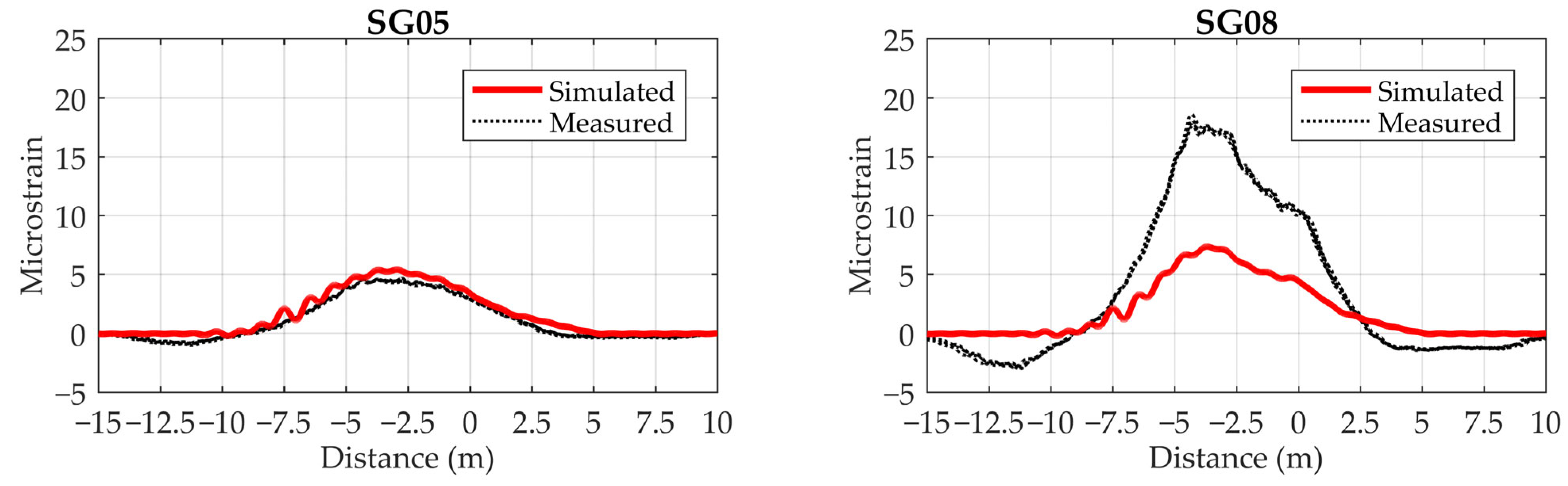
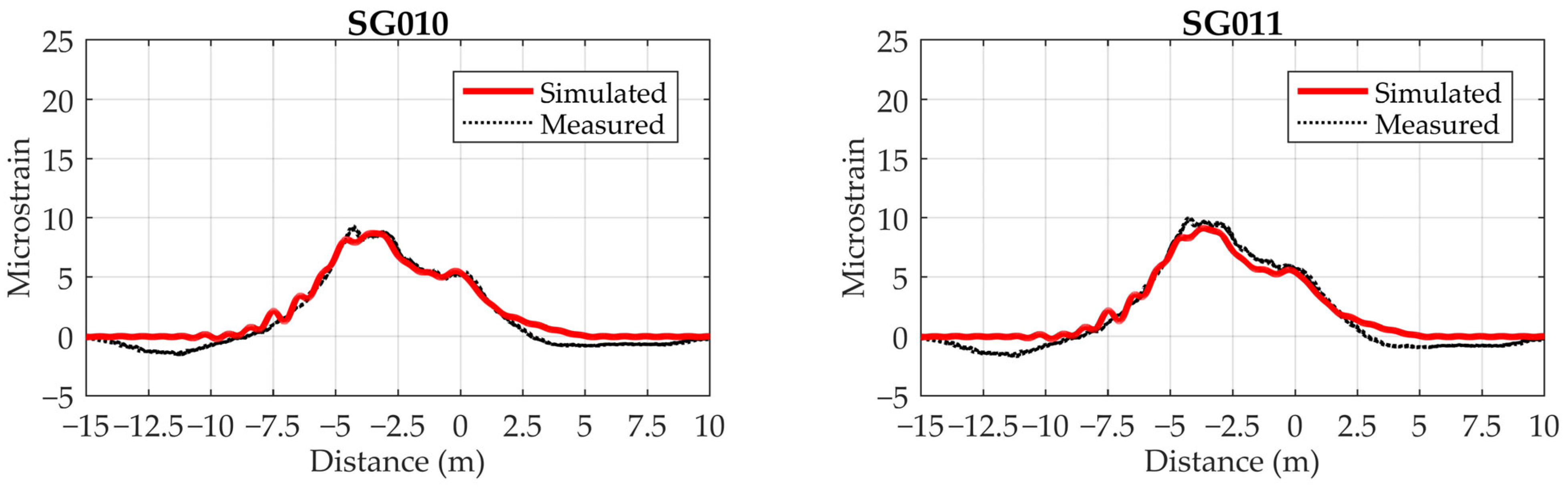
4. Results and Analyses
4.1. TLS Measurements and Verification
- The general trend in road surface unevenness indicates similar results for TLS and the IP.
- For complex road surface irregularities, it is important to have complete surface data rather than individual longitudinal profiles (even if they are very accurate) for the simulation of vehicle–bridge interaction.
4.2. Verification of the Numerical Model for VBI Considering Road Surface Unevenness
4.2.1. Bridge Model
4.2.2. Vehicle Model
4.2.3. VBI Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Normann, O.K.; Hopkins, R.C. Weighing Vehicles in Motion; Highway Research Board Bulletin 50; National Agency of Science—National Research Council: Washington, DC, USA, 1952; pp. 1–27.
- Sujon, M.; Dai, F. Application of Weigh-in-Motion Technologies for Pavement and Bridge Response Monitoring: State-of-the-Art Review. Autom. Constr. 2021, 130, 103844. [Google Scholar] [CrossRef]
- Moses, F. Weigh-in-motion system using instrumented bridges. ASCE Transp. Eng. J. 1979, 105, 233–249. [Google Scholar] [CrossRef]
- Žnidarič, A.; Kalin, J. Using Bridge Weigh-in-Motion Systems to Monitor Single-Span Bridge Influence Lines. J. Civ. Struct. Health Monit. 2020, 10, 743–756. [Google Scholar] [CrossRef]
- Hekič, D.; Anžlin, A.; Kreslin, M.; Žnidarič, A.; Češarek, P. Model Updating Concept Using Bridge Weigh-in-Motion Data. Sensors 2023, 23, 2067. [Google Scholar] [CrossRef] [PubMed]
- Oliva, J.; Goicolea, J.M.; Antolín, P.; Astiz, M.Á. Relevance of a Complete Road Surface Description in Vehicle–Bridge Interaction Dynamics. Eng. Struct. 2013, 56, 466–476. [Google Scholar] [CrossRef]
- Yang, Y.B.; Lin, C.W. Vehicle-Bridge Interaction Dynamics and Potential Applications. J. Sound Vib. 2005, 284, 205–226. [Google Scholar] [CrossRef]
- Humar, J.L.; Kashif, A.H. Dynamic Response Analysis of Slab-Type Bridges. J. Struct. Eng. 1995, 121, 48–62. [Google Scholar] [CrossRef]
- Zou, Q.; Deng, L.; Guo, T.; Yin, X. Comparative Study of Different Numerical Models for Vehicle-Bridge Interaction Analysis. Int. J. Struct. Stab. Dyn. 2016, 16, 1550057. [Google Scholar] [CrossRef]
- Li, J.A.; Feng, D. A Comparative Study of Vehicle-Bridge Interaction Dynamics with 2D and 3D Vehicle Models. Eng. Struct. 2023, 292, 116493. [Google Scholar] [CrossRef]
- OBrien, E.J.; Cantero, D.; Enright, B.; González, A. Characteristic Dynamic Increment for Extreme Traffic Loading Events on Short and Medium Span Highway Bridges. Eng. Struct. 2010, 32, 3827–3835. [Google Scholar] [CrossRef]
- Oliva, J.; Goicolea, J.M.; Astiz, M.Á.; Antolín, P. Fully Three-Dimensional Vehicle Dynamics over Rough Pavement. Proc. Inst. Civ. Eng. Transp. 2013, 166, 144–157. [Google Scholar] [CrossRef]
- Yang, Y.-B.; Lin, B.-H. Vehicle-Bridge Interaction Analysis by Dynamic Condensation Method. J. Struct. Eng. 1995, 121, 1636–1643. [Google Scholar] [CrossRef]
- Múčka, P. Current Approaches to Quantify the Longitudinal Road Roughness. Int. J. Pavement Eng. 2016, 17, 659–679. [Google Scholar] [CrossRef]
- Bitelli, G.; Simone, A.; Girardi, F.; Lantieri, C. Laser Scanning on Road Pavements: A New Approach for Characterizing Surface Texture. Sensors 2012, 12, 9110. [Google Scholar] [CrossRef] [PubMed]
- Guan, H.; Li, J.; Cao, S.; Yu, Y. Use of Mobile LiDAR in Road Information Inventory: A Review. Int. J. Image Data Fusion 2016, 7, 219–242. [Google Scholar] [CrossRef]
- De Blasiis, M.R.; Di Benedetto, A.; Fiani, M.; Garozzo, M. Assessing of the Road Pavement Roughness by Means of Lidar Technology. Coatings 2021, 11, 17. [Google Scholar] [CrossRef]
- Vezočnik, R.; Ambrožič, T.; Sterle, O.; Bilban, G.; Pfeifer, N.; Stopar, B. Use of Terrestrial Laser Scanning Technology for Long Term High Precision Deformation Monitoring. Sensors 2009, 9, 9873. [Google Scholar] [CrossRef] [PubMed]
- Luhmann, T.; Robson, S.; Kyle, S.; Harley, I. Laser-Based Measuring Systems. In Close Range Photogrammetry, Principles, Methods and Applications; Whittles Publishing: Dunbeath, UK, 2006; pp. 176–181. [Google Scholar]
- Riegl Laser Measurement Systems. Available online: http://www.riegl.com (accessed on 14 June 2017).
- Vosselman, G.; Maas, H.-G. Airborne and Terrestrial Laser Scanning; Whittles Publishing: Dunbeath, UK, 2010. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Gaussian Lowpass Filters. In Digital Image Processing; Prentice Hall, Inc.: Upper Saddle River, NJ, USA, 2006; pp. 298–299. [Google Scholar]
- Dassault Systems. Simulia Abaqus Documentation Version 2016; Dassault Systems: Providence, RI, USA, 2016. [Google Scholar]
- Daniel, Ľ.; Kortiš, J. The Comparison of Different Approaches to Model Vehicle-Bridge Interaction. Procedia Eng. 2017, 190, 504–509. [Google Scholar] [CrossRef]
- Wyss, J.C.; Su, D.; Fujino, Y. Prediction of Vehicle-Induced Local Responses and Application to a Skewed Girder Bridge. Eng. Struct. 2011, 33, 1088–1097. [Google Scholar] [CrossRef]
- Roller, M.; Betsch, P.; Gallrein, A.; Linn, J. On the Use of Geometrically Exact Shells for Dynamic Tire Simulation. Multibody Dyn. Comput. Methods Appl. 2014, 35, 205–236. [Google Scholar]
- Kwasniewski, L.; Li, H.; Wekezer, J.; Malachowski, J. Finite Element Analysis of Vehicle–Bridge Interaction. Finite Elem. Anal. Des. 2006, 42, 950–959. [Google Scholar] [CrossRef]
- Spangler, E.B.; Kelly, W.J. GMR Road Profilometer: A Method for Measuring Road Profile. Highw. Res. Rec. 1964, 121, 27–54. [Google Scholar]




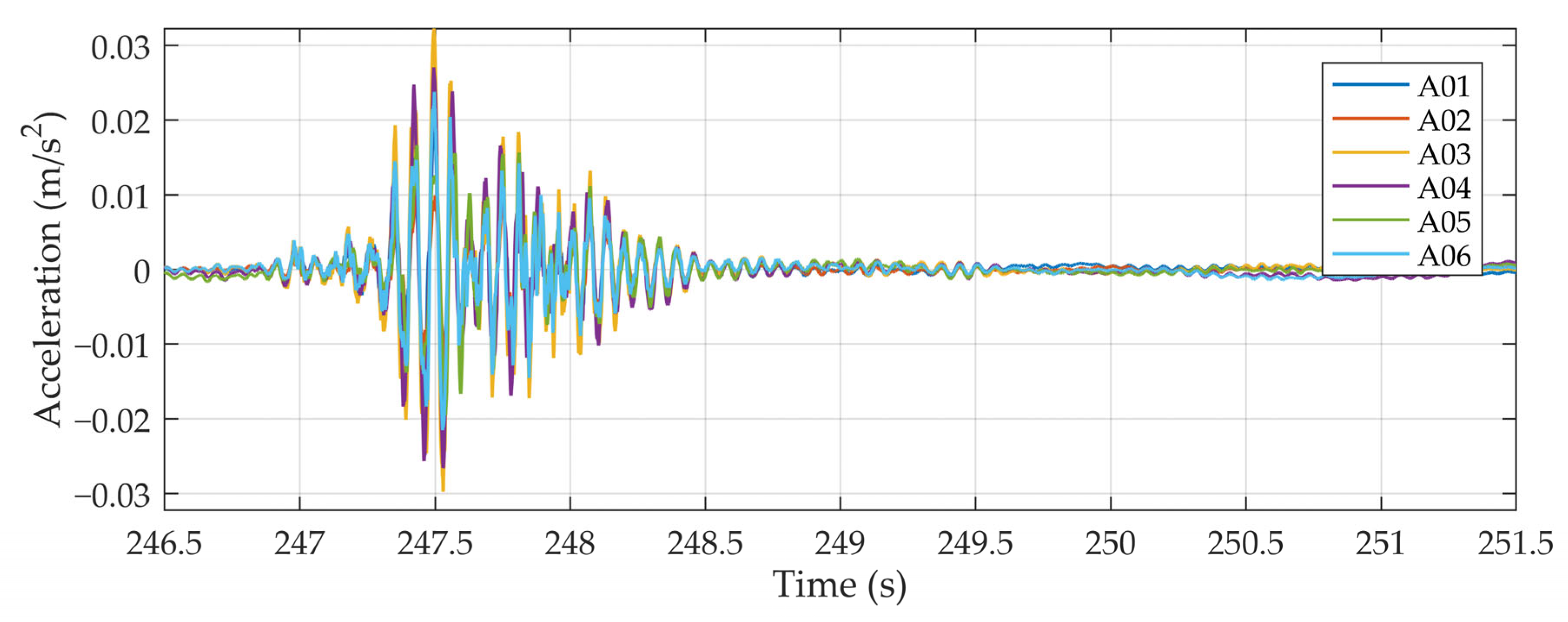

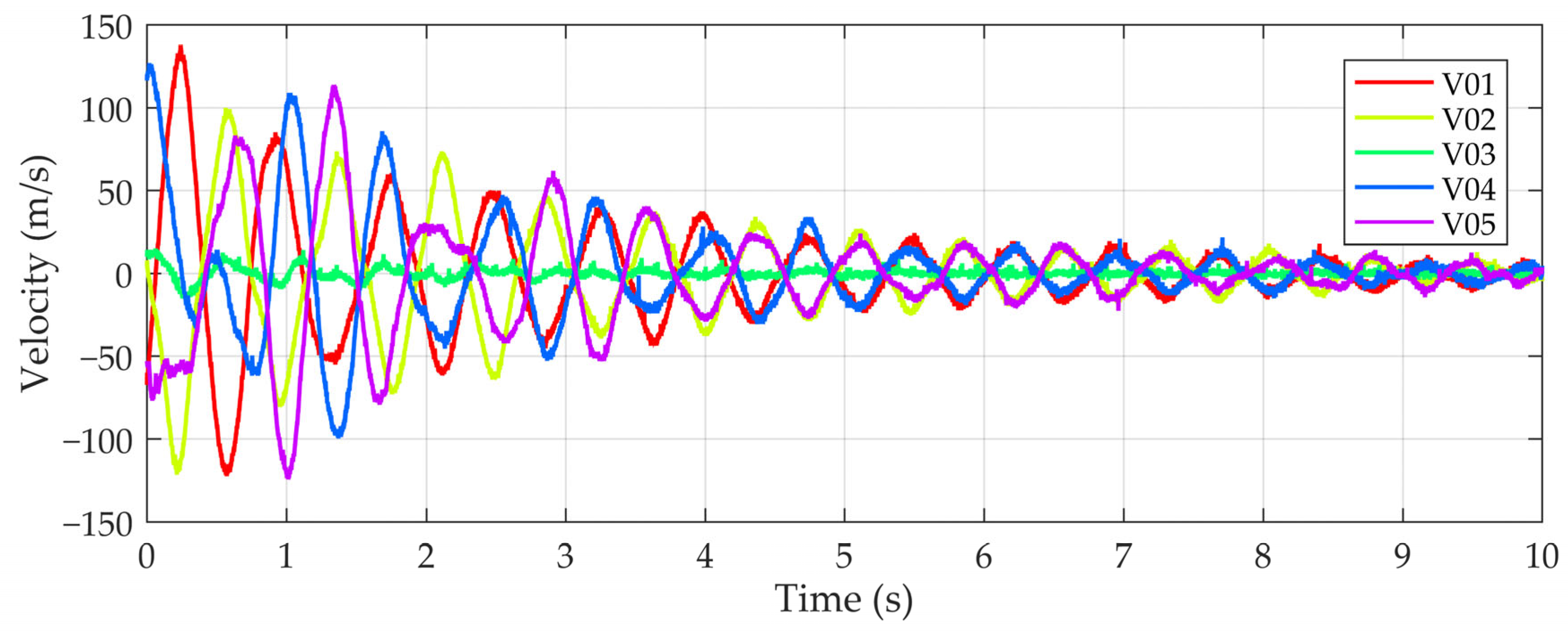
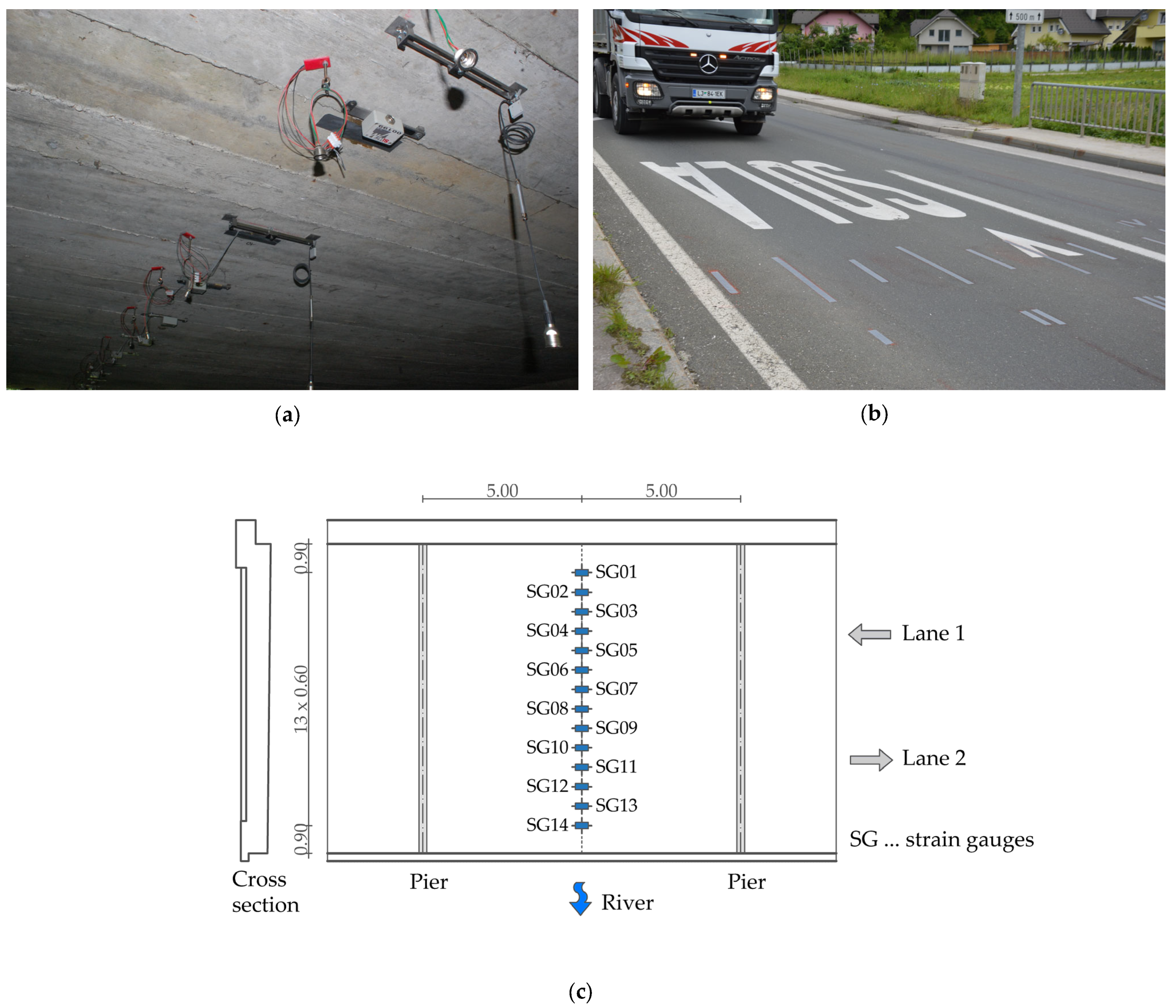



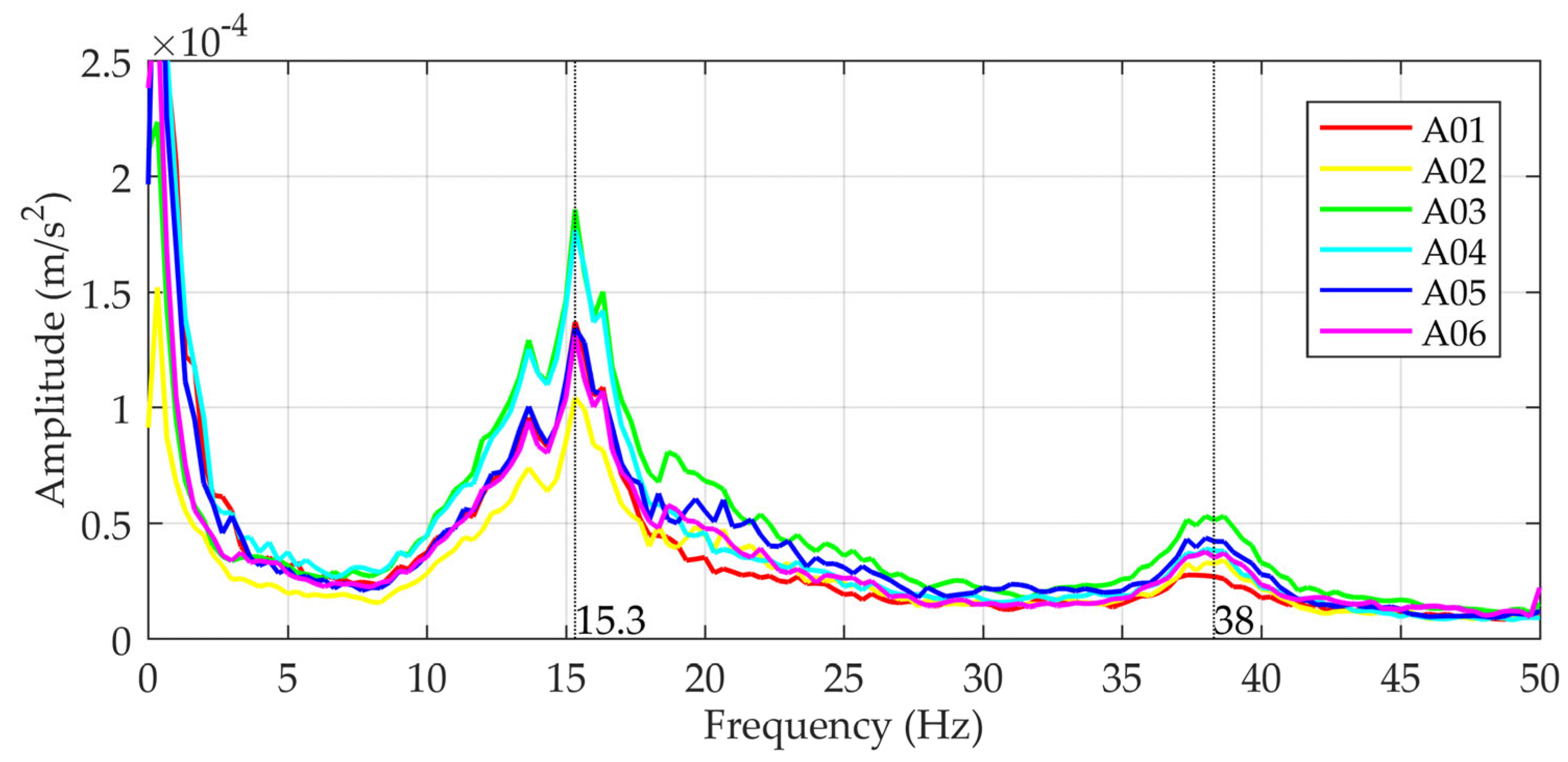





| Mode | Measurements | Numerical Model |
|---|---|---|
| 1 | 15.3 Hz | 15.8 Hz |
| 2 | / 1 | 30.9 Hz |
| 3 | 38.0 Hz | 45.4 Hz |
| Mode | Measurements | Numerical Model |
|---|---|---|
| 1 | 1.30 Hz | 1.20 Hz |
| 2 | 1.40–1.50 Hz | 1.40 Hz |
| 3 | 2.90 Hz | 2.40 Hz |
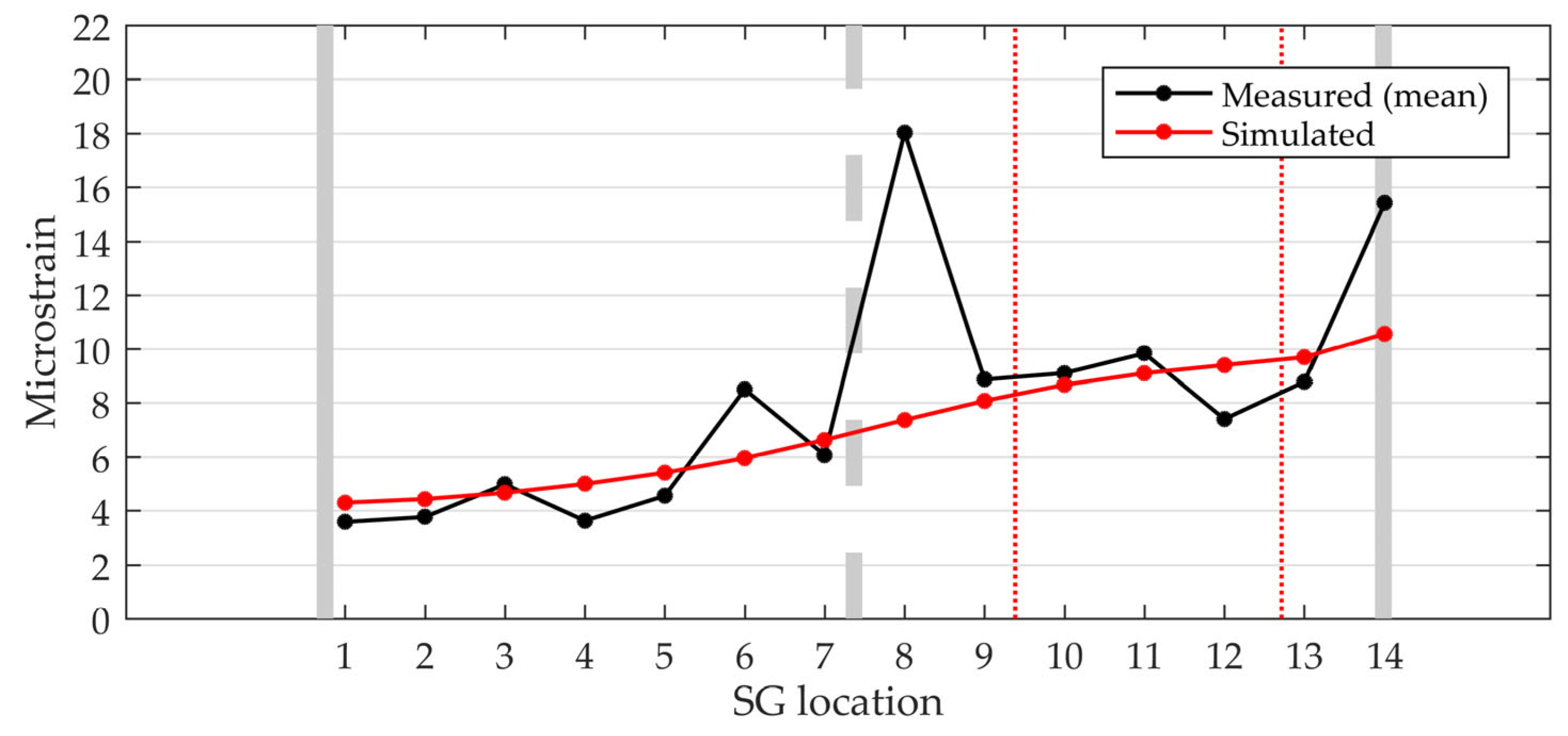
| Location | Measured Microstrain (Mean) | Simulated Microstrain | Error (%) |
|---|---|---|---|
| SG1 | 3.6 | 4.3 | 20% |
| SG2 | 3.8 | 4.4 | 18% |
| SG3 | 5.0 | 4.7 | −6% |
| SG4 | 3.6 | 5.0 | 38% |
| SG5 | 4.5 | 5.4 | 19% |
| SG6 | 8.5 | 5.9 | −30% |
| SG7 | 6.1 | 6.6 | 9% |
| SG8 | 18.0 | 7.4 | −59% |
| SG9 | 8.9 | 8.1 | −9% |
| SG10 | 9.1 | 8.7 | −5% |
| SG11 | 9.8 | 9.1 | −7% |
| SG12 | 7.4 | 9.4 | 27% |
| SG13 | 8.8 | 9.7 | 10% |
| SG14 | 15.4 | 10.6 | −31% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kreslin, M.; Češarek, P.; Žnidarič, A.; Kokot, D.; Kalin, J.; Vezočnik, R. Vehicle–Bridge Interaction Modelling Using Precise 3D Road Surface Analysis. Sensors 2024, 24, 709. https://doi.org/10.3390/s24020709
Kreslin M, Češarek P, Žnidarič A, Kokot D, Kalin J, Vezočnik R. Vehicle–Bridge Interaction Modelling Using Precise 3D Road Surface Analysis. Sensors. 2024; 24(2):709. https://doi.org/10.3390/s24020709
Chicago/Turabian StyleKreslin, Maja, Peter Češarek, Aleš Žnidarič, Darko Kokot, Jan Kalin, and Rok Vezočnik. 2024. "Vehicle–Bridge Interaction Modelling Using Precise 3D Road Surface Analysis" Sensors 24, no. 2: 709. https://doi.org/10.3390/s24020709
APA StyleKreslin, M., Češarek, P., Žnidarič, A., Kokot, D., Kalin, J., & Vezočnik, R. (2024). Vehicle–Bridge Interaction Modelling Using Precise 3D Road Surface Analysis. Sensors, 24(2), 709. https://doi.org/10.3390/s24020709








