Asymptotic Effectiveness of the Event-Based Sampling According to the Integral Criterion
Abstract
:1. Introduction
- -
- the analytical approximation of mean rate of the event-based sampling according to the integral criterion,
- -
- the formulation and the analytical proof of the theorem that evaluates the asymptotic effectiveness of the integral sampling,
- -
- the observation that the asymptotic effectiveness is a measure embedded in the sampled signal that does not depend on the sampling resolution,
- -
- the simulative validation of the analytical results,
- -
- the applications of the derived formula for common signals in dynamic systems (i.e. derivation of explicit formulas and numerical solutions for the typical transient responses),
- -
- the comparison of the effectiveness of the integral sampling to the effectiveness of the send-on-delta/level-crossing sampling.
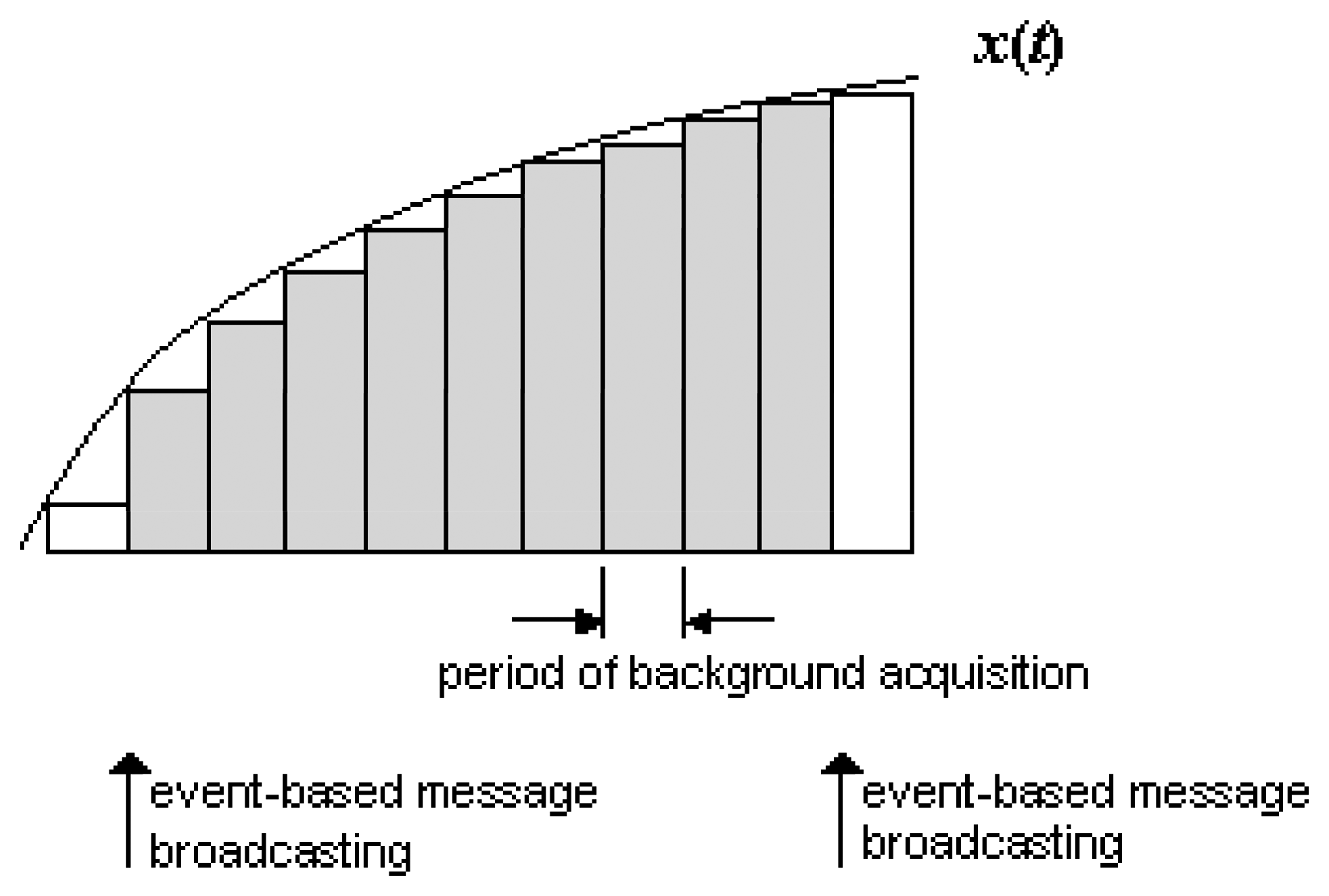
2. Event-based sampling according to the integral criterion
2.1. Motivation of use of the integral sampling
2.2. Trigger detection
3. Related works
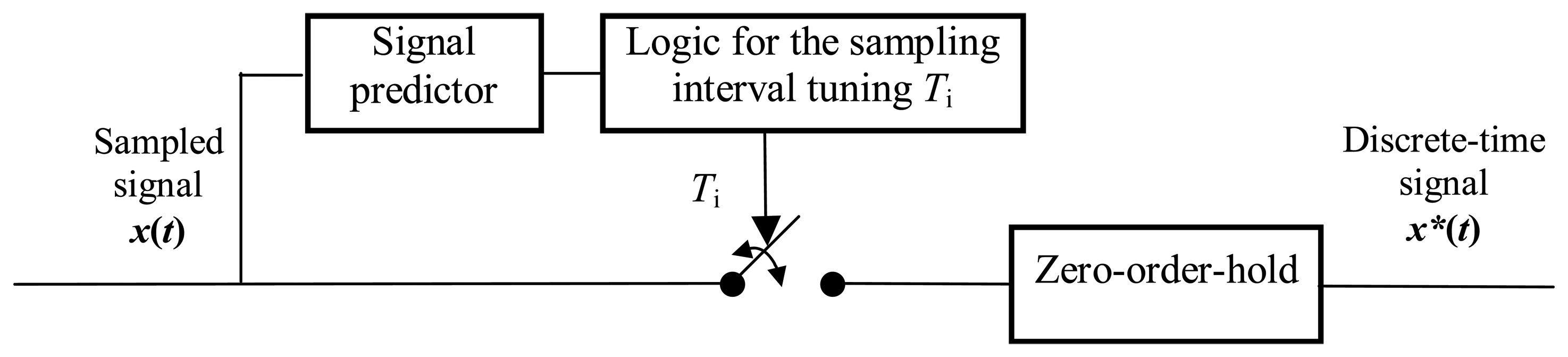
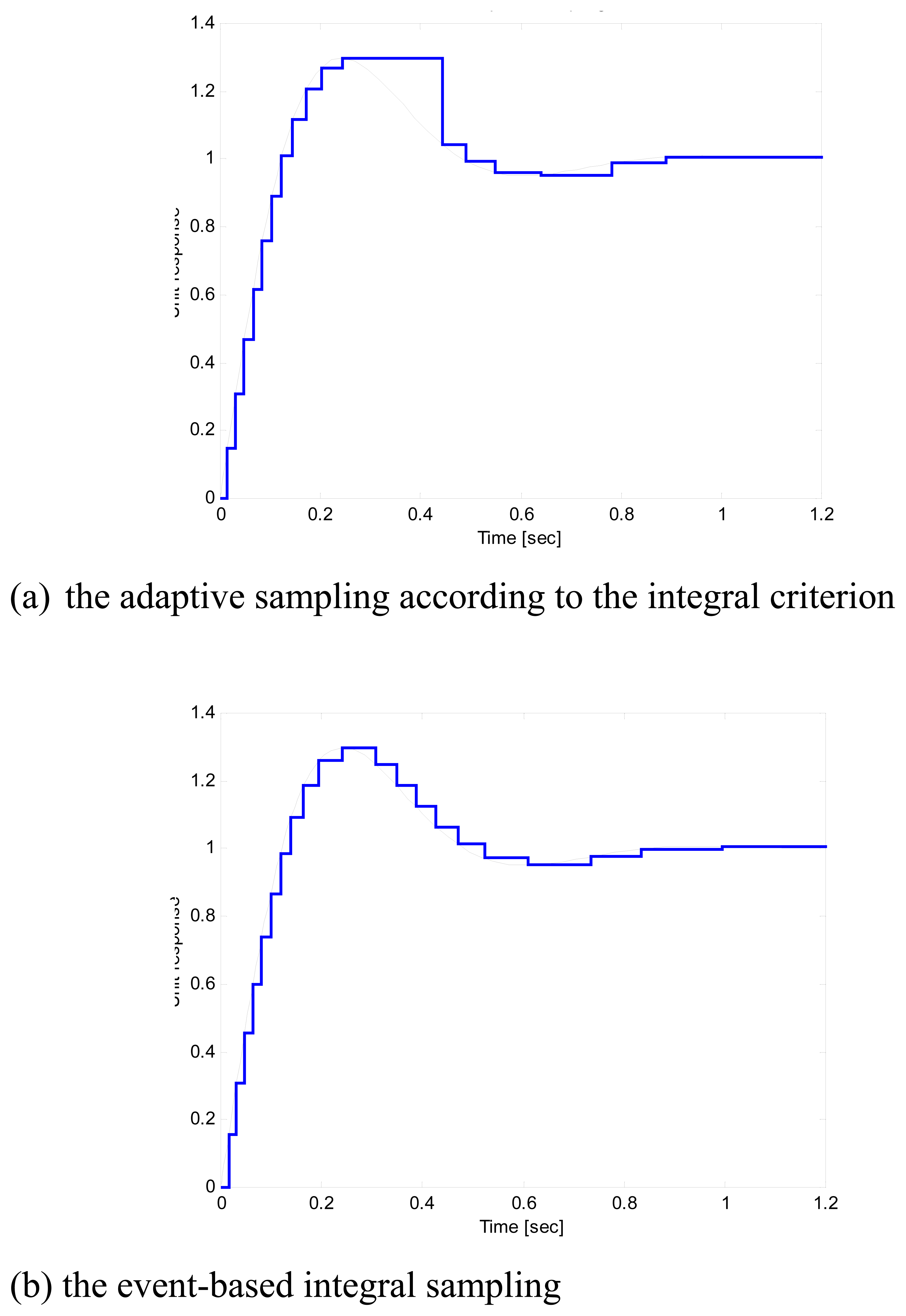
3.1. Adaptive sampling
3.2. Event-based sampling versus pulse frequency modulation (PFM)
4. Analysis of the event-based integral sampling
4.1 Sampled signal definition
Definition 1
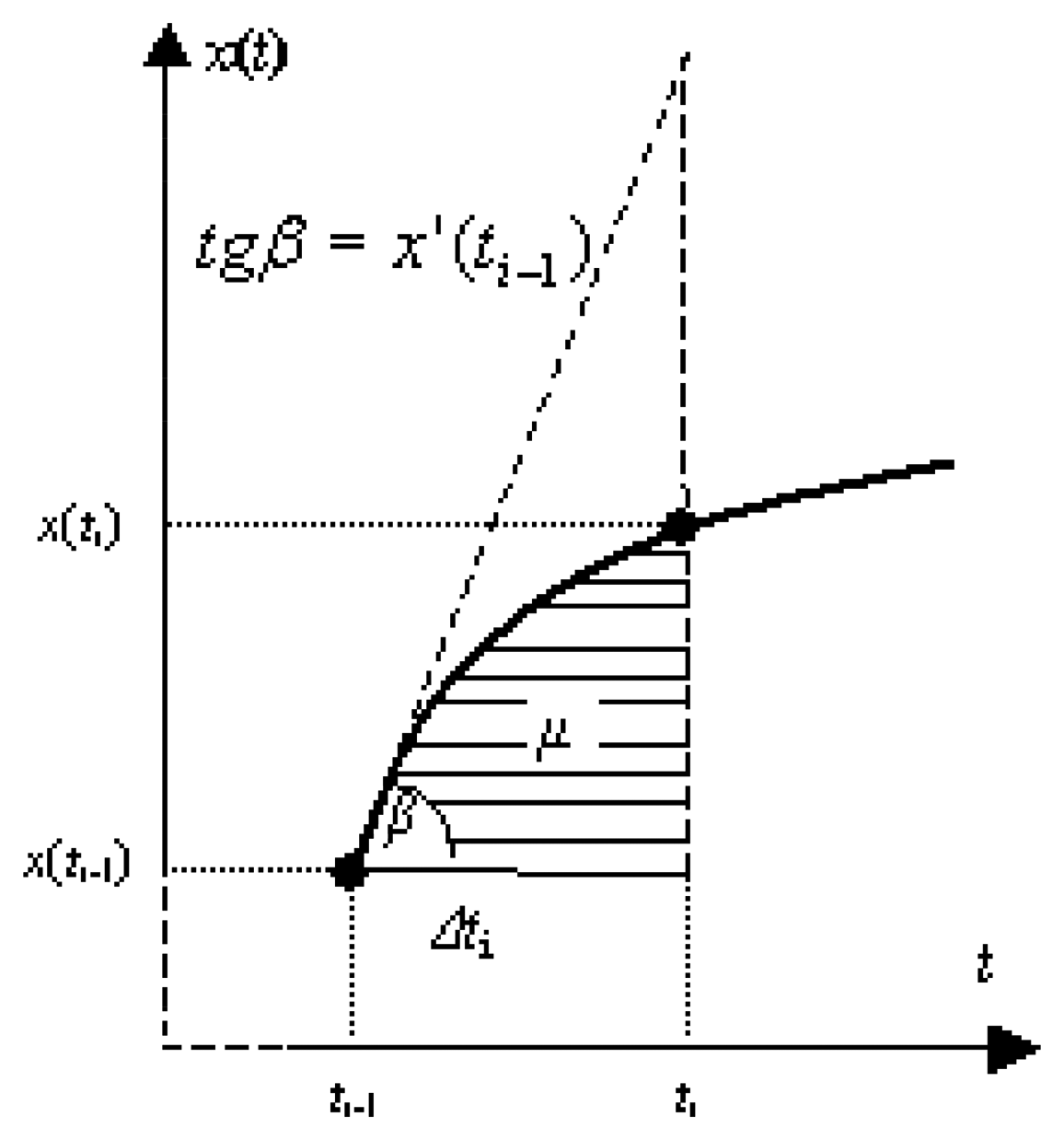
4.2. Integral sampling resolution
Definition 2
4.3. Mean and maximum sampling rate
Theorem 1
Proof
- -
- the mean of the square root of the signal derivative absolute value , which is a measure of the sampled signal x(t),
- -
- the resolution v = 1/μ of the integral event-based sampling.
4.4. Integral sampling effectiveness
Definition 3
Theorem 2
Proof
4.5. Comparing integral sampling effectiveness to send-on-delta effectiveness
Theorem 3
Proof
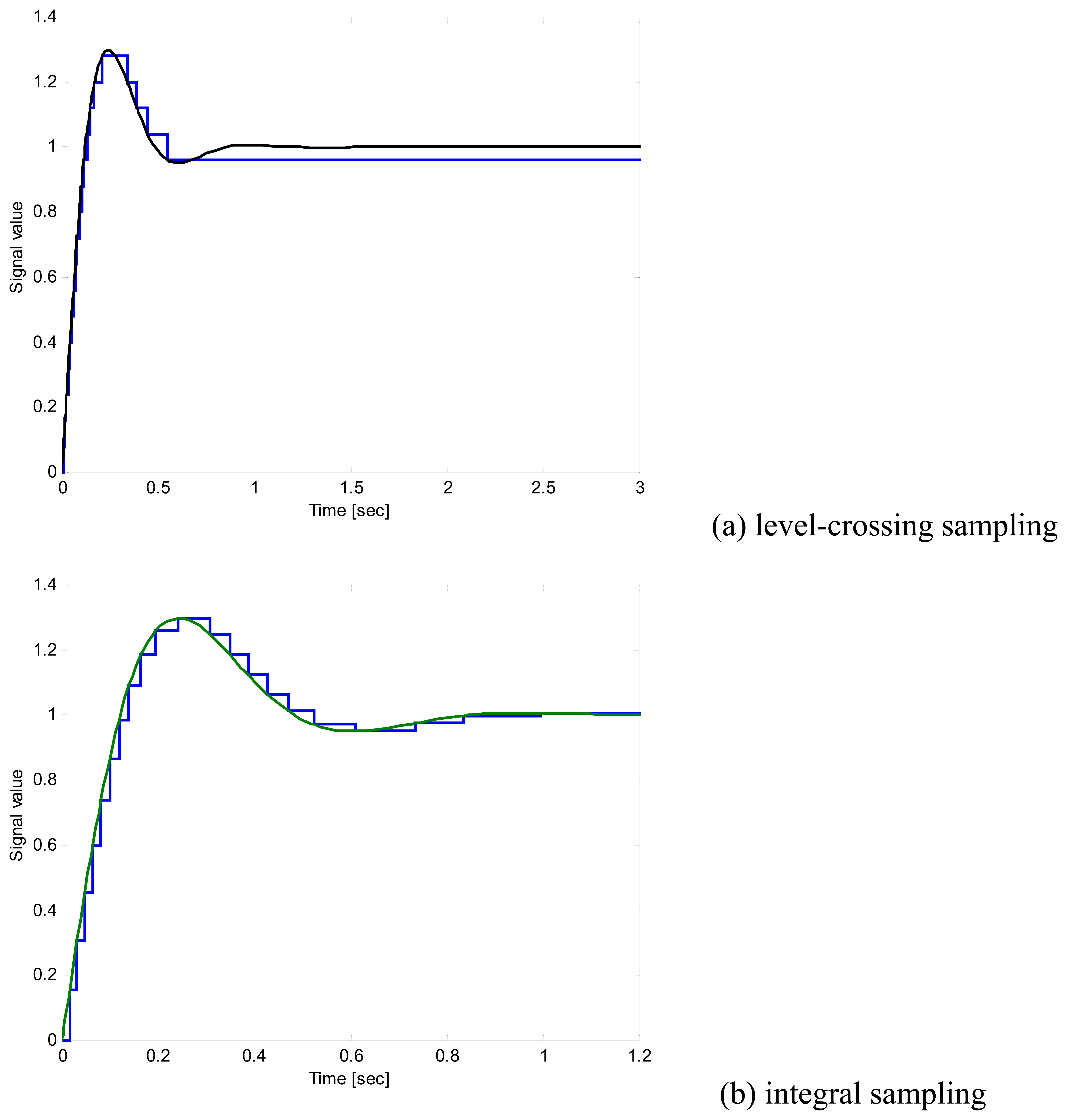
5. Simulation results
5.1. Test signal
5.2. Simulation versus analytical results for mean sampling rate
5.3. Simulation and analytical results for the integral sampling effectiveness
6. Application of the analytical formula
- -
- step responses of the first-order system, of the differentiation, and of the integration circuits,
- -
- critically damped step responses of the second-order and the nth-order systems,
- -
- second-order overdamped step response,
- -
- undamped step response (harmonic signal).
| where: | - the Gamma function, | |
| - the incomplete Gamma function, | ||
| - the error function, | ||
| - the incomplete elliptic integral of the second kind. |
7. Heartbeat sampling
Conclusions
References
- Holloway, L.E. The challenge of intelligent sensing of monitoring and control. Proceedings of the 8th IEEE International Symposium on Intelligent Control; 1993; pp. 139–43. [Google Scholar]
- LonWorks Technology Device Data; Rev. 4; Motorola, 1997.
- Miśkowicz, M. Send-on-delta concept: an event-based data reporting strategy. Sensors 2006, 6, 49–63. [Google Scholar]
- Ellis, P.H. Extension of phase plane analysis to quantized systems. IRE Transactions on Automatic Control 1959, 4, 43–59. [Google Scholar]
- Bernhardsson, B. Event triggered sampling. Research problem formulations in the DICOSMOS project; Törngren, M., Sanfridson, M., Eds.; Lund Institute of Technology, 1998. http://www.md.kth.se/∼mis/dicosmos/publications/ET-sampling.pdf.
- Aström, K.J.; Bernhardsson, B. Comparison of periodic and event based sampling for first-order stochastic systems. Proceedings of IFAC World Congress 1999, 301–306. [Google Scholar]
- Akopyan, F.; Manohar, R.; Apsel, A.B. A level-crossing flash asynchronous analog-to-digital converter. Proceedings of IEEE International Symposium on Asynchronous Circuits and Systems; 2006; pp. 12–22. [Google Scholar]
- Allier, E.; Sicard, G.; Fesquet, L.; Renaudin, M. A new class of asynchronous A/D converters based on time quantization. Proceedings of International Symposium on Asynchronous Circuits and Systems; 2003; pp. 196–205. [Google Scholar]
- Otanez, P.; Moyne, J.; Tilbury, D. Using deadbands to reduce communication in networked control systems. Proceedings of American Control Conference; 2002; 4, pp. 3015–3020. [Google Scholar]
- Layer 7 LonMark Interoperability Guidelines; Ver. 3.2. LonMark Interoperability Association, 2002. http://www.lonmark.com/press/download/LYR732.pdf.
- Arzén, K.E. A simple event-based PID controller. Proceedings of IFAC World Congress 1999, 18, 423–428. [Google Scholar]
- Henningsson, T.; Cervin, A. Event-based control over networks: some research questions and preliminary results. Proceedings of Swedish Control Conference Reglermötet'2006, Stockholm; 2006. [Google Scholar]
- Kopetz, H. Real-time systems. Design principles for distributed embedded applications; Kluwer Academic Publications, 1997. [Google Scholar]
- Miśkowicz, M. Adaptive event-triggered algorithms in distributed control network architectures (in Polish). PhD Thesis, AGH University of Science and Technology, Cracow, 2004. [Google Scholar]
- Miśkowicz, M. The event-triggered integral criterion for sensor sampling. Proceedings of IEEE International Symposium on Industrial Electronics; 2005; pp. 1061–1066. [Google Scholar]
- Dorf, R.C.; Farren, M.C.; Phillips, C.A. Adaptive sampling for sampled-data control systems. IEEE Transactions on Automatic Control 1962, 7(1), 38–47. [Google Scholar]
- De Paoli, F.; Tisato, F. On the complementary nature of event-driven and time-driven models. Control Engineering Practice 1996, 4(6), 1996. 847–854. [Google Scholar]
- Savigni, A.; Tisato, F. Kaleidoscope: A reference architecture for monitoring and control systems. Proceedings of the First Working IFIP Conference on Software Architecture; 1999; pp. 369–388. [Google Scholar]
- Mitchell, J.R.; McDaniel, W.L. Adaptive sampling technique. IEEE Transactions on Automatic Control 1969, 14(2), 200–201. [Google Scholar]
- Gupta, S.C. Increasing the sampling efficiency for a control system. IEEE Transactions on Automatic Control 1963, 8(3), 263–264. [Google Scholar]
- Hsia, T.C. Comparisons of adaptive sampling control laws. IEEE Transactions on Automatic Control 1972, 17(6), 830–831. [Google Scholar]
- Hsia, T.C. Analytic design of adaptive sampling control laws. IEEE Transactions on Automatic Control 1974, 19(1), 39–42. [Google Scholar]
- De la Sen, M.; Almansa, A. Adaptive stable control of manipulators with improved adaptation transients by using on-line supervision of the free-parameters of the adaptation algorithm and sampling rate. Informatica, Journal of the Lithuanian Academy of Sciences 2002, 13(3), 345–368. [Google Scholar]
- De la Sen, M. Non-periodic and adaptive sampling. A tutorial review. Informatica, Journal of the Lithuanian Academy of Sciences 1996, 7(2), 175–228. [Google Scholar]
- Dormido, S.; de la Sen, M.; Mellado, Mellado M. Criterios generales de determinación de leyes de maestro adaptivo (in Spanish). Revista de Informática y Automática 1978, 38, 13–29. [Google Scholar]
- Tzafestas, S.; Frangakis, G. Implementing PFM controllers. Control Engineering 1979, 91–104. [Google Scholar]
- Mateo, J.; Laguna, P. Improved heart rate variability signal analysis from the beat occurrence times according to the IPFM model. IEEE Transactions Biomedical Engineering 2000, 47(8), 997–1009. [Google Scholar]
- Jordan, C. Sur la série de Fourier; Comptes Rendus de l'Académie des Sciences. Série Mathématique; 1881; Volume 92, 5, pp. 228–230. [Google Scholar]
- Riesz, F.; Nagy, B. Functional analysis.; New York, Dover, 1990. [Google Scholar]
- Rudin, W. Real and complex analysis.McGraw-Hill Book, 3rd ed.; 1987. [Google Scholar]
- Lunze, J. Robust Multivariable Feedback Control.; Prentice-Hall, 1989. [Google Scholar]
- Boyd, S.; Barratt, C. Linear Controller Design: Limits of Performance.; Prentice-Hall, 1991. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and DesignWiley, 2nd ed.; 2005. [Google Scholar]
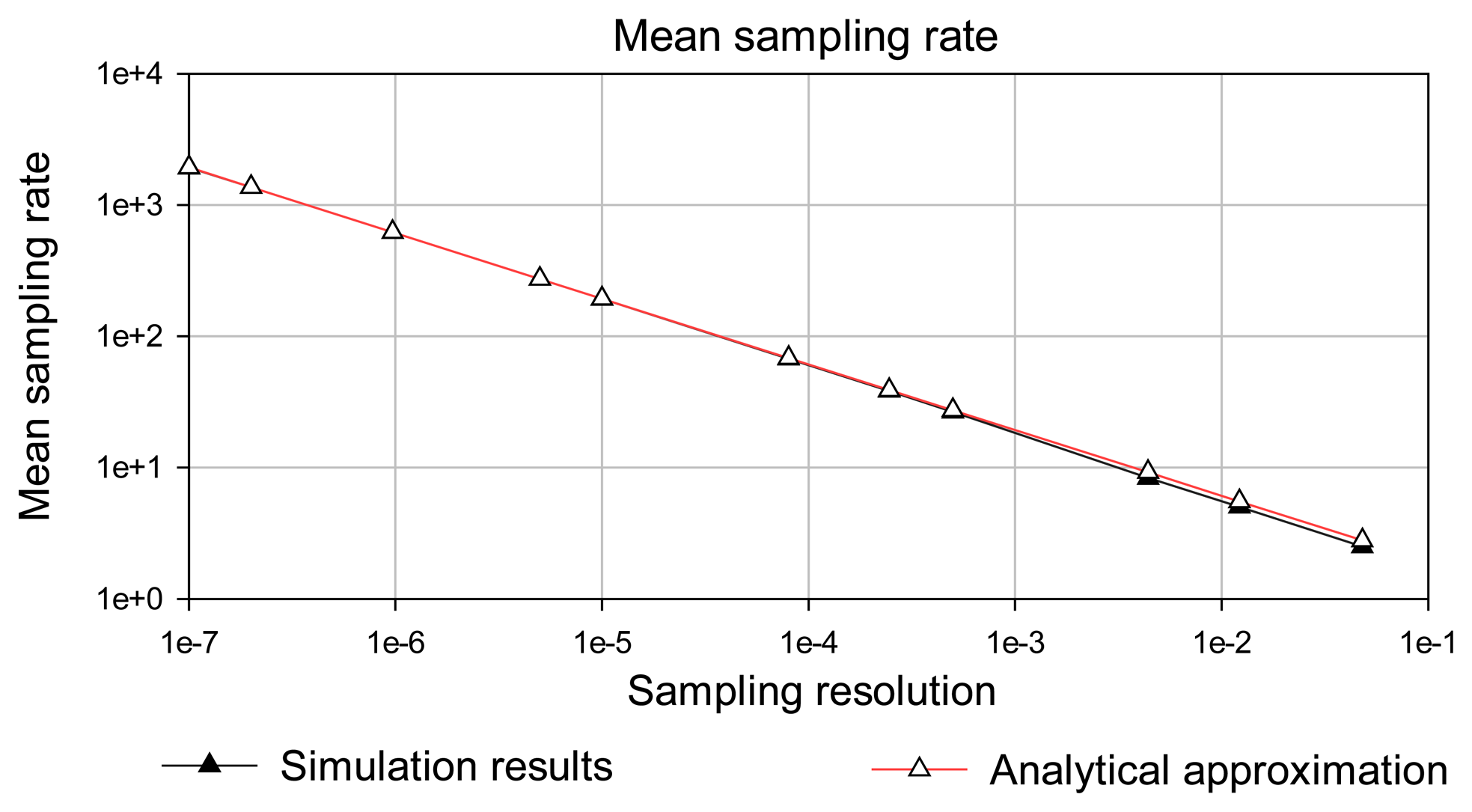

| Integral absolute error (IAE) | Simulation results | Analytical approximation |
|---|---|---|
| 0,048 | 2.5 | 2.78 |
| 1,22E-02 | 5 | 5.52 |
| 4,40E-03 | 8.33 | 9.2 |
| 5,00E-04 | 26.5 | 27.28 |
| 8,00E-05 | 67.5 | 68.2 |
| 5,00E-06 | 272.5 | 272.8 |
| 1,00E-07 | 1925 | 1929 |
| Integral absolute error (IAE) | Number of samples in event-based sampling | Number of samples in periodic sampling | Event-based sampling effectiveness |
|---|---|---|---|
| 0.048 | 3 | 12 | 4.000 |
| 5E-4 | 32 | 120 | 3.750 |
| 2.46E-4 | 46 | 171 | 3.717 |
| 8E-5 | 81 | 300 | 3.700 |
| 1E-5 | 231 | 851 | 3.684 |
| 5E-6 | 327 | 1200 | 3.675 |
| 9.7E-7 | 742 | 2727 | 3.675 |
| 1E-7 | 2310 | 8480 | 3.671 |
| Signal | Step response | Asymptotic effectiveness |
|---|---|---|
| First-order step response | ||
| Differentiation circuit | ||
| Integration circuit | ||
| Second-order critically damped step response | ||
| Second-order overdamped step response | ||
| nth-order critically damped step response | ||
| Second-order underdamped step response (0<ξ<1) | Symbolic solution is not available, the numeric solutions for a particular set of parameters can be calculated | |
| x(t) = k(1 − cos ωnt) | Harmonic signal - second-order undamped step response (ξ = 0) |
| Signal | Integral sampling effectiveness for selected time intervals |
|---|---|
x(3T) = 0.95x0 | q∞ (η= 3) = 1.93 where: η = b/T |
x(3T) = 0,05x0/T | q∞(η = 3) = 1.93 where: η = b/T |
x (20T) = 0,95·x0t | q∞ (η = 20) = 1.032 where: η = b/T |
x(5T)=0.959x0 | q∞(η = 20) = 1.46 where: η = b/T |
for T1/T2=7/5 : x(5T1=7T2) = 0.97x0 | q∞(η1 = 5, η2=7) = 1.32 where: η1 = b/T1, η2=b/T2 |
x(n = 2, η = 5) = 0.96x0 | q∞ (n = 2, η =5) = 1.46 where η = b/T |
| x(t) = x0 (1−cos ωnt) | q∞ (bωn = πm/2, m = 1,2,…) = 1.31 |
| x(t) = kt | q∞ = 1 |
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Miskowicz, M. Asymptotic Effectiveness of the Event-Based Sampling According to the Integral Criterion. Sensors 2007, 7, 16-37. https://doi.org/10.3390/s7010016
Miskowicz M. Asymptotic Effectiveness of the Event-Based Sampling According to the Integral Criterion. Sensors. 2007; 7(1):16-37. https://doi.org/10.3390/s7010016
Chicago/Turabian StyleMiskowicz, Marek. 2007. "Asymptotic Effectiveness of the Event-Based Sampling According to the Integral Criterion" Sensors 7, no. 1: 16-37. https://doi.org/10.3390/s7010016




