Novel Deployment Schemes for Mobile Sensor Networks

Abstract

Virtual Force Algorithm (VFA) is becoming a main solution to area coverage for homogeneous wireless sensor networks with random distribution of mobile sensor nodes. Consider the factors of the convergence, the boundary in Region Of Interest (ROI), effective distance of acting force and useless moving, etc, VFA is improved to overcome the above problems. Furthermore, an expression of exponential function for the relationship of virtual force is proposed to converge rapidly. Extensive simulation results indicate that these improved VFA get better performance in coverage rate, moving energy consumption, convergence etc. than original VFA.

1. Introduction

With the development and maturation of telecommunication, embedded computing and sensing technologies, a large number of miniature sensors with computing and communication abilities have been deployed around the world [1, 2]. Due to the limited computing power, sensing range, and transmission range of individual sensors, the Wireless Sensor Networks (WSNs) are formed for real-time detection, sensing and collection of various environmental parameters or information of the target under surveillance [3-5], and are studied especially of the energy-efficient aspects because the power of sensor nodes is constraint and can not be recharged [6, 7]. Clearly the integrity and accuracy of the collected information depend on the coverage ratio of the surveillance region. Furthermore, different applications may have different interpretation and requirements of the coverage [8]. To this end, Cardei and Wu have categorized the coverage problems into three different types: area coverage, point coverage and barrier coverage [9].

Area coverage is the topic being most extensively studied by using the virtual force deployment algorithms, which mainly address how to deploy the sensor nodes to achieve sufficient coverage of the Region Of Interest (ROI). This is also the focus of our research. In the area coverage problem, each point in ROI should be covered by at least one node. For instance, in the application of forest-fire forecast, the goal is to monitor the temperature of every point in ROI. At the same time, the connectivity between any two sensor nodes need to be guaranteed. Furthermore the number of the nodes should be minimized in order to reduce network cost and/or preserve network resources, in the premise of coverage and connectivity.

Since the WSNs usually work in the unknown, complex or even hostile circumstance, manual deployment is unlikely available. On the other hand, although the sensors can be conveniently deployed by dissemination, projection or spurt, they are usually not distributed to the proper locations, and thus wasting sensor resources and lowering the sensing efficiency of the whole network. Therefore, sensor deployment in WSNs has become a basic research topic in this field [10–14]. It mainly focuses on how to deploy the sensors reasonably to guarantee highly-effective coverage of ROI. Simply put, the sensor deployment problem deals with “how to maximize the coverage region for given WSNs, at the same time providing good surveillance of the coverage region”.

The sensor deployment problem is nontrivial. Clearly, a good coverage is indispensable for the effectiveness of WSNs. Given the random distribution of sensors, more sensor nodes will statistically result in a better coverage of ROI. But due to the cost, resource consumption and other factors, the number of nodes cannot be increased arbitrarily. The optimization of sensor deployment is a challenging problem that directly affects the coverage rate of ROI and accordingly the surveillance quality of ROI.

The WSNs composed of mini-robot-based mobile nodes that construct mobile sensor networks, can adjust deployment autonomously according to the location and importance of ROI, which will optimize network coverage and satisfy application requirement. A typical strategy to these kinds of deployment problems is the virtual force relationship based Algorithm(VFA) [15–17]. Originally proposed to facilitate the movement of robots to avoid obstacles, VFA has be adopted as one of the most effective algorithms to optimize the sensor deployment in WSNs. In this research we study the deficiencies of VFA by analyzing its convergence property, boundary effect and useless movement, and propose two effective improvements, dubbed Improved VFA (IVFA) and Exponential VFA (EVFA). Extensive simulations are carried out to evaluate the performance of the proposed approaches. The results show that our proposed algorithms get better performance in energy consumption, convergence and coverage rate.

The remainder of this paper is organized as follows. Section 2 describes the background of deployment problem of mobile sensor networks and analyzes the deficiencies of original VFA. Section 3 proposes two novel schemes to improve original virtual force relationship in ROI to solve deployment problem of the mobile sensor networks. Extensive simulation experiments have been done to evaluate these deployment algorithms and the results verify the proposed algorithm in section 4. Finally, we give some conclusions.

2. Analysis of Deficiencies of Virtual Force Algorithm

2.1. Problem Description

Without loss of generality, we consider the sensor deployment problem in mobile sensor networks with a N × M rectangle ROI. We adopt the plate sensing model, where the sensor can cover every point in the circle area centered at node itself and with a detection (or sensing) radius. In other words, the sensor node can detect the target appeared in its radius area. The effective communication distance is twice of the sensing radius. Each node can obtain the location of itself (through GPS or some other localization algorithms). Initially, the mobile sensor nodes are distributed randomly in the ROI plain. During the process of deployment, each node is able to move freely within certain range. Our main objective is to deploy the sensors and control their movement to achieve high coverage rate, low energy consumption and fast convergence.

2.2. Virtual Force Algorithm

VFA was elicited from the potential field algorithm used for avoiding obstacles in mobile robot movement. Zou originally combined the potential field algorithm and the plate coverage theory by abstracting the sensor node to be a particle in the potential field, which will exert forces on the nodes nearby [13]. The forces between the nodes are presented by attractive and repulsive patterns. When two nodes are close enough (i.e., smaller than a threshold D_th), the force is in repulsive pattern, which intends to separate them; When two nodes are far from each other (i.e., larger than the threshold D_th), the force becomes attractive pattern, which draws them closer. As once can see, the repulsive force is to make sensors sufficiently scarce, avoiding redundant coverage by the dense deployment of sensor nodes; while the attractive force is to keep a certain density of the nodes, avoiding blind areas.

The threshold D_th is used to control the sensor density, which is determined by the users, e.g., according to the required sensing probability of the applications. Usually it ranges between $[\sqrt{3r},2r].$ More specifically, the force exerted on Node i by Node j in the network (denoted by $\overrightarrow{F_{ij}}$) is given by Equation (1):

$$\overrightarrow{F_{ij}}=\{\begin{array}{ll}{W}_a(d_{ij}-D_{th}),{\alpha }_{ij}\hfill & \mathrm{i}\mathrm{f}{d}_{ij}>D_{th}\hfill \\ 0\hfill & \mathrm{i}\mathrm{f}{d}_{ij}=D_{th}\hfill \\ W_r{d}_{ij}^{-1},{\alpha }_{ij}+\pi \hfill & \mathrm{i}\mathrm{f}{d}_{ij}<D_{th},\hfill \end{array}$$

(1)

where W_a, W_r are the virtual force coefficients; d_ij is the Euclidean distance between sensor S_i and S_j; and α_ij is the orientation of the line segment from S_i to S_j.

The total force exerted on Node i (i.e. F_i⃗), is then calculated by adding all forces contributed by the nodes in the network.

$$\overrightarrow{F_i}=\sum _{j=1,j\ne i}^n\overrightarrow{F_{ij}},$$

(2)

where n denotes the number of mobile sensor nodes in the given ROI. The orientation of F_i⃗ is determined by the angle of the summation of all the force vectors exerted on S_i.

Once F_i⃗ and its orientation is determined, the sensor moves to its new location under the total external force, in order to maximize the coverage area in ROI.

2.3. Analysis of Virtual Force Algorithm

By analyzing the forces between sensor nodes in VFA as given by Equations (1)-(2), we find that there always exists attractive force whenever the distance between two sensors is often more than threshold D_th. However, this may result in several problems, as elaborated below.

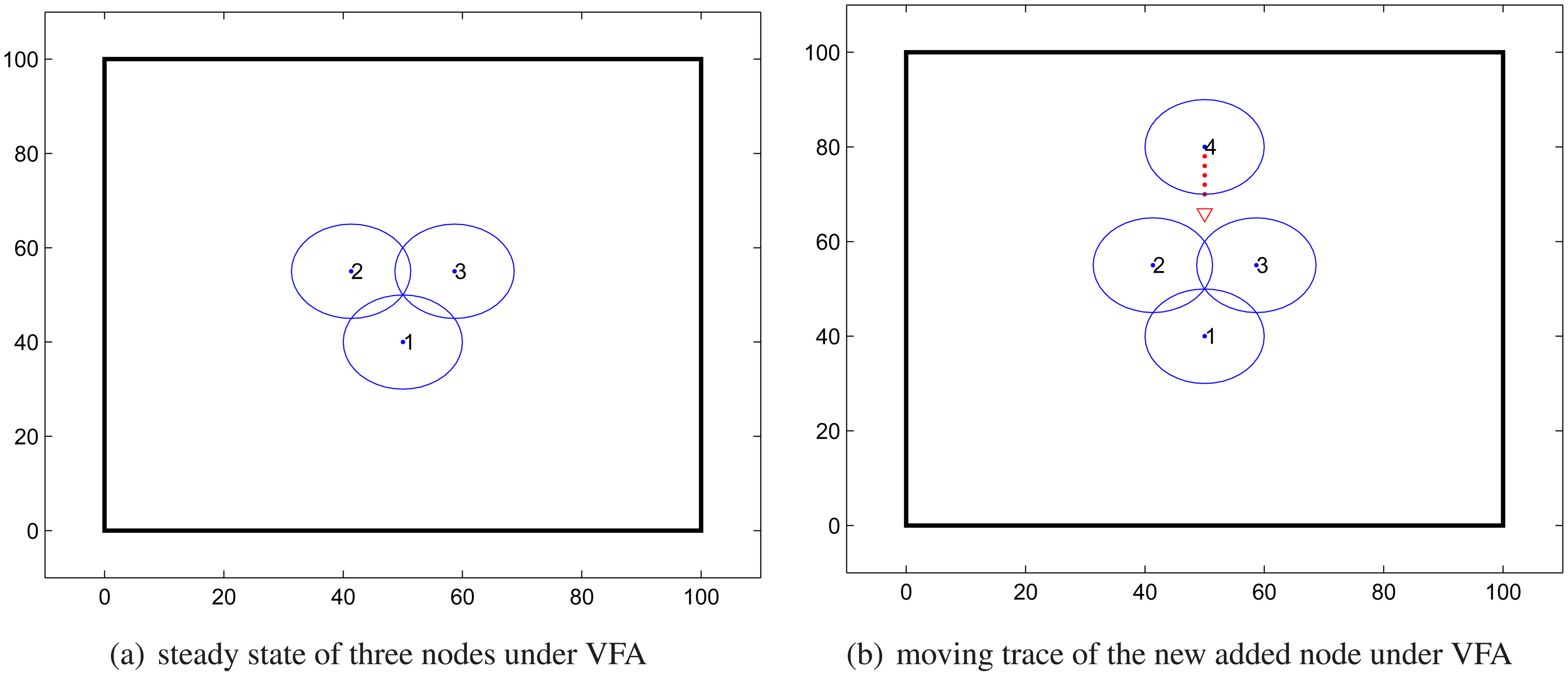
• VFA cannot always guarantee that the distance between sensors is reached at threshold D_th;
  As shown in Figure 1(a), assuming sensor nodes S₁, S₂, S₃ are located on the vertices of an equilateral triangle, when optimized coverage of ROI is achieved by using VFA. Zhang has demonstrated in [18] that in this case it ensures that not only ROI is fully covered, but also the overlap between sensing regions is minimized. When Node S₄ enters the region, as shown in Figure 1(b), S₄ moves towards S₁, S₂, and S₃ under VFA. When nodes S₂, S₃, S₄ construct an equilateral triangle, there still exist attractive force between S₁ and S₄ according to Equation (1). Thus S₁ and S₄ will continue to move towards each other under the attractive force and consequently fail to keep a force balance in the origin WSNs. In other words, none of the two nodes will stabilize at a desired threshold distance D_th.
  In fact, both Figure 1(a) and Figure 1(b) reveal that for the given ROI, the movement of S₄ cannot increase the coverage ratio. On the contrary, it reduces the coverage rate to some extent. This kind of movement will not only consume the node's energy but make the coverage rate decrease, and thus is a useless move.
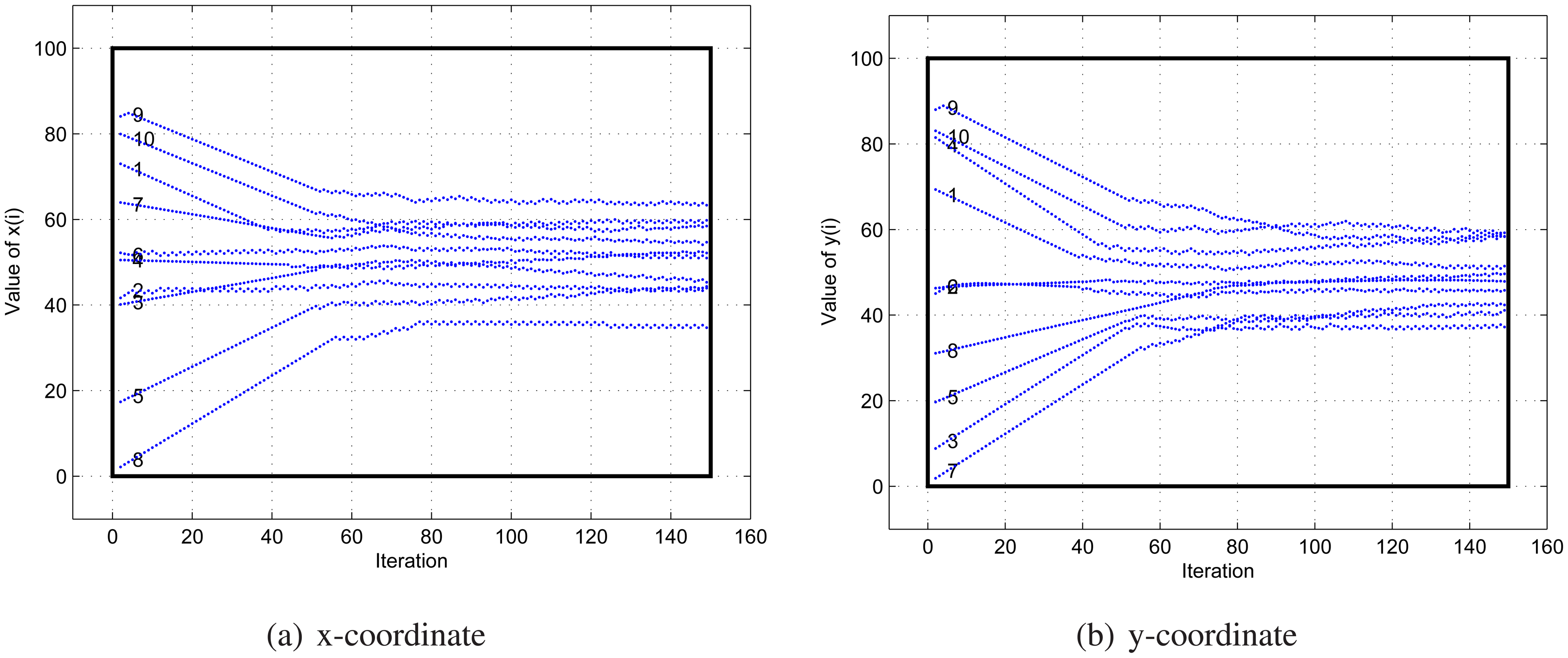
• VFA cannot converge to a steady state fastly;
  For a relatively large scale WSNs, the virtual force relationship given by equation (1) will neither make any two nodes stable at the desired threshold nor make the algorithm converged. Figure 2(a) and Figure 2(b) respectively show the changes of x and y coordinates of sensor nodes under VFA for the WSN with n = 10. It is easy to find that the nodes are not stable and their coordinates are varying all the time, being in an oscillating state.
  Therefore it is necessary to confine the virtual force between sensor nodes into an effective distance, so that no force is exerted when the distance exceed a certain range, which will facilitate sensor deployment in a fast and stable way. Also when a force effective distance is given in a coverage problem, useless moves are reduced and sensor energy is saved so that the coverage ratio of ROI in the whole networks is increased to some extent.

In addition, the boundary effect of coverage area is not discussed for VFA in [13]. Actually the sensor nodes sometimes move out of ROI under the VFA and thus the sensor resource is wasted. This problem is not obvious when the nodes are scarcely deployed; in WSNs with high density, however, the useless move near the boundary becomes a major drawback of the energy-constrainted sensor network. In this scenario the boundary effect may lower the coverage of the network or even fail to accomplish the sensing task.

In the following sections we will make two improvements on VFA, aiming to address these drawbacks.

3. Novel Deployment Schemes for Mobile Sensor Networks

3.1. Improved VFA: IVFA

In real WSNs, within an effective communication distance C_th, sensors can estimate the distance between one another using Received Signal Strength Indication (RSSI), which can be further used for computing the exerted force. When the distance between sensor nodes exceeds C_th, they cannot communicate with each other and hence fail to run VFA for analyzing the forces and adjusting locations. In addition, for those node that are separated farther than C_th, moving under the attractive force given by Equation (1) doesnt increase the coverage ratio as illustrated in Figure 1(a) and Figure 1(b). Therefore the effective communication distance C_th is helpful for making the sensor nodes in WSN converge to a steady state fast under VFA. For instance, in Figure 1(b) if there exist no forces between S₄ and S₁, S₂, and S₃, the deployment will soon come into stable in the origin network, achieving a better coverage. At the same time no extra energy consumption for the movement is needed. To this end, we propose the Improve VFA, as shown in Equation (3):

$$\overrightarrow{F_{ij}}=\{\begin{array}{ll}0\hfill & \text{if}{d}_{ij}>C_{th}\hfill \\ W_a(d_{ij}-D_{th}),{\alpha }_{ij}\hfill & \text{if}{D}_{th}\le d_{ij}\le C_{th}\hfill \\ W_r{d^{-1}}_{ij},{\alpha }_{ij}+\pi \hfill & \text{if}{d}_{ij}<D_{th}.\hfill \end{array}$$

(3)

For each iteration, the force exerted on a node is calculated by Equation (3). Once the final force exerted is calculated, the sensor node moves to a new location according to the magnitude and direction of the total force. To restrain useless move, we set the maximum movement in each iteration as Maxstep. The distance of movement of a sensor node after the force exerted on is proportional to the magnitude of the total force, but not more than Maxstep. Considering the boundary effect, we can prevent the nodes from moving out of ROI by setting a maximum coordinate of the ROI, avoiding unnecessary waste of energy and resources. The updated coordinate after a move can be calculated by Equation (4) and (5):

$$x{(i)}_{\mathit{\text{new}}}=\{\begin{array}{ll}x{(i)}_{\mathit{\text{old}}}\hfill & \mathrm{i}\mathrm{f}\left|\overrightarrow{F_i}\right|=0\hfill \\ x{(i)}_{\mathit{\text{old}}}+\mathit{\text{sign}}(\overrightarrow{F_{ix}})\left|\frac{\overrightarrow{F_{ix}}}{\overrightarrow{F_i}}\right|\times \mathit{\text{Maxstep}}\times e^{-\frac{1}{\overrightarrow{F_i}}}\hfill & \mathrm{i}\mathrm{f}0\le x{(i)}_{\mathit{\text{new}}}\le x_{\mathit{\text{ROI}}\_\mathit{\text{Max}}}\hfill \\ x_{\mathit{\text{ROI}}\_\mathit{\text{Max}}}\hfill & \mathrm{i}\mathrm{f}x{(i)}_{\mathit{\text{new}}}>x_{\mathit{\text{ROI}}\_\mathit{\text{Max}}}\hfill \\ x_{\mathit{\text{ROI}}\_\mathit{\text{Min}}}\hfill & \mathrm{i}\mathrm{f}x{(i)}_{\mathit{\text{new}}}<x_{\mathit{\text{ROI}}\_\mathit{\text{Min}}}\hfill \end{array}$$

(4)

$$y{(i)}_{\mathit{\text{new}}}=\{\begin{array}{ll}y{(i)}_{\mathit{\text{old}}}\hfill & \text{if}\left|\overrightarrow{F_i}\right|=0\hfill \\ y{(i)}_{\mathit{\text{old}}}+\left|\mathit{\text{sign}}(\overrightarrow{F_{iy}})\frac{\overrightarrow{F_{iy}}}{F_i}\right|\times \mathit{\text{Maxstep}}\times e^{-\frac{1}{\overrightarrow{F_i}}}\hfill & \text{if}0\le \text{y}{\left(i\right)}_{\mathit{\text{new}}}\le y_{\mathit{\text{ROI}}\_\mathit{\text{Max}}}\hfill \\ y_{\mathit{\text{ROI}}\_\mathit{\text{Max}}}\hfill & \text{if}y{\left(i\right)}_{\mathit{\text{new}}}>y_{\mathit{\text{ROI}}\_\mathit{\text{Max}}}\hfill \\ y_{\mathit{\text{ROI}}\_\mathit{\text{Min}}}\hfill & \text{if}y{\left(i\right)}_{\mathit{\text{new}}}<y_{\mathit{\text{ROI}}\_\mathit{\text{Min}}}\hfill \end{array}$$

(5)

where x(i)_old and y(i)_old denote the current location of S_i; x(i)_new and y(i)_new denote the next location of S_i; F_i⃗ is the magnitude of the total force exerted on S_i; $\overrightarrow{F_{ix}}$ and $\overrightarrow{F_{iy}}$ respectively denote the magnitude of the force exerted on S_i in x and y directions; x_{ROI_Max} and y_{ROI_Max} are the maximum coordinates of ROI in x and y directions.

3.2. Exponential VFA: EVFA

In order to achieve fast convergence and better coverage performance with different ways for virtual force relationship between mobile sensor nodes, we have developed another algorithm, dubbed Exponential VFA (EVFA), where the virtual force decreases exponentially with distance between mobile sensor nodes. The EVFA is illustrated in Equation (6), which is revised on the basis of Equation (3). β₁ and β₂ are constants which can be adjusted according to the types of sensors. Normally the value of 2 is used if the sensors are electrical or magnetic field based. The new coordinates are updated according to Equations (4) and (5) as the IVFA.

$$\overrightarrow{F_{ij}}=\{\begin{array}{ll}0\hfill & {\text{if d}}_{ij}>C_{th}\hfill \\ W_a{(d_{ij}-D_{th})}^{{\beta }_1},{\alpha }_{ij}\hfill & {\text{if D}}_{th}\le d_{ij}\le C_{th}\hfill \\ W_r(d_{ij}^{-{\beta }_2}-D_{th}^{-{\beta }_2}),{\alpha }_{ij}+\pi \hfill & \text{if}{d}_{ij}<D_{th}\hfill \end{array}$$

(6)

3.3. Performance Evaluation

The performance evaluation of virtual force algorithm in sensor deployment usually includes three aspects: coverage ratio, moving energy consumption and convergence.

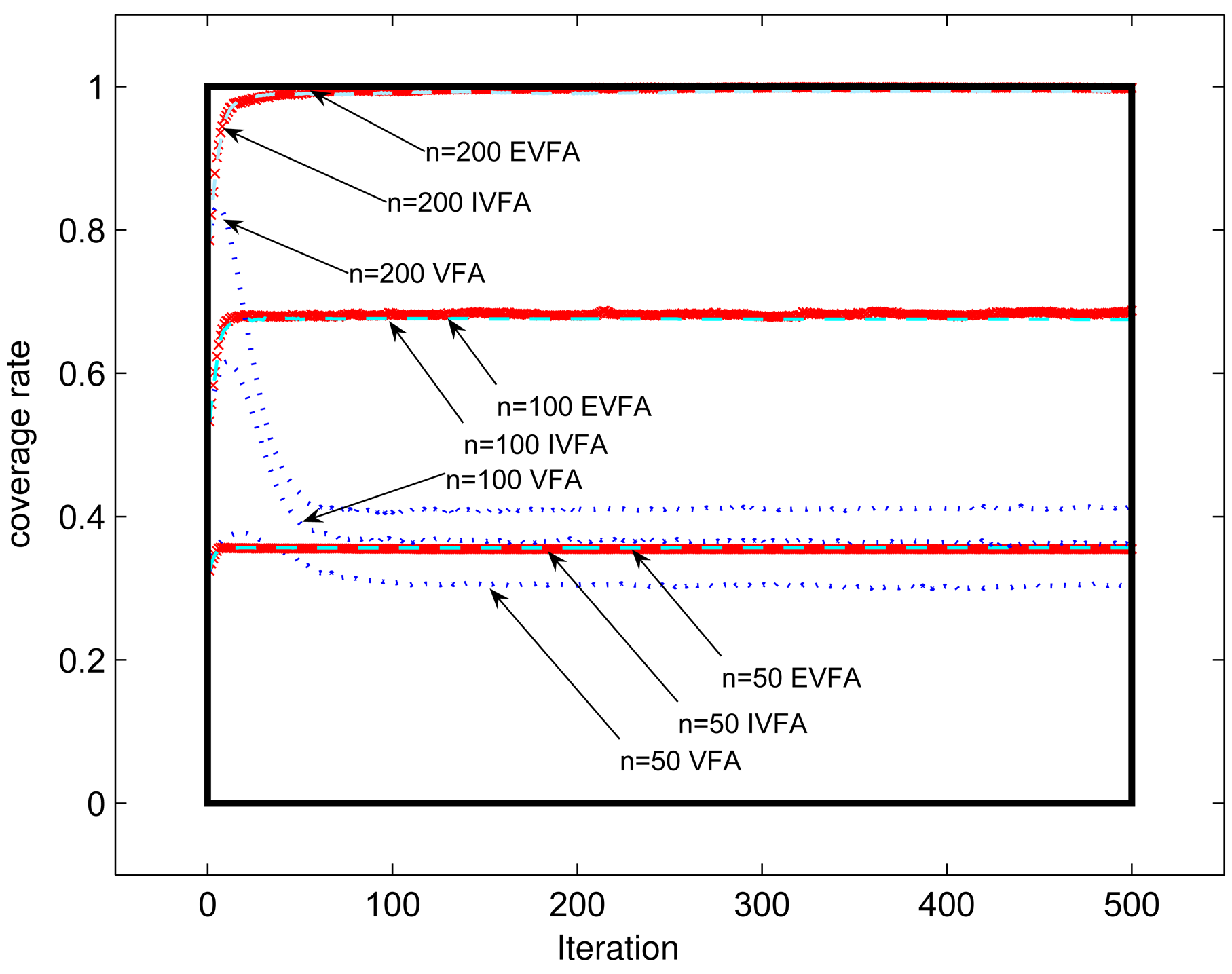
3.3.1. Coverage Rate

The coverage rate was originally proposed by Gage [19]. It is defined as the ratio of the area covered by all the nodes to the total area of ROI. Coverage rate is a measure of the coverage quality. So it is also called coverage degree. Since the total area covered by the nodes adopts the union concept, the value of coverage rate is always smaller or equal to 1:

$$C_r=\frac{{\cup }_{i=1\dots n}{A}_i}{A},$$

(7)

where C_r denotes the coverage rate; A_i denotes the covered area by node S_i; n is the number of mobile sensor nodes; and A is the total area of ROI. The computation of coverage rate adopts the Grid Scan method proposed by Shen and Chen [20]. By investigating the relationship of the distance between the center of grids and the nodes and the sensing radius of the nodes, whether a grid can be covered by a sensor or not can be determined and the coverage rate can be calculated. In this paper we assume the grid is 1 by 1.

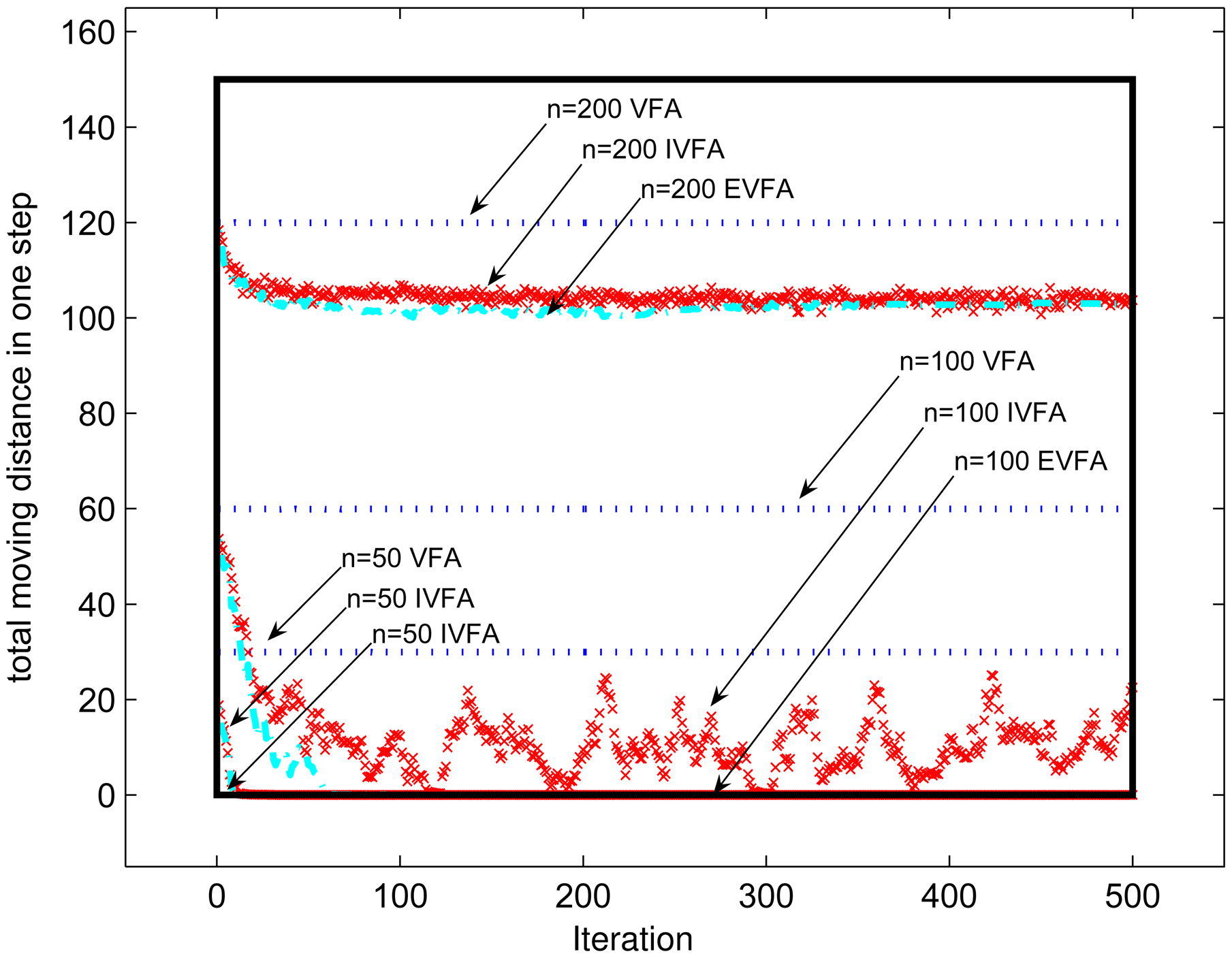
3.3.2. Moving Energy Consumption

Moving Energy Consumption is the energy used for redeploying the sensor nodes under virtual force. In this paper the moving energy consumption in simulation is represented by the overall movement of all the sensor nodes in each iteration, i.e. $E_d={\sum }_{i=1}^n\sqrt{{(x{(i)}_{\mathit{\text{new}}}-x{(i)}_{\mathit{\text{old}}})}^2+{(y{(i)}_{\mathit{\text{new}}}-y{(i)}_{\mathit{\text{old}}})}^2}$. The value of E_d represents the magnitude of the nodes' movement.

3.3.3. Convergence of Deployment Scheme

The convergence of deployment schemes is crucial to judge the accomplishment of the deployment. The deployment convergence is defined as Definition 1.

Definition 1: Virtual force based deployment schemes are convergent if each mobile sensor node can reach a steady state under a certain scheme, i.e. E_d = 0.

In distributed systems, it is not applicable to judge deployment finish by investigating whether the overall coverage rate is higher than a given threshold nor by set the iteration limits to terminate the movement. So a distributed method must be implemented to investigate the convergency and convergence speed. Usually in a densely deployed area, the virtual force algorithm cannot easily converge. Hence detailed analysis of convergency should be carried out. Generally speaking, the nodes can identify the convergency by observing the change of the coordinate of itself. We will not discuss this topic in this paper. From the simulation result, it is can be found that for scarcely deployed area, both IVFA and EVFA are deployment convergence and original VFA is not. For densely deployed area, the above algorithms are not deployment convergence if no distributed convergency algorithm is applied.

4. Simulation Results and Performance Evaluation

In this section we evaluate the performance of VFA, IVFA, EVFA by large scale simulations. The following assumptions are made in our simulation: 100 × 100 ROI, r = 5, Maxstep = 0.6, full coverage is considered, $D_{th}=\sqrt{3_r}$, and C_th = 2 r. All of the following results are the average of 100 times simulations.

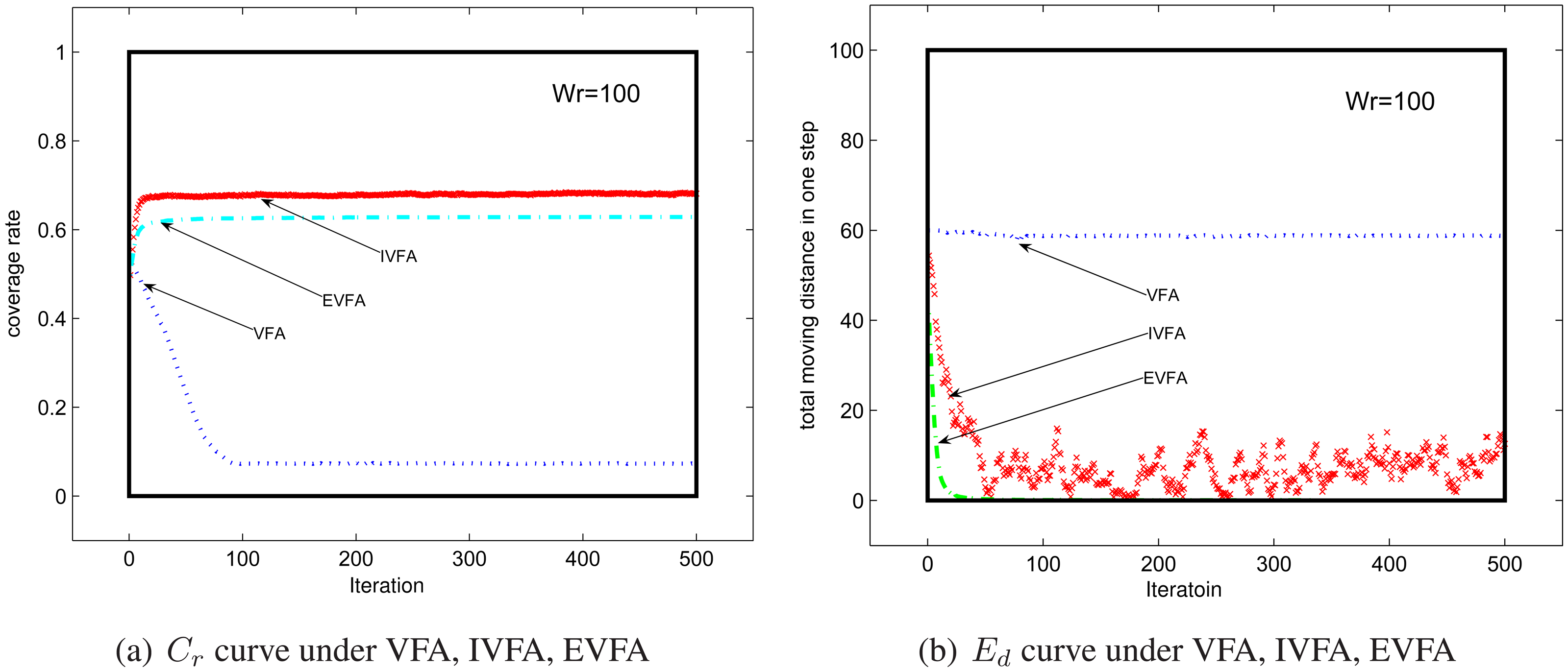
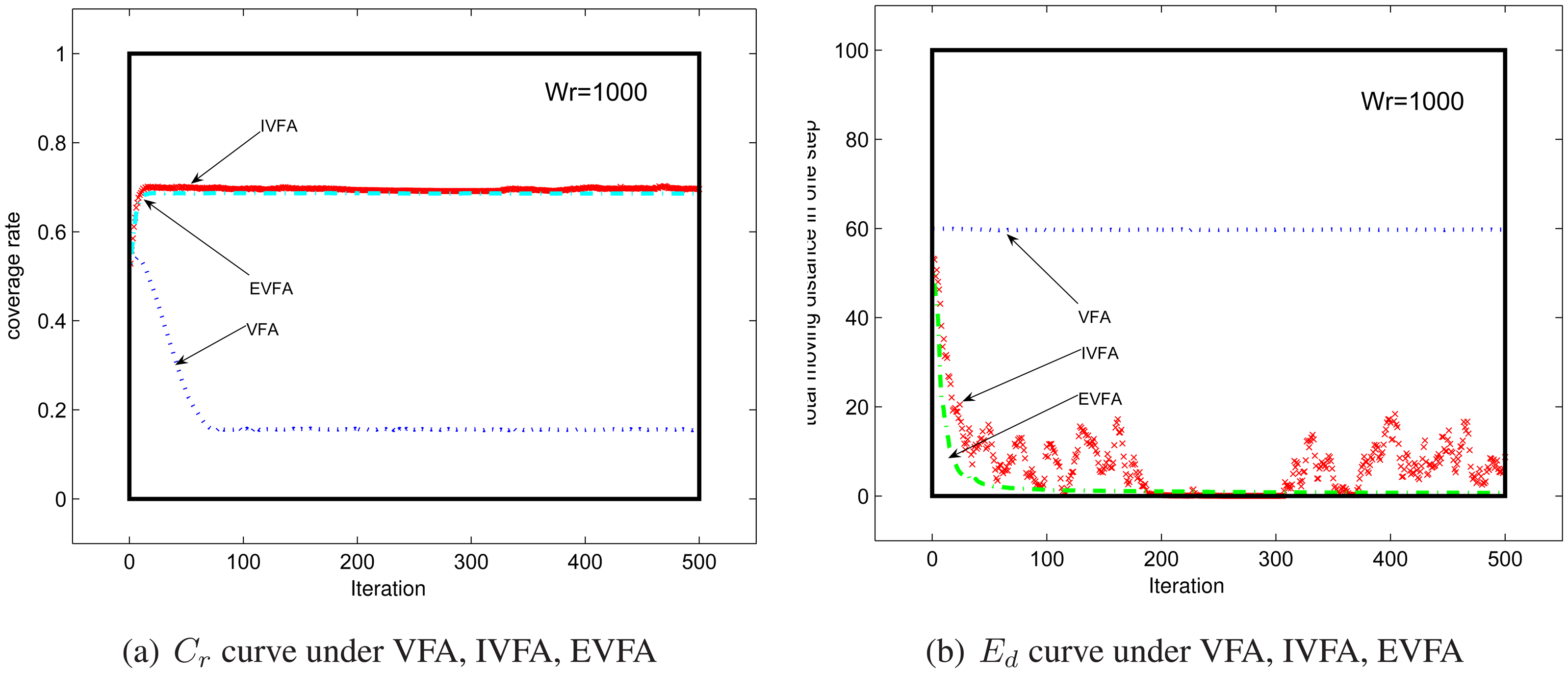
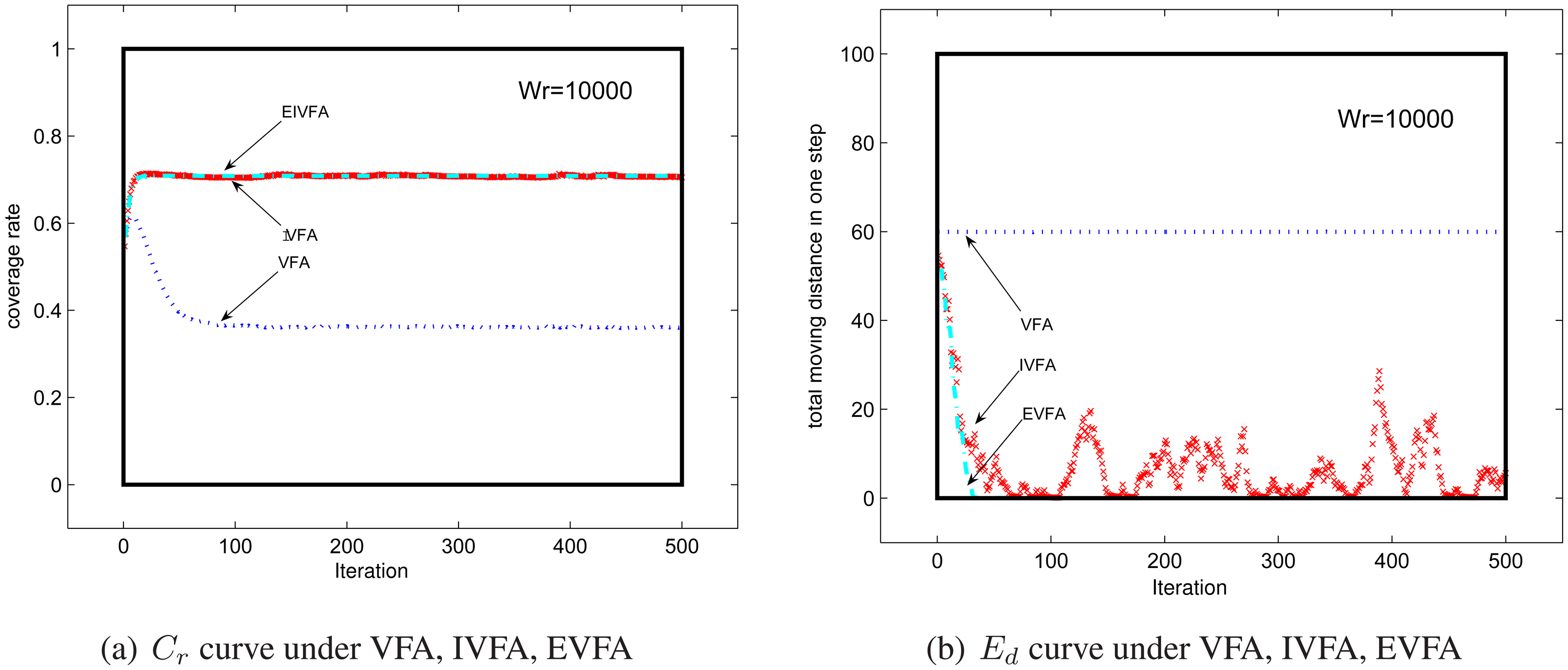
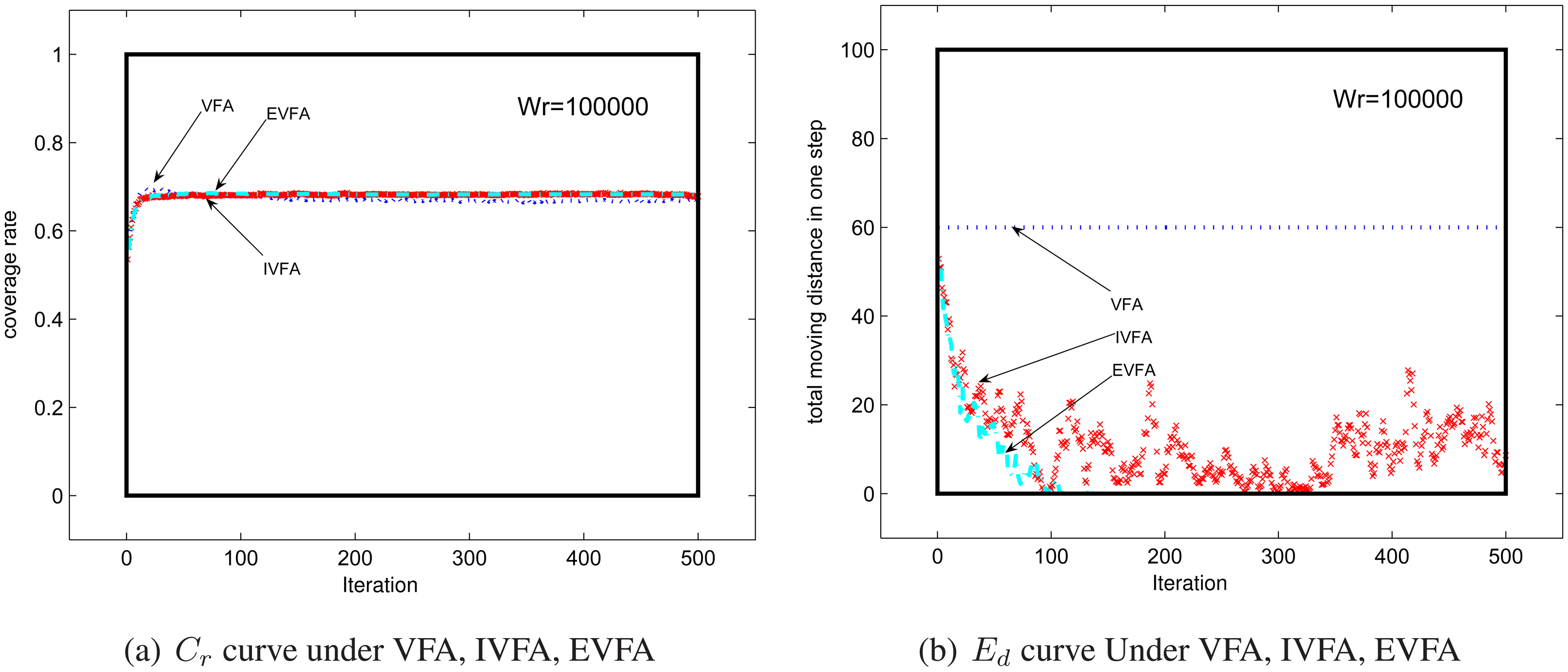
4.1. Impact of Mobile Sensor Nodes's Number

We investigate under three different network sizes with n = 50, 100, and 200, the performance of VFA, IVFA and EVFA on coverage rate, moving energy consumption and convergency. We have W_a=1, W_r = 10⁴, and β₁ = β₂ = 2. Figure 3 shows the change of coverage rate - more nodes result in higher coverage rate. For n = 50, 100, 200, both IVFA and EVFA achieve a steady coverage in 8,10,40 iterations, respectively. On the other, VFA needs 80 iterations for a steady coverage. We also observe from Figure 3 that IVFA and EVFA attain a higher coverage compared to VFA. When n = 200, the coverage rate of IVFA and EVFA is approximately 1, i.e. almost accomplish the coverage, while the rate stabilizes at 40% for VFA. (● :VFA, × :IVFA, ·– :EVFA, all the same representation in the following experiments)

Figure 4 shows the moving energy consumption for each iteration under different number of nodes in the network. The result shows that for various number of nodes n, the moving energy consumption of virtual force algorithms VFA, IVFA, and EVFA decreases respectively. In VFA since there exist forces between almost any two nodes, the sensor nodes move in Maxstep almost in every iteration, which can be observed in the simulation results. For EVFA, in the cases of n = 50, 100, the algorithm converge very well after 10, 60 iterations respectively, which results in the accomplishment of the deployment and the sensor nodes make no more moves. For IVFA in the case of n = 50, deployment is finished after about 15 iterations, achieving convergence. When n = 100, however, IVFA no longer converges as shown in the nodes' minute movement in Figure 4.

Since when n = 200 the number of sensor nodes for one-layer coverage exceeds the required number, some nodes still subject to repulsive or attractive force and move continuously even if the coverage rate remains constant under various algorithms.

From the simulation results, EVFA has the same coverage rate as IVFA but lower energy consumption and a better convergence property than IVFA. VFA performs worse than IVFA and EVFA in coverage rate, moving energy consumption and convergency.

4.2. Virtual Force Coefficient's influence on performance

The attractive and repulsive force coefficients W_a and W_r influence the algorithm's performance. Without loss of generality, we focus on the repulsive coefficient W_r only in the following discussion. In our simulation under n = 100 and W_a = 1, we respectively investigate when W_r = 10², 10³, 10⁴, 10⁵ VFA, IVFA, EVFA's performance on coverage rate, moving energy and convergency. As shown in the simulation results in Figure 5(a), Figure 6(a), Figure 7(a) and Figure 8(a), the coverage rate of IVFA and EVFA do not change much as W_r increases, i.e. the two improved algorithms are not sensitive to the coefficient W_r. While the coverage of VFA increases as W_r becomes larger. When W_r = 10⁵ (Figure 8(a)), VFA has almost the same coverage performance as IVFA and EVFA (1% lower). But it can be observed that the coverage rate of VFA is oscillating. Thus with a very large repulsive coefficient(W_r = 10⁵), VFA cannot make the sensor nodes stable.

As shown in the simulation results in Figure 5(b), Figure 6(b), Figure 7(b) and Figure 8(b), EVFA can always accomplish deployment in mobile sensor networks and make the nodes static in the end. The EVFA converges fast while the change of W_r only affects the speed of convergence to some extent and will not alter the attribute of convergence; IVFA cannot make all the nodes stable. Some (all) nodes subject to force and move all the time, which result in redeployment in every iteration. The coefficient W_r does not affect IVFA much; under different W_r, the VFA makes the nodes move in maximum step distance in every iteration. Even the same coverage rate is achieved as EVFA and IVFA, the magnitude of movement does not change at all. Besides, VFA cannot converge and its energy consumption remains in maximum condition.

5. Conclusions

In this paper different mobile medium based sensor deployment strategies are investigated in depth. We discuss the boundary effect, virtual force effective distance, useless move and convergency problems of the VFA for a given ROI. The problems are solved by setting the maximum boundary coordinates, introducing the effective communication distance and constraining maximum step size. In addition, an exponential VFA is proposed to speed up the convergence.

Simulation results show that IVFA and EVFA have better performances than the origin VFA in coverage rate and moving energy consumption. Also they are not sensitive to virtual force coefficient. Since the EVFA is expressed in exponential form, it has a better convergence property and is always able to make the mobile sensor nodes stable in scarcely deployed WSNs. The VFA cannot achieve convergence even in small-scale scarce WSNs due to its complicated force relationship. The topic of distributed convergence of the nodes is only analyzed in the simulation results while the theoretical and systematic discussion is the future work of this paper.