Near-Field Thermometry Sensor Based on the Thermal Resonance of a Microcantilever in Aqueous Medium
Abstract
:1. Introduction
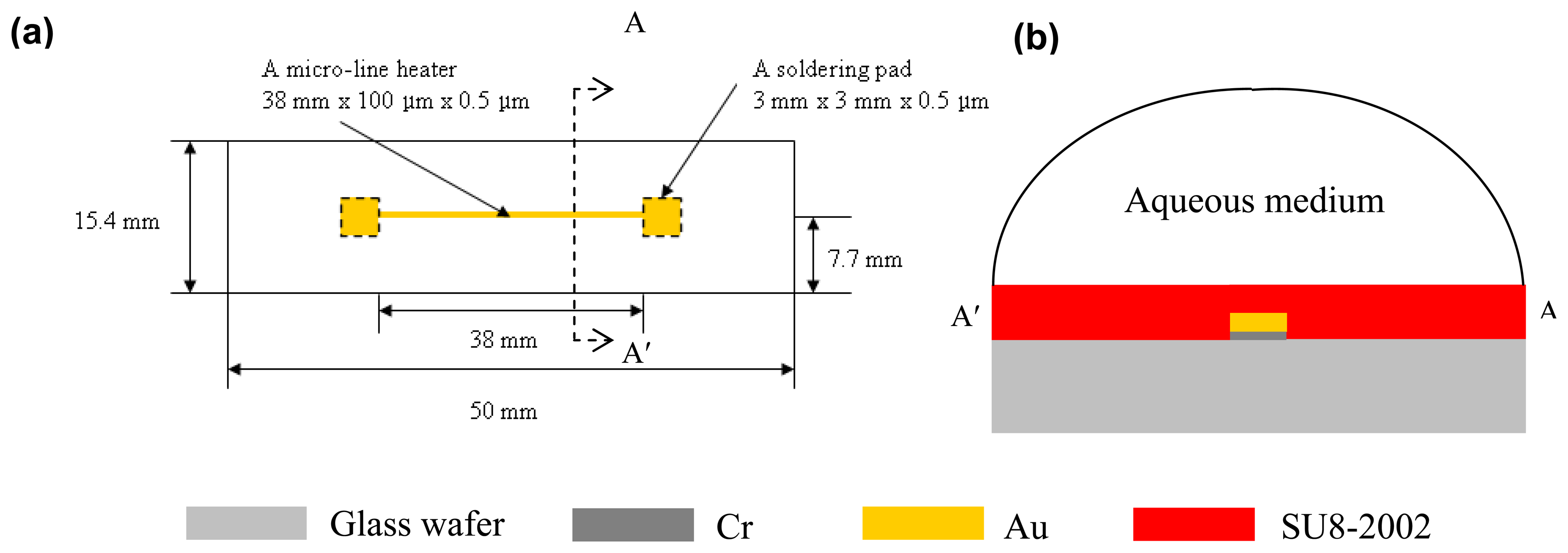
2. Materials and Methods
3. Results and Discussion
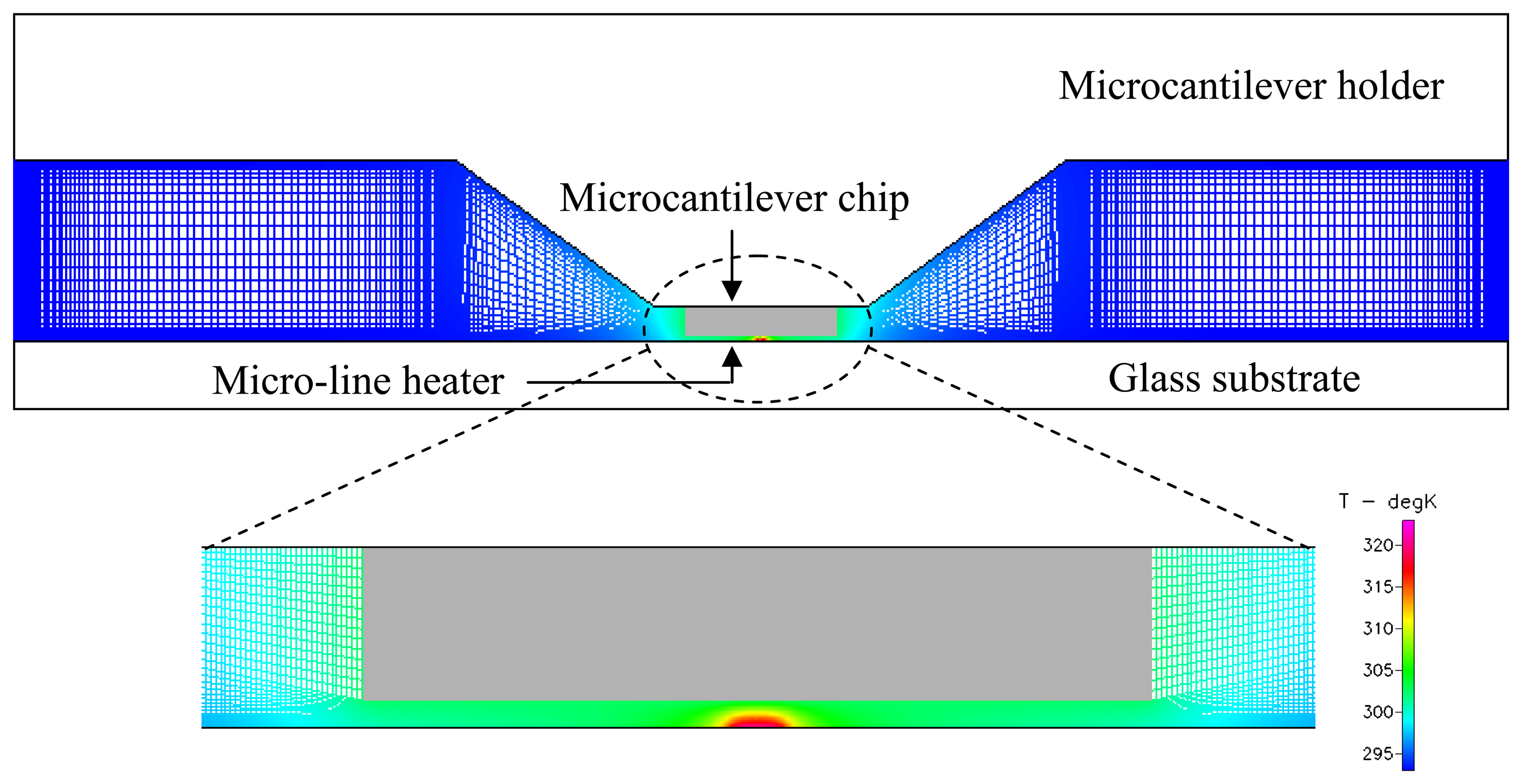
3.1. Transient temperature measurements
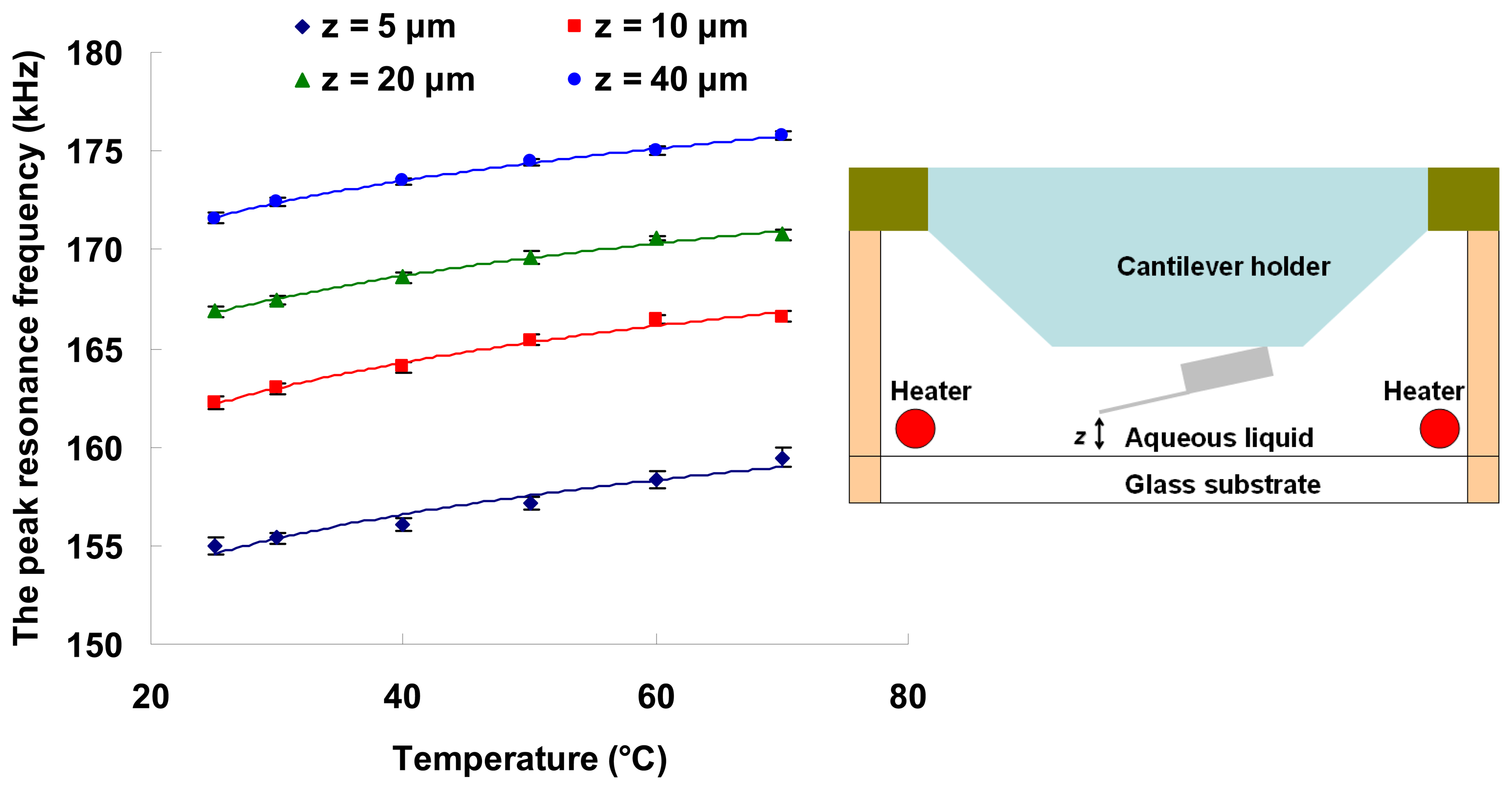
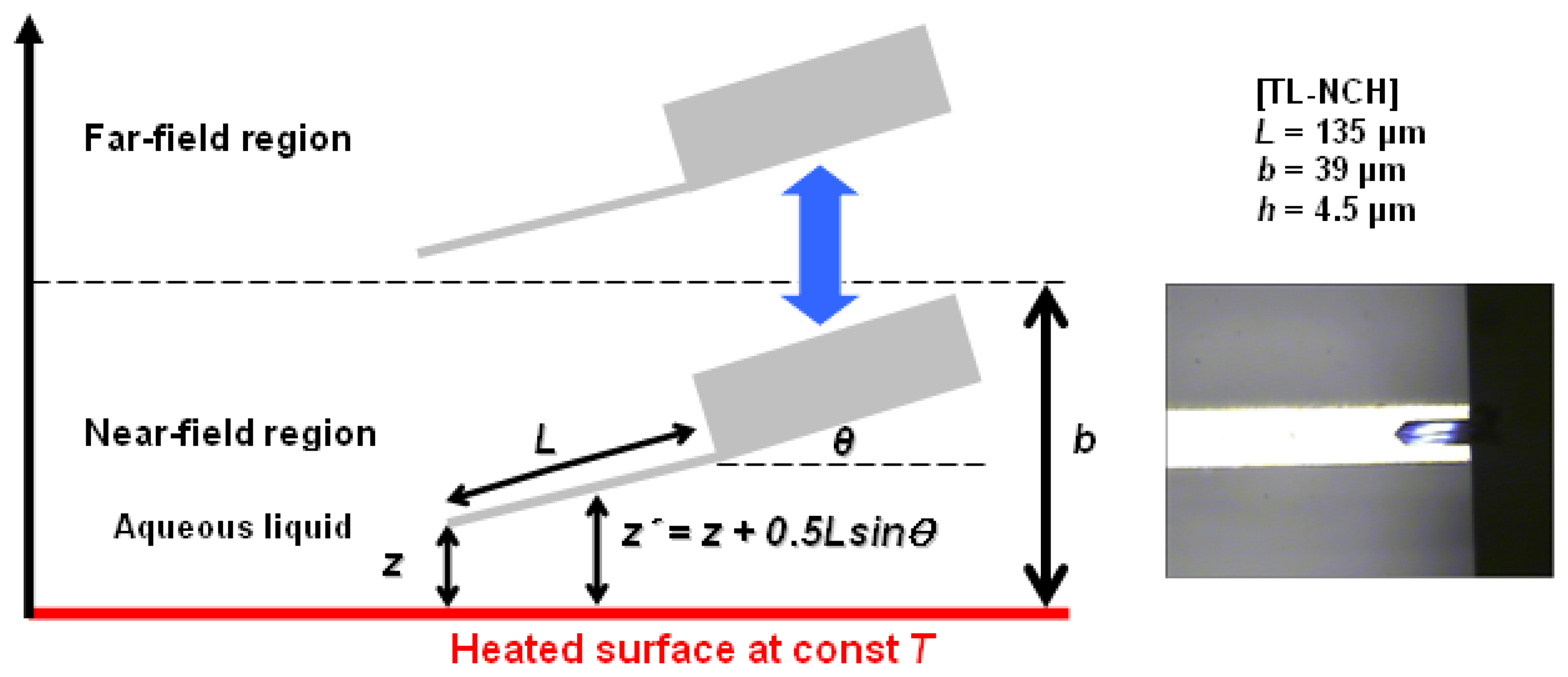
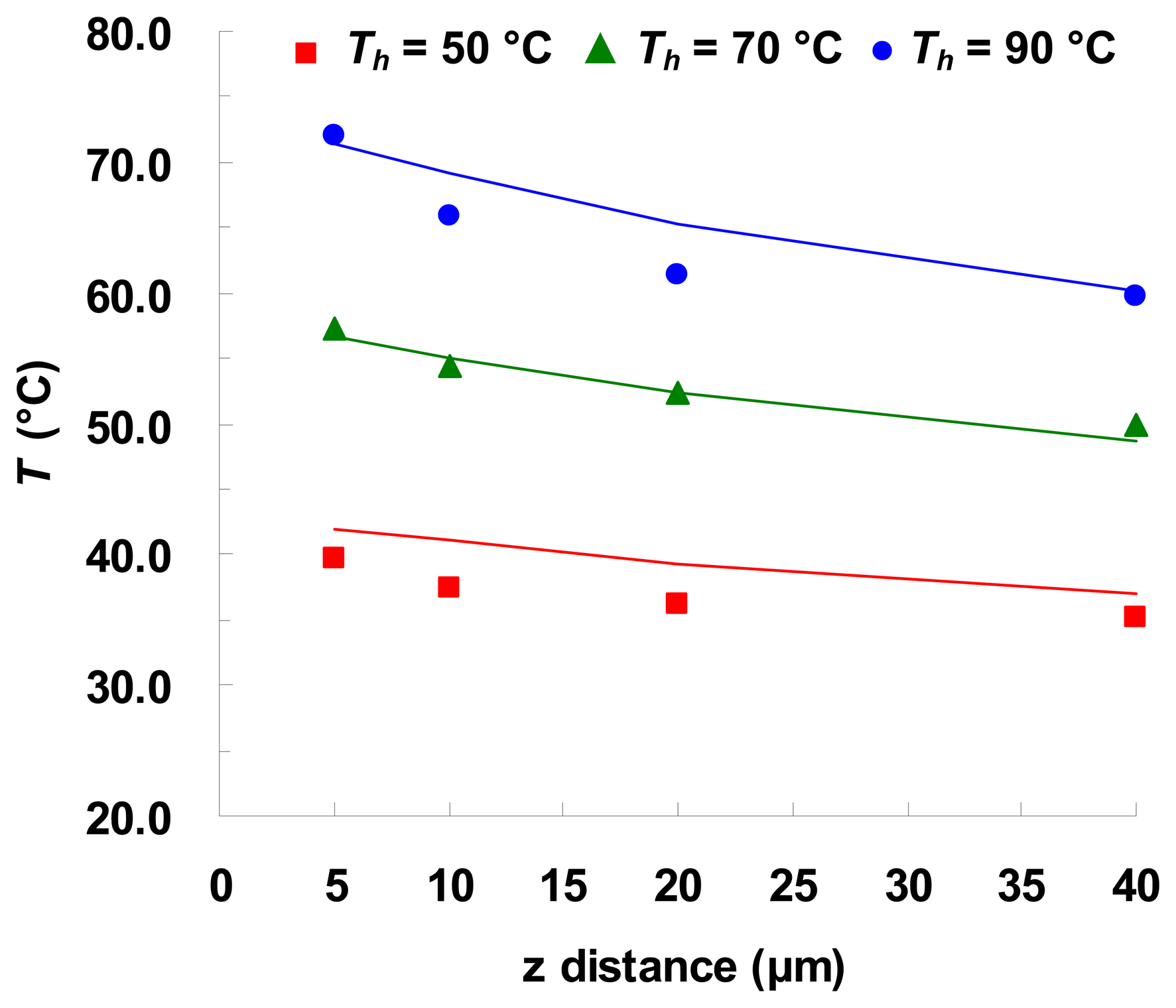
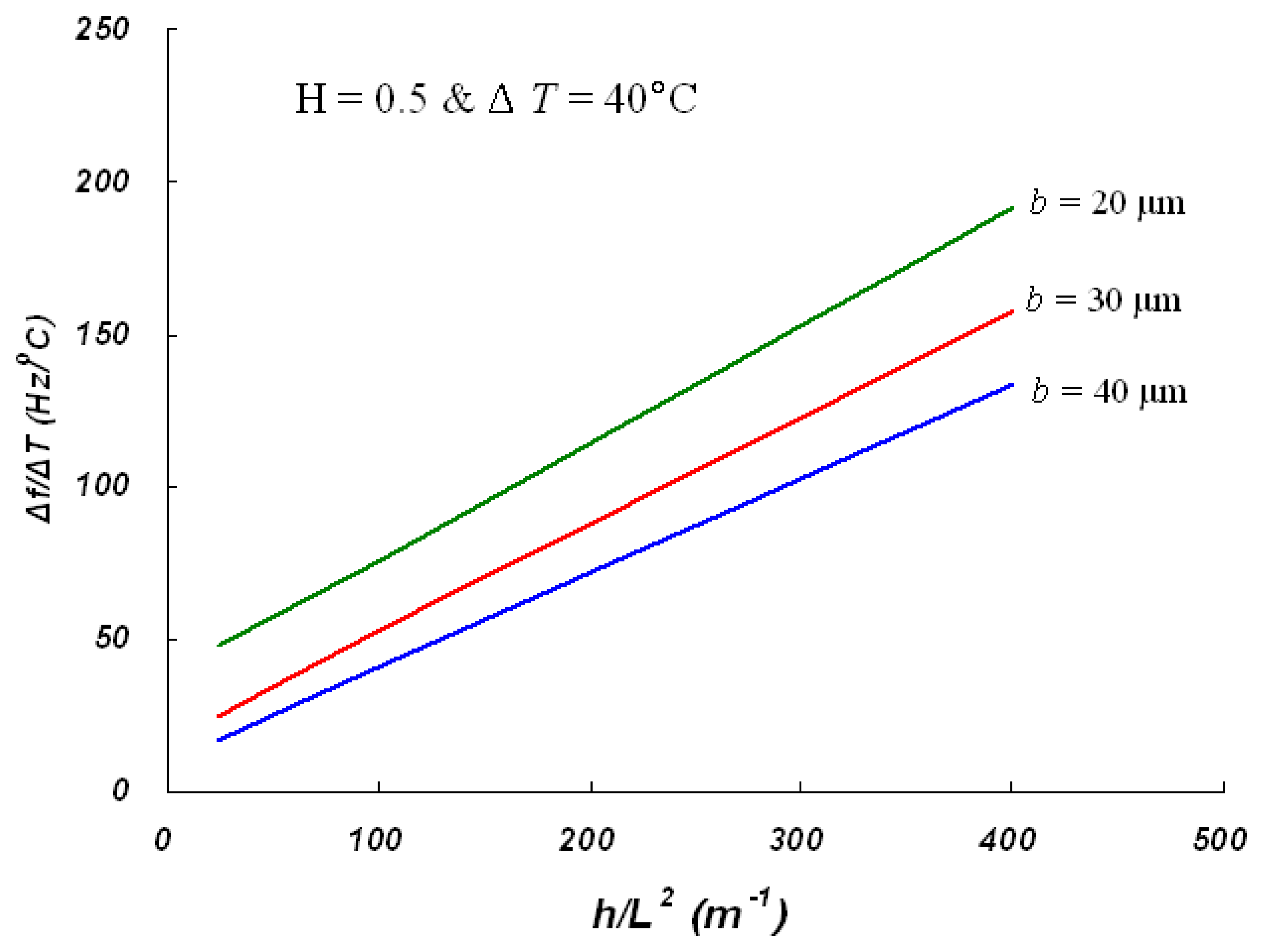
3.2. Steady-state temperature measurements
Conclusions
Acknowledgments
References and Notes
- Shi, L.; Majumdar, A. Recent developments in micro and nanoscale thermometry. Microscale Thermophys. Eng. 2001, 5, 251–265. [Google Scholar]
- Cahill, D. G.; Goodson, K.; Majumdar, A. Thermometry and thermal transport in micro/nanoscale solid-state devices and structures. J. Heat Transfer 2002, 124, 223–241. [Google Scholar]
- Shi, L.; Majumdar, A. Thermal transport mechanisms at nanoscale point contacts. J. Heat Transfer 2002, 124, 329–337. [Google Scholar]
- Roh, H. H.; Lee, J. S.; Kim, D. L.; Park, J.; Kim, K.; Kwon, O.; Park, S. H.; Choi, Y. K.; Majumdar, A. Novel nanoscale thermal property imaging technique: the 2ω method. I. principle and the 2ω signal measurement. J. Vac. Sci. Technol. B. 2006, 24, 2398–2404. [Google Scholar]
- Roh, H. H.; Lee, J. S.; Kim, D. L.; Park, J.; Kim, K.; Kwon, O.; Park, S. H.; Choi, Y. K.; Majumdar, A. Novel nanoscale thermal property imaging technique: the 2ω method. II. demonstration and comparison. J. Vac. Sci. Technol. B. 2006, 24, 2405–2411. [Google Scholar]
- Li, M. H.; Gianchandani, Y. B. Applications of a low contact force polyimide shank bolometer probe for chemical and biological diagnostics. Sens. Actuators A-Phys. 2003, 104, 236–245. [Google Scholar]
- Watanabe, M. S.; Kakuta, N.; Mabuchi, K.; Yamada, Y. Micro-thermocouple probe for measurement of cellular thermal responses, Proc. 27th Ann. Conf. 2005 IEEE EMB. 2005; pp. 4858–4861.
- Kim, H. J.; Kihm, K. D.; Allen, J. S. Examination of ratiometric laser induced fluorescence thermometry for microscale spatial measurement resolution. Int. J. Heat Mass Transfer. 2003, 46, 3967–3974. [Google Scholar]
- Park, J. S.; Choi, C. K.; Kihm, K. D. Temperature measurement for a nanoparticle suspension by detecting the Brownian motion using optical serial sectioning microscopy (OSSM). Meas. Sci. Technol. 2005, 16, 1418–1429. [Google Scholar]
- Kim, I. T.; Kihm, K. D. Full-field and real-time SPR imaging thermometry. Opt. Letters. 2007, 32, 3456–3458. [Google Scholar]
- Roters, A.; Johannsmann, D. Distance-dependent noise measurements in scanning force microscopy. J. Phys. Condens. Matter. 1996, 8, 7561–7577. [Google Scholar]
- Naik, T.; Longmire, E. K.; Mantell, S. C. Dynamic response of a cantilever in liquid near a solid wall. Sens. Actuators A-Phys. 2003, 102, 240–254. [Google Scholar]
- Kim, S.; Kihm, K. D. Experimental verification of the temperature effects on Sader's model for multilayered cantilevers immersed in an aqueous medium. Appl. Phys. Lett. 2006, 89, 061918. [Google Scholar]
- Kim, S.; Kihm, K. D. Temperature dependence of the near-wall oscillation of microcantilevers submerged in liquid environment. Appl. Phys. Lett. 2007, 90, 081908. [Google Scholar]
- Paik, S. W.; Kihm, K. D.; Lee, S. P.; Pratt, D. M. Spatially and temporally resolved temperature measurements for slow evaporating sessile drops heated by a microfabricated heater array. J. Heat Transfer 2007, 129, 966–976. [Google Scholar]
- Bruun, H. H. Hot-wire Anemometry; Oxford University Press: London, 1995; pp. 19–70. [Google Scholar]
- Goldstein, R. J. Fluid Mechanics Measurements; Hemisphere Publishing Co.: Washington D.C., 1983; pp. 99–144. [Google Scholar]
- Lee, S. P.; Kauh, S. K. A new approach to enhance the sensitivity of a hot-wire anemometer and static response analysis of a variable temperature anemometer. Exp. Fluids. 1997, 22, 212–219. [Google Scholar]
- Tamayo, J. Study of the noise of micromechanical oscillators under quality factor enhancement via driving force control. J. Appl. Phys. 2005, 97, 044903. [Google Scholar]

© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Kim, S.; Kim, K.C.; Kihm, K.D. Near-Field Thermometry Sensor Based on the Thermal Resonance of a Microcantilever in Aqueous Medium. Sensors 2007, 7, 3156-3165. https://doi.org/10.3390/s7123156
Kim S, Kim KC, Kihm KD. Near-Field Thermometry Sensor Based on the Thermal Resonance of a Microcantilever in Aqueous Medium. Sensors. 2007; 7(12):3156-3165. https://doi.org/10.3390/s7123156
Chicago/Turabian StyleKim, Seonghwan, Kyung Chun Kim, and Kenneth David Kihm. 2007. "Near-Field Thermometry Sensor Based on the Thermal Resonance of a Microcantilever in Aqueous Medium" Sensors 7, no. 12: 3156-3165. https://doi.org/10.3390/s7123156
APA StyleKim, S., Kim, K. C., & Kihm, K. D. (2007). Near-Field Thermometry Sensor Based on the Thermal Resonance of a Microcantilever in Aqueous Medium. Sensors, 7(12), 3156-3165. https://doi.org/10.3390/s7123156



