Modeling Fire Occurrence at the City Scale: A Comparison between Geographically Weighted Regression and Global Linear Regression
Abstract
:1. Introduction
2. Materials and Methods
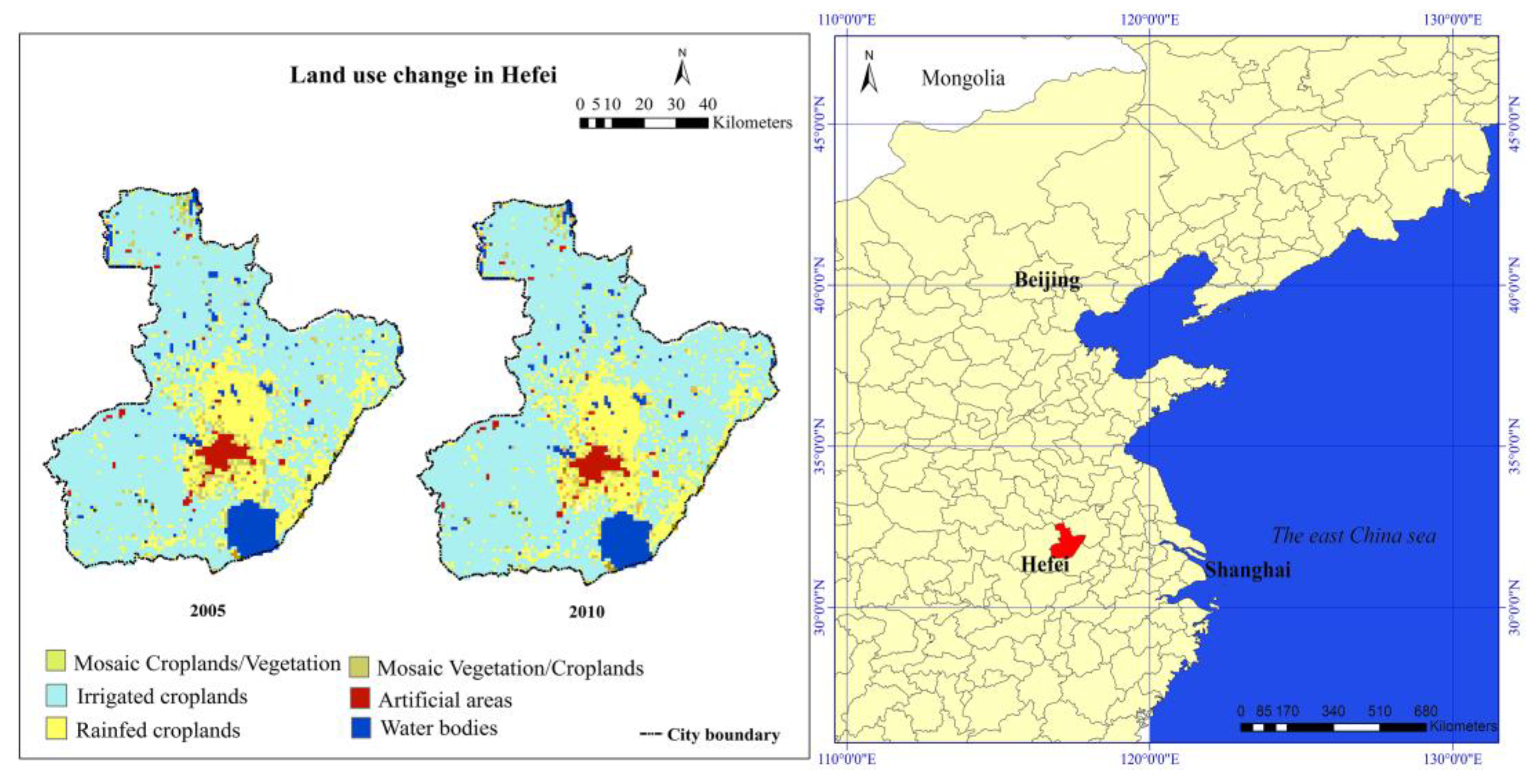
2.1. Study Area
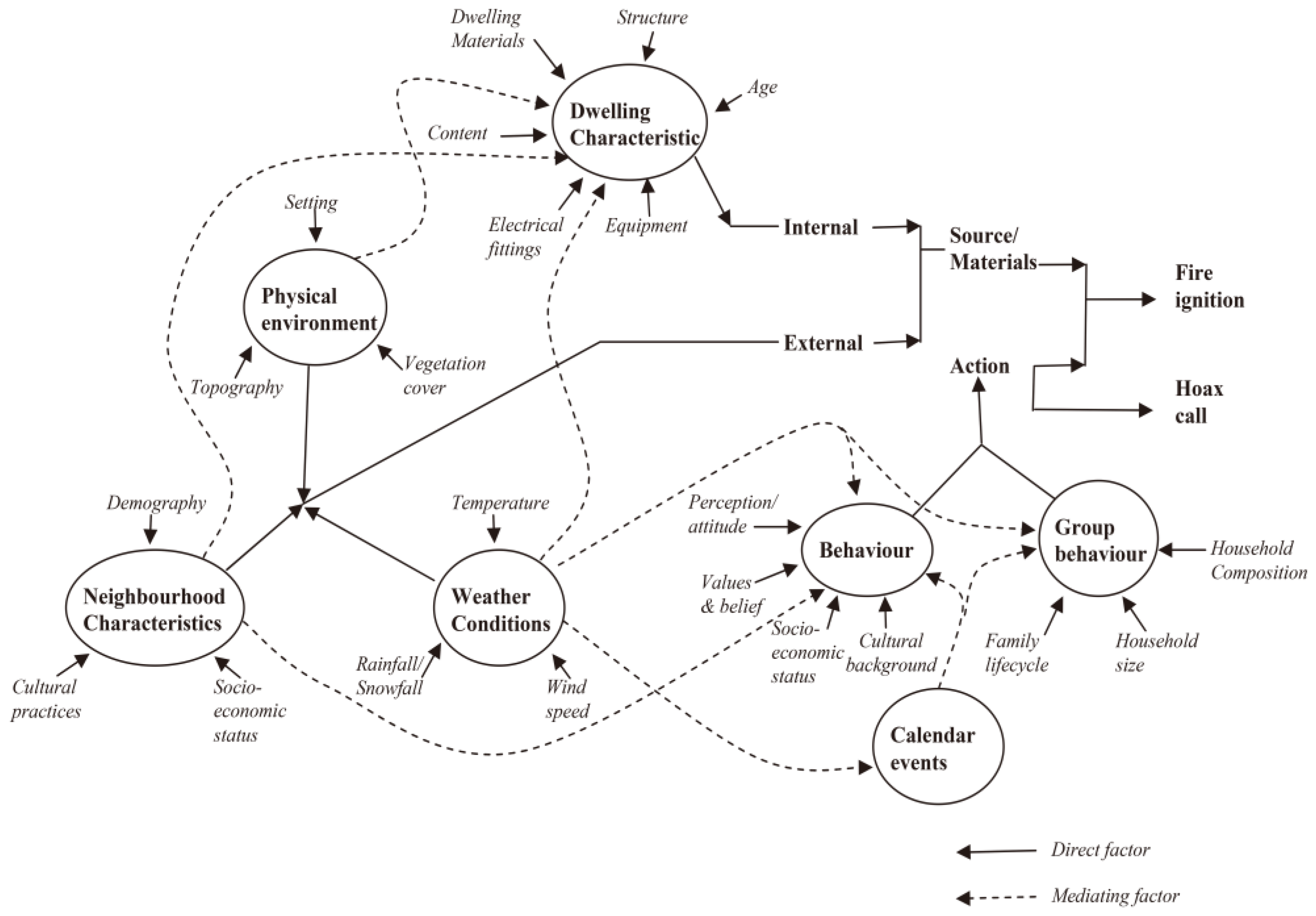
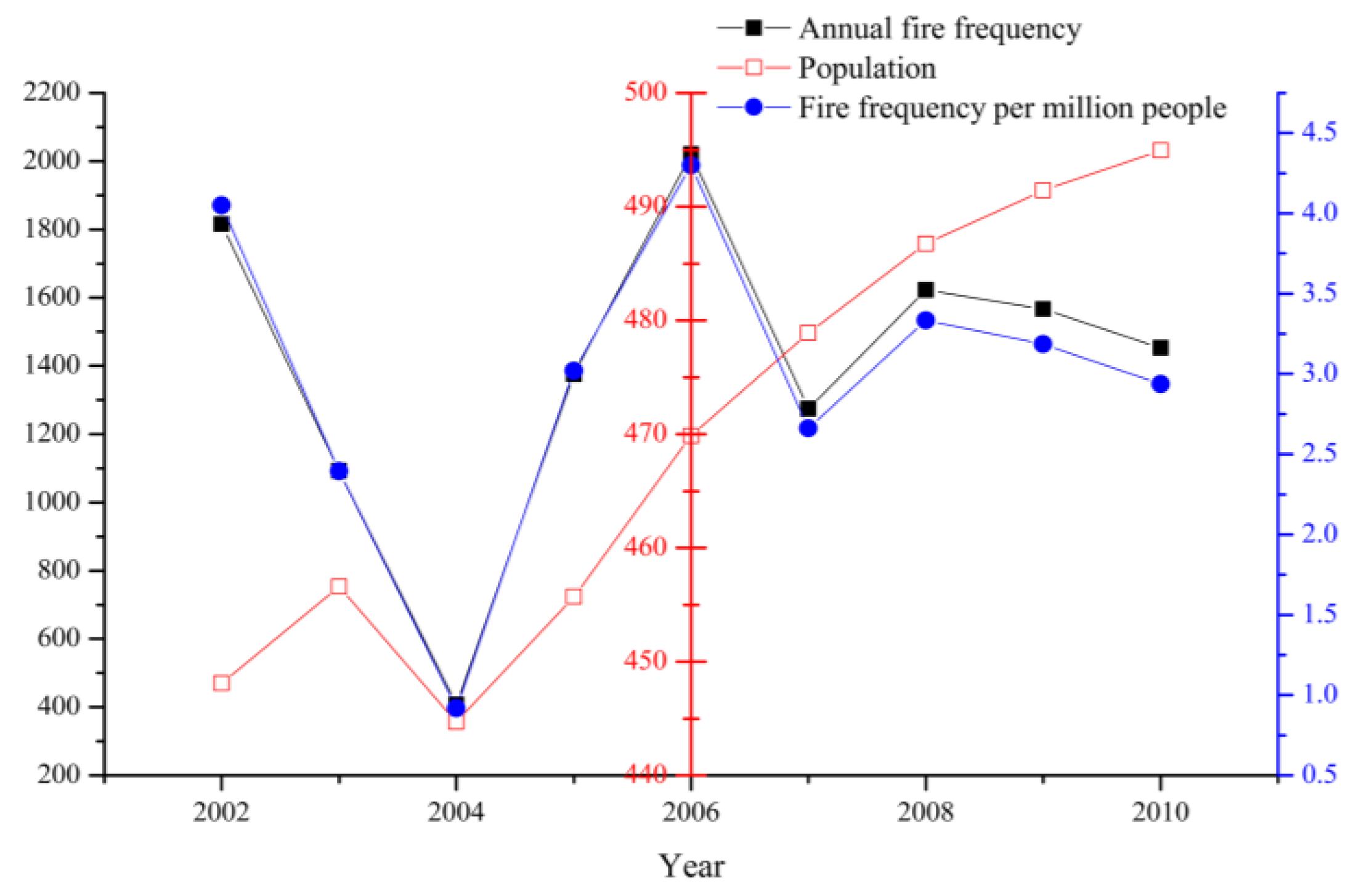
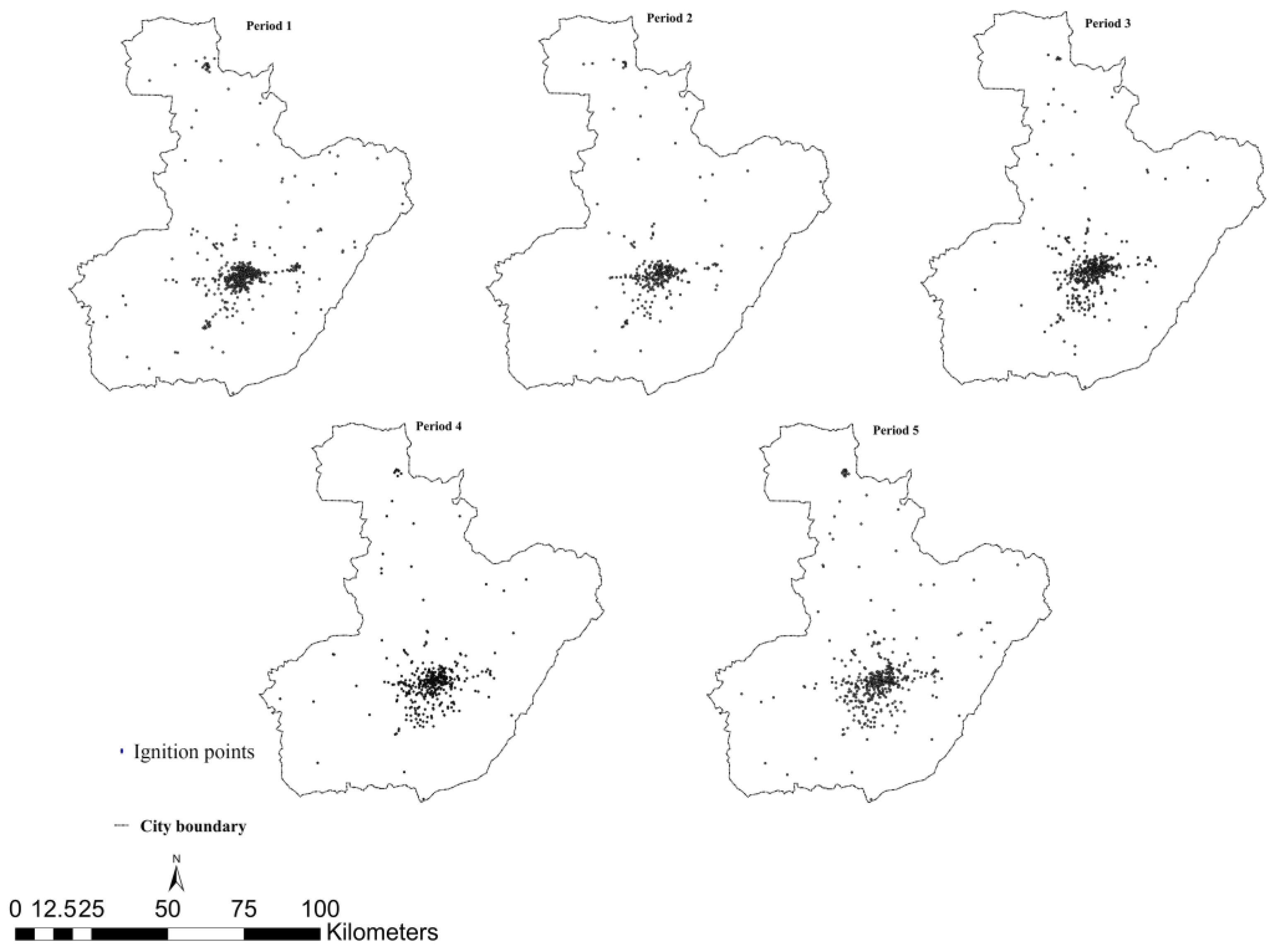
2.2. Dependent Variable and Preliminary Analysis for Infrastructure Fire Frequency
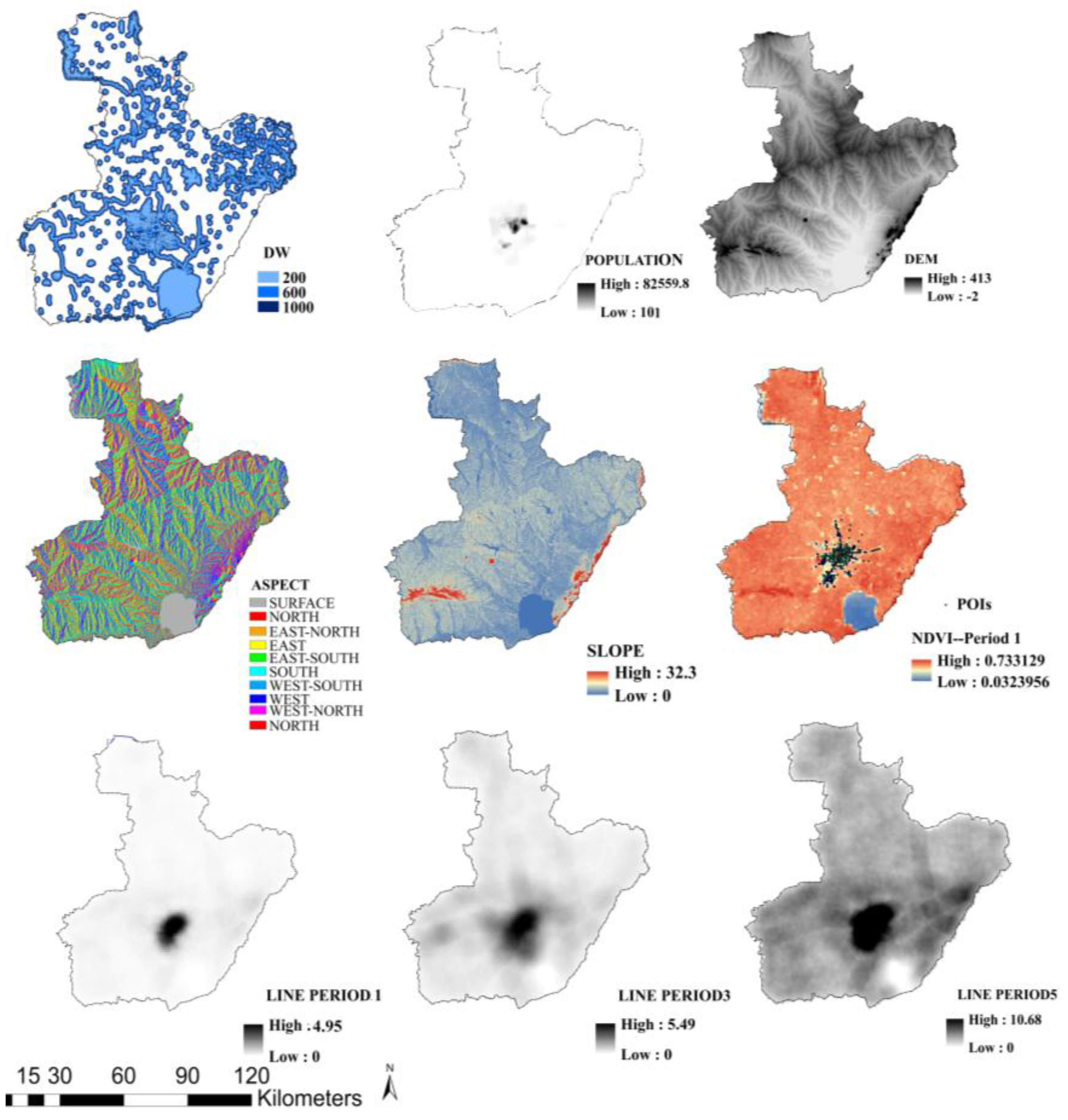
2.3. Explanatory Variables: Selection and Pre-Processing
2.3.1. Topography
2.3.2. Land Cover and NDVI
2.3.3. Temperature
2.3.4. Spatial Distribution of Population and Human Activities
2.3.5. Other Variables
2.4. Models and Methods
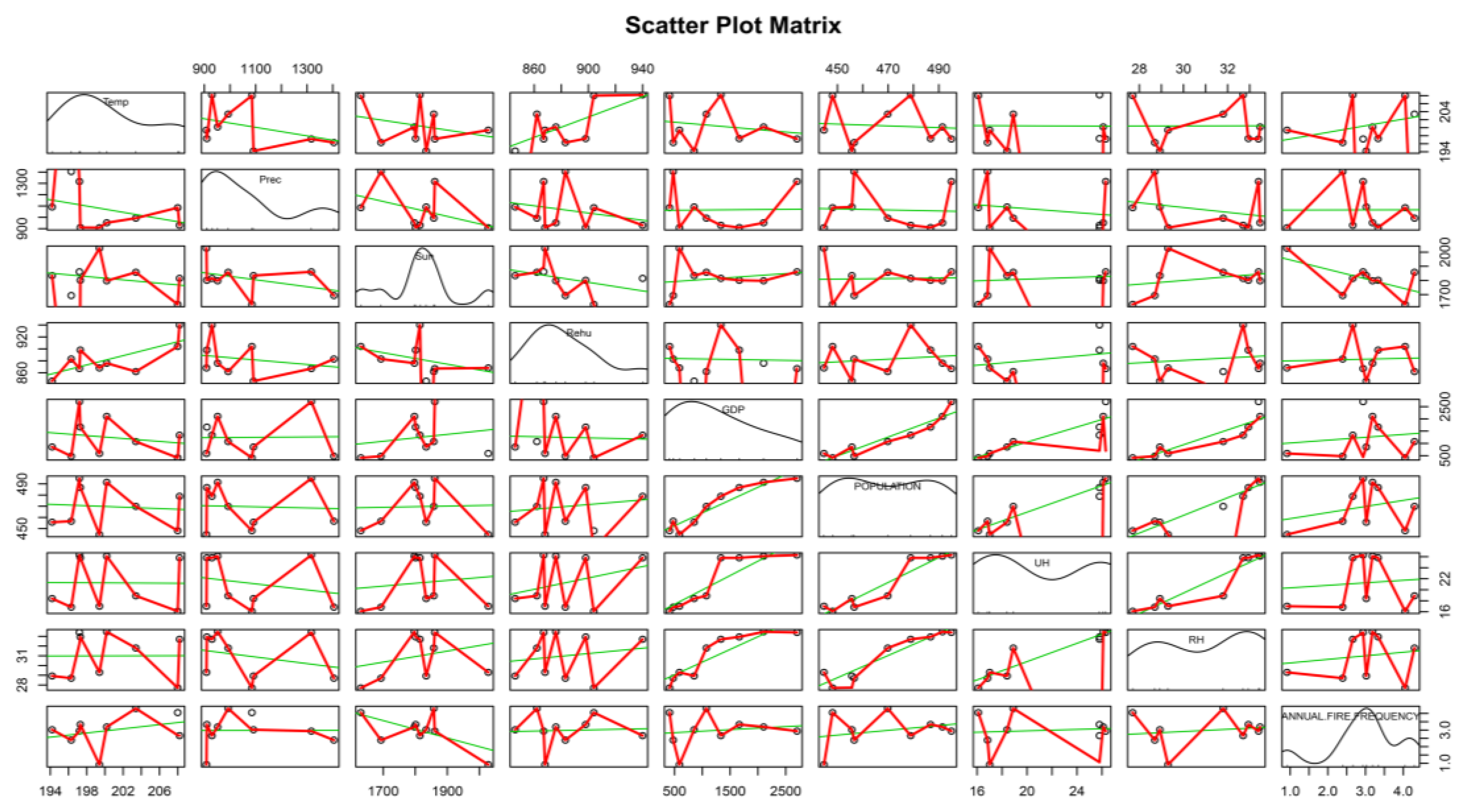
2.4.1. Data Preprocessing
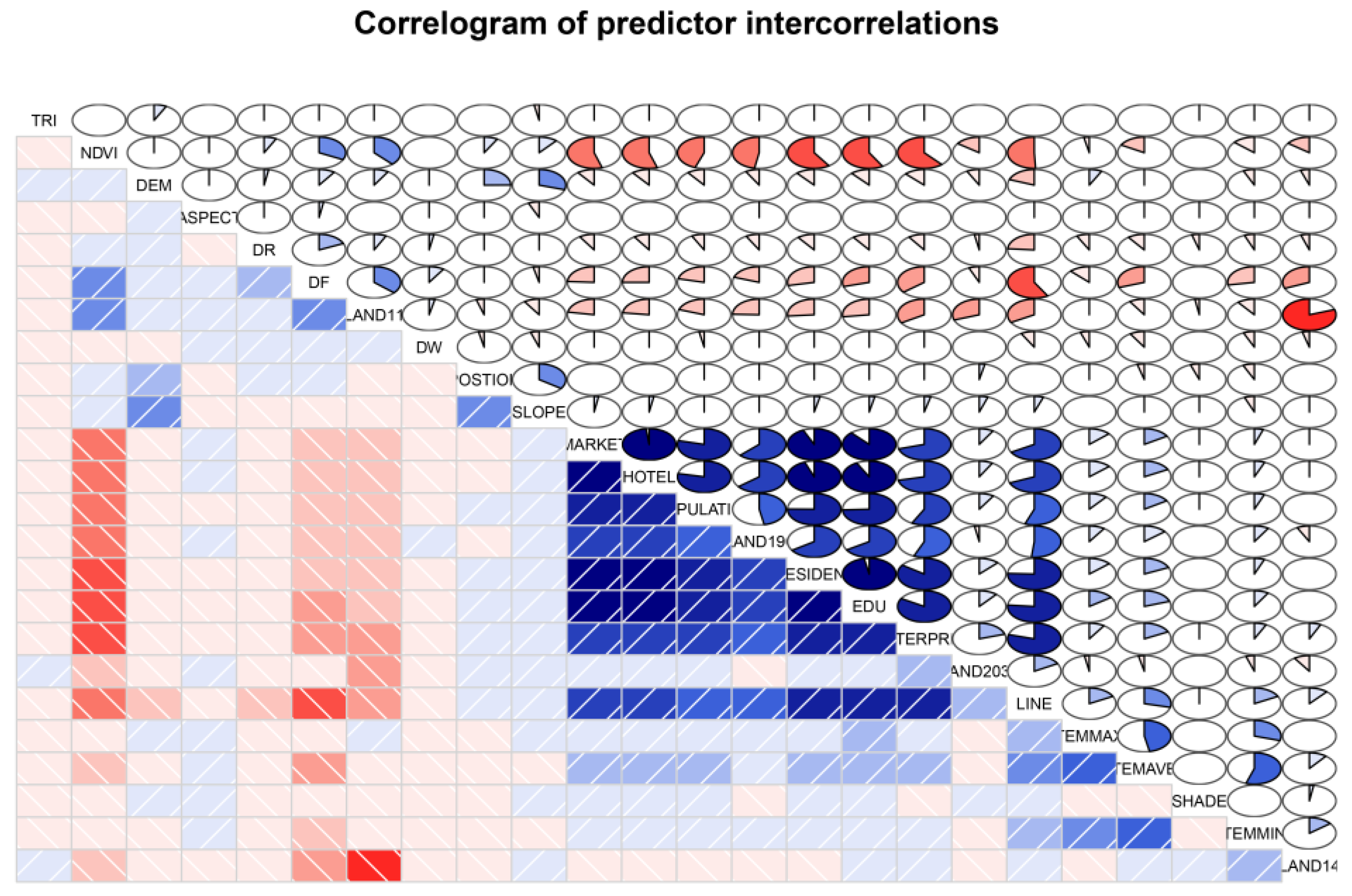
2.4.2. Variable Selection for LM
2.4.3. GWR and GTWR
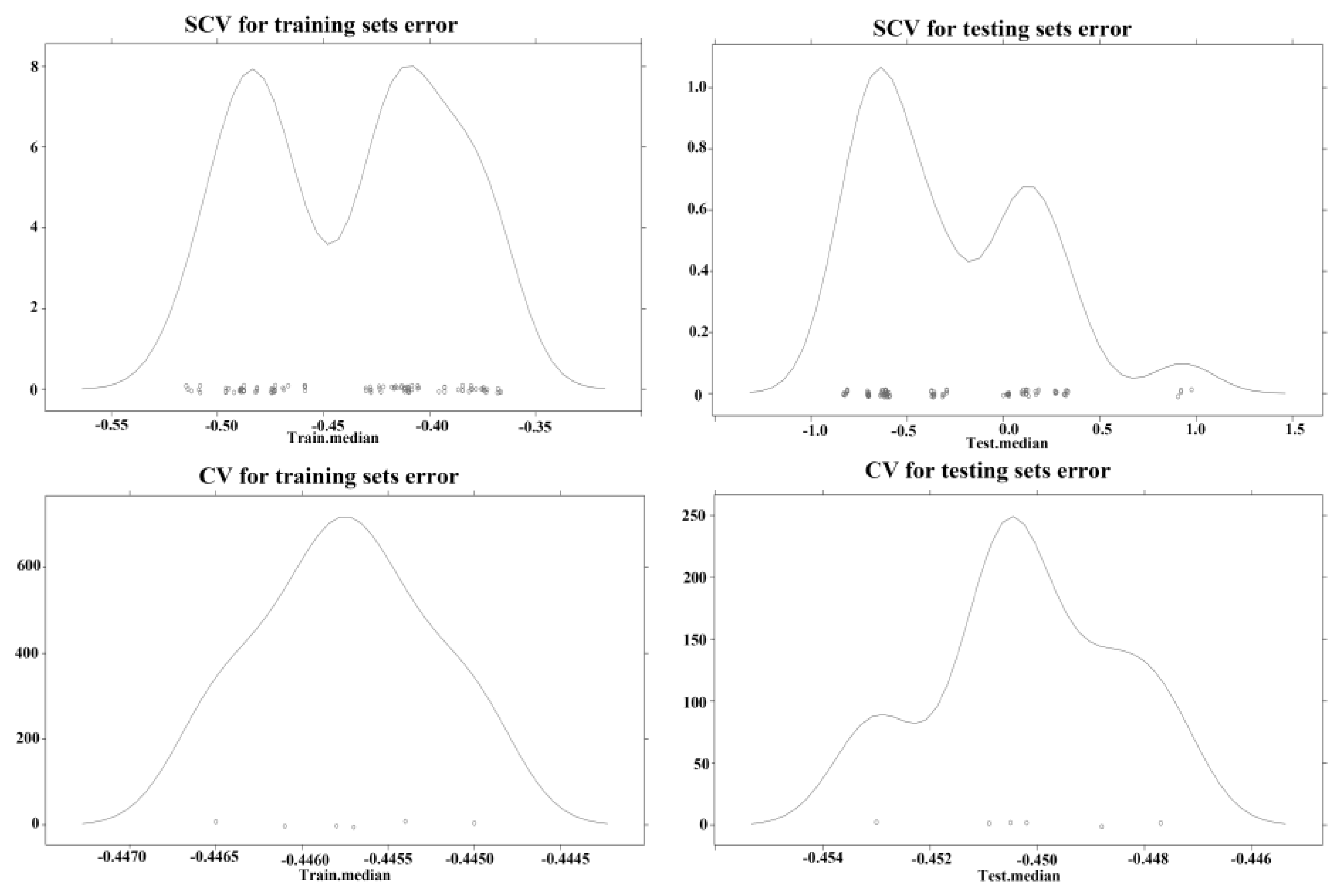
2.4.4. Model Validation
3. Results
3.1. Results of the Variables Selection for the LM
3.2. Results of the LM and the GWR-Based Model
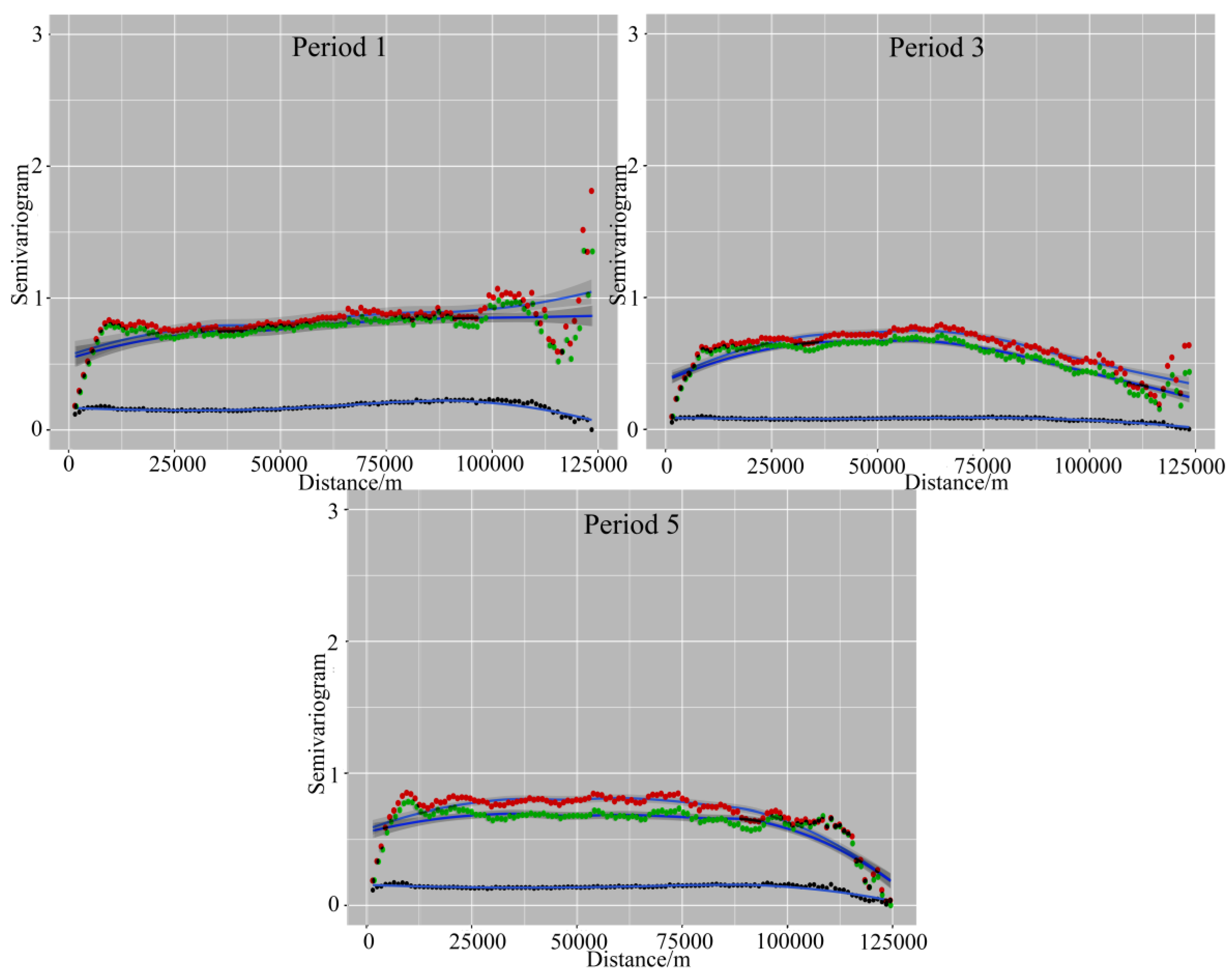
3.3. Test of Spatial Autocorrelation for Residuals
3.4. Assessment of Independent Validation for the Models
3.5. Heterogeneity of the Variable Significance Level
3.6. Spatiotemporal Changes in Fire Density
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guo, F.; Su, Z.; Wang, G.; Sun, L.; Lin, F.; Liu, A. Wildfire ignition in the forests of southeast China: Identifying drivers and spatial distribution to predict wildfire likelihood. Appl. Geogr. 2016, 66, 12–21. [Google Scholar] [CrossRef]
- Wu, Z.; He, H.S.; Yang, J.; Liang, Y. Defining fire environment zones in the boreal forests of northeastern China. Sci. Total Environ. 2015, 518–519, 106–116. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Qi, P.; Guo, G. Improvement of fire danger modelling with geographically weighted logistic model. Int. J. Wildland Fire 2014, 23, 1130–1146. [Google Scholar] [CrossRef]
- Serra, L.; Juan, P.; Varga, D.; Mateu, J.; Saez, M. Spatial pattern modelling of wildfires in Catalonia, Spain 2004–2008. Environ. Model. Softw. 2013, 40, 235–244. [Google Scholar] [CrossRef]
- Chang, Y.; Zhu, Z.; Bu, R.; Chen, H.; Feng, Y.; Li, Y.; Hu, Y.; Wang, Z. Predicting fire occurrence patterns with logistic regression in Heilongjiang Province, China. Landsc. Ecol. 2013, 28, 1989–2004. [Google Scholar] [CrossRef]
- Vilar, L.; Woolford, D.G.; Martell, D.L.; Martn, M.P. A model for predicting human-caused wildfire occurrence in the region of Madrid, Spain. Int. J. Wildland Fire 2010, 19, 325–337. [Google Scholar] [CrossRef]
- Rodrigues, M.; de la Riva, J.; Fotheringham, S. Modeling the spatial variation of the explanatory factors of human-caused wildfires in Spain using geographically weighted logistic regression. Appl. Geogr. 2014, 48, 52–63. [Google Scholar] [CrossRef]
- Oliveira, S.; Pereira, J.M.C.; San-Miguel-Ayanz, J.; Lourenço, L. Exploring the spatial patterns of fire density in southern Europe using geographically weighted regression. Appl. Geogr. 2014, 51, 143–157. [Google Scholar] [CrossRef]
- Rodrigues, M.; de la Riva, J. An insight into machine-learning algorithms to model human-caused wildfire occurrence. Environ. Model. Softw. 2014, 57, 192–201. [Google Scholar] [CrossRef]
- Corcoran, J.; Higgs, G. Special issue on spatial analytical approaches in urban fire management. Fire Saf. J. 2013, 62, 1–2. [Google Scholar] [CrossRef]
- Leone, V.; Lovreglio, R.; Martín, M.P.; Martínez, J.; Vilar, L. Human factors of fire occurrence in the Mediterranean. In Earth Observation of Wildland Fires in Mediterranean Ecosystems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 149–170. [Google Scholar]
- Romero-Calcerrada, R.; Novillo, C.J.; Millington, J.D.A.; Gomez-Jimenez, I. Gis analysis of spatial patterns of human-caused wildfire ignition risk in the SW of Madrid (Central Spain). Landsc. Ecol. 2008, 23, 341–354. [Google Scholar] [CrossRef]
- Jennings, C.R. Social and economic characteristics as determinants of residential fire risk in urban neighborhoods: A review of the literature. Fire Saf. J. 2013, 62, 13–19. [Google Scholar] [CrossRef]
- Price, O.; Bradstock, R. Countervailing effects of urbanization and vegetation extent on fire frequency on the wildland urban interface: Disentangling fuel and ignition effects. Landsc. Urban Plan. 2014, 130, 81–88. [Google Scholar] [CrossRef]
- Oliveira, S.; Oehler, F.; San-Miguel-Ayanz, J.; Camia, A.; Pereira, J.M.C. Modeling spatial patterns of fire occurrence in Mediterranean Europe using multiple regression and random forest. For. Ecol. Manag. 2012, 275, 117–129. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; Chuvieco, E.; Koutsias, N. Modelling long-term fire occurrence factors in Spain by accounting for local variations with geographically weighted regression. Nat. Hazards Earth Syst. Sci. 2013, 13, 311–327. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and temporal weighted regression (GTWR). Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Wrenn, D.H.; Sam, A.G. Geographically and temporally weighted likelihood regression: Exploring the spatiotemporal determinants of land use change. Reg. Sci. Urban Econ. 2014, 44, 60–74. [Google Scholar] [CrossRef]
- Corcoran, J.; Higgs, G.; Higginson, A. Fire incidence in metropolitan areas: A comparative study of Brisbane (Australia) and Cardiff (United Kingdom). Appl. Geogr. 2011, 31, 65–75. [Google Scholar] [CrossRef]
- Asgary, A.; Ghaffari, A.; Levy, J. Spatial and temporal analyses of structural fire incidents and their causes: A case of Toronto, Canada. Fire Saf. J. 2010, 45, 44–57. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, L.; Qin, K.; Zhang, Y.; Shen, Y.; Zhou, Y. A geographically and temporally weighted regression model for ground-level PM2.5 estimation from satellite-derived 500 m resolution AOD. Remote Sens. 2016, 8, 262. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Grömping, U. Relative importance for linear regression in R: The package relaimpo. J. Stat. Softw. 2006, 17, 1–27. [Google Scholar] [CrossRef]
- Brenning, A. Spatial cross-validation and bootstrap for the assessment of prediction rules in remote sensing: The R package sperrorest. In Proceedings of the 2012 International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 5372–5375. [Google Scholar]
- Le Rest, K.; Pinaud, D.; Monestiez, P.; Chadoeuf, J.; Bretagnolle, V. Spatial leave-one-out cross-validation for variable selection in the presence of spatial autocorrelation. Glob. Ecol. Biogeogr. 2014, 23, 811–820. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Database of Global Change Parameters, Chinese Academy of Sciences. Available online: http://globalchange.nsdc.cn (accessed on 15 September 2015).
- Mourão, P.R.; Martinho, V.D. The choices of the fire—Debating socioeconomic determinants of the fires observed at Portuguese municipalities. For. Policy Econ. 2014, 43, 29–40. [Google Scholar] [CrossRef]
- Romero-Calcerrada, R.; Barrio-Parra, F.; Millington, J.D.A.; Novillo, C.J. Spatial modelling of socioeconomic data to understand patterns of human-caused wildfire ignition risk in the SW of Madrid (Central Spain). Ecol. Model. 2010, 221, 34–45. [Google Scholar] [CrossRef]
- Sebastián-López, A.; Salvador-Civil, R.; Gonzalo-Jiménez, J.; SanMiguel-Ayanz, J. Integration of socio-economic and environmental variables for modelling long-term fire danger in Southern Europe. Eur. J. For. Res. 2008, 127, 149–163. [Google Scholar] [CrossRef]
- Butry, D.T. Economic performance of residential fire sprinkler systems. Fire Technol. 2008, 45, 117–143. [Google Scholar] [CrossRef]
- Almeida, A.F.; Moura, P.V. The relationship of forest fires to agro-forestry and socio-economic parameters in Portugal. Int. J. Wildland Fire 1992, 2, 37–40. [Google Scholar] [CrossRef]
- Kwan, M.-P. The uncertain geographic context problem. Ann. Assoc. Am. Geogr. 2012, 102, 958–968. [Google Scholar] [CrossRef]
- Center for International Earth Science Information Network-CIESIN-Columbia University. Gridded Population of the World, Version 4 (GPWV4): Population Density; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2015. [Google Scholar]
- Tian, X.; Zhao, F.; Shu, L.; Wang, M. Distribution characteristics and the influence factors of forest fires in China. For. Ecol. Manag. 2013, 310, 460–467. [Google Scholar] [CrossRef]
- Pierce, A.D.; Farris, C.A.; Taylor, A.H. Use of random forests for modeling and mapping forest canopy fuels for fire behavior analysis in Lassen Volcanic National Park, California, USA. For. Ecol. Manag. 2012, 279, 77–89. [Google Scholar] [CrossRef]
- Catry, F.X.; Rego, F.C.; Bação, F.L.; Moreira, F. Modeling and mapping wildfire ignition risk in Portugal. Int. J. Wildland Fire 2009, 18, 921–931. [Google Scholar] [CrossRef]
- Lozano, F.J.; Suárez-Seoane, S.; Kelly, M.; Luis, E. A multi-scale approach for modeling fire occurrence probability using satellite data and classification trees: A case study in a mountainous Mediterranean region. Remote Sens. Environ. 2008, 112, 708–719. [Google Scholar] [CrossRef]
- Geospatial Data Cloud. Available online: http://www.gscloud.cn (accessed on 21 September 2015).
- Wu, Z.; He, H.S.; Yang, J.; Liu, Z.; Liang, Y. Relative effects of climatic and local factors on fire occurrence in boreal forest landscapes of northeastern China. Sci. Total Environ. 2014, 493, 472–480. [Google Scholar] [CrossRef] [PubMed]
- Luo, R.; Dong, Y.; Gan, M.; Li, D.; Niu, S.; Oliver, A.; Wang, K.; Luo, Y. Global analysis of influencing forces of fire activity: The threshold relationships between vegetation and fire. Life Sci. J. 2013, 10, 15–24. [Google Scholar]
- Slavkovikj, V.; Verstockt, S.; Van Hoecke, S.; Van de Walle, R. Review of wildfire detection using social media. Fire Saf. J. 2014, 68, 109–118. [Google Scholar] [CrossRef]
- Ager, A.A.; Preisler, H.K.; Arca, B.; Spano, D.; Salis, M. Wildfire risk estimation in the Mediterranean area. Environmetrics 2014, 25, 384–396. [Google Scholar] [CrossRef]
- Fuentes-Santos, I.; Marey-Perez, M.F.; Gonzalez-Manteiga, W. Forest fire spatial pattern analysis in Galicia (NW Spain). J. Environ. Manag. 2013, 128, 30–42. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Peng, C.; Zhu, J.; Satoh, K.; Wang, D.; Wang, Y. Correlation between fire attendance time and burned area based on fire statistical data of Japan and China. Fire Technol. 2013, 50, 851–872. [Google Scholar] [CrossRef]
- Wang, D.; Lu, L.; Zhu, J.; Yao, J.; Wang, Y.; Liao, G. Study on correlation between fire fighting time and fire loss in urban building based on statistical data. J. Civ. Eng. Manag. 2016, 22, 874–881. [Google Scholar] [CrossRef]
- Brenning, A.; Schwinn, M.; Ruiz-Páez, A.P.; Muenchow, J. Landslide susceptibility near highways is increased by 1 order of magnitude in the Andes of Southern Ecuador, Loja Province. Nat. Hazards Earth Syst. Sci. 2015, 15, 45–57. [Google Scholar] [CrossRef]





| Category | Number | Proportion |
|---|---|---|
| Population-clustered places (hotel, school, market, etc.) | 2993 | 0.502941 |
| Other | 967 | 0.162494 |
| Traffic-related | 938 | 0.157621 |
| Important buildings (warehouse, gas stations, etc.) | 566 | 0.09511 |
| Electricity | 256 | 0.043018 |
| High-rise buildings | 109 | 0.018316 |
| Chemical industries | 88 | 0.014787 |
| Underground buildings | 34 | 0.005713 |
| Variable Name | Code | Data Source | Resolution/Unit |
|---|---|---|---|
| Elevation | DEM | The data set is provided by Geospatial Data Cloud site, Computer Network Information Center, Chinese Academy of Sciences (http://www.gscloud.cn) | 30 m |
| Slope | SLOPE | Calculated by ArcGis 10.2 surface analysis tool | 30 m |
| Aspect | ASPECT | The same as SLOPE | 30 m |
| Topographic Position Index | POSITION | The same as DEM | 30 m |
| Terrain Ruggedness Index | TRI | The same as DEM | 30 m |
| Shaded relief | SHADE | The same as SLOPE | 30 m |
| Normalized Difference Vegetation Index | NDVI | The same as DEM | 500 m |
| Yearly average maximum surface temperature | TEMMAX | The same as DEM | 1 km |
| Yearly average minimum surface temperature | TEMMIN | The same as DEM | 1 km |
| Yearly average mean surface temperature | TEMAVE | The same as DEM | 1 km |
| Population | POPULATION | GPWv4, NASA Socioeconomic Data and Applications Center (SEDAC) [36] | 1 km |
| Line density of roads | LINE | Product Specification of Earth Data Pacifica (Beijing) Co., Ltd. (http://www.geoknowledge.com.cn) | 1 km |
| Kernel density of residential points | RESIDENT | The same as LINE | 1 km |
| Kernel density of market points | MARKET | The same as LINE | 1 km |
| Kernel density of hotel points | HOTEL | The same as LINE | 1 km |
| Kernel density of schools, universities, etc. | EDU | The same as LINE | 1 km |
| Kernel density of enterprise points | ENTERPRISE | The same as LINE | 1 km |
| Value of 11 for land cover- Post-flooding or irrigated croplands | LAND11 | The data set is provided by Database of Global Change Parameters, Chinese Academy of Sciences. (http://globalchange.nsdc.cn) | 300 m |
| Value of 14 for land cover- Rainfed croplands | LAND14 | The same as LAND11 | 300 m |
| Value of 20 and 30 for land cover- Mosaic cropland/vegetation | LAND2030 | The same as LAND11 | 300 m |
| Value of 190 for land cover- Artificial surfaces and associated areas | LAND190 | The same as LAND11 | 300 m |
| The other values of land cover | LANDOTHER | The same as LAND11 | 300 m |
| Distance to water bodies | DW | The same as LINE and calculated by ArcMap 10.2 spatial analysis toolbox | m |
| Distance to fire stations | DF | The same as DW | m |
| Distance to roads | DR | The same as DW | m |
| Indicators | LM | |
|---|---|---|
| SCV | CV | |
| Mean of Train.error | −0.371 | −0.450 |
| Mean of Test.error | −0.426 | −0.446 |
| Mean Imp of LINE | 6.30 × 10−3 | −1.79 × 10−3 |
| Mean Imp of POPULATION | 6.03 × 10−3 | 1.11 × 10−4 |
| Mean Imp of LAND2030 | 2.55 × 10−3 | 3.39 × 10−3 |
| Mean Imp of RESIDENT | 2.10 × 10−3 | −1.37 × 10−4 |
| Mean Imp of LAND190 | 1.39 × 10−3 | 3.85 × 10−3 |
| Mean Imp of LAND14 | 1.07 × 10−3 | −6.83 × 10−3 |
| Mean Imp of POSITION | 5.72 × 10−4 | −9.51 × 10−4 |
| Mean Imp of ASPECT | 4.11 × 10−4 | 1.14 × 10−3 |
| Mean Imp of DR | 3.60 × 10−4 | 4.15 × 10−4 |
| Mean Imp of SHADE | 1.80 × 10−4 | −2.17 × 10−4 |
| Mean Imp of TEMMAX | 1.60 × 10−5 | −1.65 × 10−3 |
| Mean Imp of TRI | −8.20 × 10−4 | −5.48 × 10−4 |
| Mean Imp of DW | −9.61 × 10−4 | 2.61 × 10−4 |
| Mean Imp of DF | −1.10 × 10−3 | 3.85 × 10−2 |
| Mean Imp of SLOPE | −1.65 × 10−3 | 6.41 × 10−3 |
| Mean Imp of TEMAVE | −1.87 × 10−3 | 6.65 × 10−3 |
| Mean Imp of TEMMIN | −6.32 × 10−3 | 1.79 × 10−2 |
| Mean Imp of MARKET | −9.41 × 10−3 | 1.22 × 10−3 |
| Mean Imp of DEM | −9.81 × 10−3 | −7.00 × 10−4 |
| Mean Imp of NDVI | −1.01 × 10−2 | 1.25 × 10−2 |
| Mean Imp of ENTERPRISE | −4.53 × 10−2 | −3.43 × 10−3 |
| Explanatory Variables | Coefficient (C) | Std. Error | t Value | Pr (>|t|) | |
|---|---|---|---|---|---|
| Intercept | 0.00001 | 0.01234 | −0.001 | 0.9995 | |
| LINE | 0.12850 | 0.01465 | 8.771 | <2.0 × 10−16 | *** |
| ENTERPRISE | −0.32200 | 0.01581 | −20.364 | <2.0 × 10−16 | *** |
| DEM | −0.07834 | 0.01360 | −5.759 | 0.000001 | *** |
| NDVI | −0.07091 | 0.01416 | −5.007 | <2.0 × 10−16 | *** |
| LAND2030 | −0.02292 | 0.01262 | −1.816 | 0.0694 | † |
| TEMAVE | 0.07167 | 0.01326 | 5.404 | 0.000001 | *** |
| SLOPE | −0.02595 | 0.01324 | −1.960 | 0.0500 | † |
| Explanatory Variables | GWR | GTWR | ||
|---|---|---|---|---|
| Quantile (25%, 75%) | C ± Std. Error | Quantile (25%, 75%) | C ± Std. Error | |
| Intercept | (−0.0100, 0.2175) | (−0.0123, 0.0123) | - | - |
| LINE | (0.0862, 0.5346) | (0.1139, 0.1432) | (−0.0070, 1.4744) | (0.1139, 0.1432) |
| ENTERPRISE | (−0.3433, −0.2143) | (−0.3378, −0.3062) | (−1.7656, 0.4415) | (−0.3378, −0.3062) |
| DEM | (−0.1752, −0.0248) | (−0.0919, −0.0647) | (−0.2915, 0.2071) | (−0.0919, −0.0647) |
| NDVI | (−0.1225, 0.0117) | (−0.0851, −0.0568) | (−0.1230, 0.1369) | (−0.0851, −0.0568) |
| LAND2030 | (−0.0462, −0.0013) | (−0.0355, −0.0103) | (−0.1097, 0.1554) | (−0.0355, −0.0103) |
| TEMAVE | (0.0308, 0.0949) | (−0.0584, 0.0849) | (−0.1026, 0.3715) | (0.0584,0.0849) |
| SLOPE | (−0.0422, 0.0092) | (−0.0392, −0.0127) | (−0.1376, 0.0880) | (−0.0392, −0.0127) |
| R squared | 0.2837 | 0.8705 | ||
| RSS | 3403.22 | 646.52 | ||
| RSS improvement | GWR vs. LM: −398.01 GTWR vs. LM: −3154.71 GTWR vs. GWR: −2756.70 | |||
| Time Period | Model | ||
|---|---|---|---|
| LM | GWR | GTWR | |
| 1 | 567.517 | 567.919 | 507.709 |
| 2 | 573.082 | 574.668 | 506.101 |
| 3 | 569.504 | 570.852 | 507.263 |
| 4 | 575.697 | 572.586 | 508.224 |
| 5 | 565.234 | 571.556 | 510.529 |
| RSS Average value | 570.207 | 571.516 | 507.965 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, C.; Kwan, M.-P.; Zhu, J. Modeling Fire Occurrence at the City Scale: A Comparison between Geographically Weighted Regression and Global Linear Regression. Int. J. Environ. Res. Public Health 2017, 14, 396. https://doi.org/10.3390/ijerph14040396
Song C, Kwan M-P, Zhu J. Modeling Fire Occurrence at the City Scale: A Comparison between Geographically Weighted Regression and Global Linear Regression. International Journal of Environmental Research and Public Health. 2017; 14(4):396. https://doi.org/10.3390/ijerph14040396
Chicago/Turabian StyleSong, Chao, Mei-Po Kwan, and Jiping Zhu. 2017. "Modeling Fire Occurrence at the City Scale: A Comparison between Geographically Weighted Regression and Global Linear Regression" International Journal of Environmental Research and Public Health 14, no. 4: 396. https://doi.org/10.3390/ijerph14040396
APA StyleSong, C., Kwan, M.-P., & Zhu, J. (2017). Modeling Fire Occurrence at the City Scale: A Comparison between Geographically Weighted Regression and Global Linear Regression. International Journal of Environmental Research and Public Health, 14(4), 396. https://doi.org/10.3390/ijerph14040396







