A Normal Distribution-Based Methodology for Analysis of Fatal Accidents in Land Hazardous Material Transportation
Abstract
:1. Introduction
2. Methodology
2.1. Data Resource
2.2. Method
3. Results
3.1. Severity Analysis of Fatalities in Different Transport Mode
3.2. Severity Analysis of Fatalities in Different Country
3.3. Severity Analysis of Fatalities at Different Period
4. Discussion
4.1. Fatal Transportation Accidents by Road and Rail
4.2. The Impact of the Development Levels
4.3. The Evolution of Accident Severity
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Duan, W.L.; Chen, G.H.; Ye, Q.; Chen, Q.G. The situation of hazardous chemical accidents in China between 2000 and 2006. J. Hazard. Mater. 2011, 186, 1489–1494. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.Y.; Yan, Y.; Li, X.N.; Xie, C.J.; Wang, L.H. Analysis on tank truck accidents involved in road hazardous materials transportation in China. Traffic Inj. Prev. 2014, 15, 762–768. [Google Scholar] [CrossRef] [PubMed]
- Montiel, H.; Vílchez, J.A.; Arnaldos, J.; Casa, J. Historical analysis of accidents in the transportation of natural gas. J. Hazard. Mater. 1996, 51, 77–92. [Google Scholar] [CrossRef]
- Ellis, J. Analysis of accidents and incidents occurring during transport of packaged dangerous goods by sea. Saf. Sci. 2011, 49, 1231–1237. [Google Scholar] [CrossRef]
- Zhang, H.D.; Zheng, X.P. Characteristics of hazardous chemical accidents in China: A statistical investigation. J. Loss Prev. Process Ind. 2012, 25, 686–693. [Google Scholar] [CrossRef]
- Abdolhamidzadeh, B.; Abbasi, T.; Rashtchian, A.; Abbasi, S.A. Domino effect in process-industry accidents: An inventory of past events and identification of some patterns. J. Loss Prev. Process Ind. 2011, 24, 575–593. [Google Scholar] [CrossRef]
- Brüde, U. What is happening to the number of fatalities in road accidents? A model for forecasts and continuous monitoring of development up to the year 2000. Accid. Anal. Prev. 1995, 27, 405–410. [Google Scholar] [CrossRef]
- Savolainen, P.T.; Mannering, F.L.; Lord, D.; Quddus, M.A. The statistical analysis of highway crash-injury severities: A review and assessment of methodological alternatives. Accid. Anal. Prev. 2011, 43, 1666–1676. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Milton, J.C.; Shankar, V.N.; Mannering, F.L. Highway accident severities and the mixed logit model: An exploratory empirical analysis. Accid. Anal. Prev. 2008, 40, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Blincoe, L.; Seay, A.; Zaloshnja, E.; Miller, T.; Romano, E.; Luchter, S.; Spicer, R. The Economic Impact of Motor Vehicle Crashes; NHTSA Technical Report; NHTSA: Washington, DC, USA, 2002. [Google Scholar]
- Oggero, A.; Darbra, R.M.; Muñoz, M.; Planas, E.; Casal, J. A survey of accidents occurring during the transport of hazardous substances by road and rail. J. Hazard. Mater. A 2006, 133, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Li, F.Y.; Zhou, J.B.; Zhang, L.; Huang, L.; Bi, J. A survey on hazardous materials accidents during road transport in China from 2000 to 2008. J. Hazard. Mater. 2010, 184, 647–653. [Google Scholar] [CrossRef] [PubMed]
- Planas-Cuchi, E.; Montiel, H.; Casal, J. A survey of the origin, type and consequences of fire accidents in process plants and in the transportation of hazardous materials. Process Saf. Environ. 1997, 75, 3–8. [Google Scholar] [CrossRef]
- Vílchez, J.A.; Sevilla, S.; Montiel, H.; Casal, J. Historical analysis of accidents in chemical plants and in the transportation of hazardous materials. J. Loss Prev. Process Ind. 1995, 8, 87–89. [Google Scholar] [CrossRef]
- Rømer, H.; Haastrup, P.; Petersen, H.J.S. Accidents during marine transport of dangerous goods. Distribution of fatalities. J. Loss Prev. Process Ind. 1995, 8, 29–34. [Google Scholar] [CrossRef]
- Hemmatian, B.; Abdolhamidzadeh, B.; Darbra, R.M.; Casal, J. The significance of domino effect in chemical accidents. J. Loss Prev. Process Ind. 2014, 29, 30–38. [Google Scholar] [CrossRef]
- Darbra, R.M.; Palacios, A.; Casal, J. Domino effect in chemical accidents: Main features and accident sequences. J. Hazard. Mater. 2010, 183, 565–573. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.G.; Hu, X.Z.; Sercombe, T.; Li, Q.B.; Wu, Z.M. Prediction of ceramic fracture with normal distribution pertinent to grain size. Acta Mater. 2018, 145, 41–48. [Google Scholar] [CrossRef]
- Sedić, A.; Packović, D.; Firak, M. A methodology for normal distribution-based statistical characterization of long-term insolation by means of historical data. Sol. Energy 2015, 122, 440–454. [Google Scholar] [CrossRef]
- Hauer, E. The frequency-severity indeterminacy. Accid. Anal. Prev. 2006, 38, 78–83. [Google Scholar] [CrossRef] [PubMed]
- National Highway Traffic Safety Administration. Traffic Safety Facts: Motorcycles; DOT HS 811 159; National Highway Traffic Safety Administration: Washington, DC, USA, 2009. [Google Scholar]
- Liu, X.; Saat, M.R.; Barkan, C.P.L. Probability analysis of multiple-tank-car release incidents in railway hazardous materials transportation. J. Hazard. Mater. 2014, 276, 442–451. [Google Scholar] [CrossRef] [PubMed]
- Saccomanno, E.F.; EI-Hage, S.M. Minimizing derailments of railcars carrying dangerous commodities through effective marshaling strategies. Transp. Res. Rec. 1989, 1245, 34–51. [Google Scholar]
- Saccomanno, E.F.; EI-Hage, S.M. Estabilishing derailment profile by position for corridor shipments of dangerous goods. Can. J. Civ. Eng. 1991, 18, 67–75. [Google Scholar] [CrossRef]
- Barkan, C.P.L.; Dick, C.T.; Anderson, R.T. Railroad derailment factors affecting hazardous materials transportation risk. Transp. Res. Rec. 2003, 1825, 64–74. [Google Scholar] [CrossRef]
- Liu, X.; Saat, M.R.; Barkan, C.P.L. Analysis of causes of major train derailment and their effect on accident rates. Transp. Res. Rec. 2012, 2289, 154–163. [Google Scholar] [CrossRef]
- Carol, S.; Vílchez, J.A.; Casal, J. Study of the severity of industrial accidents with hazardous substances by historical analysis. J. Loss Prev. Process Ind. 2002, 15, 517–524. [Google Scholar] [CrossRef]
- Law, T.H.; Noland, R.B.; Evans, A.W. The sources of Kuznets relationship between road fatalities and economic growth. J. Transp. Geogr. 2011, 19, 355–365. [Google Scholar] [CrossRef]
- Zheng, W.X. Report on Occupational Safety vs Economic and Social Development; China Coal Industry Publishing House: Beijing, China, 2006. [Google Scholar]
- State Council of China. The 12th Five-Year Planning of Safety Production; State Council of China: Beijing, China, 2017.
- State Council of China. The 11th Five-Year Planning of Safety Production; State Council of China: Beijing, China, 2011.
- State Council of China. The 10th Five-Year Planning of Safety Production; State Council of China: Beijing, China, 2008.



| Ni | F | bi | Ni | F | bi | Ni | F | bi |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.000 | NA | 12 | 0.170 | −0.713 | 40 | 0.060 | −0.763 |
| 2 | 0.550 | −0.862 | 13 | 0.160 | −0.714 | 43 | 0.054 | −0.776 |
| 3 | 0.420 | −0.790 | 14 | 0.150 | −0.719 | 44 | 0.049 | −0.797 |
| 4 | 0.390 | −0.679 | 15 | 0.140 | −0.726 | 50 | 0.042 | −0.810 |
| 5 | 0.330 | −0.689 | 16 | 0.130 | −0.736 | 60 | 0.036 | −0.812 |
| 6 | 0.310 | −0.654 | 17 | 0.120 | −0.713 | 61 | 0.030 | −0.853 |
| 7 | 0.270 | −0.673 | 21 | 0.110 | −0.714 | 62 | 0.023 | −0.914 |
| 8 | 0.220 | −0.728 | 22 | 0.090 | −0.719 | 100 | 0.019 | −0.861 |
| 9 | 0.210 | −0.710 | 23 | 0.071 | −0.726 | 170 | 0.012 | −0.861 |
| 10 | 0.200 | −0.699 | 30 | 0.064 | −0.736 | 200 | 0.006 | −0.966 |
| 11 | 0.190 | −0.693 | ||||||
| Normal distribution: μ = −0.770, σ = 0.0768 | ||||||||
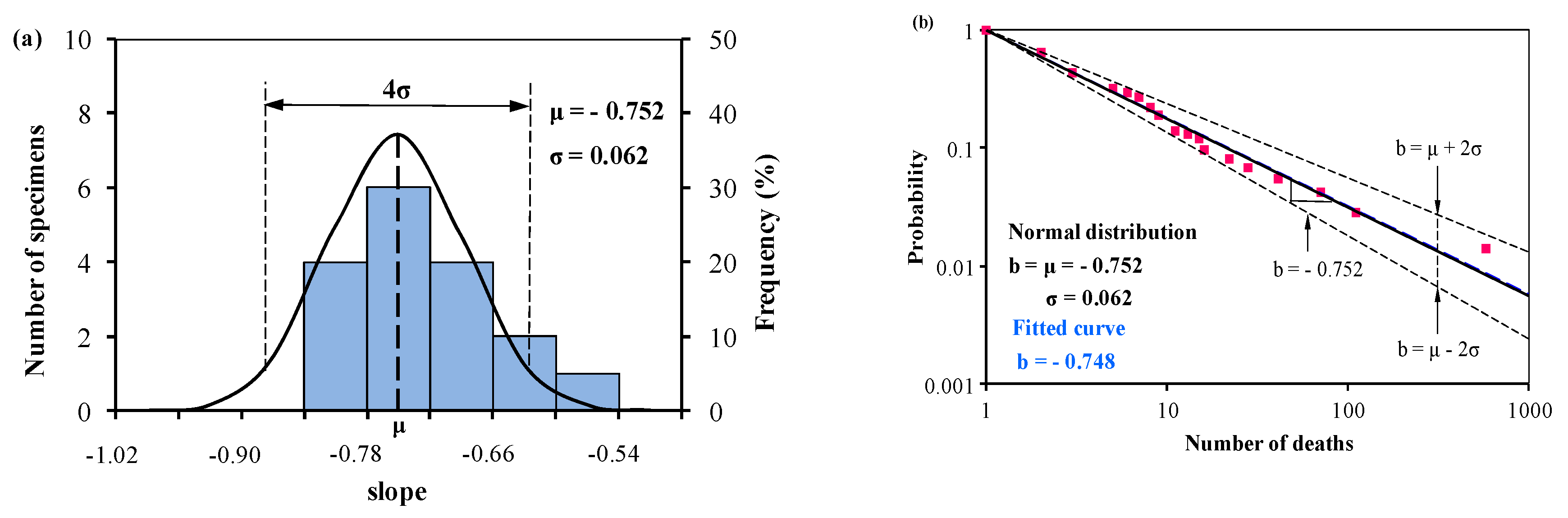
| Ni | F | bi | Ni | F | bi |
|---|---|---|---|---|---|
| 1 | 1000 | NA | 13 | 0.130 | −0.795 |
| 2 | 0.650 | −0.621 | 15 | 0.120 | −0.783 |
| 3 | 0.430 | −0.768 | 16 | 0.095 | −0.849 |
| 5 | 0.320 | −0.708 | 22 | 0.081 | −0.813 |
| 6 | 0.290 | −0.691 | 28 | 0.067 | −0.811 |
| 7 | 0.270 | −0.673 | 41 | 0.054 | −0.786 |
| 8 | 0.220 | −0.728 | 71 | 0.042 | −0.744 |
| 9 | 0.190 | −0.756 | 110 | 0.028 | −0.761 |
| 11 | 0.140 | −0.820 | 581 | 0.014 | −0.671 |
| Normal distribution: μ = −0.752, σ = 0.062 | |||||
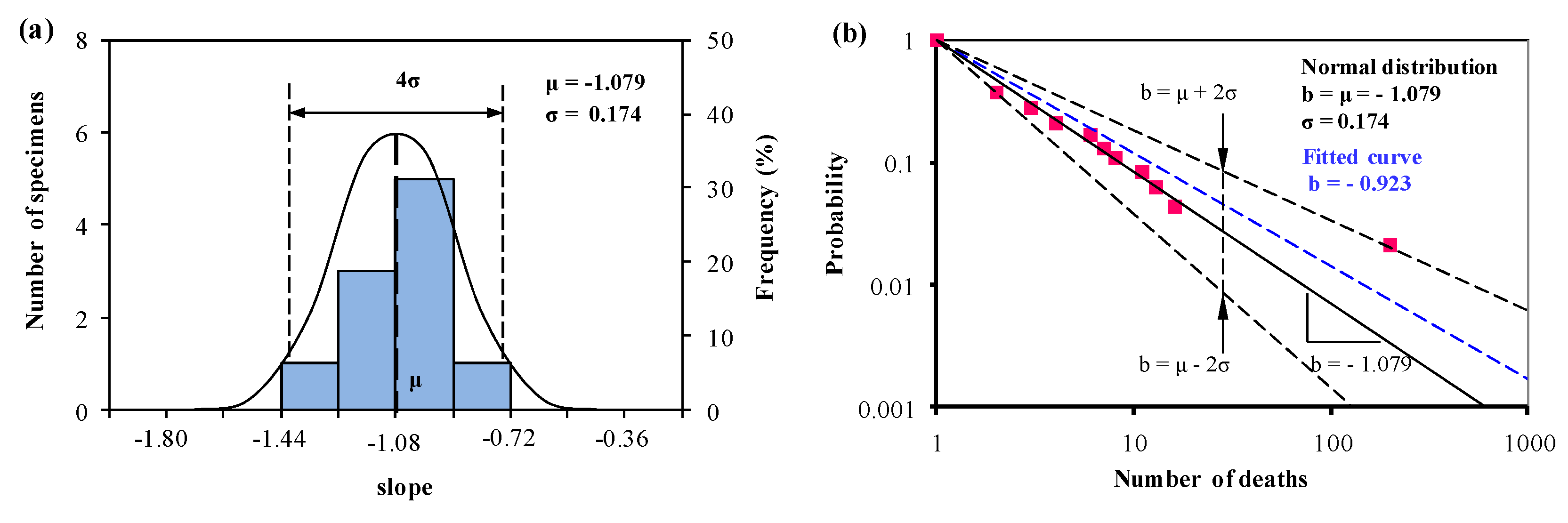
| Group 1: US, Canada, Australia, etc. | Group 2: EU | ||||||||
| Ni | F | bi | Ni | F | bi | ||||
| 1 | 1.000 | NA | 1 | 1.000 | NA | ||||
| 2 | 0.520 | −0.943 | 2 | 0.370 | −1.434 | ||||
| 3 | 0.330 | −1.009 | 3 | 0.280 | −1.159 | ||||
| 4 | 0.250 | −1.000 | 4 | 0.210 | −1.126 | ||||
| 5 | 0.210 | −0.970 | 6 | 0.170 | −0.989 | ||||
| 6 | 0.200 | −0.898 | 7 | 0.130 | −1.048 | ||||
| 7 | 0.170 | −0.911 | 8 | 0.110 | −1.061 | ||||
| 8 | 0.085 | −1.185 | 11 | 0.084 | −1.033 | ||||
| 9 | 0.070 | −1.210 | 13 | 0.064 | −1.072 | ||||
| 10 | 0.054 | −1.268 | 16 | 0.043 | −1.135 | ||||
| 11 | 0.040 | −1.342 | 200 | 0.021 | −0.729 | ||||
| 15 | 0.030 | −1.295 | |||||||
| 21 | 0.017 | −1.338 | |||||||
| Normal distribution: μ = −1.114, σ = 0.175 | Normal distribution: μ = −1.079, σ = 0.174 | ||||||||
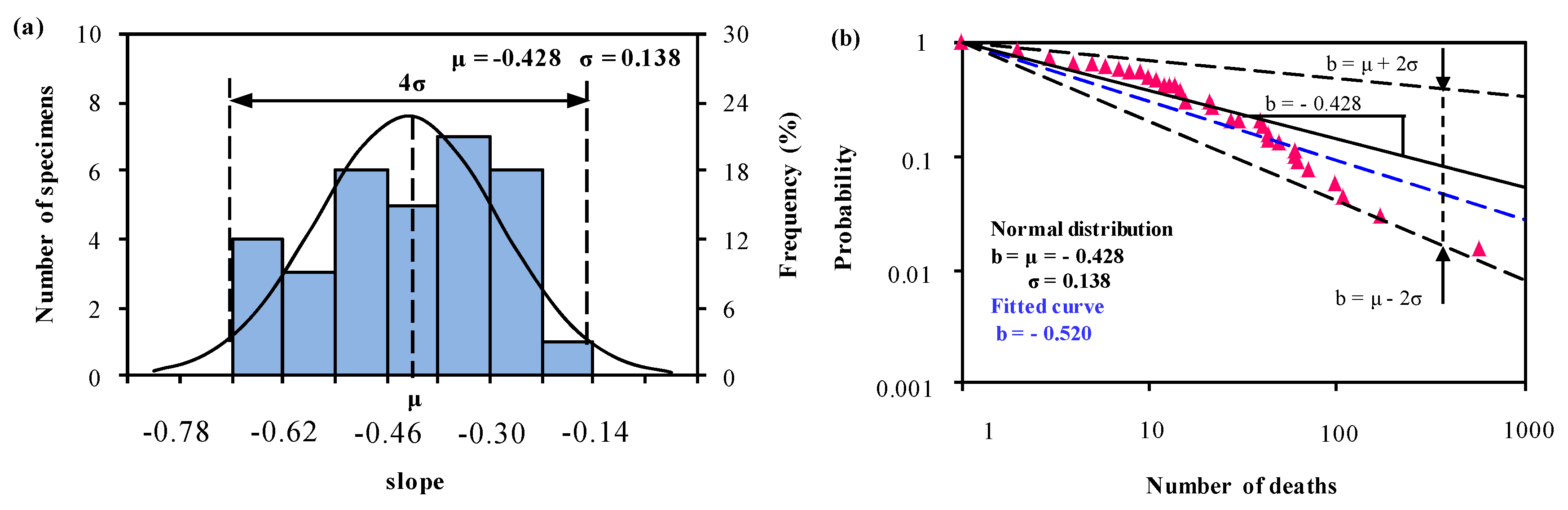
| Group 3: the Rest of the World | |||||||||
| Ni | F | bi | Ni | F | bi | Ni | F | bi | |
| 1 | 1.000 | NA | 12 | 0.430 | −0.340 | 43 | 0.160 | −0.487 | |
| 2 | 0.880 | −0.184 | 13 | 0.410 | −0.348 | 44 | 0.140 | −0.520 | |
| 3 | 0.740 | −0.274 | 14 | 0.410 | −0.338 | 50 | 0.130 | −0.522 | |
| 4 | 0.650 | −0.311 | 15 | 0.370 | −0.367 | 60 | 0.110 | −0.539 | |
| 5 | 0.640 | −0.277 | 16 | 0.310 | −0.422 | 61 | 0.100 | −0.560 | |
| 6 | 0.610 | −0.276 | 21 | 0.310 | −0.385 | 62 | 0.088 | −0.589 | |
| 7 | 0.580 | −0.280 | 22 | 0.270 | −0.424 | 71 | 0.075 | −0.608 | |
| 8 | 0.550 | −0.287 | 28 | 0.210 | −0.468 | 100 | 0.057 | −0.622 | |
| 9 | 0.540 | −0.280 | 30 | 0.210 | −0.459 | 110 | 0.043 | −0.669 | |
| 10 | 0.490 | −0.310 | 40 | 0.200 | −0.436 | 170 | 0.030 | −0.683 | |
| 11 | 0.480 | −0.306 | 41 | 0.180 | −0.462 | 581 | 0.015 | −0.660 | |
| Normal distribution: μ = −0.428, σ = 0.138 | |||||||||
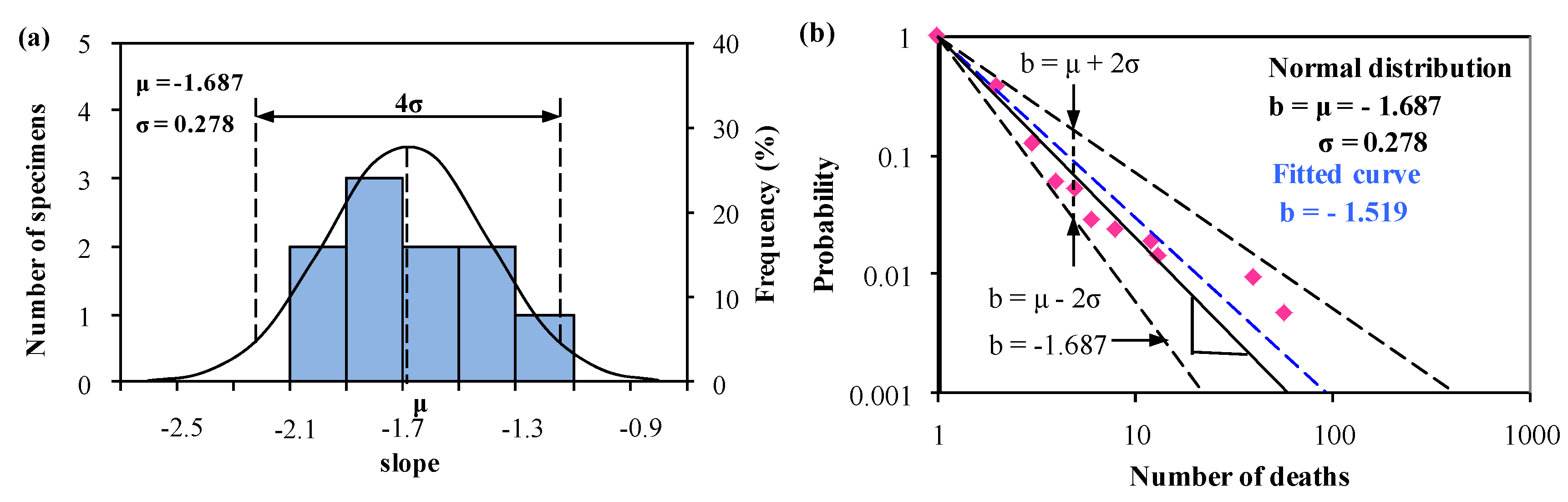
| 2000–2008 (Yang et al. [12]) | 2013–2017 (Investigated Data) | ||||
|---|---|---|---|---|---|
| Ni | F | bi | Ni | F | bi |
| 1 | 1.000 | NA | 1 | 1.000 | NA |
| 2 | 0.423 | −1.241 | 2 | 0.378 | −1.404 |
| 3 | 0.288 | −1.132 | 3 | 0.124 | −1.897 |
| 4 | 0.154 | −1.350 | 4 | 0.060 | −2.031 |
| 5 | 0.110 | −1.371 | 5 | 0.051 | −1.853 |
| 6 | 0.089 | −1.351 | 6 | 0.028 | −2.003 |
| 17 | 0.044 | −1.101 | 8 | 0.023 | −1.813 |
| 29 | 0.022 | −1.133 | 12 | 0.018 | −1.607 |
| 13 | 0.014 | −1.669 | |||
| 40 | 0.009 | −1.271 | |||
| 58 | 0.005 | −1.325 | |||
| Normal distribution: μ = −1.239, σ = 0.118 | Normal distribution: μ = −1.687, σ = 0.278 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, C.; Wu, Q.; Zhang, C.; Zhang, S. A Normal Distribution-Based Methodology for Analysis of Fatal Accidents in Land Hazardous Material Transportation. Int. J. Environ. Res. Public Health 2018, 15, 1437. https://doi.org/10.3390/ijerph15071437
Ren C, Wu Q, Zhang C, Zhang S. A Normal Distribution-Based Methodology for Analysis of Fatal Accidents in Land Hazardous Material Transportation. International Journal of Environmental Research and Public Health. 2018; 15(7):1437. https://doi.org/10.3390/ijerph15071437
Chicago/Turabian StyleRen, Cuiping, Qunqi Wu, Chunguo Zhang, and Shengzhong Zhang. 2018. "A Normal Distribution-Based Methodology for Analysis of Fatal Accidents in Land Hazardous Material Transportation" International Journal of Environmental Research and Public Health 15, no. 7: 1437. https://doi.org/10.3390/ijerph15071437
APA StyleRen, C., Wu, Q., Zhang, C., & Zhang, S. (2018). A Normal Distribution-Based Methodology for Analysis of Fatal Accidents in Land Hazardous Material Transportation. International Journal of Environmental Research and Public Health, 15(7), 1437. https://doi.org/10.3390/ijerph15071437





