1. Introduction
In general insurance, only a few large claims arising in the portfolio represent the largest part of the payments made by the insurance company. Appropriate estimation of these extreme events is crucial for the practitioner to correctly assess insurance and reinsurance premiums. On this subject, the single parameter Pareto distribution (
Arnold 1983;
Brazauskas and Serfling 2003;
Rytgaard 1990), among others has been traditionally considered as a suitable claim size distribution in relation to rating problems. Concerning this, the single parameter Pareto distribution, apart from its favourable properties, provides a good depiction of the random behaviour of large losses (e.g., the right tail of the distribution). Particularly, when calculating deductibles and excess–of–loss levels for reinsurance, the simple Pareto distribution has been demonstrated convenient, see for instance (
Boyd 1988;
Mata 2000;
Klugman et al. 2008), among others.
In this work, an alternative to the Pareto distribution will be carried out. Properties and applications of this distribution will be studied here. As far as we know, these properties have not been studied for this distribution. In particular, we concentrate our attention to results connected with financial risk and insurance.
The paper is organized as follows. In
Section 2, the new proposed distribution is shown, including some of its more relevant properties.
Section 3 presents some interesting results connecting with financial risk and insurance. Next,
Section 4 deals with parameter estimation, paying special attention to the maximum likelihood method. In
Section 5, numerical application by using real insurance data is considered. Finally, some conclusions are given in the last section.
2. The Proposed Distribution
2.1. Probability Density Function
A continuous random variable
X is said to have a generalized truncated log-gamma (GTLG) distribution if its probability density function (p.d.f.) is given by
where
is the Euler gamma function. Note that, for all
we have
As it can be easily seen, the parameter
marks a lower bound on the possible values that (
1) can take on. When
the GTLG distribution reduced to the log-gamma distribution proposed by
Consul and Jain (
1971) with p.d.f.
Note that
Consul and Jain (
1971) considered only the case
. For this case, they derived the raw moments and the distribution of the product of two independent log-gamma random variables. The p.d.f. (
1) can now be obtained by the transformation
.
Expression (
1) is a particular case of the generalized truncated log–gamma distribution proposed in
Amini et al. (
2014) and related with the family proposed by
Zografos and Balakrishnan (
2009). When
, we obtain the famous Pareto distribution. In addition, when
, we obtain a distribution reminiscent of the distribution proposed in
Gómez-Déniz and Calderín (
2014). Properties and applications of this distribution will be studied here. In particular, we concentrate attention to results connecting with financial risk and insurance.
Theorem 1. For all is decreasing (increasing-decreasing) if (.
Proof. The first derivative of
given by
which can be seen to be strictly negative if
and has a unique zero at
if
☐
Note that the mode of is given by if ( if
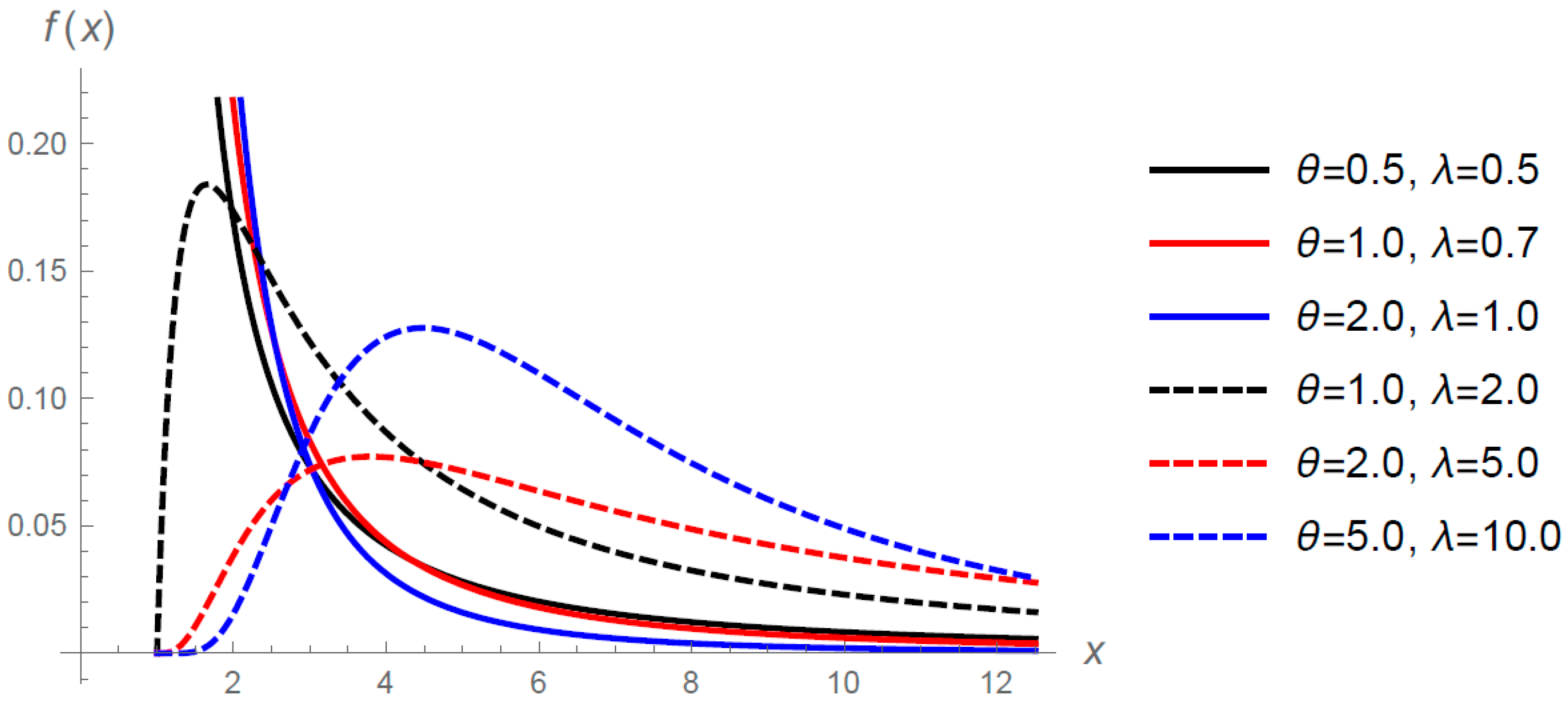
Figure 1 shows the p.d.f. (
1) for selected values of
and
when
.
2.2. Hazard Rate Function
The survival function (s.f.) of the GTLG distribution is given by
where
is the incomplete gamma function. When
is a positive integer, we have
The hazard rate function (h.r.f.) of the GTLG distribution is given by
Note that, and
Theorem 2. For all is decreasing ( increasing-decreasing) if (.
Proof. Let
It is straightforward to show that
is decreasing if
and
is increasing-decreasing if
. Now by
Glaser (
1980),
is decreasing if
and increasing-decreasing if
, since
when
☐
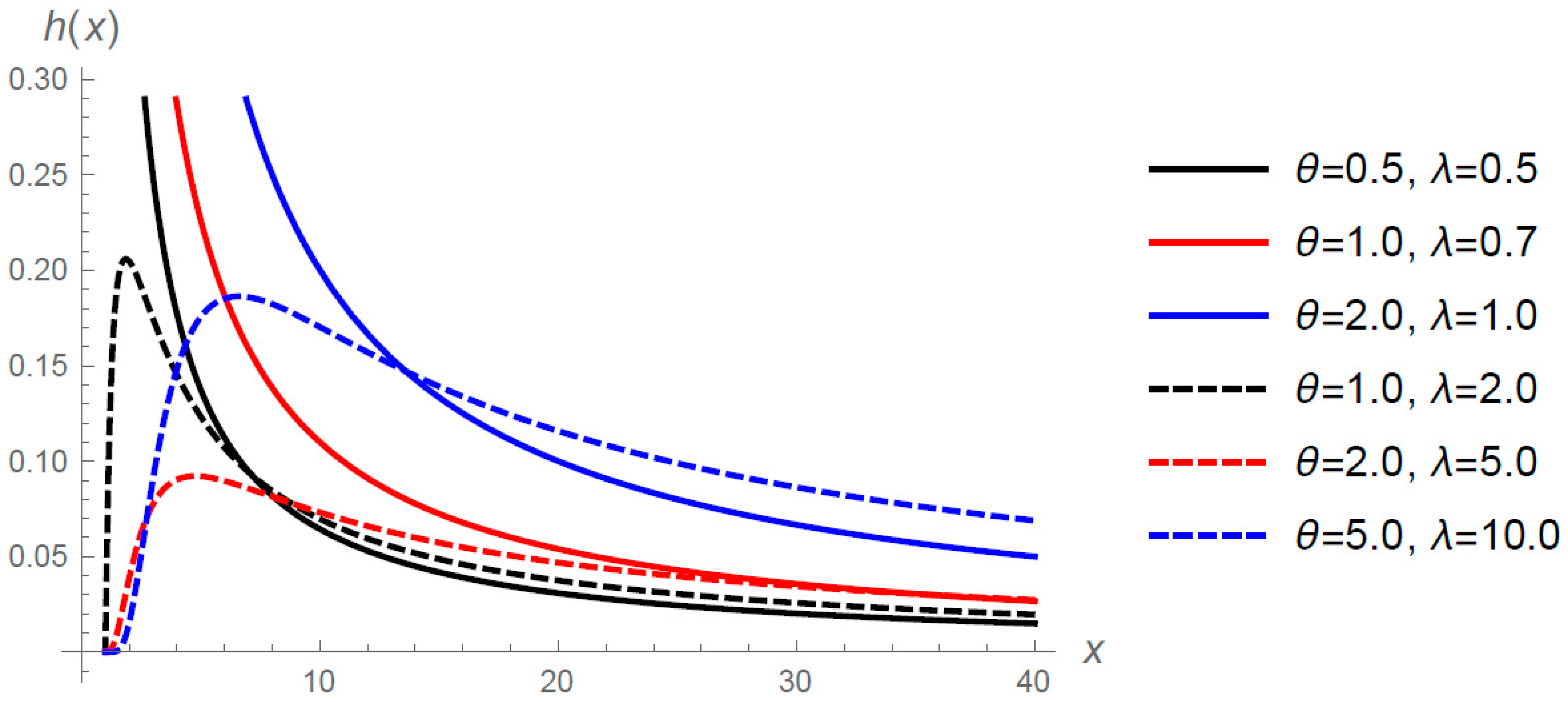
Figure 2 shows the h.r.f. (
3) for selected values of
and
when
.
2.3. Mean Residual Life Function
For the GTLG
, we have
where, for
,
is the mean of the GTLG distribution, and
(
) is the p.d.f. (
1) (s.f. (
2)) when
is replaced by
.
The mean residual life function (m.r.l.f.) of the GTLG distribution is given by
Theorem 3. For all the m.r.l.f. is increasing ( decreasing-increasing) if (.
Proof. Since
is decreasing for
it follows that, in this case,
is increasing. In addition, since
is increasing-decreasing for
and
, it follows that, in this case,
is decreasing-increasing, by
Gupta and Akman (
1995). ☐
From the point of view of a risk manager, the expression is the so-called Expected Shortfall, that is the conditional mean of X given X exceeds a given quantile value x. This is a risk measurement appropriate to evaluate the market risk or credit risk of a portfolio.
Figure 3 shows the m.r.l.f. (
4) for selected values of
and
when
.
It is noted that, unlike the classical Pareto distribution, this expression is not a linear function of x.
2.4. Moments
The GTLG distribution with p.d.f. (
1) can be obtained from a monotonic transformation of the gamma distribution, as it can be seen in the next result.
Theorem 4. Let us assume that Y follows a distribution with p.d.f. , where and . Then the random variablehas p.d.f. (1). Proof. The proof follows after a simple change of variable. ☐
Note that has a log-gamma distribution over . That is as indicated before.
Now, by using representation (
5) and the moments of the Gamma distribution, the expression for the
r-th moment about zero of distribution (
1) is easily obtained,
provided
and
.
In particular, the mean is given by
and the variance is given by
Furthermore, by using the representation given by (
5) the following result is obtained
Solving the equation
in
, we obtain
This implies that the covariates can be introduced into the model in a simple way.
2.5. Conjugate Distributions
The following results show that both the inverse Gaussian distribution and the gamma distribution are conjugate with respect to the distribution proposed in this work.
Theorem 5. Let , independent and identically distributed random variables following the p.d.f. (1). Let us suppose that θ follows a prior inverse Gaussian distribution with parameters τ and ϕ, i.e., . Then the posterior distribution of θ given the sample information is a generalized inverse Gaussian distribution , where Proof. The result follows after some computations by applying Bayes’ Theorem and arranging parameters. ☐
Theorem 6. Let , independent and identically distributed random variables following the p.d.f. (1). Let us suppose that θ follows a prior gamma distribution with a shape parameter and a scale parameter , i.e., . Then the posterior distribution of θ given the sample information is again a gamma distribution with shape parameter and scale parameter . Proof. Again, the result follows after some algebra by using Bayes’ Theorem and arranging parameters. ☐
2.6. Stochastic Ordering
Stochastic ordering of positive continuous random variables is an important tool for judging the comparative behavior. We will recall some basic definitions, see (
Shaked and Shanthikumar 2007).
Let X and Y be random variables with p.d.f.s and (s.f.s and ) (h.r.f.s and ), respectively.
A random variable X is said to be smaller than a random variable Y in the
- (i)
stochastic order (denoted by ) if for all
- (ii)
hazard rate order (denoted by ) if for all
- (iii)
likelihood ratio order (denoted by ) if decreases for all x.
The following implications are well known:
Members of the family of distributions with p.d.f. (
1) are ordered with respect to the strongest “likelihood ratio” ordering, as shown in the following theorem.
Theorem 7. Let X and Y be two continuous random variables distributed according to (1) with p.d.f.’s given by and , respectively. If , then () () Proof. Firstly, let us observe that the ratio
wih derivative
for all
, proving the theorem. ☐
Properties for higher-order stochastic dominance in financial economics can be obtained following the line of the work of (
Guo and Wong 2016). In this regard, let
X and
Y be random variables defined on
with p.d.f.’s
and s.f.’s
respectively, satisfying
where
and
.
A random variable X is said to be smaller than a random variable Y
- (i)
in the first-order descending stochastic dominance (denoted by ) iff for each .
- (ii)
in the second-order descending stochastic dominance (denoted by ) iff for each .
- (iii)
in the N-order descending stochastic dominance (denoted by ) iff for each and for , .
Theorem 8. Let X and Y be two continuous random variables distributed according to (1) with p.d.f.’s given by and , respectively. - (i)
If , then .
- (ii)
If , then .
- (iii)
If , then for .
Proof. - (i)
For
, we have
Therefore, for , .
- (ii)
For
, we have
Therefore, for , .
- (iii)
For
, we have
Also, for
, we have
Therefore, for , .
Now assume that, for , for some , i.e., for each and for , .
Now for
, we have
Also, for
, we have
Therefore, for , for all . ☐
3. Some Theoretical Financial Results
The integrated tail distribution function (also known as equilibrium distribution function):
is an important probability model that often appears in insurance and many other applied fields (see for example
Yang 2004).
For the GTLG
, we have
The integrated tail distribution of the GTLG
is given by
Under the classical model (see
Yang 2004) and assuming a positive security loading,
, for the claim size distributions with regularly varying tails we have that, by using (3), it is possible to obtain an approximation of the probability of ruin,
, when
. In this case the asymptotic approximations of the ruin function is given by
where
.
The use of heavy right-tailed distribution is of vital importance in general insurance. In this regard, Pareto and log-normal distributions have been employed to model losses in motor third liability insurance, fire insurance or catastrophe insurance. It is already known that any probability distribution, that is specified through its cumulative distribution function
on the real line, is heavy right-tailed if and only if for every
,
has an infinite limit as
x tends to infinity. On this particular subject, (
1) decays to zero slower than any exponential distribution and it is long-tailed since for any fixed
(see
Rytgaard 1990) it is verified that
Therefore, as a long-tailed distribution is also heavy right-tailed, the distribution introduced in this manuscript is also heavy right–tailed.
Another important issue in extreme value theory is the regular variation (see
Bingham 1987;
Rytgaard 1990). A distribution function is called regular varying at infinity with index
if
where the parameter
is called the tail index.
Theorem 9. The GTLG distribution is regularly varying at infinity with index .
Proof. Using L’Hospital rule, we have
for all
. ☐
As a consequence of this result we have that if
are i.i.d. random variables with common s.f. (
2) and
, then
Therefore, if
, we have that
This means that for large x the event is due to the event . Therefore, exceedance of high thresholds by the sum are due to the exceedance of this threshold by the largest value in the sample.
On the other hand, let the random variable
X represent either a policy limit or reinsurance deductible (from an insurer’s perspective); then the limited expected value function
L of
X with cdf
, is defined by
Note that represents the expected amount per claim retained by the insured on a policy with a fixed amount deductible of x.
Figure 4 shows the limited expected value function (
10) for selected values of
and
when
.
On the other hand, the new distribution can also be applied in rating excess–of–loss reinsurance as it can be seen in the next result.
Theorem 10. Let X be a random variable denoting the individual claim size taking values only for individual claims greater than d. Let us also assumed that X follows the pdf (1), then the expected cost per claim to the reinsurance layer when the losses excess of m subject to a maximum of l is given bywhere , being the exponential integral function. Proof. The result follows by having into account that
from which we get the result after some tedious algebra. ☐
4. Maximum Likelihood Estimation
In the following it will be assumed that
is a random sample selected from the GTLG distribution with known parameter
and unknown parameters
from the p.d.f. (
1). Then, the log–likelihood function is given by
The maximum likelihood estimates (MLEs)
of the parameters
are obtained by solving the score equations:
where
is the digamma function. Therefore,
where
is the solution of the equation:
The second partial derivatives are given by
The expected Fisher’s information matrix is given by
Now the estimated variance-covariance matrix of the MLEs is given by the inverse matrix .
It is known that under certain regularity conditions, the maximum likelihood estimator converges in distribution to a bivariate normal distribution with mean equal to the true parameter value and variance-covariance matrix given by the inverse of the information matrix. That is, , which provides a basis for constructing tests of hypotheses and confidence regions. The regularity conditions are verified by taking into account that the Fisher’s information matrix exists and is non-singular and that the parameter space is a subset of the real line and the range of x is independent of . Furthermore, additional computations provides that and that is bounded.
5. Numerical Application
Because the main application of the heavy tail distributions is the so-called extreme value theory, we consider a data set coming from catastrophic events. The data set represents loss ratios (yearly data in billion of dollars) for earthquake insurance in California from 1971 through 1993 for values larger than zero. The data are given in
Embrechts et al. (
1999).
For comparison with other heavy tail distributions, we consider the following models:
- (1)
- (2)
Shifted log-normal (SLN):
- (3)
- (4)
- (5)
Log-gamma distribution (LG):
Table 1 provides parameter estimates together with standard errors (in brackets) using the maximum likelihood estimation method of the parameters
and
when
. This table also gives the negative log-likelihood (NLL), Akaike’s Information Criteria (AIC), Bayesian information criterion (BIC), and Consistent Akaike’s Information Criteria (CAIC).
A lower value of these measures is desirable. These results show that the proposed GTLG distribution provides better fit than the considered competing distributions.
Table 2 shows three goodness-of-fit tests for all considered models and that the classical Pareto model is rejected for this data set.
6. Conclusions
In this paper, a continuous probability distribution function with positive support suitable for fitting insurance data has been introduced. The distribution, that arises from a monotonic transformation of the classical Gamma distribution, can be considered as a generalization of the log-gamma distribution. This new development, which has a promising approach for data modeling in the actuarial field, may be very useful for practitioners who handle large claims. For that reason, it can be deemed as an alternative to the classical Pareto distribution. Besides, an extensive analysis of its mathematical properties has been provided.
Acknowledgments
The authors would like to express their gratitude to two anonymous referees for their relevant and useful comments. Emilio Gómez-Déniz was partially funded by grant ECO2013-47092 (Ministerio de Economía y Competitividad, Spain and ECO2017-85577-P (Ministerio de Economía, Industria y Competitividad, Agencia Estatal de Investigación)).
Author Contributions
Mohamed E. Ghitany, Emilio Gómez-Déniz and Saralees Nadarajah have contributed jointly to all of the sections of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Amini, Morteza, S. M. T. K. MirMostafaee, and Jafar Ahmadi. 2014. Log-gamma-generated families of distributions. Statistics 48: 913–32. [Google Scholar] [CrossRef]
- Arnold, Barry C. 1983. Pareto Distributions. Silver Spring: International Cooperative Publishing House. [Google Scholar]
- Bingham, Nicholas H. 1987. Regular Variation. Cambridge: Cambridge University Press. [Google Scholar]
- Boyd, Albert V. 1988. Fitting the truncated Pareto distribution to loss distributions. Journal of the Staple Inn Actuarial Society 31: 151–58. [Google Scholar] [CrossRef]
- Brazauskas, Vytaras, and Robert Serfling. 2003. Favorable estimator for fitting Pareto models: A study using goodness-of-fit measures with actual data. ASTIN Bulletin 33: 365–81. [Google Scholar] [CrossRef]
- Consul, Prem C., and Gaurav C. Jain. 1971. On the log-Gamma distribution and its properties. Statistische Hefte 12: 100–6. [Google Scholar] [CrossRef]
- Embrechts, Paul, Sidney I. Resnick, and Gennady Samorodnitsky. 1999. Extreme value theory as a risk management tool. North American Actuarial Journal 3: 30–41. [Google Scholar] [CrossRef]
- Glaser, Ronald E. 1980. Bathtub and related failure rate characterizations. Journal of the American Statistical Association 75: 667–72. [Google Scholar] [CrossRef]
- Gómez-Déniz, Emilio, and Enrique Calderín. 2014. A suitable alternative to the Pareto distribution. Hacettepe Journal of Mathematics and Statistics 43: 843–60. [Google Scholar]
- Guo, Xu, and Wing-Keung Wong. 2016. Multivariate stochastic dominance for risk averters and risk seekers. RAIRO-Operations Research 50: 575–86. [Google Scholar] [CrossRef]
- Gupta, Ramesh C., and Akman H. Olcay. 1995. Mean residual life function for certain types of non-monotonic ageing. Communications in Statistics-Stochastic Models 11: 219–25. [Google Scholar]
- Klugman, Stuart A., Harry H. Panjer, and Gordon E. Willmot. 2008. Loss Models: From Data to Decisions, 3rd ed. Hoboken: Wiley. [Google Scholar]
- Mata, Ana J. 2000. Princing excess of loss reinsurance with reinstatements. ASTIN Bulletin 30: 349–68. [Google Scholar] [CrossRef]
- Rytgaard, Mette. 1990. Estimation in the Pareto distribution. ASTIN Bulletin 20: 201–16. [Google Scholar] [CrossRef]
- Shaked, Moshe, and Jeyaveerasingam G. Shanthikumar. 2007. Stochastic Orders. Series: Springer Series in Statistics; New York: Springer. [Google Scholar]
- Yang, Hailiang. 2004. Crámer-Lundberg asymptotics. In Encyclopedia of Actuarial Science. New York: Wiley, pp. 1–6. [Google Scholar]
- Zografos, Konstantinos, and Narayanaswamy Balakrishnan. 2009. On families of beta and generalized gamma-generated distributions and associated inference. Statistical Methodology 6: 344–62. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).