Models of Investor Forecasting Behavior — Experimental Evidence
Abstract
:1. Introduction
- The rational expectations hypothesis does not provide an accurate model of investor forecasting behavior, even when the earnings rate and fundamental value of the asset are known with certainty by investors.
- A simple one-parameter exponential smoothing model of investor forecasting behavior is remarkably accurate. Models with a larger number of parameters provide only a slightly better fit.
- There is strong evidence of investor overconfidence in the information content of observed price data. In the experiment, the fundamental value of the asset was known to the investors and therefore the observed prices contained no additional information regarding the fundamental value of the asset. Nevertheless, investor forecasts relied mostly on observed price data.
- Except for a few experimental investors, the price forecasts were increasing in the extrapolated prices. That is, most experimental investors did not exhibit evidence of panic, as defined in Cheriyan and Kleywegt (2016), in their forecasts.
Definition of Key Terms
2. Models of Price Forecast Formation and Literature Review
2.1. Extrapolation-Correction Models of Forecast Formation
2.1.1. Extrapolated Price
2.1.2. Price Forecast
2.2. Linear Model of Forecast Formation
2.3. Literature Review
2.3.1. Purpose of the Experiments
2.3.2. Exogenous and Endogenous Supply and Demand
2.3.3. Finite Time Horizon and Learning
2.3.4. Market Mechanism
2.3.5. Reward Mechanism
3. Design of the Behavioral Experiment
| Process Flow 1 Process flow for an asset market with a discrete-time trading mechanism. |
|
3.1. Approaches to Reduce End of Horizon Effect
3.2. Dividend Structure
3.3. Experimental Sessions
- The expected number of time periods remaining in the trading run.
- The expected total dividends paid by one unit of asset from the current period until the end of the trading run.
- The total of the expected dividend from the current period until the end of the trading run and the salvage value for one unit of asset held until the end of the trading run.
- The participant’s forecast of the price per unit of asset.
- The current state of the market (only session 3—Markov dividend case).
3.4. Incentive Mechanism
- Two randomly selected players split $300 in proportion to the value of their final amount of virtual currency, after payment of the salvage value.
- The participant with the largest final amount of virtual currency received a prize of $100.
- The participant with the smallest mean square forecast error received a prize of $100.
3.5. Participant Demographics
4. Results
4.1. Summary of Observations
4.1.1. Equilibrium Price
4.1.2. Price Forecasts
4.1.3. Earning Forecasts
Given the compensation rules and the number of participants, how much money do you think you will earn in this experiment?
4.2. Comparison of Models Fitted with Data
4.2.1. Data Used
4.2.2. Parameter Estimation Method
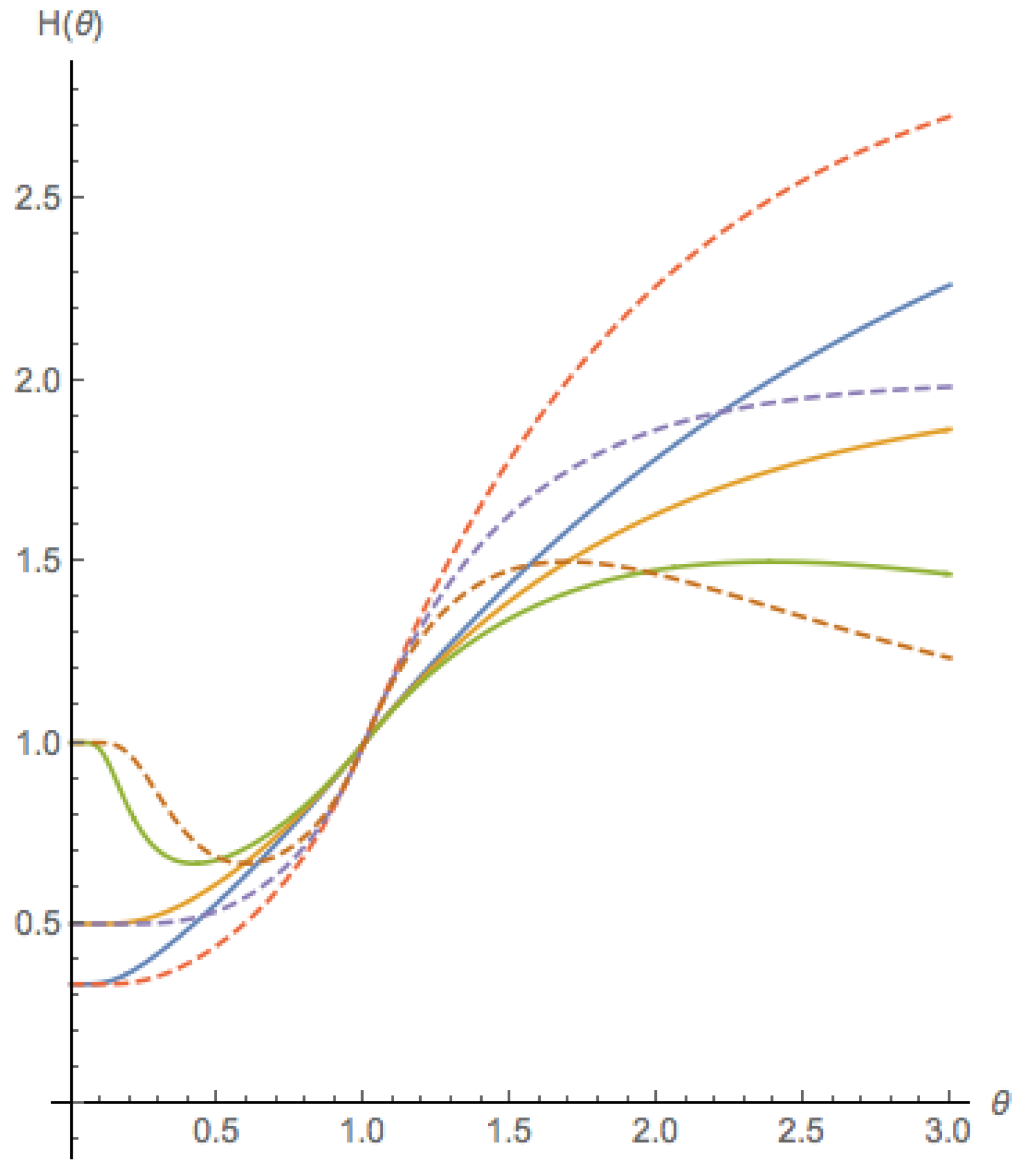
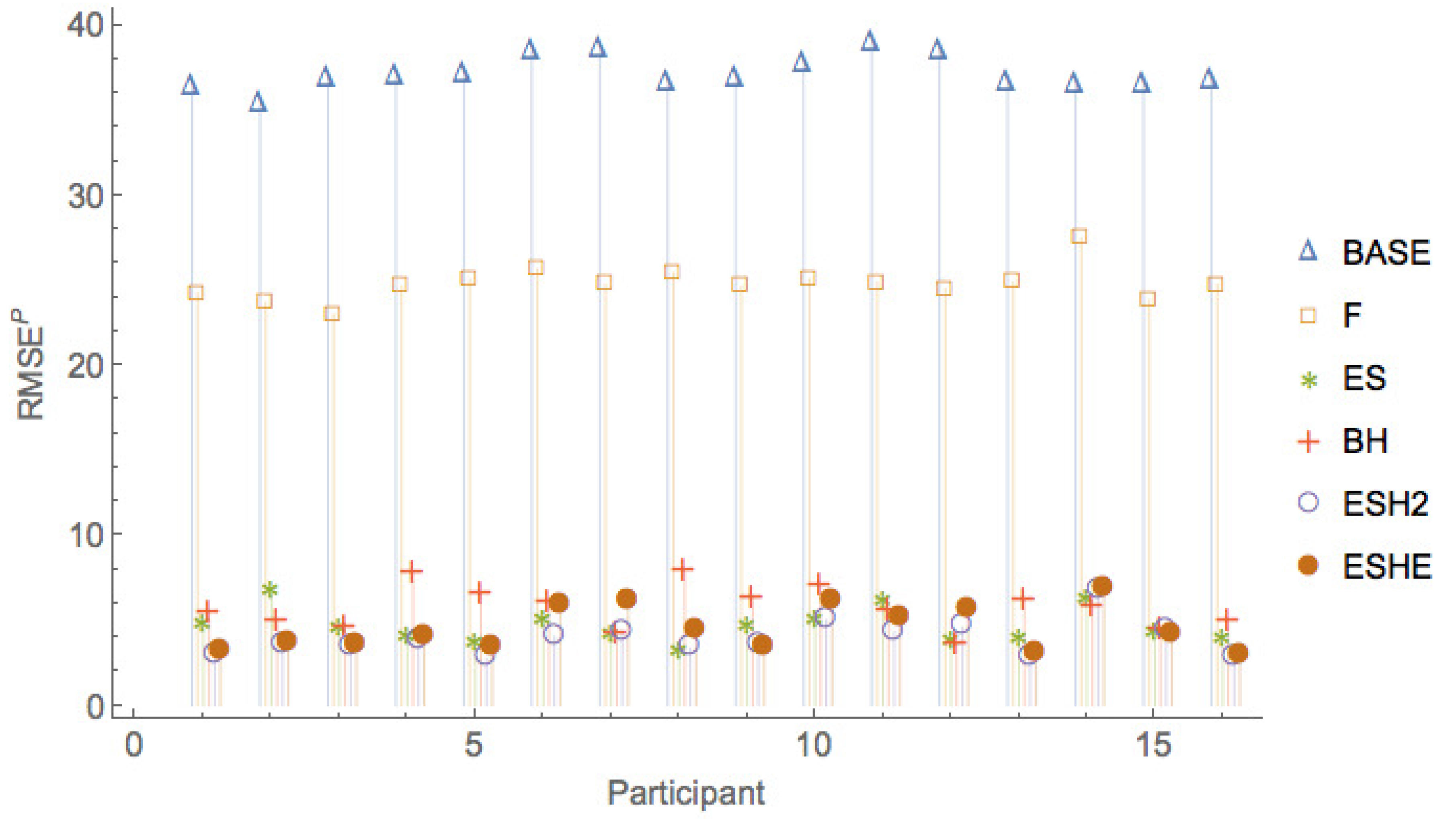
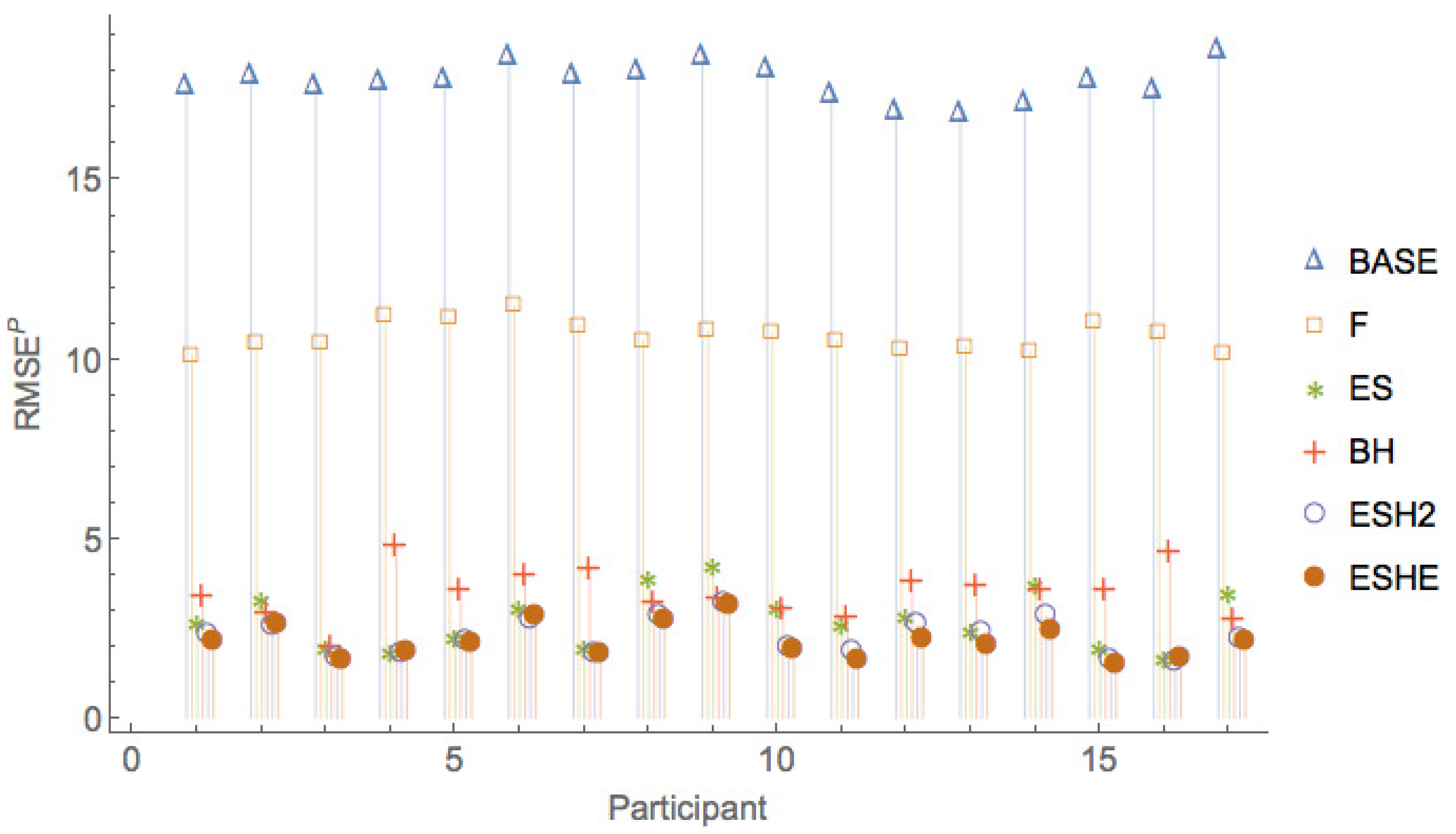
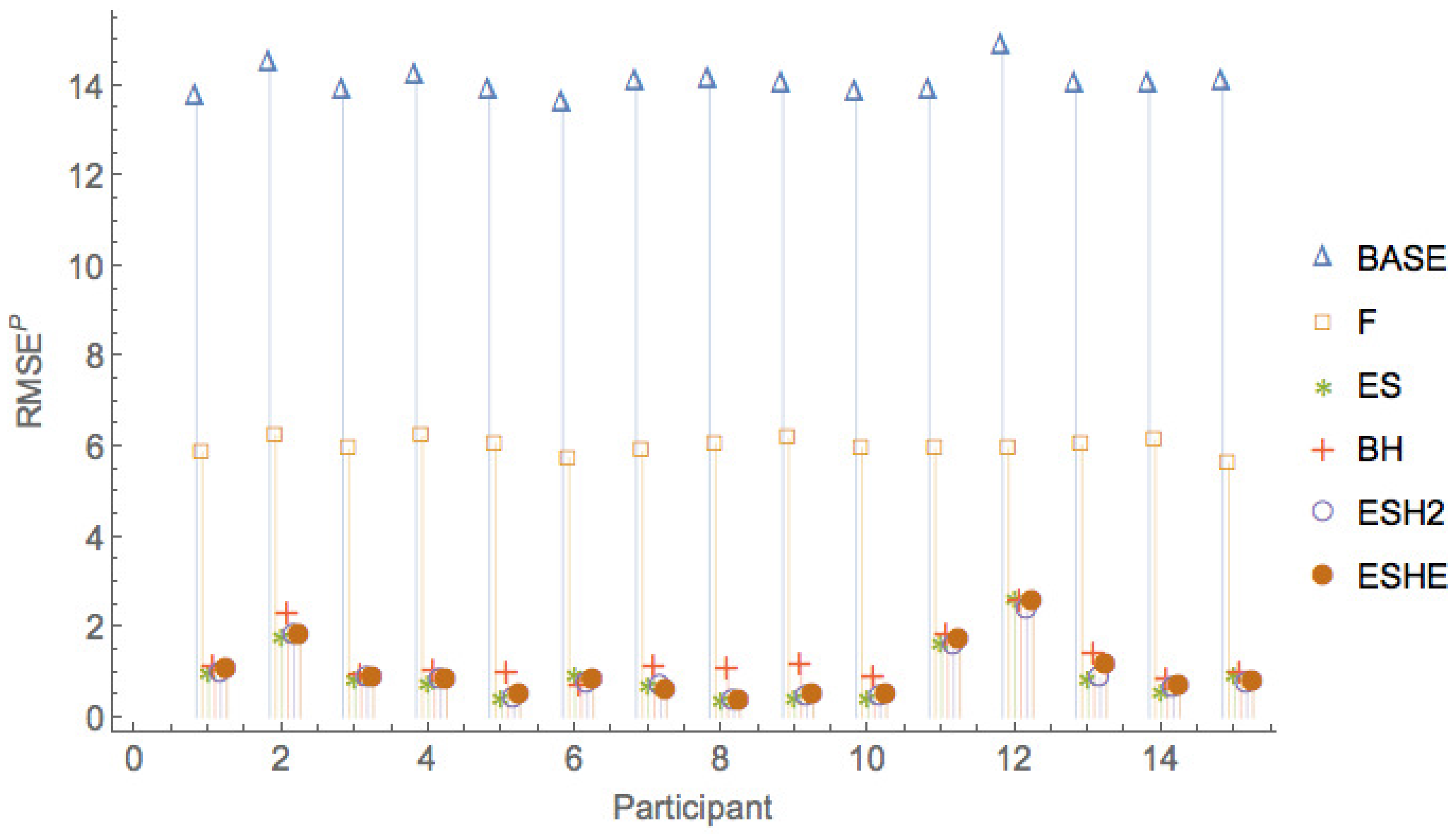
4.2.3. Comparison of Fitted Models
4.2.4. Rational Base Case
4.2.5. Modified Rational Expectations
4.2.6. Simple Exponential Smoothing
4.2.7. Brock and Hommes Model (BH)
4.2.8. Exponential Smoothing with Quadratic H (ESH2)
4.2.9. Exponential Smoothing with Non-Mononotic H (ESHE)
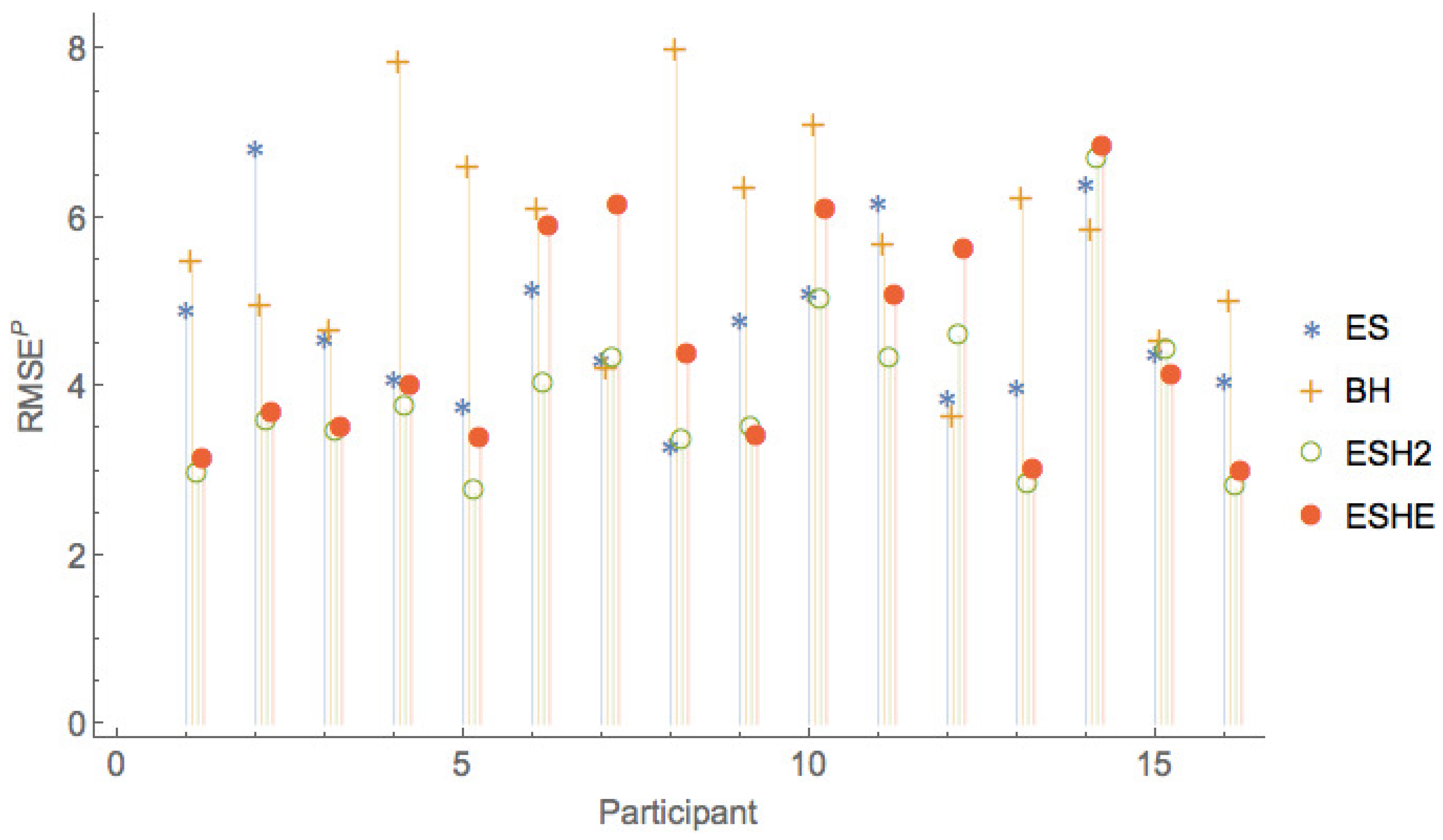
4.2.10. Comparison of Various Models
5. Interpretation and Implications of Results
6. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Fundamental Value Computations Corresponding to Different Dividend Processes
Appendix A.1. Deterministic Constant Dividend
| Algorithm A1 Market Algorithm with Deterministic Constant Dividend |
|
Appendix A.2. Markov Dividends
| Algorithm A2 Market Algorithm with Deterministic Constant Dividend |
Given:
Algorithm:
|
Appendix B. Details of Leave-One-Out-Cross-Validation Approach
Leave-One-Period-Out LOOCV
Leave-One-Session-Out LOOCV
References
- Armstrong, Scott J. 1985. Long-Range Forecasting: From Crystal Ball to Computer, 2nd ed. New York: John Wiley & Sons. [Google Scholar]
- Ball, Sheryl B., and Charles A. Holt. 1998. Classroom games: Speculation and bubbles in an asset market. The Journal of Economic Perspectives 12: 207–18. [Google Scholar] [CrossRef]
- Brock, William A., and Cars H. Hommes. 1997. A rational route to randomness. Econometrica 65: 1059–95. [Google Scholar] [CrossRef]
- Brock, William A., and Cars H. Hommes. 1998. Heterogeneous beliefs and routes to chaos in a simple asset pricing model. Journal of Economic Dynamics and Control 22: 1235–74. [Google Scholar] [CrossRef]
- Camerer, Colin F., and Keith Weigelt. 1993. Convergence in experimental double auctions in stochastically lived assets. In The Double Auction Market: Institutions, Theories and Evidence. Reading: Addison–Wesley, pp. 355–59. [Google Scholar]
- Campbell, John Y., and Robert J. Shiller. 1987. Cointegration and tests of present value models. The Journal of Political Economy 95: 1062–88. [Google Scholar] [CrossRef]
- Campbell, John Y., and Robert J. Shiller. 1988. The dividend-price ratio and expectations of future dividends and discount factors. The Review of Financial Studies 1: 195–228. [Google Scholar] [CrossRef]
- Cheriyan, Vinod, and Anton J. Kleywegt. 2016. A dynamical systems model of price bubbles and cycles. Quantitative Finance 16: 309–36. [Google Scholar] [CrossRef]
- Chuang, Wen I., and Bong-Soo Lee. 2006. An empirical evaluation of the overconfidence hypothesis. Journal of Banking & Finance 30: 2489–515. [Google Scholar]
- Hirota, Shinichi, and Shyam Sunder. 2007. Price bubbles sans dividend anchors: Evidence from laboratory stock markets. Journal of Economic Dynamics and Control 31: 1875–909. [Google Scholar] [CrossRef]
- LeRoy, Stephen F., and Richard D. Porter. 1981. The present-value relation: Tests based on implied variance bounds. Econometrica 49: 555–74. [Google Scholar] [CrossRef]
- LeRoy, Stephen F. 1989. Efficient capital markets and martingales. Journal of Economic Literature 27: 1583–621. [Google Scholar]
- Lugovskyy, Volodymyr, Daniela Puzzello, and Steven Tucker. 2009. An Experimental Study of Bubble Formation in Asset Markets Using the Tâtonnement Pricing Mechanism. Working Paper. Christchurch: University of Canterbury. [Google Scholar]
- Nickerson, Mike, Yaron Lahav, and Charles N. Noussair. 2007. Traders’ expectations in asset markets: Experimental evidence. The American Economic Review 97: 1901–20. [Google Scholar]
- Ramnath, Sundaresh, Steve Rock, and Philip Shane. 2008. The financial analyst forecasting literature: A taxonomy with suggestions for further research. International Journal of Forecasting 24: 34–75. [Google Scholar] [CrossRef]
- Scheinkman, Jose A., and Wei Xiong. 2003. Overconfidence and speculative bubbles. Journal of Political Economy 111: 1183–219. [Google Scholar] [CrossRef]
- Shiller, Robert J. 1981a. Do stock prices move too much to be justified by subsequent changes in dividends? The American Economic Review 71: 421–36. [Google Scholar]
- Shiller, Robert J. 1981b. The use of volatility measures in assessing market efficiency. The Journal of Finance 36: 291–304. [Google Scholar]
- Shiller, Robert J. 1986. The Marsh-Merton model of managers’ smoothing of dividends. The American Economic Review 76: 499–503. [Google Scholar]
- Smith, Vernon L., Gerry L. Suchanek, and Arlington W. Williams. 1988. Bubbles, crashes, and endogenous expectations in experimental spot asset markets. Econometrica: Journal of the Econometric Society 56: 1119–51. [Google Scholar] [CrossRef]
- Tversky, Amos, and Daniel Kahneman. 1974. Judgment under uncertainty: Heuristics and biases. Science 185: 1124–31. [Google Scholar] [CrossRef] [PubMed]
- West, Kenneth D. 1988a. Dividend innovations and stock price volatility. Econometrica 56: 37–61. [Google Scholar] [CrossRef]
- West, Kenneth D. 1988b. Bubbles, fads and stock price volatility tests: A partial evaluation. The Journal of Finance 43: 639–56. [Google Scholar] [CrossRef]
- Wong, Wing-Keung, and Raymond Chan. 2004. On the estimation of cost of capital and its reliability. Quantitative Finance 4: 365–72. [Google Scholar] [CrossRef]

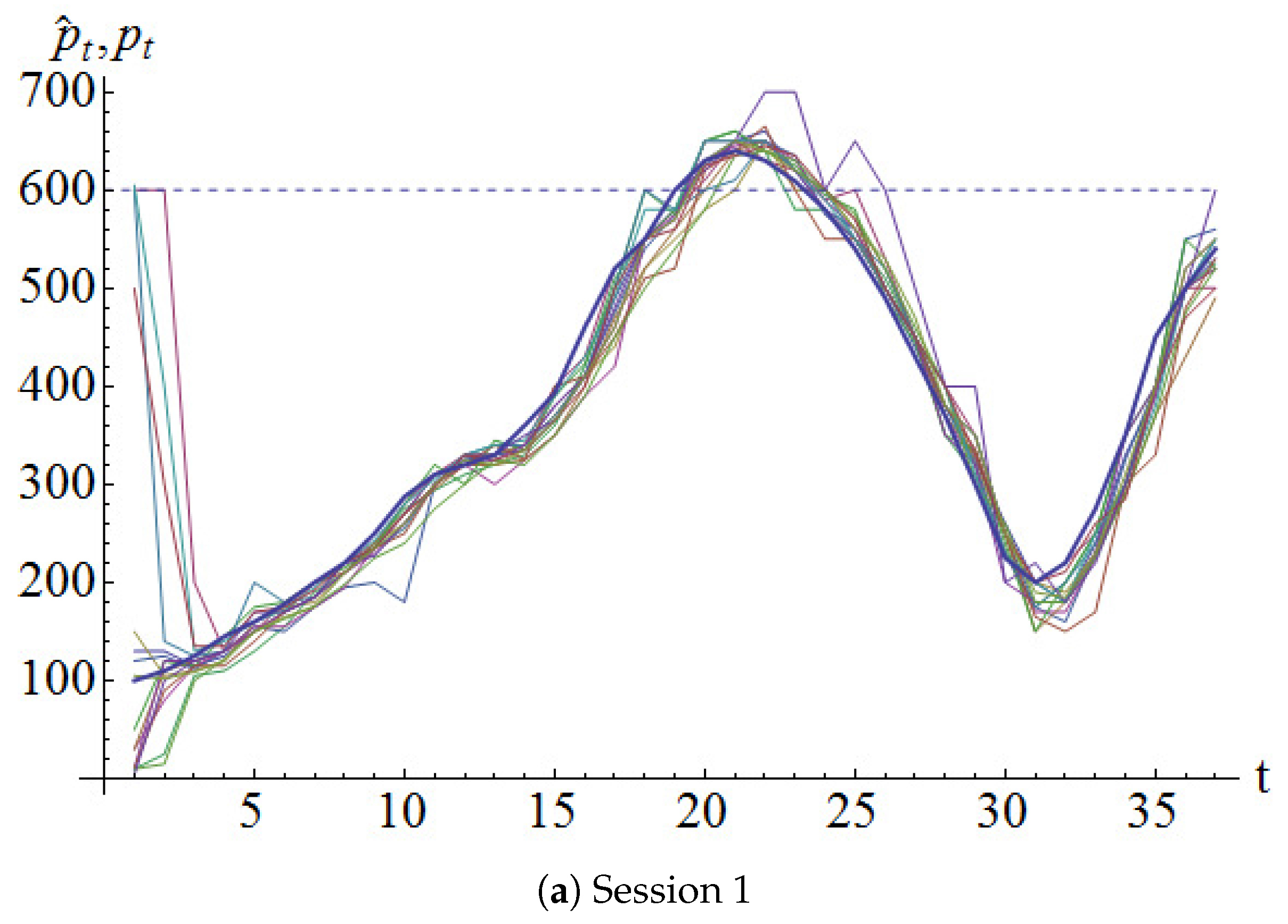
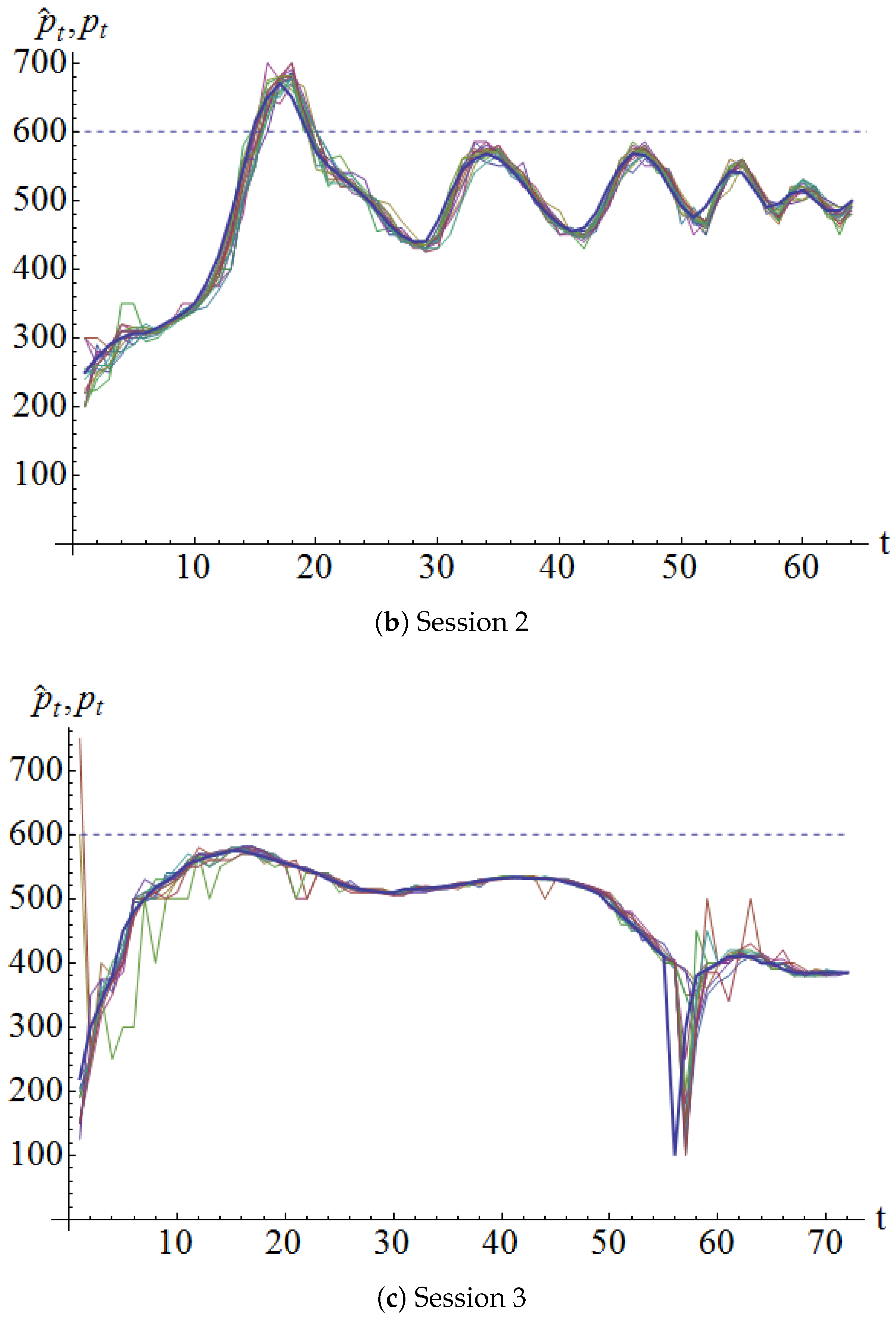
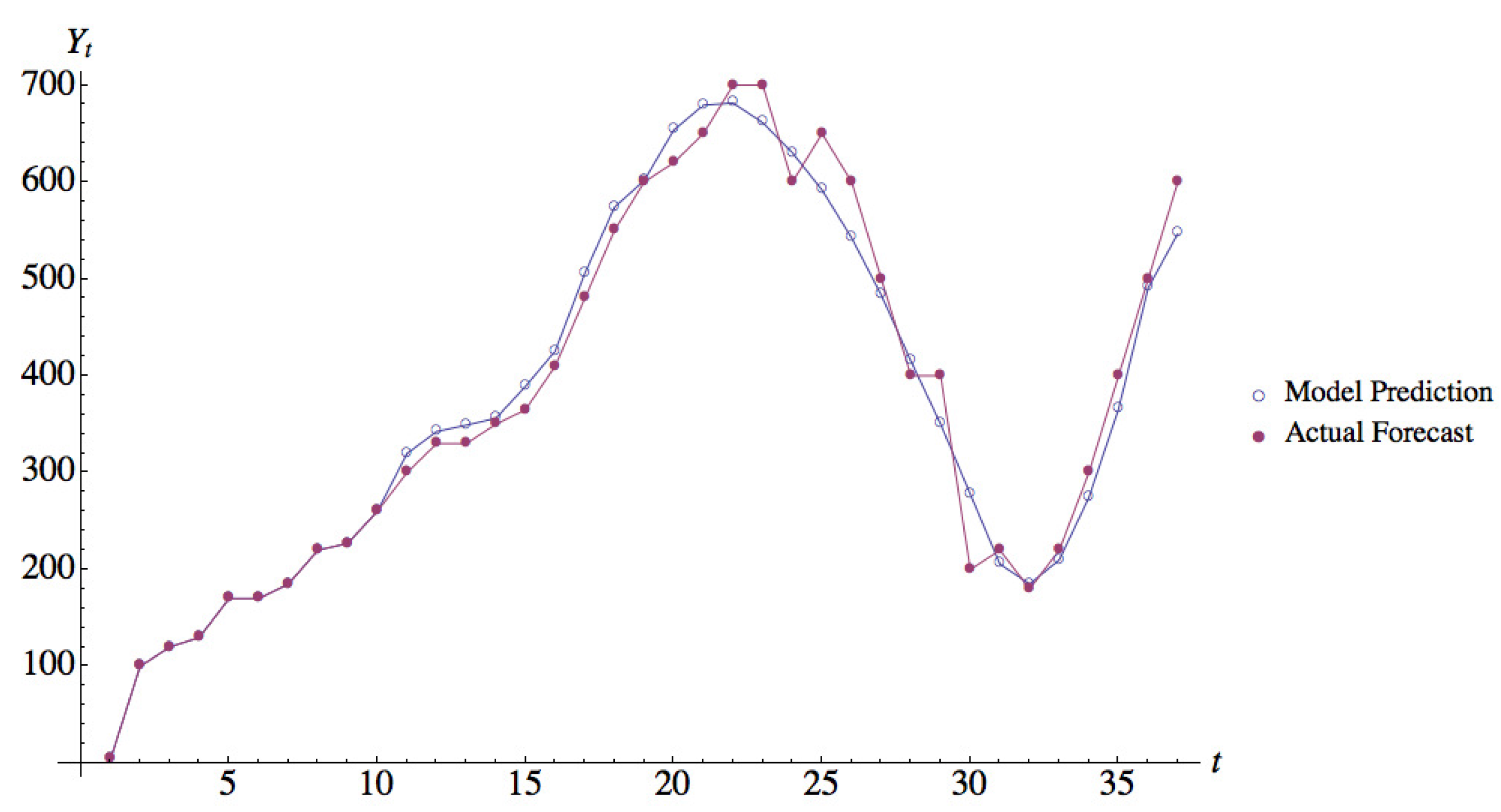


| Market State | ||||
|---|---|---|---|---|
| low | ||||
| high |
| Session | Participants | Periods | Dividend Type | Mean Dividend (ECUs) | Salvage Value (ECUs) |
|---|---|---|---|---|---|
| 1 | 16 | 37 | Constant | 10 | 100 |
| 2 | 17 | 64 | Constant | 10 | 100 |
| 3 | 15 | 72 | Markovian | 10 | 100 |
| Session | Participants | Number of Valid Responses | Average Expected Win | Average of Prize Money Per Participant |
|---|---|---|---|---|
| 1 | 16 | 14 | 90.43 | 31.25 |
| 2 | 17 | 15 | 66.07 | 29.41 |
| 3 | 15 | 13 | 68.91 | 33.33 |
| Model () | Generalized Mean (m) | Correction Function (H) | Parameters to Fit |
|---|---|---|---|
| N/A | N/A | None | |
| F | N/A | N/A | |
| Exponential Smoothing | |||
| N/A | N/A | ||
| Exponential Smoothing | |||
| Exponential Smoothing |
| Session 1 | Session 2 | Session 3 | ||||
|---|---|---|---|---|---|---|
| Part. | ||||||
| 1 | 217.66 | 36.2767 | 105.273 | 17.5455 | 82.291 | 13.7152 |
| 2 | 211.608 | 35.2679 | 107.251 | 17.8752 | 86.6954 | 14.4492 |
| 3 | 220.79 | 36.7983 | 105.178 | 17.5297 | 83.2023 | 13.8671 |
| 4 | 221.015 | 36.8358 | 106.147 | 17.6911 | 84.9293 | 14.1549 |
| 5 | 221.923 | 36.9872 | 106.301 | 17.7169 | 82.9877 | 13.8313 |
| 6 | 230.33 | 38.3883 | 110.223 | 18.3705 | 81.2825 | 13.5471 |
| 7 | 231.04 | 38.5067 | 107.187 | 17.8645 | 84.3218 | 14.0536 |
| 8 | 218.861 | 36.4768 | 107.866 | 17.9777 | 84.3693 | 14.0615 |
| 9 | 220.128 | 36.6881 | 110.193 | 18.3655 | 84.007 | 14.0012 |
| 10 | 225.415 | 37.5692 | 108.192 | 18.0321 | 82.7644 | 13.7941 |
| 11 | 233.164 | 38.8607 | 103.875 | 17.3125 | 82.9435 | 13.8239 |
| 12 | 230.39 | 38.3984 | 101.052 | 16.8421 | 88.9848 | 14.8308 |
| 13 | 218.782 | 36.4637 | 100.625 | 16.7709 | 84.0285 | 14.0048 |
| 14 | 218.338 | 36.3896 | 102.668 | 17.1114 | 83.792 | 13.9653 |
| 15 | 218.261 | 36.3769 | 106.432 | 17.7386 | 84.16 | 14.0267 |
| 16 | 219.511 | 36.5852 | 104.591 | 17.4318 | – | – |
| 17 | – | – | 111.329 | 18.5549 | – | – |
| Session 1 | Session 2 | Session 3 | ||||
|---|---|---|---|---|---|---|
| Part. | ||||||
| 1 | 145.378 | 24.2296 | 60.6133 | 10.1022 | 35.165 | 5.86083 |
| 2 | 142.013 | 23.6689 | 62.7894 | 10.4649 | 37.508 | 6.25133 |
| 3 | 138.032 | 23.0054 | 62.7262 | 10.4544 | 35.6265 | 5.93775 |
| 4 | 147.772 | 24.6287 | 67.3448 | 11.2241 | 37.2925 | 6.21542 |
| 5 | 150.402 | 25.067 | 66.8102 | 11.135 | 36.3315 | 6.05525 |
| 6 | 153.929 | 25.6548 | 68.9046 | 11.4841 | 34.4464 | 5.74107 |
| 7 | 148.482 | 24.747 | 65.6383 | 10.9397 | 35.3149 | 5.88582 |
| 8 | 152.481 | 25.4135 | 63.1547 | 10.5258 | 36.3194 | 6.05323 |
| 9 | 147.757 | 24.6262 | 64.7539 | 10.7923 | 37.0776 | 6.1796 |
| 10 | 150.344 | 25.0573 | 64.4885 | 10.7481 | 35.7969 | 5.96614 |
| 11 | 149.164 | 24.8606 | 63.1322 | 10.522 | 35.7003 | 5.95006 |
| 12 | 146.896 | 24.4826 | 61.5347 | 10.2558 | 35.776 | 5.96267 |
| 13 | 149.369 | 24.8949 | 62.0644 | 10.3441 | 36.2216 | 6.03693 |
| 14 | 164.938 | 27.4897 | 61.362 | 10.227 | 36.8212 | 6.13687 |
| 15 | 143.054 | 23.8424 | 66.0542 | 11.009 | 33.6933 | 5.61555 |
| 16 | 148.349 | 24.7248 | 64.5339 | 10.7556 | – | – |
| 17 | – | – | 60.7467 | 10.1245 | – | – |
| Session 1 | Session 2 | Session 3 | ||||
|---|---|---|---|---|---|---|
| Part. | ||||||
| 1 | 29.3523 | 4.89205 | 15.9516 | 2.65859 | 5.87511 | 0.979186 |
| 2 | 40.8778 | 6.81297 | 19.5621 | 3.26035 | 10.589 | 1.76483 |
| 3 | 27.4048 | 4.56746 | 11.6133 | 1.93555 | 4.95529 | 0.825882 |
| 4 | 24.4905 | 4.08174 | 10.7994 | 1.7999 | 4.47145 | 0.745242 |
| 5 | 22.6001 | 3.76669 | 13.1662 | 2.19436 | 2.5535 | 0.425584 |
| 6 | 30.8664 | 5.14439 | 18.1567 | 3.02612 | 5.59091 | 0.931818 |
| 7 | 25.7927 | 4.29878 | 11.5305 | 1.92175 | 4.30922 | 0.718204 |
| 8 | 19.7088 | 3.2848 | 23.1764 | 3.86274 | 2.18925 | 0.364875 |
| 9 | 28.7235 | 4.78725 | 25.3742 | 4.22903 | 2.41359 | 0.402265 |
| 10 | 30.5402 | 5.09003 | 18.3046 | 3.05077 | 2.45213 | 0.408688 |
| 11 | 37.0004 | 6.16673 | 15.4212 | 2.57019 | 9.71214 | 1.61869 |
| 12 | 23.1125 | 3.85208 | 16.7412 | 2.7902 | 15.5948 | 2.59914 |
| 13 | 23.9457 | 3.99094 | 14.3645 | 2.39408 | 5.01824 | 0.836374 |
| 14 | 38.4261 | 6.40435 | 22.18 | 3.69666 | 3.39276 | 0.56546 |
| 15 | 26.3165 | 4.38609 | 11.7149 | 1.95248 | 5.50357 | 0.917261 |
| 16 | 24.3416 | 4.05693 | 9.91197 | 1.65199 | – | – |
| 17 | – | – | 20.8576 | 3.47626 | – | – |
| Session 1 | Session 2 | Session 3 | ||||
|---|---|---|---|---|---|---|
| Part. | ||||||
| 1 | 32.8829 | 5.48048 | 20.4555 | 3.40925 | 6.66709 | 1.11118 |
| 2 | 29.7489 | 4.95815 | 17.6728 | 2.94547 | 13.8489 | 2.30816 |
| 3 | 27.9104 | 4.65174 | 12.0573 | 2.00956 | 5.62034 | 0.936723 |
| 4 | 47.0301 | 7.83836 | 28.9688 | 4.82813 | 6.04289 | 1.00715 |
| 5 | 39.5275 | 6.58791 | 21.3855 | 3.56425 | 5.9418 | 0.990301 |
| 6 | 36.5602 | 6.09336 | 23.8271 | 3.97118 | 4.24954 | 0.708256 |
| 7 | 25.3059 | 4.21766 | 25.054 | 4.17567 | 6.6485 | 1.10808 |
| 8 | 47.8765 | 7.97942 | 19.1891 | 3.19819 | 6.48157 | 1.08026 |
| 9 | 38.0958 | 6.3493 | 20.0471 | 3.34118 | 7.09285 | 1.18214 |
| 10 | 42.571 | 7.09516 | 18.366 | 3.061 | 5.41897 | 0.903162 |
| 11 | 33.9904 | 5.66506 | 16.9797 | 2.82995 | 10.8703 | 1.81171 |
| 12 | 21.7463 | 3.62438 | 22.785 | 3.7975 | 15.5483 | 2.59138 |
| 13 | 37.3059 | 6.21766 | 22.0264 | 3.67107 | 8.46553 | 1.41092 |
| 14 | 35.1063 | 5.85105 | 21.3216 | 3.5536 | 5.02028 | 0.836713 |
| 15 | 27.1887 | 4.53146 | 21.4652 | 3.57754 | 5.9336 | 0.988934 |
| 16 | 30.092 | 5.01533 | 27.8947 | 4.64912 | – | – |
| 17 | – | – | 16.5292 | 2.75487 | – | – |
| Session 1 | Session 2 | Session 3 | ||||
|---|---|---|---|---|---|---|
| Part. | ||||||
| 1 | 17.6051 | 2.93419 | 13.802 | 2.30033 | 5.51619 | 0.919365 |
| 2 | 21.4067 | 3.56779 | 15.2125 | 2.53541 | 10.6341 | 1.77234 |
| 3 | 20.5887 | 3.43145 | 9.95013 | 1.65835 | 5.08502 | 0.847504 |
| 4 | 22.3997 | 3.73329 | 10.5322 | 1.75536 | 4.72411 | 0.787352 |
| 5 | 16.3869 | 2.73115 | 12.4787 | 2.07978 | 2.33086 | 0.388477 |
| 6 | 24.1159 | 4.01932 | 16.2193 | 2.70322 | 4.31467 | 0.719111 |
| 7 | 25.7992 | 4.29986 | 10.4045 | 1.73408 | 3.99644 | 0.666073 |
| 8 | 20.0133 | 3.33556 | 16.7847 | 2.79745 | 1.7952 | 0.2992 |
| 9 | 20.9099 | 3.48498 | 19.0443 | 3.17404 | 2.51195 | 0.418658 |
| 10 | 29.9577 | 4.99294 | 11.6179 | 1.93631 | 2.45609 | 0.409348 |
| 11 | 25.8743 | 4.31238 | 10.7424 | 1.79041 | 9.38085 | 1.56348 |
| 12 | 27.5461 | 4.59102 | 15.3596 | 2.55993 | 14.0158 | 2.33596 |
| 13 | 16.84 | 2.80667 | 13.9764 | 2.3294 | 5.06343 | 0.843905 |
| 14 | 39.9483 | 6.65804 | 16.9594 | 2.82657 | 3.5487 | 0.59145 |
| 15 | 26.4518 | 4.40863 | 9.33683 | 1.55614 | 4.29295 | 0.715491 |
| 16 | 16.7662 | 2.79437 | 9.04149 | 1.50691 | – | – |
| 17 | – | – | 12.9543 | 2.15905 | – | – |
| Session 1 | Session 2 | Session 3 | ||||
|---|---|---|---|---|---|---|
| Part. | ||||||
| 1 | 18.6982 | 3.11636 | 12.5044 | 2.08407 | 6.17827 | 1.02971 |
| 2 | 21.986 | 3.66434 | 15.4513 | 2.57522 | 10.7462 | 1.79103 |
| 3 | 20.8771 | 3.47952 | 9.51516 | 1.58586 | 4.90735 | 0.817892 |
| 4 | 23.9088 | 3.9848 | 10.8678 | 1.81129 | 4.80413 | 0.800689 |
| 5 | 20.2253 | 3.37088 | 12.3063 | 2.05104 | 2.64659 | 0.441099 |
| 6 | 35.2502 | 5.87503 | 16.6865 | 2.78108 | 4.70287 | 0.783811 |
| 7 | 36.7429 | 6.12382 | 10.6514 | 1.77524 | 3.46634 | 0.577723 |
| 8 | 26.1145 | 4.35242 | 16.0153 | 2.66922 | 1.82649 | 0.304415 |
| 9 | 20.3506 | 3.39177 | 18.5346 | 3.08909 | 2.73675 | 0.456125 |
| 10 | 36.3602 | 6.06004 | 11.1061 | 1.85102 | 2.66171 | 0.443618 |
| 11 | 30.3859 | 5.06431 | 9.52843 | 1.58807 | 10.1615 | 1.69359 |
| 12 | 33.5378 | 5.58963 | 12.8078 | 2.13464 | 15.2613 | 2.54355 |
| 13 | 17.9947 | 2.99912 | 12.0823 | 2.01372 | 6.77343 | 1.12891 |
| 14 | 40.8638 | 6.81063 | 14.4793 | 2.41322 | 3.90796 | 0.651326 |
| 15 | 24.6398 | 4.10663 | 8.80488 | 1.46748 | 4.32493 | 0.720822 |
| 16 | 17.7253 | 2.95421 | 9.94192 | 1.65699 | – | – |
| 17 | – | – | 12.5098 | 2.08496 | – | – |
| Model | No. of Parameters | ||
|---|---|---|---|
| BASE | 0 | 150.34 | 25.06 |
| F | 1 | 109.04 | 18.17 |
| ES | 1 | 22.87 | 3.81 |
| BH | 2 | 23.97 | 3.99 |
| ESH2 | 3 | 19.51 | 3.25 |
| ESHE | 4 | 19.25 | 3.21 |
| Session 1 | Session 2 | Session 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Part. | CV (%) | CV (%) | CV (%) | |||||||||
| 1 | 0.35 | 0.01 | 172.32 | 2.6 | 0.73 | 0.18 | 365.69 | 1.94 | 0.6 | 2.26 | 543.41 | 0.78 |
| 2 | 0.24 | 0.52 | 407.91 | 3.03 | 0.43 | 0.36 | 395.39 | 2.34 | 0.49 | 0.03 | 312.63 | 1.7 |
| 3 | 0.29 | 0.01 | 141.31 | 3.12 | 0.15 | 0.07 | 317.4 | 1.54 | 0.56 | 1.69 | 493.54 | 0.76 |
| 4 | 0.99 | 0.01 | 186.84 | 3.52 | 0.99 | 0.11 | 413.81 | 1.71 | 0.99 | 0.61 | 488.64 | 0.72 |
| 5 | 0.49 | 0.01 | 179.32 | 2.51 | 0.62 | 0.19 | 405.06 | 1.9 | 0.72 | 0.08 | 697.33 | 0.37 |
| 6 | 0.39 | 0.01 | 167.4 | 3.86 | 0.5 | 0.01 | 214.67 | 2.48 | 0.09 | 1.69 | 452.22 | 0.6 |
| 7 | 0.17 | 0.01 | 146.57 | 3.87 | 0.99 | 0.03 | 298.27 | 1.64 | 0.84 | 1.37 | 475.69 | 0.58 |
| 8 | 0.99 | 0.01 | 250.59 | 3.23 | 0.44 | 0.23 | 370.67 | 2.52 | 0.49 | 0.89 | 472.42 | 0.25 |
| 9 | 0.38 | 0.28 | 371.52 | 2.89 | 0.49 | 0.1 | 321.78 | 2.83 | 0.94 | 0.01 | 816.76 | 0.37 |
| 10 | 0.47 | 0.01 | 168.01 | 4.01 | 0.35 | 0.06 | 302.52 | 1.78 | 0.71 | 0.19 | 643.85 | 0.31 |
| 11 | 0.25 | 0.01 | 142.26 | 3.96 | 0.42 | 0.36 | 414.8 | 1.62 | 0.51 | 1.18 | 569.84 | 1.53 |
| 12 | 0.19 | 0.01 | 143.75 | 4 | 0.99 | 1.06 | 473.49 | 2.24 | 0.99 | 3.17 | 460.64 | 2.21 |
| 13 | 0.35 | 0.01 | 184.62 | 2.58 | 0.96 | 1.08 | 490.54 | 2.04 | 0.99 | 1.95 | 498.14 | 0.78 |
| 14 | 0.19 | 0.08 | 448.71 | 5.43 | 0.51 | 0.79 | 444.85 | 2.43 | 0.47 | 0.06 | 419.71 | 0.53 |
| 15 | 0.23 | 0.42 | 394.28 | 3.55 | 0.57 | 0.12 | 370.91 | 1.37 | 0.52 | 3.45 | 482.54 | 0.6 |
| 16 | 0.35 | 0.01 | 175.67 | 2.67 | 0.99 | 0.05 | 351.82 | 1.47 | – | – | – | – |
| 17 | – | – | – | – | 0.34 | 0.09 | 291.93 | 1.99 | – | – | – | – |
| Session 1 | Session 2 | Session 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Part. | ||||||||||||
| 1 | 0.349 | −0.003 | 0.874 | 1.019 | 0.604 | −0.101 | 0.800 | 1.131 | 0.012 | −0.122 | 1.000 | 1.158 |
| 2 | 0.246 | −0.051 | 0.365 | 1.071 | 0.433 | −0.086 | 1.000 | 1.113 | 0.445 | 0.002 | 0.916 | 1.014 |
| 3 | 0.300 | 0.031 | 0.871 | 0.986 | 0.172 | 0.102 | 0.928 | 0.922 | 0.550 | −0.069 | 0.905 | 1.092 |
| 4 | 0.990 | −0.060 | 0.862 | 1.082 | 0.990 | −0.036 | 0.915 | 1.055 | 0.990 | −0.023 | 0.393 | 1.041 |
| 5 | 0.470 | −0.052 | 0.872 | 1.072 | 0.595 | −0.046 | 0.876 | 1.065 | 0.610 | −0.028 | 0.253 | 1.046 |
| 6 | 0.463 | −0.369 | 0.810 | 1.610 | 0.550 | −0.163 | 0.847 | 1.215 | 0.336 | −0.117 | 0.807 | 1.152 |
| 7 | 0.182 | −0.008 | 0.872 | 1.024 | 0.990 | 0.002 | 0.917 | 1.015 | 0.874 | −0.074 | 0.362 | 1.098 |
| 8 | 0.990 | −0.087 | 0.866 | 1.114 | 0.439 | −0.070 | 0.568 | 1.094 | 0.478 | −0.013 | 0.484 | 1.030 |
| 9 | 0.384 | −0.048 | 0.945 | 1.068 | 0.475 | −0.034 | 0.731 | 1.053 | 0.901 | −0.022 | 0.961 | 1.040 |
| 10 | 0.457 | −0.035 | 0.873 | 1.054 | 0.355 | 0.080 | 0.908 | 0.942 | 0.667 | 0.020 | 0.946 | 0.997 |
| 11 | 0.248 | −0.042 | 0.858 | 1.061 | 0.423 | −0.110 | 0.811 | 1.142 | 0.393 | −0.065 | 0.570 | 1.088 |
| 12 | 0.205 | 0.003 | 0.873 | 1.013 | 0.990 | −0.159 | 0.116 | 1.209 | 0.990 | −0.131 | 0.846 | 1.170 |
| 13 | 0.342 | −0.048 | 0.868 | 1.067 | 0.686 | −0.146 | 0.805 | 1.190 | 0.010 | −0.135 | 0.937 | 1.176 |
| 14 | 0.194 | −0.161 | 1.000 | 1.212 | 0.479 | −0.148 | 1.000 | 1.194 | 0.422 | −0.012 | 0.948 | 1.029 |
| 15 | 0.230 | 0.016 | 0.886 | 1.001 | 0.547 | −0.040 | 0.849 | 1.059 | 0.568 | −0.113 | 0.255 | 1.146 |
| 16 | 0.347 | −0.037 | 0.870 | 1.056 | 0.990 | 0.040 | 0.938 | 0.977 | – | – | – | – |
| 17 | – | – | – | – | 0.343 | −0.022 | 0.746 | 1.039 | – | – | – | – |
| Session | ||||||
|---|---|---|---|---|---|---|
| 1 | −12.87 | 4.78 | 45.11 | 0.95 | 1.02 | 1.14 |
| 2 | −12.74 | −1.69 | 4.35 | 0.93 | 0.98 | 1.05 |
| 3 | −6.63 | 4.61 | 8.59 | 1.01 | 1.09 | 1.15 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonetto, F.; Cheriyan, V.; Kleywegt, A.J. Models of Investor Forecasting Behavior — Experimental Evidence. J. Risk Financial Manag. 2018, 11, 3. https://doi.org/10.3390/jrfm11010003
Bonetto F, Cheriyan V, Kleywegt AJ. Models of Investor Forecasting Behavior — Experimental Evidence. Journal of Risk and Financial Management. 2018; 11(1):3. https://doi.org/10.3390/jrfm11010003
Chicago/Turabian StyleBonetto, Federico, Vinod Cheriyan, and Anton J. Kleywegt. 2018. "Models of Investor Forecasting Behavior — Experimental Evidence" Journal of Risk and Financial Management 11, no. 1: 3. https://doi.org/10.3390/jrfm11010003





