Emerging Market Default Risk Charge Model
Abstract
:1. Introduction
2. Default Charge Estimators
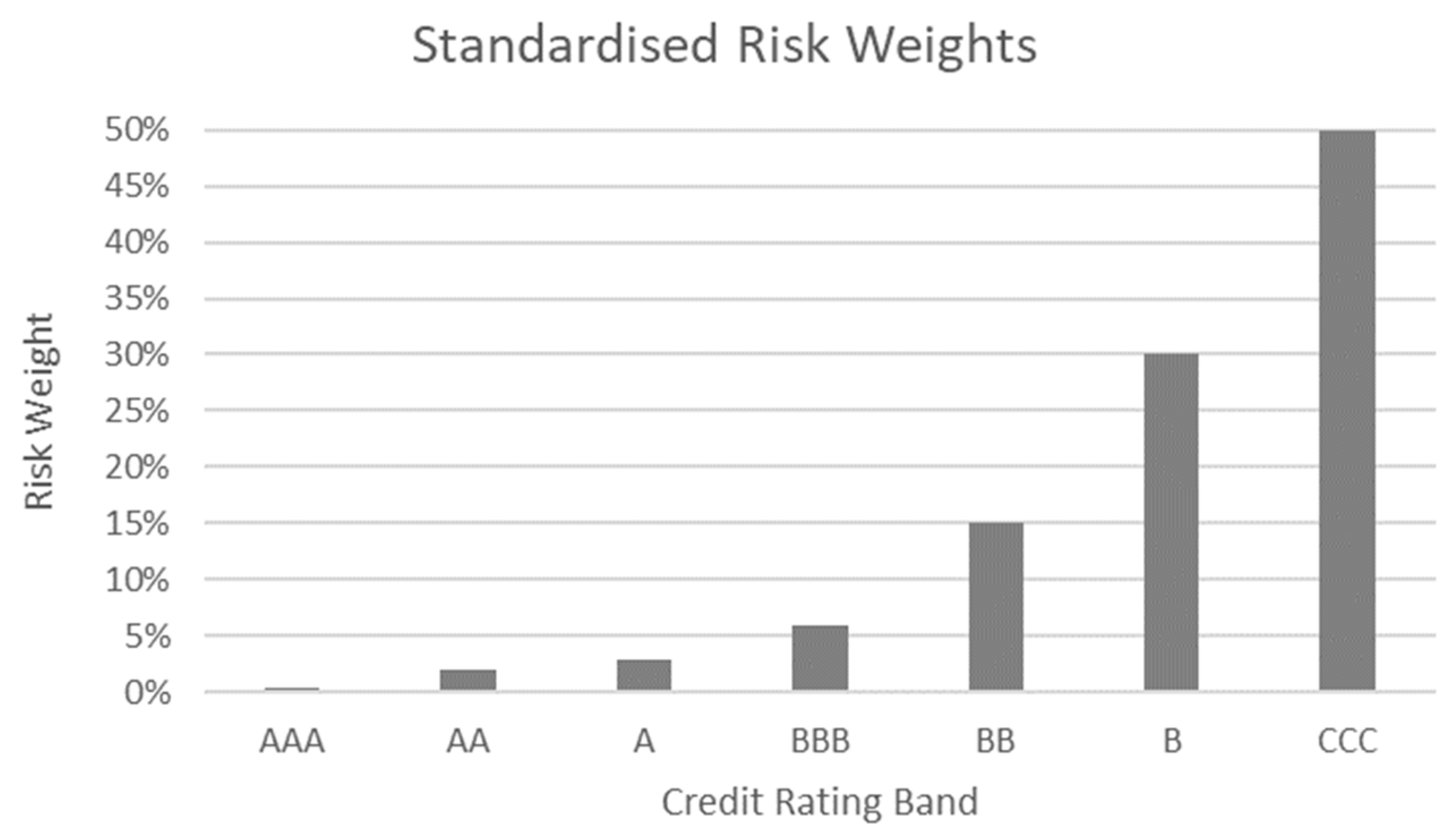
2.1. Standardised Approach
2.2. Internal Models Approach
2.2.1. DRC Rationale
2.2.2. DRC Specifications
Default Correlation
3. Emerging Market
3.1. Default Simulation
3.2. Simulation Process
4. Modelling
4.1. Default Risk Factor Modelling
Correlation Assumption
4.2. Framework
5. Results and Discussion
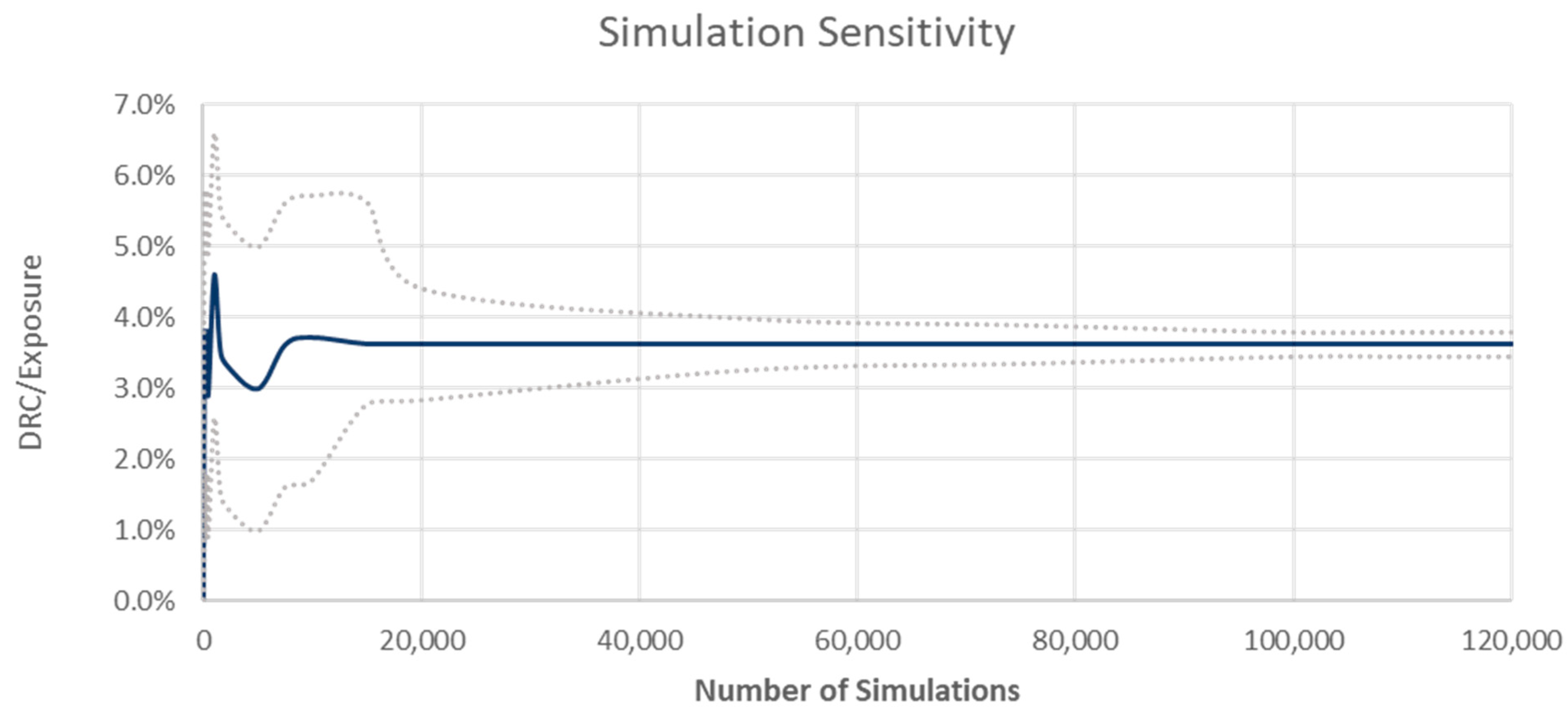
5.1. Calibration
5.2. Experimental Testing
5.2.1. Set-Up
5.2.2. Design
Market Crash Scenario
Fully Diversified Scenario
5.2.3. Test Results
6. Conclusions
- -
- The emerging market data, generally of poor quality and not abundant, prompted using equity returns to derive the default correlations. Even though this data choice seems plausible from an emerging market perspective, it may introduce some DRC variability. Using an arbitrary data choice (equity returns or CDS spreads) regarding the default calibration could lead to ill-favored variability in the DRC (Laurent et al. 2016). Apart from having two IMA DRC approaches, one for emerging markets and one for developed markets—articulating what type of data to be used, another response could be to require all banks to disclose the choice of data used for the default calibrations.
- -
- From a policy perspective, the regulator may consider dropping the 0.03% default probability floor as it may be too punitive for emerging markets. The impact of dropping the 0.03% floor is likely to be material for banking portfolios that tend to comprise significant positions in securities of well-rated sovereigns and corporates (Wilkens and Predescu 2016). In fact, in some emerging markets (like South Africa) banking portfolio default calibration data is not always available due to a scant or sporadic history of corporate credit defaults. The lower the likelihood of default, the more observations are required to produce reliable default estimates (Ferreiro 2016). Therefore, the data problem in emerging markets could translate into a default model risk problem. The probability floor of 0.03% results in a shorter distance to default for obligors with a much lower default probability (according to Equation (6) in Section 4.2). The probability floor could be thought of as some conservatism introduced to alleviate the data reliability problem. Unfortunately, the probability floor may also be argued to be introducing some fictitious conservatism in the default charge, especially for emerging markets with very well-rated bank portfolio obligors (having a default probability much less than 0.03%).
- -
- For emerging markets, the regulator may consider allowing the use of standardised LGDs (BCBS 2016) (25% for covered bonds, 75% for senior bonds, and 100% for non-senior instruments including equity) in the IMA DRC. Using the standardised LGDs in an emerging market DRC model could result in some margin of conservativism. The conservatism introduced in the emerging market DRC model is preferable from a risk perspective compared to the extra possible data uncertainty injected into the DRC via the modelling and estimating of the systemic factor-dependent LGDs. Moreover, the conservatism introduced by using the standardised LGDs in the emerging market IMA DRC model is deterministic. Thus, considering the use of standardised LGDs in the emerging market DRC model could move the regulator, supervisors, and banks closer to getting emerging market institutions to comply better and confidently adopt the IMA DRC.
- -
- Data from only one emerging market were used to calibrate the default correlations. A possible avenue for future research is to perform the default calibration on multiple emerging markets. This will not only allow direct comparisons of the calibration parameters but will also give a good idea of the measurement and management of the stability of the calibration parameters over several emerging markets.
- -
- Another limitation of the research is that the correlation calibration excluded data covering the COVID-19 epidemic period. Another possible avenue for future research is to include the epidemic period in the ten-year calibration data period. Including the epidemic data period in the calibration will allow the direct comparison of the default charge estimate under the 2008–2009 crisis and the more current epidemic period. Such a comparison can be helpful from a market risk stress management perspective.
- -
- The regulations suggest that the LGDs used in the DRC should ideally depend on the systemic factors used in the default calibration. See Figure 2. However, this research was limited to using fixed LGDs in the DRC simulation, which is not based on the derived systemic factors. The fixed LGDs were used in the emerging market DRC setting to allow for a reasonably manageable set of data assumptions in the model. Future work on emerging-market DRC modelling could explore stochastic or systemic factor based LGDs similar to the framework outlined in Section 4.2. This exercise will probably facilitate an academic contribution in that, given the data problems common to emerging markets, it could quantify and empirically show the degree to which an emerging market DRC becomes inaccurate due to too many data assumptions and approximations.
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 1 | Default correlation can be thought of as a measure of how in sync issuers of debt default in the event of a global, country or industry wide crisis, like the subprime credit crisis experienced in the years 2008 to 2009. |
| 2 | Accounting for the default charge by adding on to the overall risks are permissible since the default charge is comparable to a VaR metric (Rodrigues and Maialy 2018). |
| 3 | This limitation arises because credit correlations in markets are generally driven by more than one economic factor. |
| 4 | Interestingly, the introduction of the credit risk measure that excludes migration came against the backdrop of the global 2008–2009 financial crisis showing that most losses to the banking sector were caused not by default but by credit migration (Prorokowski and Prorokowski 2014). |
| 5 | Spread risk is more concerned with default expectations, whereas the default risk charge is concerned with the capital at risk in the event of a jump-to-default. The jump-to-default risk is analogous to jumping from a cliff (compared to a slow credit migration that allows time for credit spreads to reprice and losses to be cushioned). |
| 6 | Banks are required to seek formal approval from the supervisor to use the internal models approach for each desk; otherwise non-qualifying desks will be subject to the standardised capital framework. |
| 7 | It is counterintuitive that a default risk measure was introduced to supplement a market risk measure in the traditional sense. However, modern portfolios generally contain market and credit risks that are not fully explained by the original market capital framework (Ferreiro 2016). |
| 8 | When the correlation between issuers and the concentration risk is higher, one generally expects the DRC to increase (Slime 2018). This proportionality is not fully preserved in the standardized DRC. |
| 9 | Time series standardised to reflect a mean of 0 and standard deviation of 1. |
| 10 | Overlapping return correlations can be prone to autocorrelation effects. Moreover, the use of overlapping return correlations can distort the correlations to such an extent that the maximum, true peak correlations can go undetected. |
References
- Al Janabi, Mazin A. M. 2006. On the Inception of Sound Derivative Products in Emerging Markets, Real-world Observations and Viable Solutions. Journal of Financial Regulation and Compliance 14: 151–64. [Google Scholar] [CrossRef]
- BCBS. 2009a. Revisions to the Basel II Market Risk Framework. Available online: https://www.bis.org/publ/bcbs158.pdf (accessed on 28 February 2017).
- BCBS. 2009b. Guidelines for Computing Capital for Incremental Risk in the Trading Book. Available online: https://www.bis.org/publ/bcbs159.htm (accessed on 26 June 2018).
- BCBS. 2014. Reducing Excessive Variability in Banks’ Regulatory Capital Ratios. Available online: https://www.bis.org/bcbs/publ/d298.pdf (accessed on 22 November 2020).
- BCBS. 2016. Minimum Capital Requirements for Market Risk. Available online: https://www.bis.org/bcbs/publ/d352.htm (accessed on 28 February 2021).
- BCBS. 2019. Minimum Capital Requirements for Market Risk. Available online: https://www.bis.org/bcbs/publ/d457.htm (accessed on 10 October 2021).
- Cabrera, Emiliano. 2022. Reinventing Opportunities for Argentina, Vista Oil and Gas. Master’s thesis, Dartmouth College, Hanover, NH, USA. Available online: https://digitalcommons.dartmouth.edu/cgi/viewcontent.cgi?article=1058&context=masters_theses (accessed on 28 January 2023).
- Clift, Peter-John. 2020. Credit Curve Estimation and Corporate Bonds in South Africa. Master’s thesis, Stellenbosch University, Stellenbosch, South Africa. Available online: https://scholar.sun.ac.za/handle/10019.1/108003 (accessed on 22 November 2022).
- Düllmann, Klaus, Jonathan Küll, and Michael Kunish. 2008. Estimating Asset Correlations from Stock Prices or Default Rates—Which Method Is Superior? Banking and Financial Studies, Deutsche Bundesbank, Series 2: 04/2008, Discussion Paper. Available online: https://ideas.repec.org/p/zbw/bubdp2/7314.html (accessed on 22 November 2022).
- Economic Times. 2023. What Is Brics? Business News. Available online: https://economictimes.indiatimes.com/definition/Brics (accessed on 15 January 2023).
- Feridun, Mete, and Alper Ozün. 2020. Basel IV implementation: A review of the case of the European Union. Journal of Capital Market Studies 4: 7–24. [Google Scholar] [CrossRef]
- Ferreiro, Javier Ojea. 2016. Modelling Default Risk Charge (DRC): Internal Model Approach. Master in Banking and Finance thesis, Universidad Complutense de Madrid, Madrid, Spain. Available online: https://www.uv.es/bfc/TFM2016/TFM_JavierOjea.pdf (accessed on 10 October 2021).
- Hull, John C. 2015. Options, Futures and Other Derivatives, 9th ed. London: Pearson. ISBN 0-13-015822-4. [Google Scholar]
- Jackson, Patricia, David Maude, and William Perraudin. 1997. Bank Capital and Value at Risk. Journal of Derivatives 4: 73–90. [Google Scholar] [CrossRef]
- Klaassen, Pieter, and Idzard van Eeghen. 2009. Economic Capital, How it Works and What Every Manager Should Know, 1st ed. Amsterdam: Elsevier Finance, ISBN 13: 978-0-12-374901-7. [Google Scholar]
- Laurent, Jean-Paul, Michael Sestier, and Stéphane Thomas. 2016. Trading Book and Credit Risk: How Fundamental is the Basel Review? Journal of Banking and Finance 73: 211–23. [Google Scholar] [CrossRef] [Green Version]
- Lovreta, Lidija, and Joaquín López Pascual. 2020. Structural Breaks in the Interaction between Bank and Sovereign Default Risk. Journal of Spanish Economic Association 11: 531–59. [Google Scholar] [CrossRef]
- Merton, Robert C. 1974. On the Pricing of Corporate Debt: The Risk Structure of Interest Rates. The Journal of Finance 29: 449–70. [Google Scholar]
- Munetsi, Raramai Patience, and Pradeep Brijlal. 2021. Testing the Influence of Herding Behavior on the Johannesburg Securities Exchange (JSE) Before, During and After the Financial Crisis. International Journal of Economics and Finance Studies 13: 235–58. [Google Scholar] [CrossRef]
- Pereiro, Luis. 2010. The Beta Dilemma in Emerging Markets. Journal of Applied Corporate Finance 22: 110–23. [Google Scholar] [CrossRef]
- Prorokowski, Lukasz, and Hubert Prorokowski. 2014. Comprehensive Risk Measure—Current Challenges. Journal of Financial Regulation and Compliance 22: 271–84. [Google Scholar] [CrossRef]
- Rikhotso, Prayer M., and Beatrice D. Simo-Kengne. 2022. Dependence Structures between Sovereign Credit Default Swaps and Global Risk Factors in BRICS Countries. Journal of Risk and Financial Management 15: 109. [Google Scholar] [CrossRef]
- Rodrigues, Matheus, and Andre Maialy. 2018. Measuring Default Risk for a Portfolio of Equities. Available online: https://ssrn.com/abstract=3082021 (accessed on 26 June 2021).
- Slime, Badreddine. 2018. Concentration Risk under Default Risk Charge (DRC). Available online: https://ssrn.com/abstract=3101344 (accessed on 10 October 2020).
- Slime, Badreddine. 2022. Mathematical Modeling of Concentration Risk under the Default Risk Charge Using Probability and Statistics Theory. Journal of Probability and Statistics 2022: 1–12. [Google Scholar] [CrossRef]
- Vasicek, Alfons. 2002. The Distribution of Loan Portfolio Value. Risk Magazine 15: 160–62. [Google Scholar]
- Wikipedia. 2022. Economy of South Africa. The Free Encyclopedia. Available online: https://en.wikipedia.org/wiki/Economy_of_South_Africa (accessed on 26 June 2022).
- Wilkens, Sascha, and Mirela Predescu. 2016. Default Risk Charge: Modelling Framework for the “Basel” Risk measure. Journal of Risk 19: 23–50. [Google Scholar] [CrossRef]
- Xiao, Tim. 2009. Incremental Risk Charge Methodology. Available online: https://ssrn.com/abstract=2426836 (accessed on 22 November 2020).


| Calibration Data Frequency | t-Stat | ||
|---|---|---|---|
| Weekly | 76.08% | 14.64 | 57.89% |
| Monthly | 75.57% | 6.925 | 57.12% |
| Sector | Obligor | ||||||
|---|---|---|---|---|---|---|---|
| Secondary | 1 | 80.33% | −7.72% | 60.68% | 55.74% | 83.47% | 52.00% |
| 3.4 | −0.38 | 5.20 | 6.5 | ||||
| 2 | 48.36% | −13.23% | 69.70% | 117.11% | 49.52% | ||
| 2.03 | −0.65 | 5.93 | 5.86 | ||||
| Tertiary | 3 | 108.47% | −21.90% | 52.42% | 71.51% | 64.40% | 54.62% |
| 11.45 | −2.12 | 7.89 | 6.49 | ||||
| 4 | 85.20% | −24.77% | 62.06% | 86.01% | 68.17% | ||
| 6.80 | −1.81 | 7.05 | 6.50 | ||||
| Primary | 5 | 40.84% | 49.59% | 61.61% | 81.60% | 93.77% | 72.92% |
| 1.54 | 1.50 | 7.87 | 9.71 |
| Random Simulation | |
|---|---|
| Paths: | 1 million |
| Underlying distribution: | Gaussian |
| * Algorithm: | Mersenne Twister |
| Seed: | 456,789 |
| Scenario: | Market Crash | Fully Diversified | ||
|---|---|---|---|---|
| Correlation: | Perfect | Zero | ||
| PD: | 100% | 100% | 0 | 50% |
| Percentiles | DRC | DRC * | DRC | DRC |
| 100 | 1500 | 900 | 0 | 1300 |
| 99.9 | 1500 | 900 | 0 | 1000 |
| 99.8 | 1500 | 900 | 0 | 1000 |
| 99.5 | 1500 | 900 | 0 | 900 |
| 98 | 1500 | 900 | 0 | 800 |
| 97 | 1500 | 900 | 0 | 800 |
| 96 | 1500 | 900 | 0 | 800 |
| 95 | 1500 | 900 | 0 | 800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joseph, A.D. Emerging Market Default Risk Charge Model. J. Risk Financial Manag. 2023, 16, 194. https://doi.org/10.3390/jrfm16030194
Joseph AD. Emerging Market Default Risk Charge Model. Journal of Risk and Financial Management. 2023; 16(3):194. https://doi.org/10.3390/jrfm16030194
Chicago/Turabian StyleJoseph, Angelo D. 2023. "Emerging Market Default Risk Charge Model" Journal of Risk and Financial Management 16, no. 3: 194. https://doi.org/10.3390/jrfm16030194






