Asymmetric Effects of Financial Development on CO2 Emissions in Bangladesh
Abstract
:1. Introduction
2. Literature Review
2.1. Financial Development in Bangladesh and the Sustainable Finance Policy
2.2. Empirical Literature on Financial Development and Emissions
2.3. Asymmetry between Financial Development and CO2 Emissions
3. Data and Methods
3.1. Data
3.2. Methods
4. Results
4.1. Unit Root Test
4.2. NARDL Bounds Tests and Model Diagnostics
4.3. NARDL Long-Run and Short-Run Models
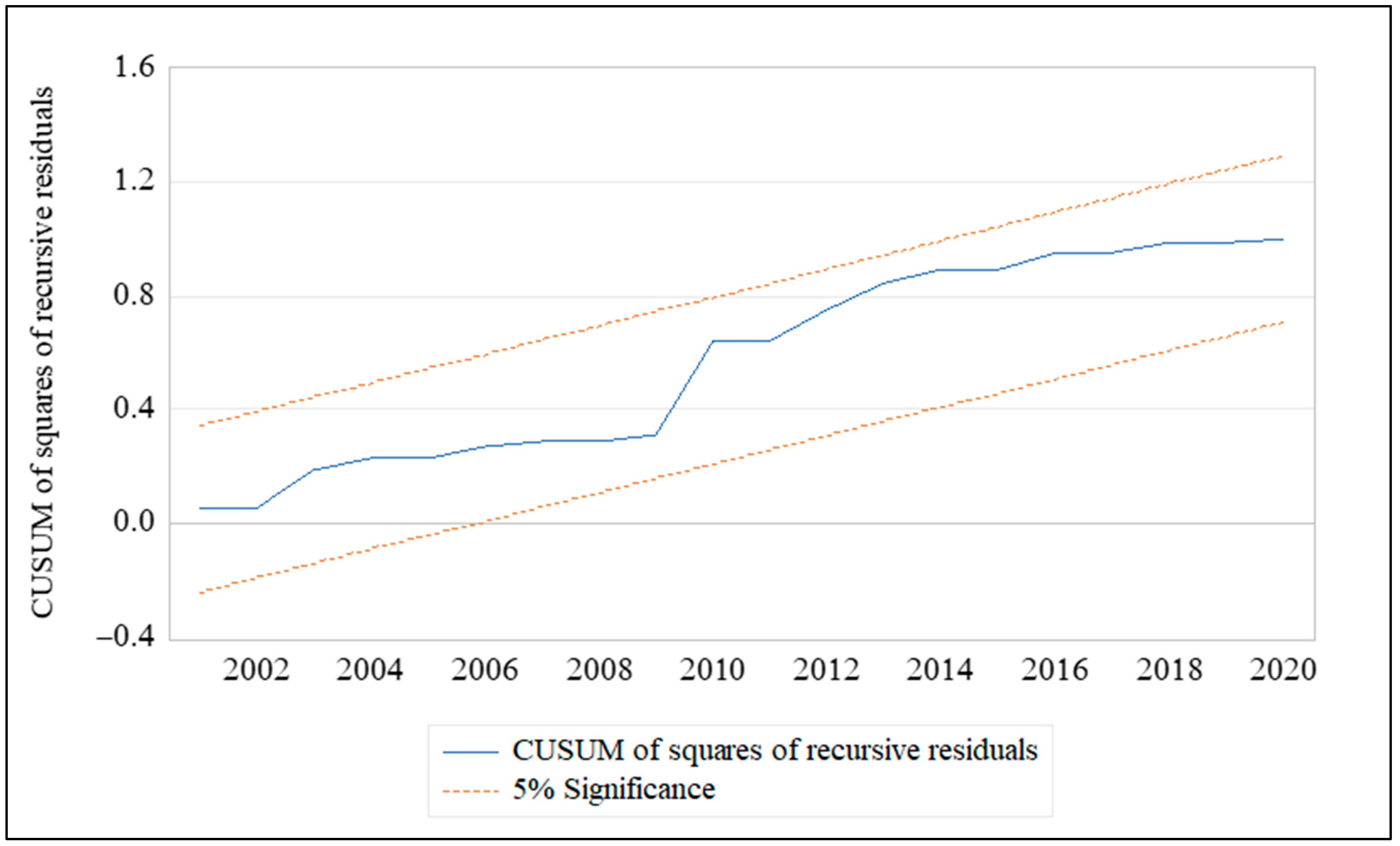
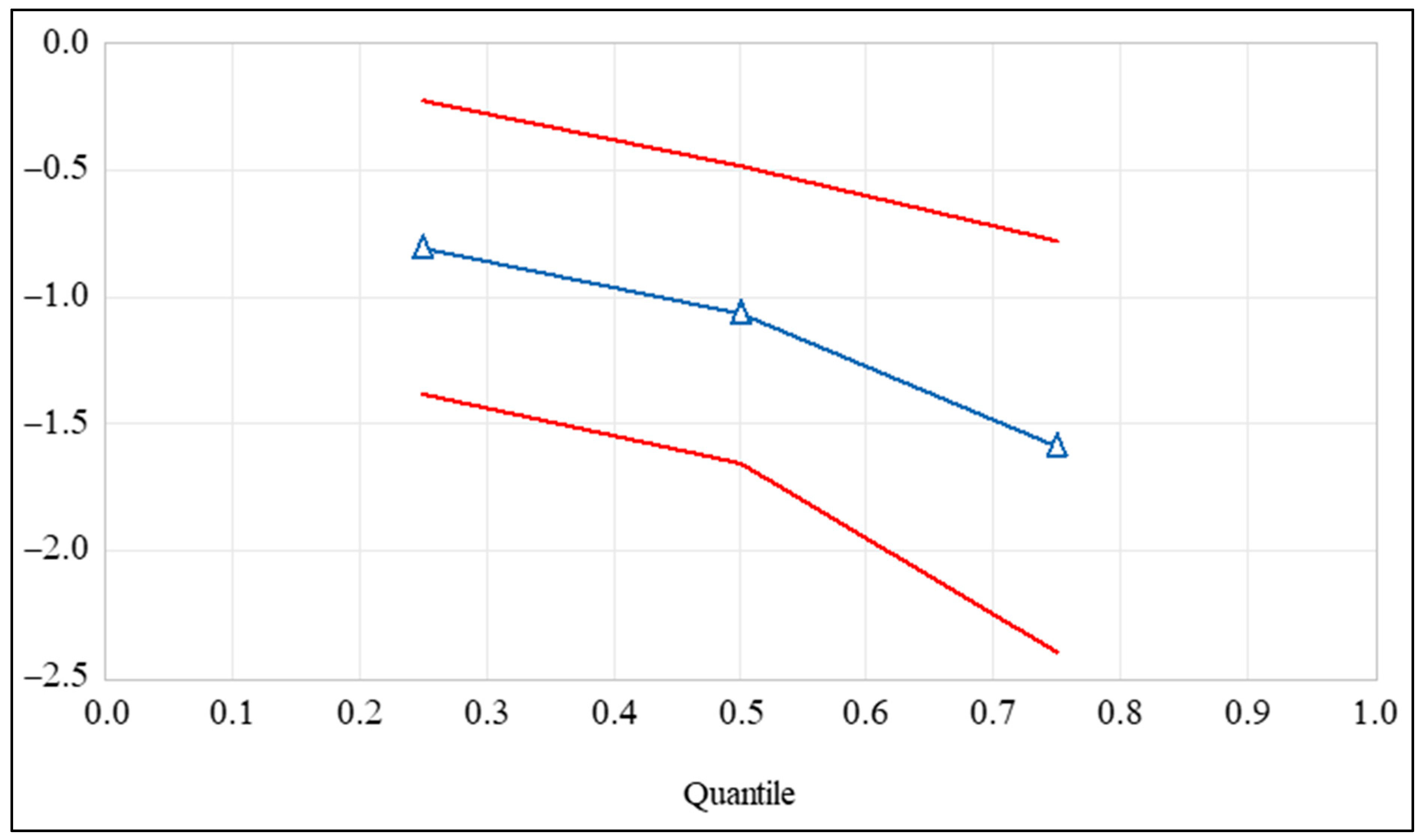
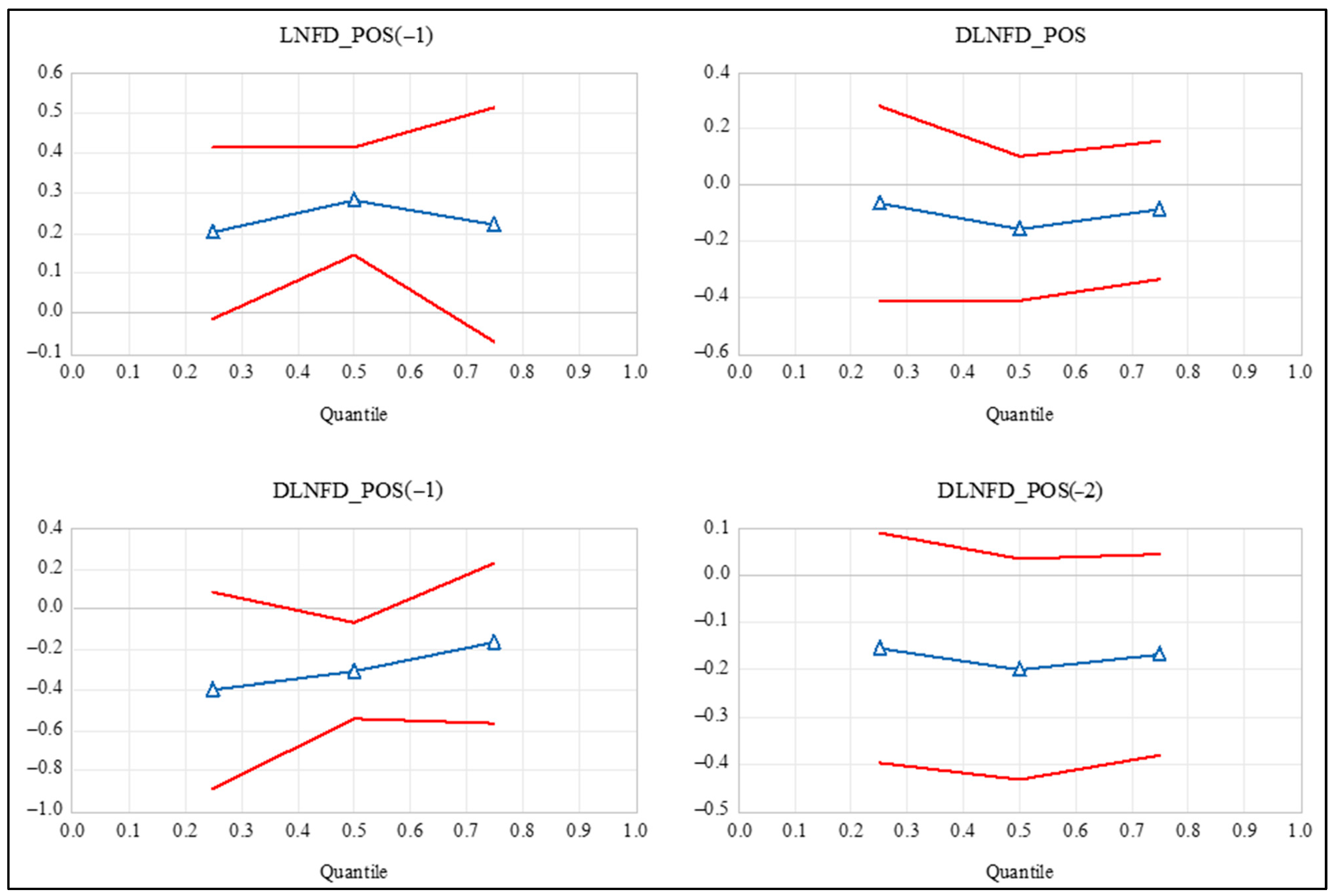
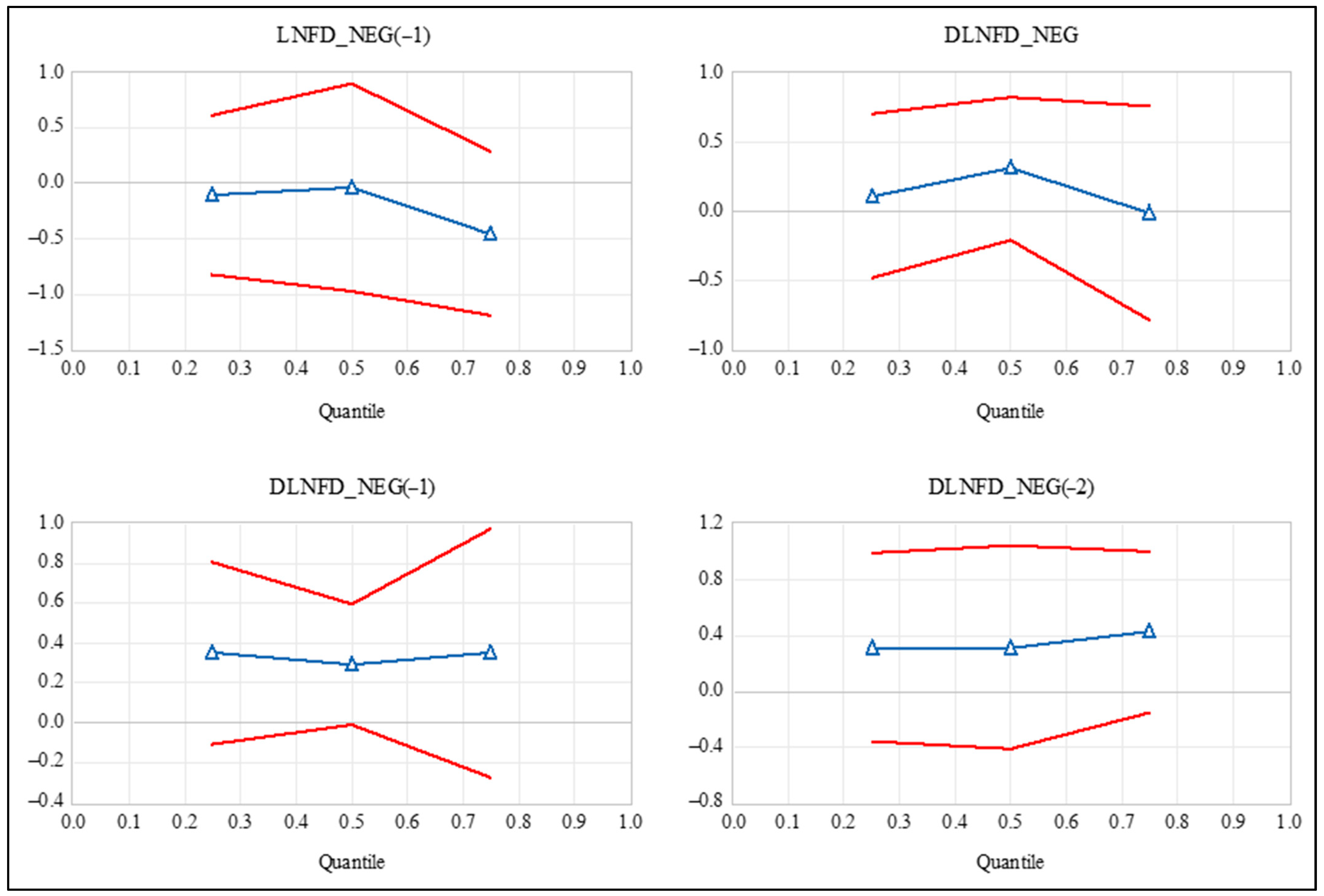
4.4. Robustness
5. Discussion
6. Conclusions and Policy Suggestions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | Details of the mechanics of the quantile autoregressive distributed lag model can be found in Cho et al. (2015) for the interested reader. |
References
- Abbasi, Faiza, and Khalid Riaz. 2016. CO2 emissions and financial development in an emerging economy: An augmented VAR approach. Energy Policy 90: 102–14. [Google Scholar] [CrossRef]
- Acheampong, Alex O. 2019. Modelling for insight: Does financial development improve environmental quality? Energy Economics 83: 156–79. [Google Scholar] [CrossRef]
- Acheampong, Alex O., Mary Amponsah, and Elliot Boateng. 2020. Does financial development mitigate carbon emissions? Evidence from heterogeneous financial economies. Energy Economics 88: 104768. [Google Scholar] [CrossRef]
- Alam, Mohammad Jahangir, Ismat Ara Begum, Jeroen Buysse, and Guido Van Huylenbroeck. 2012. Energy consumption, carbon emissions and economic growth nexus in Bangladesh: Cointegration and dynamic causality analysis. Energy Policy 45: 217–25. [Google Scholar] [CrossRef]
- Al-Mulali, Usama, Chor Foon Tang, and Ilhan Ozturk. 2015. Does financial development reduce environmental degradation? Evidence from a panel study of 129 countries. Environmental Science and Pollution Research 22: 14891–900. [Google Scholar] [CrossRef]
- Ang, James B. 2007. CO2 emissions, energy consumption, and output in France. Energy Policy 35: 4772–78. [Google Scholar] [CrossRef]
- Ang, James B. 2008. Economic development, pollutant emissions and energy consumption in Malaysia. Journal of Policy Modeling 30: 271–78. [Google Scholar] [CrossRef]
- Awal, Md Hossan, Md Aliullah, and Shishir Saidy. 2021. Green revolution in ready made garments in Bangladesh: An analytical study. International Journal of Engineering and Management Research 11: 22–29. [Google Scholar] [CrossRef]
- Bangladesh Bank. 2020. Sustainable Finance Policy for Banks and Financial Institutions. Dhaka: Bangladesh Bank. [Google Scholar]
- bdnews24.com. 2022. Bangladesh Allows Power Plants to Loan Any Amount from Banks Amid Energy Crisis. bdnews24.com. July 26. Available online: https://bdnews24.com/business/hegot77t9u (accessed on 11 February 2023).
- Bekhet, Hussain Ali, Ali Matar, and Tahira Yasmin. 2017. CO2 emissions, energy consumption, economic growth, and financial development in GCC countries: Dynamic simultaneous equation models. Renewable and Sustainable Energy Reviews 70: 117–32. [Google Scholar] [CrossRef]
- Boufateh, Talel, and Zied Saadaoui. 2020. Do asymmetric financial development shocks matter for CO2 emissions in Africa? A nonlinear panel ARDL-PMG approach. Environmental Modelling & Assessment 25: 809–30. [Google Scholar]
- Breusch, Trevor S. 1978. Testing for autocorrelation in dynamic linear models. Australian Economic Papers 17: 334–55. [Google Scholar] [CrossRef]
- Breusch, Trevor S., and Adrian R. Pagan. 1979. A simple test for heteroscedasticity and random coefficient variation. Econometrica 47: 1287–94. [Google Scholar] [CrossRef]
- Brown, Leanora, Adian McFarlane, Anupam Das, and Kaycea Campbell. 2022. The impact of financial development on carbon dioxide emissions in Jamaica. Environmental Science and Pollution Research 29: 25902–15. [Google Scholar] [CrossRef]
- Brown, Robert L., James Durbin, and James M. Evans. 1975. Techniques for Testing the Constancy of Regression Relationships over Time. Journal of the Royal Statistical Society. Series B (Methodological) 37: 149–92. [Google Scholar] [CrossRef]
- Bui, Duy Tung. 2020. Transmission channels between financial development and CO2 emissions: A global perspective. Heliyon 6: e05509. [Google Scholar] [CrossRef]
- Ceretta, Paulo Sérgio, and Marco Aurélio Vieira. 2021. CO2 emissions: A dynamic structural analysis. Revista de Administração da UFSM 14: 949–66. [Google Scholar]
- Cetin, Murat, Eyyup Ecevit, and Ali Gokhan Yucel. 2018. The impact of economic growth, energy consumption, trade openness, and financial development on carbon emissions: Empirical evidence from Turkey. Environmental Science and Pollution Research 25: 36589–603. [Google Scholar] [CrossRef] [PubMed]
- Chang, Ching-Chih. 2010. A multivariate causality test of carbon dioxide emissions, energy consumption and economic growth in China. Applied Energy 87: 3533–37. [Google Scholar] [CrossRef]
- Charfeddine, Lanouar, and Montassar Kahia. 2019. Impact of renewable energy consumption and financial development on CO2 emissions and economic growth in the MENA region: A panel vector autoregressive (PVAR) analysis. Renewable Energy 139: 198–213. [Google Scholar] [CrossRef]
- Cho, Jin Seo, Tae-hwan Kim, and Yongcheol Shin. 2015. Quantile cointegration in the autoregressive distributed-lag modeling framework. Journal of Econometrics 188: 281–300. [Google Scholar] [CrossRef]
- Das, Anupam, Adian A. McFarlane, and Murshed Chowdhury. 2013. The dynamics of natural gas consumption and GDP in Bangladesh. Renewable and Sustainable Energy Reviews 22: 269–74. [Google Scholar] [CrossRef]
- Das, Anupam, Adian McFarlane, and Luc Carels. 2021. Empirical exploration of remittances and renewable energy consumption in Bangladesh. Asia-Pacific Journal of Regional Science 5: 65–89. [Google Scholar] [CrossRef]
- DasGupta, Anirban. 2008. Asymptotic Theory of Statistics and Probability. New York: Springer. [Google Scholar]
- Ehigiamusoe, Kizito Uyi, and Hooi Hooi Lean. 2019. Effects of energy consumption, economic growth, and financial development on carbon emissions: Evidence from heterogeneous income groups. Environmental Science and Pollution Research 26: 22611–24. [Google Scholar] [CrossRef] [PubMed]
- Ehigiamusoe, Kizito Uyi, Vinitha Guptan, and Suresh Narayanan. 2021. Rethinking the impact of GDP on financial development: Evidence from heterogeneous panels. African Development Review 33: 1–13. [Google Scholar] [CrossRef]
- Godfrey, Leslie G. 1978. Testing against general autoregressive and moving average error models when the regressors include lagged dependent variables. Econometrica 46: 1293–301. [Google Scholar] [CrossRef]
- Gök, Adem. 2020. The role of financial development on carbon emissions: A meta regression analysis. Environmental Science and Pollution Research 27: 1–19. [Google Scholar] [CrossRef]
- Granger, Clive W. J., and Gawon Yoon. 2002. Hidden Cointegration. Economics Working Paper, 2002-02. Los Angeles: University of California. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=313831 (accessed on 3 February 2023).
- Grossman, Gene M., and Alan B. Krueger. 1995. Economic growth and the environment. Quarterly Journal of Economics 110: 353–77. [Google Scholar] [CrossRef]
- Hao, Yu, Zong-Yong Zhang, Hua Liao, Yi-Ming Wei, and Shuo Wang. 2016. Is CO2 emission a side effect of financial development? An empirical analysis for China. Environmental Science and Pollution Research 23: 21041–57. [Google Scholar] [CrossRef]
- Idrees, Muhammad, Umar Hayat, Magdalena Radulescu, Md Shabbir Alam, Abdul Rehman, and Mirela Panait. 2022. Measuring the financial lineralization index for Pakistan. Journal of Risk and Financial Management 15: 57. [Google Scholar] [CrossRef]
- International Monetary Fund. 2022. Financial Development Index Database. Washington, DC: International Monetary Fund. Available online: https://data.imf.org/?sk=F8032E80-B36C-43B1-AC26-493C5B1CD33B (accessed on 20 December 2022).
- Jalil, Abdul, and Mete Feridun. 2011. The impact of growth, energy and financial development on the environment in China: A cointegration analysis. Energy Economics 33: 284–91. [Google Scholar] [CrossRef]
- Jamel, Lamia, Samir Maktouf, and L. Charfeddine. 2017. The nexus between economic growth, financial development, trade openness, and CO2 emissions in European countries. Cogent Economics & Finance 5: 1–25. [Google Scholar]
- Jarque, Carlos M., and Anil K. Bera. 1980. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Economics Letters 6: 255–59. [Google Scholar] [CrossRef]
- Jiang, Chun, and Xiaoxin Ma. 2019. The impact of financial development on carbon emissions: A global perspective. Sustainability 11: 5241. [Google Scholar] [CrossRef]
- Kanas, Angelos, and Georgios P. Kouretas. 2005. A cointegration approach to the lead–lag effect among size-sorted equity portfolios. International Review of Economics and Finance 14: 181–201. [Google Scholar] [CrossRef]
- Khandker, Shahidur R., Hussain A. Samad, Zubair KM Sadeque, Mohammed Asaduzzaman, Mohammad Yunus, and AK Enamul Haque. 2014. Surge in Solar Powered Homes: Experience in Off-Grid Rural Bangladesh. Washington, DC: The World Bank. Available online: http://documents.worldbank.org/curated/en/871301468201262369/pdf/Surge-in-solar-powered-homes-experience-in-off-grid-rural-Bangladesh.pdf (accessed on 19 March 2020).
- Koenker, Roger, and Gilbert Bassett Jr. 1982. Robust tests for heteroscedasticity based on regression quantiles. Econometrica 50: 43–61. [Google Scholar] [CrossRef]
- Kripfganz, Sebastian, and Daniel C. Schneider. 2020. Response surface regressions for critical value bounds and approximate p-values in equilibrium correction models. Oxford Bulletin of Economics and Statistics 82: 1456–81. [Google Scholar] [CrossRef]
- Kripfganz, Sebastian, and Daniel C. Schneider. 2023. ARDL: Estimating Autoregressive Distributed Lag and Equilibrium Correction Models. Stata Journal. forthcoming. Available online: https://www2.econ.tohoku.ac.jp/~PDesign/dp/TUPD-2022-006.pdf (accessed on 3 February 2023).
- Lahiani, Amine. 2020. Is financial development good for the environment: An asymmetric analysis with CO2 emissions in China. Environmental Science and Pollution Research 27: 7901–9. [Google Scholar] [CrossRef]
- Ling, Gao, Asif Razzaq, Yaqiong Guo, Tehreem Fatima, and Farrukh Shahzad. 2022. Asymmetric and time-varying linkages between carbon emissions, globalization, natural resources and financial development in China. Environment, Development and Sustainability 24: 6702–30. [Google Scholar] [CrossRef]
- Majeed, Muhammad Tariq, Isma Samreen, Aisha Tauqir, and Maria Mazhar. 2020. The asymmetric relationship between financial development and CO2 emissions: The case of Pakistan. SN Applied Sciences 2: 1–11. [Google Scholar] [CrossRef]
- Maji, Ibrahim Kabiru, Muzafar Shah Habibullah, and Mohd Yusof Saari. 2017. Financial development and sectoral CO2 emissions in Malaysia. Environmental Science and Pollution Research 24: 7160–76. [Google Scholar] [CrossRef] [PubMed]
- Muhammad, Bashir. 2019. Energy consumption, CO2 emissions and economic growth in developed, emerging and Middle East and North Africa countries. Energy 179: 232–45. [Google Scholar] [CrossRef]
- Nasreen, Samia, Sofia Anwar, and Ilhan Ozturk. 2017. Financial stability, energy consumption and environmental quality: Evidence from south Asian economies. Renewable and Sustainable Energy Reviews 67: 1105–22. [Google Scholar] [CrossRef]
- Newey, Whitney K., and James L. Powell. 1987. Asymmetric least squares estimation and testing. Econometrica 55: 819–47. [Google Scholar] [CrossRef]
- Omoke, Philip C., Silva Opuala-Charles, and Chinazaekpere Nwani. 2020. Symmetric and asymmetric effects of financial development on carbon dioxide emissions in Nigeria: Evidence from linear and nonlinear autoregressive distributed lag analyses. Energy Exploration and Exploitation 38: 2059–78. [Google Scholar] [CrossRef]
- Omri, Anis, Saida Daly, Christophe Rault, and Anissa Chaibi. 2015. Financial development, environmental quality, trade and economic growth: What causes what in MENA countries. Energy Economics 48: 242–52. [Google Scholar] [CrossRef]
- Our World in Data. 2022a. CO2 Emissions. Available online: https://ourworldindata.org/co2-emissions (accessed on 20 December 2022).
- Our World in Data. 2022b. Energy. Available online: https://ourworldindata.org/energy (accessed on 20 December 2022).
- Pesaran, M. Hashem, Yongcheol Shin, and Richard J. Smith. 2001. Bounds Testing Approaches to the Analysis of Level Relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Raihan, Selim, S. R. Osmani, and M. A. Baqui Khalily. 2017. The macro impact of microfinance in Bangladesh: A CGE analysis. Economic Modelling 62: 1–15. [Google Scholar] [CrossRef]
- Ramsey, James Bernard. 1969. Tests for specification errors in classical linear least-squares regression analysis. Journal of the Royal Statistical Society. Series B (Methodological) 31: 350–71. [Google Scholar] [CrossRef]
- Salazar-Núñez, Héctor F., Francisco Venegas-Martínez, and Miguel Á. Tinoco-Zermeño. 2020. Impact of energy consumption and carbon dioxide emissions on economic growth: Cointegrated panel data in 79 countries grouped by income level. International Journal of Energy Economics and Policy 10: 218–26. [Google Scholar] [CrossRef]
- Shah, Syed Ali-Mumtaz H. 2008. Bangladesh Financial Sector: An Agenda for Further Reforms. Manila: Asian Development Bank. Available online: https://www.adb.org/sites/default/files/publication/27528/financial-sector-ban.pdf (accessed on 25 January 2023).
- Shahbaz, Muhammad, Hrushikesh Mallick, Mantu Kumar Mahalik, and Nanthakumar Loganathan. 2015. Does globalization impede environmental quality in India? Ecological Indicators 52: 379–93. [Google Scholar] [CrossRef]
- Shahbaz, Muhammad, Muhammad Ali Nasir, and David Roubaud. 2018. Environmental degradation in France: The effects of FDI, financial development, and energy innovations. Energy Economics 74: 843–57. [Google Scholar] [CrossRef]
- Shahbaz, Muhammad, Qazi Muhammad Adnan Hye, Aviral Kumar Tiwari, and Nuno Carlos Leitão. 2013a. Economic growth, energy consumption, financial development, international trade and CO2 emissions in Indonesia. Renewable and Sustainable Energy Reviews 25: 109–21. [Google Scholar] [CrossRef]
- Shahbaz, Muhammad, Sakiru Adebola Solarin, Haider Mahmood, and Mohamed Arouri. 2013b. Does financial development reduce CO2 emissions in Malaysian economy? A time series analysis. Economic Modelling 35: 145–52. [Google Scholar] [CrossRef]
- Shahbaz, Muhammad, Syed Jawad Hussain Shahzad, Nawaz Ahmad, and Shaista Alam. 2016. Financial development and environmental quality: The way forward. Energy Policy 98: 353–64. [Google Scholar] [CrossRef]
- Shin, Yongcheol, Byungchul Yu, and Matthew Greenwood-Nimmo. 2014. Modelling asymmetric cointegration and dynamic multipliers in a nonlinear ARDL framework. In Festschrift in Honor of Peter Schmidt: Econometric Methods and Applications. Edited by William C. Horrace and Robin C. Sickles. New York: Springer Science and Business Media, pp. 281–314. [Google Scholar]
- Soytas, Ugur, Ramazan Sari, and Bradley T. Ewing. 2007. Energy consumption, income, and carbon emissions in the United States. Ecological Economics 62: 482–89. [Google Scholar] [CrossRef]
- Svirydzenka, Katsiaryna. 2016. Introducing a New Broad-Based Index of Financial Development. Washington, DC: International Monetary Fund, pp. 1–43. [Google Scholar]
- Tamazian, Artur, and B. Bhaskara Rao. 2010. Do economic, financial and institutional developments matter for environmental degradation? Evidence from transitional economies. Energy Economics 32: 137–45. [Google Scholar] [CrossRef]
- Tamazian, Artur, Juan Piñeiro Chousa, and Krishna Chaitanya Vadlamannati. 2009. Does higher economic and financial development lead to environmental degradation: Evidence from BRIC countries. Energy Policy 37: 246–53. [Google Scholar] [CrossRef]
- Uddin, Gazi Salah, Muhammad Shahbaz, Mohamed Arouri, and Frédéric Teulon. 2014. Financial development and poverty reduction nexus: A cointegration and causality analysis in Bangladesh. Economic Modelling 36: 405–12. [Google Scholar] [CrossRef]
- Wald, Abraham. 1945. Sequential tests of statistical hypotheses. The Annals of Mathematical Statistics 16: 117–86. [Google Scholar] [CrossRef]
- World Bank. 2022. World Development Indicators. Washington, DC: The World Bank. Available online: https://databank.worldbank.org/source/world-development-indicators (accessed on 20 December 2022).
- Zhang, Xing-Ping, and Xiao-Mei Cheng. 2009. Energy consumption, carbon emissions, and economic growth in China. Ecological Economics 68: 2706–12. [Google Scholar] [CrossRef]
- Zhang, Yue-Jun. 2011. The impact of financial development on carbon emissions: An empirical analysis in China. Energy Policy 39: 2197–203. [Google Scholar] [CrossRef]



| Variable | C.V. at 1% | Test Statistic |
|---|---|---|
| −3.61 | 0.03 | |
| −3.61 | −8.23 *** | |
| −3.61 | 0.24 | |
| −3.61 | −4.81 *** | |
| −3.62 | 0.20 | |
| −3.62 | −5.08 *** | |
| −3.57 | −2.03 | |
| −3.59 | −3.99 *** | |
| −4.21 | −0.13 | |
| −4.21 | −6.90 *** | |
| −3.54 | 0.22 | |
| −3.54 | −6.96 *** |
| F-test, degrees of freedom = 1, 32 | |||
| F-test statistic | 9.82 *** | ||
| Significance Level | I(0) critical values | I(1) critical values | |
| 10% | 2.26 | 3.35 | |
| 5% | 2.62 | 3.79 | |
| 1% | 3.41 | 4.68 | |
| t-test, degrees of freedom = 36 | |||
| t-test statistic | −7.16 *** | ||
| Significance Level | I(0) critical values | I(1) critical values | |
| 10% | −2.57 | −3.86 | |
| 5% | −2.86 | −4.19 | |
| 1% | −3.43 | −4.79 | |
| Test | D.F. | Test Statistic | C.V. at 5% |
|---|---|---|---|
| Jarque–Bera Normality, χ2-test | 2 | 0.92 | 5.99 |
| Breusch–Godfrey Serial Correlation LM, F-test | (2, 18) | 2.72 | 3.56 |
| Breusch–Pagan–Heteroskedasticity, F-test | (16, 20) | 1.43 | 2.18 |
| Ramsey RESET, F-test | (1, 19) | 1.54 | 4.38 |
| Variable | Coefficient | Standard Error |
|---|---|---|
| Long-Run Equation | ||
| 0.17 *** | 0.04 | |
| 0.12 | 0.11 | |
| 0.81 *** | 0.04 | |
| −0.23 ** | 0.09 | |
| −0.02 | 0.03 | |
| Short-Run Equation | ||
| −0.07 | 0.05 | |
| −0.29 *** | 0.06 | |
| −0.12 | 0.06 | |
| 0.11 | 0.07 | |
| 0.28 *** | 0.08 | |
| 0.30 *** | 0.10 | |
| 0.77 *** | 0.08 | |
| −0.36 | 0.34 | |
| 0.85 | 0.41 | |
| 1.99 *** | 0.52 | |
| −1.34 *** | 0.15 | |
| Wald χ2-test of asymmetry: D.F.= 1with C.V. at 1% = 8.10 and C.V.at 5% = 4.35 | ||
| Long-run χ2-test Statistic | 5.39 ** | |
| Short-run χ2-test | 10.75 *** | |
| Adjusted R-squared | 0.80 | |
| Akaike information Criterion | −4.85 | |
| Number of observations | 37 | |
| NARDL Model | (1, 3, 3, 1, 3, 0) | |
| Coefficient(s) on | χ2--Test Statistic | D.F. | p-Value |
|---|---|---|---|
| Quantile Slope Equality | |||
| Error Correction Term | 3.83 | 2 | 0.203 |
| Positive Partial Cumulative Sums | 1.85 | 8 | 0.985 |
| Negative Partial Cumulative Sums | 4.05 | 8 | 0.852 |
| Symmetric Quantiles | |||
| Error Correction Term | 0.27 | 1 | 0.599 |
| Positive Partial Cumulative Sums | 1.53 | 4 | 0.822 |
| Negative Partial Cumulative Sums | 0.97 | 4 | 0.914 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, A.; Brown, L.; McFarlane, A. Asymmetric Effects of Financial Development on CO2 Emissions in Bangladesh. J. Risk Financial Manag. 2023, 16, 269. https://doi.org/10.3390/jrfm16050269
Das A, Brown L, McFarlane A. Asymmetric Effects of Financial Development on CO2 Emissions in Bangladesh. Journal of Risk and Financial Management. 2023; 16(5):269. https://doi.org/10.3390/jrfm16050269
Chicago/Turabian StyleDas, Anupam, Leanora Brown, and Adian McFarlane. 2023. "Asymmetric Effects of Financial Development on CO2 Emissions in Bangladesh" Journal of Risk and Financial Management 16, no. 5: 269. https://doi.org/10.3390/jrfm16050269






