A Cautionary Note on the Use of Accounting Semi-Identity-Based Models †
Abstract
:“Mistakes and errors are the discipline through which we advance.”William Ellery Channing
“Keynes’s critique of the classical economists was that they had failed to grasp how everything changes when you allow for the fact that output may be demand-constrained. They mistook accounting identities for causal relationships”.
“It is important for those who want to achieve certainty in their research, knowing how to doubt in time”.Aristotle
“Advice to Scott: Avoid Accounting Identities at ALL Costs”.
1. Introduction
2. Literature Review
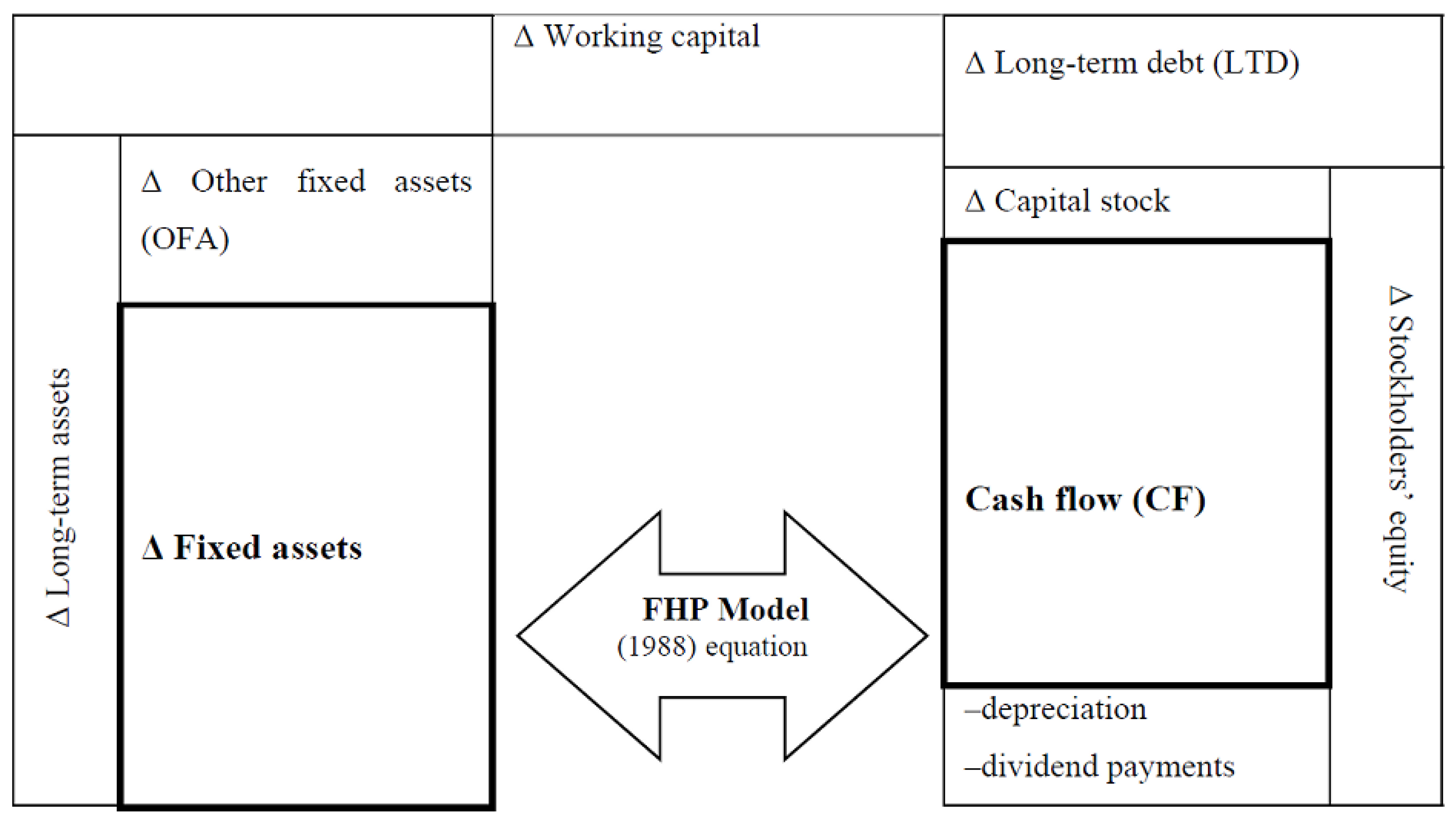
2.1. The FHP Model Is an ASI
2.2. Hypotheses
3. Materials and Methods
3.1. Research Method: Monte Carlo Simulations
3.2. Dataset
3.3. Model
4. Results
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | I contended that this will also depend on the constant, as its magnitude, if positive or negative enough, can have an impact on the overall sum and modify the results. This may also happen when adding another variable, like the Q of the FHP (1988) model. In the end, it is a question of arithmetic, and all the addends should be taken into account. |
| 2 | Again, I resorted to arbitrariness to construct this relation (Carbone 1997). Nevertheless, this example of a simulated model is similar to that which can be found in any basic Handbook of Finance, for example, the Electric Scooter Project example in Brealey and Myers (2003, p. 263). |
| 3 | Replicability is the ability to independently arrive at non-identical but at least similar results when differences in sampling, research procedures, and data analysis methods may exist. The scientific method in economics requires replicability, and its execution varies greatly among research disciplines and fields of study (see Repko 2008). Since I used Stata to produce the data and wanted to make my simulation repeatable, both the syntax and the file are available at: https://figshare.com/articles/dataset/FHP_Model_-_SAI/23112776 (accessed on 22 August 2023). |
| 4 | Results not reported but available under request. |
| 5 | Occam’s Razor is Numquam ponenda est pluralitas sine necessitate (Plurality must never be posited without necessity) (Lombardi 1495). |
References
- Adu-Ameyaw, Emmanuel, Albert Danso, Moshfique Uddin, and Samuel Acheampong. 2022. Investment-cash flow sensitivity: Evidence from investment in identifiable intangible and tangible assets activities. International Journal of Finance & Economics, 1–26. [Google Scholar] [CrossRef]
- Ağca, Şenay, and Abon Mozumdar. 2017. Investment–cash flow sensitivity: Fact or fiction? Journal of Financial and Quantitative Analysis 52: 1111–41. [Google Scholar] [CrossRef]
- Bhabra, Gurmeet Singh, Parvinder Kaur, and Ahn Seoungpil. 2018. Corporate governance and the sensitivity of investments to cash flows. Accounting & Finance 58: 367–96. [Google Scholar] [CrossRef]
- Brealey, Richard A., and Stewart C. Myers. 2003. Principles of Corporate Finance. New York: Hill Higher Education. [Google Scholar]
- Brown, James R., and Bruce Petersen. 2009. Why has the investment-cash flow sensitivity declined so sharply? Rising R&D and equity market developments. Journal of Banking & Finance 33: 971–84. [Google Scholar] [CrossRef]
- Carbone, Enrica. 1997. Discriminating between preference functionals: A Monte Carlo study. Journal of Risk and Uncertainty 15: 29–54. [Google Scholar] [CrossRef]
- Carpenter, Robert E., and Alessandra Guariglia. 2008. Cash flow, investment, and investment opportunities: New tests using UK panel. Journal of Banking and Finance 32: 1894–906. [Google Scholar] [CrossRef]
- Chen, Huafeng Jason, and Shaojun Jenny Chen. 2012. Investment-cash flow sensitivity cannot be a good measure of financial constraints: Evidence from the time series. Journal of Financial Economics 103: 393–410. [Google Scholar] [CrossRef]
- Chen, Xin, Yong Sun, and Xiadong Xu. 2016. Free cash flow, over-investment and corpo-rate governance in China. Pacific-Basin Finance Journal 37: 81–103. [Google Scholar] [CrossRef]
- Christodoulou, Demetris, and Stuart Mcleay. 2019. The double entry structural constraint on the econometric estimation of accounting variables. The European Journal of Finance 25: 1919–35. [Google Scholar] [CrossRef]
- Cleary, Sean. 1999. The relationship between firm investment and financial status. The Journal of Finance 54: 673–92. [Google Scholar] [CrossRef]
- Currie, David A. 1976. Some criticisms of the monetary analysis of balance of payments correction. The Economic Journal 86: 508–22. [Google Scholar] [CrossRef]
- De Mesnard, Louis. 2023. Input-output price indexes: Forgoing the Leontief and Ghosh models. Economic Systems Research, 1–25. [Google Scholar] [CrossRef]
- Dorman, Peter. 2007. Low Savings or a High Trade Deficit?: Which Tail Is Wagging Which? Challenge 50: 49–64. [Google Scholar] [CrossRef]
- Farooq, Umar, Mosab I. Tabash, Ahmad A. Al-Naimi, and Krzysztof Drachal. 2022. Corporate Investment Decision: A Review of Literature. Journal of Risk and Financial Management 15: 611. [Google Scholar] [CrossRef]
- Farris, Paul W., Mark E. Parry, and Frederick Webster. 1989. Accounting for the Market Share-ROI Relationship. New York: Marketing Science Institute. Available online: https://www.msi.org/working-papers/accounting-for-the-market-shareroi-relationship/ (accessed on 22 August 2023).
- Fazzari, Steven, R. Glenn Hubbard, and Bruce Petersen. 1988. Financing Constraints and Corporate Investment. Cambridge: National Bureau of Economic Research. [Google Scholar] [CrossRef]
- Felipe, Jesus, and Carsten Holz. 2001. Why do Aggregate Production Functions Work? Fisher’s simulations, Shaikh’s identity and some new results. International Review of Applied Economics 15: 261–85. [Google Scholar] [CrossRef]
- Felipe, Jesus, and John S. L. McCombie. 2001. The CES production function, the accounting identity, and Occam’s razor. Applied Economics 33: 1221–32. [Google Scholar] [CrossRef]
- Felipe, Jesus, and John S. L. McCombie. 2009. Are estimates of labour demand functions mere statistical artefacts? International Review of Applied Economics 23: 147–68. [Google Scholar] [CrossRef]
- Felipe, Jesus, and John S. L. McCombie. 2020. The illusions of calculating total factor productivity and testing growth models: From Cobb-Douglas to Solow and Romer. Journal of Post Keynesian Economics 43: 470–513. [Google Scholar] [CrossRef]
- Felipe, Jesus, John S. L. McCombie, Aashish Sunil Mehta, and Donna Faye Bajaro. 2021. Production Function Estimation: Biased Coefficients and Endogenous Regressors, or a Case of Collective Amnesia? Available online: https://ssrn.com/abstract=3857565 (accessed on 22 August 2023).
- Felipe, Jesus, Rana Hasan, and John S. L. Mccombie. 2008. Correcting for biases when estimating production functions: An illusion of the laws of algebra? Cambridge Journal of Economics 32: 441–59. [Google Scholar] [CrossRef]
- Fisher, Franklin M. 1971. Aggregate production functions and the explanation of wages: A simulation experiment. The Review of Economics and Statistics 53: 305–25. [Google Scholar] [CrossRef]
- Fisher, Franklin M., Robert M. Solow, and James M. Kearl. 1977. Aggregate production functions: Some CES experiments. The Review of Economic Studies 44: 305–20. [Google Scholar] [CrossRef]
- Gautam, Vikash, and Rajendra R. Vaidya. 2018. Evidence on the determinants of investment-cash flow sensitivity. Indian Economic Review 53: 229–44. [Google Scholar] [CrossRef]
- Giles, A. Judith, and Cara L. Williams. 2000. Export-led growth: A survey of the empirical literature and some non-causality results. Part 1. The Journal of International Trade & Economic Development 9: 261–337. [Google Scholar] [CrossRef]
- Glasner, David. 2012. Advice to Scott: Avoid Accounting Identities at ALL Costs. Available online: https://uneasymoney.com/2012/01/22/advice-to-scott-avoid-accounting-identities-at-all-costs/ (accessed on 22 August 2023).
- Guariglia, Alessandra. 2008. Internal financial constraints, external financial constraints, and investment choice: Evidence from a panel of UK firms. Journal of Banking and Finance 32: 1795–809. [Google Scholar] [CrossRef]
- Gujarati, Damodar N., and Dawn C. Porter. 2013. Basic Econometrics. New York: McGraw-Hill Irwin. [Google Scholar]
- Intriligator, Michael D. 1978. Econometric Models, Techniques and Applications. Upper Saddle River: Prentice-Hall. [Google Scholar]
- Jensen, Michael C. 1986. Agency costs of free cash flow, corporate finance, and takeovers. The American Economic Review 76: 323–29. [Google Scholar]
- Kabbach-de-Castro, Luiz Ricardo, Aquiles Elie Guimarães Kalatzis, and Aline Damasceno Pellicani. 2022a. Do financial constraints in an unstable emerging economy mitigate the opportunistic behavior of entrenched family owners? Emerging Markets Review 50: 100838. [Google Scholar] [CrossRef]
- Kabbach-de-Castro, Luiz Ricardo, Henrique Castro Martins, Eduardo Schiehll, and Paulo R. S. Terra. 2022b. Investment-cash flow sensitivity and investor protection. Journal of Business Finance & Accounting 50: 1402–38. [Google Scholar] [CrossRef]
- Kaplan, Steven N., and Luigi Zingales. 1997. Do investment-cash flow sensitivities provide useful measures of financing constraints? The Quarterly Journal of Economics 112: 169–215. [Google Scholar] [CrossRef]
- Kaplan, Steven N., and Luigi Zingales. 2000. Investment-cash flow sensitivities are not valid measures of financing constraints. The Quarterly Journal of Economics 115: 707–12. [Google Scholar] [CrossRef]
- Kashefi-Pour, Eilnaz, Shima Amini, Moshfique Uddin, and Darren Duxbury. 2020. Does cultural difference affect investment–Cash flow sensitivity? Evidence from OECD countries. British Journal of Management 31: 636–58. [Google Scholar] [CrossRef]
- Krugman, Paul. 2011. Mr Keynes and the Moderns. Available online: https://cepr.org/voxeu/columns/mr-keynes-and-moderns (accessed on 22 August 2023).
- Lambelet, Jean-Christian, and Kurt Schiltknecht. 1970. A Short-Term Forecasting Model of the Swiss Economy. Berlin: Institut für Wirtschaftsforschung. [Google Scholar]
- Lewellen, Jonathan, and Katharina Lewellen. 2016. Investment and cash flow: New evidence. Journal of Financial and Quantitative Analysis 51: 1135–64. [Google Scholar] [CrossRef]
- Lombardi, Petri. 1495. Ockham W. Quaestiones et Decisiones in Quattuor Libros Sententiarum. Lyon: Lugduni Johannes Trechsel. [Google Scholar]
- Machokoto, Michael, Umair Tanveer, Shamaila Ishaq, and Geofry Areneke. 2021. Decreasing investment-cash flow sensitivity: Further UK evidence. Finance Research Letters 38: 101397. [Google Scholar] [CrossRef]
- Marin, Dalia. 1992. Is the export-led growth hypothesis valid for industrialized countries? The Review of Economics and Statistics, 678–88. [Google Scholar] [CrossRef]
- Maskay, Nephil Matangi, Sven Steinkamp, and Frank Westermann. 2018. Do foreign currency accounts help relax credit constraints? Evidence from Nepal. Pacific Economic Review 23: 464–89. [Google Scholar] [CrossRef]
- Mattei, Aurelio. 1976. A consistent estimation of a short-term forecasting model of the Swiss economy. Empirical Economics 1: 217–30. [Google Scholar] [CrossRef]
- McCallum, John. 1995. National borders matter: Canada-US regional trade patterns. The American Economic Review 85: 615–23. Available online: https://www.jstor.org/stable/2118191 (accessed on 22 August 2023).
- Minenna, Marcello. 2022. Target 2 determinants: The role of Balance of Payments imbalances in the long run. Journal of Banking & Finance 140: 106059. [Google Scholar] [CrossRef]
- Moshirian, Fariborz, Vikram Nanda, Alexander Vadilyev, and Bohui Zhang. 2017. What drives investment–cash flow sensitivity around the World? An asset tangibility Perspective. Journal of Banking & Finance 77: 1–17. [Google Scholar]
- Peters, Ryan H., and Lucian A. Taylor. 2017. Intangible capital and the investment-q relation. Journal of Financial Economics 123: 251–72. [Google Scholar] [CrossRef]
- Repko, Allen F. 2008. Interdisciplinary Research: Process and Theory. Thousand Oaks: Sage Publications. [Google Scholar]
- Sanchez-Vidal, F. Javier. 2007. The Problem of Estimating Models Using Accounting Semi Identities. IVIE Working Paper. Available online: https://www.ivie.es/downloads/docs/wpasec/wpasec-2007-06.pdf (accessed on 22 August 2023).
- Shaikh, Anwar. 1974. Laws of production and laws of algebra: The humbug production function. The Review of Economics and Statistics 56: 115–20. [Google Scholar] [CrossRef]
- Simon, Herbert A. 1979. Rational decision making in business organizations. Nobel Memorial Lecture, December 8. [Google Scholar]
- Tettamanzi, Patrizia, Valentina Minutiello, and Michael Murgolo. 2023. Accounting education and digitalization: A new perspective after the pandemic. The International Journal of Management Education 3: 100847. [Google Scholar] [CrossRef]
- Wang, Xuan. 2023. Discussion of “The Asymmetric Impact of COVID-19: A Novel Approach to Quantifying Financial Distress across Industries”. European Economic Review 157: 104501. [Google Scholar] [CrossRef] [PubMed]
- Wang, Xun. 2022. Financial liberalization and the investment-cash flow sensitivity. Journal of International Financial Markets, Institutions and Money 77: 101527. [Google Scholar] [CrossRef]
- Wirkierman, Ariel Luis. 2023. Structural economic dynamics in actual industrial economies. Structural Change and Economic Dynamics 64: 245–62. [Google Scholar] [CrossRef]
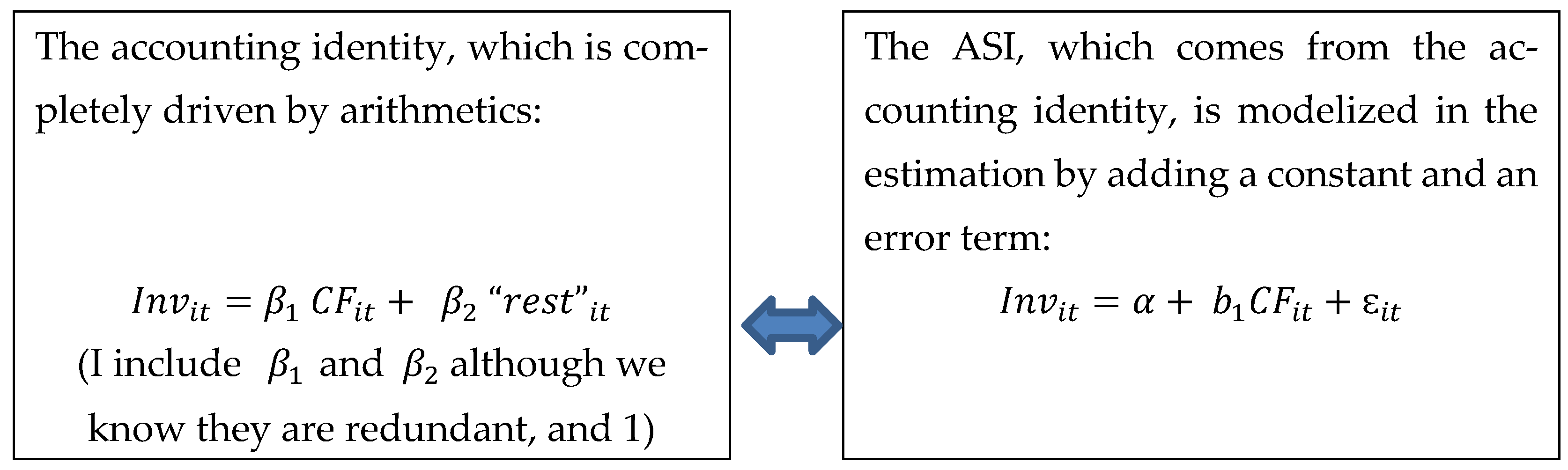
| Variable | Coef. | t |
|---|---|---|
| cash flow | 1.000 | ∞ *** |
| “rest” | 1.000 | ∞ *** |
| constant | 0.000 | ∞ *** |
| R2 | 1.000 |
| Cash Flows | Q | Investments | “Rest” | |
|---|---|---|---|---|
| Mean | 0.25 | 2.45 | 0.19 | −0.06 |
| Standard deviation | 0.10 | 0.20 | 0.11 | 0.12 |
| Whole Sample | Subsample Negative “Rest” | Subsample Positive “Rest” | Whole Sample | |||||
|---|---|---|---|---|---|---|---|---|
| Coef. | t | Coef. | t | Coef. | t | Coef. | t | |
| Cash flow | 0.452 *** (0.005) | 100.84 | 0.688 *** (0.004) | 161.85 | 0.824 *** (0.005) | 161.32 | 0.502 *** (0.003) | 150.41 |
| Dummy posit. “rest” × Cash flow | 0.666 *** (0.003) | 201.55 | ||||||
| Constant | 0.074 *** (0.001) | 61.14 | −0.033 *** (0.004) | −26.89 | 0.105 *** (0.001) | 96.08 | 0.024 *** (0.001) | 25.47 |
| R2 | 0.169 | 0.425 | 0.641 | 0.542 | ||||
| N | 50000 | 35484 | 14516 | 50000 | ||||
| I | II | III | IV | |||||
|---|---|---|---|---|---|---|---|---|
| Variable | Coef. | t | Coef. | t | Coef. | t | Coef. | t |
| cash flow | 1.500 *** (0.0013) | 1115.05 | 1.003 *** (0.005) | 201.99 | 0.461 *** (0.005) | 101.23 | 0.452 *** (0.005) | 100.99 |
| Q | −0.000 (0.0004) | −0.70 | 0.007 *** (0.002) | 3.39 | 0.031 *** (0.002) | 14.02 | 0.031 *** (0.002) | 14.00 |
| constant | 0.000 (0.0011) | 0.64 | 0.039 *** (0.005) | 8.01 | −0.006 (0.006) | −0.99 | −0.003 (0.006) | −0.47 |
| N | 187 | 12,309 | 49,651 | 50,000 | ||||
| Adj-R2 | 0.999 | 0.769 | 0.174 | 0.172 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Vidal, F.J. A Cautionary Note on the Use of Accounting Semi-Identity-Based Models. J. Risk Financial Manag. 2023, 16, 389. https://doi.org/10.3390/jrfm16090389
Sánchez-Vidal FJ. A Cautionary Note on the Use of Accounting Semi-Identity-Based Models. Journal of Risk and Financial Management. 2023; 16(9):389. https://doi.org/10.3390/jrfm16090389
Chicago/Turabian StyleSánchez-Vidal, Francisco Javier. 2023. "A Cautionary Note on the Use of Accounting Semi-Identity-Based Models" Journal of Risk and Financial Management 16, no. 9: 389. https://doi.org/10.3390/jrfm16090389






