On the Realized Risk of Foreign Exchange Rates: A Fractal Perspective
Abstract
:“There are strong pragmatic reasons to begin the study of economic distributions and time series by those that satisfy the law of Pareto.”(Benoit Mandelbrot, mathematician known for the Theory of Roughness and Fractals)
1. Introduction
2. Data
3. Methodology
3.1. Estimating Power Law Exponents Using Maximum Likelihood Estimation
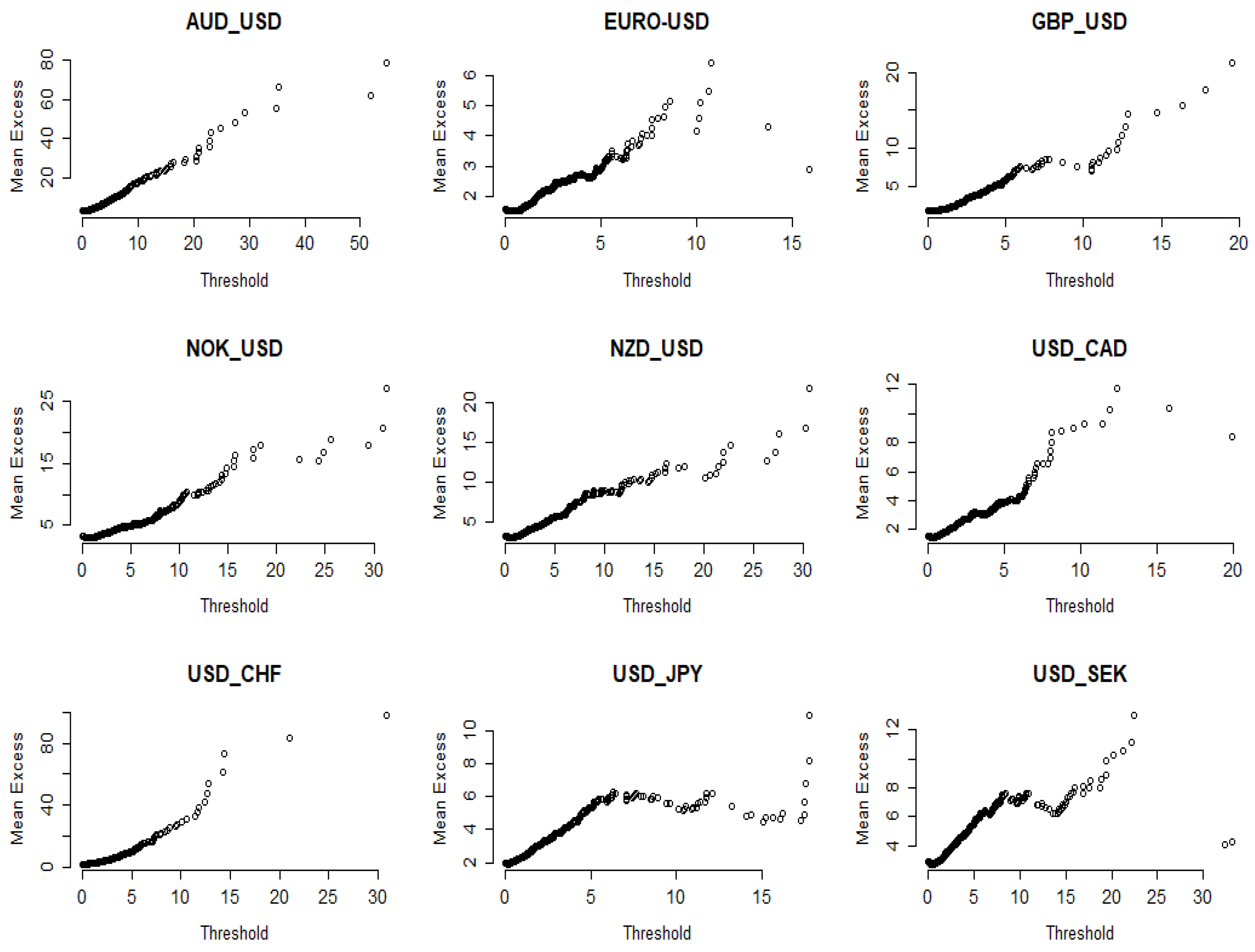
3.2. Testing the Power Law Model
3.3. An Empirical Comparison of Distributions
3.4. Robustness Checks
4. Discussion and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Panel A | ||||||
| Distribution | NPL | 95% CI | ||||
| AUD/USD | 2.4139 | 0.1666 | 6.2002 | 0.0545 | 15.65% | [2.0873, 2.7405] |
| EUR/USD | 2.4325 | 0.0934 | 1.3364 | 0.0691 | 51.09% | [2.2493, 2.6156] |
| GBP/USD | 2.5637 | 0.1196 | 1.4831 | 0.0416 | 37.17% | [2.3293, 2.7981] |
| NOK/USD | 3.2158 | 0.2432 | 6.0219 | 0.0553 | 18.04% | [2.7391, 3.6926] |
| NZD/USD | 2.4391 | 0.1085 | 3.4412 | 0.0582 | 38.26% | [2.2265, 2.6518] |
| USD/CAD | 3.0643 | 0.2522 | 3.8276 | 0.0632 | 14.57% | [2.5700, 3.5586] |
| USD/CHF | 2.7203 | 0.1640 | 2.9686 | 0.0462 | 23.91% | [2.3989, 3.0418] |
| USD/JPY | 2.4901 | 0.1268 | 2.3796 | 0.0452 | 30.00% | [2.2415, 2.7387] |
| USD/SEK | 2.3217 | 0.1058 | 3.2904 | 0.0736 | 33.91% | [2.1143, 2.5291] |
| Panel B | ||||||
| Distribution | NPL | 95% CI | ||||
| AUD/USD | 3.3773 | 0.2389 | 3.0557 | 0.0453 | 21.52% | [2.9090, 3.8456] |
| EUR/USD | 2.7133 | 0.1342 | 1.1669 | 0.0481 | 35.43% | [2.4503, 2.9764] |
| GBP/USD | 2.7723 | 0.1682 | 2.0690 | 0.0476 | 24.13% | [2.4426, 3.1020] |
| NOK/USD | 2.8486 | 0.1591 | 3.1635 | 0.0389 | 29.34% | [2.5367, 3.1604] |
| NZD/USD | 3.1287 | 0.2139 | 2.9721 | 0.0732 | 21.52% | [2.7094, 3.5481] |
| USD/CAD | 3.0508 | 0.1772 | 1.2762 | 0.0650 | 29.13% | [2.7036, 3.3981] |
| USD/CHF | 3.0085 | 0.1804 | 1.3947 | 0.0474 | 26.95% | [2.6550, 3.3620] |
| USD/JPY | 2.8305 | 0.2538 | 3.2205 | 0.0528 | 11.30% | [2.3330, 3.3281] |
| USD/SEK | 3.4147 | 0.2491 | 3.0119 | 0.0689 | 20.43% | [2.9266, 3.9029] |
| 1 | See https://www.statista.com/statistics/247328/activity-per-trading-day-on-the-global-currency-market/ (accessed on 1 January 2023). |
| 2 | Other related studies are Alexander (1995) and Bauwens et al. (2005), who used (G)ARCH-type models to explore common volatility in the foreign exchange rate market as well as the impact of scheduled and unscheduled news announcements on foreign exchange rate return volatility. |
| 3 | Note that for the sake of readability, we skip in our notation here the index j denoting the week. |
References
- Alexander, Carol O. 1995. Common volatility in the foreign exchange market. Applied Financial Economics 5: 1–10. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, and Francis X. Diebold. 2005. Roughing It Up: Including Jump Components in the Measurement, Modelling and Forecasting of Return Volatility. NBER Working Paper No. 11775. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Andersen, Torben G., Tim Bollerslev, and Nour Meddahi. 2004. Analytical evaluation of volatility forecasts. International Economic Review 45: 1079–110. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Heiko Ebens. 2001a. The distribution of realized stock return volatility. Journal of Financial Economics 61: 43–76. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys. 2001b. The distribution of realized exchange rate volatility. Journal of the American Statistical Association 96: 42–55. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys. 2003. Modeling and forecasting realized volatility. Econometrica 71: 579–625. [Google Scholar] [CrossRef]
- Baillie, Richard T., and Tim Bollerslev. 1991. Intra-day and inter-market volatility in foreign exchange rates. Review of Economic Studies 58: 565–85. [Google Scholar] [CrossRef]
- Bauwens, Luc, Walid Ben Omrane, and Pierre Giot. 2005. News announcements, market activity and volatility in the euro/dollar foreign exchange market. Journal of International Money and Finance 24: 1108–25. [Google Scholar] [CrossRef]
- Bollerslev, Tim, and Michael Melvin. 1994. Bid—Ask spreads and volatility in the foreign exchange market: An empirical analysis. Journal of International Economics 36: 355–72. [Google Scholar] [CrossRef]
- Bubák, Vít, Evžen Kočenda, and Filip Žikeš. 2011. Volatility transmission in emerging European foreign exchange markets. Journal of Banking and Finance 35: 2829–41. [Google Scholar] [CrossRef]
- Calvet, Laurent E., and Adlai J. Fisher. 2004. Regime-switching and the estimation of multifractal processes. Journal of Financial Econometrics 2: 44–83. [Google Scholar] [CrossRef]
- Clauset, Aaron, Cosma Rohilla Shalizi, and Mark E. J. Newman. 2009. Power law distributions in empirical data. SIAM Review 51: 661–703. [Google Scholar] [CrossRef]
- Corsi, Fulvio. 2004. A Simple Long Memory Model of Realized Volatility. Working Paper. Lugano: Institute of Finance, University of Lugano. [Google Scholar]
- Corsi, Fulvio, Stefan Mittnik, Christian Pigorsch, and Uta Pigorsch. 2008. The volatility of realized volatility. Econometric Reviews 27: 46–78. [Google Scholar] [CrossRef]
- Embrechts, Paul, Claudia Klüppelberg, and Thomas Mikosch. 1997. Modelling Extremal Events for Insurance and Finance. New York: Springer. [Google Scholar]
- Fama, Eugene F. 1963. Mandelbrot and the stable Paretian hypothesis. Journal of Business 36: 420–29. [Google Scholar] [CrossRef]
- Gabaix, Xavier, and Rustam Ibragimov. 2011. Rank—1/2: A simple way to improve the OLS estimation of tail exponents. Journal of Business and Economic Statistics 29: 24–39. [Google Scholar] [CrossRef]
- Grobys, Klaus. 2021. What do we know about the second moment of financial markets? International Review of Financial Analysis 78: 101891. [Google Scholar] [CrossRef]
- Grobys, Klaus. 2023. Correlation versus co-fractality: Evidence from foreign-exchange-rate variances. International Review of Financial Analysis 86: 102531. [Google Scholar] [CrossRef]
- Grobys, Klaus, James W. Kolari, and Niranjan Sapkota. 2021. On the stability of stablecoins. Journal of Empirical Finance 64: 207–23. [Google Scholar] [CrossRef]
- Hamermesh, Daniel S. 2007. Viewpoint: Replication in economics. Canadian Journal of Economics 40: 715–33. [Google Scholar] [CrossRef]
- Hou, Kewei, Chen Xue, and Lu Zhang. 2020. Replicating anomalies. Review of Financial Studies 33: 2019–133. [Google Scholar] [CrossRef]
- Ibragimov, Marat, Rustam Ibragimov, and Paul Kattuman. 2013. Emerging markets and heavy tails. Journal of Banking and Finance 37: 2546–59. [Google Scholar] [CrossRef]
- Jorion, Philippe. 1995. Predicting volatility in the foreign exchange market. Journal of Finance 50: 507–28. [Google Scholar] [CrossRef]
- Lux, Thomas, Leonardo Morales-Arias, and Cristina Sattarhoff. 2014. A Markov-switching multifractal approach to forecasting realized volatility. Journal of Forecasting 33: 532–41. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit B. 1963. The variation of certain speculative prices. Journal of Business 36: 394–419. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit B. 2008. The (Mis)behavior of Markets. A Fractal View of Risk, Ruin and Reward. London: Profile Books. [Google Scholar]
- Renò, Roberto, and Rosario Rizza. 2003. Is volatility lognormal? Evidence from Italian futures. Physica A: Statistical Mechanics and Its Applications 322: 620–28. [Google Scholar] [CrossRef]
- Serra-Garcia, Marta, and Uri Gneezy. 2021. Nonreplicable publications are cited more than replicable ones. Science Advances 7: 1705. [Google Scholar] [CrossRef]
- Taleb, Nassim Nicholas. 2020. Statistical Consequences of Fat Tails: Real World Preasymptotics, Epistemology, and Applications. Papers and Commentary, STEM. Cambridge: Academic Press. [Google Scholar]
- Wang, Jianxin, and Minxian Yang. 2009. Asymmetric volatility in the foreign exchange markets. Journal of International Financial Markets, Institutions and Money 19: 597–615. [Google Scholar] [CrossRef]
- White, Ethan P., Brian J. Enquist, and Jessica L. Green. 2008. On estimating the exponent of power law frequency distributions. Ecology 89: 905–12. [Google Scholar] [CrossRef]
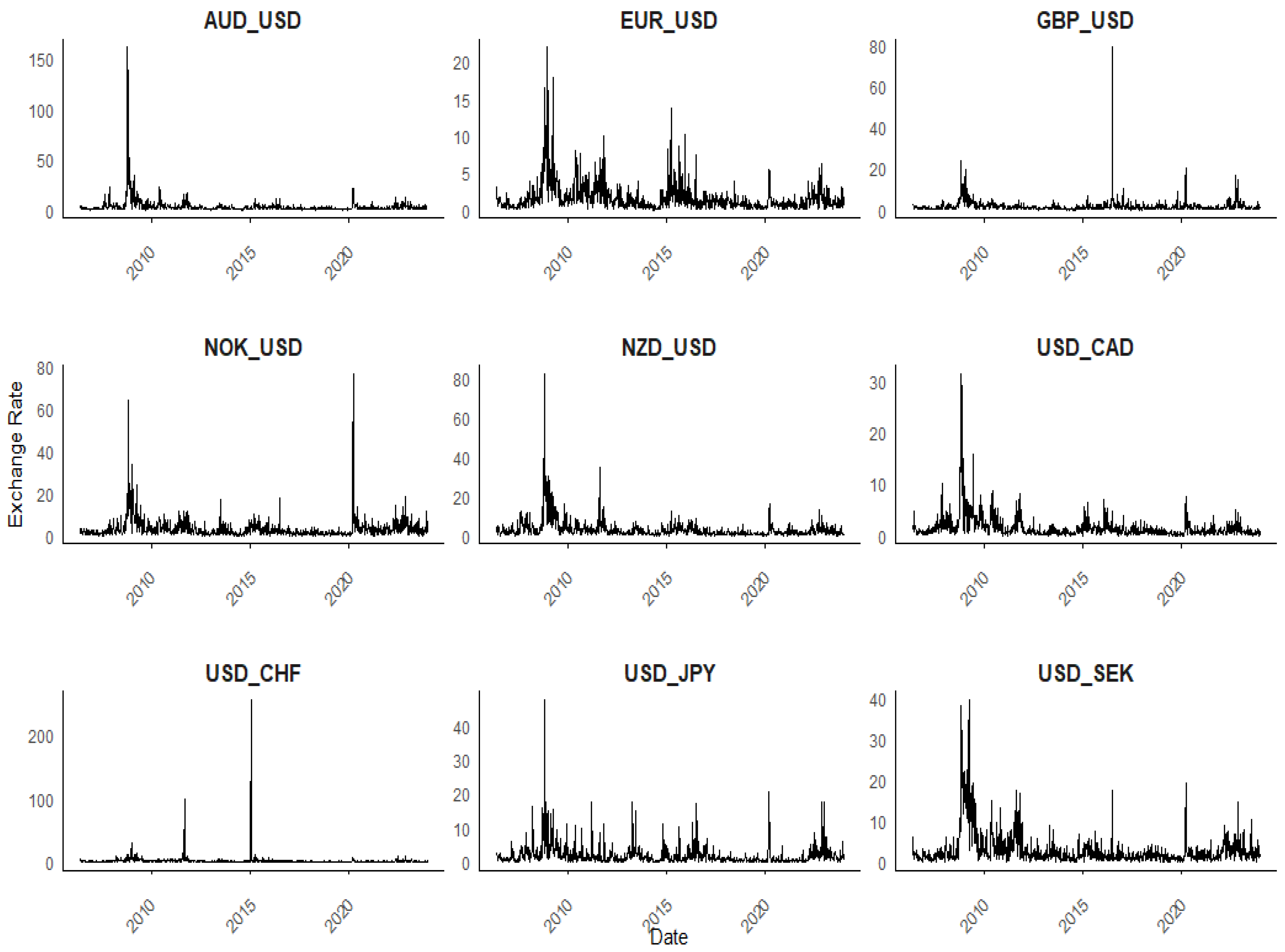



| AUD/USD | EUR/USD | GBP/USD | NOK/USD | NZD/USD | USD/CAD | USD/CHF | USD/JPY | USD/SEK | |
|---|---|---|---|---|---|---|---|---|---|
| Mean | 3.3170 | 1.6138 | 1.8063 | 3.2683 | 3.2357 | 1.5839 | 2.1195 | 1.9851 | 2.9710 |
| Median | 1.6427 | 1.0225 | 1.1017 | 1.9579 | 1.8758 | 0.9303 | 1.0874 | 1.0876 | 1.7309 |
| Std.Dev. | 8.7209 | 1.9674 | 3.3995 | 4.8487 | 4.8140 | 2.3482 | 9.2697 | 3.1163 | 4.0658 |
| Kurtosis | 187.8401 | 27.0404 | 289.4048 | 90.3521 | 91.2411 | 64.0870 | 618.1327 | 57.6324 | 25.8182 |
| Skewness | 12.3553 | 4.1499 | 13.9099 | 7.5595 | 7.2678 | 6.5452 | 23.5305 | 5.7512 | 4.3111 |
| Minimum | 0.0676 | 0.0333 | 0.0427 | 0.0398 | 0.0641 | 0.0230 | 0.0081 | 0.0155 | 0.0870 |
| Maximum | 161.8294 | 21.9666 | 78.6839 | 77.0604 | 82.8622 | 31.4039 | 255.0862 | 47.5975 | 39.5884 |
| Obs | 920 | 920 | 920 | 920 | 920 | 920 | 920 | 920 | 920 |
| Distribution | NPL | 95% CI | ||||
|---|---|---|---|---|---|---|
| AUD/USD | 2.4834 | 0.0911 | 2.9452 | 0.0242 | 28.80% | [2.3048, 2.6620] |
| EUR/USD | 3.5968 | 0.3126 | 4.3242 | 0.0497 | 7.50% | [2.9841, 4.2095] |
| GBP/USD | 2.6704 | 0.1092 | 1.9530 | 0.0319 | 25.43% | [2.4563, 2.8844] |
| NOK/USD | 3.1845 | 0.1978 | 6.1729 | 0.0389 | 13.26% | [2.7968, 3.5721] |
| NZD/USD | 2.8648 | 0.1617 | 5.4697 | 0.0509 | 14.46% | [2.5479, 3.1818] |
| USD/CAD | 2.5048 | 0.0869 | 1.4408 | 0.0535 | 32.61% | [2.3345, 2.6751] |
| USD/CHF | 2.7312 | 0.1256 | 2.4059 | 0.0275 | 20.65% | [2.4851, 2.9774] |
| USD/JPY | 2.5888 | 0.1276 | 3.0011 | 0.0485 | 16.85% | [2.3387, 2.8390] |
| USD/SEK | 2.5553 | 0.1019 | 3.2868 | 0.0462 | 25.33% | [2.3556, 2.7550] |
| Power Law | Lognormal | Exponential | |
|---|---|---|---|
| EUR/USD | 0.96 | 0.05 | 0.00 |
| AUD/USD | 0.76 | 0.40 | 0.08 |
| GBP/USD | 0.64 | 0.38 | 0.14 |
| NOK/USD | 0.86 | 0.60 | 0.00 |
| NZD/USD | 0.30 | 0.90 | 0.10 |
| USD/CAD | 0.00 | 0.46 | 0.00 |
| USD/CHF | 0.98 | 0.26 | 0.44 |
| USD/JPY | 0.16 | 0.64 | 0.32 |
| USD/SEK | 0.04 | 0.86 | 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathi, M.; Grobys, K.; Kolari, J.W. On the Realized Risk of Foreign Exchange Rates: A Fractal Perspective. J. Risk Financial Manag. 2024, 17, 79. https://doi.org/10.3390/jrfm17020079
Fathi M, Grobys K, Kolari JW. On the Realized Risk of Foreign Exchange Rates: A Fractal Perspective. Journal of Risk and Financial Management. 2024; 17(2):79. https://doi.org/10.3390/jrfm17020079
Chicago/Turabian StyleFathi, Masoumeh, Klaus Grobys, and James W. Kolari. 2024. "On the Realized Risk of Foreign Exchange Rates: A Fractal Perspective" Journal of Risk and Financial Management 17, no. 2: 79. https://doi.org/10.3390/jrfm17020079
APA StyleFathi, M., Grobys, K., & Kolari, J. W. (2024). On the Realized Risk of Foreign Exchange Rates: A Fractal Perspective. Journal of Risk and Financial Management, 17(2), 79. https://doi.org/10.3390/jrfm17020079







