Action-Based Fiscal Consolidations and Economic Growth
Abstract
:1. Introduction
2. Related Literature
3. Data and Estimation Framework for: Are Action-Based Fiscal Consolidations Exogenous?
3.1. Data
3.1.1. Action-Based Fiscal Consolidations
“We examine policymakers’ intentions and actions as described in contemporaneous policy documents, and identify measures motivated primarily by deficit reduction…Following Romer and Romer (2010), we use the contemporaneous estimates contained in these sources since retrospective estimates are rarely available.”
3.1.2. Exogenous Variables
3.1.3. Descriptive Statistics
3.2. Estimation Framework
4. Empirical Results for: Are Action-Based Fiscal Consolidations Exogenous?
4.1. Contemporaneous Effects of Temperature Changes
4.2. Contemporaneous Effects of GDP Growth of Trading Partners
4.3. Contemporaneous Effects of an International Commodity Price Index
5. Estimation Framework: Identification of a Simultaneous System of Two Equations
- (1)
- FiscalConsolidation = αGDPGrowth + u,
- (2)
- GDPGrowth = β*FiscalConsolidation + e,
- (I)
- βLS = β + cov(FiscalConsolidation,u) = β + α(1 − α β)−1σ2(e)/σ2(F),
- (2’)
- GDPGrowth = β*FiscalConsolidation + φZ + e’
- (II)
- βIV = cov(ures,GDPGrowth)/cov(ures,FiscalConsolidation)= β + cov(ures,e)/cov(ures,FiscalConsolidation)= β + cov(u,e)/cov(u,FiscalConsolidation)= β
6. Instrumental Variables’ Estimates of the Simultaneous System of Equations
6.1. The Contemporaneous Effect of GDP Growth on Fiscal Consolidations
6.1.1. Overidentified Model
6.1.2. Just-Identified Model
6.1.3. Tests for Direct Effects of the Instruments on Fiscal Consolidations
6.1.4. A Dynamic Simultaneous System of Equations
- (1)
- FiscalConsolidationit = ai + bt + αGDPGrowthit + Γ1Xit−1 + Γ2Xit−2 + uit
- (2)
- GDPGrowthit = ci + dt + βFiscalConsolidationit + Π1Xit−1 + Π1Xit−2 + ΘZit + eit
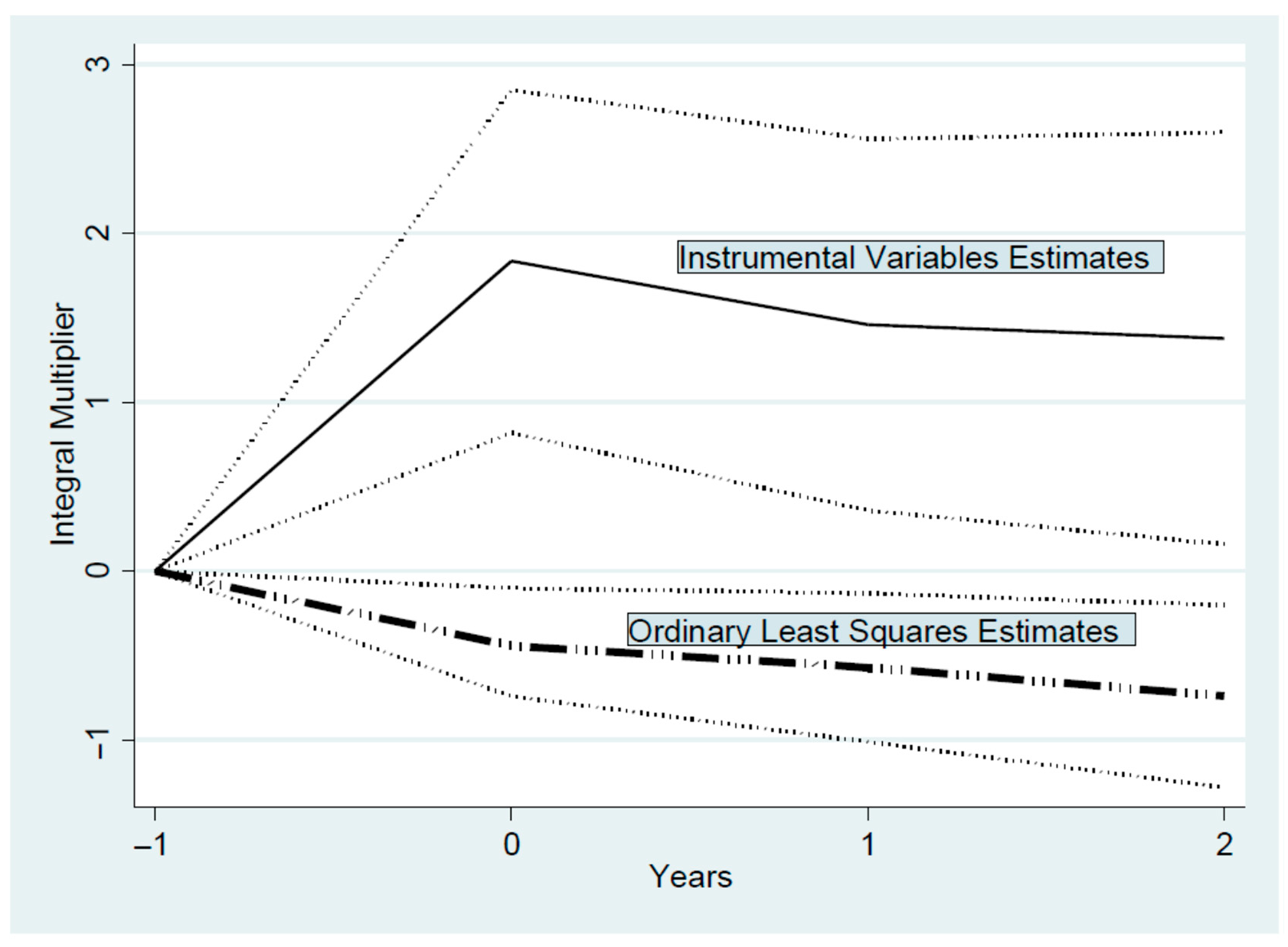
6.1.5. Integral Multipliers
- (1)
- FiscalConsolidation(h)it = ai + bt + αhGDPGrowth(h)it + Γ1Xit−1 + Γ2Xit−2 + uit
- (2)
- GDPGrowth(h)it = ci + dt + βhFiscalConsolidation(h)it + Π1Xit−1 + Π1Xit−2 + ΘZ(h)it + eit
- i.
- For h = 0, a one standard deviation (equivalent to 4.2) increase in contemporaneous GDP growth over a horizon of one year reduces the magnitude of a fiscal consolidation over a horizon of one year by about 0.3 percent of GDP. This is equivalent to about 0.5 standard deviations.
- ii.
- For h = 1, a one standard deviation (equivalent to 7.2) increase in contemporaneous GDP growth over a horizon of two years reduces the magnitude of a fiscal consolidation over a horizon of two years by 0.5 percent of GDP. This is equivalent to about 0.4 standard deviations.
- iii.
- For h = 2, a one standard deviation (equivalent to 9.5) increase in contemporaneous GDP growth over a horizon of three years reduces the magnitude of a fiscal consolidation over a horizon of three years by 0.7 percent of GDP. This is equivalent to about 0.5 standard deviations.
6.2. The Response of GDP Growth to Fiscal Consolidations
6.3. Mechanisms
7. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Variable | Source | Mean | Std. Dev. | Obs. |
|---|---|---|---|---|
| Fiscal Consolidation | DeVries et al. (2011); David and Leigh (2018) | 0.32 | 0.74 | 1016 |
| Tax-based | DeVries et al. (2011); David and Leigh (2018) | 0.15 | 0.44 | 984 |
| Expenditure-based | DeVries et al. (2011); David and Leigh (2018) | 0.16 | 0.44 | 984 |
| Temperature Change | FAOSTAT (2021) | 0.68 | 0.6 | 994 |
| Temperature Change | Dell et al. (2012) | 0.03 | 0.65 | 745 |
| GDP Growth of Trading Partners | Vegh and Vulletin (2015) | 0.66 | 0.51 | 913 |
| Commodity Price Index | Vegh and Vulletin (2015) | 0.83 | 3.62 | 908 |
| Commodity Price Index | Gruss and Kebhaj (2019) | 100.5 | 3.99 | 995 |
| Terms of Trade | World Bank (2021) | 99.6 | 18.5 | 1012 |
| GDP Growth | PWT version 10.0 | 3.41 | 4.24 | 1016 |
| Total Factor Productivity Growth | PWT version 10.0 | 0.39 | 2.11 | 1016 |
| Investment Growth | PWT version 10.0 | 3.46 | 10.7 | 1016 |
| Consumption Growth | PWT version 10.0 | 3.31 | 3.75 | 1016 |
| Change in GDP Share of Net-Exports | PWT version 10.0 | −0.02 | 3.27 | 1016 |
| Inflation | PWT version 10.0 | 2.82 | 10.15 | 1016 |
| Real Effective Exchange Rate Growth | World Bank (2021) | −0.08 | 617 | 836 |
| GDP Share of Tax Revenues | Vegh and Vulletin (2015) | 21.8 | 8.8 | 793 |
| GDP Share of Government Expenditures | PWT version 10.0 | 16 | 4.3 | 1016 |
| 1 | For temperature, examples of papers that document a significant effect on GDP growth are Dell et al. (2012), Burke et al. (2015), and Gallic and Vermandel (2020). In IV estimations of the contemporaneous effects of annual GDP growth on tax rates, Vegh and Vulletin (2015) showed that GDP growth of trading partners and an international commodity price index are relevant instruments for GDP growth. There are many other papers that have documented a significant effect of these variables on GDP, such as Kose (2002), Acemoglu et al. (2008), Brueckner et al. (2012), and Fernandez et al. (2017). |
| 2 | The narrative approach was pioneered by Friedman and Schwartz (1963) and has since been applied to monetary policy, fiscal policy, and macroprudential policy. See Ramey (2016) for a discussion of recent papers that have applied a narrative approach to various types of economic policy. |
| 3 | See https://ideas.repec.org/r/imf/imfwpa/2011-128.html (accessed on 15 January 2024). |
| 4 | For more details on how these variables are constructed and justification for why they are exogenous to GDP growth, see page 351 of Vegh and Vulletin (2015). |
| 5 | Vegh and Vulletin (2015) also used the US real interest rate as an instrument for GDP growth. I do not report results for the US real interest rate because my panel models include time fixed effects. The US real interest rate is perfectly collinear with the time fixed effects. I have estimated panel models without time fixed effects and included the US real interest rate on the right-hand side. I found a significant positive effect of the US real interest rate on the magnitude of action-based fiscal consolidations in the sample that excludes the US economy: a one percentage point increase in the US real interest rate in year t increases the magnitude of an action-based fiscal consolidation by about 0.03 percent of GDP. |
| 6 | Carrière-Swallow et al. (2021) included, in addition to the first and second lags of GDP growth and fiscal consolidations, current and lagged values of a commodity price index. Carrière-Swallow et al. (2021) did not include temperature changes or GDP growth of trading partners in Equation (2). Note that even with a commodity price index as a control variable in Equation (2), OLS of Equation (2) still yields a downward-biased estimate of βh if, in Equation (1), αh < 0. |
References
- Acemoglu, Daron, Simon Johnson, James Robinson, and Pierre Yared. 2008. Income and Democracy. American Economic Review 98: 808–42. [Google Scholar] [CrossRef]
- Alesina, Alberto, Carlo Favero, and Francesco Giavazzi. 2015. The output effect of fiscal consolidation plans. Journal of International Economics 96: S19–S42. [Google Scholar] [CrossRef]
- Alesina, Alberto, Carlo Favero, and Francesco Giavazzi. 2018. What Do We Know about the Effects of Austerity? AEA Papers and Proceedings 108: 524–30. [Google Scholar] [CrossRef]
- Alesina, Alberto, Carlo Favero, and Francesco Giavazzi. 2019a. Effects of Austerity: Expenditure- and Tax-based Approaches. Journal of Economic Perspectives 33: 141–62. [Google Scholar] [CrossRef]
- Alesina, Alberto, Carlo Favero, and Francesco Giavazzi. 2019b. Austerity: When It Works and When It Doesn’t. Princeton: Princeton University Press. [Google Scholar]
- Alesina, Alberto, Roberto Perotti, and Jose Tavares. 1998. The Political Economy of Fiscal Adjustments. Brookings Papers on Economic Activity 1998: 197–266. [Google Scholar] [CrossRef]
- Barnichon, Regis, and Davide Debortoli. 2022. Understanding the Size of the Government Spending Multiplier: It’s in the Sign. Review of Economic Studies 89: 87–117. [Google Scholar] [CrossRef]
- Blanchard, Oliver, and Roberto Perotti. 2002. An empirical characterization of the dynamic effects of changes in government spending and taxes on output. Quarterly Journal of Economics 117: 1329–68. [Google Scholar] [CrossRef]
- Blanchard, Oliver. 1990. Comment: Can Severe Fiscal Contractions Be Expansionary? Tales of Two Small European Countries. NBER Macroeconomics Annual 5: 75–122. [Google Scholar] [CrossRef]
- Brueckner, Markus. 2012. An instrumental variables approach to estimating tax revenue elasticities: Evidence from Sub-Saharan Africa. Journal of Development Economics 98: 220–27. [Google Scholar] [CrossRef]
- Brueckner, Markus, Alberto Chong, and Mark Gradstein. 2012. Estimating the permanent income elasticity of government expenditures: Evidence on Wagner’s law based on oil price shocks. Journal of Public Economics 96: 1025–35. [Google Scholar] [CrossRef]
- Burke, Marshall, Solomon Hsiang, and Edward Miguel. 2015b. Global non-linear effect of temperature on economic production. Nature 527: 235–39. [Google Scholar] [CrossRef]
- Cloyne, James, Oscar Jorda, and Alan Taylor. 2020. Decomposing the Fiscal Multiplier. NBER Working Paper 26939. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Carrière-Swallow, Yan, Antonio C. David, and Daniel Leigh. 2021. Macroeconomic Effects of Fiscal Consolidation in Emerging Economies: New Narrative Evidence from Latin America and the Caribbean. Journal of Money, Credit and Banking 6: 1313–35. [Google Scholar] [CrossRef]
- David, Antonio, and Daniel Leigh. 2018. A New Action-Based Dataset of Fiscal Consolidation in Latin America and the Caribbean. IMF Working Papers 18/94. Washington, DC: International Monetary Fund. [Google Scholar]
- Dell, Melissa, Ben Jones, and Ben Olken. 2012. Temperature Shocks and Economic Growth: Evidence from the Last Half Century. American Economic Journal: Macroeconomics 4: 66–95. [Google Scholar] [CrossRef]
- DeVries, Paul, Jaime Guajardo, Daniel Leigh, and Andrea Pescatori. 2011. A New Action-Based Dataset of Fiscal Consolidation. IMF Working Paper No. 11/128. Washington, DC: International Monetary Fund. [Google Scholar]
- Food and Agriculture Organization Corporate Statistical Database. 2021. Available online: http://www.fao.org/faostat/en/#data/QC (accessed on 2 April 2024).
- Fernandez, Andres, Stephanie Schmitt-Grohe, and Martin Uribe. 2017. World shocks, world prices, and business cycles: An Empirical Investigation. Journal of International Economics 108: S2–S14. [Google Scholar] [CrossRef]
- Friedman, Milton, and Anna Jacobson Schwartz. 1963. A Monetary History of the United States, 1867–1960. Princeton: Princeton University Press. [Google Scholar]
- Gallic, Ewen, and Gallier Vermandel. 2020. Weather Shocks. European Economic Review 124: 103409. [Google Scholar] [CrossRef]
- Giavazzi, Francesco, and Marco Pagano. 1990. Can Severe Fiscal Contractions Be Expansionary? Tales of Two Small European Countries. NBER Macroeconomics Annual 5: 75–122. [Google Scholar] [CrossRef]
- Gruss, Bertrand, and Suhaib Kebhaj. 2019. Commodity Terms of Trade: A New Database. IMF Working Paper No. 19/21. Washington, DC: International Monetary Fund. [Google Scholar]
- Guajardo, Jaime, Daniel Leigh, and Andrea Pescatori. 2014. Expansionary Austerity? International Evidence. Journal of the European Economic Association 12: 949–68. [Google Scholar] [CrossRef]
- Hausman, Jerry, Whitney Newey, and William Taylor. 1987. Efficient Estimation and Identification of Simultaneous Equation Models with Covariance Restrictions. Econometrica 55: 849–74. [Google Scholar] [CrossRef]
- International Monetary Fund. 2024. Fiscal Monitor. Washington, DC: International Monetary Fund. [Google Scholar]
- Jordà, Oscar, and Alan Taylor. 2016. The Time for Austerity: Estimating the Average Treatment Effect of Fiscal Policy. Economic Journal 126: 219–55. [Google Scholar] [CrossRef]
- Kose, Ayhan. 2002. Explaining business cycles in small open economies: How much do world prices matter? Journal of International Economics 56: 299–327. [Google Scholar] [CrossRef]
- Montiel, Jose, and Mikkel Plagborg-Møller. 2021. Local Projection Inference is Simpler and More Robust Than You Think. Econometrica 89: 1789–823. [Google Scholar] [CrossRef]
- Mountford, Andrew, and Harald Uhlig. 2009. What are the Effects of Fiscal Policy Shocks? Journal of Applied Econometrics 24: 960–92. [Google Scholar] [CrossRef]
- Plagborg-Møller, Mikkel, and Christian Wolf. 2021. Local Projections and VARs Estimate the Same Impulse Responses. Econometrica 89: 955–80. [Google Scholar] [CrossRef]
- Pappa, Evi, Rana Sajedi, and Eugenia Vella. 2015. Fiscal consolidation with tax evasion and corruption. Journal of International Economics 1: 56–75. [Google Scholar] [CrossRef]
- Ramey, Valerie. 2011. Identifying Government Spending Shocks: It’s All in the Timing. The Quarterly Journal of Economics 126: 51–102. [Google Scholar] [CrossRef]
- Ramey, Valerie. 2016. Macroeconomic Shocks and Their Propagation. In Handbook of Macroeconomics. Edited by John B. Taylor and Harald Uhlig. Amsterdam: North Holland, vol. 2A, chp. 2. pp. 71–162. [Google Scholar]
- Ramey, Valerie. 2019. Ten Years After the Financial Crisis: What Have We Learned from the Renaissance in Fiscal Research? Journal of Economic Perspectives 33: 89–114. [Google Scholar] [CrossRef]
- Ramey, Valerie, and Sarah Zubairy. 2018. Government Spending Multipliers in Good Times and in Bad: Evidence from US Historical Data. Journal of Political Economy 126: 850–901. [Google Scholar] [CrossRef]
- Romer, Christina, and David Romer. 2010. The Macroeconomic Effects of Tax Changes: Estimates Based on a New Measure of Fiscal Shocks. American Economic Review 100: 763–801. [Google Scholar] [CrossRef]
- Stock, James, and Mark Watson. 2018. Identification and Estimation of Dynamic Causal Effects in Macroeconomics Using External Instruments. Economic Journal 128: 917–48. [Google Scholar] [CrossRef]
- Vegh, Carlos, and Guillermo Vulletin. 2015. How Is Tax Policy Conducted over the Business Cycle? American Economic Journal: Economic Policy 7: 327–70. [Google Scholar] [CrossRef]
- World Bank. 2021. World Development Indicators. Online Database. Available online: https://databank.worldbank.org/source/world-development-indicators (accessed on 19 February 2021).
- Yared, Piere. 2019. Rising Government Debt: Causes and Solutions for a Decades-Old Trend. Journal of Economic Perspectives 33: 115–40. [Google Scholar] [CrossRef]
| Fiscal Consolidation | Fiscal Consolidation | GDP | GDP | |
|---|---|---|---|---|
| Growth | Growth | |||
| (1) | (2) | (3) | (4) | |
| Whole Sample | Excluding Large Economies | Whole Sample | Excluding Large Economies | |
| Temperature Change, t | −0.07 ** (0.04) | −0.10 ** (0.04) | 0.71 *** (0.2) | 0.75 *** (0.22) |
| Country Fixed Effects | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes |
| Observations | 986 | 805 | 986 | 805 |
| Countries | 31 | 26 | 31 | 26 |
| Fiscal Consolidation | Fiscal Consolidation | GDP Growth | GDP Growth | |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Whole Sample | Excluding Large Economies | Whole Sample | Excluding Large Economies | |
| GDP Growth of Trading Partners, t | −0.25 *** (0.08) | −0.25 *** (0.09) | 2.65 *** (0.45) | 2.61 *** (0.46) |
| Country Fixed Effects | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes |
| Observations | 913 | 733 | 913 | 733 |
| Countries | 30 | 25 | 30 | 25 |
| Fiscal Consolidation | Fiscal Consolidation | GDP Growth | GDP Growth | |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Whole Sample | Excluding Large Economies | Whole Sample | Excluding Large Economies | |
| Commodity Price Index, t | −0.02 ** (0.01) | −0.02 ** (0.01) | 0.20 *** (0.06) | 0.18 *** (0.07) |
| Country Fixed Effects | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes |
| Observations | 908 | 728 | 908 | 728 |
| Countries | 30 | 25 | 30 | 25 |
| Fiscal Consolidation (Tax and Expenditure) | Fiscal Consolidation (Tax and Expenditure) | Fiscal Consolidation (Tax) | Fiscal Consolidation (Tax) | Fiscal Consolidation (Expenditure) | Fiscal Consolidation (Expenditure) | |
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Whole Sample | Excluding Large Economies | Whole Sample | Excluding Large Economies | Whole Sample | Excluding Large Economies | |
| GDP Growth, t | −0.07 ** (0.02) | −0.08 *** (0.03) | −0.05 ** (0.02) | −0.05 ** (0.02) | −0.03 ** (0.01) | −0.03 * (0.02) |
| Cragg–Donald F-Stat | 19.7 | 13.9 | 19.7 | 13.9 | 19.7 | 13.9 |
| Kleibergen–Paap F-Stat | 17 | 13.7 | 17 | 13.7 | 17 | 13.7 |
| Hansen J, p-value | 0.99 | 0.75 | 0.87 | 0.79 | 0.63 | 0.37 |
| First-Stage Estimates for GDP Growth, t | ||||||
| GDP Growth of Trading Partners, t | 2.21 *** (0.51) | 2.13 *** (0.52) | 2.21 *** (0.51) | 2.13 *** (0.52) | 2.21 *** (0.51) | 2.13 *** (0.52) |
| Commodity Price Index, t | 0.17 ** (0.07) | 0.14 * (0.07) | 0.17 ** (0.07) | 0.14 * (0.07) | 0.17 ** (0.07) | 0.14 * (0.07) |
| Temperature Change, t | 0.71 *** (0.22) | 0.71 *** (0.26) | 0.71 *** (0.22) | 0.71 *** (0.26) | 0.71 *** (0.22) | 0.71 *** (0.26) |
| Country Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 850 | 670 | 850 | 670 | 850 | 670 |
| Countries | 29 | 24 | 29 | 24 | 29 | 24 |
| Fiscal Consolidation | ||||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Whole Sample | Excluding Large Economies | Whole Sample | Excluding Large Economies | Whole Sample | Excluding Large Economies | |
| GDP Growth, t | −0.09 *** (0.03) | −0.10 *** (0.03) | −0.08 ** (0.04) | −0.10 ** (0.05) | −0.10 * (0.05) | −0.14 ** (0.06) |
| Cragg–Donald F-Stat | 48.8 | 13.7 | 27.9 | 13.7 | 8.7 | 7 |
| Kleibergen–Paap F-Stat | 33.65 | 13.9 | 9.1 | 13.9 | 12.9 | 11.1 |
| First-Stage Estimates for GDP Growth, t | ||||||
| GDP Growth of Trading Partners, t | 2.65 *** (0.45) | 2.61 *** (0.45) | ||||
| Commodity Price Index, t | 0.20 *** (0.07) | 0.18 *** (0.07) | ||||
| Temperature Change, t | 0.71 *** (0.19) | 0.75 *** (0.22) | ||||
| Country Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 913 | 733 | 908 | 728 | 990 | 670 |
| Countries | 30 | 24 | 30 | 25 | 31 | 24 |
| Fiscal Consolidation | ||||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Whole Sample | Excluding Large Economies | |||||
| GDP Growth, t | −0.08 *** (0.02) | −0.09 * (0.05) | −0.07 ** (0.03) | −0.08 ** (0.02) | −0.11 ** (0.06) | −0.07 ** (0.03) |
| Temperature Change, t | 0.01 (0.04) | −0.01 (0.04) | ||||
| GDP Growth of Trading Partners, t | 0.04 (0.17) | 0.1 (0.2) | ||||
| Commodity Price Index, t | −0.00 (0.01) | −0.01 (0.01) | ||||
| Hansen J, p-value | 0.73 | 0.68 | 0.98 | 0.61 | 0.86 | 0.61 |
| Cragg–Donald F-Stat | 29.3 | 11.1 | 21.7 | 20.9 | 7.3 | 17 |
| Kleibergen–Paap F-Stat | 16.1 | 10.4 | 23 | 14 | 7.4 | 21 |
| First-Stage Estimates for GDP Growth | ||||||
| Temperature Change, t | 0.73 *** (0.21) | 0.73 *** (0.21) | 0.74 *** (0.25) | 0.74 *** (0.25) | ||
| GDP Growth of Trading Partners, t | 2.28 *** (0.47) | 2.28 *** (0.47) | 2.25 *** (0.49) | 2.25 *** (0.49) | ||
| Commodity Price Index, t | 0.16 *** (0.07) | 0.16 ** (0.07) | 0.13 * (0.07) | 0.13 * (0.07) | ||
| Country Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 882 | 882 | 882 | 702 | 702 | 702 |
| Countries | 30 | 30 | 30 | 25 | 25 | 25 |
| Fiscal Consolidation | ||||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Whole Sample | Excluding Large Economies | |||||
| GDP Growth, t | −0.08 *** (0.03) | −0.07 *** (0.02) | −0.07 *** (0.02) | −0.09 *** (0.03) | −0.08 *** (0.02) | −0.08 *** (0.02) |
| CONTROL VARIABLES | ||||||
| Fiscal Consolidations, | 0.40 *** (0.05) | 0.40 *** (0.05) | 0.40 *** (0.05) | 0.40 *** (0.05) | 0.41 *** (0.05) | 0.41 *** (0.05) |
| t − 1 | ||||||
| Fiscal Consolidations, | −0.00 (0.07) | 0.01 (0.06) | −0.00 (0.07) | 0.01 (0.07) | ||
| t − 2 | ||||||
| GDP Growth, t − 1 | 0.02 (0.01) | 0.02 (0.01) | ||||
| GDP Growth, t − 2 | −0.02 ** (0.01) | −0.02 ** (0.01) | ||||
| Hansen J, p-value | 0.97 | 0.99 | 0.98 | 0.89 | 0.72 | 0.83 |
| Cragg–Donald F-Stat | 13 | 20.4 | 22 | 9.4 | 14.7 | 15.5 |
| Kleibergen–Paap F-Stat | 14 | 13.7 | 13.8 | 12.6 | 12.4 | 12.1 |
| First-Stage Estimates for GDP Growth, t | ||||||
| Temperature Change | 0.60 *** (0.2) | 0.60 *** (0.21) | 0.58 *** (0.21) | 0.63 *** (0.24) | 0.60 *** (0.26) | 0.59 ** (0.26) |
| GDP Growth of Trading Partners | 1.64 *** (0.37) | 2.16 *** (0.49) | 2.04 *** (0.49) | 1.61 *** (0.38) | 2.14 *** (0.51) | 1.99 *** (0.51) |
| Commodity Price Index | 0.14 ** (0.07) | 0.20 *** (0.07) | 0.22 *** (0.06) | 0.13 * (0.07) | 0.18 ** (0.07) | 0.20 *** (0.06) |
| Country Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 797 | 797 | 824 | 627 | 627 | 649 |
| Countries | 29 | 29 | 29 | 24 | 24 | 24 |
| Fiscal Consolidation (h) | ||||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| h = 0 | h = 1 | h = 2 | h = 0 | h = 1 | h = 2 | |
| Whole Sample | Excluding Large Economies | |||||
| GDP Growth (h) | −0.08 *** (0.03) | −0.07 *** (0.02) | −0.07 *** (0.02) | −0.09 *** (0.03) | −0.06 *** (0.02) | −0.06 *** (0.02) |
| CONTROL VARIABLES | ||||||
| Fiscal Consolidation, t − 1 | 0.40 *** (0.05) | 0.53 ** (0.11) | 0.54 *** (0.13) | 0.41 *** (0.05) | 0.55 ** (0.12) | 0.56 *** (0.14) |
| Fiscal Consolidation, t − 2 | −0.00 (0.06) | −0.02 (0.07) | −0.00 (0.07) | −0.00 (0.06) | −0.03 (0.07) | −0.01 (0.07) |
| GDP Growth, t − 1 | 0.02 (0.02) | 0.01 (0.02) | −0.01 (0.02) | 0.02 (0.02) | −0.00 (0.02) | −0.02 (0.02) |
| GDP Growth, t − 2 | −0.02 ** (0.00) | −0.03 ** (0.01) | −0.04 *** (0.02) | −0.02 ** 0 | −0.04 *** (0.02) | −0.05 *** (0.02) |
| First-Stage Estimates for GDP Growth (h) | ||||||
| Temperature Change (h) | 0.60 *** (0.2) | 0.76 ** (0.37) | 1.41 *** (0.54) | 0.63 *** (0.24) | 0.68 * (0.4) | 1.21 ** (0.06) |
| GDP Growth of Trading Partners (h) | 1.64 *** (0.37) | 2.35 *** (0.56) | 3.01 *** (0.73) | 1.61 *** (0.38) | 2.34 *** (0.57) | 3.08 *** (0.74) |
| Commodity Price Index (h) | 0.14 ** (0.07) | 0.21 *** (0.07) | 0.22 *** (0.08) | 0.13 * (0.07) | 0.19 *** (0.07) | 0.20 *** (0.07) |
| Cragg–Donald F-Stat | 14 | 16.5 | 19.1 | 9.4 | 15.9 | 23.01 |
| Kleibergen–Paap F-Stat | 13 | 22.7 | 32.1 | 12.6 | 16.5 | 23.76 |
| Hansen J, p-value | 0.97 | 0.58 | 0.42 | 0.89 | 0.43 | 0.27 |
| Country Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 797 | 768 | 739 | 627 | 603 | 579 |
| Countries | 29 | 29 | 29 | 24 | 24 | 24 |
| GDP Growth (h) | ||||||
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| h = 0 | h = 1 | h = 2 | t = 0 | t = 1 | t = 2 | |
| Whole Sample | Excluding Large Economies | |||||
| Panel A: Two-Stage Least Squares | ||||||
| Fiscal Consolidation (h) | 1.84 *** (0.51) | 1.46 *** (0.55) | 1.38 ** (0.61) | 2.00 *** (0.58) | 1.61 *** (0.62) | 1.52 ** (0.7) |
| [Wild Restricted Efficient Cluster Bootstrapped 95% Confidence Interval] | ||||||
| [0.72, 2.83] | [0.35, 2.69] | [0.20, 3.08] | [0.67, 3.26] | [0.31, 3.01] | [0.11, 3.49] | |
| First Stage for Fiscal Consolidation (h) | ||||||
| ures | 0.88 *** (0.03) | 0.91 *** (0.03) | 0.91 *** (0.03) | 0.86 *** (0.03) | 0.90 *** (0.04) | 0.89 *** (0.05) |
| Cragg–Donald F-Stat | 4253.7 | 5376.2 | 4590.9 | 2878.5 | 3467.7 | 2830.2 |
| Kleibergen–Paap F-Stat | 807.4 | 887.7 | 633 | 550.9 | 569.5 | 378.2 |
| Panel B: Least Squares | ||||||
| Fiscal Consolidation (h) | −0.44 *** (0.15) | −0.57 ** (0.22) | −0.74 *** (0.27) | −0.45 ** (0.19) | −0.60 ** (0.24) | −0.80 *** (0.28) |
| Controls and Observations in Panels A and B | ||||||
| Country Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Additional Controls | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 827 | 797 | 767 | 657 | 632 | 607 |
| Countries | 30 | 30 | 30 | 25 | 25 | 25 |
| Total Factor Productivity Growth | Investment Growth | Consumption Growth | Change in Net-Exports GDP Share | |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Panel A: Whole Sample | ||||
| Fiscal Consolidation, t | 0.62 ** (0.26) | 2.34 ** (1.08) | 0.48 (0.41) | 0.81 *** (0.24) |
| Cragg–Donald F-Stat | 3799.3 | 3826.8 | 3999.3 | 3840.4 |
| Kleibergen–Paap F-Stat | 690 | 689.7 | 701.9 | 690.8 |
| Observations | 797 | 797 | 797 | 797 |
| Countries | 29 | 29 | 29 | 29 |
| Country Fixed Effects | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes |
| Additional Controls | Yes | Yes | Yes | Yes |
| Panel B: Excluding 5 Largest Economies | ||||
| Fiscal Consolidation, t | 0.62 ** (0.28) | 2.35 ** (1.15) | 0.42 (0.42) | 0.82 *** (0.25) |
| Cragg–Donald F-Stat | 2963.2 | 2989.8 | 3146.3 | 2997.2 |
| Kleibergen–Paap F-Stat | 603.3 | 609.5 | 622 | 608.5 |
| Observations | 627 | 627 | 627 | 627 |
| Countries | 24 | 29 | 29 | 29 |
| Country Fixed Effects | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes |
| Additional Controls | Yes | Yes | Yes | Yes |
| Inflation | Inflation | Real Exchange Rate | Real Exchange Rate | |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Whole Sample | Excluding 5 Largest Economies | Whole Sample | Excluding 5 Largest Economies | |
| Fiscal Consolidation, t | −2.33 *** (0.75) | −2.44 *** (0.82) | −0.95 ** (0.46) | −1.10 ** (0.48) |
| Cragg–Donald F-Stat | 3793.9 | 2976.4 | 3604.4 | 2758.9 |
| Kleibergen–Paap F-Stat | 676.1 | 600.4 | 918 | 893.9 |
| Observations | 797 | 627 | 674 | 517 |
| Countries | 29 | 25 | 25 | 20 |
| Country Fixed Effects | Yes | Yes | Yes | Yes |
| Time Fixed Effects | Yes | Yes | Yes | Yes |
| Additional Controls | Yes | Yes | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brueckner, M. Action-Based Fiscal Consolidations and Economic Growth. J. Risk Financial Manag. 2024, 17, 194. https://doi.org/10.3390/jrfm17050194
Brueckner M. Action-Based Fiscal Consolidations and Economic Growth. Journal of Risk and Financial Management. 2024; 17(5):194. https://doi.org/10.3390/jrfm17050194
Chicago/Turabian StyleBrueckner, Markus. 2024. "Action-Based Fiscal Consolidations and Economic Growth" Journal of Risk and Financial Management 17, no. 5: 194. https://doi.org/10.3390/jrfm17050194





