Operation Optimization of Steam Accumulators as Thermal Energy Storage and Buffer Units
Abstract
:1. Introduction
2. Principle of SA and Classification of SSs
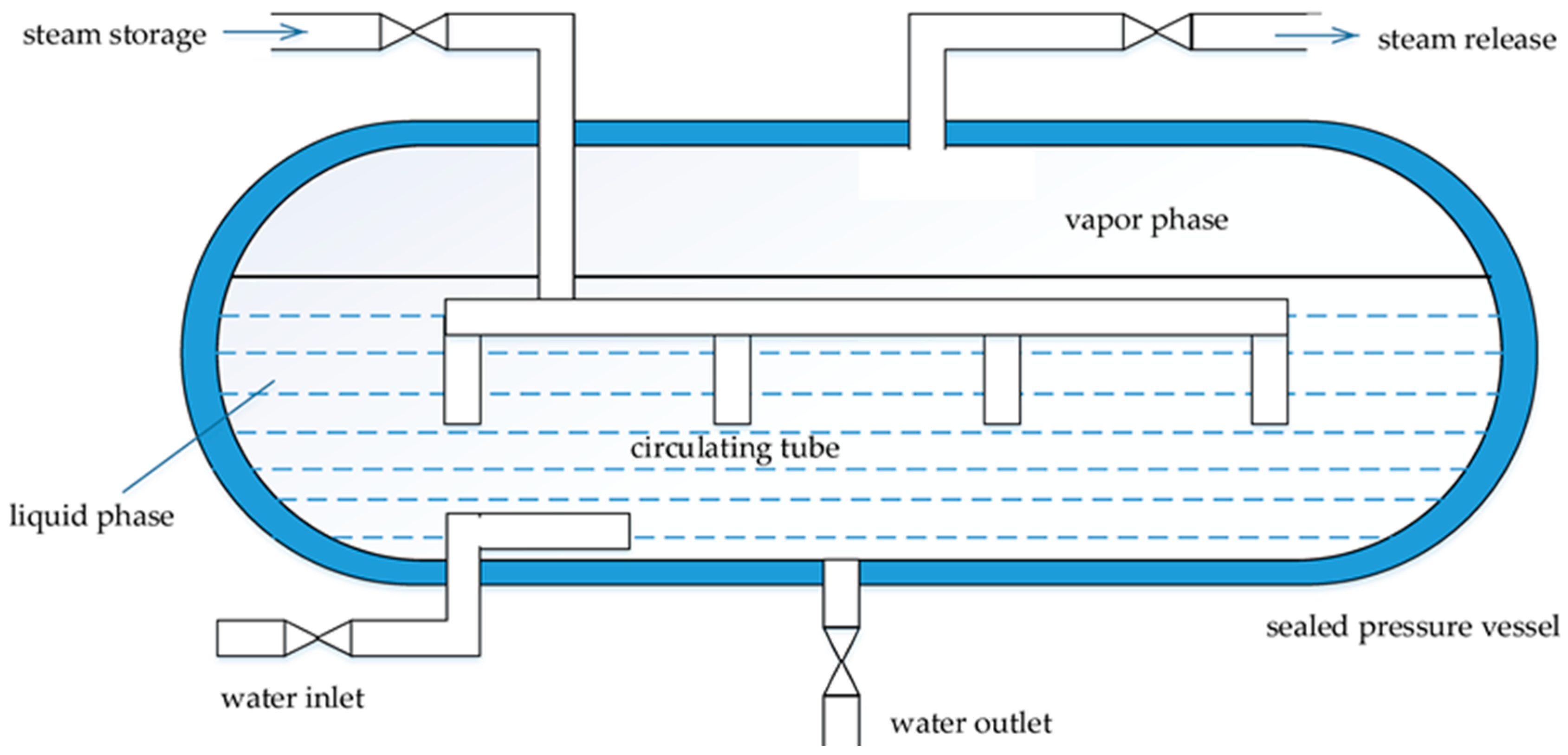
2.1. SA Operation Principle
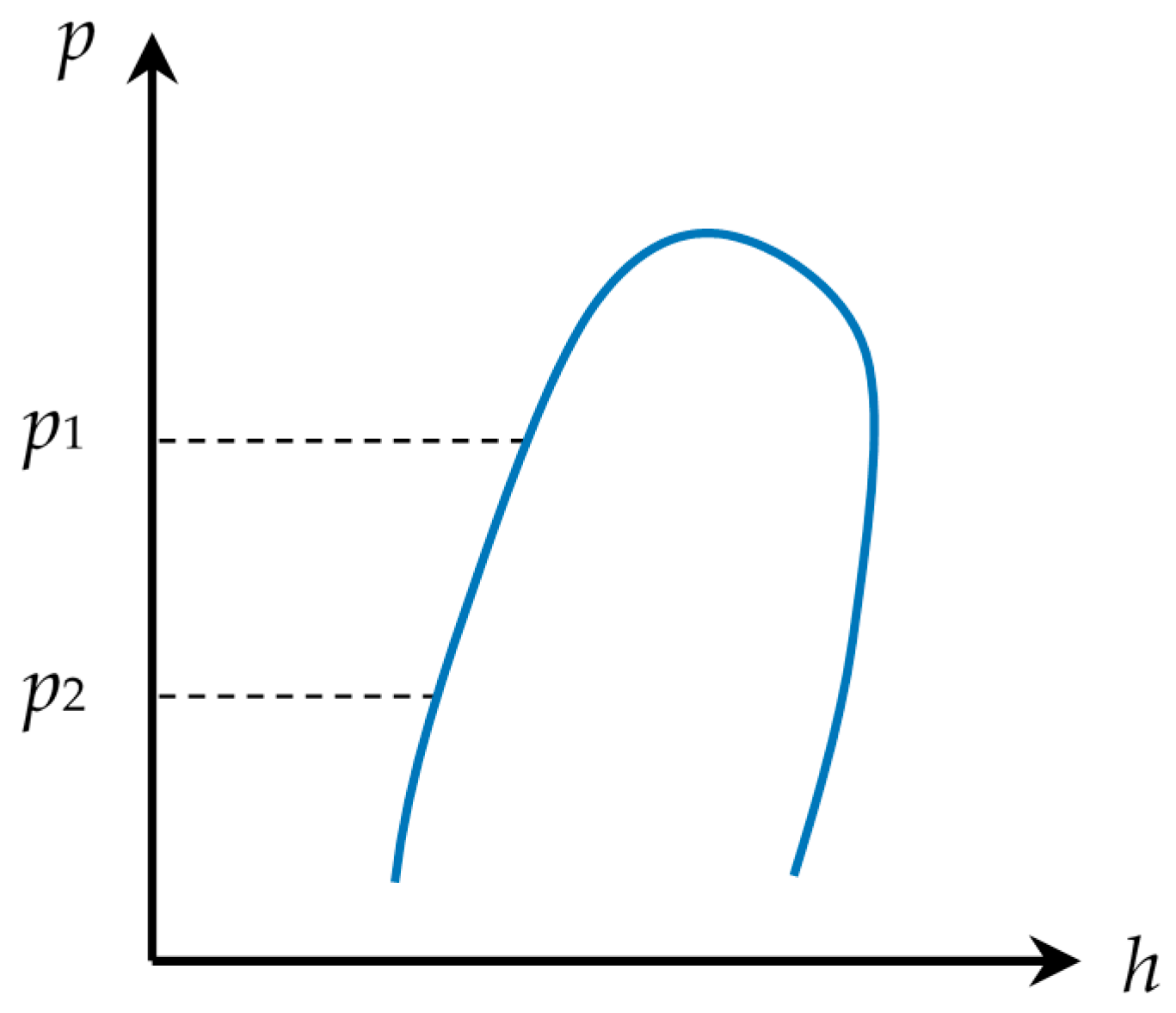
- Steam storage process: The pressure of steam from a high-temperature SS is higher than that inside the SA. When the steam inlet valve is open, steam flows into the SA automatically. The saturated water and saturated steam with relatively low temperature and pressure is stored in the SA, to which high-temperature steam is added. Through rapid heat exchange, the high-temperature steam is cooled, and the previously mentioned saturated water and steam are heated to a higher temperature to form a new equilibrium state. As the steam storage process continues, it sees a steady rise in the temperature of the water and steam inside the SA, followed by an increasing pressure and water level. Once the internal pressure reaches the specified maximum value, the steam inlet valve closes, and the steam storage process ends. As shown in Figure 2, during the steam storage process, the pressure rises from the specified minimum value p2 to the maximum p1, and the steam is condensed, leading to an increase in the water enthalpy along the saturated liquid line at the left side of Figure 2.
- Steam release process: This is an inverse process of the steam storage process detailed above. When the SA provides steam for users, the valve at the steam outlet is open. Since the pressure in the steam pipe is lower than that in the SA, the saturated steam in the SA releases automatically under the pressure difference, resulting in a lower pressure inside the SA. When the internal pressure is lower than the saturation pressure corresponding to the temperature of water stored, the saturated water becomes superheated, and the water boils immediately to evaporate as saturated steam. At this point the water temperature and water level in the SA drop until they have decreased to the specified minimum value, at which point the steam outlet valve closes, and the steam release process ends. During this process, the pressure decreases from p1 to p2, as shown in Figure 2, meaning that the superheated water converts to saturated water, and thus, the water enthalpy reduces along the saturated liquid line.
2.2. SS Classification
- Controllable steam source (CSS): The steam generation process is of considerable controllability, and therefore, the steam’s flow rate, pressure, and temperature are steady, change periodically, or can be controlled easily, e.g., coal-fired boiler and other station boilers.
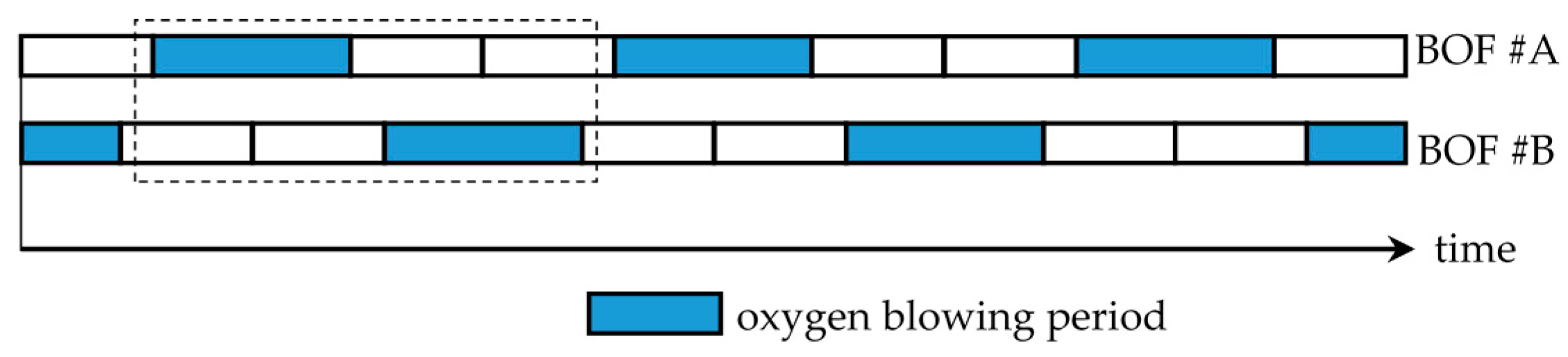
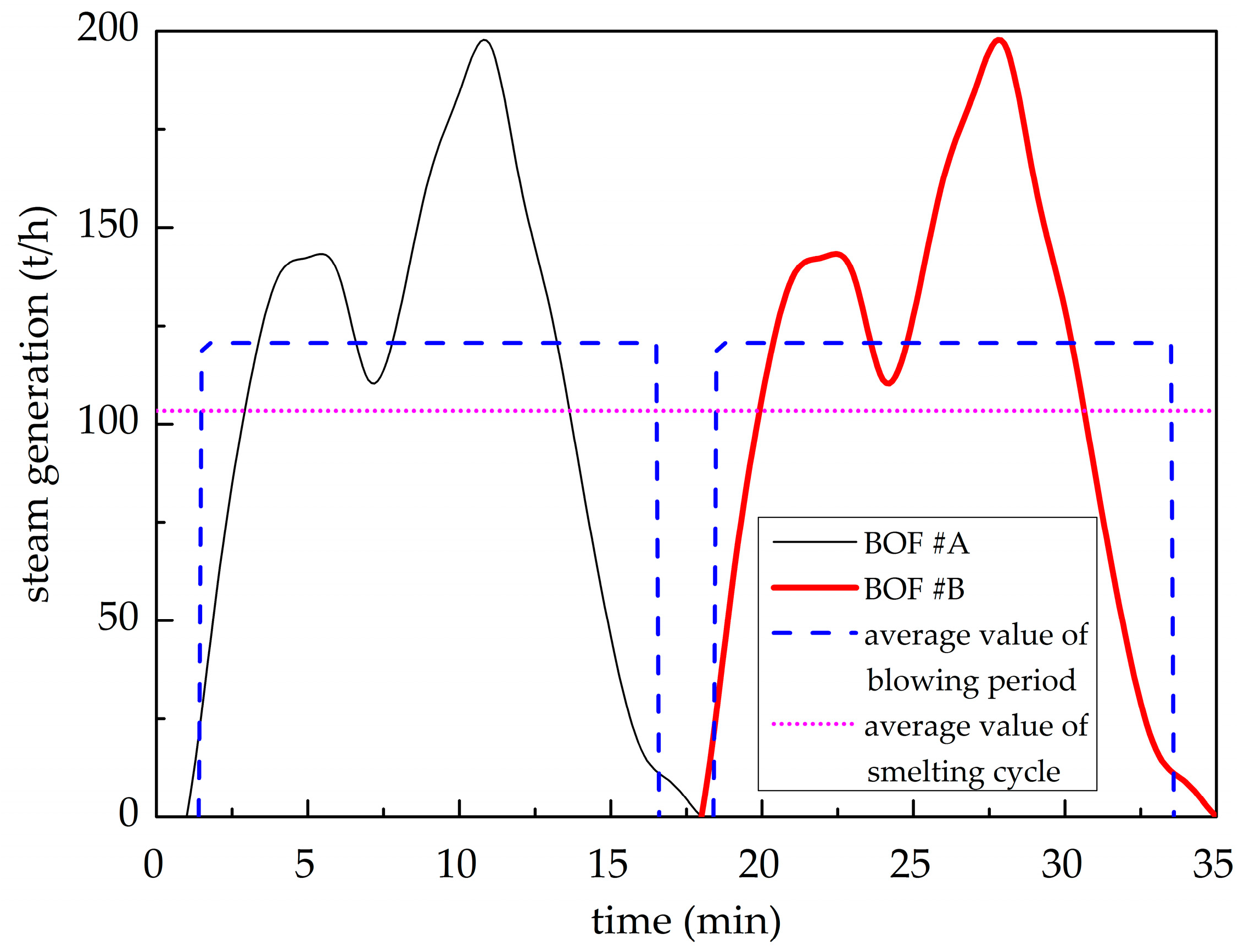
- Uncontrollable steam source (UCSS): This type generally has the following characteristics: (a) The generation of the steam is influenced by other factors, even randomly intermittent factors; (b) the flow rate of the steam supplied fluctuates frequently; and (c) the temperature and pressure of the steam supplied vary significantly over a large range. It is hard to control the flow rate, pressure, and temperature of steam from UCSSs. Examples include solar thermal plants, incinerators fueled by municipal solid wastes, and basic oxygen furnace (BOF) waste heat power generation.
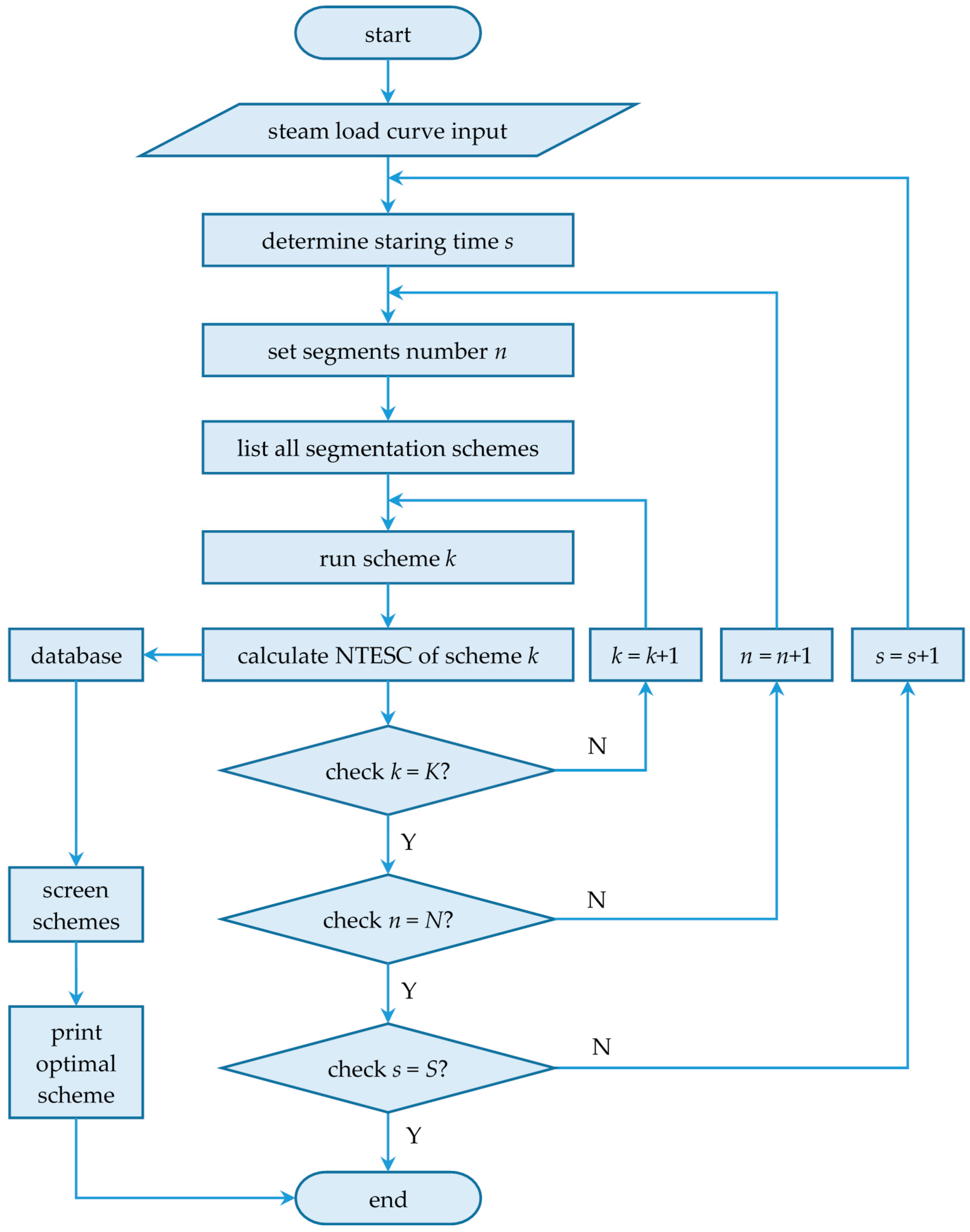
3. Mathematical Model of Steam Accumulator (SA) Operation Optimization
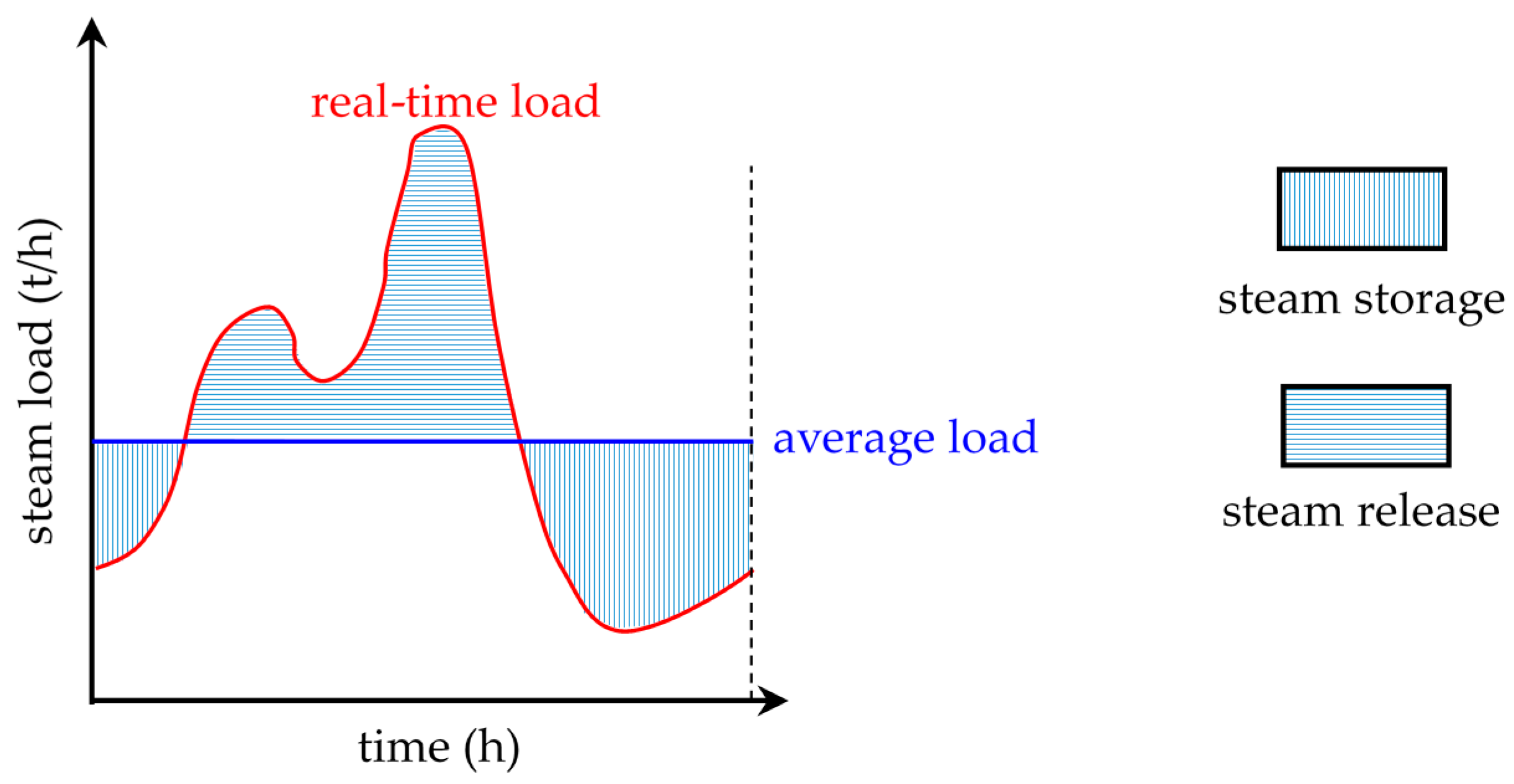
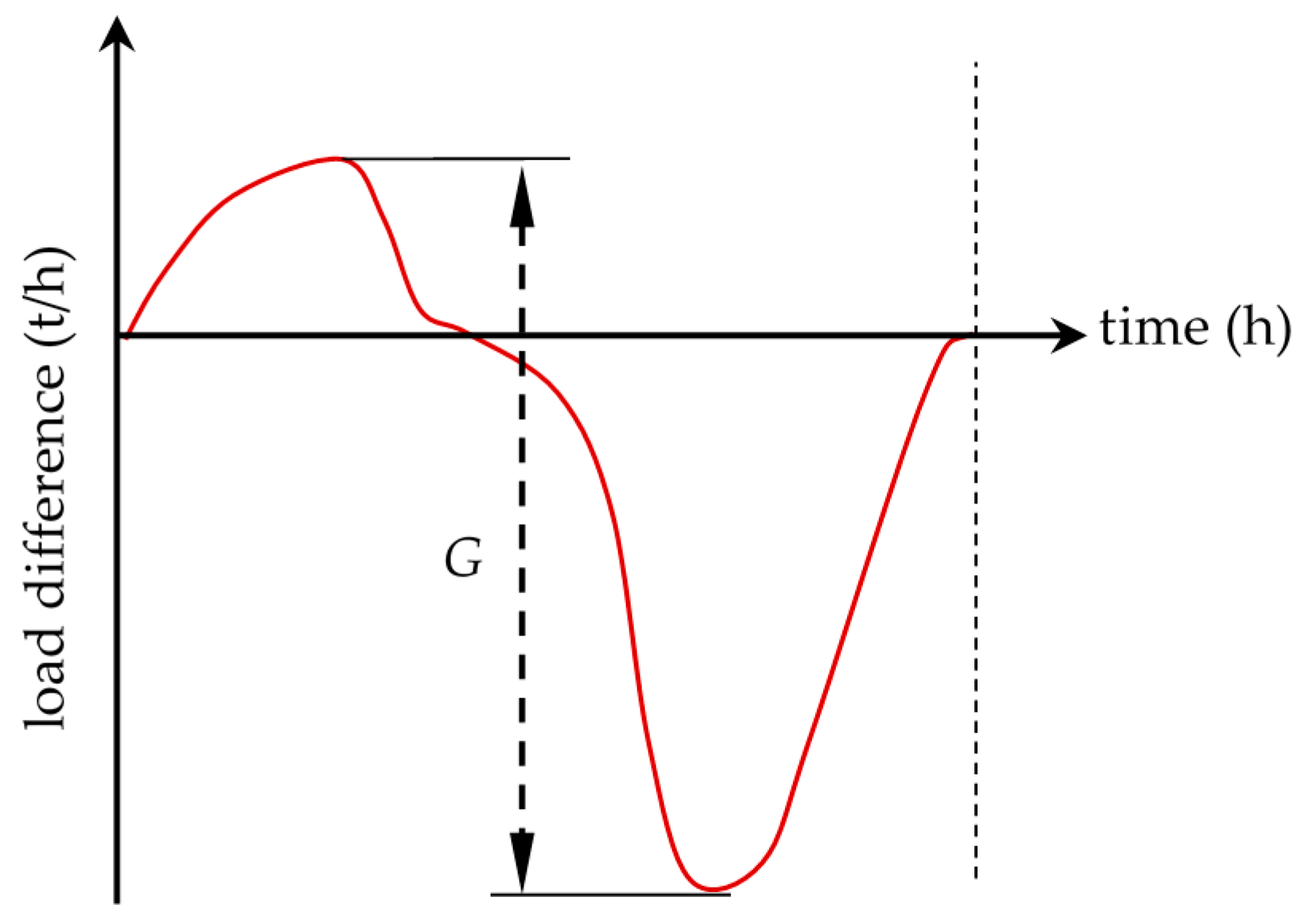
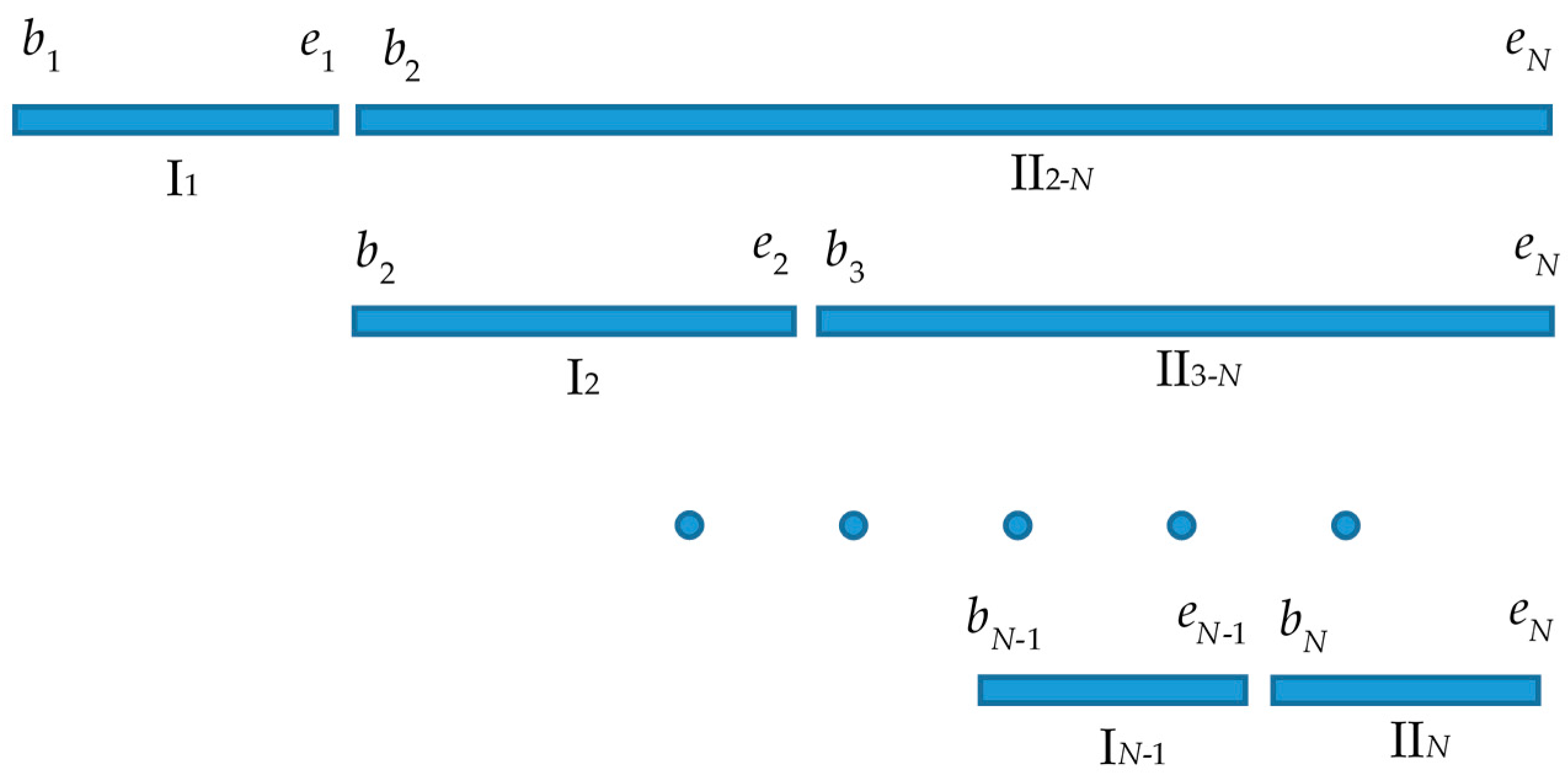
3.1. SA Operation Optimization for UCSS
3.2. SA Operation Optimization for CSS
4. Case Results and Discussion
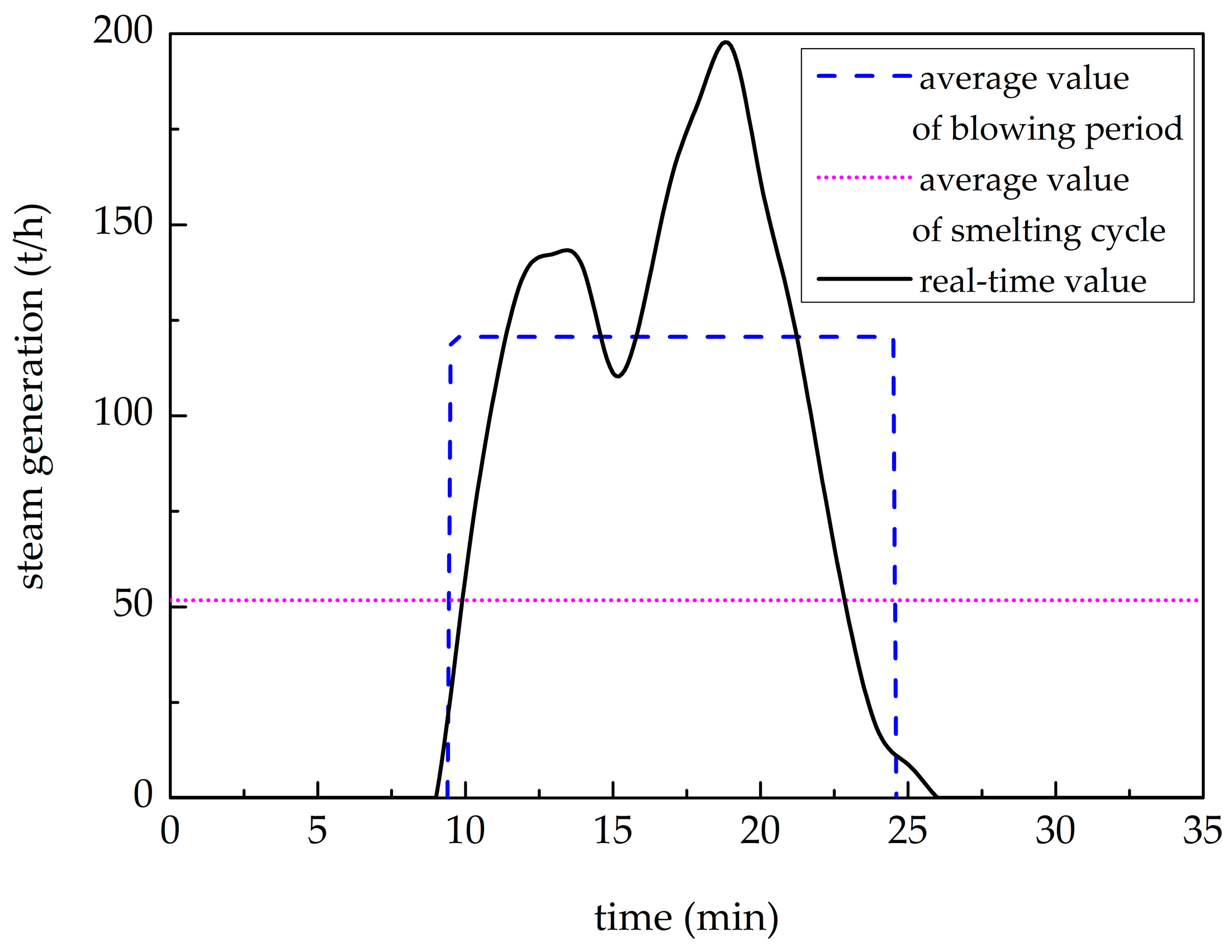
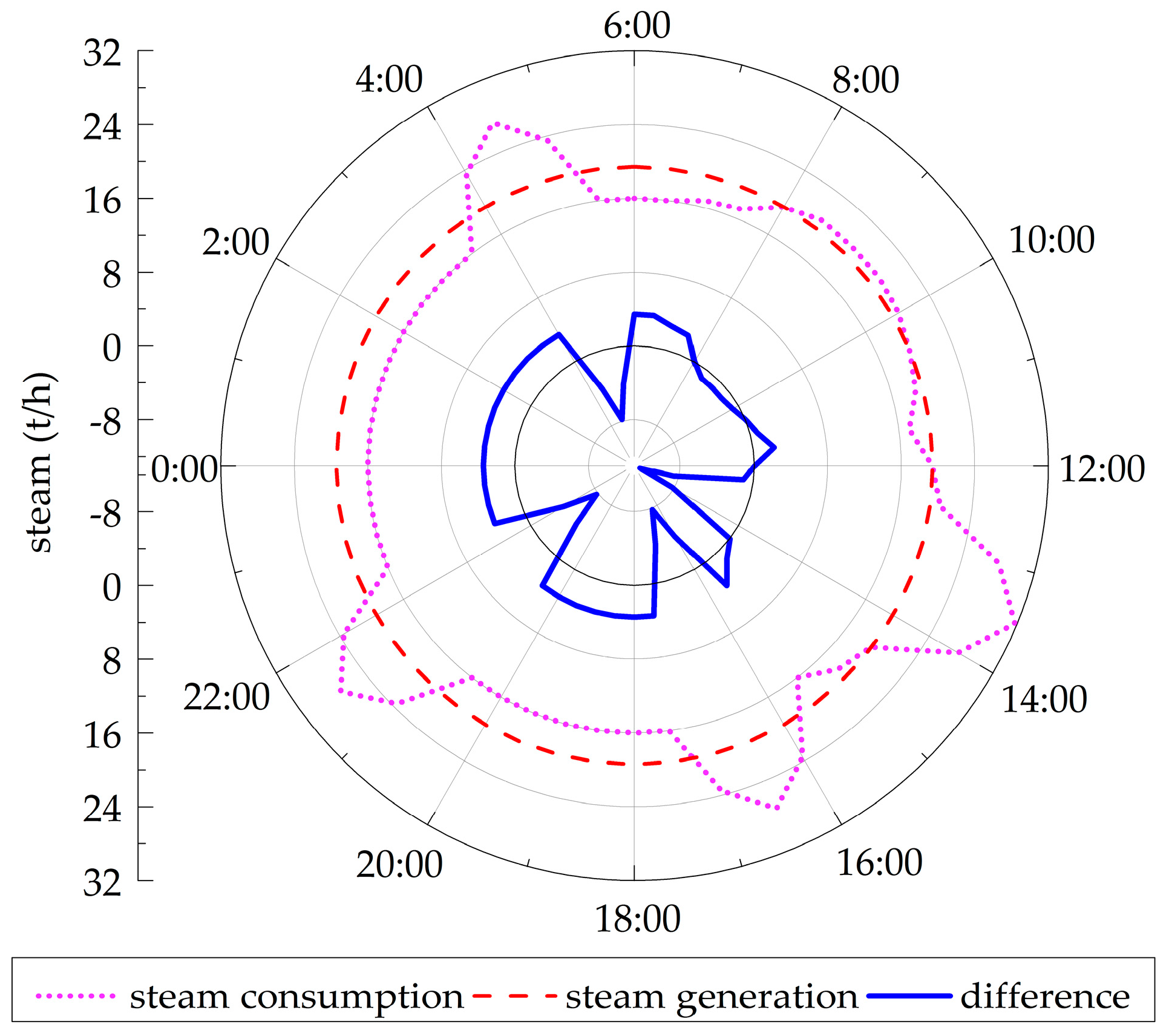
4.1. SA Cooperating with a UCSS
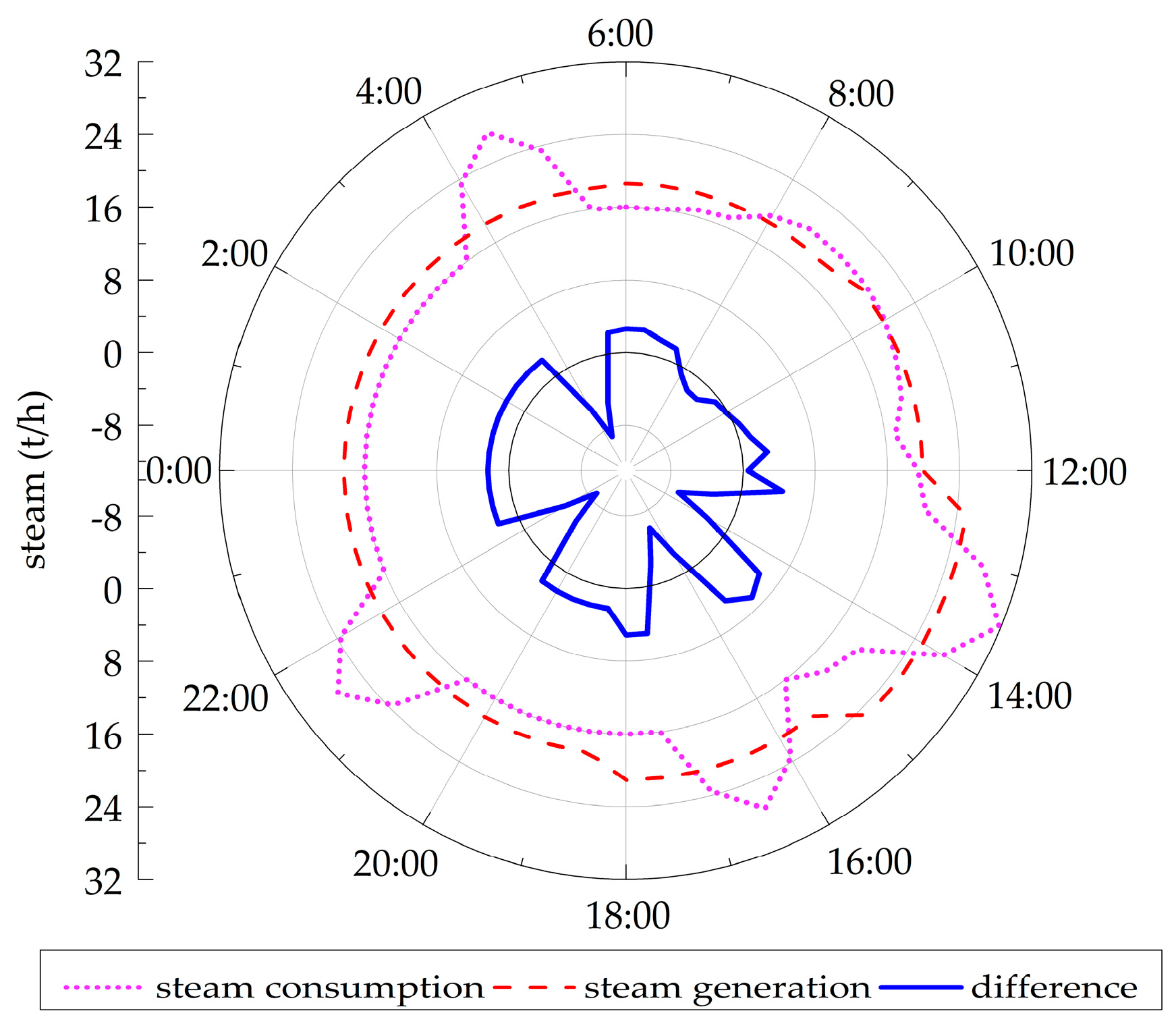
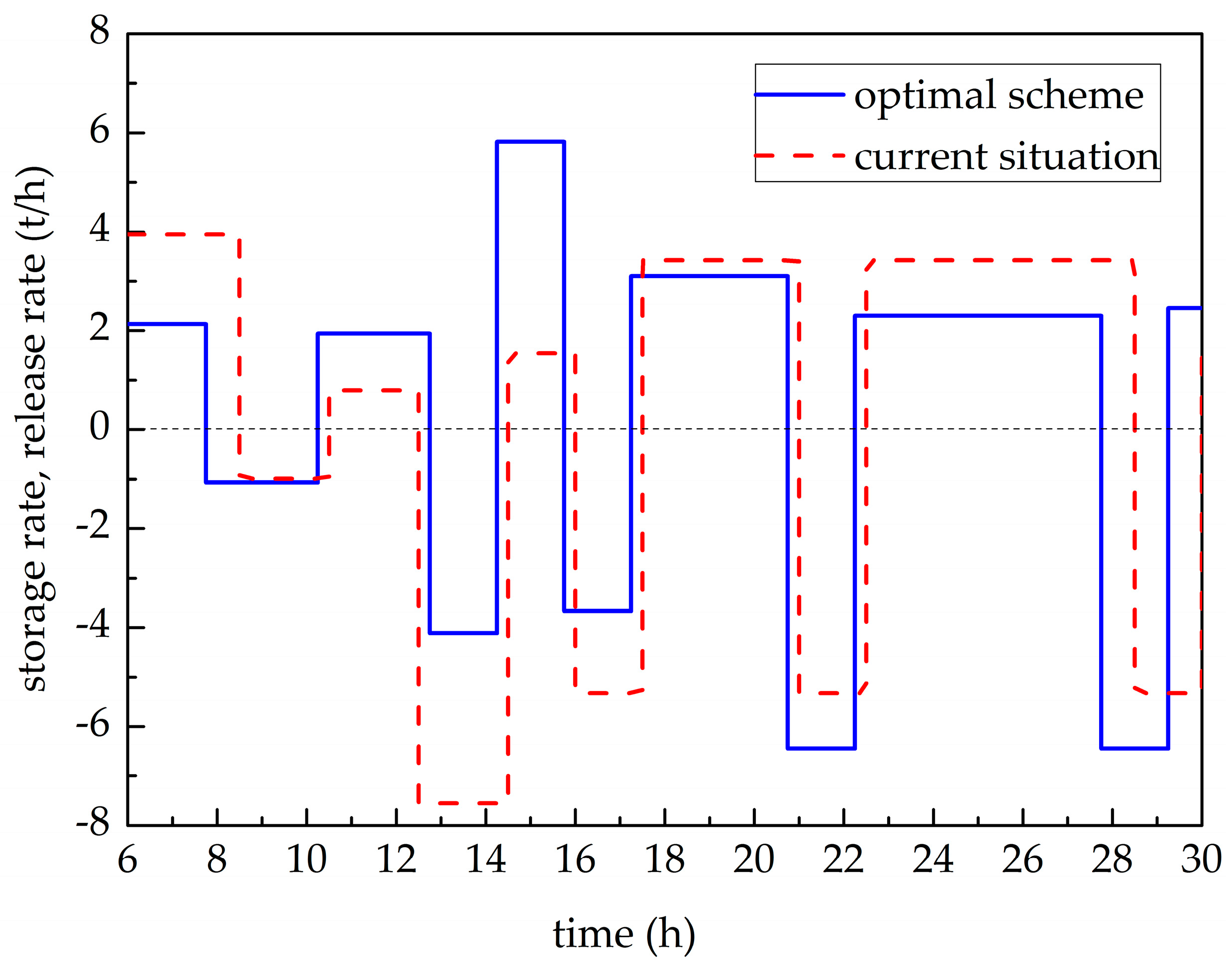
4.2. SA Cooperating with a CSS
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BOF | basic oxygen furnace |
| CSS | controllable steam source |
| NTESC | necessary thermal energy storage capacity |
| SA | steam accumulator |
| SS | steam source |
| STESC | specific thermal energy storage capacity |
| TESC | thermal energy storage capacity |
| UCSS | uncontrollable steam source |
References
- Castro-Dominguez, B.; Mardilovich, I.P.; Ma, L.C.; Ma, R.; Dixon, A.G.; Kazantzis, N.K.; Ma, Y.H. Integration of methane steam reforming and water gas shift reaction in a Pd/Au/Pd-based catalytic membrane reactor for process intensification. Membranes 2016, 6, 44. [Google Scholar] [CrossRef] [PubMed]
- Kessy, H.N.E.; Hu, Z.; Zhao, L.; Zhou, M. Effect of steam blanching and drying on phenolic compounds of litchi pericarp. Molecules 2016, 21, 729. [Google Scholar] [CrossRef] [PubMed]
- Shamsi, S.; Omidkhah, M.R. Optimization of steam pressure levels in a total site using a thermoeconomic method. Energies 2012, 5, 702–717. [Google Scholar] [CrossRef]
- Sun, W.; Zhao, Y.; Wang, Y. Electro- or turbo-driven?—Analysis of different blast processes of blast furnace. Processes 2016, 4, 28. [Google Scholar] [CrossRef]
- Ma, G.; Cai, J.; Zhang, L.; Sun, W. Influence of steam recovery and consumption on energy consumption per ton of steel. Energy Procedia 2012, 14, 566–571. [Google Scholar] [CrossRef]
- Yu, J. Status and transformation measures of industrial coal-fired boiler in China. Clean Coal Technol. 2012, 18, 89–91. (In Chinese) [Google Scholar]
- Tanton, D.M.; Cohen, R.R.; Probert, S.D. Improving the effectiveness of a domestic central-heating boiler by the use of heat storage. Appl. Energy 1987, 27, 53–82. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Sabihuddin, S.; Kiprakis, A.E.; Mueller, M. A numerical and graphical review of energy storage technologies. Energies 2015, 8, 172–216. [Google Scholar] [CrossRef]
- Shnaider, D.A.; Divnich, P.N.; Vakhromeev, I.E. Modeling the dynamic mode of steam accumulator. Auto Remote Control 2010, 71, 1994–1998. [Google Scholar] [CrossRef]
- Bai, F.; Xu, C. Performance analysis of a two-stage thermal energy storage system using concrete and steam accumulator. Appl. Therm. Eng. 2011, 31, 2764–2771. [Google Scholar] [CrossRef]
- Xu, E.; Yu, Q.; Wang, Z.; Yang, C. Modeling and simulation of 1 MW DAHAN solar thermal power tower plant. Renew. Energy 2011, 36, 848–857. [Google Scholar] [CrossRef]
- Chen, G.Q.; Yang, Q.; Zhao, Y.H.; Wang, Z.F. Nonrenewable energy cost and greenhouse emissions of a 1.5 MW solar power tower plant in China. Renew. Sustain. Energy Rev. 2011, 15, 1961–1967. [Google Scholar] [CrossRef]
- Price, N. Steam accumulators provide uniform loads on boilers. Chem. Eng. 1982, 89, 131–135. [Google Scholar]
- Studovic, M.; Stevanovic, V. Non-equilibrium approach to the analysis of steam accumulator operation. Thermophys. Aeromech. 1994, 1, 53–60. [Google Scholar]
- Stevanovic, V.D.; Maslovaric, B.; Prica, S. Dynamics of steam accumulation. Appl. Therm. Eng. 2012, 37, 73–79. [Google Scholar] [CrossRef]
- Stevanovic, V.D.; Petrovic, M.M.; Milivojevic, S.; Maslovaric, B. Prediction and control of steam accumulation. Heat Transf. Eng. 2015, 36, 498–510. [Google Scholar] [CrossRef]
- Maklakov, N.N.; Khramov, S.M. Application of a heat hydraulic accumulator to thermal stabilization of the evaporation zone of a heat pipe. J. Eng. Phys. Thermophys. 2003, 76, 1–5. [Google Scholar] [CrossRef]
- Walter, H.; Linzer, W. Flow stability of heat recovery steam generators. J. Eng. Gas Turbines Power 2006, 128, 840–848. [Google Scholar] [CrossRef]
- Liu, X.; Gong, C.; Liu, S.; Nie, Q. Analytical calculation and experimental study on temperature rising process of steam accumulator. Acta Energiae Solaris Sin. 1998, 19, 102–104. [Google Scholar]
- Yang, S.; Manning, B.W. Fitness for service evaluation of cracked divider plate bolt locking tabs for nuclear steam generators. Nucl. Eng. Des. 2009, 239, 2242–2264. [Google Scholar] [CrossRef]
- Steinmann, W.D.; Eck, M. Buffer storage for direct steam generation. Sol. Energy 2006, 80, 1277–1282. [Google Scholar] [CrossRef]
- Su, S.; Huang, S.Y.; Wang, X.M. Experiments and homogeneous turbulence model of boiling flow in narrow channels. Heat Mass Transf. 2005, 41, 773–779. [Google Scholar]
- Engelhardt, G.R.; Macdonald, D.D.; Millett, P.J. Transport processes in steam generator crevices. II. A simplified method for estimating impurity accumulation rates. Corros. Sci. 1999, 41, 2191–2211. [Google Scholar] [CrossRef]
- Cao, J. Optimization of thermal storage based on load graph of thermal energy system. Int. J. Thermodyn. 2000, 3, 91–97. [Google Scholar]
- Valenzuela, L.; Zarza, E.; Berenguel, M.; Camacho, E.F. Direct steam generation in solar boilers. IEEE Control Syst. Mag. 2004, 24, 15–29. [Google Scholar] [CrossRef]


| Disharing Pressure (MPa) | Charging Pressure (MPa) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.7 | 0.8 | 0.9 | 1.0 | 1.2 | 1.4 | 1.5 | 1.6 | 1.8 | 2.0 | 2.2 | 2.4 | |
| 0.2 | 66 | 74 | 81 | 87 | 99 | 110 | 115 | 119 | 127 | 136 | 143 | 149 |
| 0.3 | 48 | 57 | 65 | 71 | 84 | 95 | 99 | 104 | 113 | 121 | 127 | 134 |
| 0.4 | 33 | 42 | 50 | 57 | 69 | 81 | 86 | 91 | 100 | 108 | 116 | 122 |
| 0.5 | 22 | 31 | 39 | 46 | 59 | 70 | 76 | 80 | 90 | 97 | 106 | 112 |
| 0.6 | - | - | 28 | 34 | 47 | 59 | 65 | 69 | 78 | 87 | 95 | 102 |
| 0.7 | - | - | - | - | 38 | 50 | 56 | 61 | 70 | 78 | 86 | 92 |
| 0.8 | - | - | - | - | - | - | 47 | 53 | 63 | 71 | 78 | 84 |
| 0.9 | - | - | - | - | - | - | - | 44 | 55 | 63 | 70 | 76 |
| 1.0 | - | - | - | - | - | - | - | - | 47 | 56 | 64 | 70 |
| 1.1 | - | - | - | - | - | - | - | - | - | 49 | 57 | 63 |
| 1.2 | - | - | - | - | - | - | - | - | - | 43 | 50 | 56 |
| Item | Value | Unit |
|---|---|---|
| nominal capacity of BOF | 260 | t |
| smelting cycle of BOF | 35 | min |
| oxygen blowing period of BOF | 15 | min |
| pressure of generated steam | 2.45 | MPa |
| temperature of generated steam | 223 | °C |
| charging pressure of SA | 2.40 | MPa |
| discharging pressure of SA | 1.05 | MPa |
| water filling coefficient of SA | 0.90 | - |
| thermal efficiency of SA | 0.99 | - |
| Item | Value | Unit |
|---|---|---|
| charging pressure of SA | 1.50 | MPa |
| discharging pressure of SA | 0.40 | MPa |
| water filling coefficient of SA | 0.90 | - |
| thermal efficiency of SA | 0.99 | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Hong, Y.; Wang, Y. Operation Optimization of Steam Accumulators as Thermal Energy Storage and Buffer Units. Energies 2017, 10, 17. https://doi.org/10.3390/en10010017
Sun W, Hong Y, Wang Y. Operation Optimization of Steam Accumulators as Thermal Energy Storage and Buffer Units. Energies. 2017; 10(1):17. https://doi.org/10.3390/en10010017
Chicago/Turabian StyleSun, Wenqiang, Yuhao Hong, and Yanhui Wang. 2017. "Operation Optimization of Steam Accumulators as Thermal Energy Storage and Buffer Units" Energies 10, no. 1: 17. https://doi.org/10.3390/en10010017
APA StyleSun, W., Hong, Y., & Wang, Y. (2017). Operation Optimization of Steam Accumulators as Thermal Energy Storage and Buffer Units. Energies, 10(1), 17. https://doi.org/10.3390/en10010017






