Harmonic Analyzing of the Double PWM Converter in DFIG Based on Mathematical Model
Abstract
:1. Introduction
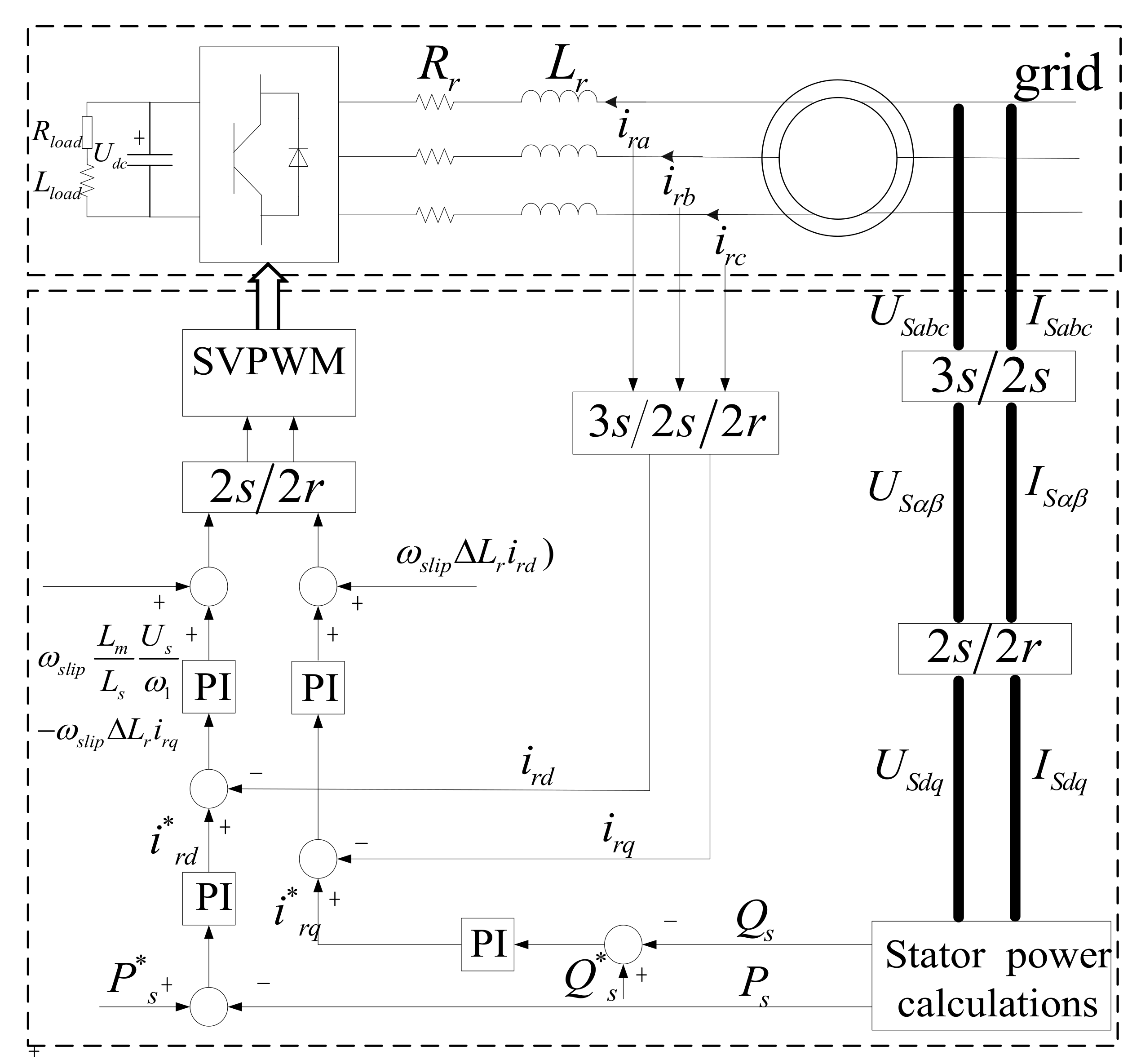
2. Harmonic Modeling of Double PWM Converter
2.1. Low-Order Harmonic Modeling
2.1.1. The Low-Order Harmonic Modeling of GSC in Sub-Synchronous State
2.1.2. The Low-Order Harmonic Modeling of RSC in Super-Synchronous State
2.1.3. The Low-Order Harmonic Modeling of the Inverter
2.2. High-Order Harmonic Modeling
3. Simulations and Experimental Results
3.1. The Low-Order Harmonics of GSCin Sub-Synchronous State
3.2. The Low-Order Harmonics of RSCin Sub-Synchronous State
3.3. The Low-Order Harmonics of RSC in Super-Synchronous State
3.4. The Low-Order Harmonics of GSC in Super-Synchronous State
3.5. The High-Order Harmonics of Current in Converter
4. Conclusions
- (1)
- In sub-synchronous state, both dc link voltage and grid current of GSC contain only the fundamental component.
- (2)
- In super-synchronous state, the rotor current contains only the fundamental component with an offset.
- (3)
- In the inverter side, the output current contains 5th, 7th, 17th order harmonics.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kwon, J.; Wang, X.; Bak, C.L.; Blaabjerg, F. Harmonic instability analysis of single-phase grid connected converter using Harmonic State Space (HSS) modeling method. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Fahad, L.; Anwar, S.S. Optimal configuration analysis for a campus microgrid—A case study. Prot. Control Mod. Power Syst. 2017, 2, 23. [Google Scholar]
- Chen, L.; Deng, C.; Zheng, F. Fault ride-through capability enhancement of DFIG-based wind turbine with a flux-coupling-type SFCL employed at different locations. IEEE Trans. Appl. Superconduct. 2015, 25. [Google Scholar] [CrossRef]
- Wen, Y. Short-Term Wind Power Forecasting Using the Enhanced Particle Swarm Optimization Based Hybrid Method. Energies 2013, 6, 4879–4896. [Google Scholar]
- Morgan, R.; Eduard, D.; Senad, A. Evaluation of a Blade Force Measurement System for a Vertical Axis Wind Turbine Using Load Cells. Energies 2015, 8, 5973–5996. [Google Scholar]
- Sungsu, P.; Yoonsu, N. Two LQRI based Blade Pitch Controls for Wind Turbines. Energies 2012, 5, 1998–2016. [Google Scholar]
- Muller, S.; Deicke, M.; De Doncker, R.W. Doubly Fed Induction Generator Systems for Wind Turbines. IEEE Ind. Appl. Mag. 2002, 8, 26–33. [Google Scholar] [CrossRef]
- Dimitrios, G.; Giaourakis, D.; Safacas, A. Quantitative and Qualitative Behavior Analysis of a DFIG Wind Energy Conversion System by Wind Gust and Converter Faults. Wind Energy 2016, 19, 527–546. [Google Scholar]
- Li, J.; Corzine, K. Harmonic compensation for variable speed DFIG wind turbines using multiple reference frame theory. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015. [Google Scholar]
- Jun, Y.; Qing, L.; Zhe, C.; Aolin, L. Coordinated Control of a DFIG-Based Wind-Power Generation System with SGSC under Distorted Grid Voltage Conditions. Energies 2013, 6, 2541–2561. [Google Scholar]
- Muthana, A.; Mohamed, Z.; Mohamed, R. Feedback Linearization Controller for a Wind Energy Power System. Energies 2016, 9, 771. [Google Scholar]
- Fan, L.; Yuvarajan, S.; Kavasseri, R. Harmonic analysis of a DFIG for a wind energy conversion system. IEEE Trans. Energy Convers. 2010, 25, 181–190. [Google Scholar]
- Li, J.; Nader, S.; Stephen, W. Modeling of Large Wind Farm Systems for Dynamic and Harmonics Analysis. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008. [Google Scholar]
- Fan, L.; Miao, Z.; Yuvarajan, S. A Unified Model of DFIG for Simulating Acceleration with Rotor Injection and Harmonics in Wind Energy Conversion Systems. In Proceedings of the IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Abniki, H.; Nateghi, S. Harmonic Analyzing of Wind Farm Based on Harmonic Modeling of Power System Components. In Proceedings of the 11th International Conference on Environment and Electrical Engineering (EEEIC), Venice, Italy, 18–25 May 2012. [Google Scholar]
- Vandai, L.; Xinran, L.; Yong, L.; Tran, L.; Thang, D.; Caoquyen, L. An Innovative Control Strategy to Improve the Fault Ride-Through Capability of DFIGs Based on Wind Energy Conversion Systems. Energies 2016, 9, 69. [Google Scholar]
- Jabr, H.M.; Lu, D.; Kar, N.C. Design and implementation of neuro-fuzzy vector control for wind-driven doubly-fed induction generator. IEEE Trans. Sustain. Energy 2011, 2, 404–413. [Google Scholar] [CrossRef]
- Li, S.; Haskew, T.A.; Williams, K.A. Control of DFIG wind turbine with direct-current vector control configuration. IEEE Trans. Sustain. Energy 2012, 3, 1–11. [Google Scholar] [CrossRef]
- Mohammadi, J.; Vaez-Zadeh, S.; Afsharnia, S.; Daryabeigi, E. A combined vector and direct power control for DFIG-based wind turbines. IEEE Trans. Sustain. Energy 2014, 5, 767–775. [Google Scholar] [CrossRef]
- Ajami, A.; Oskuee, M.R.J.; Mokhberdoran, A.O. Implementation of Novel Technique for Selective Harmonic Elimination in Multilevel Inverters Based on ICA. Adv. Power Electron. 2013, 10, 847365. [Google Scholar] [CrossRef]
- Junbum, K.; Xiongfei, W.; Frede, B. Harmonic Instability Analysis of a Single-PhaseGrid-Connected Converter Using a HarmonicState-Space Modeling Method. IEEE Trans. Ind. Appl. 2016, 52, 4188–4200. [Google Scholar]
- Gupta, N.P.; Gupta, P.; Masand, D. Power Quality Improvement Using Hybrid Active Power Filter for a DFIG Based Wind Energy Conversion System. In Proceedings of the 3rd Nirma University International Conference on Engineering (NUiCONE), Ahmedabad, India, 6–8 December 2012. [Google Scholar]
- Nian, H.; Song, Y.; Zhou, P.; He, Y. Improved direct power control of a wind turbine driven doubly fed induction generator during transient grid voltage unbalance. IEEE Trans. Energy Convers. 2011, 26, 976–986. [Google Scholar] [CrossRef]
- Li, D.; Song, X. Research on control strategy and modeling-simulation for tracking maximum power point in VSCF wind generation system. In Proceedings of the Electric Information and Control Engineering (ICEICE), Wuhan, China, 15–17 April 2011. [Google Scholar]
- Chen, W.; Xie, S.; Zhu, Z.; Li, L. Multi-channel three-phase converter based on phase-shift space vector modulation. Electr. Power Autom. Equip. 2015, 35, 9–14. [Google Scholar]
- Kostic, D.J.; Avramovic, Z.Z.; Ciric, N.T. A new approach to theoretical analysis of harmonic content of PWM waveforms of single-and multiple-frequency modulators. IEEE Trans. Power Electron. 2013, 28, 4557–4567. [Google Scholar] [CrossRef]
- Beres, R.; Wang, X.; Blaabjerg, F. A review of passive filters for grid-connected voltage source converters. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 16–20 March 2014. [Google Scholar]
- Tooth, D.J.; Finney, S.J.; Williams, B.W. Fourier theory of jumps applied to converter harmonic analysis. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 109–122. [Google Scholar] [CrossRef]
- Huang, Z.A.; Zou, X.B.; Li, F.C.; Zou, Y.D.; Tong, L.E. A novel filter for harmonics and inter-harmonics analysis and suppression in AC electronic load. In Proceedings of the 8th International Conference on Power Electronics (ICPE & ECCE), Jeju, Korea, 30 May–3 June 2011. [Google Scholar]
- Peng, L.; Ming, D.; Jianxun, W.; Xiaolong, L. Analysis about the parameters calculation of characteristic interharmonic in the voltage source type AC/DC/AC frequency converter. In Proceedings of the China International Conference on Electricity Distribution (CICED), Shanghai, China, 10–14 September 2012. [Google Scholar]
- Longchang, W.; Houlei, G.; Guibin, Z. Modeling methodology and fault simulation of distribution networks integrated with inverter-based DG. Prot. Control Mod. Power Syst. 2017, 2, 31. [Google Scholar]
- Zhu, R.; Zhe, C.; Yi, T. Dual-loop control strategy for DFIG-based Wind turbines under grid voltage disturbances. IEEE Trans. Power Electron. 2016, 31, 2239–2253. [Google Scholar] [CrossRef]
- Alaboudy, A.H.K.; Zeineldin, H.H. Flicker minimization of DFIG based wind turbines with optimal reactive current management. In Proceedings of the IEEE PES Conference on Innovative Smart Grid Technologies-Middle East (ISGT Middle East), Jeddah, Saudi Arabia, 17–20 December 2011. [Google Scholar]














| A0n | n | A0n | |
|---|---|---|---|
| 3 | 0.095 | 11 | 0 |
| 4 | 0 | 12 | 0 |
| 5 | 0.1 | 13 | 0 |
| 6 | 0 | 14 | 0 |
| 7 | 0.0475 | 15 | 0.0235 |
| 8 | 0 | 16 | 0 |
| 9 | 0.0475 | 17 | 0.0235 |
| 10 | 0 | 18 | 0 |
| A0c | n | A0c | |
|---|---|---|---|
| 3 | 0 | 11 | 0 |
| 4 | 0 | 12 | 0 |
| 5 | 0.1 | 13 | 0 |
| 6 | 0 | 14 | 0 |
| 7 | 0.0475 | 15 | 0 |
| 8 | 0 | 16 | 0 |
| 9 | 0 | 17 | 0.0235 |
| 10 | 0 | 18 | 0 |
| n | A0na | A0nc | cn | cna |
|---|---|---|---|---|
| 3 | 18 | 19 | 0.5% | 5.6% |
| 5 | 21 | 20 | 0.5% | 4.8% |
| 7 | 10.5 | 9.5 | 0.5% | 9.5% |
| 9 | 12.5 | 9.5 | 1.5% | 24% |
| 15 | 6.5 | 4.7 | 0.9% | 27.7% |
| 17 | 7.8 | 4.7 | 1.55% | 39.7% |
| n | A0ca | A0cc | cc | cca |
|---|---|---|---|---|
| 5 | 32 | 31.5 | 0.16% | 1.6% |
| 7 | 17 | 15 | 0.63% | 11.8% |
| 17 | 11 | 7.5 | 1.11% | 31.8% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Liu, Z. Harmonic Analyzing of the Double PWM Converter in DFIG Based on Mathematical Model. Energies 2017, 10, 2087. https://doi.org/10.3390/en10122087
Liu J, Liu Z. Harmonic Analyzing of the Double PWM Converter in DFIG Based on Mathematical Model. Energies. 2017; 10(12):2087. https://doi.org/10.3390/en10122087
Chicago/Turabian StyleLiu, Jing, and Zhigang Liu. 2017. "Harmonic Analyzing of the Double PWM Converter in DFIG Based on Mathematical Model" Energies 10, no. 12: 2087. https://doi.org/10.3390/en10122087




