Impact of Distributed Generation Grid Code Requirements on Islanding Detection in LV Networks
Abstract
:1. Introduction
2. Present Standard and Requirements for Distributed Generators (DGs) Connected to Low Voltage (LV) Networks
2.1. P/f and Q/V Regulations
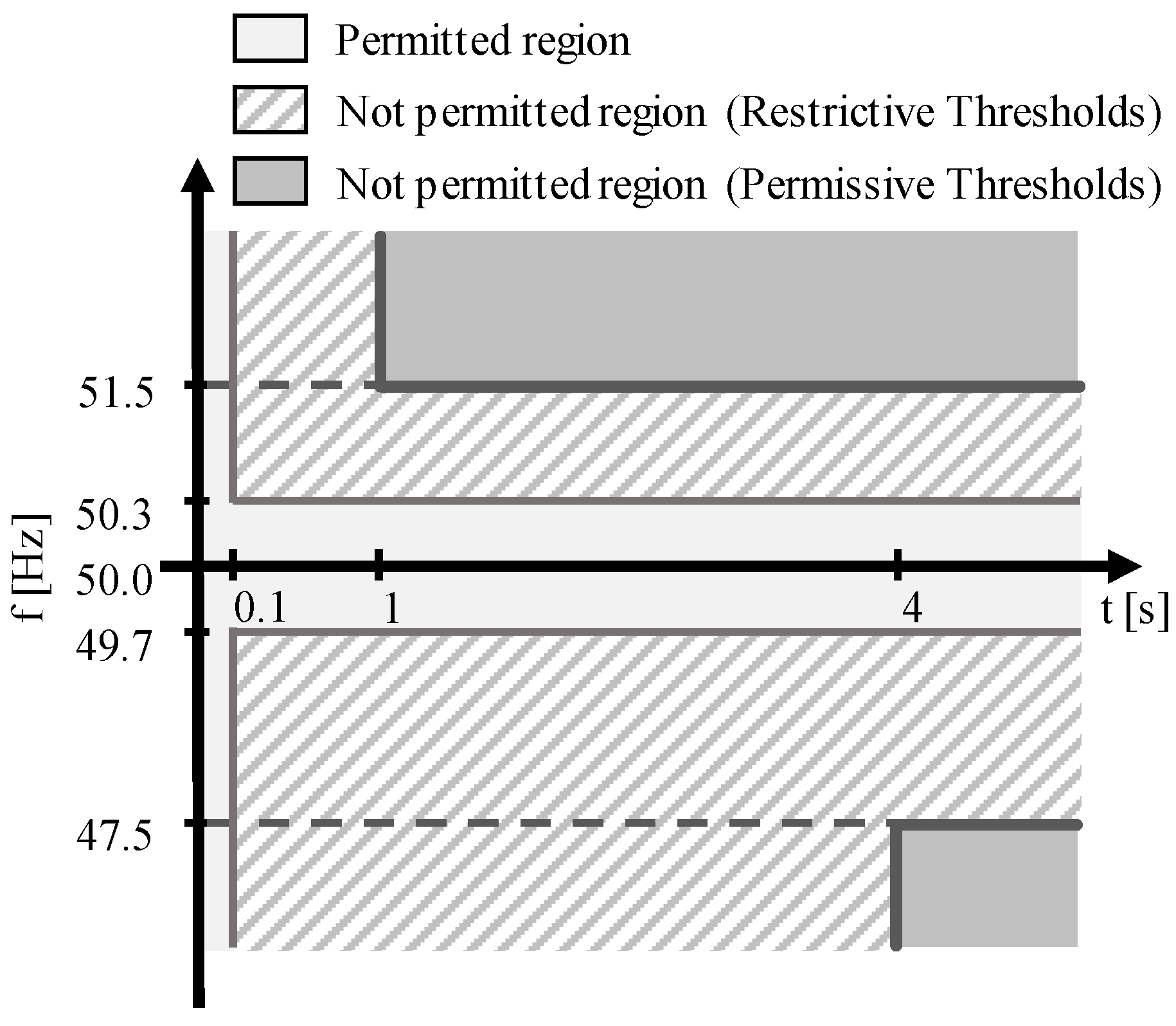
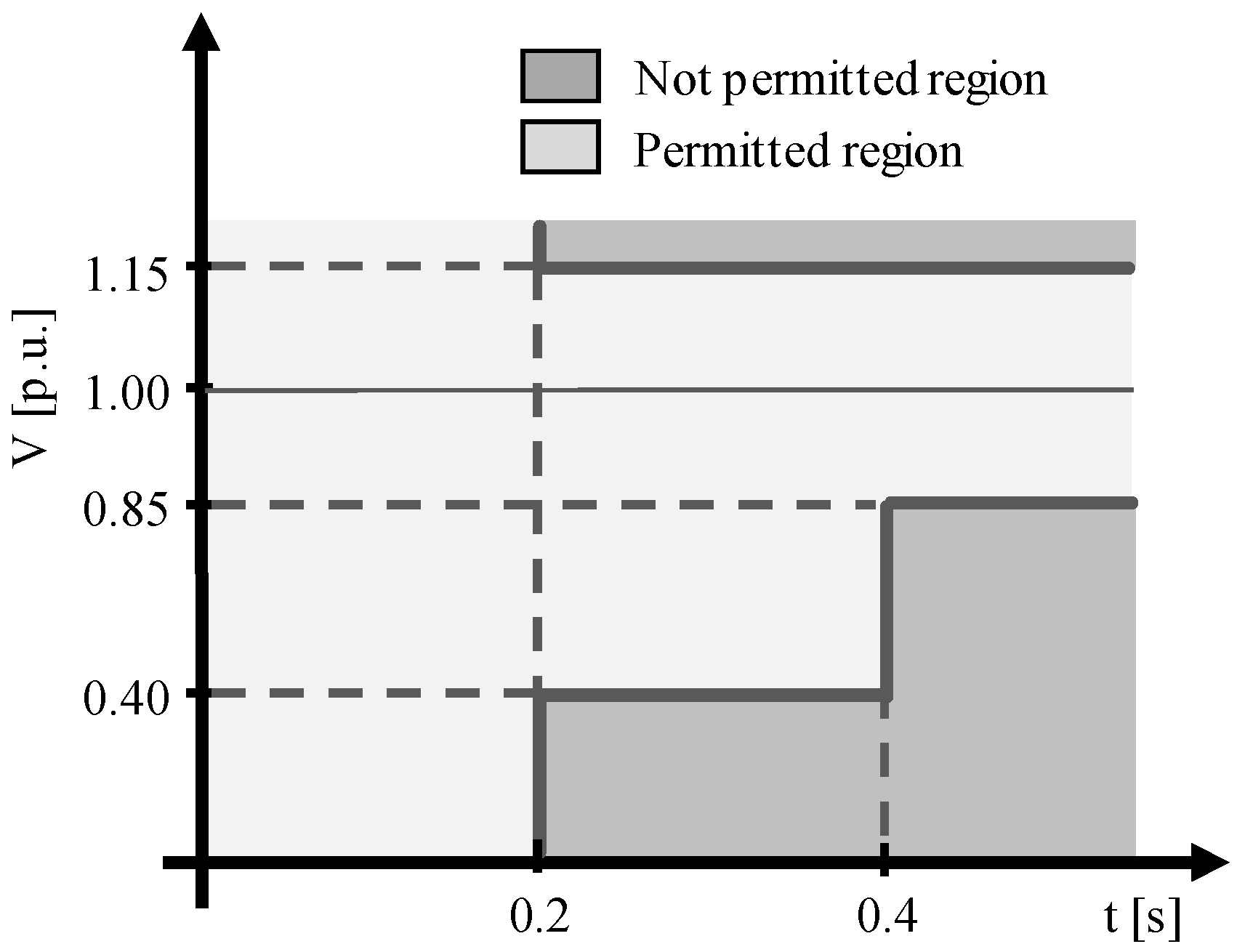
2.2. Interface Protection System
3. Additional LV DGs Stabilizing Functions
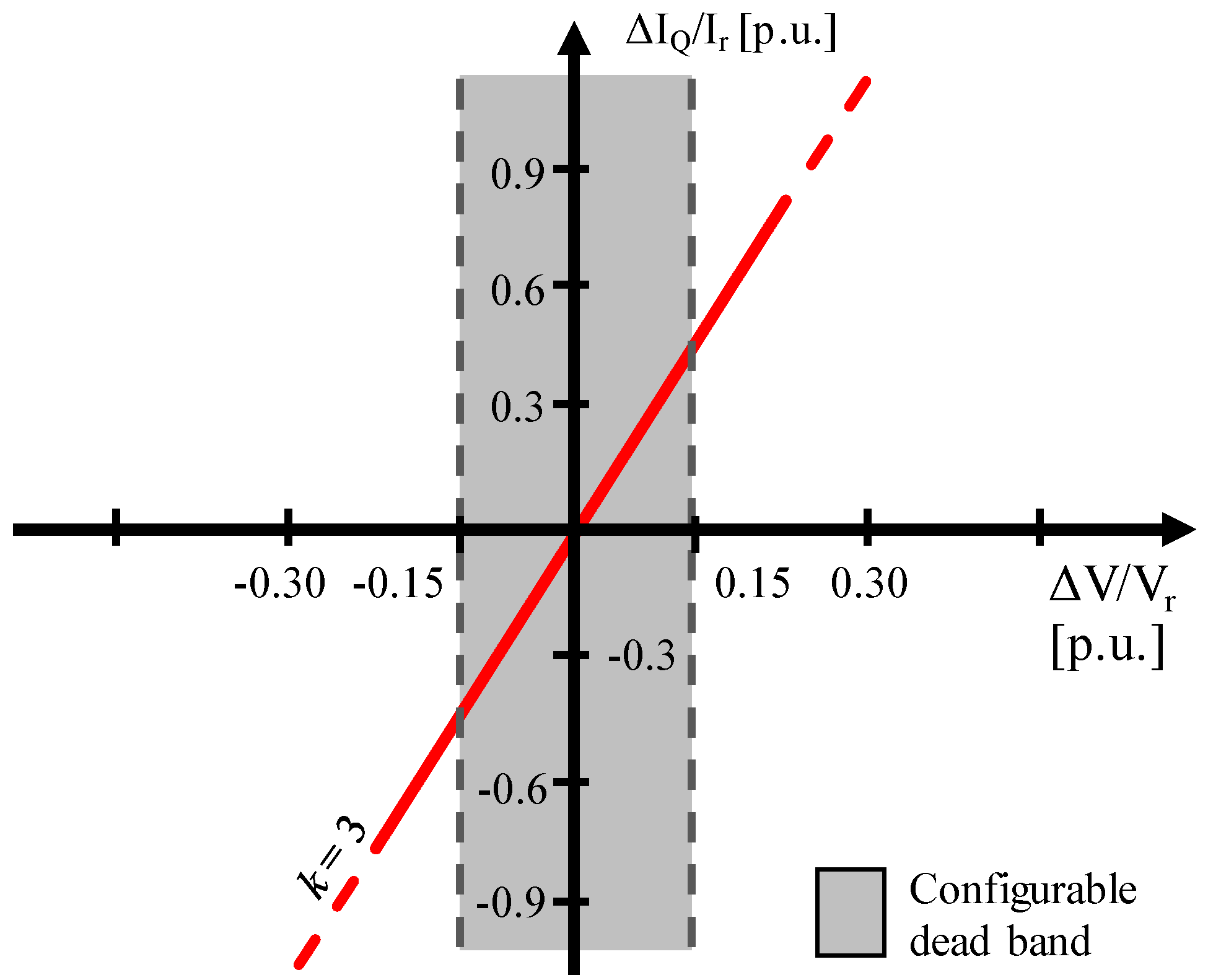
3.1. Voltage Support Strategies
3.2. Synthetic Inertia
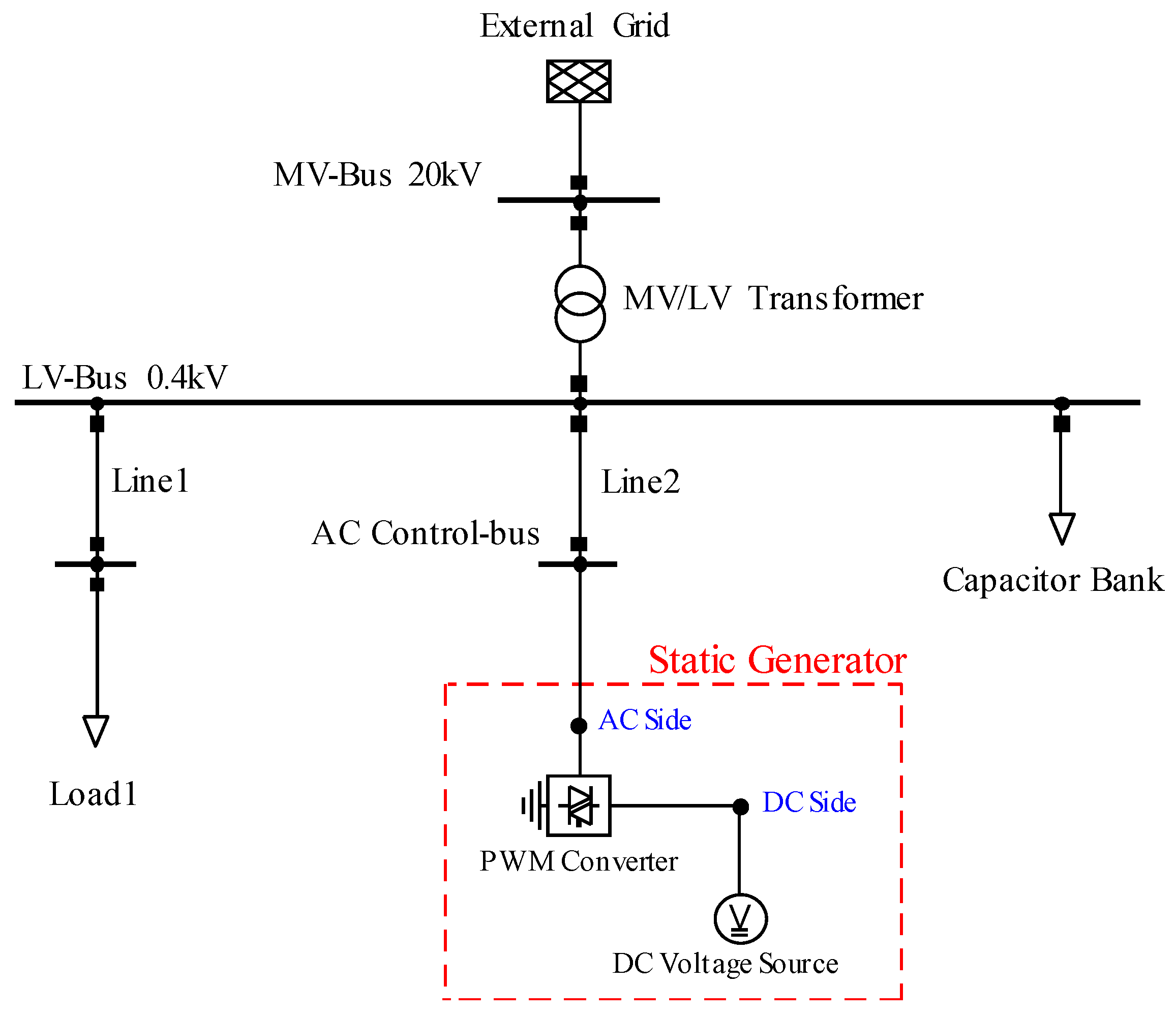
4. Low Voltage Network Study Case
4.1. Network Data
- An active end-user: the unexpected islanding is analysed in terms of potential safety issues for untrained people.
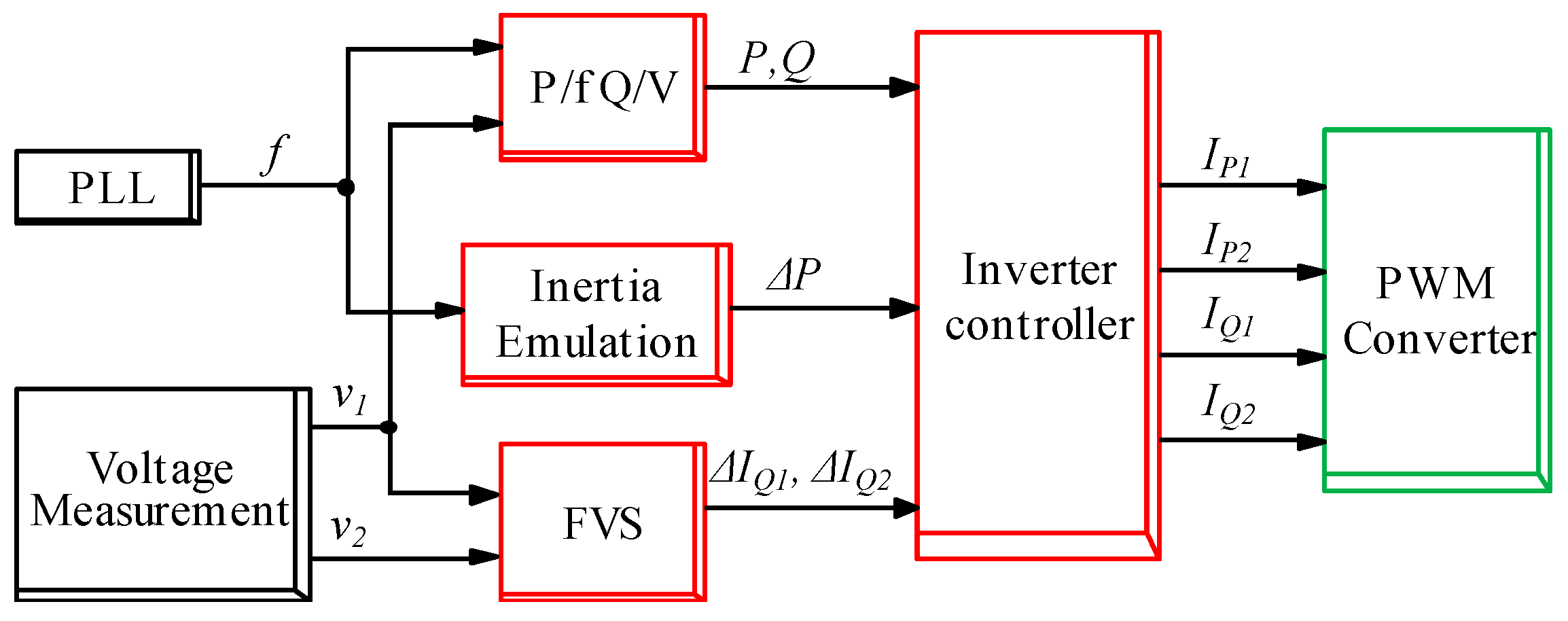
4.2. Generator Model
5. Results
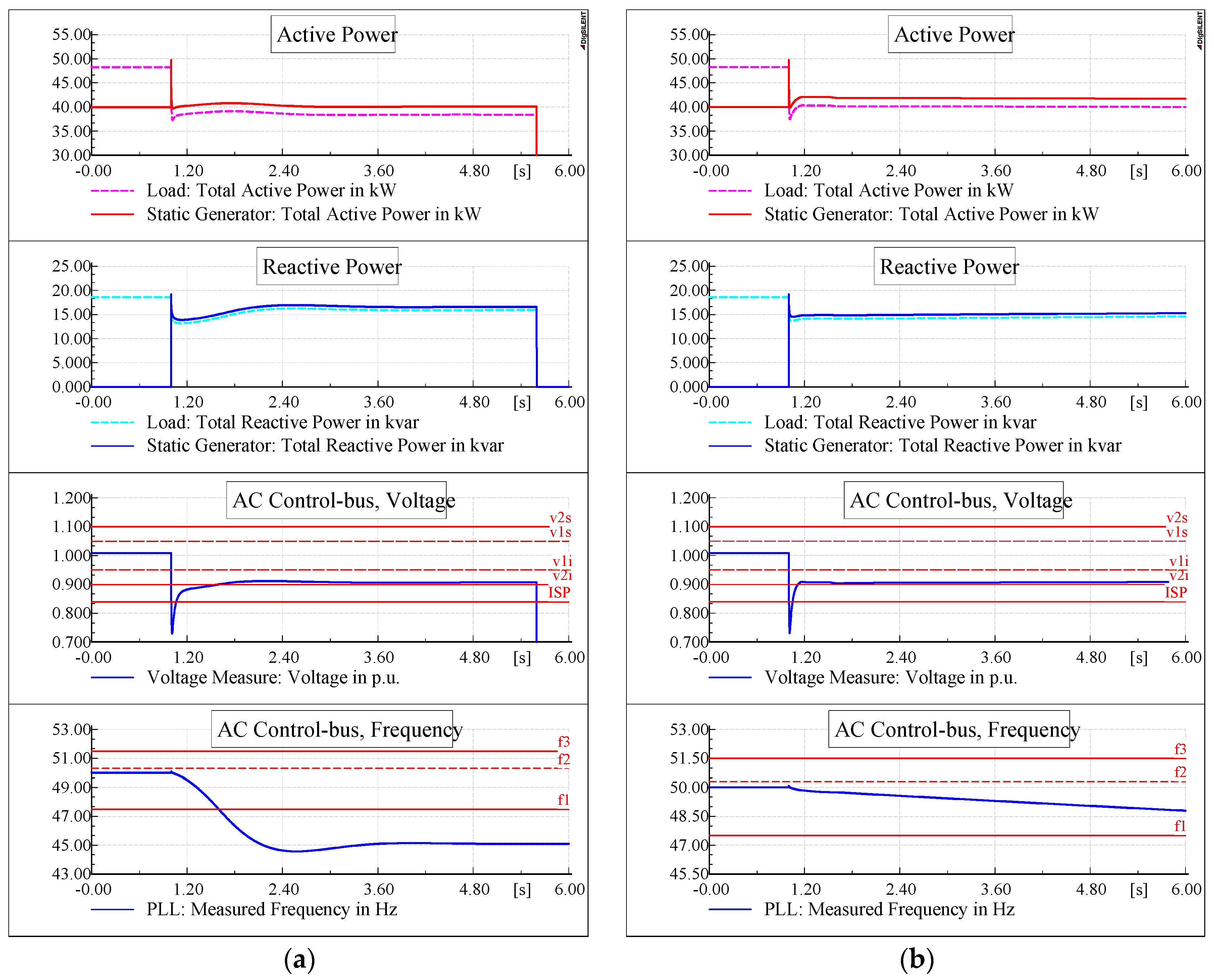
5.1. Islanded Network Stability
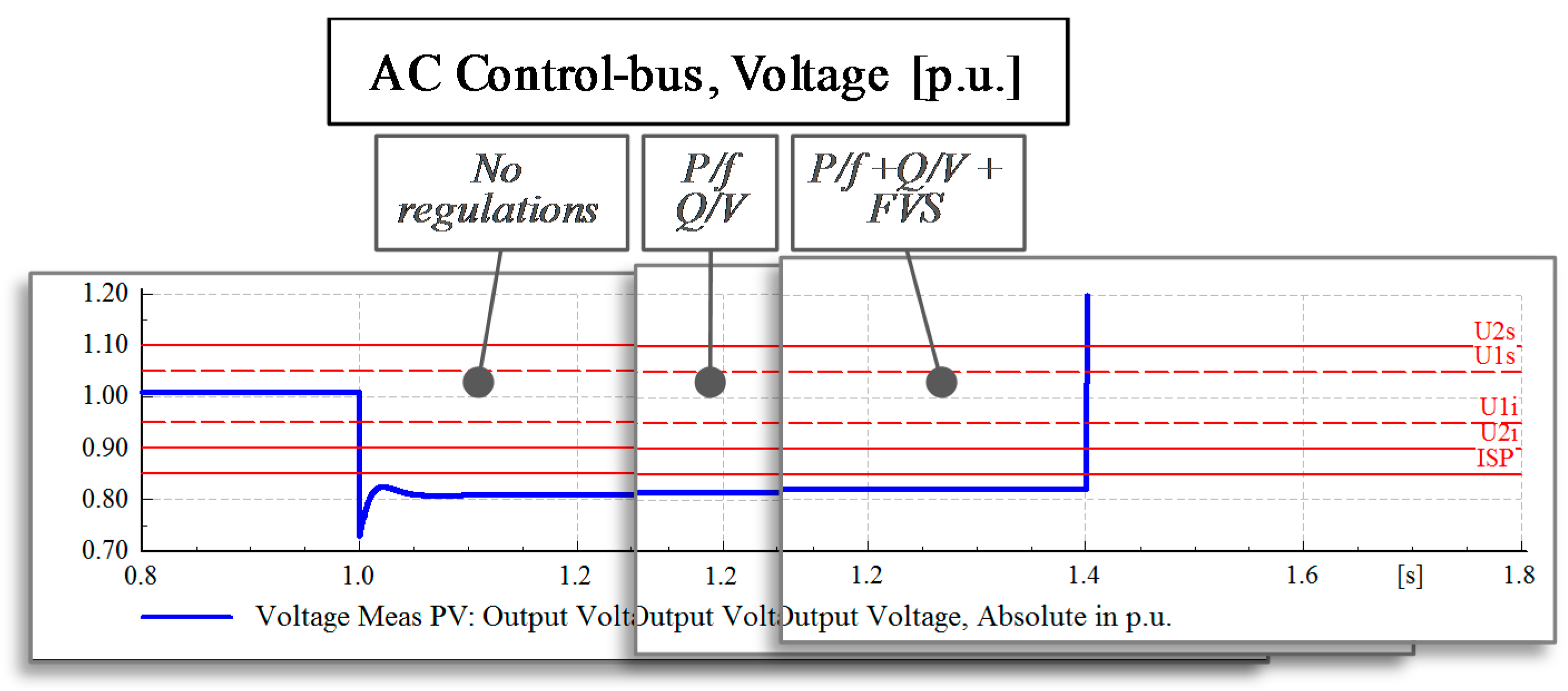
5.2. Voltage Levels during Faults
6. Conclusions
Author Contributions
Conflicts of Interest
References
- European Committee for Electrotechnical Standardization. Requirements for Generating Plants to Be Connected in Parallel with Distribution Networks—Part 1: Connection to a LV Distribution Network above 16 A; Technical Specification CENELEC TS 50549-1; European Committee for Electrotechnical Standardization (CENELEC): Brussels, Belgium, 2015. [Google Scholar]
- European Committee for Electrotechnical Standardization. Requirements for Generating Plants to Be Connected in Parallel with Distribution Networks–Part 2: Connection to a MV Distribution System; Technical Specification CENELEC TS 50549-2; CENELEC: Brussels, Belgium, 2015. [Google Scholar]
- European Committee for Electrotechnical Standardization. Requirements for Micro-Generating Plants to Be Connected in Parallel with Public Low-Voltage Distribution Networks; European Standard CENELEC EN 50438; CENELEC: Brussels, Belgium, 2013. [Google Scholar]
- Comitato Elettrotecnico Italiano. Reference Technical Rules for the Connection of Active and Passive Consumers to the HV and MV Electrical Networks of Distribution Company; CEI 0-16; CEI: Milan, Italy, 2016. [Google Scholar]
- Comitato Elettrotecnico Italiano. Reference Technical Rules for the Connection of Active and Passive Users to the LV Electrical Utilities; CEI 0-21; CEI: Milan, Italy, 2016. [Google Scholar]
- Bignucolo, F.; Caldon, R.; Prandoni, V. Radial MV networks voltage regulation with distribution management system coordinated controller. Electr. Power Syst. Res. 2008, 78, 634–645. [Google Scholar] [CrossRef]
- Bignucolo, F.; Caldon, R.; Carradore, L.; Sacco, A.; Turri, R. Role of storage systems and market based ancillary services in active distribution networks management. In Proceedings of the 43rd International Conference on Large High Voltage Electric Systems (CIGRE), Paris, France, 22–27 August 2010; p. 9.
- Kang, H.-K.; Chung, I.-Y.; Moon, S.-I. Voltage control method using distributed generators based on a multi-agent system. Energies 2015, 8, 14009–14025. [Google Scholar] [CrossRef]
- Yang, J.-S.; Choi, J.-Y.; An, G.-H.; Choi, Y.-J.; Kim, M.-H.; Won, D.-J. Optimal scheduling and real-time state-of-charge management of energy storage system for frequency regulation. Energies 2016, 9, 1010. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Yuan, W.; Han, H.; Zhong, C.; Guerrero, J.M. Conventional P-ω/Q-V droop control in highly resistive line of low-voltage converter-based ac microgrid. Energies 2016, 9, 943. [Google Scholar] [CrossRef]
- Vandoorn, T.L.; Renders, B.; Degroote, L.; Meersman, B.; Vandevelde, L. Active load control in islanded microgrids based on the grid voltage. IEEE Trans. Smart Grid 2011, 2, 139–151. [Google Scholar] [CrossRef]
- Latif, A.; Gawlik, W.; Palensky, P. Quantification and mitigation of unfairness in active power curtailment of rooftop photovoltaic systems using sensitivity based coordinated control. Energies 2016, 9, 436. [Google Scholar] [CrossRef]
- Blazic, B.; Papic, I. Voltage profile support in distribution networks—Influence of the network R/X ratio. In Proceedings of the 13th Power Electronics and Motion Control (EPE-PEMC) Conference, Poznan, Poland, 1–3 September 2008; pp. 2510–2515.
- Caldon, R.; Coppo, M.; Turri, R. Voltage unbalance compensation in LV networks with inverter interfaced distributed energy resources. In Proceedings of the IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 527–532.
- Caldon, R.; Coppo, M.; Turri, R. Coordinated voltage control in MV and LV distribution networks with inverter-interfaced users. In Proceedings of the IEEE Grenoble Conference (PowerTech), Grenoble, France, 16–20 June 2013.
- Bignucolo, F.; Bertoluzzo, M.; Fontana, C. Applications of the solid state transformer concept in the electrical power system. In Proceedings of the International Annual Conference (AEIT), Napoli, Italy, 14–16 October 2015.
- Savio, A.; Bignucolo, F.; Caldon, R. Contribution of MV static distributed generation to voltage unbalance mitigation. In Proceedings of the AEIT International Annual Conference, Capri, Italy, 5–7 October 2016.
- Bignucolo, F.; Caldon, R.; Frigo, M.; Morini, A.; Pitto, A.; Silvestro, F. Impact of distributed generation on network security: Effects on loss-of-main protection reliability. In Proceedings of the Universities Power Engineering Conference (UPEC), Padova, Italy, 1–4 September 2008.
- Caldon, R.; Coppo, M.; Sgarbossa, R.; Turri, R. Risk of unintentional islanding in LV distribution networks with inverter-based DGs. In Proceedings of the 48th International Power Engineering Conference, Dublin, UK, 2–5 September 2013; pp. 1–6.
- Sgarbossa, R.; Lissandron, S.; Mattavelli, P.; Turri, R.; Cerretti, A. Analysis of ΔP-ΔQ area of uncontrolled islanding in low voltage grids with PV generators. IEEE Trans. Ind. Appl. 2016, 52, 2387–2396. [Google Scholar] [CrossRef]
- Cerretti, A.; D’Orazio, L.; Pezzato, C.; Sapienza, G.; Valvo, G.; Camalleri, N.; Mattavelli, P.; Sgarbossa, R.; Turri, R.; De Berardinis, E. Uncontrolled islanding operations of MV/LV active distribution networks. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6.
- Amadei, F.; Cerretti, A.; Coppo, M.; Mattavelli, P.; Sgarbossa, R.; Turri, R. Temporary islanding operations of MV/LV active distribution networks under fault conditions. In Proceedings of the 49th International Universities Power Engineering Conference, Cluj-Napoca, Romania, 2–5 September 2014; pp. 1–6.
- Bignucolo, F.; Savio, A.; Turri, R.; Cerretti, A. Undesired islanding of MV networks sustained by LV dispersed generators compliant with present grid code requirements. In Proceedings of the 51st International Universities UPEC, Coimbra, Portugal, 6–9 September 2016.
- Sundar, D.J.; Kumaran, M.S. A comparative review of islanding detection schemes in distributed generation systems. Int. J. Renew. Energy Res. 2015, 5, 1016–1023. [Google Scholar]
- Fazio, A.R.D.; Russo, M.; Valeri, S. A new protection system for islanding detection in LV distribution systems. Energies 2015, 8, 3775–3793. [Google Scholar] [CrossRef]
- Ahmad, A.; Rajaji, L. Anti islanding technique for grid connected residential solar inverter system. In Proceedings of the Institution of Engineering and Technology (IET) Chennai Fourth International Conference on Sustainable Energy and Intelligent Systems (SEISCON), Chennai, India, 12–14 December 2013; pp. 114–118.
- Cataliotti, A.; Cosentino, V.; Guaiana, S.; Di Cara, D.; Panzavecchia, N.; Tinè, G. An interface protection system with power line communication for distributed generators remote control. In Proceedings of the 2014 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 24–26 September 2014; pp. 1–6.
- Bufano, V.; D’Adamo, C.; D’Orazio, L.; D’Orinzi, C. Innovative solutions to control unintentional islanding on LV network with high penetration of distributed generation. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED), Stockholm, Sweden, 10–13 June 2013; pp. 1–4.
- Bufano, V.; Camalleri, N.; Cerretti, A.; D’Adamo, C.; D’Orazio, L.; Pezzato, C.; De Berardinis, E. Risk of uncontrolled islanding on active distribution networks short term countermeasures taken by Enel Distribuzione. In Proceedings of the 23nd International Conference and Exhibition on Electricity Distribution, Lyon, France, 15–18 June 2015.
- Kniccic, S.; Chandra, A.; Lagacé, P.; Papic, M. Dynamic voltage support of the transmission network from distribution level. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006.
- Marinopoulos, A.; Papandrea, F.; Reza, M.; Norrga, S.; Spertino, F.; Napoli, R. Grid integration aspects of large solar PV installations: LVRT capability and reactive power/voltage support requirements. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 18–19 May 2011; pp. 1–8.
- Lammert, G.; Heß, T.; Schmidt, M.; Schegner, P.; Braun, M. Dynamic grid support in low voltage grids-fault ride-through and reactive power/voltage support during grid disturbances. In Proceedings of the Power Systems Computation Conference (PSCC), Wroclaw, Poland, 18–22 August 2014; pp. 1–7.
- Camacho, A.; Castilla, M.; Miret, J.; Vasquez, J.; Alarcon-Gallo, E. Flexible voltage support control for three-phase distributed generation inverters under grid fault. IEEE Trans. Ind. Electron. 2013, 60, 1429–1441. [Google Scholar] [CrossRef]
- Camacho, A.; Castilla, M.; Miret, J.; Guzman, R.; Borreli, A. Reactive power control for distributed generation power plants to comply with voltage limits during grid faults. IEEE Trans. Power Electron. 2014, 29, 6224–6234. [Google Scholar] [CrossRef]
- Sulla, F.; Svensson, J.; Samuelsson, O. Wind turbines voltage support in weak grids. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5.
- Rahmann, C.; Jara, J.; Salles, M.B. Effects of inertia emulation in modern wind parks on isolated power systems. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5.
- Gonzales-Longatt, F.; Chikuni, E.; Rashayi, E. Effects of the synthetic inertia from wind power on the total system inertia after a frequency disturbance. In Proceedings of the 2013 IEEE International Conference on Industrial Technology (ICIT), Cape Town, South Africa, 25–28 February 2013; pp. 826–832.
- Mentesidi, K.; Garde, R.; Aguado, M.; Rikos, E. Implementation of a fuzzy logic controller for virtual inertia emulation. In Proceedings of the 2015 International Symposium on Smart Electric Distribution Systems and Technologies (EDST), Vienna, Austria, 8–11 September 2015; pp. 606–611.
- Gavriluta, C.; Candela, I.; Rocabert, J.; Exteberria-Otadui, I.; Rodriguez, P. Storage system requirements for grid supporting PV-power plants. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 5323–5330.
- Thiesen, H.; Jauch, C.; Gloe, A. Design of a system substituting today’s inherent inertia in the European continental synchronous area. Energies 2016, 9, 582. [Google Scholar] [CrossRef]
- Visconti, I.F.; Lima, D.A.; de Sousa Costa, J.M.C.; de B.C. Sobrinho, N.R. Measurement-Based load modeling using transfer functions for dynamic simulations. IEEE Trans. Power Syst. 2014, 29, 111–120. [Google Scholar]
- Vignesh, V.; Chakrabarti, S.; Srivastava, S.C. Power system load modelling under large and small disturbances using phasor measurement units data. IET Gener. Transm. Dis. 2015, 9, 1316–1323. [Google Scholar]
- Savio, A.; Bignucolo, F.; Sgarbossa, R.; Mattavelli, P.; Cerretti, A.; Turri, R. A novel measurement-based procedure for load dynamic equivalent identification. In Proceedings of the 2015 IEEE 1st International Forum on Research and Technologies for Society and Industry Leveraging a better tomorrow (RTSI), Turin, Italy, 16–18 September 2015; pp. 274–279.
- Milanović, J.; Matevosiyan, J.; Gaikwad, A. TB 566: Modeling and Aggregation of Loads in Flexible Power Networks —WG C4.605; Technical Report; International Council on Large Electric systems (CIGRE): Paris, France, 2014. [Google Scholar]
- Cocchi, L.; Cerretti, A.; Deberardinis, E.; Bignucolo, F.; Savio, A.; Sgarbossa, R. Influence of average power factor management on active distribution networks. In Proceedings of the 23nd International Conference and Exhibition on Electricity Distribution (CIRED), Lyon, France, 15–18 June 2015.
- Bignucolo, F.; Savio, A.; Caldon, R. Effects of average power factor management in distribution systems with dispersed generation. In Proceedings of the 2016 International Annual Conference (AEIT), Capri, Italy, 5–7 October 2016.
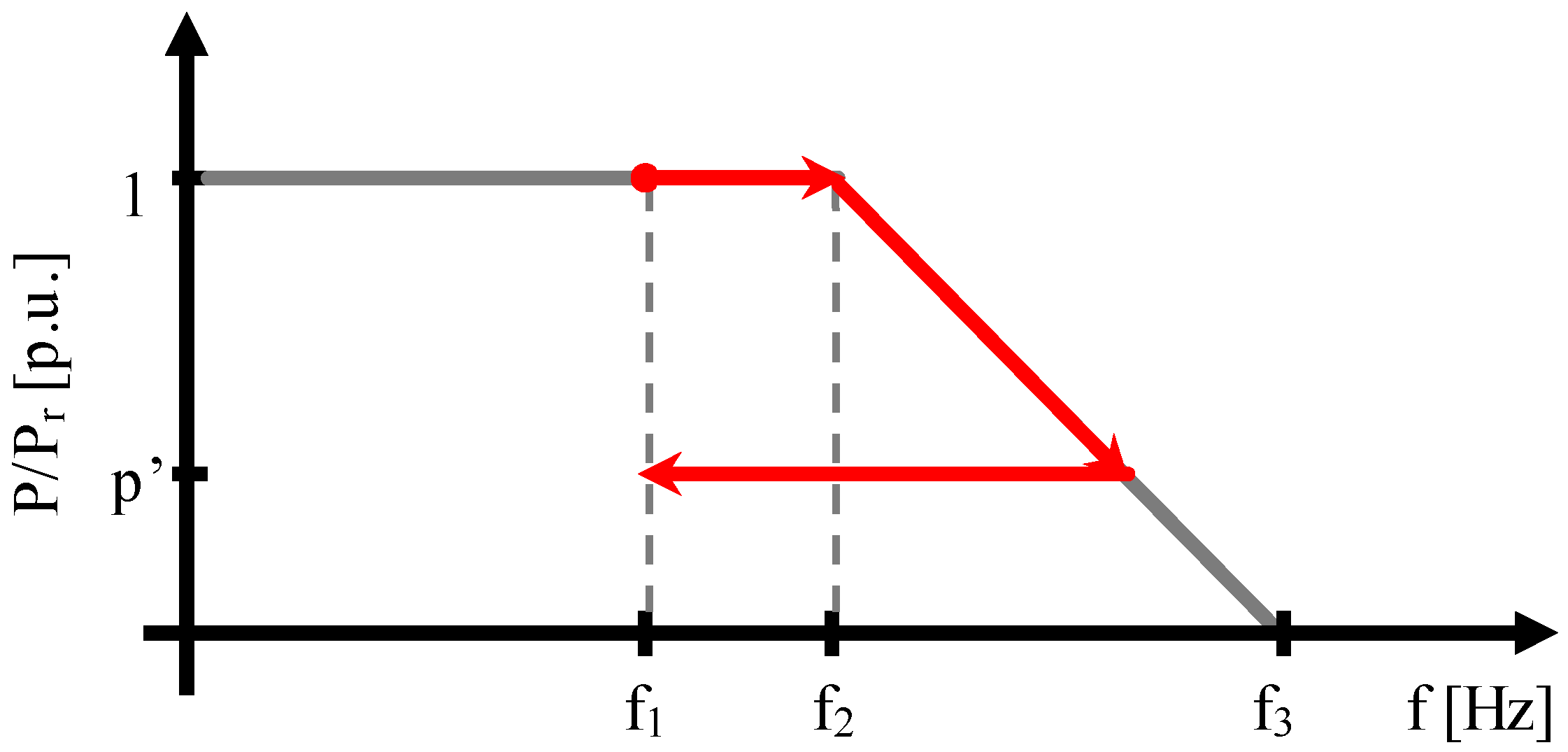
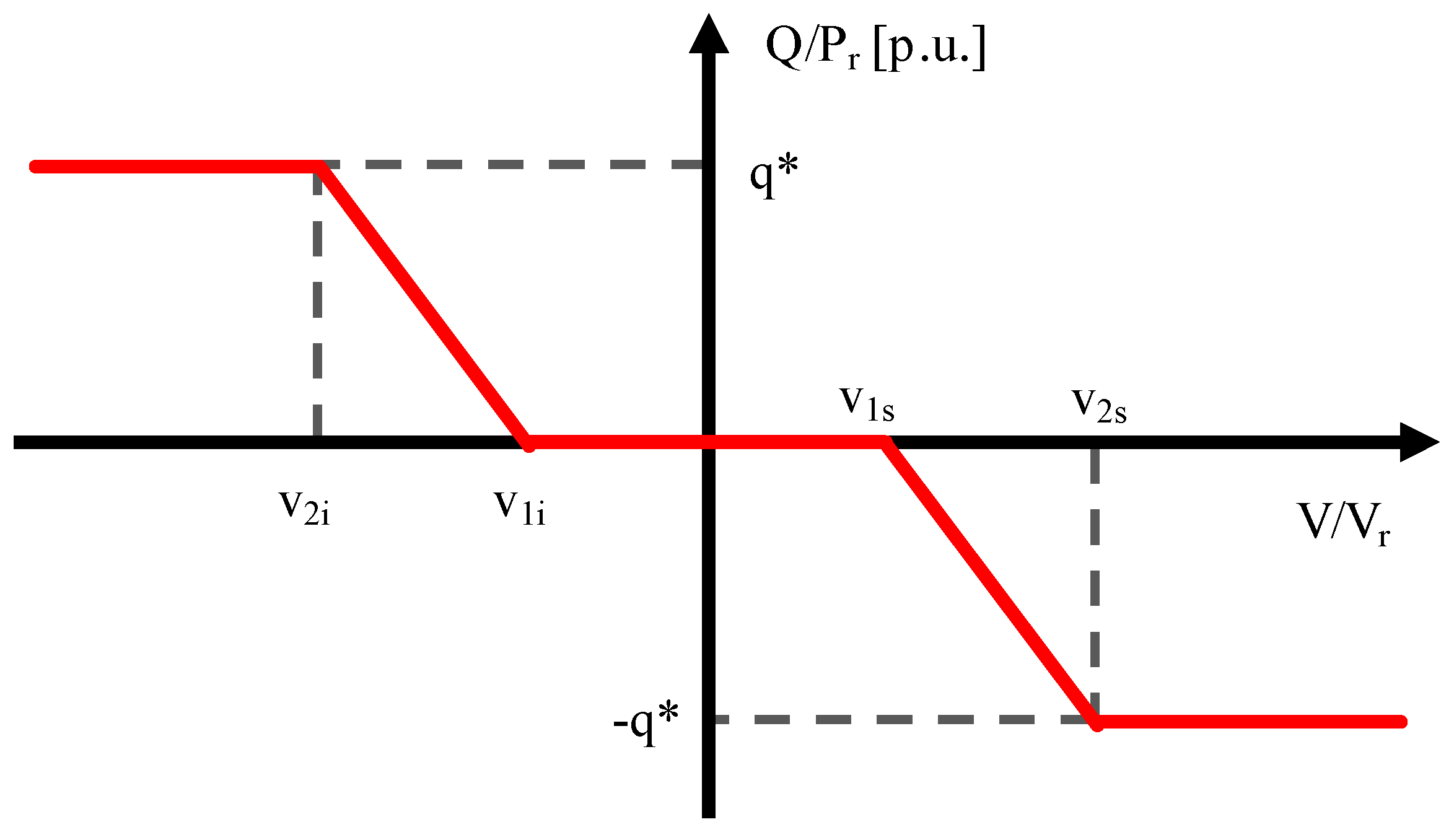

| P/f Regulation Characteristic | Q/V Regulation Characteristic | ||
|---|---|---|---|
| f1 | 50.0 Hz | v2s | 1.10 p.u. |
| f2 | 50.3 Hz | v1s | 1.05 p.u. |
| f3 | 51.5 Hz | v1i | 0.95 p.u. |
| ‑ | ‑ | v2s | 0.90 p.u. |
| ‑ | ‑ | q* | 0.4843 p.u. |
| Generator Psetpoint | Case | P/f and Q/V | Synthetic Inertia | IPS Correct Action (without CB) | IPS Correct Action (with CB) |
|---|---|---|---|---|---|
| 40 kW (80% of Pload) | i.a | OFF | OFF | YES | NO |
| i.b | ON | OFF | YES | YES | |
| i.c | ON | ON | NO | NO | |
| 50 kW (100% of Pload) | ii.a | OFF | OFF | YES | NO |
| ii.b | ON | OFF | NO | NO | |
| ii.c | ON | ON | NO | NO | |
| 60 kW (120% of Pload) | iii.a | OFF | OFF | YES | YES |
| iii.b | ON | OFF | NO | NO | |
| iii.c | ON | ON | NO | NO |
| P/f and Q/V | Synthetic Inertia | Load Power Factor | Ranges of DG Active Power Psetpoint Involving a IPS Failure, Compared with Pload |
|---|---|---|---|
| OFF | OFF | 0.928 (no compensation) | --- |
| 0.95 (3.6 kVAr) | --- | ||
| 0.98 (9.9 kVAr) | --- | ||
| 1.00 (20 kVAr) | 76%–116% of Pload | ||
| ON | OFF | 0.928 (no compensation) | 82%–164% of Pload |
| 0.95 (3.6 kVAr) | 82%–164% of Pload | ||
| 0.98 (9.9 kVAr) | 84%–168% of Pload | ||
| 1.00 (20 kVAr) | 86%–172% of Pload | ||
| ON | ON | 0.928 (no compensation) | 74%–186% of Pload |
| 0.95 (3.6 kVAr) | 74%–86% of Pload | ||
| 0.98 (9.9 kVAr) | 76%–188% of Pload | ||
| 1.00 (20 kVAr) | 79%–190% of Pload |
| Generator Psetpoint | P/f and Q/V | FVS | IPS Correct Action |
|---|---|---|---|
| 40 kW (80% of Pload) | OFF | OFF | YES |
| ON | OFF | YES | |
| ON | ON | YES | |
| 50 kW (100% of Pload) | OFF | OFF | YES |
| ON | OFF | YES | |
| ON | ON | YES | |
| 60 kW (120% of Pload) | OFF | OFF | YES |
| ON | OFF | YES | |
| ON | ON | YES |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bignucolo, F.; Cerretti, A.; Coppo, M.; Savio, A.; Turri, R. Impact of Distributed Generation Grid Code Requirements on Islanding Detection in LV Networks. Energies 2017, 10, 156. https://doi.org/10.3390/en10020156
Bignucolo F, Cerretti A, Coppo M, Savio A, Turri R. Impact of Distributed Generation Grid Code Requirements on Islanding Detection in LV Networks. Energies. 2017; 10(2):156. https://doi.org/10.3390/en10020156
Chicago/Turabian StyleBignucolo, Fabio, Alberto Cerretti, Massimiliano Coppo, Andrea Savio, and Roberto Turri. 2017. "Impact of Distributed Generation Grid Code Requirements on Islanding Detection in LV Networks" Energies 10, no. 2: 156. https://doi.org/10.3390/en10020156
APA StyleBignucolo, F., Cerretti, A., Coppo, M., Savio, A., & Turri, R. (2017). Impact of Distributed Generation Grid Code Requirements on Islanding Detection in LV Networks. Energies, 10(2), 156. https://doi.org/10.3390/en10020156









