Wind Turbine Power Curve Design for Optimal Power Generation in Wind Farms Considering Wake Effect
Abstract
:1. Introduction
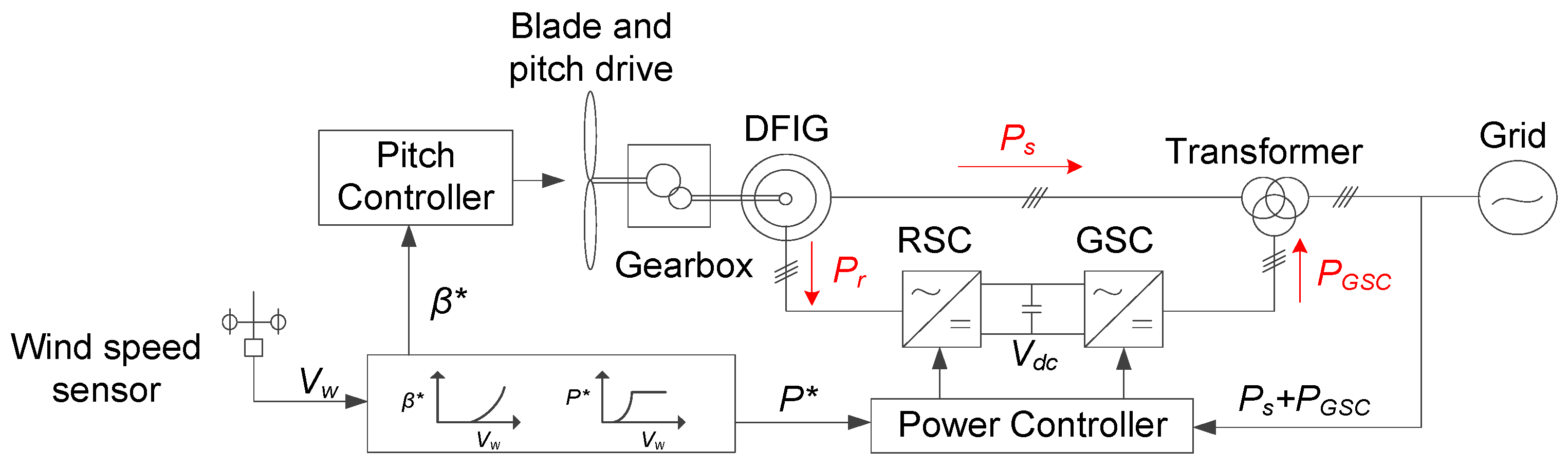
2. DFIG Wind Turbine and MPPT
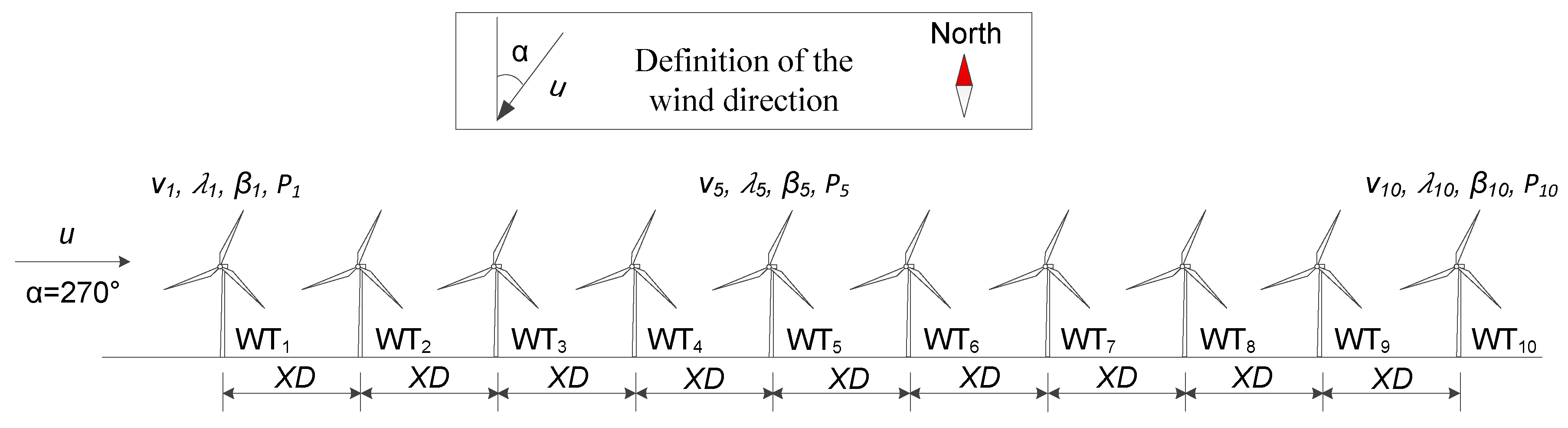
3. Wake Effect and Active Power Maximization in a Two-Turbine Wind Farm
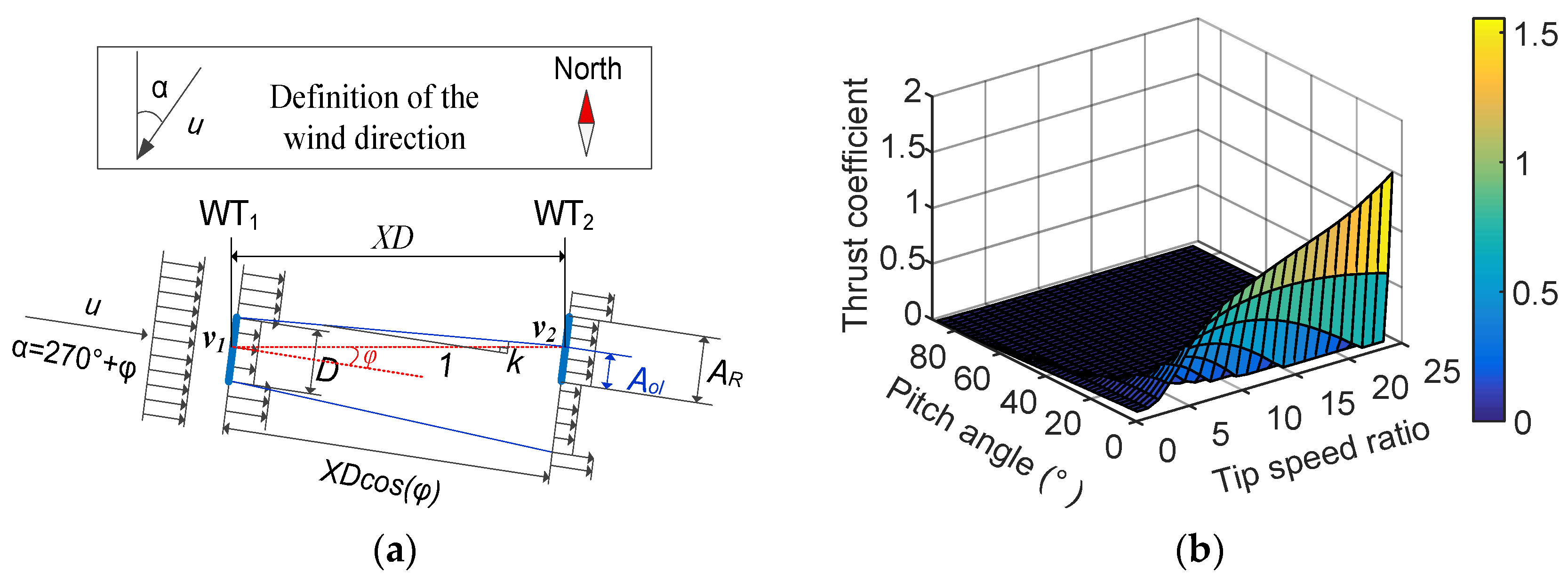
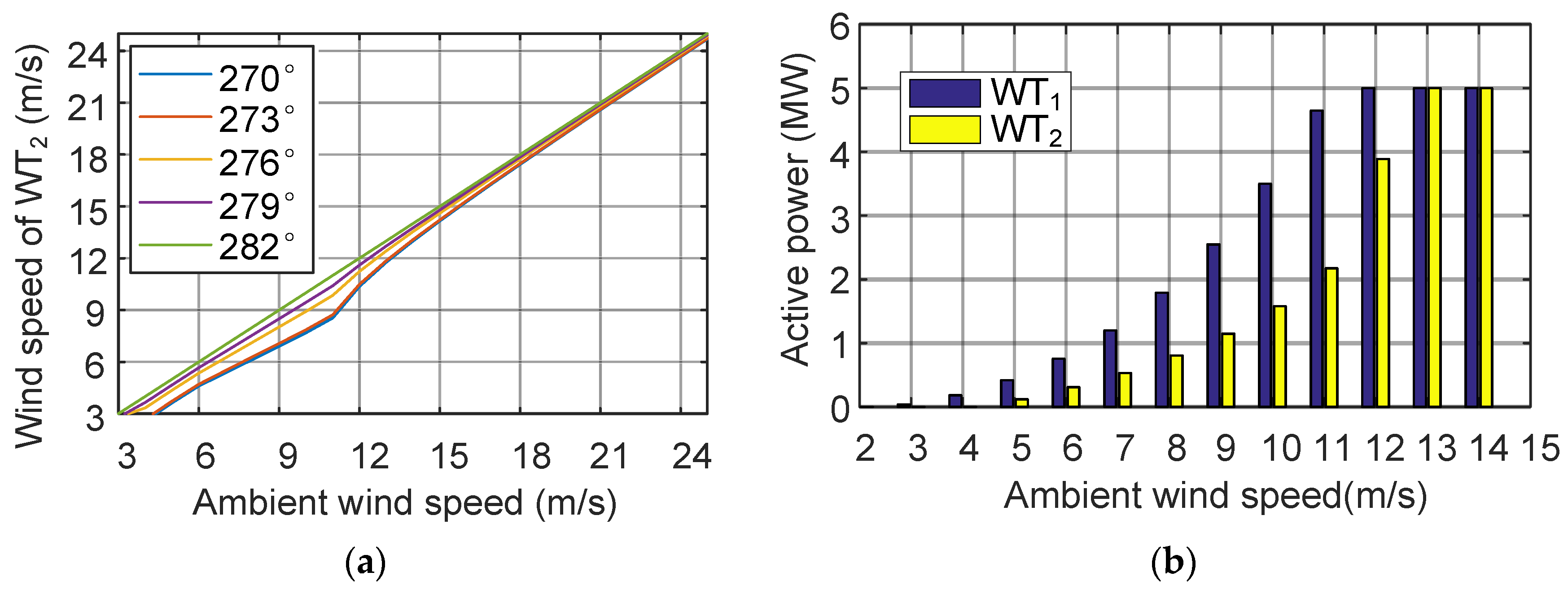
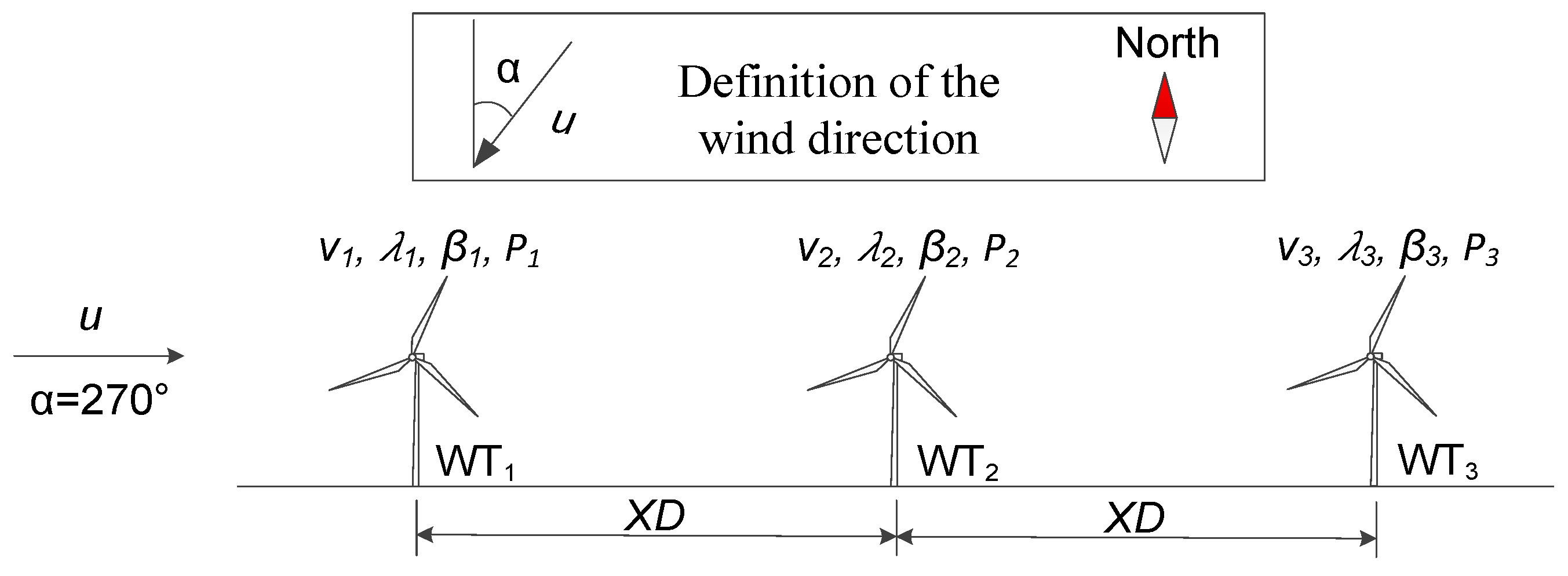
3.1. Wake Effect in Two-Turbine Wind Farm
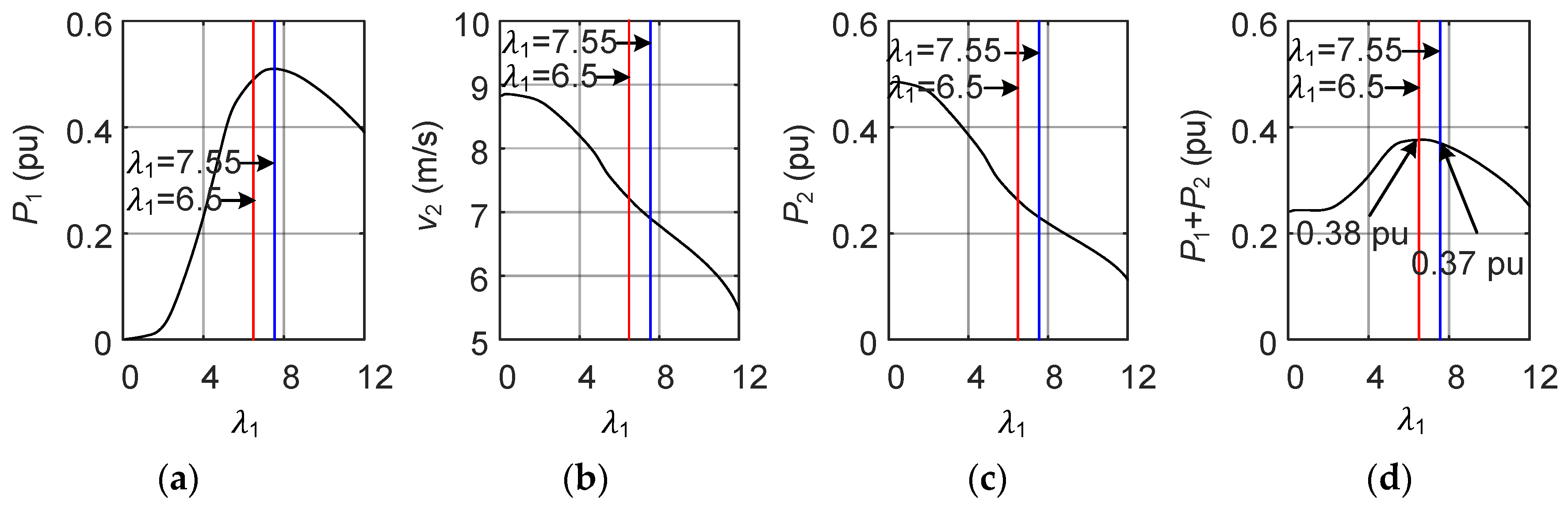
3.2. Active Power Maximization
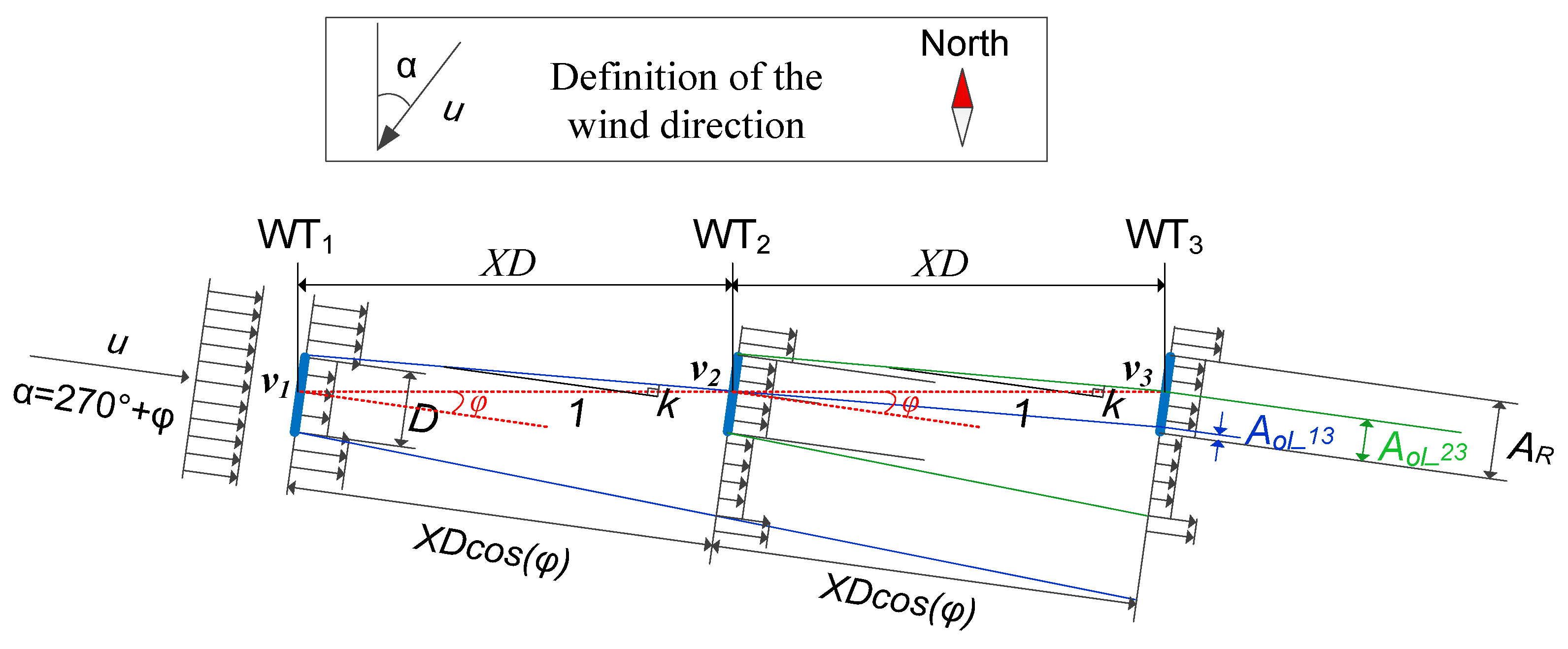
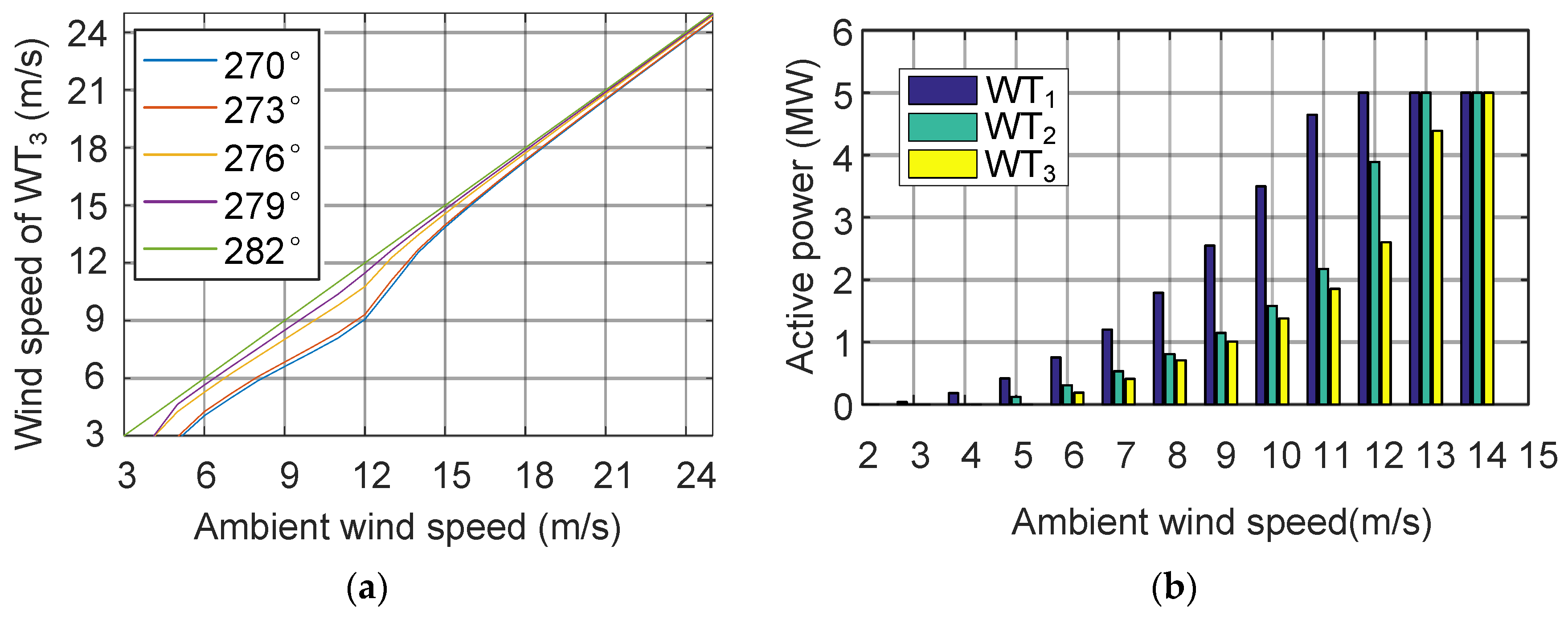
4. Wake Effect and Active Power Maximization in a Three-Turbine Wind Farm
4.1. Multi-Wake Effect
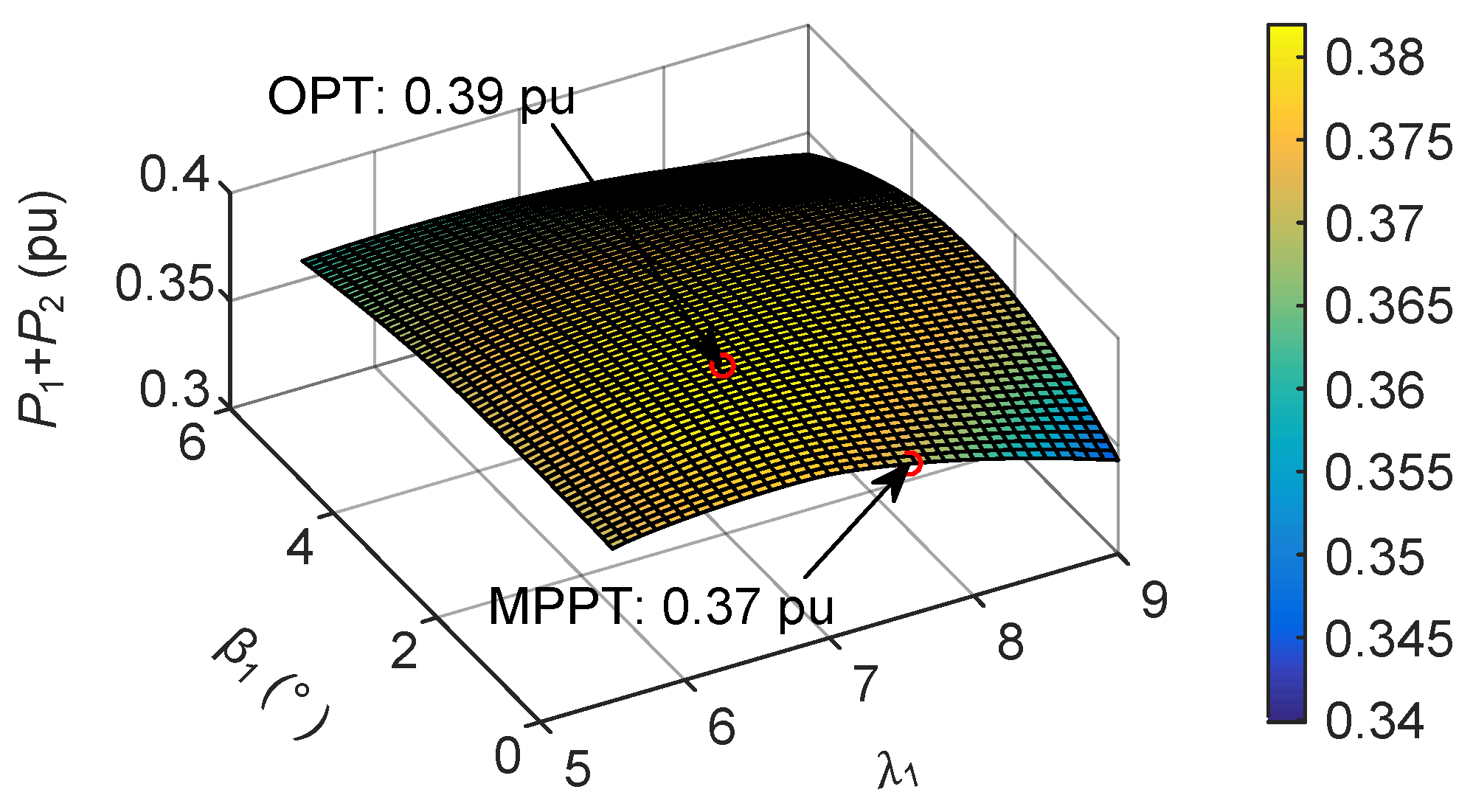
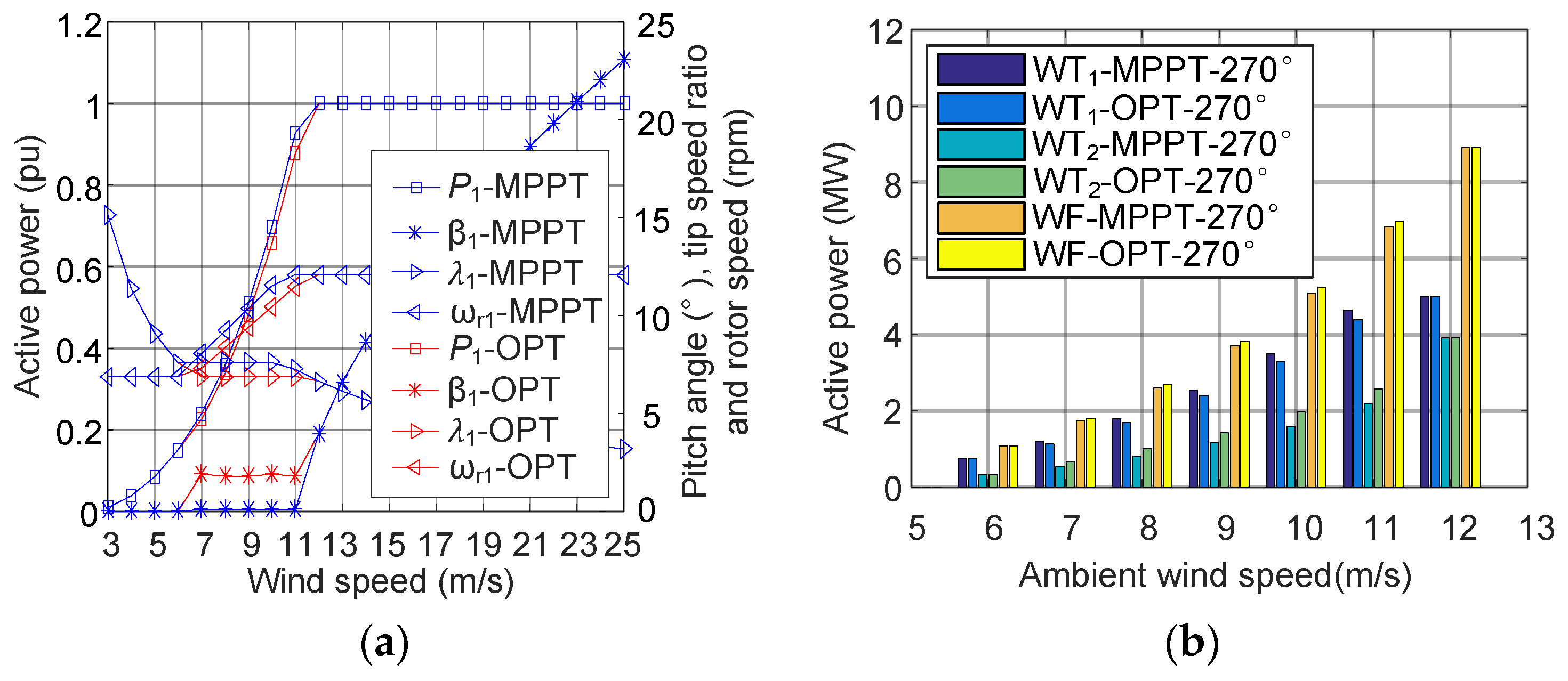
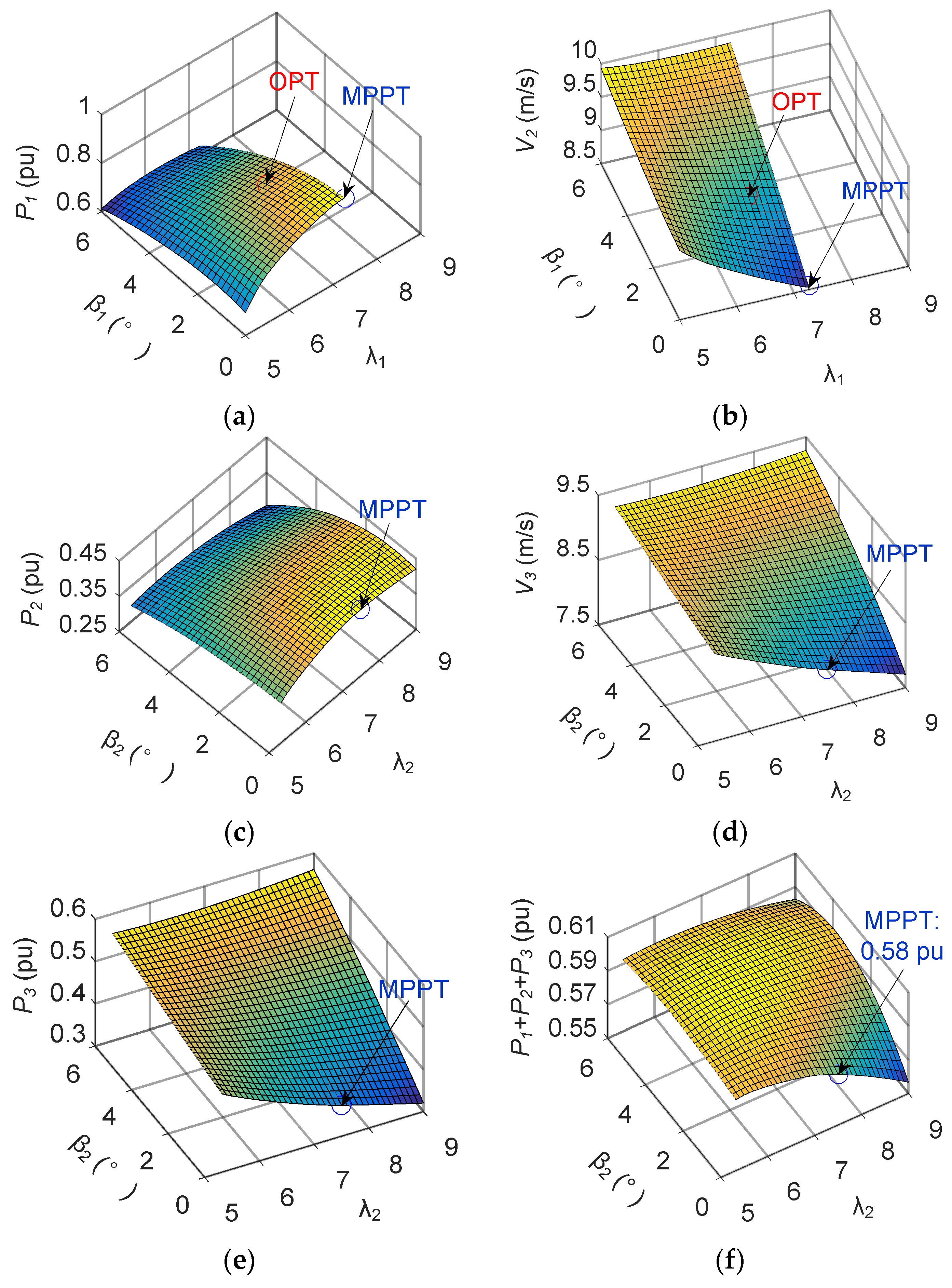
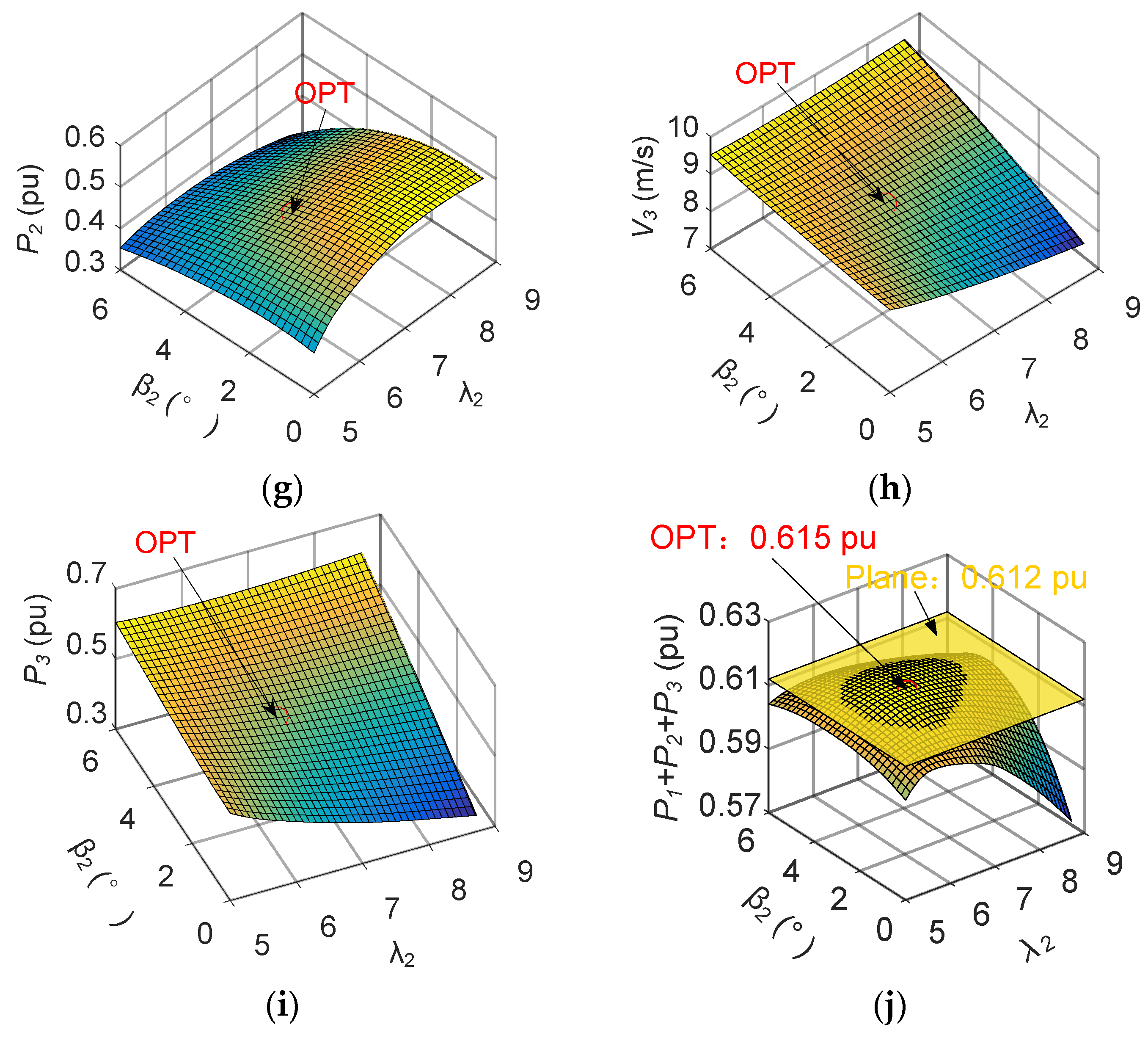
4.2. Active Power Maximization
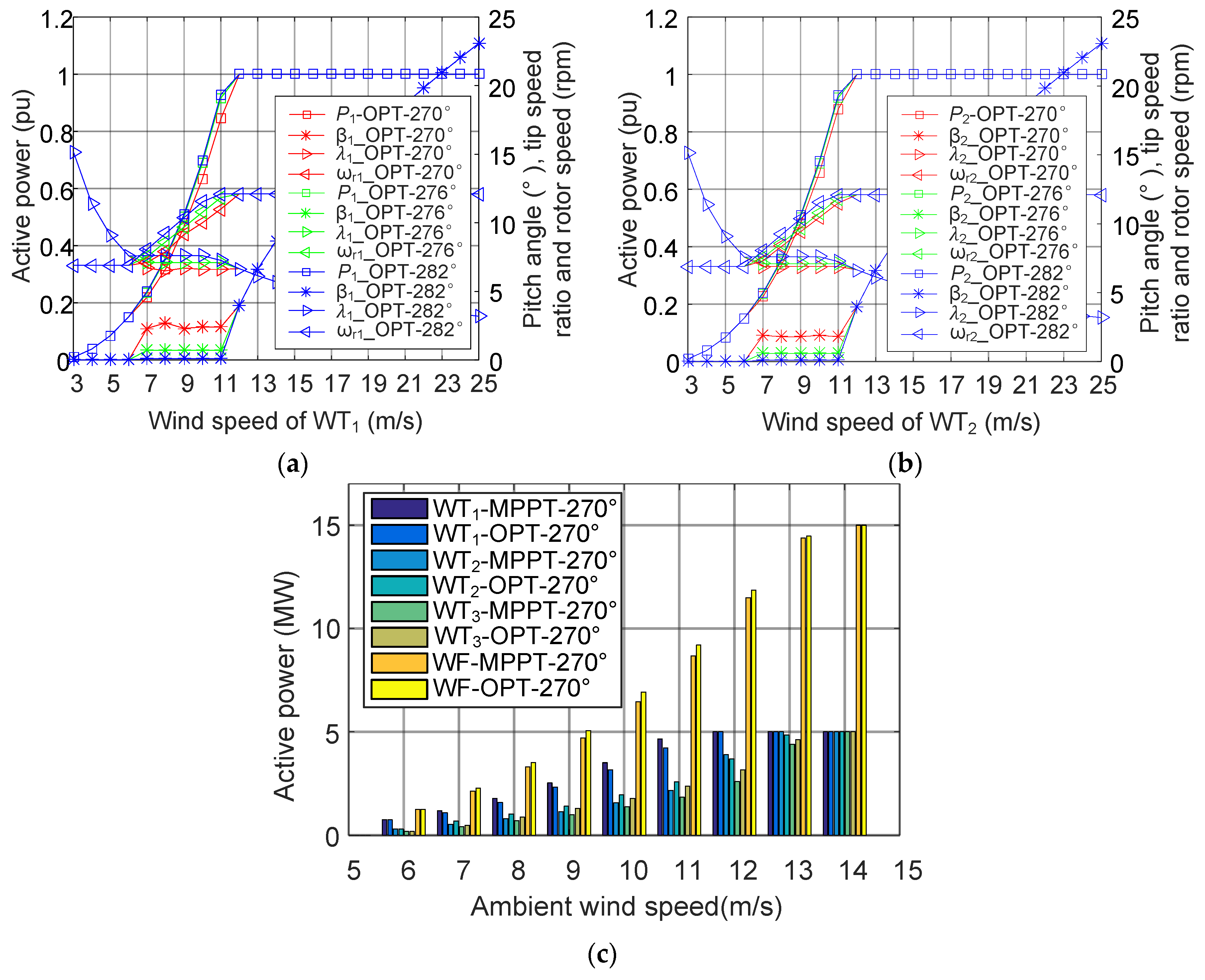
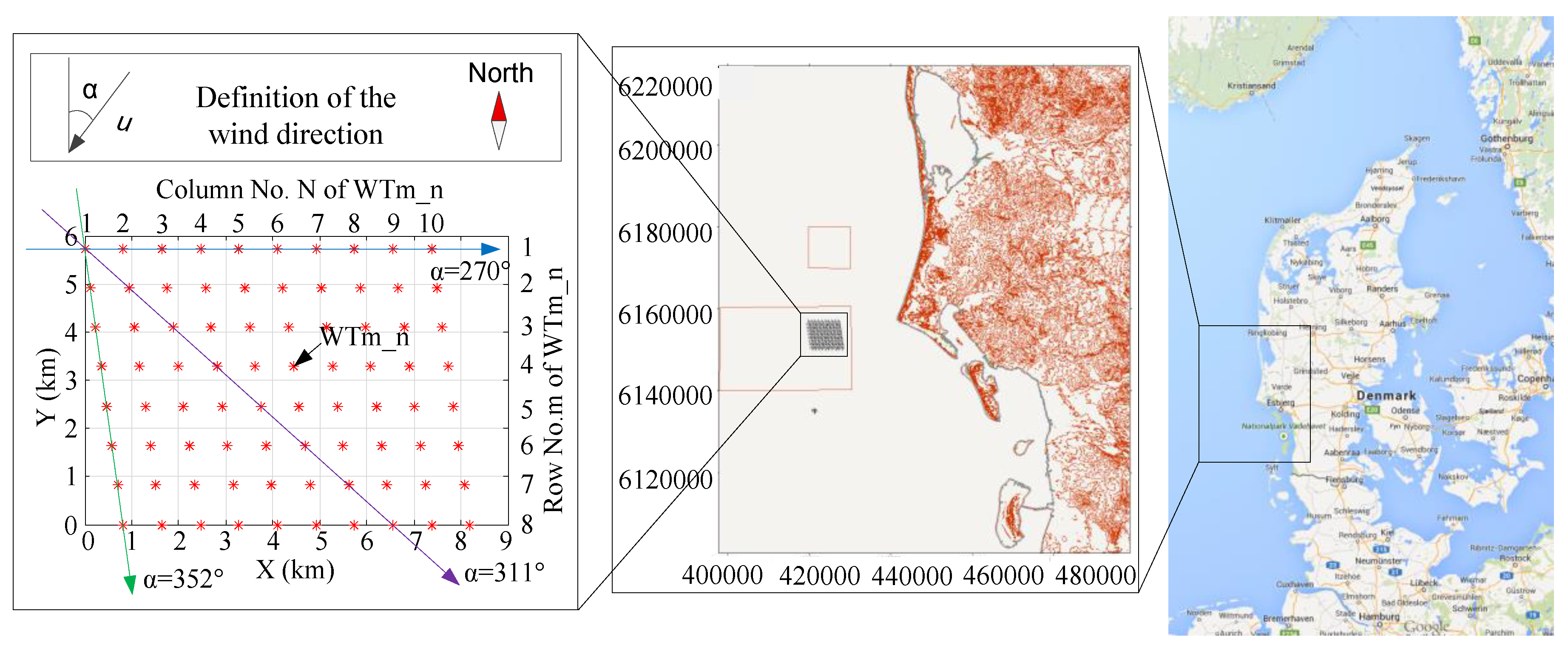
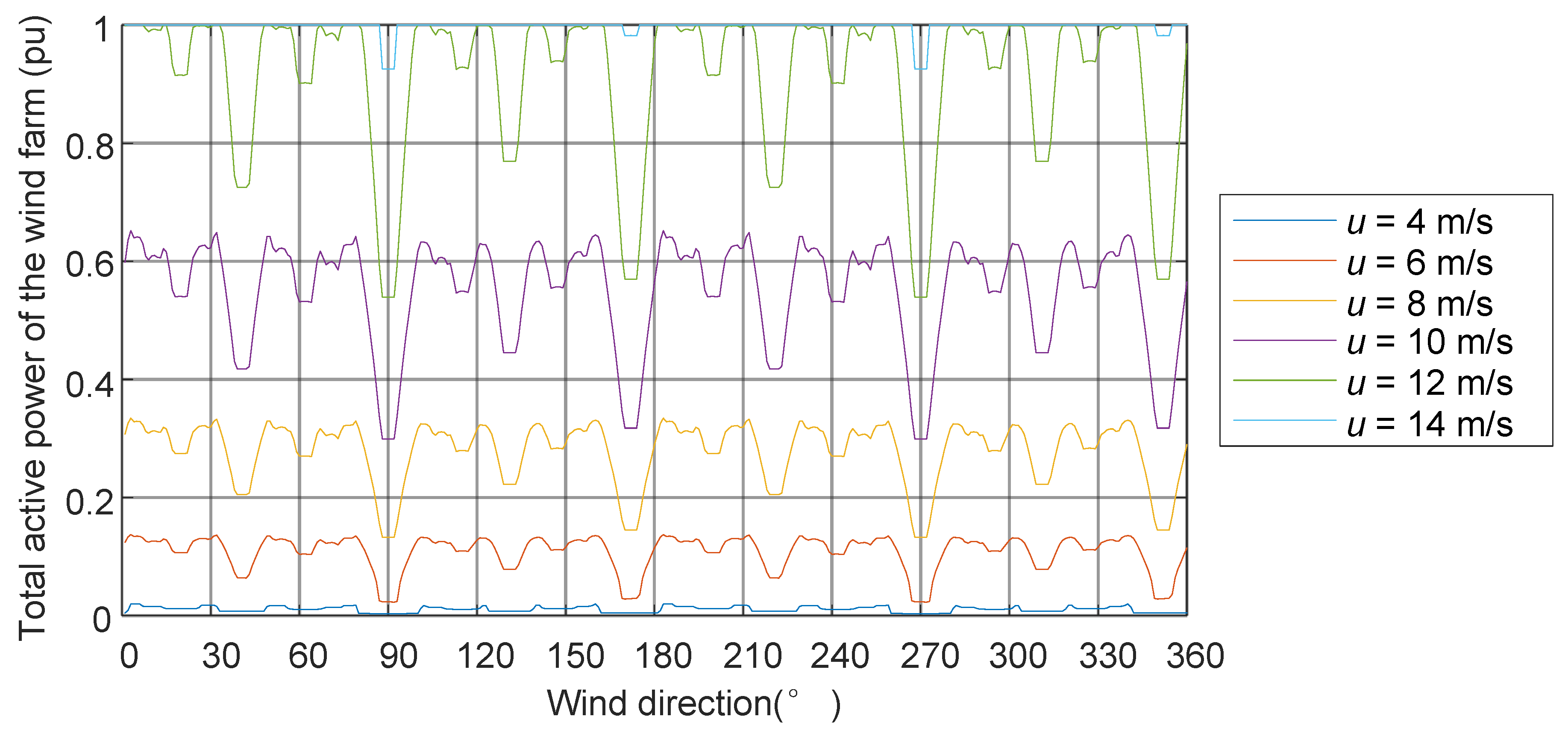
5. Wake Effect and Active Power Maximization in a Large-Scale Wind Farm
5.1. Wake Effect
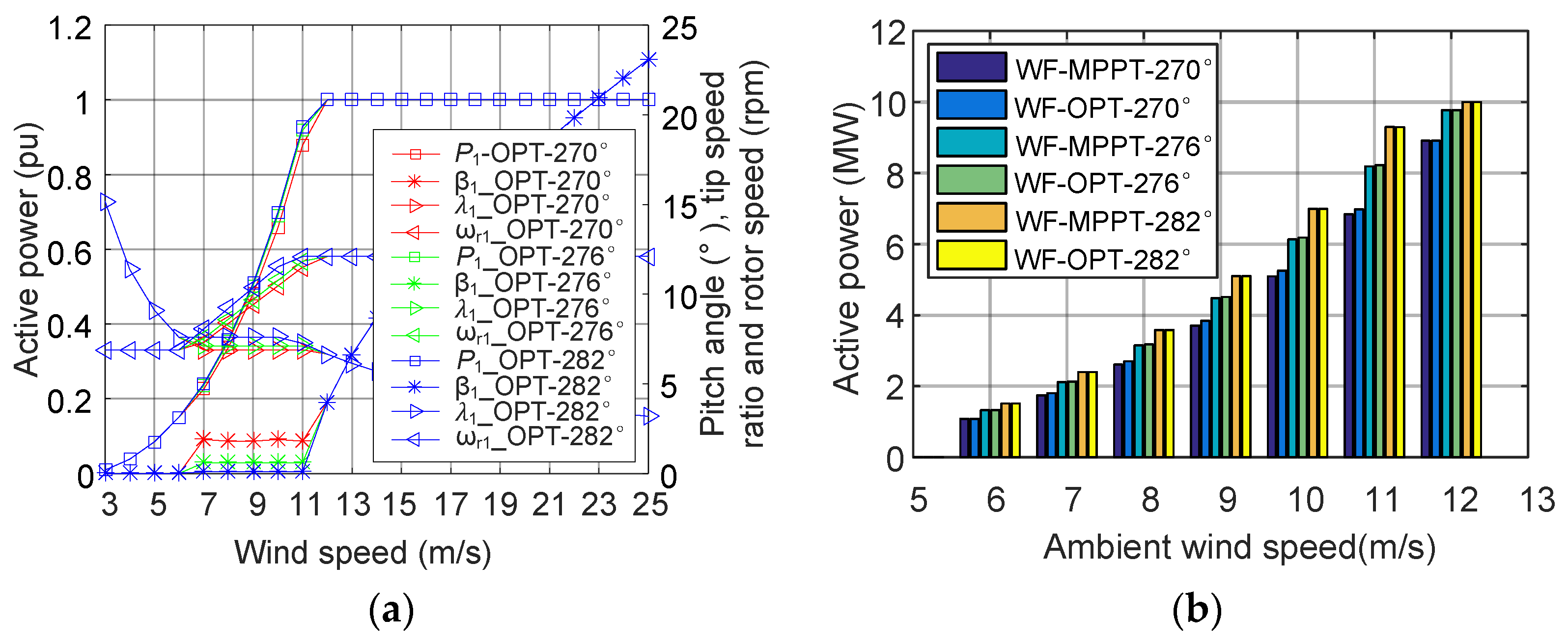
5.2. Active Power Maximization
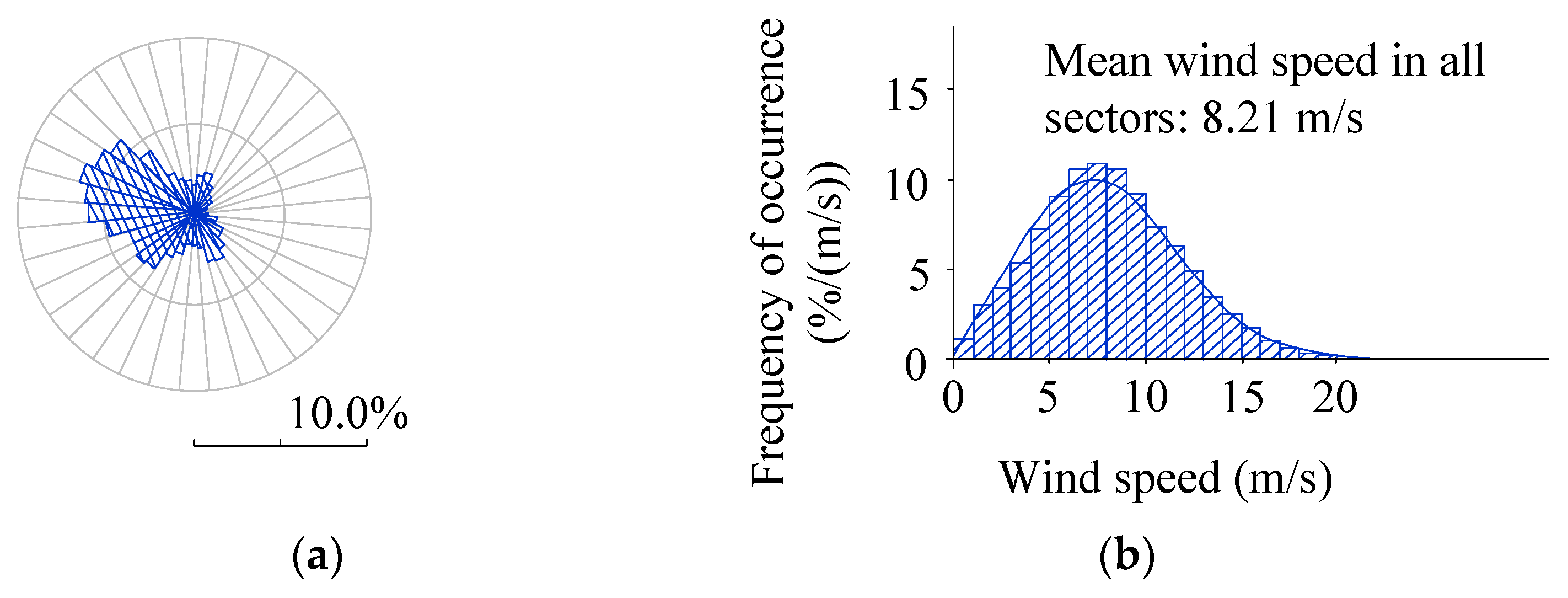
5.3. Annual Energy Production
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- IEA Wind Annual Report. August 2016. Available online: http://www.ieawind.org (accessed in 2 August 2016).
- Krohn, S.; Morthorst, P.E.; Awerbuch, S. The Economics of Wind Energy; European Wind Energy Association (EWEA): Brussels, Belgium, 2009. [Google Scholar]
- Barthelmie, R.J.; Folkerts, L.; Larsen, G.C.; Rados, K.; Pryor, S.C.; Frandsen, S.T.; Lange, B.; Schepers, G. Comparison of wake model simulations with offshore wind turbine wake profiles measured by Sodar. J. Atmos. Ocean. Technol. 2006, 23, 888–901. [Google Scholar] [CrossRef]
- Gebraad, P.M.O.; Teeuwisse, F.W.; van Wingerden, J.W.; Fleming, P.A.; Ruben, S.D.; Marden, J.R.; Pao, L.Y. Wind plant power optimization through yaw control using a parametric model for wake effects—A CFD simulation study. Wind Energy 2014, 23, 95–114. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Sun, Y.Z.; Lin, J.; Li, G.J. Coordinated frequency regulation by doubly fed induction generator-based wind power plants. IET Renew. Power Gen. 2012, 6, 38–47. [Google Scholar] [CrossRef]
- Slootweg, J.G.; de Haan, S.W.H.; Polinder, H.; Kling, W.L. General model for representing variable speed wind turbines in power system dynamics simulations. IEEE Trans. Power Syst. 2003, 18, 144–151. [Google Scholar] [CrossRef]
- Steinbuch, M.; de Boer, W.W.; Bosgra, O.H.; Peters, S.; Ploeg, J. Optimal control of wind power plants. J. Wind Eng. Ind. Aerodyn. 1988, 27, 237–246. [Google Scholar] [CrossRef]
- Corten, G.P.; Schaak, P. More power and less loads in wind farms: ‘Heat and flux’. In Proceedings of the European Wind Energy Conference & Exhibition, London, UK, 22–25 November 2004; pp. 1–10.
- Larsen, G.C.; Madsen, H.A.; Troldborg, N.; Larsen, T.J.; Réthoré, P.E.; Fuglsang, P.; Ott, S.; Mann, J.; Buhl, T.; Nielsen, M. TOPFARM-Next Generation Design Tool for Optimisation of Wind Farm Topology and Operation; Technical Report Risø-R-1805(EN); RisØ National Laboratory: Roskilde, Denmark, 2011. [Google Scholar]
- Tian, J.; Su, C.; Soltani, M.; Chen, Z. Active power dispatch method for a wind farm central controller considering wake effect. In Proceedings of the 2014 40th IEEE Industrial Electronics Society Conference, Dallas, TX, USA, 29 October–1 November 2014; pp. 5450–5456.
- González, J.S.; Payán, M.B.; Santos, J.R.; Rodríguez, Á.G.G. Maximizing the overall production of wind farms by setting the individual operating point of wind turbines. Renew. Energy 2015, 80, 219–229. [Google Scholar] [CrossRef]
- Abad, G.; Lopez, J.; Rodriguez, M.; Marroyo, L.; Iwanski, G. Doubly Fed Induction Machine; Wiley: Hoboken, NJ, USA, 2011; p. 19. [Google Scholar]
- Soleimanzadeh, M.; Wisniewski, R.; Brand, A. State-space representation of the wind flow model in wind farms. Wind Energy 2014, 17, 627–639. [Google Scholar] [CrossRef]
- Marden, J.R.; Ruben, S.D.; Pao, L.Y. A model-free approach to wind farm control using game theoretic methods. IEEE Trans. Control Syst. Technol. 2013, 21, 1207–1214. [Google Scholar] [CrossRef]
- Gebraad, P.M.O.; Wingerden, J.W. Maximum power-point tracking control for wind farms. Wind Energy 2015, 18, 429–447. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report NREL/TP-500-38060; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Barthelmie, R.J.; Hansen, K.; Frandsen, S.T.; Rathmann, O.; Schepers, J.G.; Schlez, W.; Phillips, J.; Rados, K.; Zervos, A.; Politis, E.S.; et al. Modelling and measuring flow and wind turbine wakes in large wind farms offshore. Wind Energy 2009, 12, 431–444. [Google Scholar] [CrossRef]
- Duckworth, A.; Barthelmie, R.J. Investigation and validation of wind turbine wake models. Wind Eng. 2008, 32, 459–475. [Google Scholar] [CrossRef]
- Katic, I.; Højstrup, D.; Jensen, N.O. A sample model for cluster efficiency. In Proceedings of the 1986 European Wind Energy Association Conference, Rome, Italy, 7–9 October 1986; pp. 407–410.
- Jensen, N.O. A Note on wind Generator Interaction; Technical Report RisØ M-2411; RisØ National Laboratory: Roskilde, Denmark, 1983. [Google Scholar]
- Mortensen, N.G.; Heathfield, D.N.; Myllerup, L.; Landberg, L.; Rathmann, O. Wind Atlas Analysis and Application Program: WAsP 8 Help Facility; Risø National Laboratory: Roskilde, Denmark, 2005. [Google Scholar]
- Kristoffersen, J.R.; Christiansen, P. Horns rev off shore windfarm: Its main controller and remote control system. Wind Eng. 2003, 27, 351–366. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, A.G.; Burgos-Payan, M.; Riquelme-Santos, J.; Serrano-Gonzalez, J. Reducing computational effort in the calculation of annual energy produced in wind farms. Renew. Sustain. Energy Rev. 2015, 43, 656–665. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Rated power | 5 MW |
| Rotor diameter | 126 m |
| Cut-in, rated, Cut-out wind speed | 3 m/s, 11.4 m/s, 25 m/s |
| Min. and Max. rotor speed | 6.9 rpm, 12.1 rpm |
| Gearbox ratio | 97:1 |
| Number of pole-pairs | 3 |
| Synchronous frequency | 50 Hz |
| Electrical generator efficiency | 94.4% |
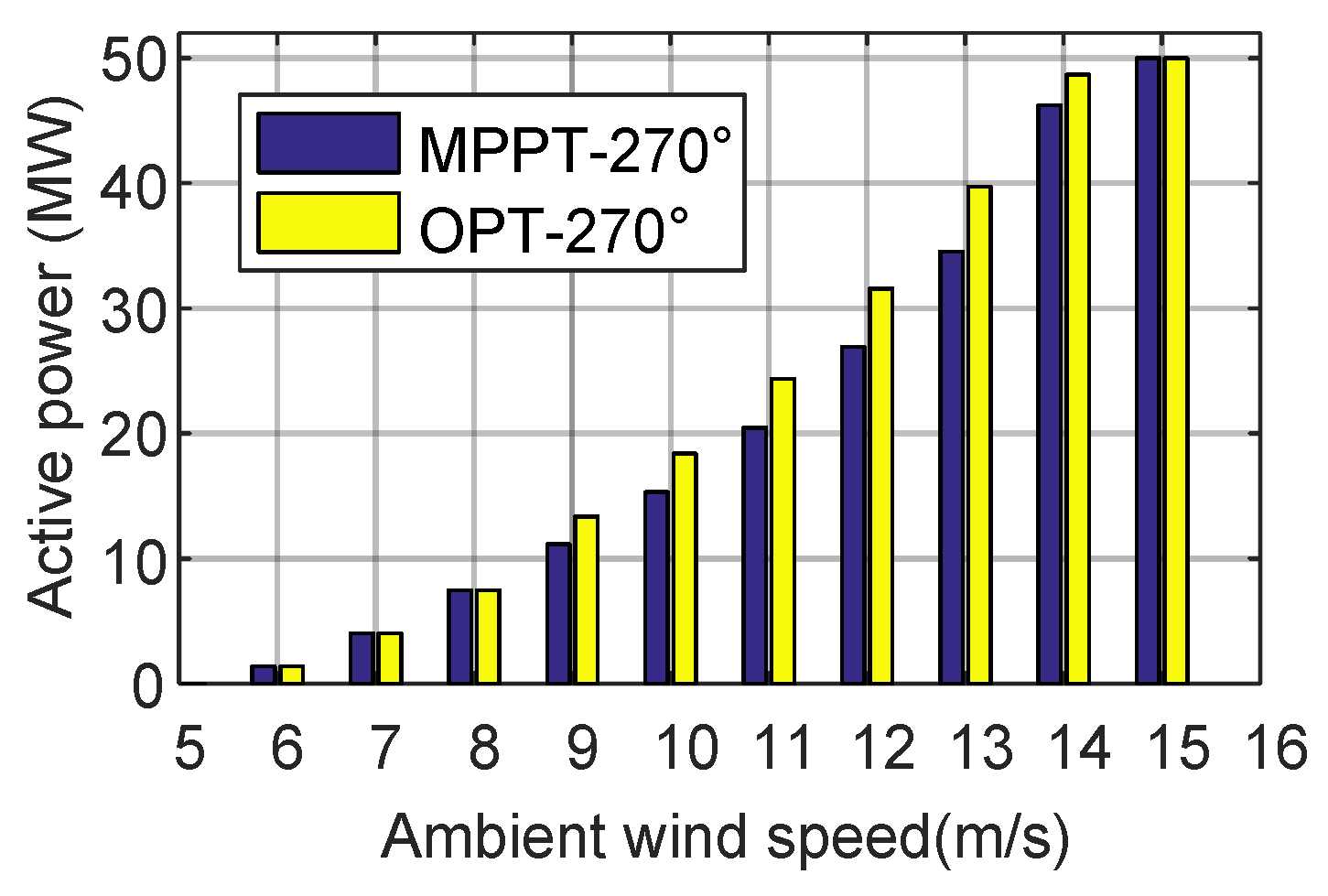
| AEP | 265°–275° Sector | 85°–95° Sector | ||
|---|---|---|---|---|
| MPPT | OPT | MPPT | OPT | |
| WT1_1 | 1356.6 | 1280.9 | 85.5 | 142.3 |
| WT1_2 | 977.8 | 949.7 | 86.8 | 130.7 |
| WT1_3 | 835.4 | 880.7 | 88.7 | 122.5 |
| WT1_4 | 760.8 | 840.4 | 90.5 | 123.4 |
| WT1_5 | 713.9 | 815.6 | 94.5 | 125.6 |
| WT1_6 | 689.1 | 798.6 | 99.1 | 128.8 |
| WT1_7 | 669.2 | 786.8 | 108.9 | 134.2 |
| WT1_8 | 658.7 | 780.4 | 127.1 | 143.3 |
| WT1_9 | 642.7 | 814.0 | 167.4 | 161.0 |
| WT1_10 | 631.2 | 859.3 | 288.4 | 262.8 |
| Total | 63,482.2 | 70,450.4 | 9895.4 | 11,795.4 |
| Increased | 11.0% | 19.2% | ||
| AEP | 345°–355° Sector | 165°–175° Sector | ||
|---|---|---|---|---|
| MPPT | OPT | MPPT | OPT | |
| WT1_1 | 382.9 | 348.4 | 169.9 | 248.7 |
| WT2_1 | 234.1 | 232.1 | 173.0 | 233.8 |
| WT3_1 | 185.3 | 208.8 | 180.1 | 222.7 |
| WT4_1 | 162.5 | 195.5 | 187.7 | 228.1 |
| WT5_1 | 148.4 | 188.1 | 203.9 | 237.0 |
| WT6_1 | 142.3 | 183.4 | 230.1 | 252.0 |
| WT7_1 | 136.1 | 194.1 | 283.7 | 278.4 |
| WT8_1 | 134.0 | 207.0 | 435.2 | 400.0 |
| Total | 15,255.2 | 17,573.2 | 18,635.2 | 21,006.9 |
| Increased | 15.2% | 12.7% | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, J.; Zhou, D.; Su, C.; Soltani, M.; Chen, Z.; Blaabjerg, F. Wind Turbine Power Curve Design for Optimal Power Generation in Wind Farms Considering Wake Effect. Energies 2017, 10, 395. https://doi.org/10.3390/en10030395
Tian J, Zhou D, Su C, Soltani M, Chen Z, Blaabjerg F. Wind Turbine Power Curve Design for Optimal Power Generation in Wind Farms Considering Wake Effect. Energies. 2017; 10(3):395. https://doi.org/10.3390/en10030395
Chicago/Turabian StyleTian, Jie, Dao Zhou, Chi Su, Mohsen Soltani, Zhe Chen, and Frede Blaabjerg. 2017. "Wind Turbine Power Curve Design for Optimal Power Generation in Wind Farms Considering Wake Effect" Energies 10, no. 3: 395. https://doi.org/10.3390/en10030395
APA StyleTian, J., Zhou, D., Su, C., Soltani, M., Chen, Z., & Blaabjerg, F. (2017). Wind Turbine Power Curve Design for Optimal Power Generation in Wind Farms Considering Wake Effect. Energies, 10(3), 395. https://doi.org/10.3390/en10030395










