1. Introduction
For the past two decades, global climate change and the greenhouse effect have caused huge impacts on the Earth’s environment, which has motivated and pushed the research and development of energy sources and storage systems worldwide. Among the various energy storage devices, the Li-ion battery has been accepted and widely implemented in electronic products and is considered as the main power source for electric vehicles (EVs). Compared to conventional batteries such as lead-acid and Ni-H batteries, the Li-ion battery is the most attractive energy storage device due to its higher energy density, higher power density, longer cycle life, and lower self-discharge rate [
1]. The Li-ion battery is the fastest growing and most widely used battery in consumer low-power products in the field of electronics, such as cell phones and laptops, and in high-power applications such as electric vehicles, trams, bicycles, etc. [
2,
3].
Although the electrical performance of Li-ion batteries, such as the energy density and c-rate, has improved significantly, the non-uniformity of their capacity and the retention ratio with aging has been a big problem in terms of a battery pack with a large amount of cells in series. A battery management system (BMS) protects the overall system and provides optimal performance management of the energy storage. In addition to on-line monitoring of the terminal voltage of each single cell, a BMS is required to predict and provide each cell’s SOC and SOH, which are the most important indicators for adapting each cell’s optimized loading timely for extending the whole pack life. For example, in EVs applications, the battery SOC can be employed in the figurative sense as a replacement for the fuel gauge used in conventional vehicles. Similarly, the SOH can be likened to the odometer. A BMS with accurate estimation of SOC and SOH can prevent each cell in a battery pack from overcharging or over-discharging, and can extend the whole pack’s life [
4,
5,
6,
7,
8,
9]. Online estimation of a battery’s SOC and SOH is also essential for safe and reliable EVs. However, it is not possible to perform a direct measurement of these states by any electrical gauge. Instead, it is estimated by the measured battery variables, such as the time-varying voltage and the charging/discharging current. There have been various SOC and SOH estimation methods, and each has its own merits and limitations [
10,
11].
The existing SOC estimation methods are usually divided into three classifications, including data-driven, adaptive, and hybrid methods [
12,
13]. Data-driven methods can be divided into the direct measurement and the model-based methods. Direct measurement methods include the Coulomb counting method (CCM) [
14], open circuit voltage (OCV) method [
15,
16], and impedance method [
17]. The CCM is performed through measuring the discharging current over time and then making an I-t integration to obtain an estimated SOC value [
14]. The disadvantages of CCM are that it relies on the accuracy of the current sensor and it can accumulate errors due to its open-loop nature. The OCV method is relatively accurate but needs a sufficient rest time, and it becomes less accurate if a battery has a flat OCV-SOC curve [
15]. In the model-based approach, one measures the battery’s online data and applies these signals as model inputs to calculate the SOC (output). Two types of battery models have been widely employed: electrical and electrochemical models. However, all SOC estimation methods based on electrical models have a common disadvantage that the model parameters can only be applied on fresh cells, but are invalid on aged cells.
Adaptive methods provide an improved solution for a battery’s SOC estimation with a non-linear SOC caused by chemical factors [
12]. The adaptive approaches consider the self-designing effect and can automatically adapt to discharging conditions. Various new adaptive methods for SOC estimation have been developed, including Kalman filter (KF), fuzzy logic methods, support vector machine (SVM), neural network, etc. The most widely used adaptive filter technique is the KF [
18,
19]. The application of the KF method on estimations of SOC is proven to be verifiable through the real-time state estimation [
20]. Singh et al. developed a fuzzy logic-based SOC estimation method for Li-ion batteries which proved its potential in portable defibrillators [
21], in which the AC impedance and voltage recovery measurements were made and used as the input parameters for this fuzzy logic model.
The hybrid models benefit from the advantages of each of the data-driven and adaptive SOC estimation methods and allow a globally optimal estimation performance [
11]. A multiscale framework with extended Kalman filter (EKF) was proposed to estimate SOC and capacity [
6]. Simulation results with synthetic data based on a valid cell dynamic model suggest that the proposed framework, as a hybrid of CCM and adaptive filtering techniques, achieves higher accuracy and efficiency than the joint/dual EKF.
The SOH of a battery is usually described as the battery performance at the present time compared with the performance at ideal conditions and the battery’s fresh state. The estimation of the battery’s SOH has to take into consideration both the battery capacity fade and the impedance increase. The determination of the SOH can be done by two different approaches including data-driven and adaptive systems. In the data-driven part, with the cycling data and the main parameters affecting the battery lifetime, an estimation of the SOH can be performed. A deep understanding of the correlation between the operation and degradation through physical analysis or the evaluation of large data sets is needed for this approach.
The SOH can be determined by monitoring the internal resistance of a battery [
22,
23,
24]. However, the measurement of real-time battery internal resistance is difficult. Adaptive systems determine the SOH through calculations from parameters that are sensitive to the degradation of the battery. These parameter data must be measurable or should be examined throughout the operation of the battery. There are several ways the SOH can be estimated, e.g., KF, EKF [
16,
17,
18], genetic algorithm (GA) [
25], particle filter [
26], fuzzy logic [
21], artificial neural networks (ANNs) [
27], and the least-squares method (LSM) [
28]. The EKF method is easy to implement and commonly used in battery prognosis. He et al. [
17] proposed an electromotive force (EMF) method combined with recursive least-squares (RLS) for online estimation of OCV and SOC of Li-ion batteries. Nuhic et al. [
29] used SVM to estimate the SOH by using load collectives as the training and test data. Chen et al. [
25] used GA to estimate the battery model parameters, including the diffusion capacitance in real time, and then determined the battery SOH using the identified diffusion capacitance. However, adaptive systems also operate with the drawback of having a high computational load, which complicates the online running of the model on a real application [
30].
Capacity decrease and power fading do not originate from one single cause. Most of these processes cannot be studied independently. Because a battery’s maximum capacity decreases with age, accurate SOC estimation relies on a battery degradation model. Similarly, an inaccurate SOC estimation may mislead a battery’s SOH calibration. Simultaneous estimation of SOC and SOH appears to be necessary and beneficial for battery management systems [
10,
31,
32]. Kim and Cho [
18] proposed a method based on EKF to identify suitable SOC and SOH model parameters for Li-ion batteries. Hung et al. [
31] proposed a dynamic impedance method to estimate the SOC and a projection method to estimate the SOH of Li-ion batteries. The dynamic impedance is defined as the changes in voltage over the changes in current during charging/discharging. The rate of change in dynamic impedance with respect to SOC was then projected to determine SOH. Experimental data verified that the SOC estimations were bounded within a 5% error but the detail of SOH accuracy was not described in that paper.
The capacity quantifies the available energy stored in a battery. After continuous operation, the active materials in both the cathode and anode are reduced or blocked, which leads to the battery capacity decline. The laboratory measurements and off-line analysis are essential to evaluate the effect of capacity fading [
33,
34]. The most common method of determining the degree of battery aging is based on the OCV–SOC curve [
34]. However, it requires fully charging or discharging the battery at a low rate (e.g., 1/25 C). These methods need time-consuming tests so they cannot meet the online real-time requirements for BMSs. An alternative approach to estimate capacity loss is the so-called incremental capacity analysis (ICA). The concept of ICA originates from the study of the lithium intercalation process [
35,
36]. ICA is more sensitive to gradual change with battery aging compared to those methods based on conventional charging or discharging curves [
37,
38]. ICA was shown to be an effective tool for analyzing battery capacity fading. Wang et al. proved that their incremental capacity analysis with the SVM model can reduce the computation load, and the model built from one single cell was able to predict the SOH of the other cells within a 1% error bound [
38]. However, this methodology still needs to collect a wide range of charging data typically from 3 to 3.6 V during a charging process.
To overcome these issues described above, this paper defines a new variable V′, which is the unit time voltage drop in the discharging process due to its timely responsive and on-line measureable features, and proposes a novel model that employs V and 1/V′ as the main variables. The SOC is expressed as a linear relation of the two variables with three undetermined coefficients. Data regression from test cells yielded the values of the coefficients. The SOH was found to be linear with 1/V′ by a modification factor that is a function of the SOC. The derived model, which can simultaneously estimate the battery’s instantaneous SOC and SOH, is promising for online real-time applications. The robustness of the model is checked as well. Most important is that it was demonstrated that this model, which was fitted by the data from one battery of a batch, can be applied to the other batteries of the same batch without any need of sophisticated model-updating algorithms, such as EKF or SVM. Random samplings from the tested data to simulate the online SOC and SOH estimations are performed, and satisfactory results are obtained.
2. Experimental Data Analysis
Four lithium cobalt oxide (LiCoO2) batteries (numbered A–D) of nominal capacity 1.10 Ah were tested at 25 °C. The charging process follows the standard CCCV protocol, i.e., constant current (CC) at 0.5 C until the voltage reaches its designated value of 4.2 V, then constant voltage (CV) charging takes over until the current falls below 50 mA. The discharging current is kept at a 1 C rate and terminated at a cut-off voltage of 2.7 V. The voltages of the tested cells were logged at 30-s intervals. The battery’s latest maximum capacity, denoted Qm, was evaluated by CCM at the end of every discharging process. With the evaluated Qm, the SOC at any previous time instant was calculated backwards. SOH was evaluated by dividing the latest Qm by the nominal one (Qnom) at the end of every discharging cycle.
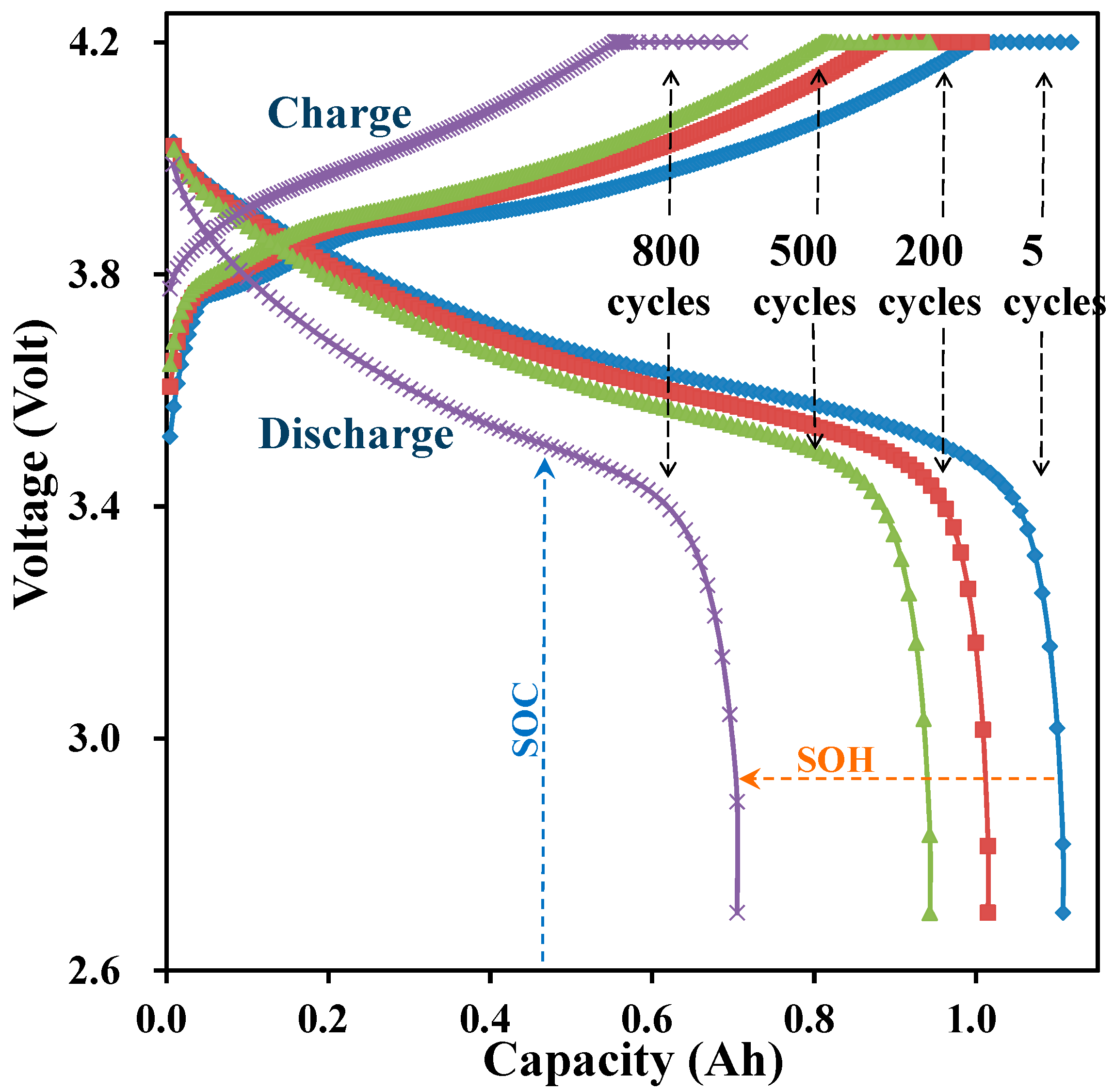
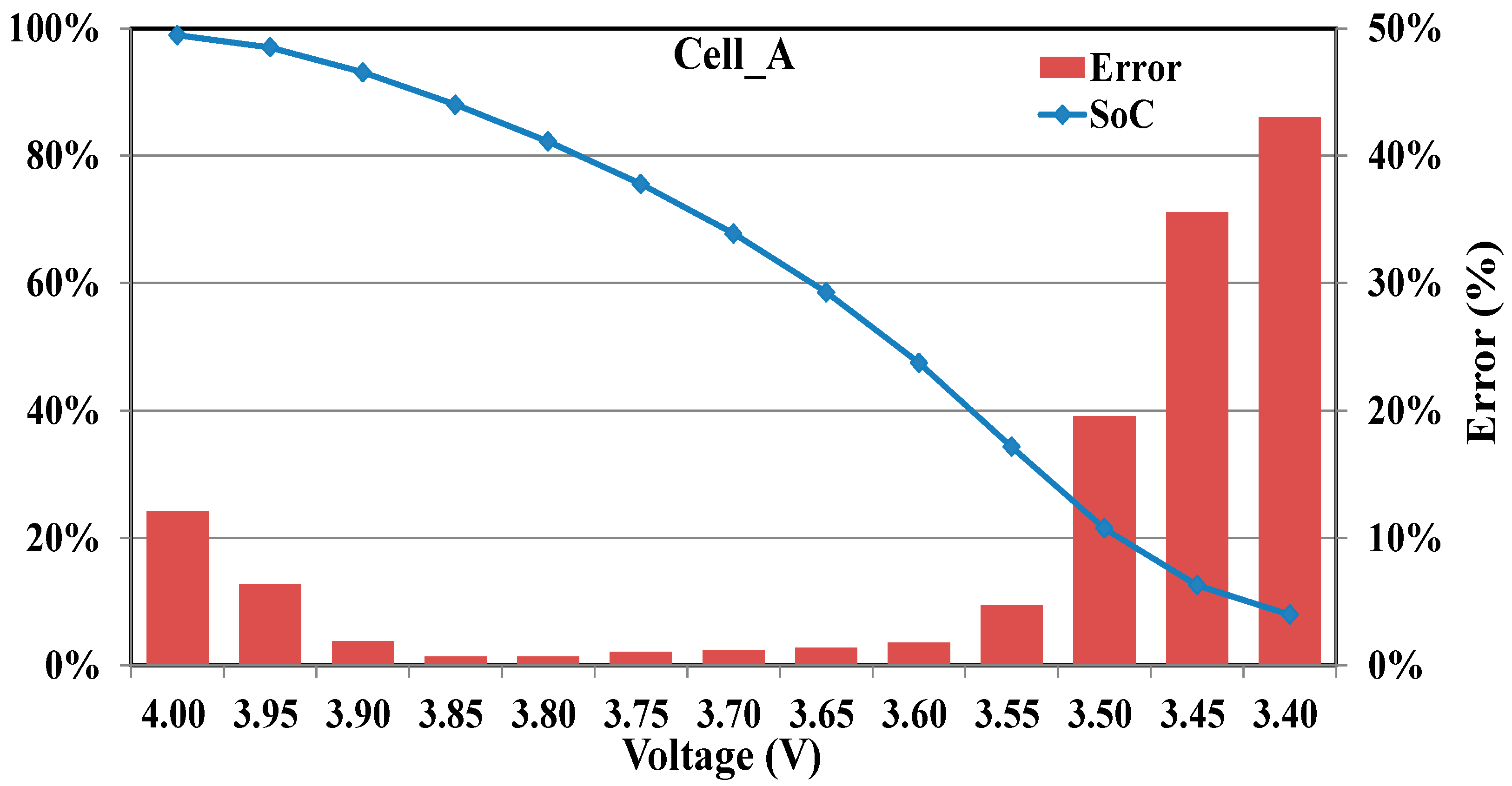
Figure 1 illustrates the typical curve of voltage versus capacity for the tested cell A at certain test cycles. The left-shifting of the discharging curves implies the capacity fade and is an indicator of the battery’s health (SOH). The voltage declining with the discharging time can be used as an indicator for the battery SOC. Nonetheless, every instantaneous voltage could reflect multiple SOC values unless the cycle number
N is known. The present research is aimed at a battery’s online real-time SOC and SOH estimation model without fully conducting a charging/discharge cycle, i.e., without
N as a parameter. It is necessary to look for extra parameters for SOC and SOH modeling in addition to instantaneous voltage. Therefore, a new variable, V′, which is the unit time voltage drop in the discharging process, was defined and used to derive the model for SOC and SOH prediction.
2.1. Battery States
The definitions of SOC, SOH, and some terminologies are briefly described as follows:
is defined as the ratio of the remaining capacity over the maximum capacity, and SOC can provide a timely charge warning.
Figure 1 shows that a battery’s
Qm gradually decreases with battery aging. According to the degradation of
Qm, SOH is defined as:
A battery’s SOH normally ranges within 0–100%, but when it is new, the SOH can be slightly larger than 100% due to product variations. The end of life of a Li-ion battery is commonly defined by the maximum cycles when the SOH drops to 80%. SOH is a key indicator of safe operation because it provides a timely warning that replacement is required.
2.2. New Parameter for SOC and SOH Model
OCV has been proven as a proper indicator for SOC and SOH evaluation, but the measurement of OCV requires a long relaxation time to reach a steady state under thermodynamic equilibrium, which is called EMF and is more suitable for off-line evaluation. Our previous study [
39] adopted the fully discharged voltage as a replacement for OCV, and combined it with the resistance for the SOH model construction. That model predicted a battery’s remaining useful life (RUL) within reasonable accuracy, but the voltage and resistance at a fully discharged state are apparently inappropriate aging parameters for an on-line, real-time model. The present study is intended to develop a suitable model for the real-time, on-line monitoring of a battery in use, and thus any parameter associated with the fully discharged state is hazardous and should be avoided. The most convenient and direct outputs from a battery in use are voltage, current, and time. A single voltage value, as shown in
Figure 1, is never enough to identify a battery’s SOC because the voltage shifts with battery aging. Therefore, this paper proposes a new parameter called the
unit time voltage drop,
V′ for SOC and SOH modeling, i.e.,
Note that in Equation (3), Δ
V is the voltage drop in the discharging process, i.e., Δ
V =
V1 −
V2.
2.3. SOC and SOH Regression Model
The correlation of SOC with
V and
V′ is first checked from the test data so as to judge its appropriateness for model construction. The average correlation of SOC vs.
V is 0.988, and that of SOC vs. 1/
V′ is 0.984. The relations of SOC vs.
V and 1/
V′ are also found to be approximately linear. As depicted previously, both variables of
V and 1/
V′ are needed to estimate the SOC because there are multiple SOCs for a given
V or a given
V′.
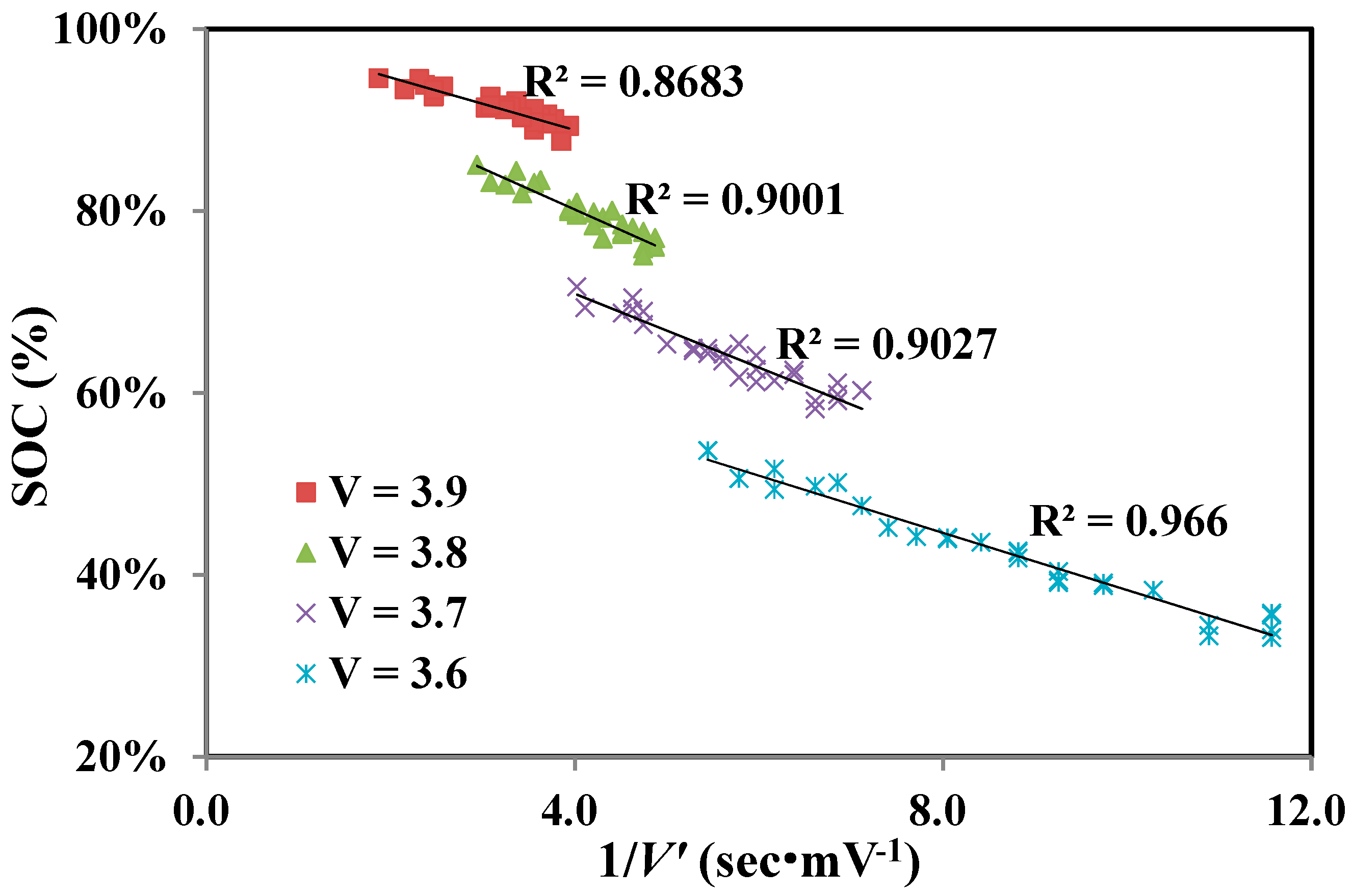
Figure 2 illustrates the correlations of SOC vs. 1/
V′ at different fixed voltages, and the values appear high enough except for
V = 3.9.
Figure 2 also shows that when modeling by employing both parameters
V and 1/
V′, only a single correspondent SOC is obtained for a specific
V′ under a given voltage,
V.
To further explore the physical meaning of the parameter
V′, we tried to correlate
V′ to the internal resistance of the battery by the following equation
If the change of
Veq in a short discharge time duration is negligible, it can be assumed that Δ
V is approximate to Δ
η.
where
η is the overpotential which includes two parts, the reversible and the irreversible, representing the degree of deviation from the equilibrium voltage,
Veq (the value of Voc).
If Equation (6) is divided by the current
I, it can be rewritten as:
where
R is the equivalent resistance of the battery and
V′ is proportional to Δ
R under a short discharge time duration and a discharging current
I. That means for a given
V and fixed Δ
t, a lower
V′ has a lower Δ
R.
V′ is related to the increasing rate of internal resistance caused by battery discharging and aging. Therefore, for a given cell voltage,
V′ is sensitive to battery aging and changes with different charge-discharge cycles. Equation (9) uses
V′ to correlate SOC with battery aging so that the cycle number
N can be removed. Accordingly, the SOC equation is assumed to be
where
a,
b, and
c are undetermined coefficients to be fitted from test data regression.
Accurate SOC estimation relies on the precise evaluation of
Qm, which diminishes with battery age. Provided
Qm is not instantly updated, the estimated SOC would misguide the BMS operation. Therefore, SOC cannot be separately evaluated without considering SOH at the same time. Fortunately, it was seen that the battery’s aging information is, in fact, imbedded in the new parameter
V′. To see how the newly defined parameter
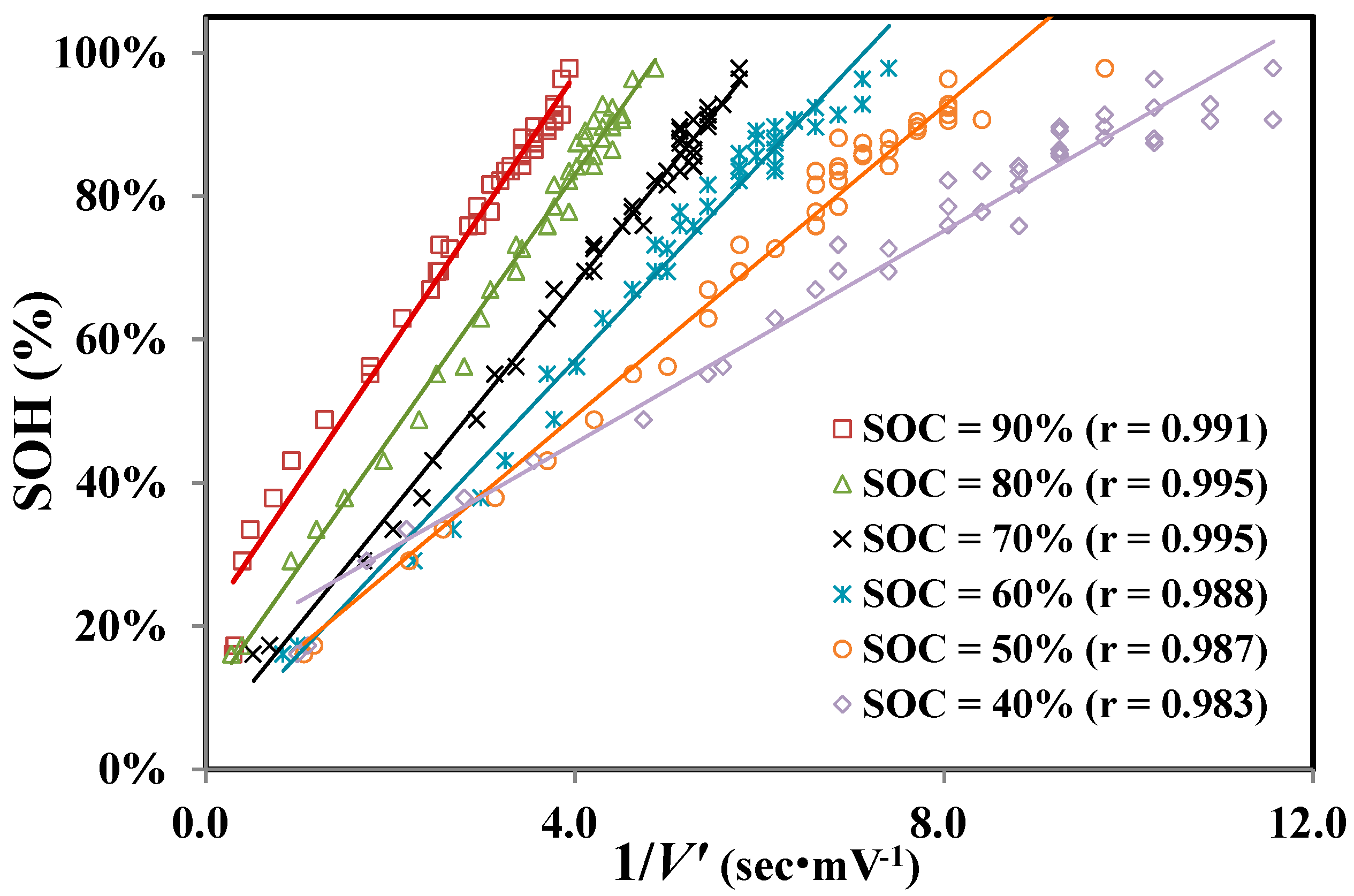
V′ related to SOH, their correlations at several SOC levels are illustrated in
Figure 3. The results show a surprisingly good correlation (>0.99) for all fixed SOCs ranging from 40% to 90%.
Figure 3 also shows that SOH-(1/
V′) has an approximately linear relationship for all different SOC levels. Therefore, the SOH regression model for a specific SOC level can be assumed to be
Similarly,
A and
B are regression coefficients to be determined. Take SOC = 70% as a typical example and solve for the coefficients
A = 0.5192 and
B = 0.0405 from cell
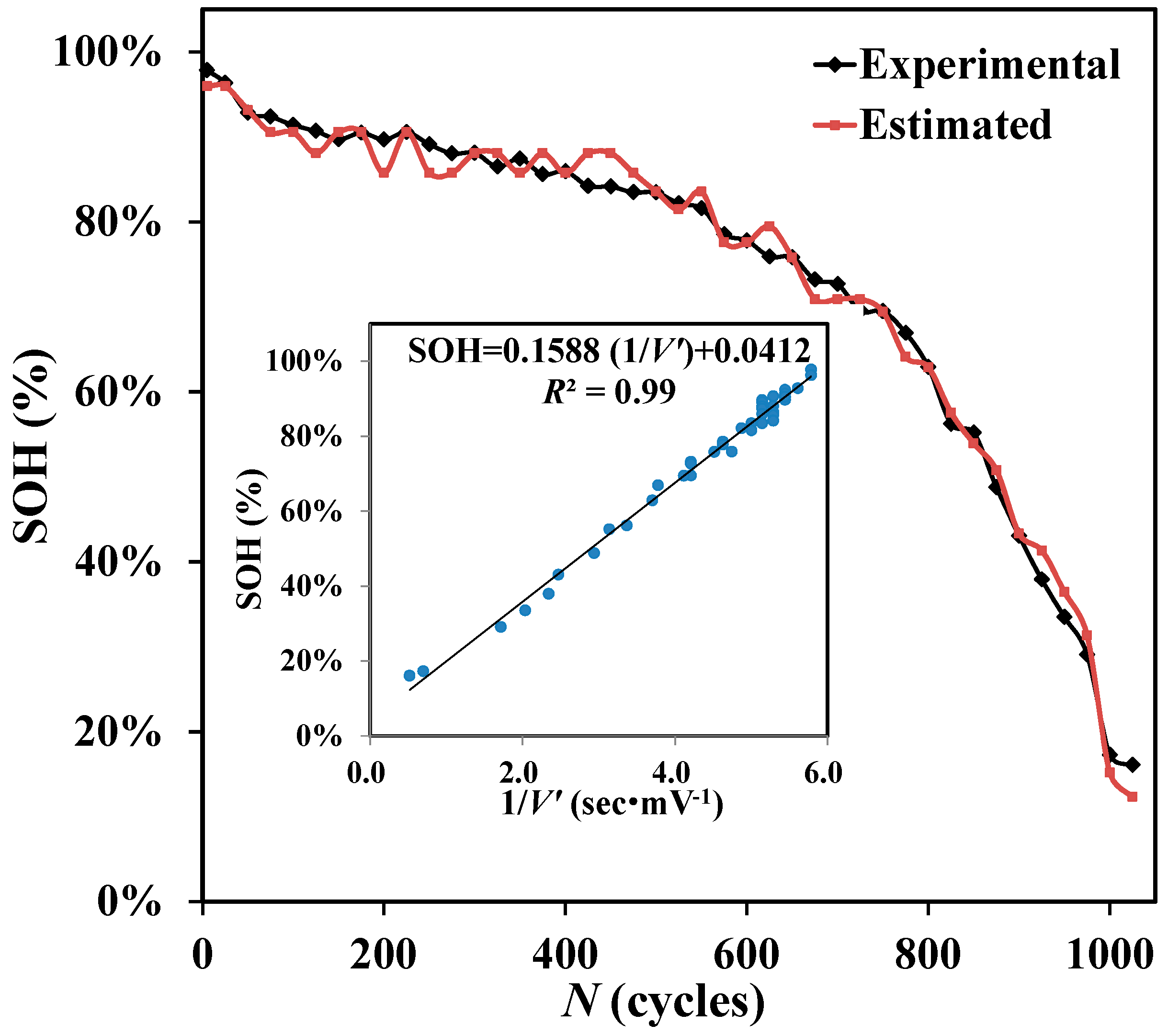
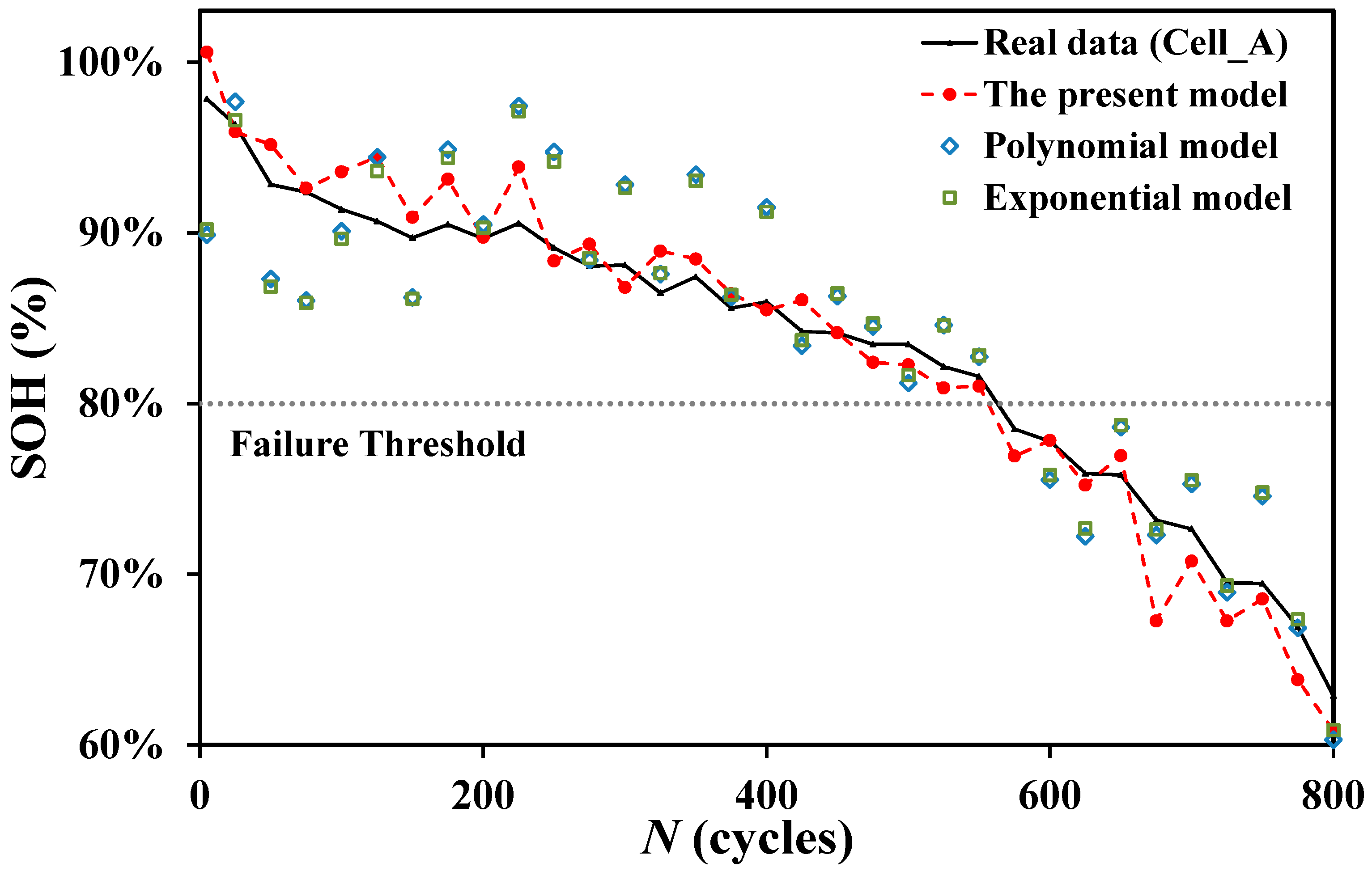
A’s test data. Substitute Equation (10) for the estimated SOH vs.
N, and compare it against the real values in
Figure 4. The coefficient of determination (
R2) is as high as 0.9907. This result enhances the adequacy of the SOH model, shown by Equation (10). Nonetheless, this is valid only for the case of SOC = 70%, and new coefficients for
A and
B need to be derived if SOC is other than 70%. It is impractical to have numerous sets of coefficients for different SOC levels. Therefore, an alternative approach to account for SOC variation is necessary.
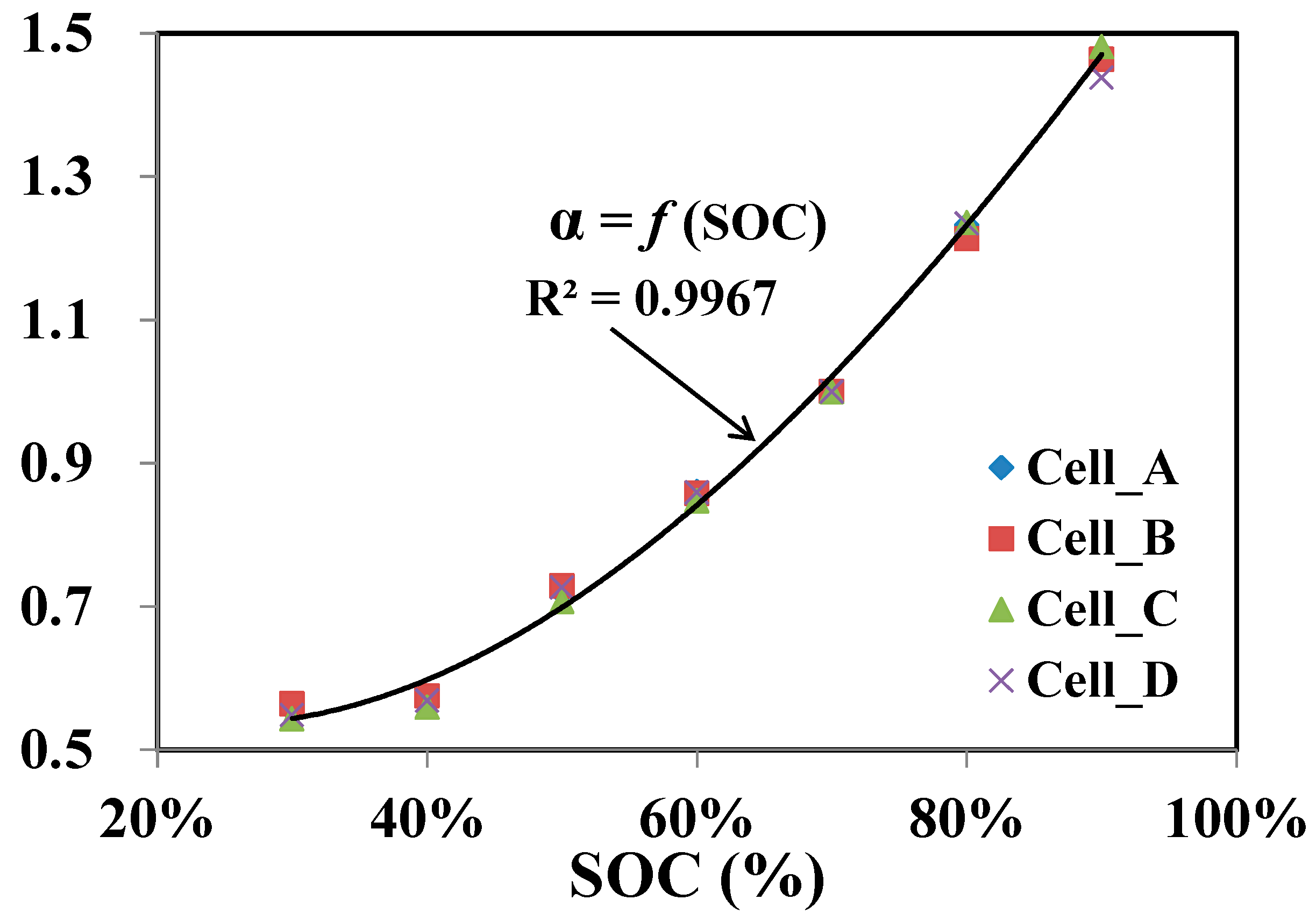
After thorough inspection of the test data, we multiplied a modification factor
α onto Equation (10) without recalculating the regression coefficients
A and
B. Equation (10) is hence modified to become
where
α(SOC) is the newly defined modification factor as a function of SOC. Since
α does not monotonically change with SOC, interpolation is required and a third degree of polynomials is found to be accurate enough, as follows:
The fitted curve of Equation (12) derived from cell A with SOC, ranging from 40% to 90%, shows excellent agreement with the other three tested cells, as seen in
Figure 5. The reason for choosing SOC = 70% as the basis (
α = 1) is because that state seems to be the most prevalent state of an in-use battery. The authors have used other SOCs or other cell as the basis, and the estimation error level remained the same, although the regression coefficients of the model and modification factor were different. This consistency partially proves the robustness of the derived model.
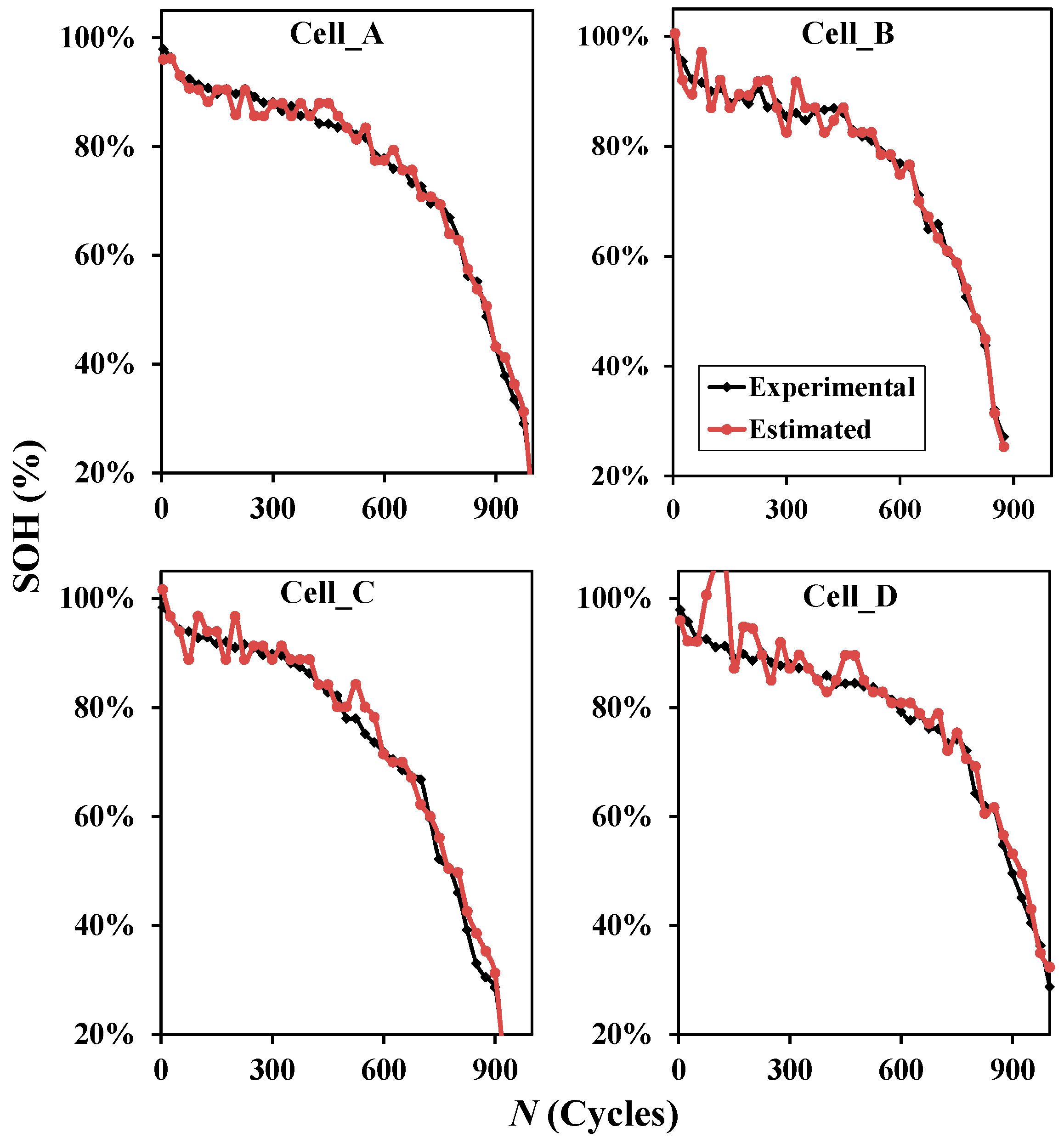
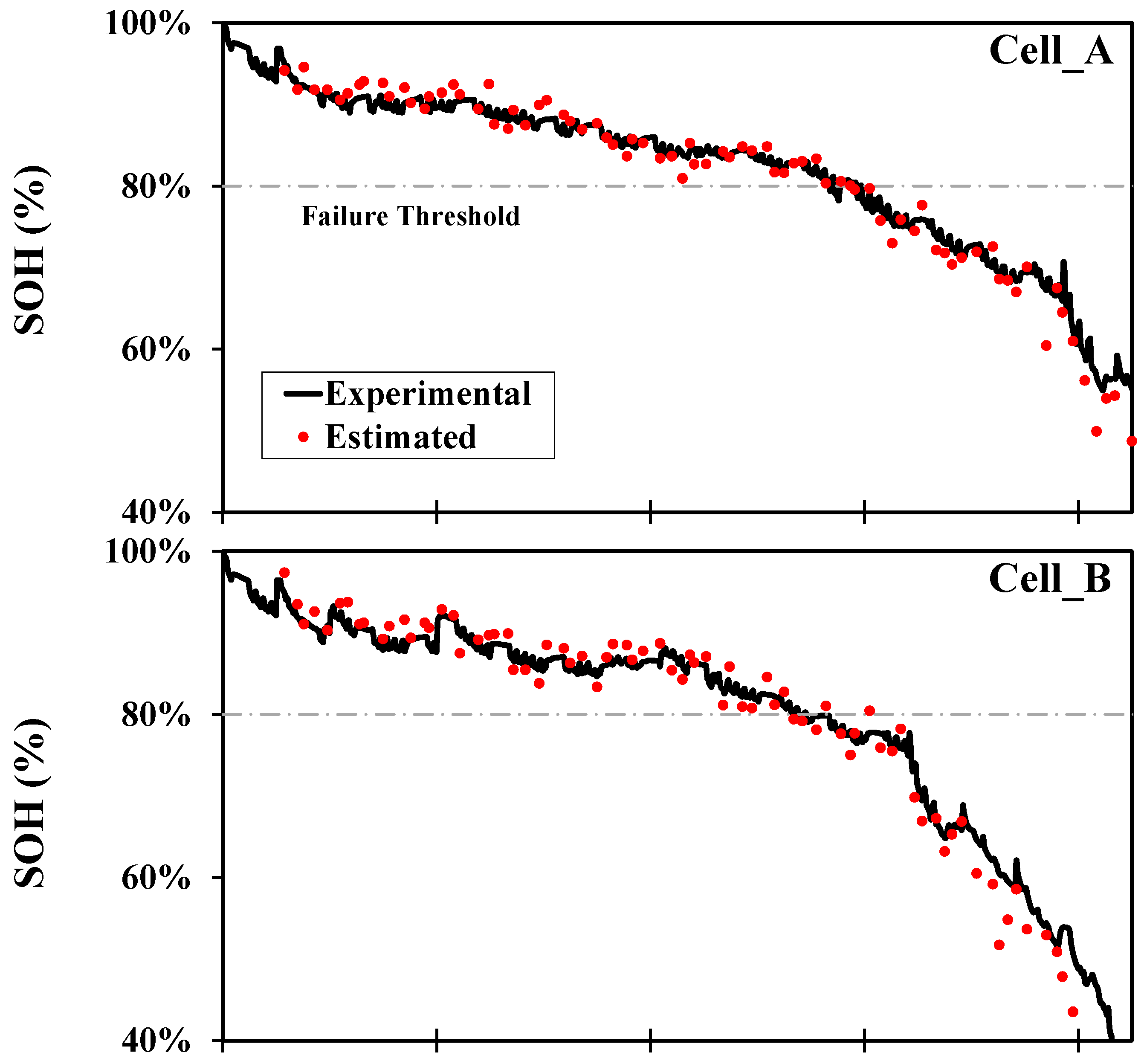
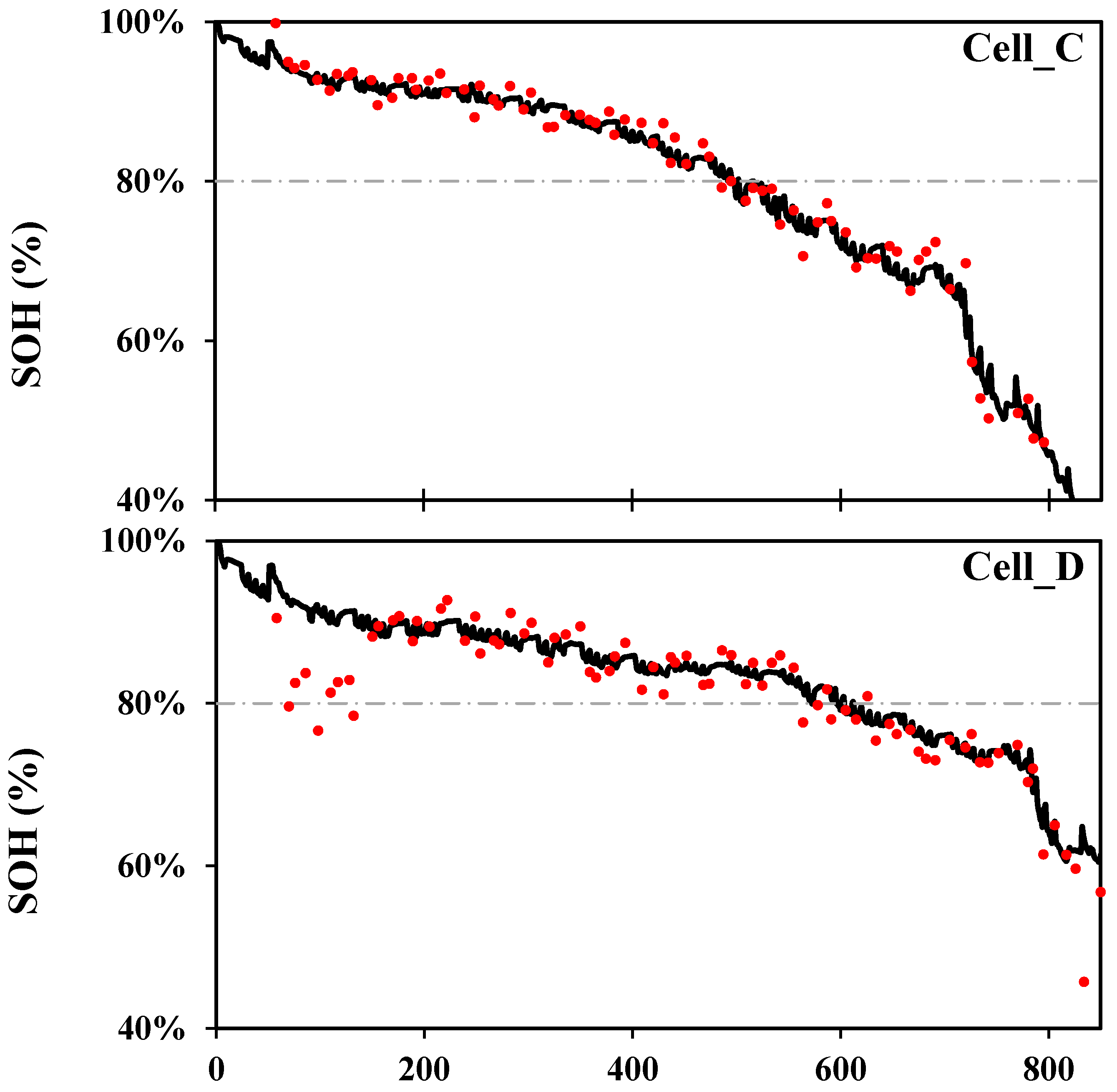
2.4. Model Construction and Verification
This study aimed to employ battery outputs such as voltage and current to build up a new model suitable for SOC and SOH online estimation. The newly developed SOC and SOH models (Equations (9), (11), and (12)) do not use the cycle number
N as the aging parameter. The batteries were undergoing the common cycle life test in the study so as to have
N as a reference to do a comparison within the models. The process of model construction is shown in
Figure 6, in which the test data of the instantaneous voltage, discharging current (constant), time, and resistance in each cycle were logged at 30-s intervals. 1/
V′ is calculated from every two adjacent outputs.
Qm is evaluated at the end of every discharging process, and SOH is calculated from Equation (2) accordingly. The SOC for each data point is obtained by back-substituting
Qm into Equation (1).
The coefficients of the SOC and SOH models, based on the four tested cells in this study, were calculated from data regression. The equations were then applied back to the four cells to estimate the SOC and SOH values and to compare against the real data for verification. The accuracy of the models was defined by R2 and root mean square error (RMSE). The SOC and SOH were estimated from the battery’s random sampling of discharging voltages to simulate an in-use situation.