Power-Smoothing Scheme of a DFIG Using the Adaptive Gain Depending on the Rotor Speed and Frequency Deviation
Abstract
:1. Introduction
2. Proposed Power-Smoothing Scheme of a DFIG
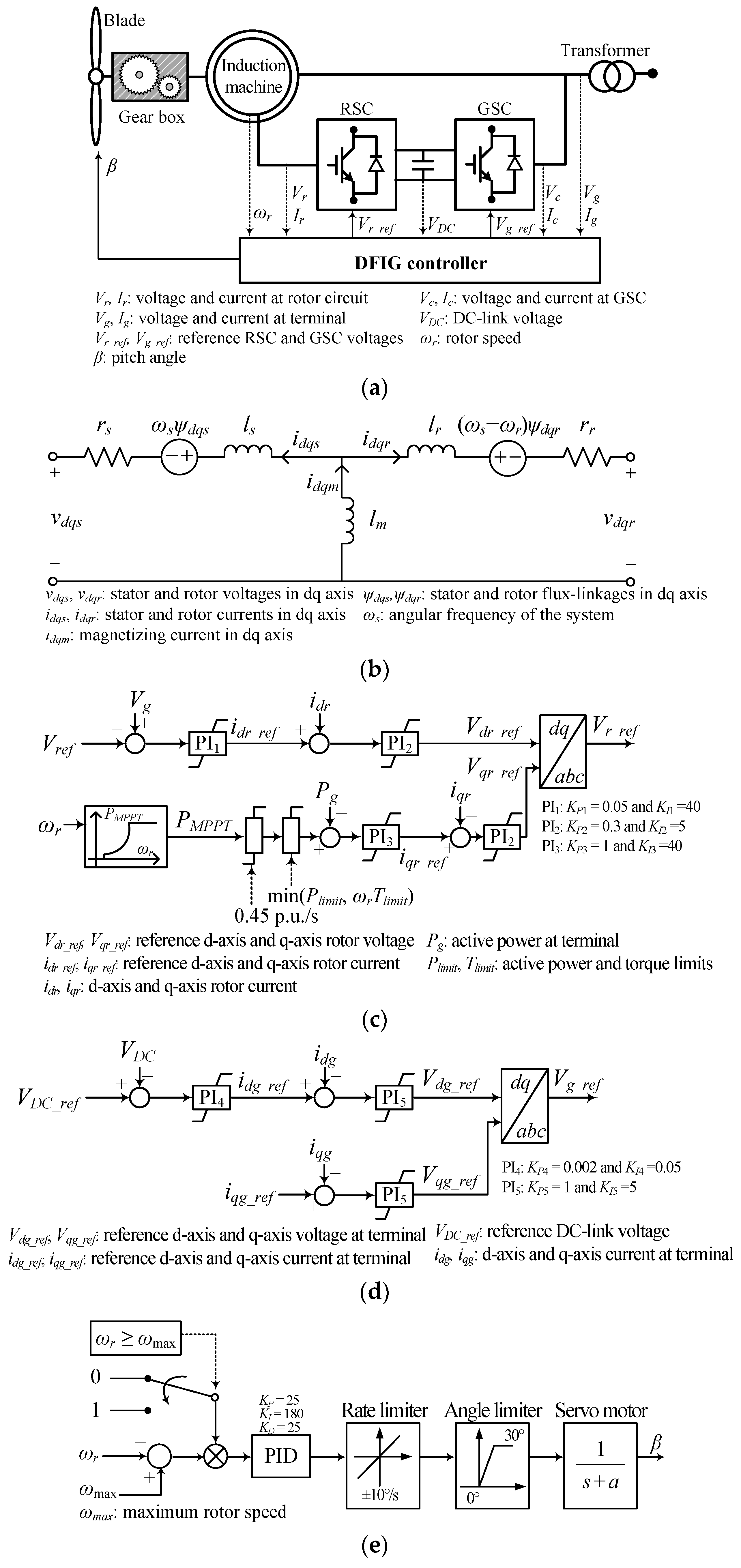
2.1. DFIG Model
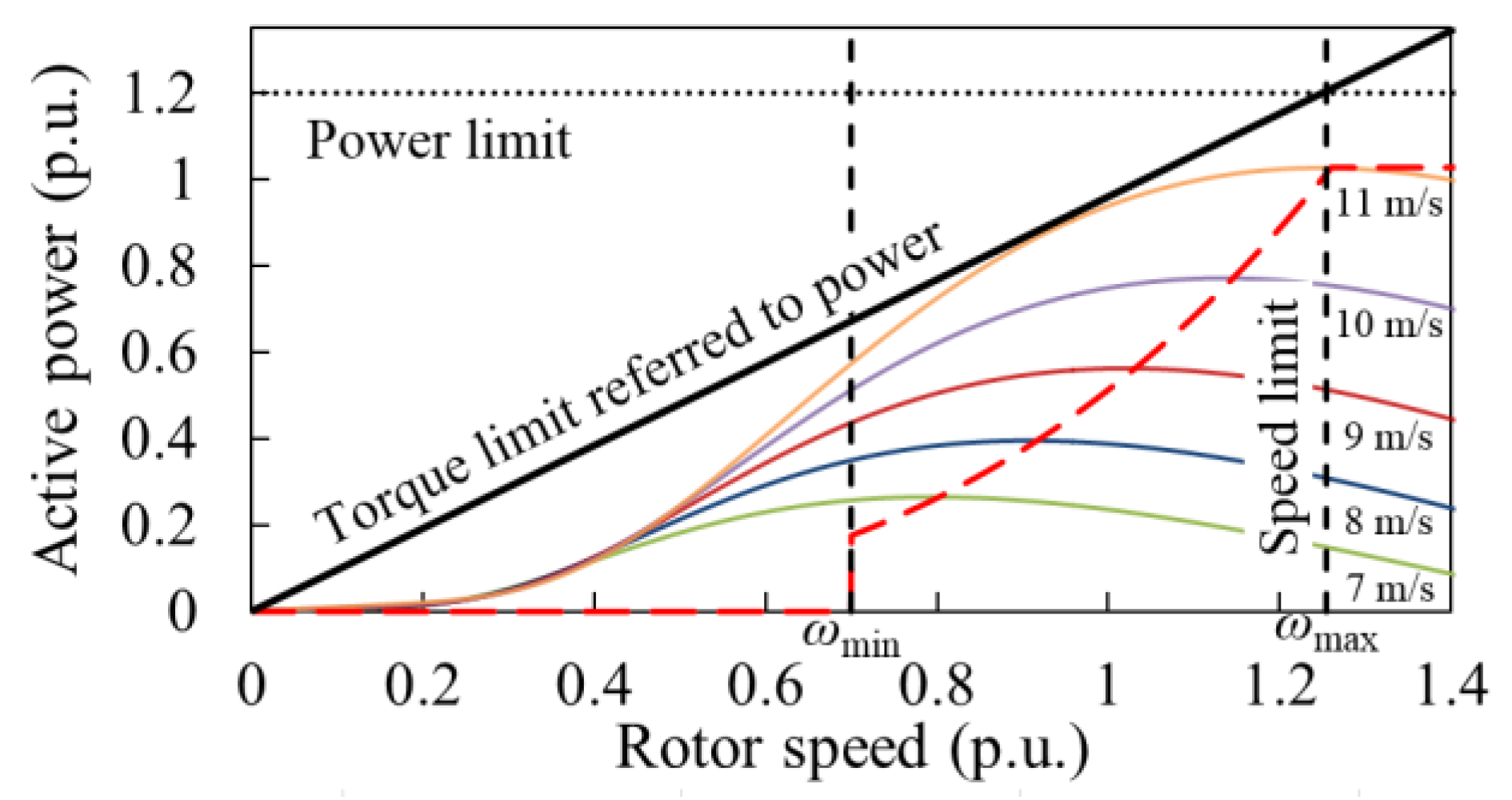
2.2. Conventional Power-Smoothing Scheme in [12]
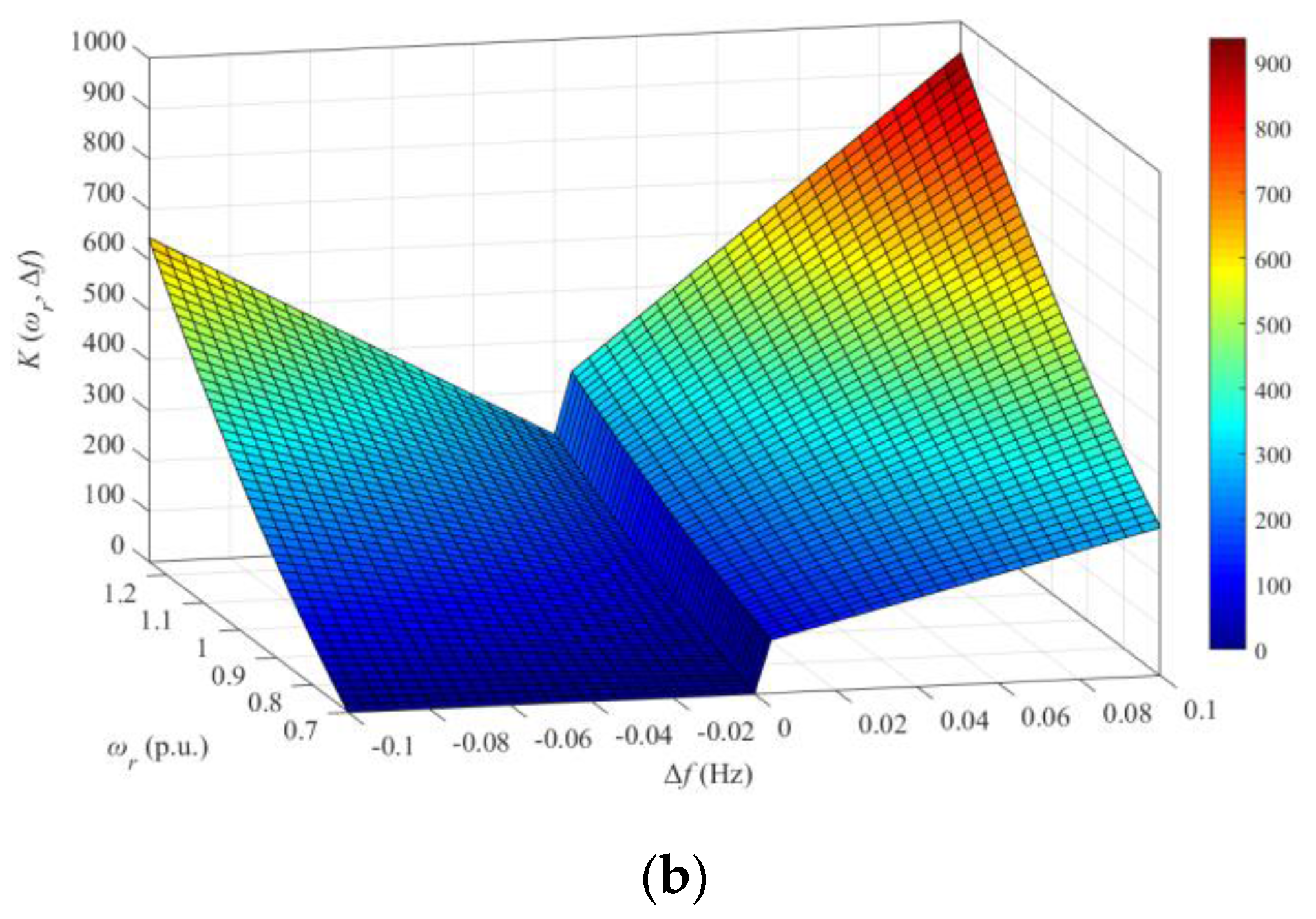
2.3. Proposed Power-Smoothing Scheme Using the Adaptive Gain with the Rotor Speed and Δf
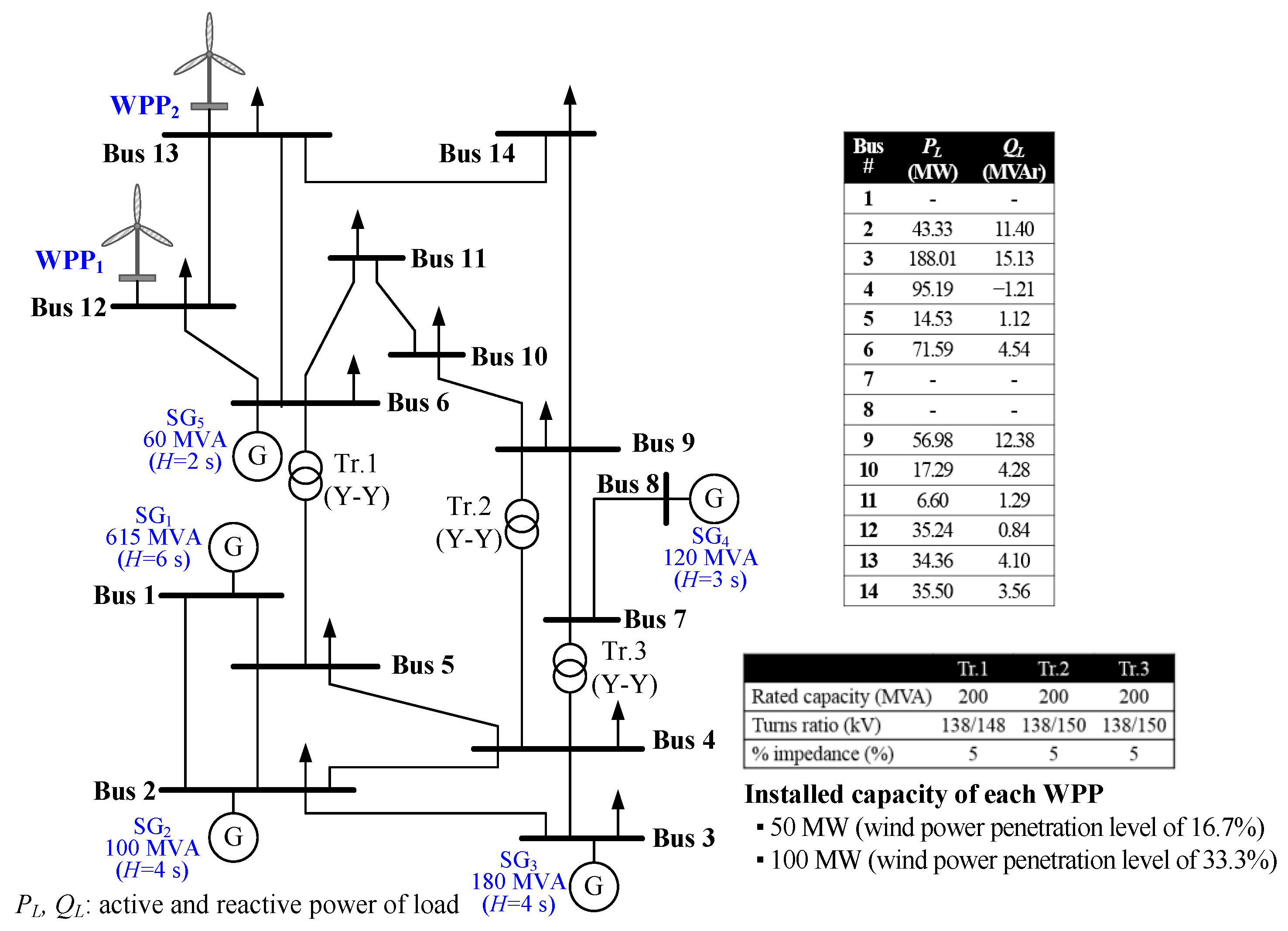
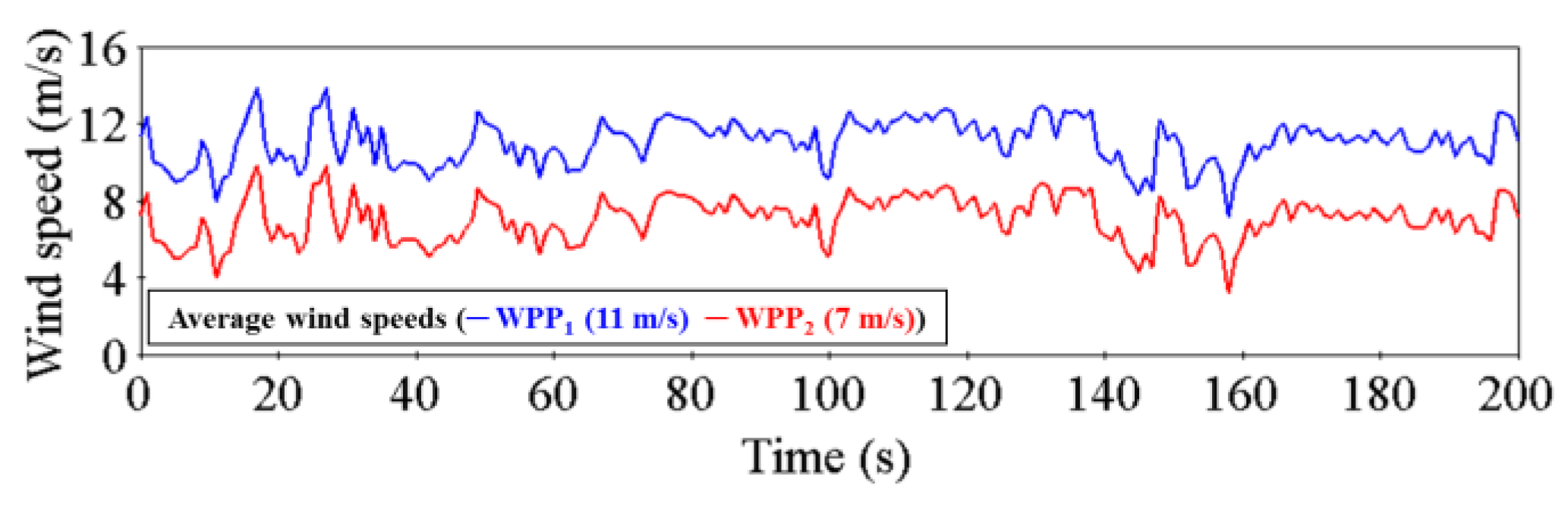
3. Model System
4. Case Studies
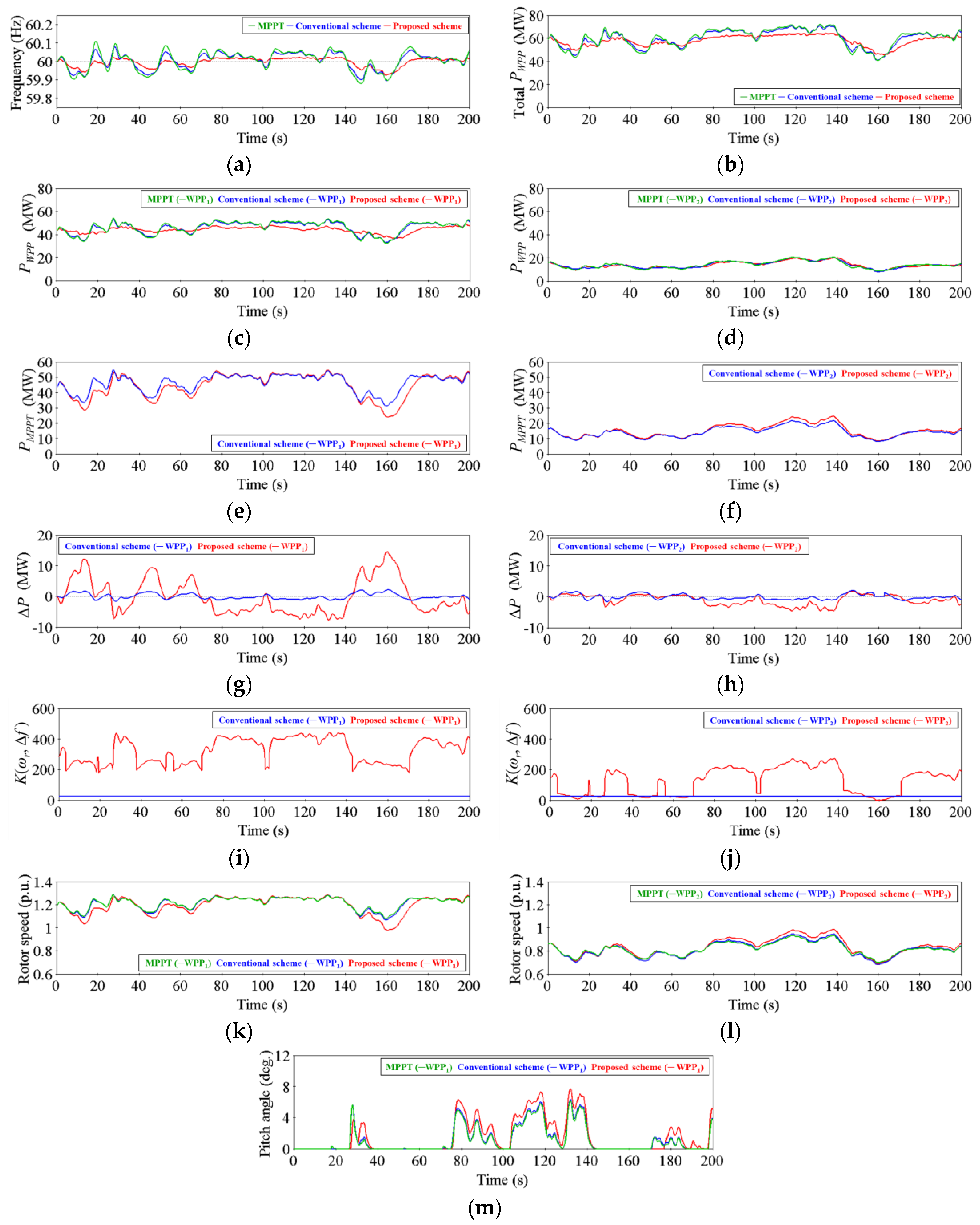
4.1. Case 1: Wind Power Penetration Level of 16.7%
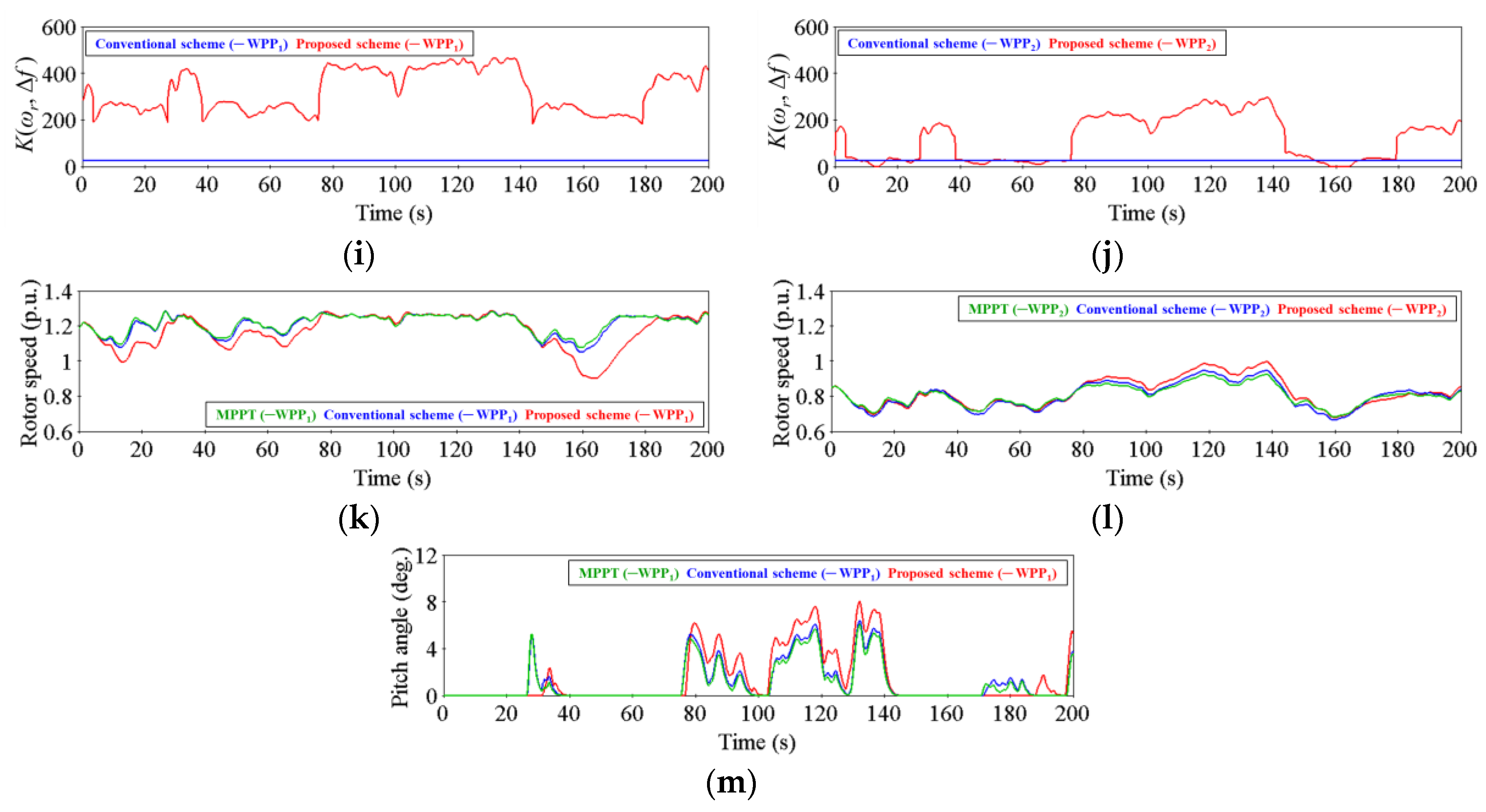
4.2. Case 2: Wind Power Penetration Level of 33.3%
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bevrani, H. Robust Power System Frequency Control, 2nd ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Alegría, I.M.; Andreu, J.; Martín, J.L.; Ibañez, P.; Villate, J.L.; Camblong, H. Connection requirements for wind farms: A survey on technical requirements and regulation. Renew. Sustain. Energy Rev. 2007, 11, 1858–1872. [Google Scholar] [CrossRef]
- Eriksen, P.B.; Ackermann, T.; Abildgaard, H.; Smith, P.; Winter, W.; Garcia, J.R. System operation with high wind penetration. IEEE Power Energy Mag. 2005, 3, 65–74. [Google Scholar] [CrossRef]
- Liserre, M.; Cardenas, R.; Molinas, M.; Rodriguez, J. Overview of multi-MW wind turbines and wind parks. IEEE Trans. Ind. Electron. 2011, 58, 1081–1095. [Google Scholar] [CrossRef]
- Ekanayake, J.B.; Jenkins, N. Comparison of the response of doubly-fed and fixed-speed induction generator wind turbines to changes in network frequency. IEEE Trans. Energy Convers. 2004, 19, 800–802. [Google Scholar] [CrossRef]
- Lalor, G.; Mullane, A.; O’Malley, M. Frequency control and wind turbine technologies. IEEE Trans. Power Syst. 2005, 20, 1905–1913. [Google Scholar] [CrossRef]
- Fagan, E.; Grimes, S.; McArdle, J.; Smith, P.; Stronge, M. Grid code provisions for wind generators in Ireland. In Proceedings of the 2005 IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 12–16 June 2005. [Google Scholar]
- D’ıaz-Gonz’alez, F.; Bianchi, F.D.; Sumper, A.; Gomis-Bellmunt, O. Control of a flywheel energy storage system for power smoothing in wind power plants. IEEE Trans. Energy Convers. 2014, 29, 204–214. [Google Scholar] [CrossRef]
- Pegueroles-Queralt, J.; Bianchi, F.D.; Gomis-Bellmunt, O. A power smoothing system based on supercapacitors for renewable distributed generation. IEEE Trans. Ind. Electron. 2015, 62, 343–350. [Google Scholar] [CrossRef]
- Xiangjun, L.; Dong, H.; Xiaokang, L. Battery energy storage station (BESS)-based smoothing control of photovoltaic (PV) and wind power generation fluctuations. IEEE Trans. Sustain. Energy 2013, 4, 464–473. [Google Scholar]
- Margaris, I.D.; Papathanassiou, S.A.; Hatziargyriou, N.D.; Hansen, A.D.; Sørensen, P. Frequency control in autonomous power systems with high wind power penetration. IEEE Trans. Sustain. Energy 2012, 3, 189–199. [Google Scholar] [CrossRef]
- Wang-hansen, M.; Josefsson, R.; Mehmendovic, H. Frequency controlling wind power modeling of control strategies. IEEE Trans. Sustain. Energy 2013, 4, 954–959. [Google Scholar] [CrossRef]
- Yang, S. Novel Sensorless Generator Control and Grid Fault Ride-through Strategies for Variable-Speed Wind Turbines and Implementation on a New Real-Time Simulation Platform. Ph.D. Thesis, Department of Electrical and Computer Engineering, Iowa State University, Ames, Iowa, 2010. [Google Scholar]
- Ye, R.-J.; Li, H.; Chen, Z.; Gao, Q. Comparison of transient behaviors of wind turbines with DFIG considering the shaft flexible models. In Proceedings of the 2008 IEEE International Conference on Electrical Machines and Systems (ICEMS), Wuhan, China, 17–20 October 2008. [Google Scholar]
- Lie, X.; Yi, W. Dynamic modelling and control of DFIG-based wind turbines under unbalanced network conditions. IEEE Trans. Power Syst. 2007, 22, 314–323. [Google Scholar]
- Shen, B.; Mwinyiwiwa, B.; Zhang, Y.; Ooi, B. Sensorless maximum power point tracking of wind by DFIG using rotor position phase lock loop. IEEE Trans. Power Electron. 2009, 24, 942–951. [Google Scholar] [CrossRef]
- Wang, Y.; Delille, G.; Bayem, H.; Guilaud, X.; Francois, B. High wind power penetration in isolated power systems—Assessment of wind inertial and primary frequency responses. IEEE Trans. Power Syst. 2013, 28, 2412–2420. [Google Scholar] [CrossRef]
- Mauricio, J.M.; Marano, A.; Gómez-Expósito, A.; Ramos, J.L.M. Frequency regulation contribution through variable-speed wind energy conversion systems. IEEE Trans. Power Syst. 2009, 24, 173–180. [Google Scholar] [CrossRef]
- Clark, K.; Miller, N.W.; Sanchez-Gasca, J.J. Modeling of GE Wind Turbine-Generators for Grid Studies, version 4.5; GE Energy: Schenectady, NY, USA, 2010. [Google Scholar]
- Sutter, J.; Maleche, J.; Muriithi, C. Analysis of power system transient stability due to increased integration of geothermal power. In Proceedings of the 39th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 24–26 February 2014. [Google Scholar]
- Byerly, R.T.; Aanstad, O.; Berry, D.H.; Dunlop, R.D.; Ewart, D.N.; Fox, B.M.; Johnson, L.H.; Tschappat, D.W. Dynamic models for steam and hydro turbines in power system studies. IEEE Trans. Power Appar. Syst. 1973, 92, 1904–1915. [Google Scholar]
- Ackermann, T. Wind Power in Power Systems, 2nd ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2012. [Google Scholar]



| Parameter | MPPT Operation | Conventional Scheme | Proposed Scheme |
|---|---|---|---|
| RMS {Δf} (Hz) | 0.051 | 0.043 | 0.024 |
| Δfmax (Hz) | 0.108 | 0.079 | 0.022 |
| Δfmin (Hz) | −0.121 | −0.106 | −0.075 |
| Operating Range of ωr for WPP1 (p.u.) | 0.205 | 0.218 | 0.308 |
| Operating Range of ωr for WPP2 (p.u.) | 0.237 | 0.267 | 0.297 |
| Parameter | MPPT Operation | Conventional Scheme | Proposed Scheme |
|---|---|---|---|
| RMS {Δf} (Hz) | 0.098 | 0.076 | 0.037 |
| Δfmax (Hz) | 0.196 | 0.128 | 0.026 |
| Δfmin (Hz) | −0.235 | −0.191 | −0.113 |
| Operating Range of ωr for WPP1 (p.u.) | 0.209 | 0.235 | 0.385 |
| Operating Range of ωr for WPP2 (p.u.) | 0.245 | 0.285 | 0.320 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Hwang, M.; Muljadi, E.; Sørensen, P.; Kang, Y.C. Power-Smoothing Scheme of a DFIG Using the Adaptive Gain Depending on the Rotor Speed and Frequency Deviation. Energies 2017, 10, 555. https://doi.org/10.3390/en10040555
Lee H, Hwang M, Muljadi E, Sørensen P, Kang YC. Power-Smoothing Scheme of a DFIG Using the Adaptive Gain Depending on the Rotor Speed and Frequency Deviation. Energies. 2017; 10(4):555. https://doi.org/10.3390/en10040555
Chicago/Turabian StyleLee, Hyewon, Min Hwang, Eduard Muljadi, Poul Sørensen, and Yong Cheol Kang. 2017. "Power-Smoothing Scheme of a DFIG Using the Adaptive Gain Depending on the Rotor Speed and Frequency Deviation" Energies 10, no. 4: 555. https://doi.org/10.3390/en10040555
APA StyleLee, H., Hwang, M., Muljadi, E., Sørensen, P., & Kang, Y. C. (2017). Power-Smoothing Scheme of a DFIG Using the Adaptive Gain Depending on the Rotor Speed and Frequency Deviation. Energies, 10(4), 555. https://doi.org/10.3390/en10040555






