A Method for Thermal Dimensioning and for Energy Behavior Evaluation of a Building Envelope PCM Layer by Using the Characteristic Days
Abstract
:1. Introduction
2. Methodology
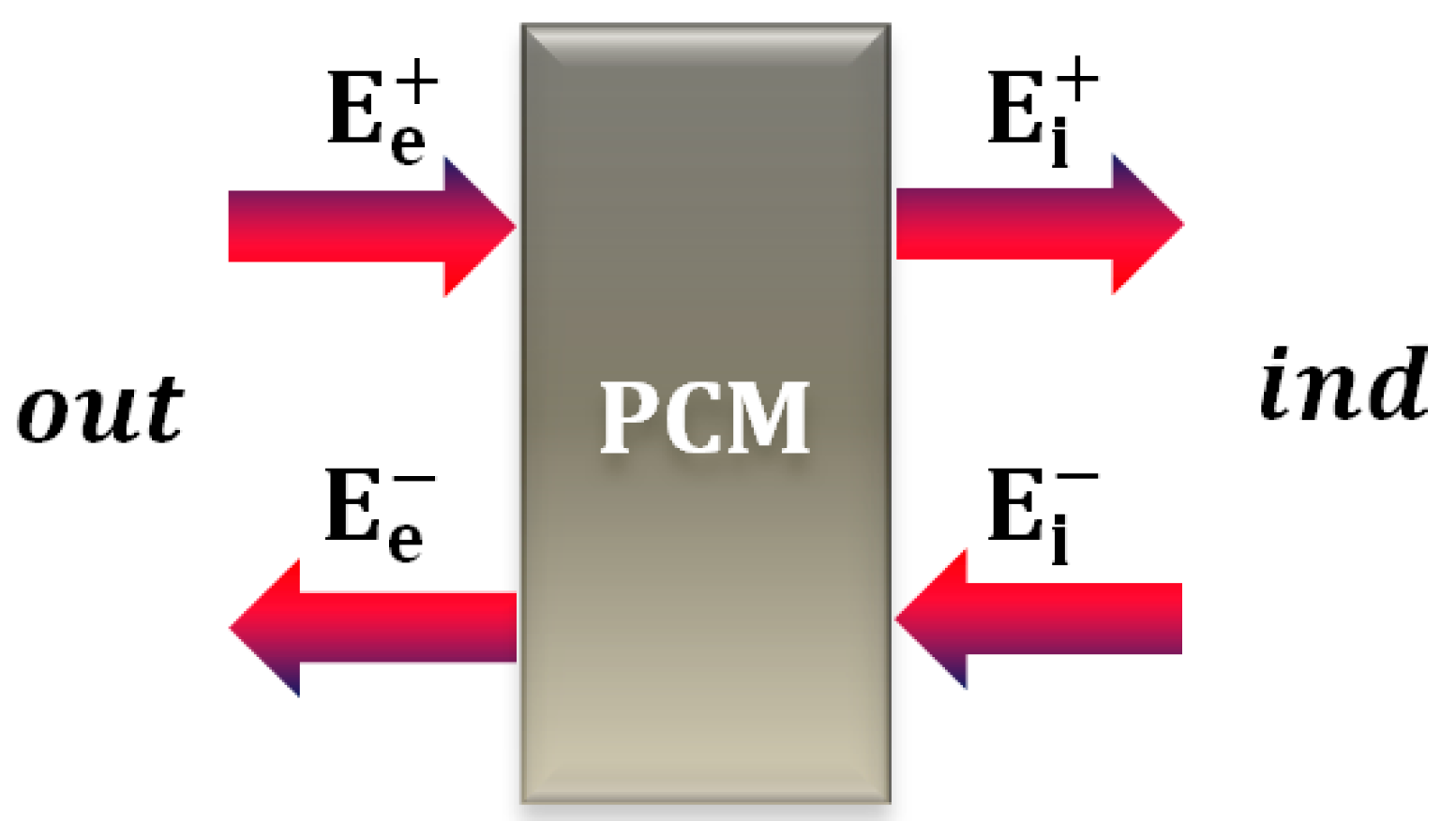
2.1. Calculation Model
2.2. Transferred and Stored Energy
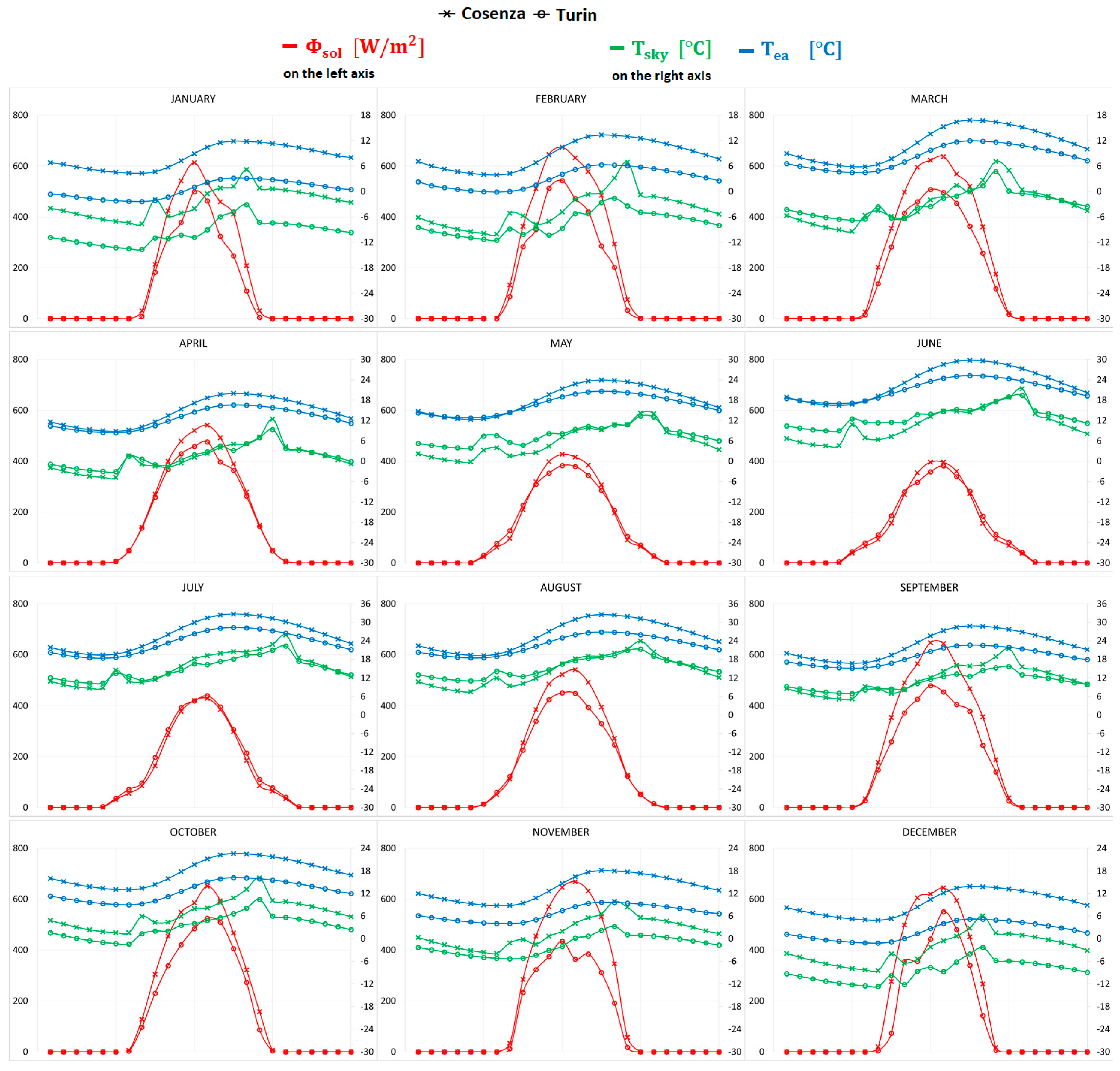
3. Case Study Description
4. Results and Discussion
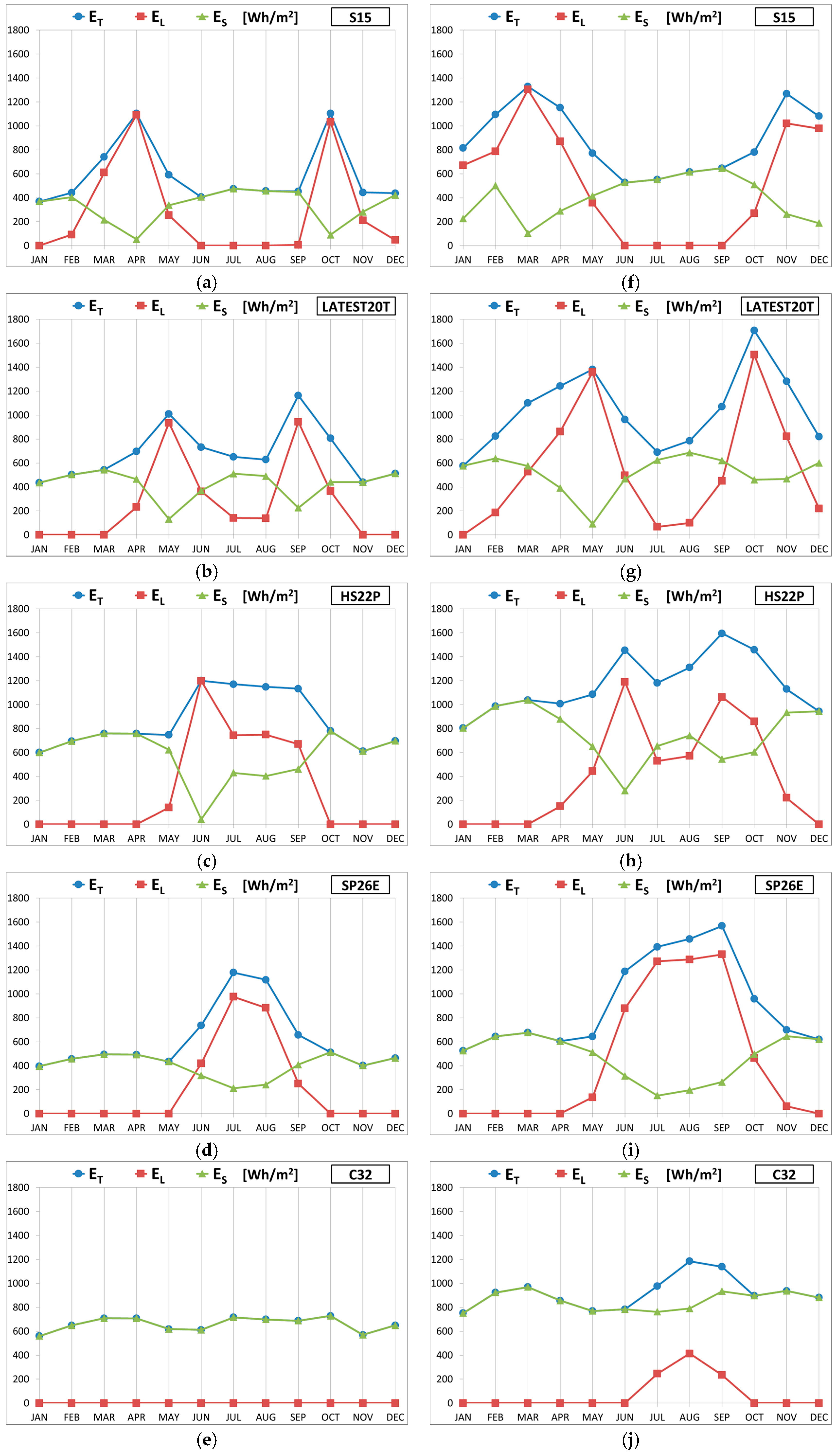
4.1. Monthly Energy Behaviour of the Layer
4.1.1. Number of Bi-Phase Interfaces in the PCM Layer
4.1.2. Stored Energy
4.1.3. Transferred Energy
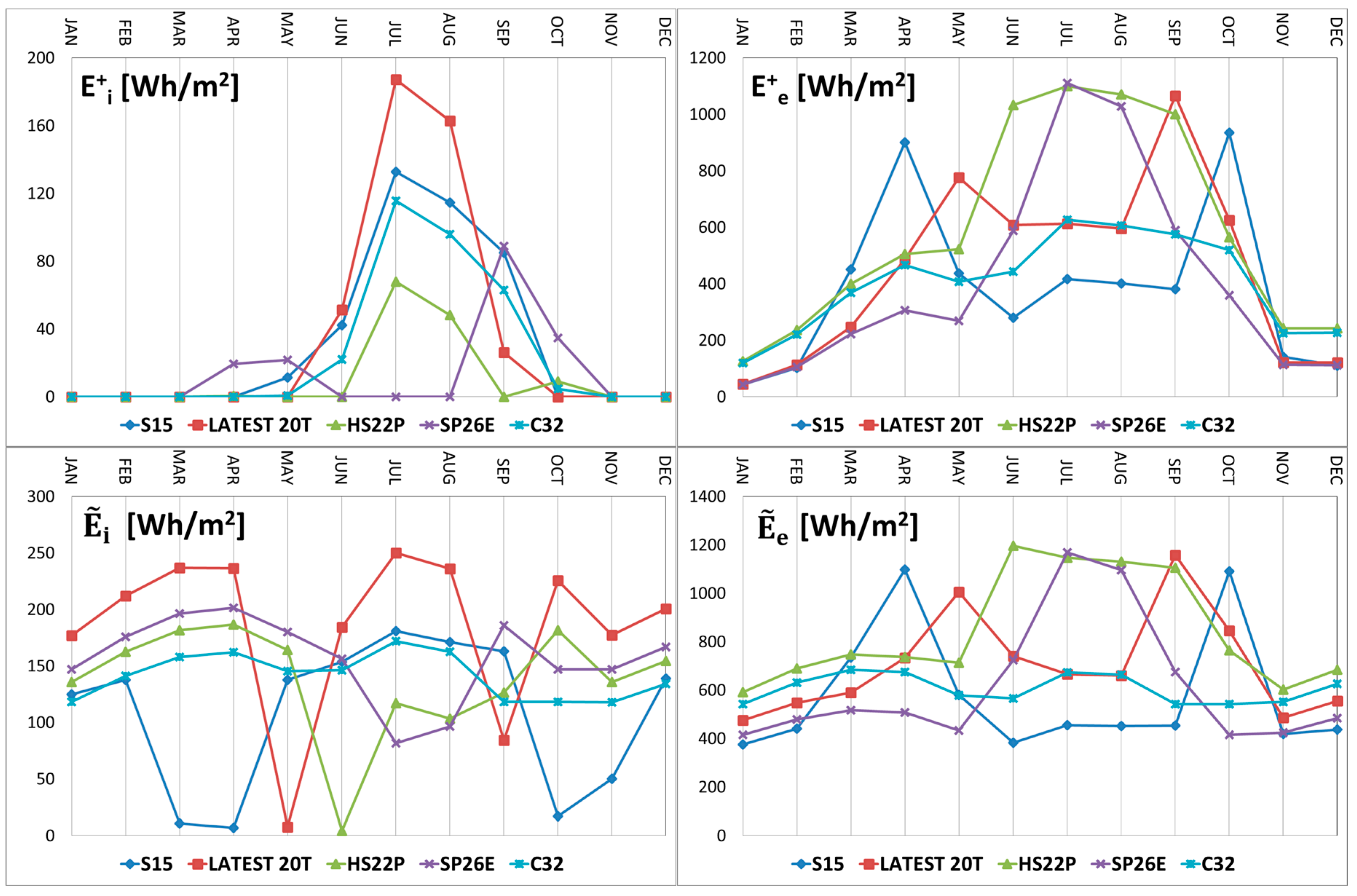
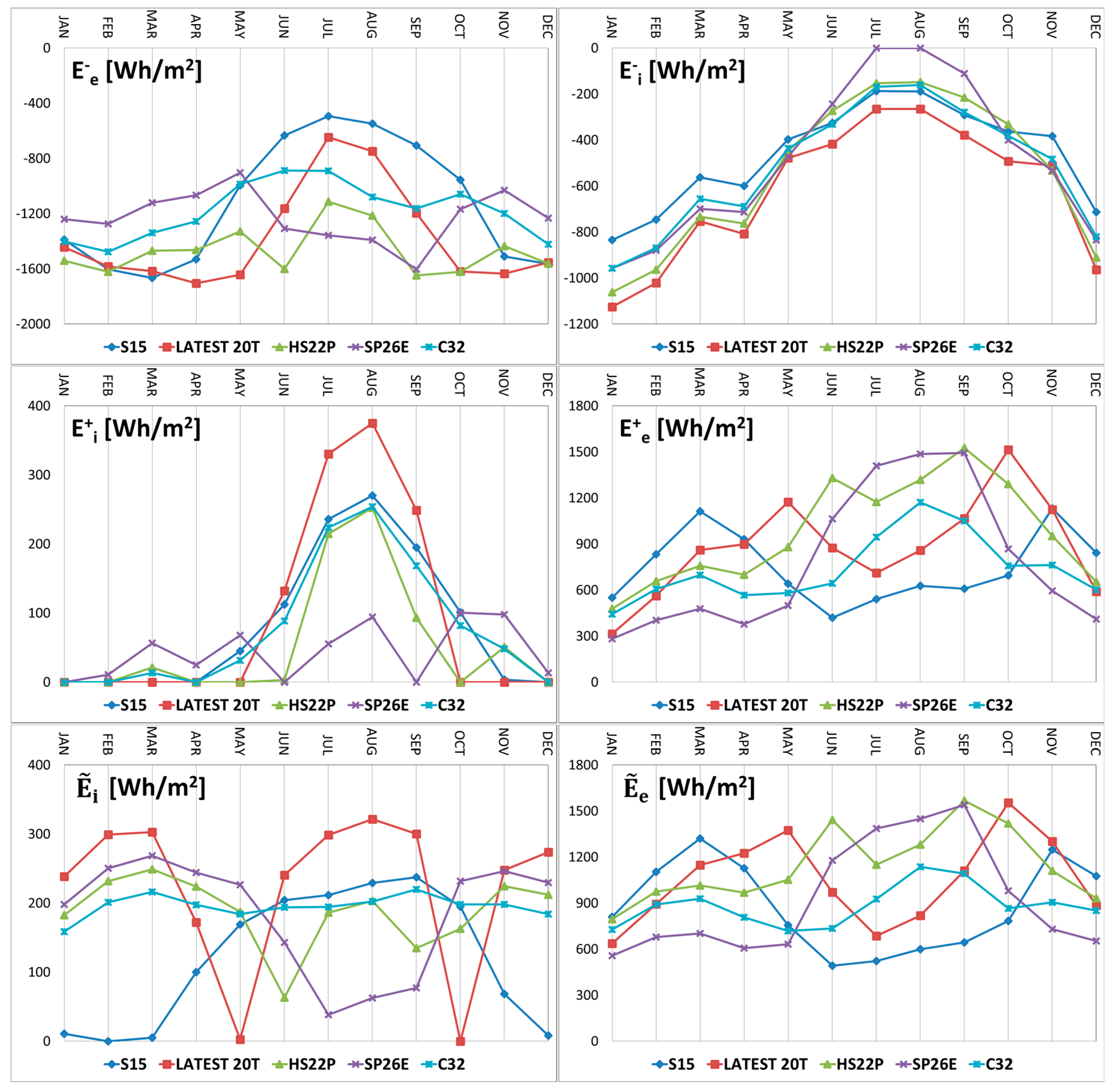
- shows a regular trend with a minimum value in the summer months and it increases in a monotonous way, proceeding towards the winter months with maximum values in January and December; the PCM LATEST20T provides the highest values in all months, while the lowest values are obtained in July and August with the PCM SP26E and in the other months with the PCM S15;
- shows high values during the winter months and lower values in the summer and intermediate months, with a regular trend in absence of phase change, as in the case of PCM C32. The presence of bi-phase interfaces gives rise to a sharp increase of the energy lost through the external surface. In particular, such an increase moves with increasing melting temperature from intermediate months to the summer months. PCM HS22P provides the highest values from November to March and from June to August, S15 in April and in October, and LATEST20T during the other months. The lowest values occur with PCM S15 between November and February and between June and September, and in the other months with SP26E;
- shows, usually, the highest values during summer months, with a peak in June, and nil values between November and March. PCM LATEST20T records during June, July and August show the highest values. The behaviour of PCM SP26 is quite different, recording nil values during summer months and the highest values during the intermediate months;
- shows low values during winter months and higher values during intermediate and summer months. The irregular trend is due to the phase changes, which cause a sharp increase of the energy entering the layer. The monthly behaviour of different PCMs is totally analogous to that illustrated regarding the energy exiting from the layer toward the outdoor environment , with higher values and lower values obtained by the same PCMs during the different months;
- and show a slightly variable monthly trend in absence of bi-phase interfaces, as highlighted by PCM C32. The phase change determines a modification of the previous trend with significant monthly variations of the heat flux fluctuating components on the internal and external surface. Particularly, the stored and then released latent energy causes a sharp reduction of the fluctuating energy through the internal surface and a marked increase of the fluctuating energy through the external surface.
- for the different PCMs shows the same trend with lower values in the different months. Even in this case, the highest values are obtained with PCM LATEST20T. The lowest values are recorded from June to September with PCM SP26E, from November to May with the PCM S15, and in October with PCM HS22P;
- shows the same trend with lower values and, during the months in which phase change occurs, the increase switches with the rise in melting temperature from winter to summer months. PCM S15 shows the highest values in March, LATEST20T in April, May and November, SP26E in July and August, and HS22P in all the other months. The lowest values occur with PCM S15 between June and October and with SP26E from November to May;
- shows a similar trend with higher values and with a maximum in August. PCM LATEST20T records higher values from June to September and, in all other months, nil values. The behaviour of PCM SP26E is quite different, showing lower values in the summer months and higher values during intermediate months;
- shows higher values and the increases switch, due to the phase changes according to the rise of the melting temperature from winter to summer months. Even in Cosenza, the highest and the lowest values during the different months are obtained with the same PCMs highlighted in the comment about exiting energy;
- and show analogous behaviour as that experienced for Turin.
4.1.4. Influence of Latent Storage on the Energy Behavior of the Layer
4.2. Criterion of Choice of the PCM Layer
4.2.1. Seasonal Transferred Energy
4.2.2. Yearly Stored Energy
5. Conclusions
- With the increase of the melting temperature, for both locations, the highest values of the stored latent energy switch from winter and intermediate months to summer months. The quantity of latent energy stored, during the months in which phase change is recorded, depends on the number of bi-phase interfaces, on the size of the portion of the layer involved in the phase change, on the density and on the latent heat of fusion.
- The sensible energy storage shows a reduction during the months in which the phase change occurs, while during the other months, it depends on the volumetric heat capacity ρc of the PCM.
- The total stored energy increases during the months in which the phase change occurs, despite the reduction of the sensible contribution; during the other months, it is determined by only sensible energy.
- The lowest energy exiting from the indoor environment is ensured by a PCM with a melting temperature of 15 °C (S15);
- The highest contribution of energy entering the indoor environment, mainly due to solar radiation, is recorded for a PCM with a melting temperature of 26 °C (SP26).
- The lowest value of energy entering the indoor environment is obtained by SP26;
- The highest value of energy exiting from the indoor environment is ensured by LATEST20 (with a melting temperature equal to 20 °C).
Author Contributions
Conflicts of Interest
Nomenclature
| a | Thermal diffusivity (m2/s) |
| c | Specific heat capacity (J/kg K) |
| E | Energy per square meter (J/m2) |
| Ee | Energy on the external surface (J/m2) |
| Ei | Energy on the internal surface (J/m2) |
| h | Heat transfer coefficient (W/(m2 K)) |
| H | Latent heat of fusion (J/kg) |
| k | Thermal conductivity (W/m K) |
| L | Layer thickness (m) |
| P | Period (s) |
| t | Time (s) |
| T | Temperature (K) |
| x | Spatial coordinate (m) |
| XM | Position of the bi-phase interface (m) |
Greek symbols
| Solar absorption coefficient (-) | |
| Finite difference time step (s) | |
| Heat flux (W/m2) | |
| ρ | Density (kg/m3) |
Subscripts
| c | Convective |
| e | External |
| ea | Referring to the external air load |
| ia | Referring to the internal air |
| k | k-th bi-phase interface |
| l | Liquid |
| L | Referring to the latent energy stored |
| M | Melting |
| r | Radiative |
| s | Solid |
| S | Referring to the sensible energy stored |
| s,i | Referring to the internal surface |
| s,e | Referring to the external surface |
| sky | Referring to the sky load |
| sol | Referring to the solar load |
Superscripts
| + | Entering |
| − | Exiting |
| n | Current time instant |
| n+1 | Successive time instant |
Symbols
| ~ | Fluctuating value |
References
- Souayfane, F.; Fardoun, F.; Biwole, P.-H. Phase change materials (PCM) for cooling applications in buildings: A review. Energy Build. 2016, 129, 396–431. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, C.Y.; Tian, Y. Review on thermal energy storage with phase change materials (PCMs) in building applications. Appl. Energy 2012, 92, 593–605. [Google Scholar] [CrossRef]
- Kalnæs, S.E.; Jelle, B.P. Phase change materials and products for building applications: A state-of-the-art review and future research opportunities. Energy Build. 2015, 94, 150–176. [Google Scholar] [CrossRef]
- Han, Y.; Taylor, J.E. Simulating the Inter-Building Effect on energy consumption from embedding phase change materials in building envelopes. Sustain. Cities Soc. 2016, 27, 287–295. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; De Masi, R.F.; de’ Rossi, F.; Vanoli, G.P. Energy refurbishment of existing buildings through the use of phase change materials: Energy savings and indoor comfort in the cooling season. Appl. Energy 2014, 113, 990–1007. [Google Scholar] [CrossRef]
- Halford, C.K.; Boehm, R.F. Modeling of phase change material peak load shifting. Energy Build. 2007, 39, 298–305. [Google Scholar] [CrossRef]
- Mazzeo, D.; Oliveti, G.; De Simone, M.; Arcuri, N. Analytical model for solidification and melting in a finite PCM in steady periodic regime. Int. J. Heat Mass Transf. 2015, 88, 844–861. [Google Scholar] [CrossRef]
- Mazzeo, D.; Oliveti, G.; Arcuri, N. Multiple bi-phase interfaces in a PCM layer subject to periodic boundary conditions characteristic of building external walls. Energy Procedia 2015, 82, 472–479. [Google Scholar] [CrossRef]
- Mazzeo, D.; Oliveti, G.; Arcuri, N. Definition of a new set of parameters for the dynamic thermal characterization of PCM layers in the presence of one or more liquid-solid interfaces. Energy Build. 2017, 141, 379–396. [Google Scholar] [CrossRef]
- Diaconu, B.M.; Cruceru, M. Novel concept of composite phase change material wall system for year-round thermal energy savings. Energy Build. 2010, 42, 1759–1772. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Li, L.; Zhao, M. Experimental assessment on the use of phase change materials (PCMs)-bricks in the exterior wall of a full-scale room. Energy Convers. Manag. 2016, 120, 81–89. [Google Scholar] [CrossRef]
- Chen, C.; Guo, H.; Liu, Y.; Yue, H.; Wang, C. A new kind of phase change material (PCM) for energy-storing wallboard. Energy Build. 2008, 40, 882–890. [Google Scholar] [CrossRef]
- Qureshi, W.A.; Nair, N.-K.C.; Farid, M.M. Impact of energy storage in buildings on electricity demand side management. Energy Convers. Manag. 2011, 52, 2110–2120. [Google Scholar] [CrossRef]
- Peippo, K.; Kauranen, P.; Lund, P.D. A multicomponent PCM wall optimized for passive solar heating. Energy Build. 1991, 17, 259–270. [Google Scholar]
- Athienitis, A.K.; Liu, C.; Hawes, D.; Banu, D.; Feldman, D. Investigation of the thermal performance of a passive solar test-room with wall latent heat storage. Build. Environ. 1997, 32, 405–410. [Google Scholar] [CrossRef]
- Hammou, Z.A.; Lacroix, M. A new PCM storage system for managing simultaneously solar and electric energy. Energy Build. 2006, 38, 258–265. [Google Scholar] [CrossRef]
- Castell, A.; Martorell, I.; Medrano, M.; Pérez, G.; Cabeza, L.F. Experimental study of using PCM in brick constructive solutions for passive cooling. Energy Build. 2010, 42, 534–540. [Google Scholar] [CrossRef]
- Lei, J.; Yang, J.; Yang, E.-H. Energy performance of building envelopes integrated with phase change materials for cooling load reduction in tropical Singapore. Appl. Energy 2016, 162, 207–217. [Google Scholar] [CrossRef]
- Kosny, J.; Kossecka, E.; Brzezinski, A.; Tleoubaev, A.; Yarbrough, D. Dynamic thermal performance analysis of fiber insulations containing bio-based phase change materials (PCMs). Energy Build. 2012, 52, 122–131. [Google Scholar] [CrossRef]
- Neeper, D.A. Thermal dynamics of wallboard with latent heat storage. Sol. Energy 2000, 68, 393–403. [Google Scholar] [CrossRef]
- Heim, D.; Clarke, J.A. Numerical modelling and thermal simulation of PCM-gypsum composites with ESP-r. Energy Build. 2004, 36, 795–805. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Y.; Lin, K.; Di, H.; Yang, R. Modeling and simulation on the thermal performance of shape-stabilized phase change material floor used in passive solar buildings. Energy Build. 2005, 37, 1084–1091. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, Y.; Wang, X.; Lin, K.; Xiao, W. An assessment of mixed type PCM-gypsum and shape-stabilized PCM plates in a building for passive solar heating. Sol. Energy 2007, 81, 1351–1360. [Google Scholar] [CrossRef]
- Jiang, F.; Wang, X.; Zhang, Y. A new method to estimate optimal phase change material characteristics in a passive solar room. Energy Convers. Manag. 2011, 52, 2437–2441. [Google Scholar] [CrossRef]
- Ye, H.; Long, L.; Zhang, H.; Zou, R. The performance evaluation of shape-stabilized phase change materials in building applications using energy saving index. Appl. Energy 2014, 113, 1118–1126. [Google Scholar] [CrossRef]
- Arnault, A.; Mathieu-Potvin, F.; Gosselin, L. Internal surfaces including phase change materials for passive optimal shift of solar heat gain. Int. J. Therm. Sci. 2010, 49, 2148–2156. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Q.; Medina, M.A.; Lee, K.O. Energy and economic analysis of a building enclosure outfitted with a phase change material board (PCMB). Energy Convers. Manag. 2014, 83, 73–78. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Q.; Medina, M.A.; Lee, K.O.; Liao, S. Parameter design for a phase change material board installed on the inner surface of building exterior envelopes for cooling in China. Energy Convers. Manag. 2016, 120, 100–108. [Google Scholar] [CrossRef]
- Thiele, A.M.; Sant, G.; Pilon, L. Diurnal thermal analysis of microencapsulated PCM-concrete composite walls. Energy Convers. Manag. 2015, 93, 215–227. [Google Scholar] [CrossRef]
- Zhou, D.; Shire, G.S.F.; Tian, Y. Parametric analysis of influencing factors in Phase Change Material Wallboard (PCMW). Appl. Energy 2014, 119, 33–42. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Heating and Cooling of Buildings—Climatic Data; UNI 10349; Italian Organization for Standardization (UNI): Milan, Italy, 1994.
- TRNSYS; Version 17; Solar Energy Laboratory University of Wisconsin-Madison: Madison, WI, USA, 2012.
- Energy Performance of Buildings—Calculation of Energy Use for Space Heating and Cooling; EN ISO 13790; European Committee for Standardization (CEN): Geneva, Switzerland, 2008.
- Energy Performance of Buildings Part 1—Evaluation of Energy Need for Space Heating and Cooling; UNI TS 11300-1; Italian Organization for Standardization (UNI): Milan, Italy, 2008.
- Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Method; EN ISO 6946; International Organization for Standardization: Geneva, Switzerland, 1997.
- Oliveti, G.; Arcuri, N.; De Simone, M.; Bruno, R. Experimental evaluations of the building shell radiant exchange in clear sky conditions. Sol. Energy 2012, 86, 1785–1795. [Google Scholar] [CrossRef]




| Company | PCM | TM (°C) | H (kJ/kg) | ρ (kg/m3) | k (W/(m K)) | c (J/(kg K)) |
|---|---|---|---|---|---|---|
| EPS Yaxley (UK) | S15 | 15 | 160 | 1510 | 0.43 | 1900 |
| TEAP Mumbai (India) | LATEST20T | 20 | 175 | 1490 | 1 | 2000 |
| savENRG Arden, NC (USA) | HS22P | 23 | 185 | 1690 | 0.815 | 3060 |
| RUBITHERM Berlin (Germany) | SP26E | 26 | 190 | 1450 | 0.6 | 2000 |
| CLIMATOR Skövde (Sweden) | C32 | 32 | 162 | 1420 | 0.6 | 3600 |
| Turin | |||||
| S15 | LATEST20T | HS22P | SP26E | C32 | |
| JAN | sol | sol | sol | sol | sol |
| FEB | 1 | sol | sol | sol | sol |
| MAR | 3 | sol | sol | sol | sol |
| APR | 3 | 2 | sol | sol | sol |
| MAY | 2 | 3 | 1 | sol | sol |
| JUN | liq | 2 | 2 | 2 | sol |
| JUL | liq | 1 | 2 | 2 | sol |
| AUG | liq | 2 | 2 | 2 | sol |
| SEP | 1 | 2 | 2 | 2 | sol |
| OCT | 2 | 2 | sol | sol | sol |
| NOV | 2 | sol | sol | sol | sol |
| DEC | 1 | sol | sol | sol | sol |
| Cosenza | |||||
| S15 | LATEST20T | HS22P | SP26E | C32 | |
| JAN | 3 | sol | sol | sol | sol |
| FEB | 3 | 2 | sol | sol | sol |
| MAR | 3 | 2 | sol | sol | sol |
| APR | 2 | 3 | 2 | sol | sol |
| MAY | 2 | 3 | 2 | 2 | sol |
| JUN | liq | 2 | 2 | 2 | sol |
| JUL | liq | 1 | 2 | 2 | 2 |
| AUG | liq | 1 | 2 | 2 | 2 |
| SEP | liq | 2 | 2 | 2 | 2 |
| OCT | 2 | 3 | 2 | 2 | sol |
| NOV | 2 | 2 | 2 | 1 | sol |
| DEC | 3 | 2 | sol | sol | sol |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazzeo, D.; Oliveti, G.; Arcuri, N. A Method for Thermal Dimensioning and for Energy Behavior Evaluation of a Building Envelope PCM Layer by Using the Characteristic Days. Energies 2017, 10, 659. https://doi.org/10.3390/en10050659
Mazzeo D, Oliveti G, Arcuri N. A Method for Thermal Dimensioning and for Energy Behavior Evaluation of a Building Envelope PCM Layer by Using the Characteristic Days. Energies. 2017; 10(5):659. https://doi.org/10.3390/en10050659
Chicago/Turabian StyleMazzeo, Domenico, Giuseppe Oliveti, and Natale Arcuri. 2017. "A Method for Thermal Dimensioning and for Energy Behavior Evaluation of a Building Envelope PCM Layer by Using the Characteristic Days" Energies 10, no. 5: 659. https://doi.org/10.3390/en10050659
APA StyleMazzeo, D., Oliveti, G., & Arcuri, N. (2017). A Method for Thermal Dimensioning and for Energy Behavior Evaluation of a Building Envelope PCM Layer by Using the Characteristic Days. Energies, 10(5), 659. https://doi.org/10.3390/en10050659








