Numerical Study on Melting Heat Transfer in Dendritic Heat Exchangers
Abstract
1. Introduction
2. Mathematical Model
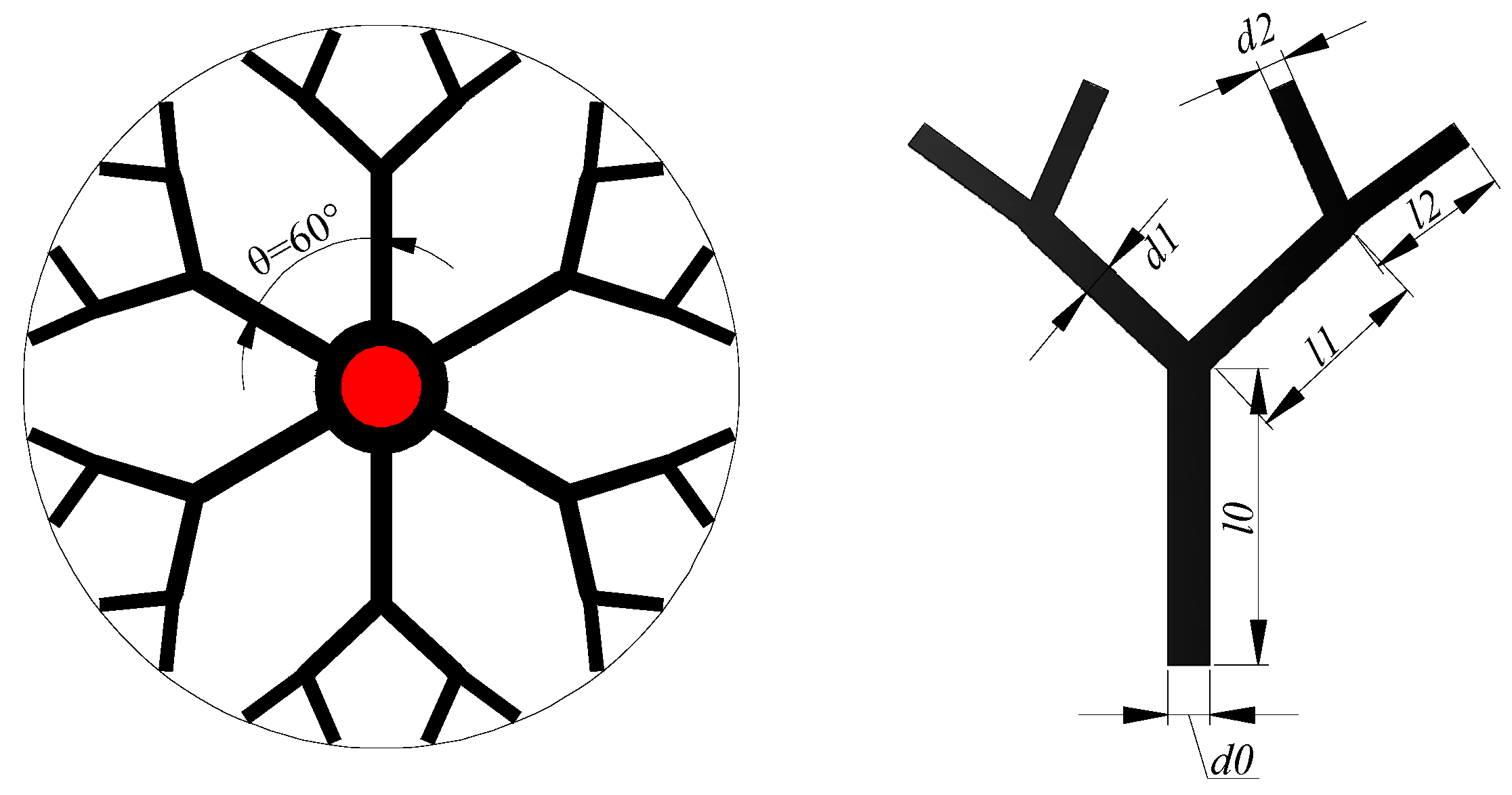
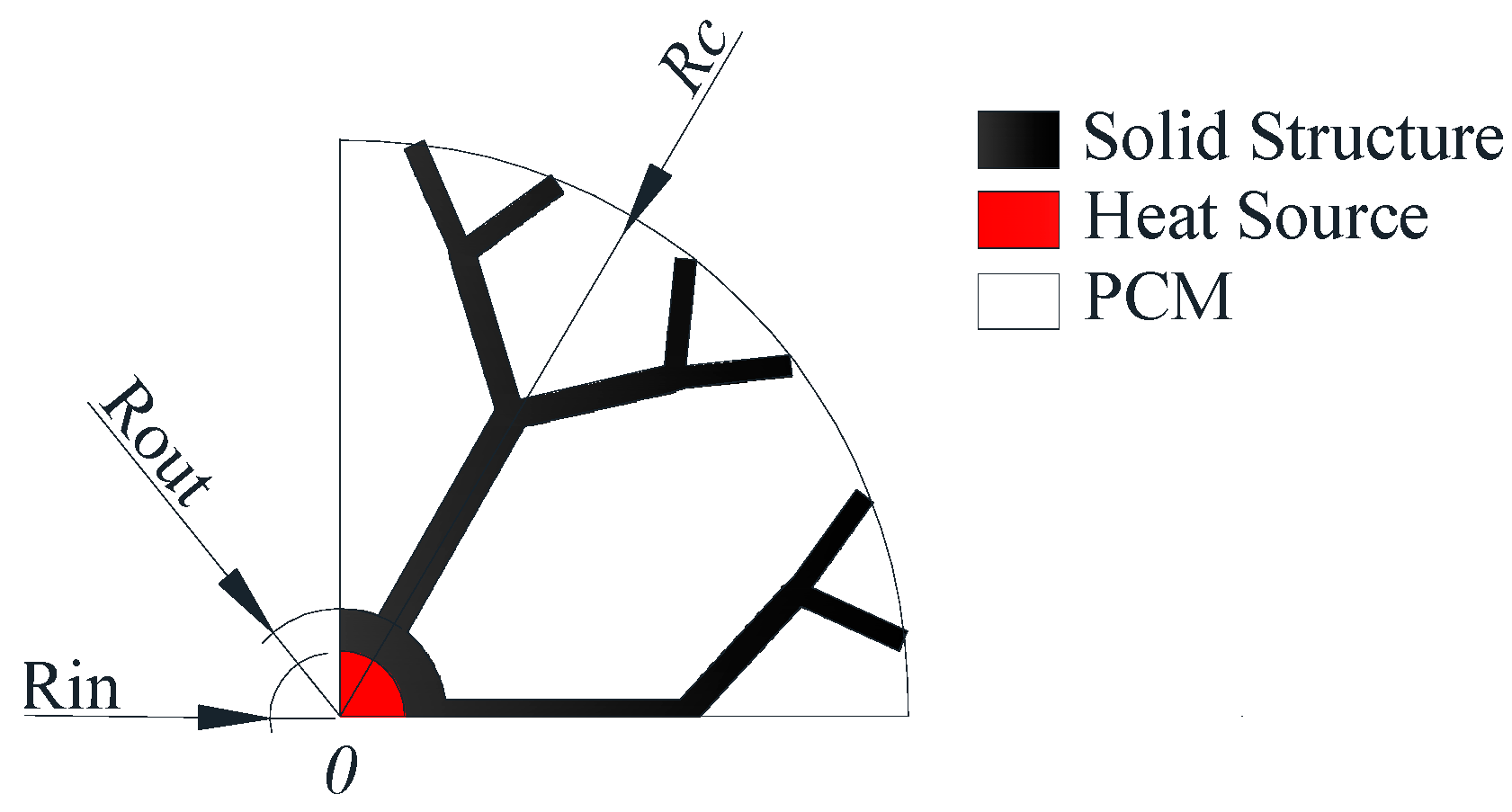
2.1. Dendritic Heat Exchanger
2.2. Control Equations and Boundary Conditions
- (1)
- The physical properties (density, thermal conductivity, etc.) of the PCM are considered as constant;
- (2)
- Natural convection in the PCM liquid phase zone is ignored;
- (3)
- In the phase change process of PCM, there is solid state, liquid state, and solid-liquid coexistence state.
- (4)
- The specific heat capacity and thermal conductivity of the PCM in the mushy zone change linearly;
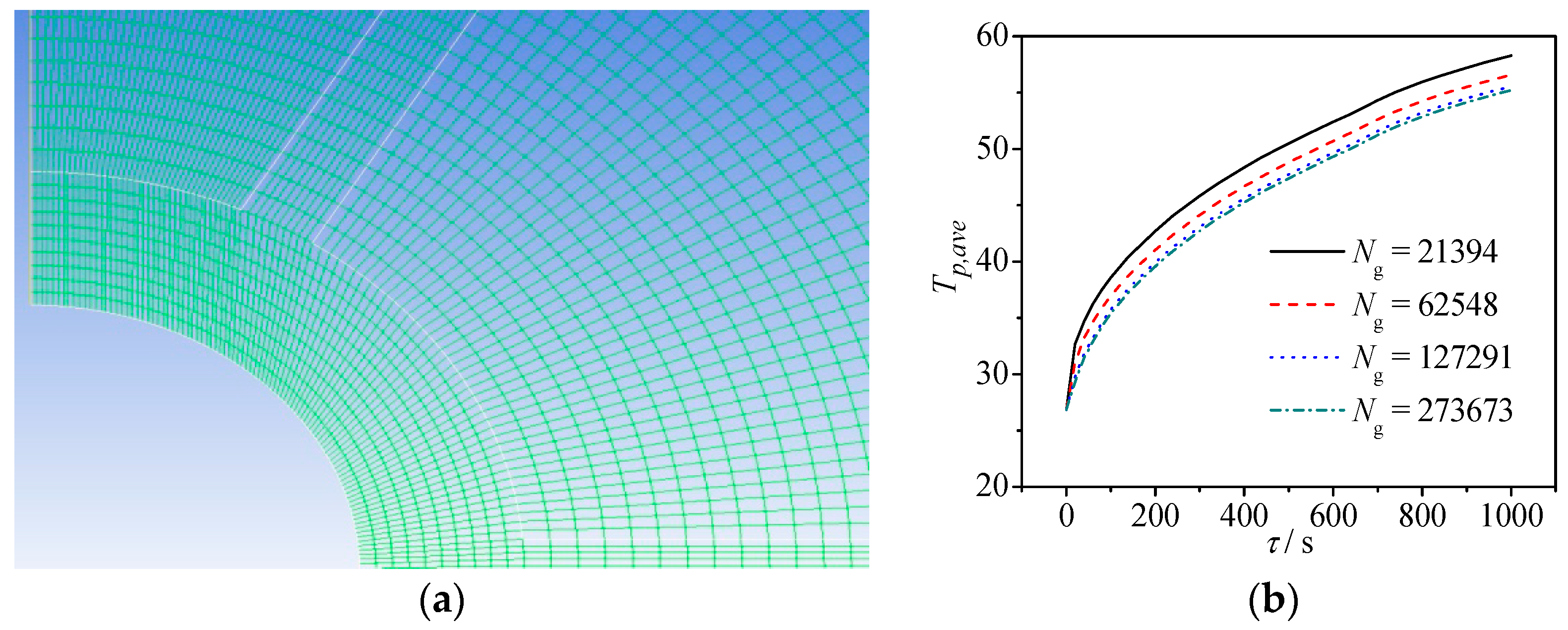
2.3. Numerical Solutions
3. Results and Discussion
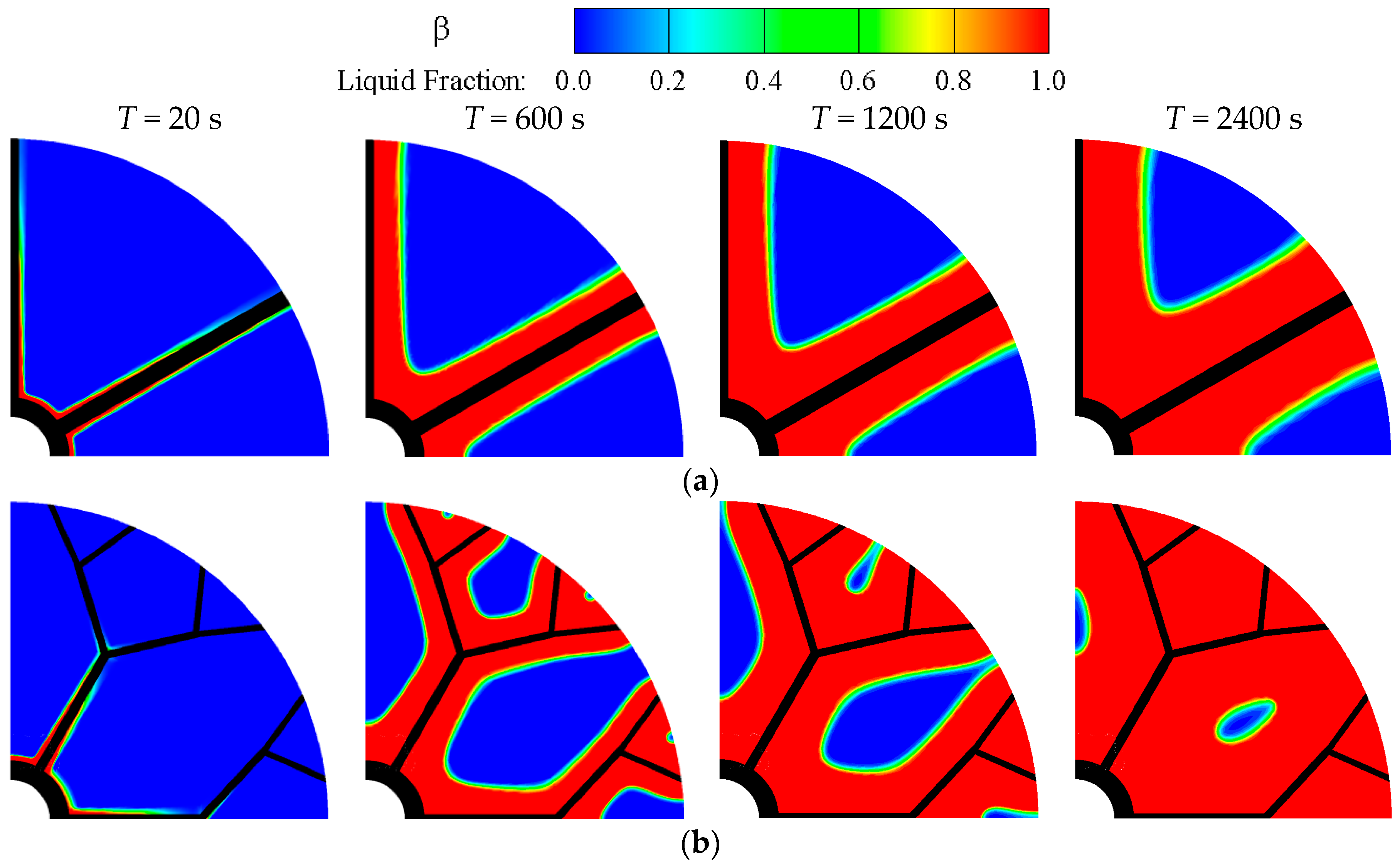
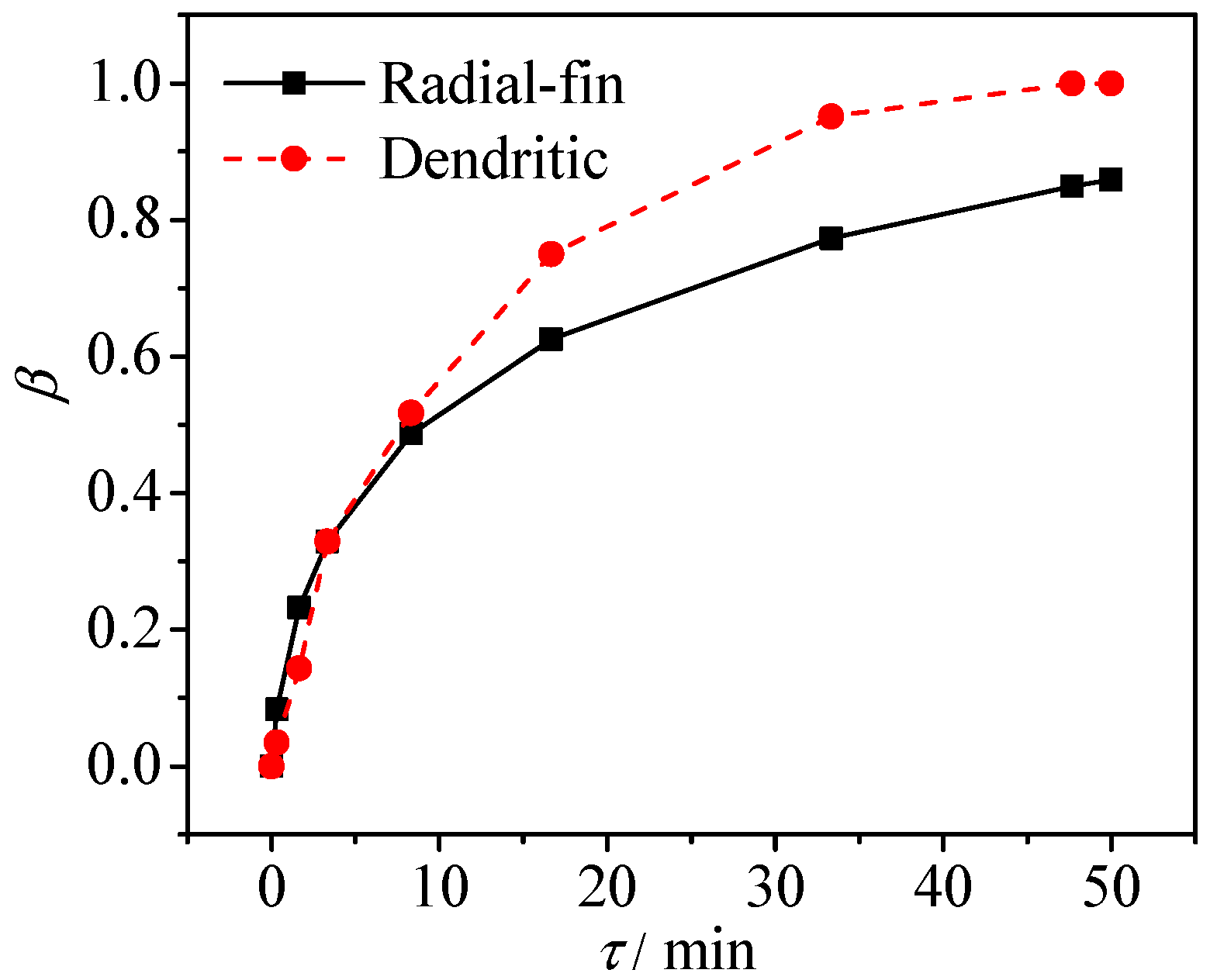
3.1. Melt Phase Change Characteristics
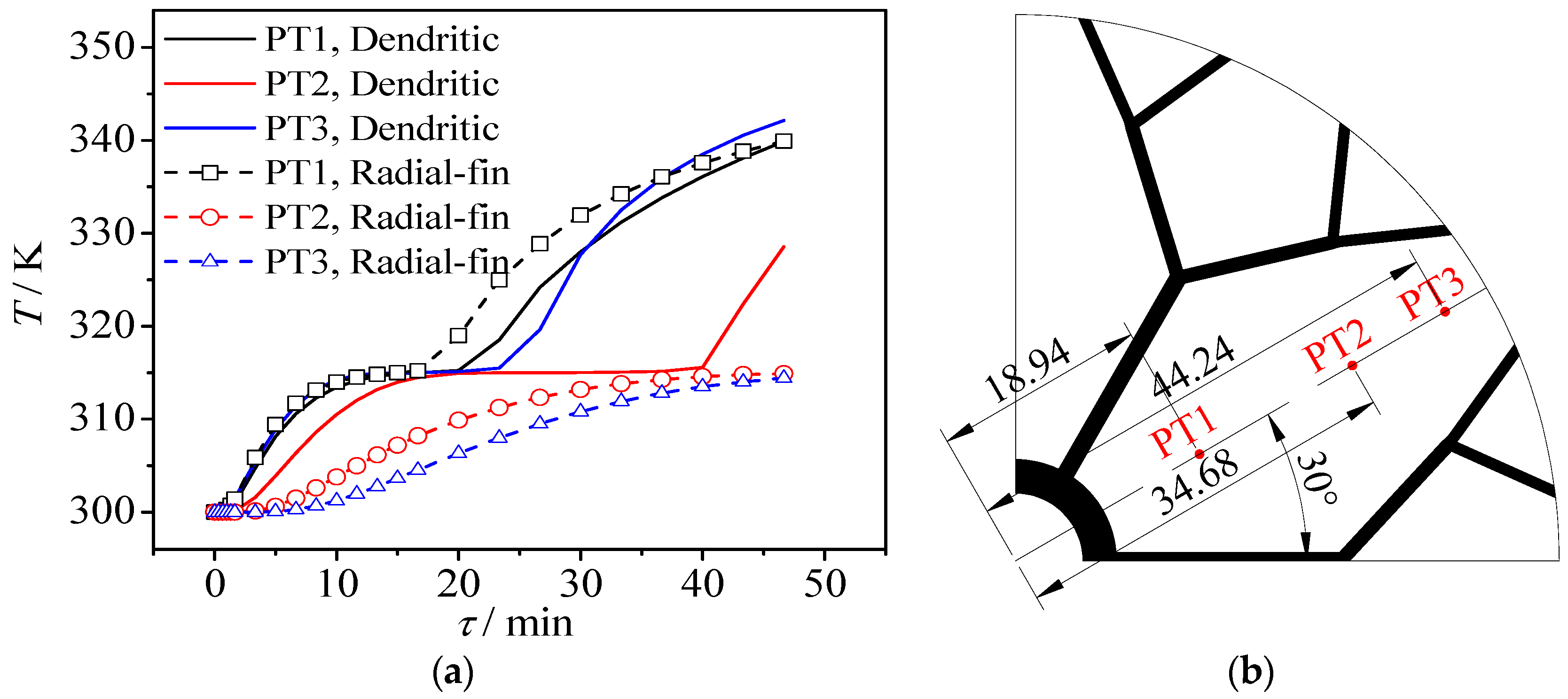
3.2. Dynamic Temperature Changes
4. Conclusions
- (1)
- The solid-liquid phase interface in the heat exchanger with plain radial fin moves very slowly and almost straight along the vertical direction of the fins towards the outer area. However, the presence of dendritic fin leads to the formation of multiple independent PCM zones, and make the PCM far away from heat sources melt earlier and faster.
- (2)
- The whole heat transfer performance in dendritic heat exchanger is superior owing to additional fin surface-area and better fin configuration. The time required for the complete melting of the PCM in dendritic heat exchanger is shorter than that of the radial-fin heat exchanger.
- (3)
- The temperature difference in the whole region of PCM within heat exchangers with radial plain fin is clear, however, the dendritic structure makes the PCM temperature distribution over the entire zone more uniform inside heat exchangers due to the highly-efficient heat flow distribution of dendritic fins.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| cp | specific heat capacity |
| D | fractal dimension of bifurcation length |
| d | fin width |
| hT | sensible heat |
| h | enthalpy |
| Lp | latent heat |
| l | fin length |
| N | bifurcation number |
| Ng | grid number |
| Rc | outer diameter of heat exchange |
| Rin | inner radius of tube |
| Rout | outer radius of tube |
| T0 | initial temperature |
| Tl | liquidus temperature |
| Tp | temperature of solid-liquid interface |
| Tref | reference temperature |
| Ts | solidus temperature |
| Tw | wall temperature |
| Greek Symbols | |
| β | liquid phase ratio |
| Δ | fractal dimension of fin width |
| θ | angle between each fin |
| λ | thermal conductivity |
| ρ | density |
| τ | time |
References
- Shon, J.; Kim, H.; Lee, K. Improved heat storage rate for an automobile coolant waste heat recovery system using phase-change material in a fin–tube heat exchanger. Appl. Energy 2014, 113, 680–689. [Google Scholar] [CrossRef]
- Merlin, K.; Soto, J.; Delaunay, D.; Traonvouez, L. Industrial waste heat recovery using an enhanced conductivity latent heat thermal energy storage. Appl. Energy 2016, 183, 491–503. [Google Scholar] [CrossRef]
- Dal Magro, F.; Jimenez-Arreola, M.; Romagnoli, A. Improving energy recovery efficiency by retrofitting a PCM-based technology to an ORC system operating under thermal power fluctuations. Appl. Energy 2017, 208, 972–985. [Google Scholar] [CrossRef]
- Deng, Z.L.; Liu, X.D.; Zhang, C.B.; Huang, Y.P.; Chen, Y.P. Melting behaviors of PCM in porous metal foam characterized by fractal geometry. Int. J. Heat Mass Transf. 2017, 113, 1031–1042. [Google Scholar] [CrossRef]
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Liu, X.D.; Chen, Y.P.; Shi, M.H. Dynamic performance analysis on start-up of closed-loop pulsating heat pipes (CLPHPs). Int. J. Therm. Sci. 2013, 65, 224–233. [Google Scholar] [CrossRef]
- Behi, H.; Ghanbarpour, M.; Behi, M. Investigation of PCM-assisted heat pipe for electronic cooling. Appl. Therm. Eng. 2017, 127, 1132–1142. [Google Scholar] [CrossRef]
- Wu, J.F.; Shi, M.H.; Chen, Y.P.; Li, X. Visualization study of steam condensation in wide rectangular silicon microchannels. Int. J. Therm. Sci. 2010, 49, 922–930. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Sheremet, M.A. Conjugate heat transfer in the PCM-based heat storage system with finned copper profile: Application in electronics cooling. Int. J. Heat Mass Transf. 2018, 124, 1275–1284. [Google Scholar] [CrossRef]
- Saffari, M.; de Gracia, A.; Fernández, C.; Cabeza, L.F. Simulation-based optimization of PCM melting temperature to improve the energy performance in buildings. Appl. Energy 2017, 202, 420–434. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Gao, D.Y.; Shi, J. Experimental and numerical study on melting of phase change materials in metal foams at pore scale. Int. J. Heat Mass Transf. 2014, 72, 646–655. [Google Scholar] [CrossRef]
- Tong, X.L.; Khan, J.A.; RuhulAmin, M. Enhancement of heat transfer by inserting a metal matrix into a phase change material. Numer. Heat Transf. Part A Appl. 1996, 30, 125–141. [Google Scholar] [CrossRef]
- Feng, S.S.; Zhang, Y.; Shi, M.; Wen, T.; Lu, T.J. Unidirectional freezing of phase change materials saturated in open-cell metal foams. Appl. Therm. Eng. 2015, 88, 315–321. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, C.Y. A numerical investigation of heat transfer in phase change materials (PCMs) embedded in porous metals. Energy 2011, 36, 5539–5546. [Google Scholar] [CrossRef]
- Li, W.Q.; Qu, Z.G.; He, Y.L.; Tao, W.Q. Experimental and numerical studies on melting phase change heat transfer in open-cell metallic foams filled with paraffin. Appl. Therm. Eng. 2012, 37, 1–9. [Google Scholar] [CrossRef]
- Zhang, C.B.; Chen, Y.P.; Deng, Z.L.; Shi, M.H. Role of rough surface topography on gas slip flow in microchannels. Phys. Rev. E 2012, 86, 016319. [Google Scholar] [CrossRef] [PubMed]
- Bejan, A.; Errera, M.R. Deterministic tree networks for fluid flow: Geometry for minimal flow resistance between a volume and one point. Fractals 1997, 5, 685–695. [Google Scholar] [CrossRef]
- Errera, M.; Bejan, A. Deterministic tree networks for river drainage basins. Fractals 1998, 6, 245–261. [Google Scholar] [CrossRef]
- Zhang, C.B.; Deng, Z.L.; Chen, Y.P. Temperature jump at rough gas–solid interface in Couette flow with a rough surface described by Cantor fractal. Int. J. Heat Mass Transf. 2014, 70, 322–329. [Google Scholar] [CrossRef]
- Pelletier, J.D.; Turcotte, D.L. Shapes of river networks and leaves: Are they statistically similar? Philos. Trans. R. Soc. B-Biol. Sci. 2000, 355, 307–311. [Google Scholar] [CrossRef] [PubMed]
- Neagu, M.; Bejan, A. Constructal-theory tree networks of “constant” thermal resistance. J. Appl. Phys. 1999, 86, 1136–1144. [Google Scholar] [CrossRef]
- Gabryś, E.; Rybaczuk, M.; Kędzia, A. Blood flow simulation through fractal models of circulatory system. Chaos Solitons Fractals 2006, 27, 1–7. [Google Scholar] [CrossRef]
- Zhang, C.B.; Chen, Y.P.; Wu, R.; Shi, M.H. Flow boiling in constructal tree-shaped minichannel network. Int. J. Heat Mass Transf. 2011, 54, 202–209. [Google Scholar] [CrossRef]
- Zimparov, V.; Da Silva, A.; Bejan, A. Constructal tree-shaped parallel flow heat exchangers. Int. J. Heat Mass Transf. 2006, 49, 4558–4566. [Google Scholar] [CrossRef]
- Chen, Y.P.; Zhang, C.B.; Wu, R.; Shi, M.H. Methanol steam reforming in microreactor with constructal tree-shaped network. J. Power Source 2011, 196, 6366–6373. [Google Scholar] [CrossRef]
- Senn, S.; Poulikakos, D. Laminar mixing, heat transfer and pressure drop in tree-like microchannel nets and their application for thermal management in polymer electrolyte fuel cells. J. Power Source 2004, 130, 178–191. [Google Scholar] [CrossRef]
- Senn, S.; Poulikakos, D. Tree network channels as fluid distributors constructing double-staircase polymer electrolyte fuel cells. J. Appl. Phys. 2004, 96, 842–852. [Google Scholar] [CrossRef]
- Chen, Y.P.; Deng, Z.L. Hydrodynamics of a droplet passing through a microfluidic T-junction. J. Fluid Mech. 2017, 819, 401–434. [Google Scholar] [CrossRef]
- Chen, Y.P.; Liu, X.D.; Shi, M.H. Hydrodynamics of double emulsion droplet in shear flow. Appl. Phys. Lett. 2013, 102, 051609. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Mujumdar, A.S.; Yap, C. Thermal characteristics of tree-shaped microchannel nets for cooling of a rectangular heat sink. Int. J. Therm. Sci. 2006, 45, 1103–1112. [Google Scholar] [CrossRef]
- Chen, Y.P.; Zhang, C.B.; Shi, M.H.; Yang, Y.C. Thermal and hydrodynamic characteristics of constructal tree-shaped minichannel heat sink. AIChE J. 2010, 56, 2018–2029. [Google Scholar] [CrossRef]
- Wechsatol, W.; Lorente, S.; Bejan, A. Tree-shaped flow structures with local junction losses. Int. J. Heat Mass Transf. 2006, 49, 2957–2964. [Google Scholar] [CrossRef]
- Chen, Y.P.; Gao, W.; Zhang, C.B.; Zhao, Y.J. Three-dimensional splitting microfluidics. Lab Chip 2016, 16, 1332–1339. [Google Scholar] [CrossRef] [PubMed]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Brent, A.; Voller, V.; Reid, K. Enthalpy-porosity technique for modeling convection-diffusion phase change: application to the melting of a pure metal. Numer. Heat Transf. Part A Appl. 1988, 13, 297–318. [Google Scholar]

| Material | Density P (Kg/M3) | Specific Heat Capacity C (J/Kg·K) | Thermal Conductivity Λ (W/M·K) | Latent Heat of Phase Change Lp (J/Kg) | Phase Change Temperature Tp (K) |
|---|---|---|---|---|---|
| Lauric acid (C12H24O2) | 1000 | 2150 | 0.15 | 178,000 | 315 (Solid Phase) 317 (Liquid phase) |
| Aluminum | 2719 | 871 | 202.4 | / | / |
| Fin Shape | Length, l (mm) | Width, d (mm) |
|---|---|---|
| Radial-fin | 39.5 | 4.8 |
| Dendritic | l0 = 9.3 | d0 = 2.47 |
| l1 = 13.15 | d1 = 1.96 | |
| l2 = 18.6 | d2 = 1.56 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Liao, S. Numerical Study on Melting Heat Transfer in Dendritic Heat Exchangers. Energies 2018, 11, 2504. https://doi.org/10.3390/en11102504
Luo X, Liao S. Numerical Study on Melting Heat Transfer in Dendritic Heat Exchangers. Energies. 2018; 11(10):2504. https://doi.org/10.3390/en11102504
Chicago/Turabian StyleLuo, Xinmei, and Shengming Liao. 2018. "Numerical Study on Melting Heat Transfer in Dendritic Heat Exchangers" Energies 11, no. 10: 2504. https://doi.org/10.3390/en11102504
APA StyleLuo, X., & Liao, S. (2018). Numerical Study on Melting Heat Transfer in Dendritic Heat Exchangers. Energies, 11(10), 2504. https://doi.org/10.3390/en11102504




