Large-Signal Stability Modeling for the Grid-Connected VSC Based on the Lyapunov Method
Abstract
:1. Introduction
- Proposing a systematic way in order to find the Lyapunov function of the grid-connected VSC based on the system state variables.
- Parametric analysis of the energy function for the stability of the grid-connected VSC.
- Studying the effect of the linearization on determining the stability margin of the grid-connected VSC.
2. Lyapunov-Based Stability Assessment
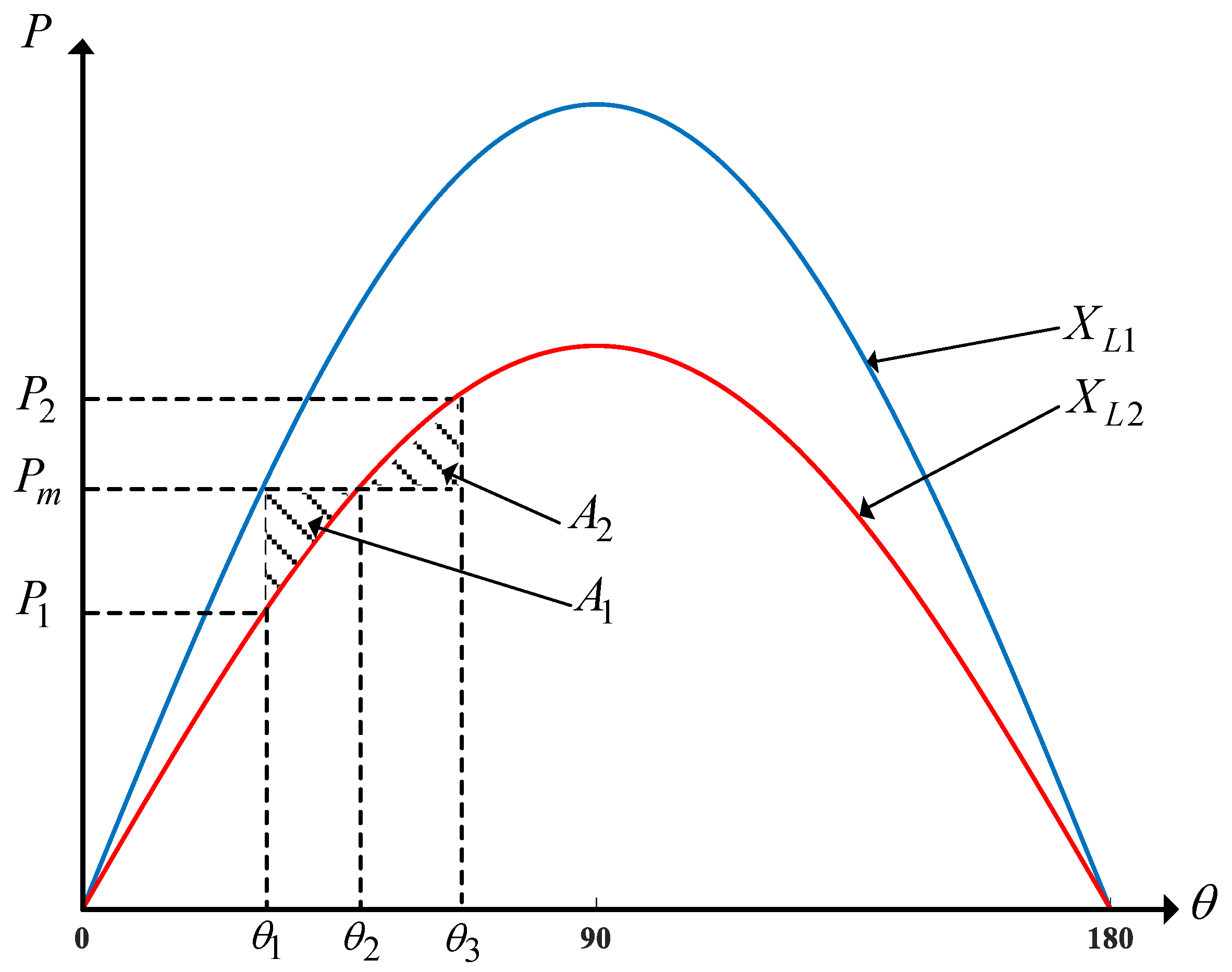
3. Parametric Lyapunov-Based Stability Analysis of the Grid-Connected Voltage Source Converter (VSC)
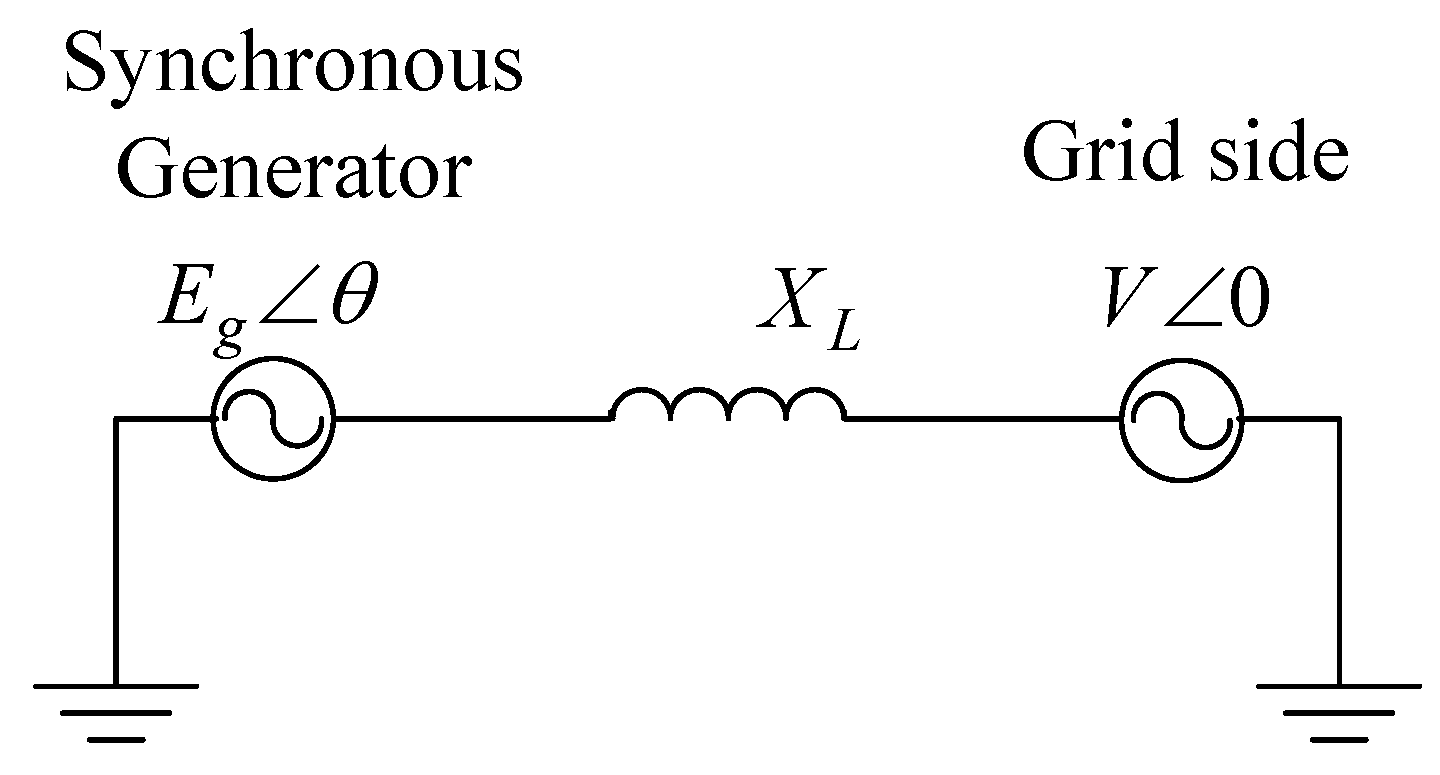
3.1. Modeling of the Grid-Connected VSC
3.2. Systematic Lyapunov-Based Stability Method
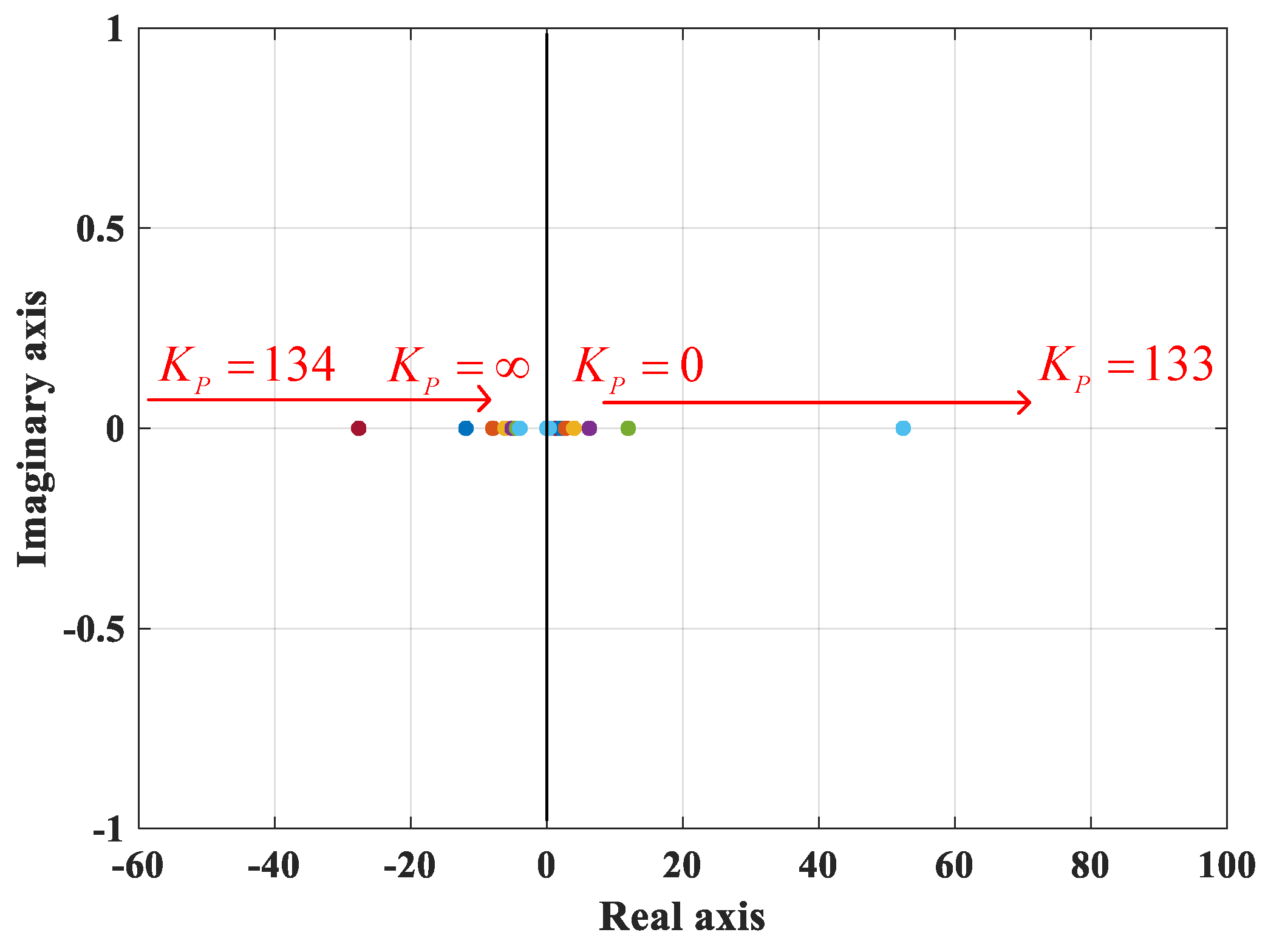
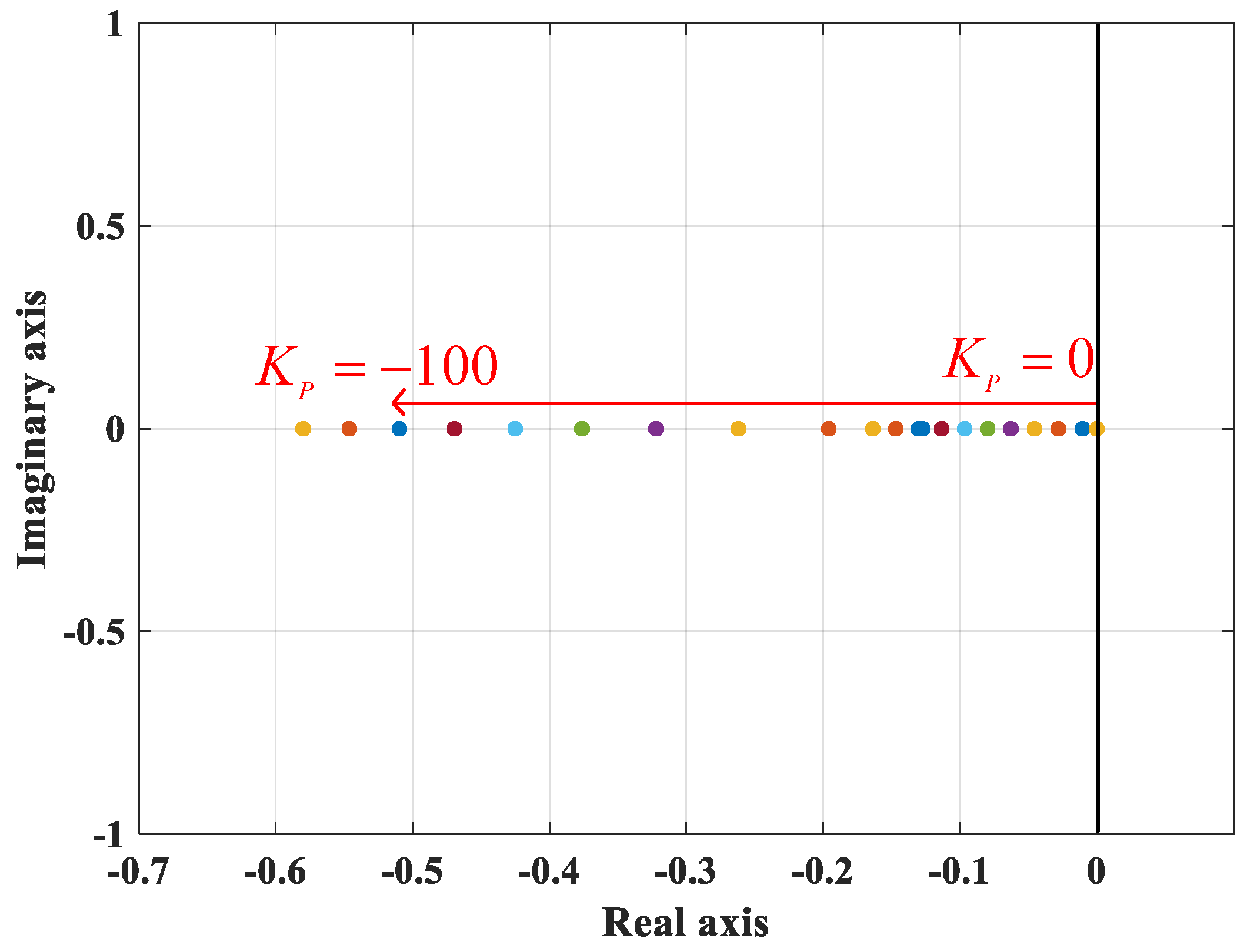
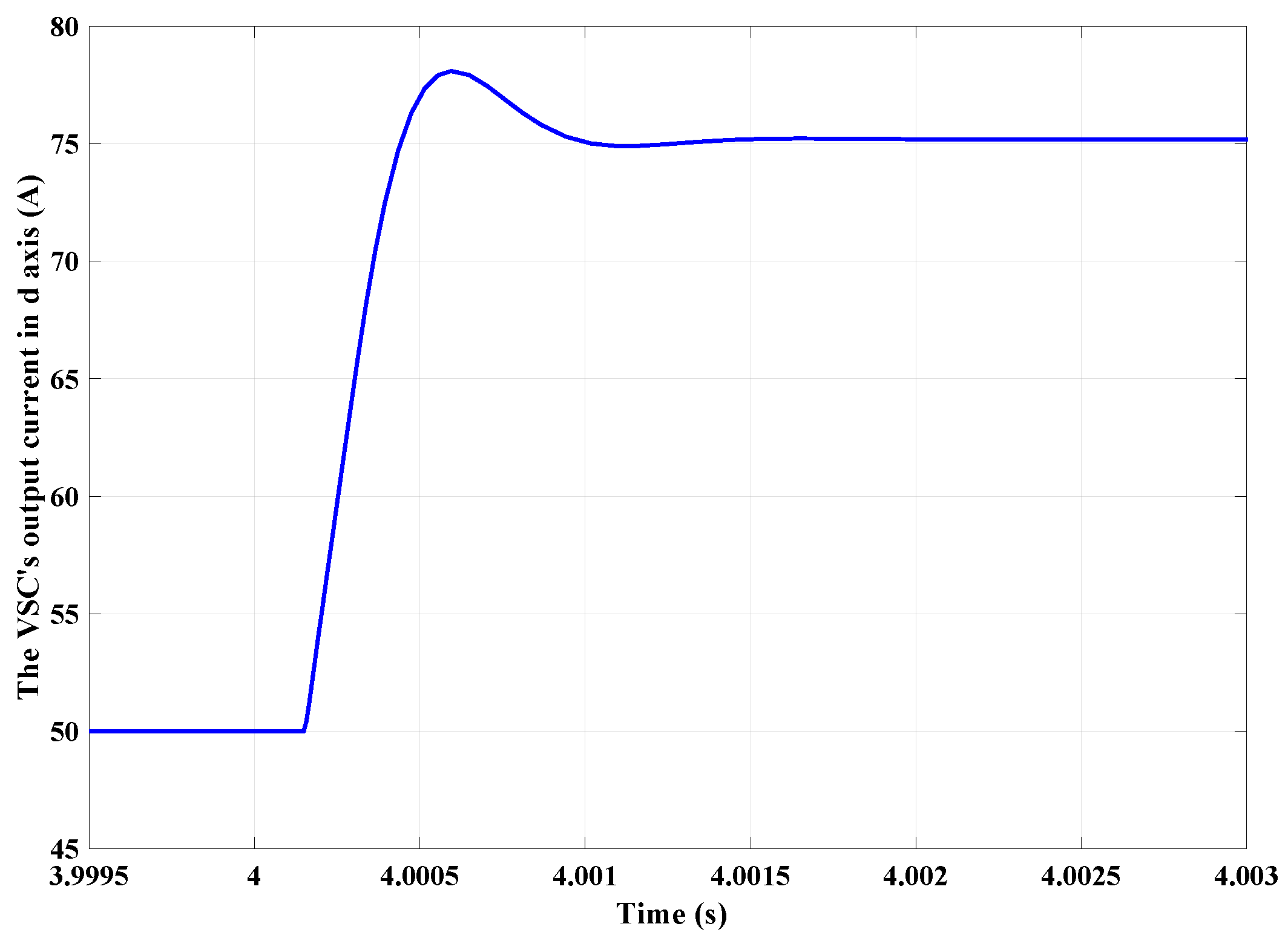
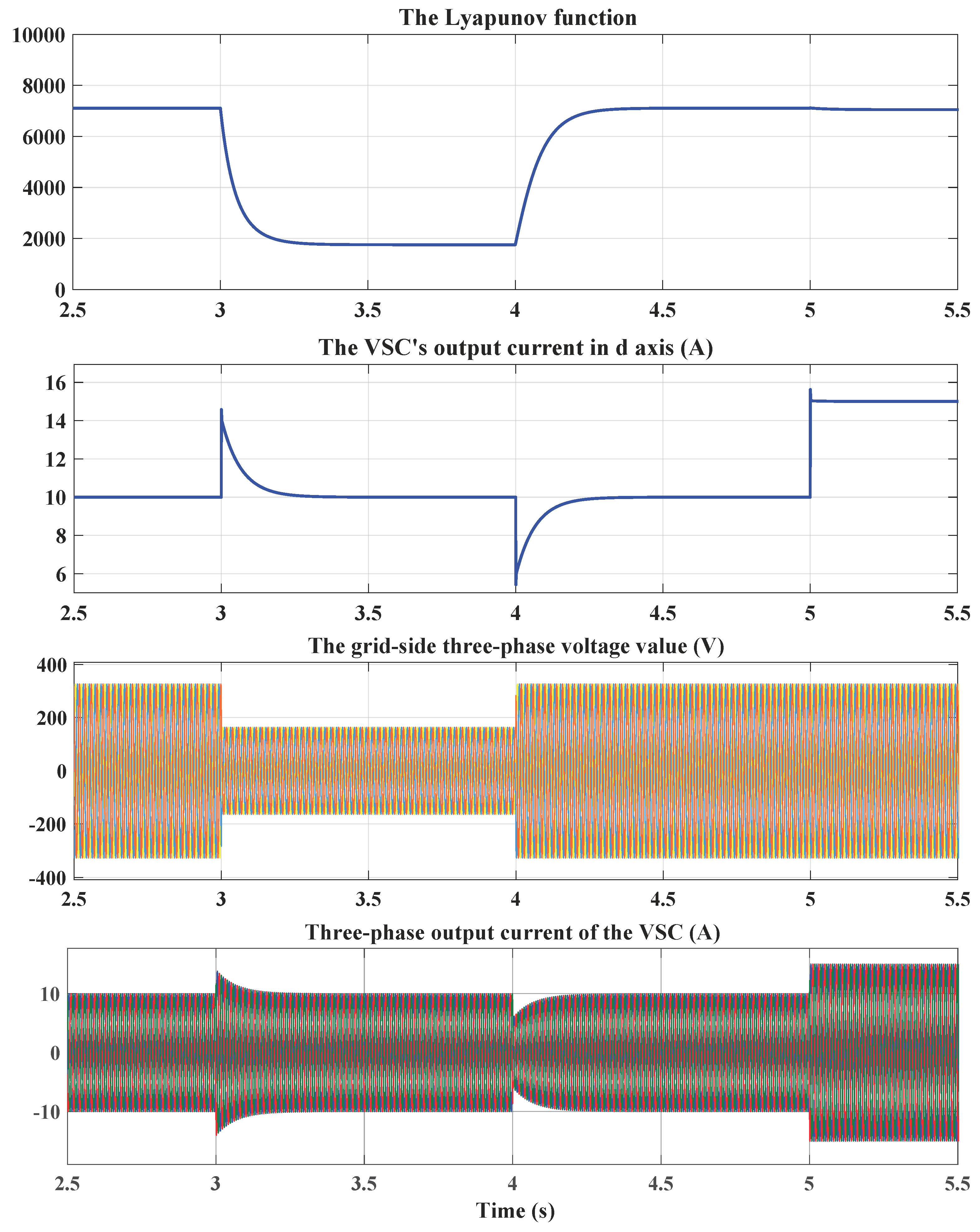
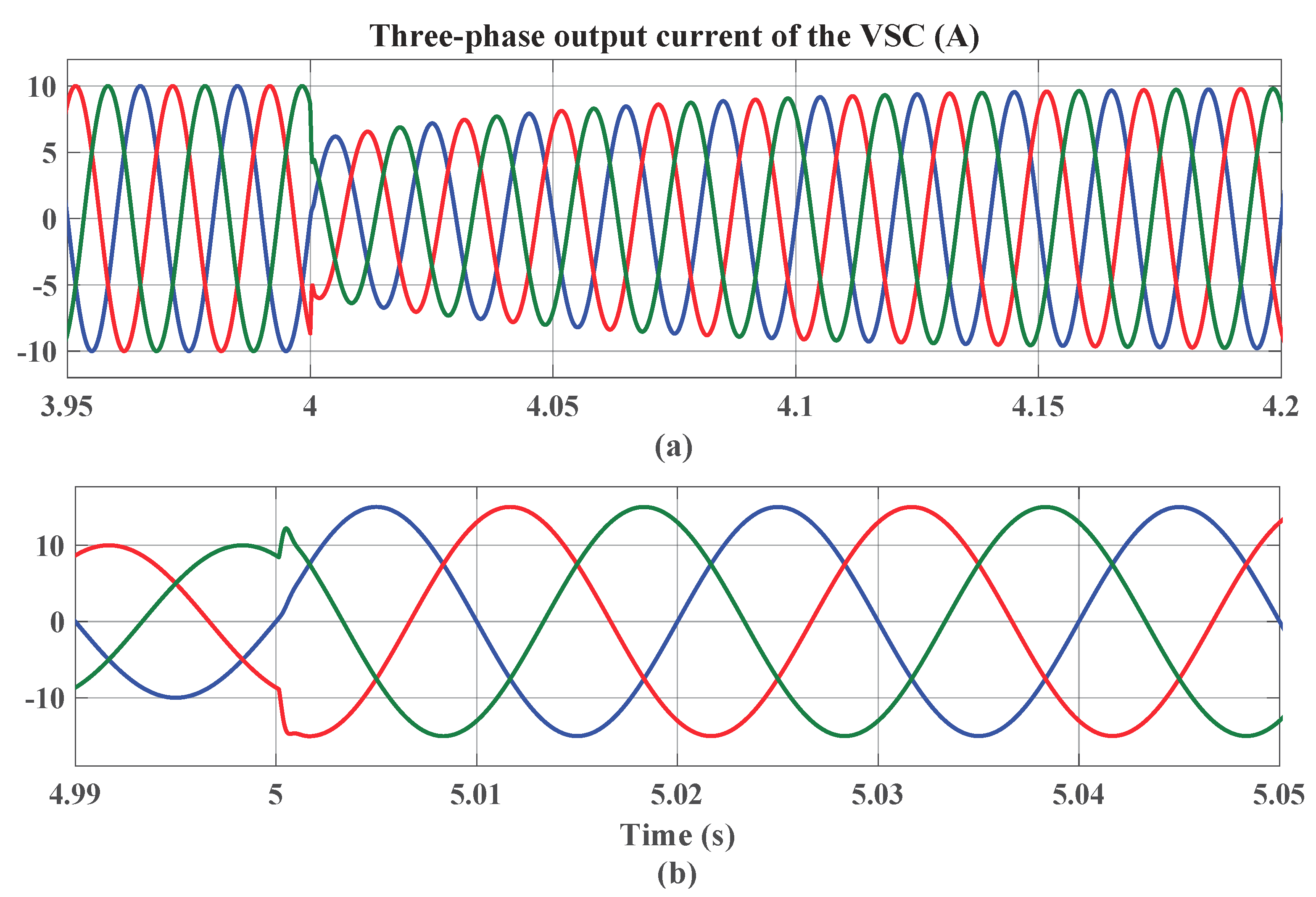
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodriguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Altin, M.; Göksu, Ö.; Teodorescu, R.; Rodriguez, P.; Jensen, B.B.; Helle, L. Overview of recent grid codes for wind power integration. In Proceedings of the 2010 12th International Conference on Optimization of Electrical and Electronic Equipment, Piscataway, NJ, USA, 20–22 May 2010. [Google Scholar] [CrossRef] [Green Version]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [Green Version]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Ogata, K. Modern Control Engineering; Prentice-Hall: Boston, MA, USA, 2010; Volume 5. [Google Scholar]
- Zarei, S.F.; Mokhtari, H.; Ghasemi, M.A.; Blaabjerg, F. Reinforcing Fault Ride Through Capability of Grid Forming Voltage Source Converters Using an Enhanced Voltage Control Scheme. IEEE Trans. Power Deliv. 2018. [Google Scholar] [CrossRef]
- Bottrell, N.; Prodanovic, M.; Green, T.C. Dynamic Stability of a Microgrid With an Active Load. IEEE Trans. Power Electron. 2013, 28, 5107–5119. [Google Scholar] [Green Version]
- Kabalan, M.; Singh, P.; Niebur, D. Large Signal Lyapunov-Based Stability Studies in Microgrids: A Review. IEEE Trans. Smart Grid 2017, 8, 2287–2295. [Google Scholar]
- Andrade, F.; Kampouropoulos, K.; Romeral Martínez, J.L.; Vasquez Quintero, J.C.; Guerrero, J.M. Study of large-signal stability of an inverter-based generator using a Lyapunov function. In Proceedings of the 40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 30 October–1 November 2014. [Google Scholar]
- Li, X.; Hua, L. Stability Analysis of Grid-Connected Converters with Different Implementations of Adaptive PR Controllers under Weak Grid Conditions. Energies 2018, 11, 2004. [Google Scholar]
- Harnefors, L.; Finger, R.; Wang, X.; Bai, H.; Blaabjerg, F. VSC Input-Admittance Modeling and Analysis Above the Nyquist Frequency for Passivity-Based Stability Assessment. IEEE Trans. Ind. Electron. 2017, 64, 6362–6370. [Google Scholar] [CrossRef]
- Safaee, A.; Woronowicz, K. Time-Domain Analysis of Voltage-Driven Series–Series Compensated Inductive Power Transfer Topology. IEEE Trans. Power Electron. 2017, 32, 4981–5003. [Google Scholar] [CrossRef]
- Wang, J.; Liang, J.; Gao, F.; Dong, X.; Wang, C.; Zhao, B. A Closed-Loop Time-Domain Analysis Method for Modular Multilevel Converter. IEEE Trans. Power Electron. 2017, 32, 7494–7508. [Google Scholar]
- Raza, M.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Small-Signal Stability Analysis of Offshore AC Network Having Multiple VSC-HVDC Systems. IEEE Trans. Power Deliv. 2018, 33, 830–839. [Google Scholar]
- Khalil, H.K. Noninear Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Yepes, A.G.; Freijedo, F.D.; López, Ó.; Doval-Gandoy, J. Analysis and Design of Resonant Current Controllers for Voltage-Source Converters by Means of Nyquist Diagrams and Sensitivity Function. IEEE Trans. Ind. Electron. 2011, 58, 5231–5250. [Google Scholar] [CrossRef]
- Aldhaheri, A.; Etemadi, A. Impedance Decoupling in DC Distributed Systems to Maintain Stability and Dynamic Performance. Energies 2017, 10, 470. [Google Scholar] [CrossRef]
- Freytes, J.; Akkari, S.; Dai, J.; Gruson, F.; Rault, P.; Guillaud, X. Small-signal state-space modeling of an HVDC link with modular multilevel converters. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016. [Google Scholar]
- Amin, M.; Molinas, M. Small-Signal Stability Assessment of Power Electronics Based Power Systems: A Discussion of Impedance- and Eigenvalue-Based Methods. IEEE Trans. Ind. Appl. 2017, 53, 5014–5030. [Google Scholar] [CrossRef]
- Freijedo, F.D.; Rodriguez-Diaz, E.; Golsorkhi, M.S.; Vasquez, J.C.; Guerrero, J.M. A Root-Locus Design Methodology Derived From the Impedance/Admittance Stability Formulation and Its Application for LCL Grid-Connected Converters in Wind Turbines. IEEE Trans. Power Electron. 2017, 32, 8218–8228. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Wang, X. Transient angle stability analysis of grid-connected converters with the first-order active power loop. Presented at 2018 IEEE Applied Power Electronics Conference and Exposition, San Antonio, TX, USA, 4–8 March 2018. [Google Scholar]
- Dasgupta, S.; Mohan, S.N.; Sahoo, S.K.; Panda, S.K. Lyapunov Function-Based Current Controller to Control Active and Reactive Power Flow From a Renewable Energy Source to a Generalized Three-Phase Microgrid System. IEEE Trans. Ind. Electron. 2013, 60, 799–813. [Google Scholar] [CrossRef]
- Mehrasa, M.; Adabi, M.E.; Pouresmaeil, E.; Adabi, J.; Jørgensen, B.N. Direct Lyapunov control (DLC) technique for distributed generation (DG) technology. Electr. Eng. 2014, 96, 309–321. [Google Scholar] [CrossRef]
- Dasgupta, S.; Sahoo, S.K.; Panda, S.K. A novel current control scheme using Lyapunov function to control the active and reactive power flow in a single phase hybrid PV inverter system connected to the grid. Presented at the 2010 International Power Electronics Conference, Sapporo, Japan, 21–24 June 2010. [Google Scholar]
- Li, M.; Huang, W.; Tai, N.; Yu, M. Lyapunov-Based Large Signal Stability Assessment for VSG Controlled Inverter-Interfaced Distributed Generators. Energies 2018, 11, 2273. [Google Scholar] [CrossRef]
- Shang, J.; Li, H.; You, X.; Zheng, T.Q.; Wang, S. A novel stability analysis approach based on describing function method using for DC-DC converters. Presented at 2015 IEEE Applied Power Electronics Conference and Exposition, Charlotte, NC, USA, 15–19 March 2015. [Google Scholar]
- Karimipour, D.; Salmasi, F.R. Stability Analysis of AC Microgrids With Constant Power Loads Based on Popov’s Absolute Stability Criterion. IEEE Trans. Circuits Syst. 2015, 62, 696–700. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, X.; Hu, J.; Zhou, P. Modeling of VSC Connected to Weak Grid for Stability Analysis of DC-Link Voltage Control. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1193–1204. [Google Scholar] [CrossRef]
- Luís, B. Lyapunov Exponents; Springer International Publishing: New York, NY, USA, 2017. [Google Scholar]
- Moussa, H.; Martin, J.P.; Pierfederici, S.; Nahid-Mobarakeh, B. Modeling and large signal stability analysis for islanded AC-microgrids. Presented at 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 4–5 October 2017. [Google Scholar]
- Hart, P.; Lesieutre, B. Energy function for a grid-tied, droop-controlled inverter. In Proceedings of the 2014 North American Power Symposium (NAPS), Pullman, WA, USA, 7–9 September 2014. [Google Scholar]
- Zhang, L.; Harnefors, L.; Nee, H.P. Power-Synchronization Control of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Yao, G.; Lu, Z.; Wang, Y.; Benbouzid, M.; Moreau, L. A Virtual Synchronous Generator Based Hierarchical Control Scheme of Distributed Generation Systems. Energies 2017, 10, 2049. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M. Universal Integrated Synchronization and Control for Single-Phase DC/AC Converters. IEEE Trans. Power Electron. 2015, 30, 1544–1557. [Google Scholar] [CrossRef]
- Komurcugil, H.; Kukrer, O. Lyapunov-based control for three-phase PWM AC/DC voltage-source converters. IEEE Trans. Power Electron. 1998, 13, 801–813. [Google Scholar] [CrossRef]
- Huang, M.; Peng, Y.; Chi, K.T.; Liu, Y.; Sun, J.; Zha, X. Bifurcation and Large-Signal Stability Analysis of Three-Phase Voltage Source Converter Under Grid Voltage Dips. IEEE Trans. Power Electron. 2017, 32, 8868–8879. [Google Scholar] [CrossRef]
- Shuai, Z.; Peng, Y.; Guerrero, J.M.; Li, Y.; Shen, J.Z. Transient Response Analysis of Inverter-based Microgrids under Unbalanced Conditions using Dynamic Phasor Model. IEEE Trans. Ind. Electron. 2018. [Google Scholar] [CrossRef]
- Sauer, P.W.; Pai, M.A.; Chow, J.H. Power System Dynamics and Stability: With Synchrophasor Measurement and Power System Toolbox; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
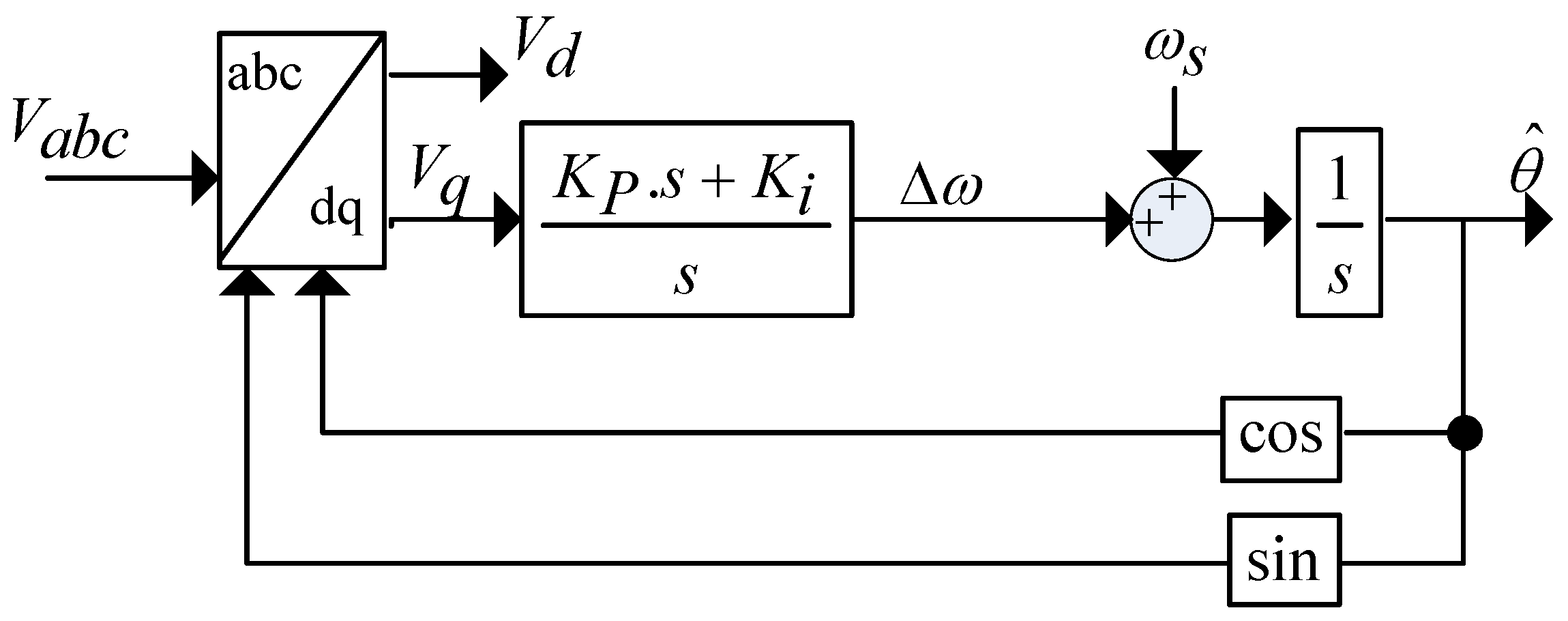
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. Three-Phase PLLs: A Review of Recent Advances. IEEE Trans. Power Electron. 2017, 32, 1894–1907. [Google Scholar] [CrossRef]





| Power Electronic-Based Power System Stability Assessment | |||
|---|---|---|---|
| Linear-Based Method [5] | Nonlinear-Based Methods [15] | ||
| Techniques | |||
| Characteristic | |||
| Global equilibrium point | Only valid for one equilibrium point | Valid for all equilibrium points | |
| Model accuracy | An approximation of the system will be modeled using linearizaing techniques [28]. | The exact model of the system will be evaluated. | |
| Computation complexity | They are mostly easy to implement and assess. | Nonlinear-based methods are more complex than linear techniques. Their computational burden increase as the system size increases. | |
| System Parameters | Value | Explanation |
|---|---|---|
| L-filter | 10 mH | The VSC output includes only an L-filter. Alternatively, an LCL filter may be used. |
| Vgrid | 400 V (rms phase to phase) | An ideal voltage source is used as the grid equivalent. |
| System Frequency | 50 Hz | - |
| Controlling system time delay | 1.5 | delay is caused by the computation process and 0.5 is due to the PWM. |
| 10 s | The sampling frequency is chosen to be equal to 10 kHz. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakerighadi, B.; Ebrahimzadeh, E.; Blaabjerg, F.; Leth Bak, C. Large-Signal Stability Modeling for the Grid-Connected VSC Based on the Lyapunov Method. Energies 2018, 11, 2533. https://doi.org/10.3390/en11102533
Shakerighadi B, Ebrahimzadeh E, Blaabjerg F, Leth Bak C. Large-Signal Stability Modeling for the Grid-Connected VSC Based on the Lyapunov Method. Energies. 2018; 11(10):2533. https://doi.org/10.3390/en11102533
Chicago/Turabian StyleShakerighadi, Bahram, Esmaeil Ebrahimzadeh, Frede Blaabjerg, and Claus Leth Bak. 2018. "Large-Signal Stability Modeling for the Grid-Connected VSC Based on the Lyapunov Method" Energies 11, no. 10: 2533. https://doi.org/10.3390/en11102533





