Stochastic Programming-Based Fault Diagnosis in Power Systems Under Imperfect and Incomplete Information

Abstract

When a fault occurs in a section or a component of a given power system, the malfunctioning of protective relays (PRs) and circuit breakers (CBs), and the false and missing alarms, may manifestly complicate the fault diagnosis procedure. It is necessary to develop a methodologically appropriate framework for this application. As a branch of stochastic programming, the well-developed chance-constrained programming approach provides an efficient way to solve programming problems fraught with uncertainties. In this work, a novel fault diagnosis analytic model is developed with the ability of accommodating the malfunctioning of PRs and CBs, as well as the false and/or missing alarms. The genetic algorithm combined with Monte Carlo simulations are then employed to solve the optimization model. The feasibility and efficiency of the developed model and method are verified by a real fault scenario in an actual power system. In addition, it is demonstrated by simulation results that the computation speed of the developed method meets the requirements for the on-line fault diagnosis of actual power systems.

1. Introduction

A flood of alarm information could be produced when a fault occurs in a certain section of a power system, which makes it difficult for the operators to identify the fault sections and components rapidly and accurately, especially with severe faults. Fault diagnosis, based on the protective devices, is used to address this challenge by employing the alarming signals and other relevant information. A lot of efforts have already been engaged in this field, and many fault diagnosis methods have been proposed, such as the expert system (ES) [1,2], analytic model [3,4,5,6,7], artificial neural network (ANN) [8], fuzzy set (FS) [9], Petri net [10], multi-agent system (MAS) [11], abductive reasoning network [12], waveform matching [13], Bayesian network [14], logic cause-effect model [15], and flexible model-based method [16]. In [17], RS, ANN, and ES are incorporated to overcome respective deficiency and exert respective excellence. The Hebb’s rule and continuous genetic algorithm are applied in [18]. Additionally, a pattern recognition approach is proposed in [19]. Recently, a new method has been proposed using history driven differential evolution and stochastic time domain simulation [20]. Besides, wide area measurements can provide synchronized data and improve the capability of fault section estimation [21,22]. Up to now, only the expert system and the analytic model-based methods have been well developed and applied in practice.

For methods based on an analytic model, different combinations of all the primary devices in the outage region are regarded as the fault hypotheses. Then, an objective function is built up according to the structure of the power network, the protection scheme, and the collected operation information of protective relays (PRs) and circuit breakers (CBs), in order to reflect the discrepancy between the actual and expected states of PRs and CBs. Consequently, the fault diagnosis can be formulated as an unconstrained 0–1 integer programming problem, and optimization algorithms can be employed to minimize the objective function, i.e., the discrepancy, with the optimum solution as the fault diagnosis result.

Because the analytic model strictly complies with mathematical logics, it usually provides an accurate diagnosis result, even for a fault with a small quantity of false and/or missing alarms [3,4]. Potential malfunctioning of PRs and CBs was taken into account in [8]. The proposed model could not only estimate the outage section(s), but also identify the malfunctioned PRs and CBs and the false and/or missing alarms. Nevertheless, the reliability of the PR and CB operations was not considered.

The main difficulty in current research on power system fault diagnosis lies in the existence of the malfunctioning of PRs and CBs, in addition to the false and/or missing alarms with uncertainties. Therefore, when constructing the mathematical framework of power system fault diagnosis, the only way to improve the performance is to include every possible uncertainty to the maximum extent.

Chance-constrained programming (CCP) is proposed by Charnes and Cooper [23] as a branch of stochastic programming. Through modeling the uncertainties into random variable forms, the CCP provides a new way to approach the programming problems fraught with uncertain factors, like fault diagnosis of power systems. Under this circumstance, the authors propose a novel analytic model applying chance-constrained programming techniques. With the developed model, the malfunctioning of PRs and CBs, and the false and/or missing alarms, are denoted by random variables and the genetic algorithm based on Monte Carlo simulation is employed to attain the solution. Since the uncertain factors in the fault diagnosis are fully considered, the fault tolerance of the model is ensured theoretically. In the paper, an actual fault scenario is used to demonstrate the effectiveness and feasibility of the proposed method.

2. Chance-Constrained Programming

The CCP is applicable for optimization problems where random variables are included in the constraints and the objective function and the decision should be made before these random variables are observed. Since the decision thereby obtained may sometimes not accommodate the constraints, the following principle should be retained: while decisions not accommodating the constraints to a certain extent are allowed, the probability of their obeying the constraints should be no less than a prescribed confidence level. The CCP method has been applied in many areas of the power system [24,25,26,27,28,29,30]. In general, the mathematical model can be described as follows:

$$\{\begin{array}{ll}\min & \overline{f}\\ s.t.& P_r\{f(x,\xi )\le f_{\min }\}\ge \beta \\ & P_r\{g_j(x,\xi )\le 0,j=1,2,\cdots ,p\}\ge \alpha \end{array}$$

(1)

where x is a vector of decision variables; ξ is the stochastic vector with a given probability density function Φ(ξ); f(x,ξ) is the objective function; g_j(x,ξ)(j = 1, 2, …, p) is the constraint function; P_r{∙} is the probability of the events in the set; α and β are the prescribed confidence levels of the constraints and the objective function, respectively; and min $\overline{f}$ is the minimum value of f(x,ξ) with the confidence level β.

3. Analytic Model of Power System Fault Diagnosis Based on CPP

This section discusses the analytic model for power system fault diagnosis, the uncertain factors involved, and the expected states of them.

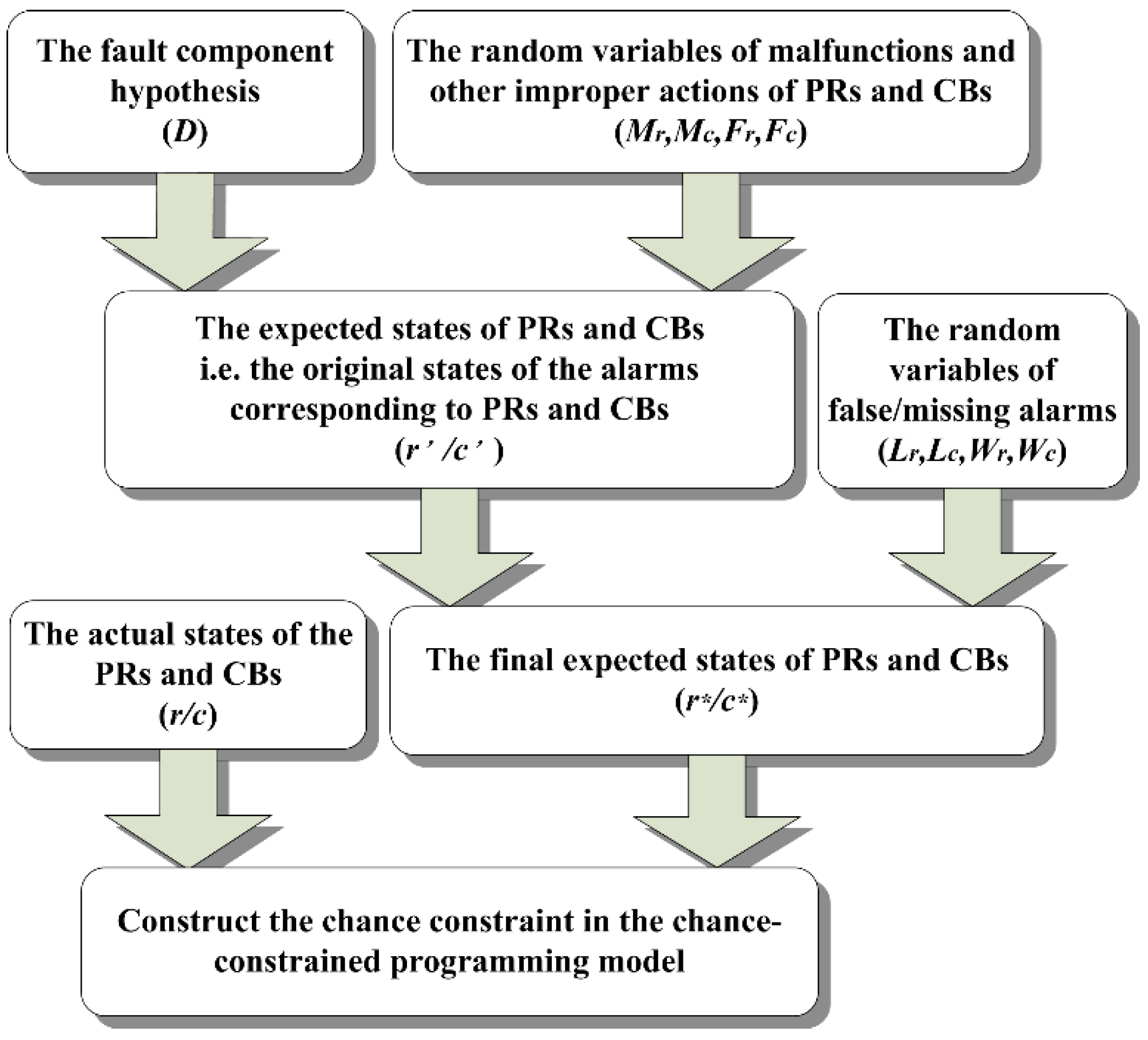
3.1. Modeling of Uncertain Factors

Most uncertain factors can be modeled into a probabilistic form such as probability density functions, the parameters of which can be acquired from the historical data and the operation status of the devices. In the fault diagnosis of power systems, as aforementioned, the related PRs and CBs can operate properly or improperly. Meanwhile, due to device and communication problems, false and/or missing alarms may occur occasionally. Both of the two scenarios described above contain uncertainties. Therefore, the malfunctioning and other improper actions of PRs and CBs, as well as the false and/or missing alarms, are regarded as uncertain factors, which, together with other types of uncertainties in the developed model, can be handled using the methods discussed below.

In fact, the action of different PRs/CBs only reflects the states of the corresponding components, so there are no interferences between them. For the same PR/CB, the precondition of its malfunction is that the PR/CB is not expected to trip, while the precondition of its refusing action is that the PR/CB is expected to trip. The preconditions of the malfunction and the refusing action are different, so there are no interferences between them. As a result, these uncertainties are independent from each other. Thus, these uncertainties are taken as independent random variables with only two possible states (1/0) and are described with discrete probability distributions. Assume that the probabilities of the malfunction ($m_{ri}=1$) and the refusing action ($f_{ri}=1$) of the ith PR(r_i) are $p_{mri}$ and $p_{fri}$, respectively. Similarly, the probabilities of the malfunction ($m_{cj}=1$) and the refusing action ($f_{ci}=1$) of the jth CB (c_j) are $p_{mcj}$ and $p_{fcj}$, respectively.

Likewise, false and missing alarms are also denoted by discrete probability distributions. The probabilities of the false alarm ($w_{ri}=1$) and the missing alarm ($l_{ri}=1$) of $r_i$ are $p_{wri}$ and $p_{lri}$, and the probabilities of the false alarm ($w_{cj}=1$) and the missing alarm ($l_{cj}=1$) of $c_j$ are $p_{wcj}$ and $p_{lcj}$, respectively.

3.2. Analytic Model

Suppose that there are $n_d$ components in the outage area, $n_r$ configured PRs, and $n_c$ CBs connected to the outage components before the fault. Hence, there are $n_r$ and $n_c$ alarms corresponding to the PRs and the CBs, respectively.

In the process of fault diagnosis, the discrepancy between the actual and the expected states of PRs and CBs can be expressed as:

$${\displaystyle \sum _i^{n_r}\left|r_i-r_i^{\ast }(H)\right|}+{\displaystyle \sum _j^{n_c}\left|c_j-c_j^{\ast }(H)\right|}$$

(2)

where $H=[D,F,M,L,W]$ is the fault hypothesis; $D=[d_1,d_2,\cdots ,d_{nd}]$ is randomly generated at the beginning of the solving procedure and is updated during the process; d_i = 1 and d_i = 0 respectively represent the faulty and normal states of the ith component d_i in the outage area; $M=[m_{r_1},m_{r_2},\cdots ,m_{r_{nr}},m_{c_1},m_{c_2},\cdots ,m_{c_{nc}}]$ and $F=[f_{r_1},f_{r_2},\cdots ,f_{r_{nr}},f_{c_1},f_{c_2},\cdots ,f_{c_{nc}}]$ are the random vectors of the malfunctioning and the refusing actions of the PRs and CBs, respectively; $W=[w_{r_1},w_{r_2},\cdots ,w_{r_{nr}},w_{c_1},w_{c_2},\cdots ,w_{c_{nc}}]$ and $L=[l_{r_1},l_{r_2},\cdots ,l_{r_{nr}},l_{c_1},l_{c_2},\cdots ,l_{c_{nc}}]$ are the random vectors of the false and the missing alarms, respectively; $r_i$ and $r_i^{\ast }(H)$ are the actual and expected states of PRs, respectively; $c_j$ and $c_j^{\ast }(H)$ are the actual and expected states of CBs, respectively; and $r_i$ and $c_j$ are observed during the faulty state.

Consequently, all the malfunctioned/improper-acted PRs and CBs, and the false/missing alarms, make up the objective function of the analytic model:

$$E(H)={\displaystyle \sum _{i=1}^{n_r}\left(\left|m_{r_i}\right|+\left|f_{r_i}\right|\right)}+{\displaystyle \sum _{j=1}^{n_c}\left(\left|m_{c_j}\right|+\left|f_{c_j}\right|\right)}+{\displaystyle \sum _{i=1}^{n_r}\left(\left|l_{r_i}\right|+\left|w_{r_i}\right|\right)}+{\displaystyle \sum _{j=1}^{n_c}\left(\left|l_{c_j}\right|+\left|w_{c_j}\right|\right)}$$

(3)

Furthermore, the discrepancy between the actual and the expected states of PRs and CBs is taken as the chance constraint:

$$P_r\left\{{\displaystyle \sum _i^{n_r}\left|r_i-r_i^{\ast }(H)\right|}+{\displaystyle \sum _j^{n_c}\left|c_j-c_j^{\ast }(H)\right|}=0\right\}\ge \alpha$$

(4)

where $P_r\{•\}$ is the probability of $\{•\}$ and $\alpha$ is the confidence level of the chance constraint.

In traditional chance-constrained programming, $\alpha$ is prescribed. Nevertheless, it is difficult to find a fixed and widely applied $\alpha$ in power system fault diagnosis because of the diversity of fault components, in addition to the complexity of fault conditions, malfunctioned/false-acted devices, and missing/false alarms. When PRs and CBs act properly without false/missing alarms, a larger $\alpha$ is beneficial for finding an accurate fault diagnosis, while a smaller $\alpha$ may give misleading results; when malfunctioning and other improper actions of PRs and CBs, and false and/or missing alarms, exist, a smaller $\alpha$ rather than a larger one should be adopted to obtain a satisfactory diagnosis result. Thus, $\alpha$ should be handled as an adaptive variable, with a large initial value, and be adjusted through the iterations until a satisfactory diagnosis is achieved (Figure 1). The adjustment of $\alpha$ is as follows:

$$\alpha ={\alpha }_0·\exp \left(3(1-n)/N\right)$$

(5)

where ${\alpha }_0$ is the initial value of $\alpha$, $n$ is the number of the iterations, and $N$ is the maximum number of iterations set in advance.

The chance constraint is gradually built up with the fault hypotheses and the random variables, as illustrated by the procedures shown in Figure 2. The expected states of PRs and CBs in Figure 2 will be discussed in Section 3.3 and Section 3.4.

Finally, the mathematical model based on the chance-constrained programming for fault diagnosis of a power system is formulated as below:

$$\{\begin{array}{ll}\min & \overline{E}\\ s.t.& P_r\{E(H)\le \overline{E}\}\ge \beta \\ & P_r\left\{{\displaystyle \sum _i^{n_r}\left|r_i-r_i^{\ast }(H)\right|+{\displaystyle \sum _j^{n_c}\left|c_j-c_j^{\ast }(H)\right|=0}}\right\}\ge \alpha \end{array}$$

(6)

where $\beta$ is the confidence level of the objective function and $\overline{E}$ is the minimum of the objective function $E(H)$ with the confidence level $\beta$.

3.3. Determination of the Expected States of PRs and CBs with Potential Malfunctions

Malfunctioning and other improper actions are taken into account in the evaluation of the expected states of PRs and CBs.

3.3.1. PRs

The expected states of different types of PRs are discussed below, where $\otimes$ and $\oplus$ denote the logic multiplication and summation.

(1) Main Protection (MP)

Suppose that $r_i$ is the MP of $d_k$ and it should operate if a fault occurs on $d_k(d_k=1)$. By taking into account the malfunctioning and other improper actions, the expected state of MP is determined by:

$$r_i^{\prime }=d_k\otimes \overline{f_{r_i}}\oplus m_{r_i}$$

(7)

(2) Primary Backup Protection (PBP)

Suppose that $r_i$ is the PBP of $d_k$. $r_i$ should operate if the MP $r_x$ failed to do so ($m_{r_x}=1$) when a fault occurred on $d_k$ ($d_k=1$). By taking into account the malfunctioning and other improper actions, the expected state of PBP is determined by:

$$r_i^{\prime }=d_k\otimes \overline{r_x^{\prime }}\otimes \overline{f_{r_i}}\oplus m_{r_i}$$

(8)

(3) Secondary Backup Protection (SBP)

Suppose that $r_i$ is the SBP of $d_k$. The expected state of $r_i$ is determined as follows:

(a)

If a fault occurred on $d_k$, and both MP $r_x$ and BPB $r_y$ failed to operate, then $r_i$ should operate, i.e.,

$$r_i^{\prime }=d_k\otimes \overline{r_x^{\prime }}\otimes \overline{r_y^{\prime }}$$

(9)

(b)

If a fault occurred on the related device d_j in the protection zone of r_i, and all CBs along the related path $p\left(r_i,d_j\right)$ from $r_i$ to $d_j$ were closed, i.e., the fault has not been cleared yet, then ri should operate. $Z(r_i)$ denotes the set of related sections in the protection zone, $d_j\in Z(r_i)$. So there is

$$r_i^{\prime }={\displaystyle \sum _{d_j\in Z\left(r_i\right)}\left(d_j\otimes {\displaystyle \prod _{c_p\in p\left(r_i,d_j\right)}\overline{c_p}}\right)}$$

(10)

The related path from $r_i$ to $d_j$ is the acyclic electrical path from the location of $r_i$ to its related section $d_j$ denoted by $p\left(r_i,d_j\right)$. Taking into account the malfunctioning and other improper actions, and using the above Equations (7)–(10), the expected state of SBP can be expressed by:

$$r_i^{\prime }=\left[d_k\otimes \overline{r_x^{\prime }}\otimes \overline{r_y^{\prime }}\oplus {\displaystyle \sum _{d_j\in Z\left(r_i\right)}\left(d_j\otimes {\displaystyle \prod _{c_p\in p\left(r_i,d_j\right)}\overline{c_p}}\right)}\right]\otimes \overline{f_{r_i}}\oplus m_{r_i}$$

(11)

(4) Breaker Failure Protection (BFP)

Suppose that $r_i$ is the BFP of CB $c_j$ that failed to trip when a fault occurred and the tripping signal had been sent to it; then, $r_i$ should operate. Thus, the refusing actions of the CBs with BFPs cannot be taken as random variables and the expected state of BFP should be the same as the refusing action of its CB, i.e.,

$$r_i^{″}=f_{c_j}=\left(r_x^{\prime }\oplus r_y^{\prime }\oplus r_z^{\prime }\right)\otimes \overline{c_j}\otimes r_i$$

(12)

where $r_x^{\prime }$, $r_y^{\prime }$, and $r_z^{\prime }$ are the expected states of MP, PBP, and SBP, respectively; and $c_j$ and $r_i$ are the actual states of CB and its BFP, respectively. Taking into account the malfunctioning and other improper actions of PRs, the expected state of BFP is given by:

$$r_i^{\prime }=f_{c_j}\otimes \overline{f_{r_i}}\oplus m_{r_i}$$

(13)

3.3.2. CBs

If $c_j$ has received tripping signals from $r_x$, it should trip off. $R\left(c_j\right)$ denotes the set of PRs related to $c_j$ and $r_x\in R\left(c_j\right)$. Taking into account the malfunctioning and other improper actions of CBs, the expected state of $c_j$ is given as:

$$c_j^{\prime }=\left({\displaystyle \sum _{r_x\in R\left(c_j\right)}{r}_x^{\prime }}\right)\otimes \overline{f_{c_j}}\oplus m_{c_j}$$

(14)

3.4. The Final Expected States of PRs and CBs

In the process employed to determine the expected states of PRs and CBs discussed in Section 3.3, the false and missing alarms have been ignored. As shown in Figure 2, the expected states deduced by considering the malfunctioning and other improper actions of PRs and CBs should be further processed by including the false and missing alarms that can also be denoted by random variables. Thus, there are:

$$r_i^{\ast }=r_i^{\prime }\otimes \overline{l_{r_i}}\oplus w_{r_i}$$

(15)

$$c_j^{\ast }=c_j^{\prime }\otimes \overline{l_{c_j}}\oplus w_{c_j}$$

(16)

where $r_i^{\prime }$ and $c_j^{\prime }$ are the expected states of the corresponding PR and CB (Section 3.3) when considering the malfunctioning and other improper actions; and $r_i^{\ast }$ and $c_j^{\ast }$ are the final expected states of the corresponding PR and CB.

4. Solving the Fault Diagnosis Problem

This section discusses the methods and procedures used for solving the fault diagnosis problem.

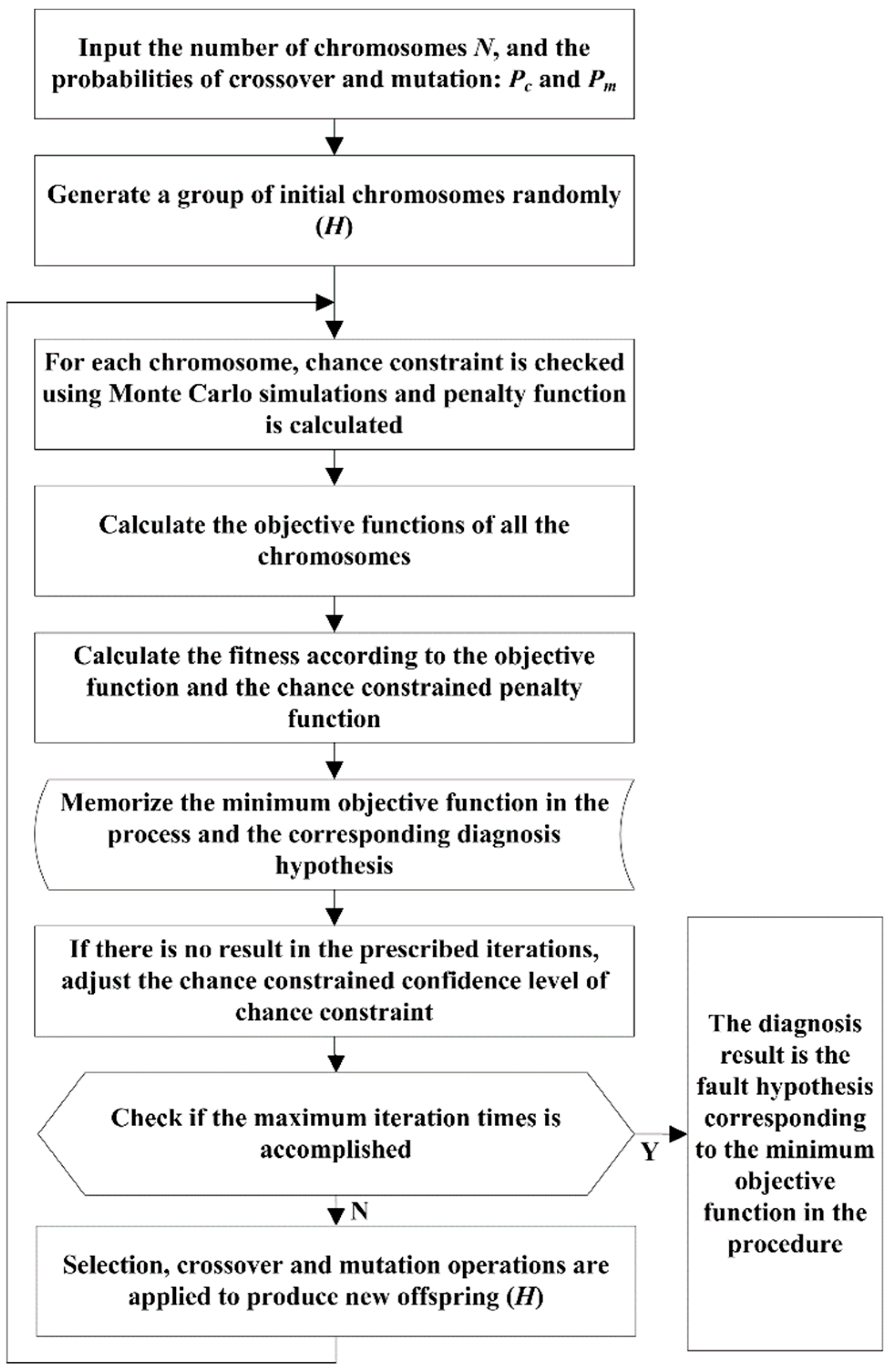
4.1. Constraint Checking

The chance constraint shown in Equation (4) can be checked using the Monte Carlo simulation method [24].

4.2. The Calculation of the Objective Function

For any given fault hypothesis D, the Monte Carlo simulation method is employed to search for the minimum $\overline{E}$, which accommodates the following constraint:

$$P_r\left\{E(H)\le \overline{E}\right\}\ge \beta$$

(17)

The following is the procedure of searching $\overline{E}$ using the Monte Carlo simulation method:

(a)

The random variables are sampled $N_{max}$ times, and $E$ is calculated by using Equation (3) to obtain the sequence $\{E_1,E_2,\cdots E_{N_{max}}\}$.

(b)

Set $N^{\prime }$ as the integer part of $\beta N_{max}$.

(c)

Select the $N_{th}^{\prime }$ smallest element in the sequence $\{E_1,E_2,\cdots E_{N_{max}}\}$ to be the objective value $\overline{E}$.

Finally, the genetic algorithm (GA) based on Monte Carlo simulations is employed to solve the chance-constrained programming model for the fault diagnosis problem described by Equation (6). The well-known GA techniques are not discussed in the paper. Please refer to [24] for detail if necessary.

4.3. The Solving Procedure

To solve the fault diagnosis chance-constrained programming model of Equation (6) using the genetic algorithm based on Monte Carlo simulations, the penalty functions should be constructed by employing the chance constraint in the first place. The fitness function can then be formed by the penalty function in conjunction with the objective function. The solving procedure is shown in Figure 3.

5. Application Examples

An actual fault is adopted in this section to verify the developed model and the method. The fault occurred at Tangling Substation in Zhejiang province, China, on 28 August 2009. Figure 4 shows the involved part of the power network. As illustrated by the diagram, the outage area contains five components and ten CBs. They are L4333, L4339, L4335, L4336 and B1-I, and C2, C3, C6, C7, C10, C11, C12, C13, C14, and C18.

In the real scenario, faults occurred on both L4335 (d₂) and L4336 (d₃). The analysis showed that C10 of Tangling Substation refused to trip and the differential protection alarm on the Tangling side of Jianshan L4336 was missing.

The reported alarms after the fault are listed in

Table 1. Received Alarm.

Timestamp (ms)	Substation	Alarms	Timestamp (ms)	Substation	Alarms
28	Tangling	DP of L4335 operated	665	Tangling	Phase A of C18 was tripped
31	Jianshan	DP of L4335 operated	665	Tangling	Phase B of C18 was tripped
75	Tangling	Phase C of C10 was tripped	666	Tangling	Phase C of C18 was tripped
79	Jianshan	Phase C of C11 was tripped	667	Tangling	Phase A of C14 was tripped
383	Tangling	Acceleration Protection of C10 operated	667	Tangling	Phase B of C14 was tripped
480	Jianshan	DP of L4336 operated	668	Tangling	Phase C of C14 was tripped
523	Tangling	Phase A of C12 was tripped	873	Tangling	Phase A of C3 was tripped
523	Tangling	Phase B of C12 was tripped	873	Tangling	Phase B of C3 was tripped
524	Tangling	Phase C of C12 was tripped	874	Tangling	Phase C of C3 was tripped
529	Jianshan	Phase A of C13was tripped	874	Tangling	Phase A of C6 was tripped
529	Jianshan	Phase B of C13 was tripped	875	Tangling	Phase B of C6 was tripped
529	Jianshan	Phase C of C13 was tripped	875	Tangling	Phase C of C6 was tripped
617	Tangling	BFP of C10 operated

Note: DP and BFP denote Differential Protection and Breaker Failure Protection.

. For convenience of description, the related components, PRs, and CBs are encoded as shown in

Table 2. The Encoding of the Component.

L4333	L4339	L4335	L4336	B1-I
d0	d1	d2	d3	d4

,

Table 3. The Encoding of Relays.

	L4333	L4339	L4335	L4336	B1-I
MP	r0	r1	r2	r3	r4
PBP	r5	r6	r7	r8	—
SBP	r9	r10	r11	r12	—
BFP	C3	C6	C10	C14	C18
	r13	r14	r15	r16	r17

and

Table 4. The Encoding of Breakers.

C2	C3	C6	C7	C10	C11	C12	C13	C14	C18
c0	c1	c2	c3	c4	c5	c6	c7	c8	c9

. According to the received alarms, the actual states of PRs and CBs after the fault are shown in

Table 5. The States of the Relays and Breakers.

Alarm Type	MP	PBP	SBP	BFP	CB
Actual state	00100	0000	0000	00100	0110011111

.

In the software simulation, the parameters selection is as follows:

• the number of chromosomes is set to 20;
• the times of Monte Carlo simulations is set to 1000;
• the initial value of confidence level $\alpha$ is set to 0.3;
• $\beta$ is set to 0.7;
• the times of iterations is set to 1000;
• the probabilities of crossover and mutation are set to 0.5 and 0.3.

The probabilities of all the malfunctioning and other improper actions of PRs and CBs, and the false/missing alarms, are set to 0.05.

The outcome produced by the fault diagnosis software based on the proposed method is in a sequence form 00110, which implies that faults occurred on L4335 and L4336 at the same time. Through the analysis, the fault procedure can be reproduced as below.

When a fault occurred on Phase C of L4335, both sides of the Differential Protection of L4335 operated and then Phase C of C10 and C11 were tripped. After a very short delay, Phase C of C10 was resumed. Therefore, the Acceleration Protection of C10 operated but failed to trip. Afterward, the Breaker Failure Protection of C10 operated and all the CBs connected to B1-I were tripped. Meanwhile, a fault occurred on the L4336. Then, both sides of the Differential Protection of L4336 still operated and in turn, the three phases of C12 and C13 were tripped. However, the differential protection alarm on the Tangling side of Jianshan L4336 was missing.

The fault diagnosis results are consistent with what really happened.

6. Conclusions

In order to handle uncertain factors, including malfunctioning and other improper actions of PRs and CBs, in addition to false and/or missing alarms, a chance-constrained programming model is introduced into power system fault diagnosis. The Monte Carlo simulation-based genetic algorithm is employed to solve the developed optimization model. An actual complicated fault scenario at a substation in Zhejiang province, China, is presented to test the proposed method. As shown by the case study, the diagnosis result is consistent with the real fault, and the high fault tolerance capability is demonstrated. Furthermore, the computation speed of the developed method meets the requirements of on-line fault diagnosis applications.

An extension of this work by employing temporal information of alarm messages [31] will be carried out in our following research work.