Assessing the Effect of Incentive Policies on Residential PV Investments in Colombia
Abstract
:1. Introduction
2. Literature Review
3. Simulation Model
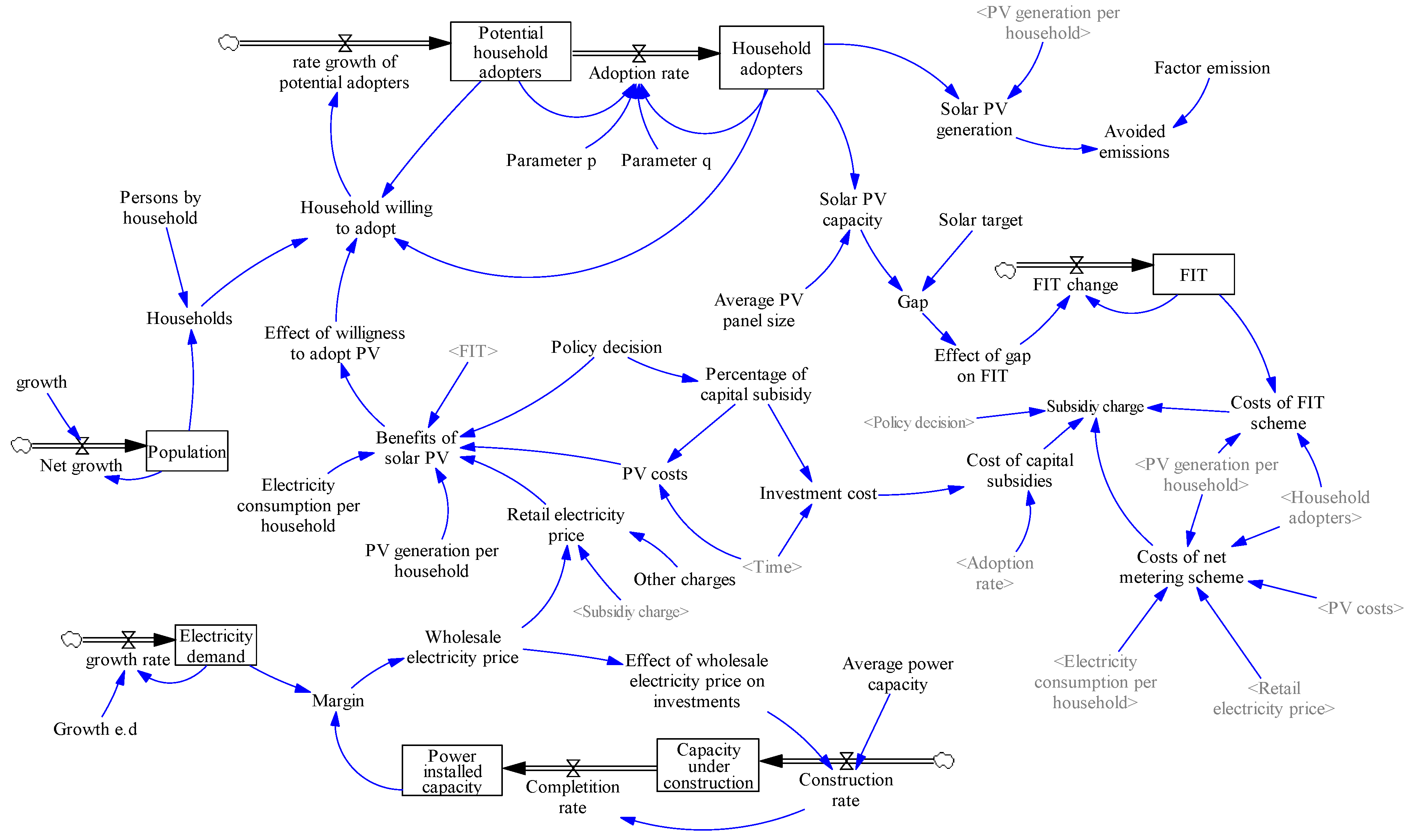
3.1. Dynamic Hypothesis
3.2. Mathematical Model
3.2.1. Wholesale Electricity Market
3.2.2. PV Adoption
3.2.3. PV Policies
3.2.4. Environmental Indicators
3.2.5. Simulation Model
3.2.6. Data
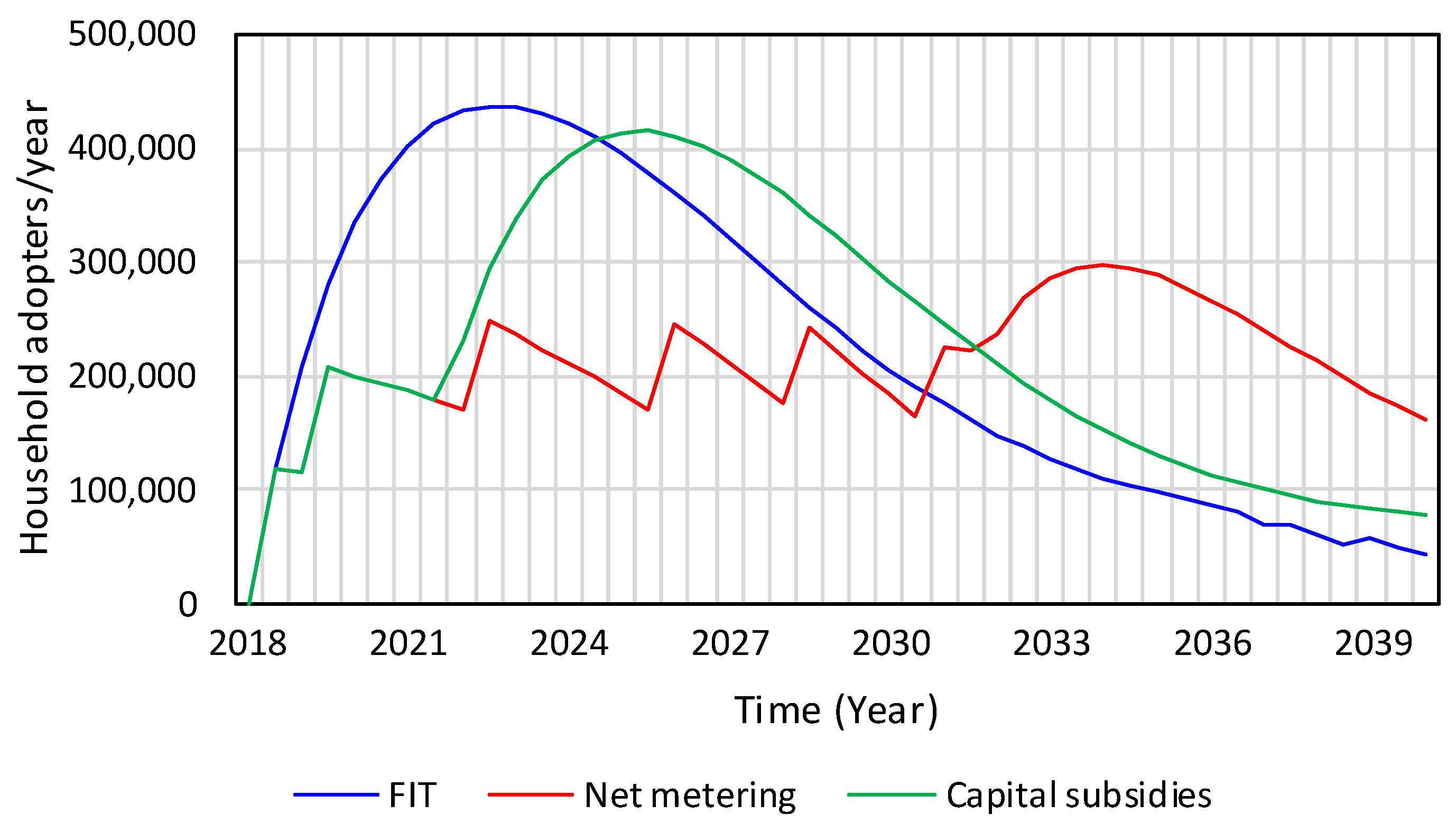
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- REN21. Renewable Energy Policy Network for the 21st Century; Renewables 2018 Global Status Report; REN21: Paris, France, 2018. [Google Scholar]
- Masson, G.; Kaizuka, I.; Brunisholz, M. 2018 Snapshot of global photovoltaic markets; International Energy Agency: Paris, France, 2018. [Google Scholar]
- International Renewable Energy Agency (IRENA). Global Renewable Generation Continues its Strong Growth, New IRENA Capacity Data Shows. Available online: http://www.irena.org/newsroom/pressreleases/2018/Apr/Global-Renewable-Generation-Continues-its-Strong-Growth-New-IRENA-Capacity-Data-Shows (accessed on 8 August 2018).
- Taylor, M.; Ralon, P.; Ilas, A. The Power to Change: Solar and Wind Cost Reduction Potential to 2025; IRENA: Abu Dhabi, UAE, 2016. [Google Scholar]
- Pepermans, G.; Driesen, J.; Haeseldonckx, D.; Belmans, R.; D’haeseleer, W. Distributed generation: definition, benefits and issues. Energy Policy 2005, 33, 787–798. [Google Scholar] [CrossRef]
- Ackermann, T. Distributed generation: A definition. Electr. Power Syst. Res. 2001, 57, 195–204. [Google Scholar] [CrossRef]
- Australian Energy Council. Renewable Energy in Australia—How Do We Really Compare? Australian Energy Council: Melbourne, Australia, 2016. [Google Scholar]
- Sioshansi, F.; Weinberg, C. Lessons from other industries facing disruptive technology. In Distributed Generation and Its Implications for the Utility Industry; Elsevier Inc.: Amsterdam, The Netherlands, 2014; pp. 141–162. ISBN 9780128002407. [Google Scholar]
- El Chaar, L.; Lamont, L.A.; El Zein, N. Review of photovoltaic technologies. Renew. Sustain. Energy Rev. 2011, 15, 2165–2175. [Google Scholar] [CrossRef]
- Anzalchi, A.; Sarwat, A. Overview of technical specifications for grid-connected photovoltaic. Energy Convers. Manag. 2017, 152, 312–327. [Google Scholar] [CrossRef]
- Tayal, D.; Rauland, V. Future business models for Western Australian electricity utilities. Sustain. Energy Technol. Assess. 2017, 19, 59–69. [Google Scholar] [CrossRef]
- Pérez-Arriaga, I.J.; Ruester, S.; Schwenen, S.; Battle, C.; Glachant, J.-M. From Distribution Networks to Smart Distribution Systems: Rethinking the Regulation of European Electricity DSOs; European University Institute: Fiesole, FI, Italy, 2013; ISBN 9789290841432. [Google Scholar]
- Thiam, D.R. An energy pricing scheme for the diffusion of decentralized renewable technology investment in developing countries. Energy Policy 2011, 39, 4284–4297. [Google Scholar] [CrossRef]
- Kumar, B. A study on global solar PV energy developments and policies with special focus on the top ten solar PV power producing countries. Renew. Sustain. Energy Rev. 2015, 43, 621–634. [Google Scholar] [CrossRef]
- De Boeck, L.; Van Asch, S.; De Bruecker, P.; Audenaert, A. Comparison of support policies for residential photovoltaic systems in the major EU markets through investment profitability. Renew. Energy 2016, 87, 42–53. [Google Scholar] [CrossRef]
- Dusonchet, L.; Telaretti, E. Comparative economic analysis of support policies for solar PV in the most representative EU countries. Renew. Sustain. Energy Rev. 2015, 42, 986–998. [Google Scholar] [CrossRef]
- Cansino, J.M.; Pablo-Romero, M.D.P.; Román, R.; Yñiguez, R. Promoting renewable energy sources for heating and cooling in EU-27 countries. Energy Policy 2011, 39, 3803–3812. [Google Scholar] [CrossRef]
- Del Río, P.; Mir-Artigues, P. Support for solar PV deployment in Spain: Some policy lessons. Renew. Sustain. Energy Rev. 2012, 16, 5557–5566. [Google Scholar] [CrossRef]
- Sarasa-Maestro, C.J.; Dufo-López, R.; Bernal-Agustín, J.L. Photovoltaic remuneration policies in the European Union. Energy Policy 2013, 55, 317–328. [Google Scholar] [CrossRef]
- Karneyeva, Y.; Wüstenhagen, R. Solar feed-in tariffs in a post-grid parity world: The role of risk, investor diversity and business models. Energy Policy 2017, 106, 445–456. [Google Scholar] [CrossRef]
- Bale, C.S.E.; Varga, L.; Foxon, T.J. Energy and complexity: New ways forward. Appl. Energy 2015, 138, 150–159. [Google Scholar] [CrossRef] [Green Version]
- Qudrat-ullah, H. Modelling and Simulation in Service of Energy Policy. Energy Procedia 2015, 75, 2819–2825. [Google Scholar] [CrossRef]
- Dyner, I.; Larsen, E.R. From planning to strategy in the electricity industry. Energy Policy 2001, 29, 1145–1154. [Google Scholar] [CrossRef]
- Movilla, S.; Miguel, L.J.; Blázquez, L.F. A system dynamics approach for the photovoltaic energy market. Energy Policy 2013, 60, 142–154. [Google Scholar] [CrossRef]
- Campoccia, A.; Dusonchet, L.; Telaretti, E.; Zizzo, G. An analysis of feed’ in tariffs for solar PV in six representative countries of the European Union. Sol. Energy 2014, 107, 530–542. [Google Scholar] [CrossRef]
- Verbruggen, A.; Lauber, V. Assessing the performance of renewable electricity support instruments. Energy Policy 2012, 45, 635–644. [Google Scholar] [CrossRef]
- Sovacool, B.K. The importance of comprehensiveness in renewable electricity and energy-efficiency policy. Energy Policy 2009, 37, 1529–1541. [Google Scholar] [CrossRef]
- Haas, R.; Resch, G.; Panzer, C.; Busch, S.; Ragwitz, M.; Held, A. Efficiency and effectiveness of promotion systems for electricity generation from renewable energy sources—Lessons from EU countries. Energy 2010, 36, 2186–2193. [Google Scholar] [CrossRef]
- Castaneda, M.; Jimenez, M.; Zapata, S.; Franco, C.J.; Dyner, I. Myths and facts of the utility death spiral. Energy Policy 2017, 110, 105–116. [Google Scholar] [CrossRef]
- Castaneda, M.; Franco, C.J.; Dyner, I. Evaluating the effect of technology transformation on the electricity utility industry. Renew. Sustain. Energy Rev. 2017, 80, 341–351. [Google Scholar] [CrossRef]
- Jimenez, M.; Franco, C.J.; Dyner, I. Diffusion of renewable energy technologies: The need for policy in Colombia. Energy 2016, 111, 818–829. [Google Scholar] [CrossRef]
- Sovacool, B.K.; Agostino, A.L.D.; Bambawale, M.J. The socio-technical barriers to Solar Home Systems (SHS) in Papua New Guinea: “Choosing pigs, prostitutes, and poker chips over panels”. Energy Policy 2011, 39, 1532–1542. [Google Scholar] [CrossRef]
- Hsu, A.; Rosengarten, C.; Weinfurter, A.; Xie, Y. Renewable Energy and Energy Efficiency in Developing Countries: Contributions to Reducing Global Emissions Third Report; UNEP: Nairobi, Kenya, 2017; ISBN 978-9-291426515. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Mitigation of Climate Change: Contribution of Working Group III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2007; ISBN 0521880114. [Google Scholar]
- Verbruggen, A. Performance evaluation of renewable energy support policies, applied on Flanders’ tradable certificates system. Energy Policy 2009, 37, 1385–1394. [Google Scholar] [CrossRef]
- Del Río, P. The dynamic efficiency of feed-in tariffs: The impact of different design elements. Energy Policy 2012, 41, 139–151. [Google Scholar] [CrossRef]
- Weitzman, M.L. Prices vs. Quantities. Rev. Econ. Stud. 1974, 1974, 477–491. [Google Scholar] [CrossRef]
- Franz, S. Regulatory Trends in Renewable Energy Self-Supply Título: Regulatory Trends in Renewable Energy Self-Supply Proyecto Energía Solar para la Generación de Electricidad y Calor Página 3; Ministerio de Energía de Chile: Santiago, Chile, 2016.
- La Monaca, S.; Ryan, L. Solar PV where the sun doesn’t shine: Estimating the economic impacts of support schemes for residential PV with detailed net demand pro fi ling. Energy Policy 2017, 108, 731–741. [Google Scholar] [CrossRef]
- Yamamoto, Y. Pricing electricity from residential photovoltaic systems: A comparison of feed-in tariffs, net metering, and net purchase and sale. Sol. Energy 2012, 86, 2678–2685. [Google Scholar] [CrossRef]
- Poullikkas, A. A comparative assessment of net metering and feed in tariff schemes for residential PV systems. Sustain. Energy Technol. Assess. 2013, 3, 1–8. [Google Scholar] [CrossRef]
- Ahmad, S.; Tahar, R.M.; Muhammad-Sukki, F.; Munir, A.B.; Rahim, R.A. Role of feed-in tariff policy in promoting solar photovoltaic investments in Malaysia: A system dynamics approach. Energy 2015, 84, 808–815. [Google Scholar] [CrossRef] [Green Version]
- Radomes, A.A.; Arango, S. Renewable energy technology diffusion: An analysis of photovoltaic-system support schemes in Medellín, Colombia. J. Clean. Prod. 2015, 2009. [Google Scholar] [CrossRef]
- Hsu, C.-W. Using a system dynamics model to assess the effects of capital subsidies and feed-in tariffs on solar PV installations. Appl. Energy 2012, 100, 205–217. [Google Scholar] [CrossRef]
- Mahajan, V.; Muller, E.; Bass, F.M. New product diffusion models in marketing: A review and directions for research. J. Mark. 1990, 54, 125–177. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2014: Mitigation of Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Congreso Colombia Ley 1715 de 2014. Available online: http://www.comunidadcontable.com/BancoMedios/Imagenes/ley%201715%20de%202014.pdf (accessed on 30 September 2018).
- Zapata, S.; Castaneda, M.; Garces, E.; Franco, C.J.; Dyner, I. Assessing security of supply in a largely hydroelectricity-based system: The Colombian case. Energy 2018, 156, 444–457. [Google Scholar] [CrossRef]
- Franco, C.J.; Castaneda, M.; Dyner, I. Simulating the new British Electricity-Market Reform. Eur. J. Oper. Res. 2015, 245, 273–285. [Google Scholar] [CrossRef]
- CREG. Resolución 31 de 1997—Formula tarifaria; Ministry of Justice and Law: Bogotá, Colombia, 1997; pp. 1–14.
- Branker, K.; Pathak, M.J.M.; Pearce, J.M. A review of solar photovoltaic levelized cost of electricity. Renew. Sustain. Energy Rev. 2011, 15, 4470–4482. [Google Scholar] [CrossRef]
- Sterman, J.D. Business Dynamics: Systems Thinking and Modeling for a Complex World; McGraw-Hill Higher Education: Columbus, OH, USA, 2000; ISBN 0-07-231135-5. [Google Scholar]
- Bass, F. A new product growth for model consumer durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- IPCC. IPCC Guidelines for National Greenhouse Gas Inventories 2006. Available online: https://www.ipcc-nggip.iges.or.jp/public/2006gl/index.html (accessed on 5 January 2018).
- Estimaciones y proyección de población (DANE). Estimaciones y Proyecciónes de Hogares y Viviendas; DANE: Bogotá, Colombia, 2010. Available online: http://www.dane.gov.co/index.php/poblacion-y-demografia/proyecciones-de-poblacion (accessed on 3 November 2015).
- Departamento Administrativo Nacional de Estadisticas (DANE). Proyecciones Nacionales y Departamentales de Poblacion 2005–2020; DANE: Bogotá, Colombia, 2009; ISBN 9789586240789. [Google Scholar]
- UPME; IDEAM. Atlas de Radiación solar de Colombia; Ministerio de Minas y Energía: Bogotá, Colombia, 2005.
- UPME; BID. Integración de las Energías Renovables no Convencionales en Colombia. Available online: https://www.senado.gov.co/historia/item/download (accessed on 8 August 2018).
- XM Portal BI. Available online: https://www.portalbi.org (accessed on 1 August 2018).
- SUI. Sistema unico de Informacion de Servicios Publicos Domiciliarios. Available online: http://www.sui.gov.co/web (accessed on 8 March 2018).
- Costello, K.W. Major Challenges of Distributed Generation for State Utility Regulators. Electr. J. 2015, 28, 8–25. [Google Scholar] [CrossRef]
- Brown, A.; Lund, L. Distributed Generation: How Green? How Efficient? How Well-Priced? Electr. J. 2013, 26, 28–34. [Google Scholar] [CrossRef]
- Kirsch, L.D.; Morey, M.J. Pricing Retail Electricity in a Distributed Energy Resources World. Electr. J. 2015, 28, 1–10. [Google Scholar] [CrossRef]
- Eid, C.; Reneses, J.; Frías, P.; Hakvoort, R. The economic effect of electricity net-metering with solar PV: Consequences for network cost recovery, cross subsidies and policy objectives. Energy Policy 2014, 75, 244–254. [Google Scholar] [CrossRef]









| Variable | Value | Source |
|---|---|---|
| Population | 49,834,240 (people) | [55] |
| Population growth | 2% | [56] |
| Sunshine hours | 4.5 kWh/m2/day | [57] |
| Levelized Cost of Energy (LCOE) of solar PV | 0.15 USD/ kWh | [58] |
| Installed capacity | 17.34 GW | [59] |
| Peak electricity demand | 10 GW | [59] |
| Retail electricity tariff | 0.15 USD/kWh | [60] |
| Average energy consumption per household | 188 kWh-month | [60] |
| PV Installed Capacity (MW) | Total Avoided Emissions (Millions t CO2) | Average PV Charges (USD/kWh) | Cost of PV Installed (USD/MW) | |
|---|---|---|---|---|
| Feed-in tariff | 7522 | 4,792,823 | 0.0033 | 133,335 |
| Net metering | 7029 | 3,312,580 | 0.0003 | 20,298 |
| Capital subsidy | 7544 | 4,493,053 | 0.0125 | 509,616 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castaneda, M.; Zapata, S.; Aristizabal, A. Assessing the Effect of Incentive Policies on Residential PV Investments in Colombia. Energies 2018, 11, 2614. https://doi.org/10.3390/en11102614
Castaneda M, Zapata S, Aristizabal A. Assessing the Effect of Incentive Policies on Residential PV Investments in Colombia. Energies. 2018; 11(10):2614. https://doi.org/10.3390/en11102614
Chicago/Turabian StyleCastaneda, Monica, Sebastian Zapata, and Andres Aristizabal. 2018. "Assessing the Effect of Incentive Policies on Residential PV Investments in Colombia" Energies 11, no. 10: 2614. https://doi.org/10.3390/en11102614
APA StyleCastaneda, M., Zapata, S., & Aristizabal, A. (2018). Assessing the Effect of Incentive Policies on Residential PV Investments in Colombia. Energies, 11(10), 2614. https://doi.org/10.3390/en11102614





