Analytical Determination of Energy Release in a Coal Mass

Abstract

In underground mining, it is not currently feasible to forecast a coal burst incident. A coal burst usually includes suddenly abrupt energy release in line with the significant deformed shape in a coal mass as well as coal ejection. The major source of the released energy is the energy stored in the coal. The effect of geological characteristics in the coal on the possible released energy due to material and joint damping is classified as a current silent issue. Therefore, innovative research is needed to understand the influence of coal’s joint and cleat characters (directions and densities) on the possible energy release and/or dissipation. A simple and novel analytical solution is developed in this paper to calculate the amount of released energy due to varying joint density. A broad validation is conducted by comparing the outcomes of the developed analytical model with the results of a three-dimensional numerical simulation using the commercial discrete element package 3DEC. An appropriate agreement has been observed between the results from the numerical modelling and the suggested closed form solution. The paper derives a novel analytical solution to calculate the amount of released energy in coal with different joint densities.

1. Introduction

Coal bursts have been identified as one of the major catastrophic failures in underground coal mines, causing a significant threat to safety and production. Many researchers define coal bursts as abrupt, sudden fractures of the rock mass with a brittle, unstable release of elastic or strain energy from the mining excavation area due to seismic incident as well as the mining activities. The coal burst source is the mechanism that triggers or induces the damage mechanism visible on the excavation surface. The coal burst source is generally associated with a seismic event that can be performed at a wide range of local magnitudes [1,2,3,4,5,6]. Indeed, mining-induced seismicity can reach moderate values of ground velocity and acceleration, and in some cases on the surface may lead to the generation of low-intensity earthquakes [7]. The mechanism that produces the seismic event is a sudden release of the strain energy that has been stored above a critical level within the rock/coal mass. Some portion of this energy can be dissipated by the crack development, and the rest of the energy is converted into kinetic energy [8,9]. When the energy source is located near the roadway, the released energy may lead to coal fragmentation. When the major source of the energy is located in a plane of weakness inside the coal mass, the released energy may considerably cause to create a shear displacement along the plane. This sudden shear displacement can result in the generation of vibrations that cause coal ejections when they are situated near the excavation boundaries [5]. Tarasov and Randolph [6] devoted special attention to comprehensively elaborating the individual and inconsistent behaviours of hard rock at the significant depth, which are directly in line with the rock fracture condition in deep excavations. Tarasov and Randolph [6] broadly indicated that the shear failure procedures, under the significantly low frictional condition between the engaged surfaces, can be classified as the main reason for the release of energy. Based on the suggested frictionless mechanism, the level of the brittleness of the confined rock/coal masses might be increased under high stress conditions. This may result in reduced overall ductility which would be in line with the abrupt fracture failure. Under an energy-balance approach, the methods to predict coal burst risk are based on energy indexes such as energy release rate (ERR) [1,8], energy storage rate (ESR), strain energy storage index [9], potential energy of elastic strain (PES) or strain energy density (SED) (i.e., the elastic strain energy in a unit volume of the coal mass, which can be computed by the uniaxial compressive strength of the coal and the relevant unloading tangential modulus [8]), and burst potential index (BPI) [10]. Comprehensive reviews of research on the chemical and physical properties of a coal samples have been conducted [11,12], however, there is a critical need to undertake research on the physical responses of the joint and cleat densities on the energy absorption and dissipation in a coal sample under different loading conditions. This paper analyses the role of the joint and cleat characters on energy release in coal samples with respect to the different joint densities and quantifies the strain energy and the release energy that potentially contribute to coal bursts.

2. Calculation of the Three Dimensional Strain Energy in a Coal Mass

An analytical model is suggested to calculate the strain energy. The proposed model is based on the Novozhilove approach [13]. According to Novozhilove [13], strain and plastic work may be calculated by reference to an element, the deformed volume, which is:

$$dA=\mathrm{\Im }\left({\epsilon }_{xx},{\epsilon }_{yy},{\epsilon }_{zz},{\epsilon }_{xy},{\epsilon }_{yz},{\epsilon }_{zx}\right)dxdydz$$

(1)

where ε_xx, ε_yy, ε_zz are the tensorial strains in different directions.

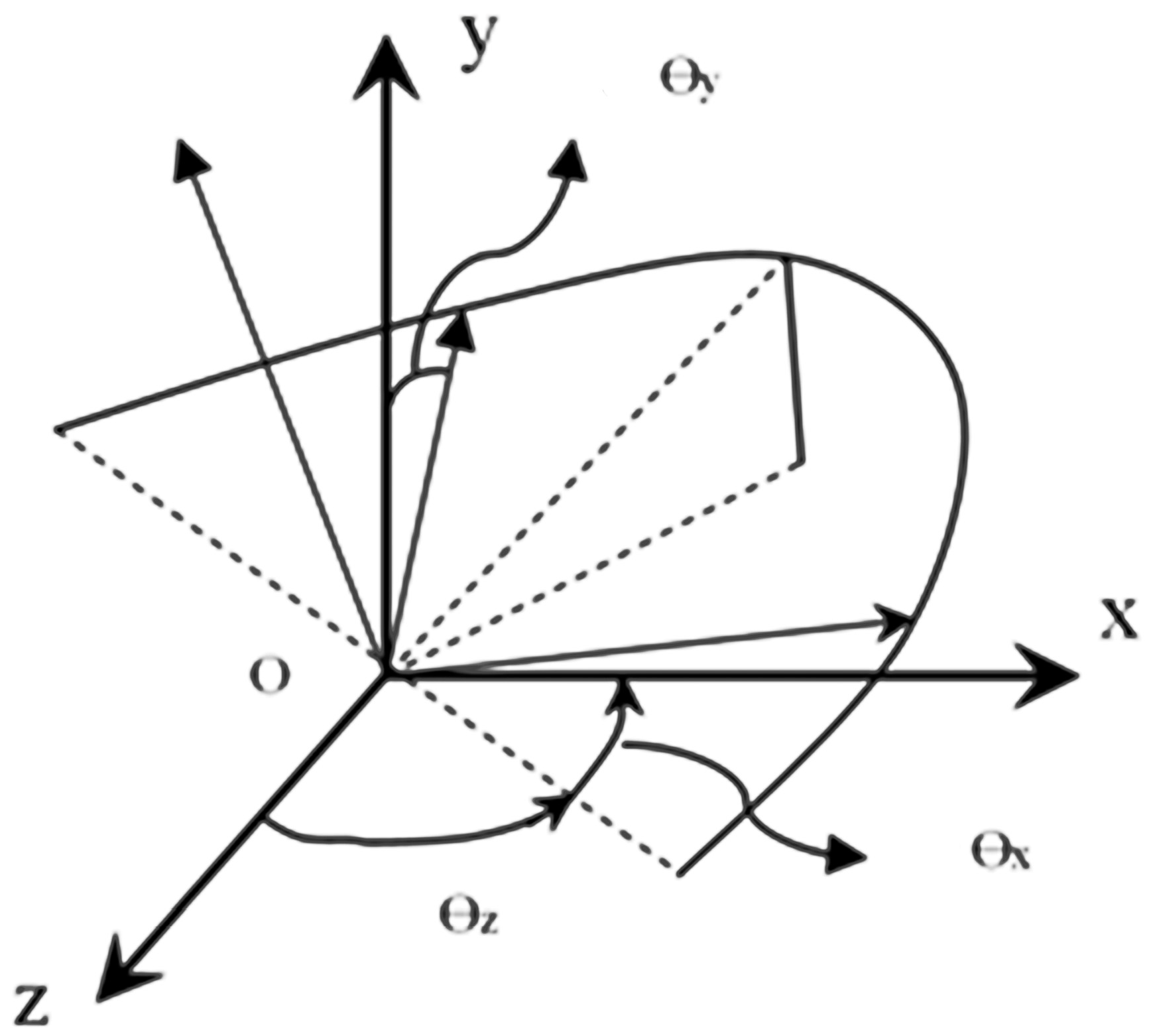
The deformed volume is equal to the product of the undeformed volume dx, dy, dz and a function of the six strain components. The form of this function depends on the physical properties of the dimensions and shape of the body. Alternatively, the strain components can be expressed in terms of the three principal strains ε₁, ε₂, ε₃ and the direction cosines of the principal axes of strain ε₁, ε₂, ε₃ with respect to the X, Y and Z axes. Thus, the direction cosines might be regarded as a function of three independent quantities, the Euler angles (Figure 1) θ, ϕ, Ψ which determine the orientation of the trihedral ε₁, ε₂, ε₃ relative to the trihedral X, Y and Z. Therefore, dA can be written as:

$$dA=\mathrm{\Im }\left({\epsilon }_1,{\epsilon }_2,{\epsilon }_3,\theta ,\phi ,\Psi \right)dxdydz$$

(2)

$$dA=\mathrm{\Im }({\epsilon }_1,{\epsilon }_2,{\epsilon }_3)dxdydz$$

(3)

The three independent invariants ε₁, ε₂, ε₃ are important, as they have a simple physical meaning, individually, in the case of small deformations. The strain components can be expressed by a₀, a₁, a₂ factors, and thus it is more expedient to indicate the work of deformation on an element of an isotropic body as a function of the three invariants a₀, a₁, a₂:

$${{\displaystyle a}}_0={{\displaystyle \epsilon }}_{xx}{{\displaystyle \epsilon }}_{yy}{{\displaystyle \epsilon }}_{zz}-\frac{1}{4}\left({{\displaystyle \epsilon }}_{xx}{{\displaystyle \epsilon }}_{yz}^2+{{\displaystyle \epsilon }}_{yy}{{\displaystyle \epsilon }}_{xz}^2+{{\displaystyle \epsilon }}_{zz}{{\displaystyle \epsilon }}_{xy}^2-{{\displaystyle \epsilon }}_{xy}{{\displaystyle \epsilon }}_{xz}{{\displaystyle \epsilon }}_{yz}\right)$$

(4)

$${{\displaystyle a}}_1={{\displaystyle \epsilon }}_{xx}{{\displaystyle \epsilon }}_{yy}+{{\displaystyle \epsilon }}_{xx}{{\displaystyle \epsilon }}_{zz}+{{\displaystyle \epsilon }}_{yy}{{\displaystyle \epsilon }}_{zz}-\frac{1}{4}({{\displaystyle \epsilon }}_{xy}^2+{{\displaystyle \epsilon }}_{xz}^2+{{\displaystyle \epsilon }}_{yz}^2)={{\displaystyle \epsilon }}_1{{\displaystyle \epsilon }}_2+{{\displaystyle \epsilon }}_1{{\displaystyle \epsilon }}_3+{{\displaystyle \epsilon }}_2{{\displaystyle \epsilon }}_3$$

(5)

$${{\displaystyle a}}_2={{\displaystyle \epsilon }}_{xx}+{{\displaystyle \epsilon }}_{yy}+{{\displaystyle \epsilon }}_{zz}={{\displaystyle \epsilon }}_1+{{\displaystyle \epsilon }}_2+{{\displaystyle \epsilon }}_3$$

(6)

Thus, the induced work by considering the possible deforming of an elementary parallelepiped of an isotropic body can be calculated by:

$$dA=\mathsf{\Phi }\left(a_2,a_1,a_0\right)dxdydz$$

(7)

Therefore, for the entire body:

$$A={\displaystyle \int {\displaystyle \int {\displaystyle \int \mathsf{\Phi }\left(a_2,a_1,a_0\right)dxdydz}}}$$

(8)

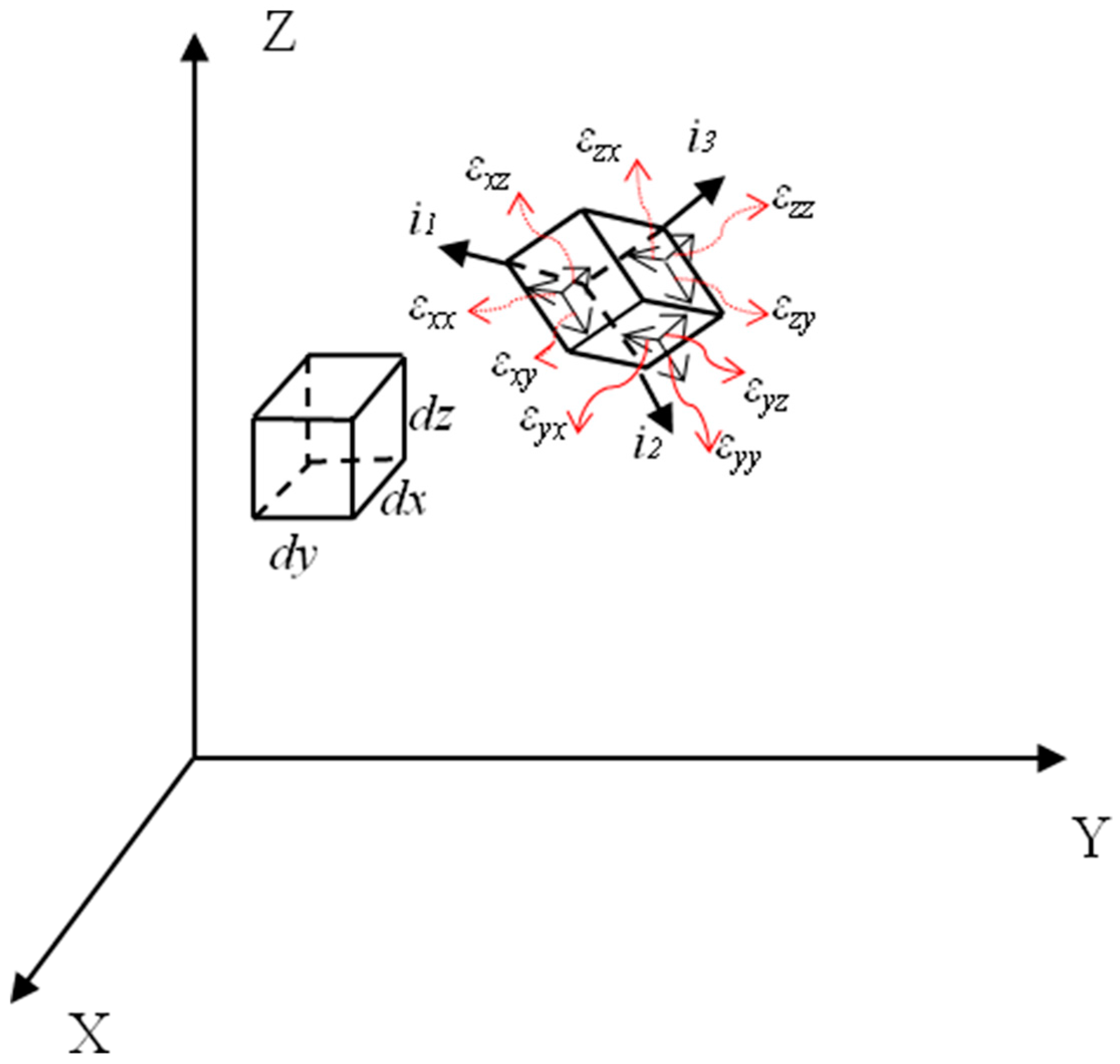
where the integration extends over the volume of the body in its unstrained state, as dxdydz is the volume of an elementary parallelepiped in that state. The function Φ(a₂, a₁, a₀) is the strain energy of a unit volume of the body in its unstrained state, specific strain energy. To calculate all of the possible induced energy inside the entire element due to the different deformations in the different directions, the application of the principle of virtual displacement to a deformed body in a state of equilibrium is considered. The arbitrary vectors including $\overrightarrow{u}\left(x,y,z\right)$, $\overrightarrow{v}\left(x,y,z\right)$ and $\overrightarrow{\omega }\left(x,y,z\right)$ were assigned to the displacements and dξ, dζ, dη are virtual displacement (Figure 2), respectively, which can be considered as arbitrary continuous functions of x, y, z equal to zero at those points where the values of the displacement are known.

Thus, the rate of change strain energy will be in line with δA, where it would be equal to the work done by all the exterior forces applied to the body in affecting the indicated virtual displacement (Figure 3). Thus, δA can be written by:

$$\delta A=\delta R_1+\delta R_2$$

(9)

where δR₁ is the virtual work due to the body forces and δR₂ is the virtual work done by the surface forces. The virtual work done by the body forces is equal to:

$$\delta R_1={\displaystyle \int {\displaystyle \int {\displaystyle \int \left[F_{\xi }^{*}\delta u+F_{\eta }^{*}\delta v+F_{\varsigma }^{*}\delta w\right]}}}Ddxdydz$$

(10)

where $F_{\xi }^{*},F_{\eta }^{*},F_{\zeta }^{*}$ are the components along the X, Y, Z axes of the force referred to as a unit volume of the deformed body, dxdydz is the volume element of the unstrained body, and Ddxdydz = (V*/V)dxdydz is the corresponding volume element of the strained body:

$$\delta R_2={\displaystyle \int \left[f_{\xi }^{*}\delta u+f_{\eta }^{*}\delta v+f_{\varsigma }^{*}\delta w\right]d\Omega \prime }$$

(11)

where $f_{\xi }^{*},f_{\eta }^{*},f_{\zeta }^{*}$ are the components along the X, Y, Z axes of the force acting on a unit area of the surface of the deformed body, while dΩ’ is the differential of the area in the strained state.

To calculate δR₂ over the surface of the body in its strained state, it would be possible to replace dΩ’ in terms of dΩ, the differential of surface area in the unstrained state by considering an elementary rectangular area with sides $d\overrightarrow{a},d\overrightarrow{b}$ on the bounding elementary rectangle has an area equal to d$\overrightarrow{\Omega }=d\overrightarrow{a}\times d\overrightarrow{b}$ and the relevant orientation can be determined by the direction of the unit normal vector ${\overrightarrow{i}}_n=-\frac{d\overrightarrow{a}\times d\overrightarrow{b}}{\left|d\overrightarrow{\Omega }\right|}$. Thus, as a result of the deformation, the rectangular area is transformed into a surface of the deformed body having the form of a parallelogram with sides (1 + E_a)da, (1 + E_b)db. The cosine of the angle formed by these sides is:

$$\cos (da\prime ,db\prime )=\frac{{\overrightarrow{\epsilon }}_{ab}}{(1+E_a)(1+E_b)}=\frac{{\overrightarrow{\epsilon }}_{ab}}{\sqrt{(1+2\times {\overrightarrow{\epsilon }}_{aa})\times (1+2\times {\overrightarrow{\epsilon }}_{bb})}}$$

(12)

where E_a, E_b are the relative elongations in the directions da, db and ε_aa, ε_bb, ε_ab are the corresponding tangential strain components. Therefore, an element on the surface of the strained body has an area equal to:

$$d\Omega \prime =\sqrt{(1+2{\epsilon }_{aa})(1+2{\epsilon }_{bb})-{\epsilon }_{ab}^2}d\Omega =\frac{s_n^{*}}{s_n}d\Omega$$

(13)

The coefficient $\frac{s_n^{*}}{s_n}$ which is equal to the ratio of the elements of area in the terminal and initial states can be expressed in terms of the strain components relative to the X, Y, Z axes and the three direction cosines of the normal to the surface in the unstrained state. Thus, it is necessary to replace the strain components ε_aa, ε_bb, ε_ab in the formula:

$$\frac{s_n^{*}}{s_n}=\sqrt{(1+2{\epsilon }_{aa})(1+2{\epsilon }_{bb})-{\epsilon }_{ab}^2}$$

(14)

by their expressions in terms of ε_xx, …, ε_yz and the direction cosines of da, db and n, then, by considering the relevant transformations:

$$\frac{s_n^{*}}{s_n}=\sqrt{{\gamma }_{xx}{\cos }^2(n,x)+{\gamma }_{yy}{\cos }^2(n,y)+{\gamma }_{zz}{\cos }^2(n,z)+{\gamma }_{xy}\cos (n,x)\cos (n,y)+{\gamma }_{xz}\cos (n,x)\cos (n,z)+{\gamma }_{yz}\cos (n,y)\cos (n,z)}$$

(15)

$$\mathrm{where}{\gamma }_{xx}={\left(\frac{S_x^{*}}{S_x}\right)}^2,{\gamma }_{yy}={\left(\frac{S_y^{*}}{S_y}\right)}^2,{\gamma }_{zz}={\left(\frac{S_z^{*}}{S_z}\right)}^2$$

(16)

$$\frac{1}{2}{\gamma }_{xy}=-{\epsilon }_{xy}+{\epsilon }_{xz}{\epsilon }_{yz}-2{\epsilon }_{xy}{\epsilon }_{zz}$$

(17)

$$\frac{1}{2}{\gamma }_{xz}=-{\epsilon }_{xz}+{\epsilon }_{xy}{\epsilon }_{yz}-2{\epsilon }_{xz}{\epsilon }_{yy}$$

(18)

$$\frac{1}{2}{\gamma }_{yz}=-{\epsilon }_{yz}+{\epsilon }_{xz}{\epsilon }_{xy}-2{\epsilon }_{yz}{\epsilon }_{xx}$$

(19)

and $n\widehat{x},n\widehat{y},n\widehat{z}$ are the direction angles of the normal to the bounding surface in the unstrained state relative to the X, Y, Z axes. The virtual work done by the external surface through the virtual displacements δu, δv, δω is of the form:

$$\delta R_2={\displaystyle \int {\displaystyle \int \left[f_{\xi }^{*}\delta u+f_{\eta }^{*}\delta v+f_{\zeta }^{*}\delta w\right]\frac{S_n^{*}}{S_n}d}\Omega }$$

(20)

where $\left|d\overrightarrow{\Omega }\right|=\left|d\overrightarrow{a}\times d\overrightarrow{b}\right|$ is the area of a surface element in the initial state. Thus, in order to calculate the value δR₂, the integration should be carried out over the surface in the unstrained state. The key parameters $f_{\xi }^{*},f_{\eta }^{*},f_{\zeta }^{*}$ can be also calculated based on the Euler-Bernoulli beam model Ranzi and Gilbert [14]. An analytical method is developed to evaluate shear stress and strain distributions between the engaged surfaces throughout different joint layers by considering the beam theory method in different directions with respect to the different planes, where it can independently calculate shear forces between the different layers and shear strain as well as the curvature distribution along the different layers that have been extracted. The main concept to derive the following equations was extracted from Ranzi and Gilbert [14] and Ranzi et al. [15]. According to Ranzi and Gilbert [14], the cross-sectional (Figure 4) analysis is based on the assumption of the Euler-Bernoulli beam model.

The strain distribution across the section can be calculated by ε = ε_r − y × κ where ε_r is the strain at the reference point (which can be determined at any point), y is the distance between the selected point and location of the neutral axis of the cross-section and κ is the curvature across the section in different strata layers. A vector can be introduced by K(D) which will be included in the internal action N (axial forces) and M (internal moment). External loads, which might be due to the effect of the self-weight of the strata layers as well as the possible applied forces due to the vertical or horizontal displacement in the different layers, can induce the external axial force N_e, external moment M_e and dA is the differentiate of the engaged surfaces. The relationship between the internal and external actions can be presented by:

$$\epsilon =\left[\begin{array}{c}{\epsilon }_r\\ \kappa \end{array}\right]$$

(21)

$$r\left(\epsilon \right)=\left[\begin{array}{c}N\\ M\end{array}\right]$$

(22)

$$r_e=\left[\begin{array}{c}{N}_e\\ M_e\end{array}\right]$$

(23)

$$r\left(\epsilon \right)=r_e,\left(\mathrm{This}\mathrm{is}\mathrm{the}\mathrm{vector}\mathrm{for}\mathrm{strain}\right)$$

(24)

By considering the nonlinear interactions, the presented equations can be re-written by:

$$r\left({\epsilon }^{(i+1)}\right)=r\left({\epsilon }^{(i)}\right)+r_t\left({\epsilon }^{(i)}\right)\times \Delta {\epsilon }^{(i)}=r_e$$

(25)

$$r_t\left({\epsilon }^{(i)}\right)r_t\left({\epsilon }^{(i)}\right)\times \Delta {\epsilon }^{(i)}=r_R^{(i)}$$

(26)

$$\frac{\partial N\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)}{\partial {\epsilon }_r}\times \Delta {\epsilon }_r^{(i)}+\frac{\partial N\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)}{\partial \kappa }\times \Delta \kappa =N_R^{(i)}$$

(27)

$$r_R^{(i)}=r_e-r\left({\epsilon }^{(i)}\right)$$

(28)

$$N_R^{(i)}=N_e-N\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)$$

(29)

$$M_R^{(i)}=M_e-M\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)$$

(30)

All the equations can be re-presented in matrix format:

$$r_t\left({\epsilon }^{(i)}\right)=\left[\begin{array}{cc}\frac{\partial N\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)}{\partial {\epsilon }_r}& \frac{\partial N\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)}{\partial \kappa }\\ \frac{\partial M\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)}{\partial {\epsilon }_r}& \frac{\partial M\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)}{\partial \kappa }\end{array}\right]$$

(31)

$$\Delta {\epsilon }^{(i)}=\left[\begin{array}{c}\Delta {\epsilon }_r^{(i)}\\ \Delta {\kappa }^{(i)}\end{array}\right],(\mathrm{changing}\mathrm{strain}\mathrm{and}\mathrm{curvature})$$

(32)

The partial derivatives of N and M with respect to ε_r and κ can be re-arranged in a:

$$r_R^{(i)}=\left[\begin{array}{c}{N}_R^{(i)}\\ M_R^{(i)}\end{array}\right]$$

(33)

more practical form, recalling the definitions of internal actions as:

$$\frac{\partial N\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)}{\partial {\epsilon }_r}={\displaystyle \int \frac{\partial \sigma }{\partial {\epsilon }_r}d\mathrm{A}}$$

(34)

$$\frac{\partial N\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)}{\partial \kappa }={\displaystyle \int \frac{\partial \sigma }{\partial \kappa }d\mathrm{A}}$$

(35)

$$\frac{\partial M\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)}{\partial {\epsilon }_r}=-{\displaystyle \int y\frac{\partial \sigma }{\partial {\epsilon }_r}d\mathrm{A}}$$

(36)

$$\frac{\partial M\left({\epsilon }_r^{(i)},{\kappa }^{(i)}\right)}{\partial \kappa }=-{\displaystyle \int y\frac{\partial \sigma }{\partial \kappa }d\mathrm{A}}$$

(37)

where the values of the stress depend on the constitutive models adopted for the materials and on the magnitude of the strain [14]:

$$\frac{\partial N({{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial {{\displaystyle \epsilon }}_r}={\displaystyle \int \frac{\partial \sigma }{\partial {{\displaystyle \epsilon }}_r}}d\mathrm{A}={\displaystyle \int \frac{\partial \sigma }{\partial \epsilon }}\times \frac{\partial \epsilon }{\partial {{\displaystyle \epsilon }}_r}d\mathrm{A}={\displaystyle \int \frac{\partial \sigma }{\partial \epsilon }}\times \frac{\partial ({{\displaystyle \epsilon }}_r-y\times \kappa )}{\partial {{\displaystyle \epsilon }}_r}d\mathrm{A}={\displaystyle \int \frac{\partial \sigma }{\partial \epsilon }}d\mathrm{A}$$

(38)

$$\frac{\partial N({{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial \kappa }={\displaystyle \int \frac{\partial \sigma }{\partial \kappa }}d\mathrm{A}={\displaystyle \int \frac{\partial \sigma }{\partial \epsilon }}\times \frac{\partial ({{\displaystyle \epsilon }}_r-y\times \kappa )}{\partial \kappa }d\mathrm{A}=-{\displaystyle \int y\times \frac{\partial \sigma }{\partial \epsilon }}d\mathrm{A}$$

(39)

$$\frac{\partial M({{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial {{\displaystyle \epsilon }}_r}=-{\displaystyle \int y\times \frac{\partial \sigma }{\partial {{\displaystyle \epsilon }}_r}}d\mathrm{A}=-{\displaystyle \int y\times \frac{\partial \sigma }{\partial \epsilon }}\times \frac{\partial ({{\displaystyle \epsilon }}_r-y\times \kappa )}{\partial {{\displaystyle \epsilon }}_r}d\mathrm{A}=-{\displaystyle \int y\times \frac{\partial \sigma }{\partial \epsilon }}d\mathrm{A}$$

(40)

$$\frac{\partial M({{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial \kappa }=-{\displaystyle \int y\times \frac{\partial \sigma }{\partial {{\displaystyle \epsilon }}_r}}d\mathrm{A}=-{\displaystyle \int y\times \frac{\partial \sigma }{\partial \epsilon }}\times \frac{\partial ({{\displaystyle \epsilon }}_r-y\times \kappa )}{\partial \kappa }d\mathrm{A}={\displaystyle \int {{\displaystyle y}}^2\times \frac{\partial \sigma }{\partial \epsilon }}d\mathrm{A}$$

(41)

$$\sigma =E\times \epsilon \mathrm{for}\left|\epsilon \right|\le {\epsilon }_p\left(\mathrm{elastic}\mathrm{strain}\right)$$

(42)

$$\sigma =f_p\mathrm{for}\left|\epsilon \right|>{\epsilon }_p\left(\mathrm{plastic}\mathrm{strain}\right)$$

(43)

$$\frac{\partial \sigma }{\partial \epsilon }=\frac{\partial (E\times \epsilon )}{\partial \epsilon }=E\mathrm{for}\left|\epsilon \right|\le {\epsilon }_p(\mathrm{elastic}\mathrm{strain})$$

(44)

$$\frac{\partial \sigma }{\partial \epsilon }=\frac{\partial ({{\displaystyle f}}_p)}{\partial \epsilon }=0\mathrm{for}\left|\epsilon \right|>{\epsilon }_p(\mathrm{plastic}\mathrm{strain})$$

(45)

$$N({{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})={\displaystyle \int \sigma d\mathrm{A}={\displaystyle \sum _{j=1}^{n_j}\sigma ({{\displaystyle y}}_j}},{{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})\times {\mathrm{A}}_j$$

(46)

$$M({{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})=-{\displaystyle \int y\sigma d\mathrm{A}=-{\displaystyle \sum _{j=1}^{{{\displaystyle n}}_j}{{\displaystyle y}}_j\times \sigma ({{\displaystyle y}}_j}},{{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})\times {\mathrm{A}}_j$$

(47)

$$\frac{\partial N({{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial {{\displaystyle \epsilon }}_r}={\displaystyle \int \frac{\partial \sigma }{\partial \epsilon }}d\mathrm{A}={\displaystyle \sum _{j=1}^{{{\displaystyle n}}_j}\frac{\partial \sigma ({{\displaystyle y}}_j,{{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial \epsilon }}\times {\mathrm{A}}_j$$

(48)

$$\frac{\partial N({{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial \kappa }=-{\displaystyle \int y\times \frac{\partial \sigma }{\partial {{\displaystyle \epsilon }}_r}}d\mathrm{A}=-{\displaystyle \sum _{j=1}^{{{\displaystyle n}}_j}{{\displaystyle y}}_j\times \frac{\partial \sigma ({{\displaystyle y}}_j,{{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial \epsilon }}\times {\mathrm{A}}_j$$

(49)

$$\frac{\partial M({{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial {{\displaystyle \epsilon }}_r}=-{\displaystyle \int y\times \frac{\partial \sigma }{\partial {{\displaystyle \epsilon }}_r}}d\mathrm{A}=-{\displaystyle \sum _{j=1}^{{{\displaystyle n}}_j}{{\displaystyle y}}_j\times \frac{\partial \sigma ({{\displaystyle y}}_j,{{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial \epsilon }}\times {\mathrm{A}}_j$$

(50)

$$\frac{\partial M({{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial \kappa }={\displaystyle \int y^2\times \frac{\partial \sigma }{\partial \epsilon }}d\mathrm{A}={\displaystyle \sum _{j=1}^{{{\displaystyle n}}_j}{{\displaystyle y}}_j^2\times \frac{\partial \sigma ({{\displaystyle y}}_j,{{\displaystyle \epsilon }}_r^{(i)},{{\displaystyle \kappa }}^{(i)})}{\partial \epsilon }}\times {\mathrm{A}}_j$$

(51)

Thus, by calculating stress and strain at the different points at the different layers of the overburden, the internal axial forces as well as internal moments can be calculated. It was assumed that strain energy (A) can be calculated by:

$$A={\displaystyle \int {\displaystyle \int {\displaystyle \int \mathsf{\Phi }\left(a_2,a_1,a_0\right)dxdydz}}}$$

(52)

$$\delta A=\delta {\displaystyle \int {\displaystyle \int {\displaystyle \int \mathsf{\Phi }\left(a_2,a_1,a_0\right)dxdydz}}}={\displaystyle \int {\displaystyle \int {\displaystyle \int \delta \left[\mathsf{\Phi }\left(a_2,a_1,a_0\right)\right]dxdydz}}}$$

(53)

Furthermore:

$$\delta \left[\mathsf{\Phi }\left(a_2,a_1,a_0\right)\right]=\frac{\partial \mathsf{\Phi }}{\partial {\epsilon }_{xx}}\delta {\epsilon }_{xx}+\frac{\partial \mathsf{\Phi }}{\partial {\epsilon }_{yy}}\delta {\epsilon }_{yy}+\frac{\partial \mathsf{\Phi }}{\partial {\epsilon }_{zz}}\delta {\epsilon }_{zz}+\frac{\partial \mathsf{\Phi }}{\partial {\epsilon }_{xy}}\delta {\epsilon }_{xy}+\frac{\partial \mathsf{\Phi }}{\partial {\epsilon }_{xz}}\delta {\epsilon }_{xz}+\frac{\partial \mathsf{\Phi }}{\partial {\epsilon }_{yz}}\delta {\epsilon }_{yz}$$

(54)

where, in accordance with the former equations and substituting for a₀, a₁ and a₂ according to Equations (4)–(6),

$$\frac{\partial \mathsf{\Phi }}{\partial {\epsilon }_{xx}}=\frac{\partial \mathsf{\Phi }}{\partial a_2}\frac{\partial a_2}{\partial {\epsilon }_{xx}}+\frac{\partial \mathsf{\Phi }}{\partial a_1}\frac{\partial a_1}{\partial {\epsilon }_{xx}}+\frac{\partial \mathsf{\Phi }}{\partial a_0}\frac{\partial a_0}{\partial {\epsilon }_{xx}}=\frac{\partial \mathsf{\Phi }}{\partial a_2}+\frac{\partial \mathsf{\Phi }}{\partial a_1}\left({\epsilon }_{yy}+{\epsilon }_{zz}\right)+\frac{\partial \mathsf{\Phi }}{\partial a_0}\left({\epsilon }_{yy}{\epsilon }_{zz}-\frac{1}{4}{\epsilon }_{yz}^2\right)$$

(55)

and similarly for ε_yy and ε_zz, furthermore:

$$\frac{\partial \mathsf{\Phi }}{\partial {\epsilon }_{xy}}=\frac{\partial \mathsf{\Phi }}{\partial a_2}\frac{\partial a_2}{\partial {\epsilon }_{xy}}+\frac{\partial \mathsf{\Phi }}{\partial a_1}\frac{\partial a_1}{\partial {\epsilon }_{xy}}+\frac{\partial \mathsf{\Phi }}{\partial a_0}\frac{\partial a_0}{\partial {\epsilon }_{xy}}=-\frac{1}{2}\frac{\partial \mathsf{\Phi }}{\partial a_1}{\epsilon }_{xy}+\frac{1}{2}\frac{\partial \mathsf{\Phi }}{\partial a_0}\left(\frac{1}{2}{\epsilon }_{xx}{\epsilon }_{yz}-{\epsilon }_{xy}{\epsilon }_{zz}\right)$$

(56)

and similarly for ε_xz and ε_yz. Moreover, by taking into account:

$$\begin{array}{l}\delta \left({\epsilon }_{xx}\right)=\left(1+\frac{\partial u}{\partial x}\right)\delta \left(\frac{\partial u}{\partial x}\right)+\frac{\partial v}{\partial x}\delta \left(\frac{\partial v}{\partial x}\right)+\frac{\partial w}{\partial x}\delta \left(\frac{\partial w}{\partial x}\right)=\left(1+e_{xx}\right)\frac{\partial \left(\delta u\right)}{\partial x}\\ +\left(\frac{1}{2}{e}_{xy}+w_z\right)\frac{\partial \left(\delta v\right)}{\partial x}+\left(\frac{1}{2}{e}_{xz}-w_y\right)\frac{\partial \left(\delta w\right)}{\partial x}\end{array}$$

(57)

and similarly for ε_yy and ε_zz, furthermore:

$$\begin{array}{l}\delta \left({\epsilon }_{xy}\right)=\frac{\partial u}{\partial y}\delta \left(\frac{\partial u}{\partial x}\right)+\left(1+\frac{\partial v}{\partial y}\right)\delta \left(\frac{\partial v}{\partial x}\right)+\left(\frac{\partial w}{\partial y}\right)\delta \left(\frac{\partial w}{\partial x}\right)+\left(1+\frac{\partial u}{\partial x}\right)\delta \left(\frac{\partial u}{\partial y}\right)\\ +\frac{\partial v}{\partial x}\delta \left(\frac{\partial v}{\partial y}\right)+\frac{\partial w}{\partial x}\delta \left(\frac{\partial w}{\partial y}\right)=\left(\frac{1}{2}{e}_{xy}-w_z\right)\frac{\partial \left(\delta u\right)}{\partial x}+\left(1+e_{yy}\right)\frac{\partial \left(\delta v\right)}{\partial x}+\left(\frac{1}{2}{e}_{yz}+w_x\right)\frac{\partial \left(\delta w\right)}{\partial x}\\ +\left(1+e_{xx}\right)\frac{\partial \left(\delta u\right)}{\partial y}+\left(\frac{1}{2}{e}_{xy}+w_z\right)\frac{\partial \left(\delta v\right)}{\partial y}+\left(\frac{1}{2}{e}_{xz}-w_y\right)\frac{\partial \left(\delta w\right)}{\partial y}\end{array}$$

(58)

and similarly for ε_xz and ε_yz. And by substituting these values of $\delta ({\epsilon }_{xx}),\dots ,\delta ({\epsilon }_{yz})$:

$$\begin{array}{l}\delta \left[\mathsf{\Phi }\left(a_2,a_1,a_0\right)\right]=\frac{\partial \mathsf{\Phi }}{\partial u_x}\frac{\partial \left(\delta u\right)}{\partial x}+\frac{\partial \mathsf{\Phi }}{\partial u_y}\frac{\partial \left(\delta u\right)}{\partial y}+\frac{\partial \mathsf{\Phi }}{\partial u_z}\frac{\partial \left(\delta u\right)}{\partial z}\\ +\frac{\partial \mathsf{\Phi }}{\partial v_x}\frac{\partial \left(\delta v\right)}{\partial x}+\frac{\partial \mathsf{\Phi }}{\partial v_y}\frac{\partial \left(\delta v\right)}{\partial y}+\frac{\partial \mathsf{\Phi }}{\partial v_z}\frac{\partial \left(\delta v\right)}{\partial z}+\frac{\partial \mathsf{\Phi }}{\partial w_x}\frac{\partial \left(\delta w\right)}{\partial x}+\frac{\partial \mathsf{\Phi }}{\partial w_y}\frac{\partial \left(\delta w\right)}{\partial y}+\frac{\partial \mathsf{\Phi }}{\partial w_z}\frac{\partial \left(\delta w\right)}{\partial z}\end{array}$$

(59)

$$\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle u}}_x}=\frac{\partial \mathsf{\Phi }}{\partial (\frac{\partial u}{\partial x})}=(1+{{\displaystyle e}}_{xx})\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle \epsilon }}_{xx}}+(\frac{1}{2}{{\displaystyle e}}_{xy}-{{\displaystyle \omega }}_z)\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle \epsilon }}_{xy}}+(\frac{1}{2}{{\displaystyle e}}_{xx}+{{\displaystyle \omega }}_y)\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle \epsilon }}_{xz}}$$

(60)

$$\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle v}}_x}=\frac{\partial \mathsf{\Phi }}{\partial (\frac{\partial v}{\partial x})}=(\frac{1}{2}{{\displaystyle e}}_{xy}+{{\displaystyle \omega }}_z)\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle \epsilon }}_{xx}}+(1+{{\displaystyle e}}_{yy})\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle \epsilon }}_{xy}}+(\frac{1}{2}{{\displaystyle e}}_{yz}-{{\displaystyle \omega }}_x)\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle \epsilon }}_{xz}}$$

(61)

$$\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle \omega }}_x}=\frac{\partial \mathsf{\Phi }}{\partial (\frac{\partial \omega }{\partial x})}=(\frac{1}{2}{{\displaystyle e}}_{xz}-{{\displaystyle \omega }}_y)\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle \epsilon }}_{xx}}+(\frac{1}{2}{{\displaystyle e}}_{yz}+{{\displaystyle \omega }}_x)\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle \epsilon }}_{xy}}+(1+{{\displaystyle e}}_{zz})\frac{\partial \mathsf{\Phi }}{\partial {{\displaystyle \epsilon }}_{xz}}$$

(62)

and similarly for u_y, u_z; v_y, v_z and w_y, w_z. Thus, the strain energy (A) can be calculated by:

$$A=\frac{1}{2}\times {\displaystyle \iiint ({{\displaystyle \sigma }}_{xx}\times {{\displaystyle \epsilon }}_{xx}}+{{\displaystyle \sigma }}_{yy}\times {{\displaystyle \epsilon }}_{yy}+{{\displaystyle \sigma }}_{zz}\times {{\displaystyle \epsilon }}_{zz}+{{\displaystyle \sigma }}_{xy}\times {{\displaystyle \epsilon }}_{xy}+{{\displaystyle \sigma }}_{xz}\times {{\displaystyle \epsilon }}_{xz}+{{\displaystyle \sigma }}_{yz}\times {{\displaystyle \epsilon }}_{yz})dxdydz$$

(63)

where σ_xx × ε_xx, …, σ_yz × ε_yz (Figure 5) can be calculated according to the principal of the virtual work and virtual deformation δA = δR₁ + δR₂ when the induced stresses and strains cannot be directly extracted from the simulated model.

3. Calculating the Released Energy

Initially, in order to calculate the released energy, an assumption was made based on the principle of thermodynamics. The accuracy of the assumption is validated in line with the analytical model validation. Provided that there is an exponential relationship between the changing rate of the released energy as well as the changing rate of the strain energy and the joint density per unit volume of a sample, thus α is the significant coefficient where it can represent the rating of the differences between the released and strain energy over the changing rate of the strain energy with respect to the total strain:

$$\left({\epsilon }_{tot}=\sqrt{\left({\epsilon }_{xx}^2+{\epsilon }_{yy}^2+{\epsilon }_{zz}^2\right)}\right)$$

(64)

$$D=e^{\frac{\alpha }{\Psi }}$$

(65)

$$\alpha =\frac{\left(\frac{\partial \left(\frac{\Delta A-\Delta E_{released}}{\Delta {\epsilon }_{tot}}\right)}{\partial {\epsilon }_{tot}}\right)}{\frac{\partial \left(\frac{\Delta A}{\Delta {\epsilon }_{tot}}\right)}{\partial {\epsilon }_{tot}}}$$

(66)

It can be represented by:

$$D=exp\left(\frac{1}{\Psi }\times \left(1-\frac{\frac{\partial \left(\frac{E_{release{d}_i}-E_{release{d}_{i-1}}}{\Delta {\epsilon }_{tot}}\right)}{\partial {\epsilon }_{tot}}}{\frac{\partial \left(\frac{A_i-A_{i-1}}{\Delta {\epsilon }_{tot}}\right)}{\partial {\epsilon }_{tot}}}\right)\right)$$

(67)

where A is the strain energy and $A_i$, $A_{i-1}$ are the strain energy in the different increments, $\Psi$ is the damping factor $\left(0.1\le \Psi \le 0.25\right)$ and D is the joint density per unit volume of the sample. Also, $E_{release{d}_i}$ and $E_{release{d}_{i-1}}$ are the released energy in the different increments. Besides, ${\epsilon }_{tot}=\sqrt{\left({\epsilon }_{xx}^2+{\epsilon }_{yy}^2+{\epsilon }_{zz}^2\right)}$ where it is the strain component in all of the directions. Thus, we have:

$$\ln \left(D\right)=\left(\frac{1}{\Psi }\times \left(1-\frac{\frac{\partial \left(\frac{E_{release{d}_i}-E_{release{d}_{i-1}}}{\Delta {\epsilon }_{tot}}\right)}{\partial {\epsilon }_{tot}}}{\frac{\partial \left(\frac{A_i-A_{i-1}}{\Delta {\epsilon }_{tot}}\right)}{\partial {\epsilon }_{tot}}}\right)\right)$$

(68)

Furthermore, it is clear that:

$$\begin{array}{l}\frac{\partial \left(E_{released}\right)}{\partial {\epsilon }_{tot}}=\frac{\left(E_{release{d}_i}-E_{release{d}_{i-1}}\right)}{\Delta {\epsilon }_{tot}} \mathrm{and} \frac{\partial \left(A\right)}{\partial {\epsilon }_{tot}}=\frac{\left(A_i-A_{i-1}\right)}{\Delta {\epsilon }_{tot}}\\ \mathrm{if} \Delta {\epsilon }_{tot}\to 0\end{array}$$

(69)

$$\ln \left(D\right)=\frac{1}{\Psi }\times \left(1-\frac{\frac{{\partial }^2{E}_{released}}{\partial {\epsilon }_{tot}^2}}{\frac{{\partial }^{2}A}{\partial {\epsilon }_{tot}^2}}\right)$$

(70)

$$\ln \left(D\right)\times \Psi \times \frac{{\partial }^{2}A}{\partial {\epsilon }_{tot}^2}=\frac{{\partial }^{2}A}{\partial {\epsilon }_{tot}^2}-\frac{{\partial }^2{E}_{released}}{\partial {\epsilon }_{tot}^2}$$

(71)

$${\displaystyle \int \ln \left(D\right)\times \Psi \times \frac{{\partial }^{2}A}{\partial {\epsilon }_{tot}^2}d{\epsilon }_{tot}}={\displaystyle \int \frac{{\partial }^{2}A}{\partial {\epsilon }_{tot}^2}d{\epsilon }_{tot}}-{\displaystyle \int \frac{{\partial }^2{E}_{released}}{\partial {\epsilon }_{tot}^2}d{\epsilon }_{tot}}$$

(72)

$$\ln \left(D\right)\times \Psi \times \frac{\partial A}{\partial {\epsilon }_{tot}}+C_1=\frac{\partial A}{\partial {\epsilon }_{tot}}-\frac{\partial E_{released}}{\partial {\epsilon }_{tot}}+C_2$$

(73)

Provided that we assume that the constant values are C₁ = 0, C₂ = 0 based on the initial conditions:

$$\ln \left(D\right)\times \Psi \times \frac{\partial A}{\partial {\epsilon }_{tot}}=\frac{\partial A}{\partial {\epsilon }_{tot}}-\frac{\partial E_{released}}{\partial {\epsilon }_{tot}}$$

(74)

By integrating in both parts of the equations:

$$\ln \left(D\right)\times \Psi \times {\displaystyle \int \frac{\partial A}{\partial {\epsilon }_{tot}}d{\epsilon }_{tot}}={\displaystyle \int \frac{\partial A}{\partial {\epsilon }_{tot}}d{\epsilon }_{tot}}-{\displaystyle \int \frac{\partial E_{released}}{\partial {\epsilon }_{tot}}d{\epsilon }_{tot}}$$

(75)

$$\mathrm{Therefore},\ln \left(D\right)\times \Psi \times A+C_3=A-E_{released}+C_4$$

(76)

Provided that we assume that the constant values are C₃ = 0, C₄ = 0 based on the initial:

$$\ln \left(D\right)\times \Psi \times A=A-E_{released}\mathrm{or}\frac{E_{released}}{A}=\left(1-\Psi \times \ln \left(D\right)\right)$$

(77)

Equation (77) is the significant equation to calculate the amount of the released energy based on the value of the strain energy. The suggested equation can indicate the relationship between the released energy as well as the strain energy due to different joint density per unit volume of a sample as well as the damping coefficient. Developing the current equation is the major contribution of the paper. It can also help calculate the amount of the released/dissipated energy as well as help determine zones of high risk of coal bursts.

4. Validation of the Suggested Analytical Approach

A discrete element method, using commercial package 3DEC, has been developed to validate the proposed analytical method. A number of coal samples of different sizes (a cubic coal sample ranging from 1 m × 1 m × 1 m to 15 m × 15 m × 15 m) as well as different joint and cleat density have been numerically examined. A Mohr-Coulomb (MC) material that presents a constant strength after failure and a Mohr-Coulomb strain-softening material that can reach the peak strength and then decrease to a residual strength have been considered. A Coulomb Slip (CS) joint interface property was considered to simulate the interface properties between the engaged surfaces.

Table 1. Coal and joint properties.

Material	Young’s Modulus (GPa)		Cohesion (MPa)		Friction Angle (°)		Plastic Strain
		Material	Peak	Residual	Peak	Residual
		Coal
		Poisson’s Ratio
Coal	2.5	0.3	1.1	0.1	25	12	0.012
Joint Properties	Normal stiffness = 100 GPa/m, Shear stiffness = 50 GPa/m Cohesion = 0.5 MPa, Internal friction angle = 30°

presents the available coal as well as the developed joint properties.

A quasi-static loading as a velocity was applied on the top and bottom of the model. The velocity slowly applied to the model to represent a relatively loading system to promote a model of a coal failure that progresses gradually. Simulating the acceptable loading condition is significantly important to soundly obtain a better understanding of the structural performance of a single coal mass the quasi-static loading conditions. No boundary and restrain conditions were applied around the lateral sides of the simulated cubes. Figure 6 illustrates a typical coal cubic sample with different density (a cubic coal sample ranging from 1 m × 1 m × 1 m to 15 m × 15 m × 15 m). As the number of the crossed joint sets increases, the role of the joint properties becomes more critical.

5. Discussion of the Results

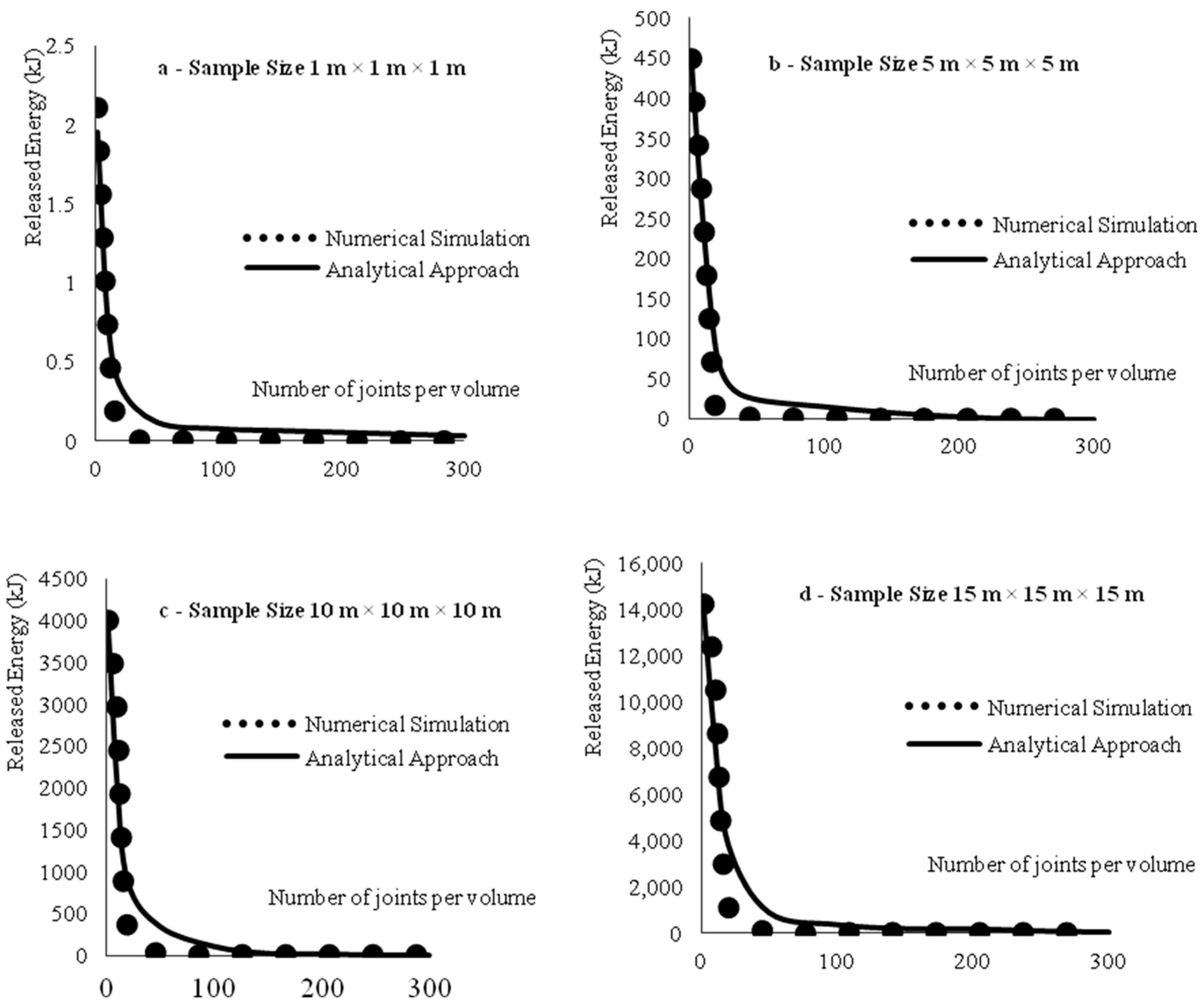
Figure 7 presents the estimated amount of released energy in different coal samples with different joint densities using both the analytical and numerical methods. As illustrated, there is a good agreement between the numerical and analytical solutions. As the number of joints increases, the amount of the released energy in the simulated coal samples significantly decreases. This is due to the effect of the physical and damping interaction between the engaged surfaces of the joints which creates an internal released energy. It is also found that by increasing the number of joints, the global integrity of the simulated samples is considerably reduced, which may lead to reducing the amount of released energy in the coal.

Existing rock and coal discontinuities can seriously affect the mechanical properties of coal materials. Research on the behaviour of coal discontinuities has been carried out in line with studies of the behaviour of coal properties. Knowledge of the behaviour of geological discontinuities such as joints and faults is essential for understanding slip-type coal bursts. One important aspect of the behaviour of a joint is its deformability. The discussed approach can lead to a sound understanding of the impact of coal local mechanical properties on energy released or absorbed. 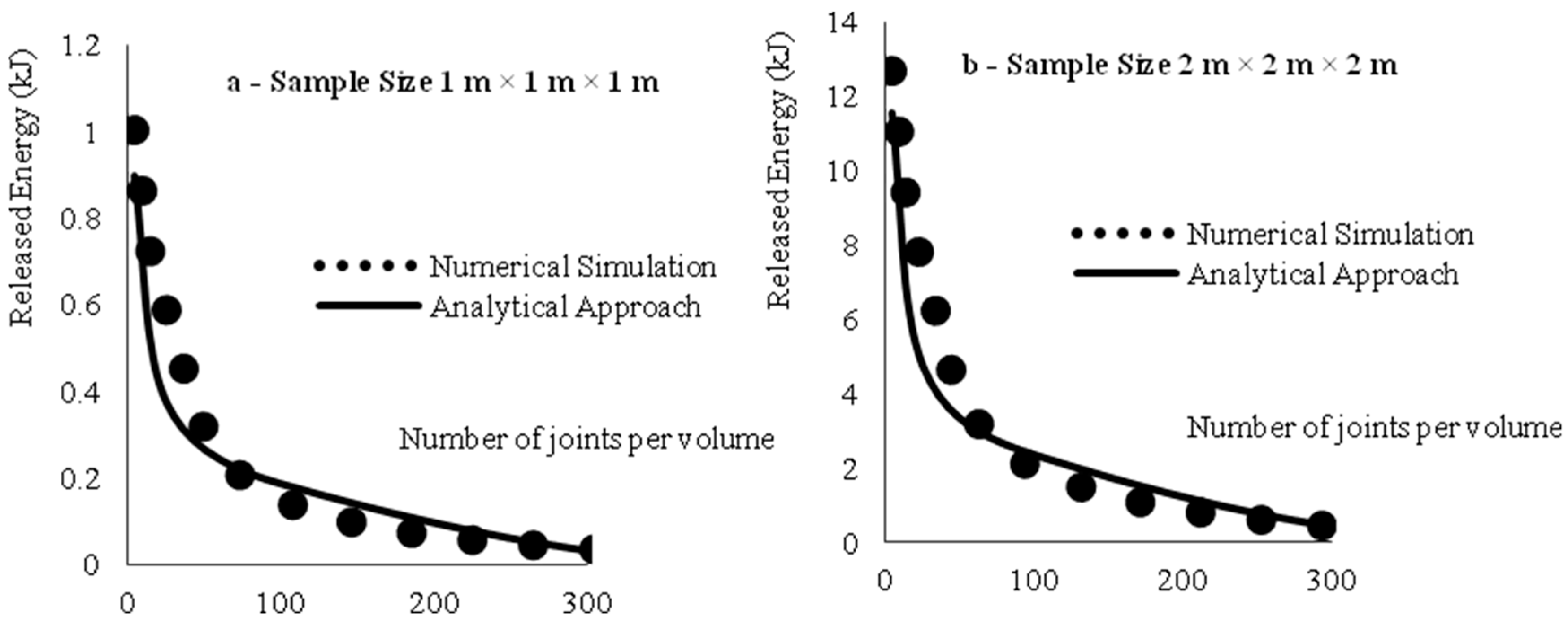Figure 8 presents a comparison between the suggested analytical solution and the numerical simulation while considering different crossed joint set densities.

Based on the observed results from Figure 6, a proper agreement can be found between the discussed analytical solution and the numerical simulation. More realistic and complex conditions, such as multiple, intersecting coal discontinuities under the influence of sequential mining operations, can also be studied based on the established methodologies and validated numerical program. By comparing the single joint results against crossed joints, it is shown that the developed analytical model has better prediction for the crossed joints condition. As the density of the joints increases in multiple directions, the condition in the numerical models comes close to the proposed assumption in the suggested closed form solution. According to the inductive approach, it proves the reliability of the initial hypothesis where there is an exponential relationship between the changing rate of the released energy as well as the changing rate of the strain energy and the joint density per unit volume of a sample. The current research developed a number of innovative analytical and numerical techniques and has advanced the current knowledge of energy calculations applied to coal bursts. In general, energy release in coal mining can occur passively in the form of heat and sound or dynamically in the form of coal bursts. The sudden energy release values are related to the energy changes in the materials that take place between mining steps. For the vast majority of elements, energy changes are associated with changes in the element’s stress and deformation state while staying on the same material curve.

It was also hypothesised that energy calculations may provide a strong extrapolative capability to determine the possible location and timing of a coal burst. However, from past experiences documented in the literature, it appears that coal burst prediction based on energy calculations has practical limitations due to the extreme sensitivity of the energy calculations to the value of uncertain input parameters. This sensitivity of the calculated energy results to the input properties of the geologic material may reflect the true situation underground where small anomalies in geology or rock properties may ultimately determine the precise location and timing of coal burst. Nevertheless, this sensitivity of the energy calculations to uncertain material properties appears to be a practical limitation to forecasting coal bursts using calculated energy values. Obtaining sufficient geological data, such as properties of roof and floor strata, stress fields and properties and locations of existing rock discontinuities, can improve the quality of analyses of unstable failures in underground mining. Due to the lack of relevant geological data, performing an analytical and a numerical simulation can be classified as a good tool to improve the understanding of rock and coal mass behaviour against possible abnormal loading. The established methodologies can be extended in more detail in three-dimensional modelling. With three-dimensional models, back analyses of unstable failures in historical cases can be performed to calibrate the parameters in the models. The calibrated models may be able to provide useful information about possible locations and intensities of unstable failures in future mining operations and prevent serious coal bursts from occurring. Different coal burst proneness indexes were suggested by different researchers [16]. Xie et al. [16] indicated that dissipated and released energy can play a significant role. A sudden release of the strain energy may lead to a catastrophic failure, which clearly indicates a certain condition where the coal mass collapses. Based on the failure mechanism, the fracture procedure of a coal mass might be started from a partial fracture which would be followed by local damage. This procedure will be finally resulting in collapsing the mining structures. The failure process is thermodynamically permanent, which includes released and dissipated energy. By calculating released energy, it is possible to calculate the amount of dissipated energy which can help calculate different energy index impact factors. This is a significant step towards forecasting coal burst-prone zones and reducing threats to safety and production.

6. Conclusions

This paper has analytically assessed the effect of joint densities on consistently predicting the energy released and dissipated in a coal mass. A precise closed form solution was developed to analytically determine the key aspects to calculate the released energy in a coal sample due to a possible applied high stress condition. The developed analytical approach was validated by comparing the simulated results from the discrete element code using three-dimensional modelling. The suggested analytical model to calculate the released energy is a function of the strain energy and damping as well as the joint density per volume of the coal sample. A two-dimensional closed form solution was also developed to calculate the in-plane shear stress and strain between the different joint layers. A comprehensive three-dimensional analytical method was suggested to calculate strain energy based on the virtual work. The suggested analytical solution to calculate strain energy is independent of access to stress and strain in different increments. The major contribution of the current research is to combine two different analytical methods to calculate the released energy in a coal mass due to the different joint density per unit of volume. Analytical methods are an important part of coal burst evaluation and forecasting. Identifying coal burst-prone zones in underground excavations is important to properly estimate the in situ stress state of the rock mass and the mining-induced stress changes, as well as released and dissipated energy. Analytical forecasting methods, either alone or combined with numerical simulations, can be used to estimate both in situ stress and induced stress, which leads to the prediction of failure-prone areas and calculation of critical values of the energies.