3.1. J-Tube and Cable Parameters
The design parameters of the submarine cable considered in this research are given in
Table 1. They are based on a 630 mm
2, 64/110 kV single-core XLPE insulated cable, which is often used in Chinese OWF export systems [
10,
11]. Only one phase of the export circuit is modeled. Within the modeled cable, heat is generated in the conductor, dielectric, sheath, and armoring [
12]. These heat sources are defined according to IEC 60287-1 [
13]. The sheath and armoring loss factor values are 0.4095 and 1.2703, respectively, with a dielectric loss of 1.4219 W/m.
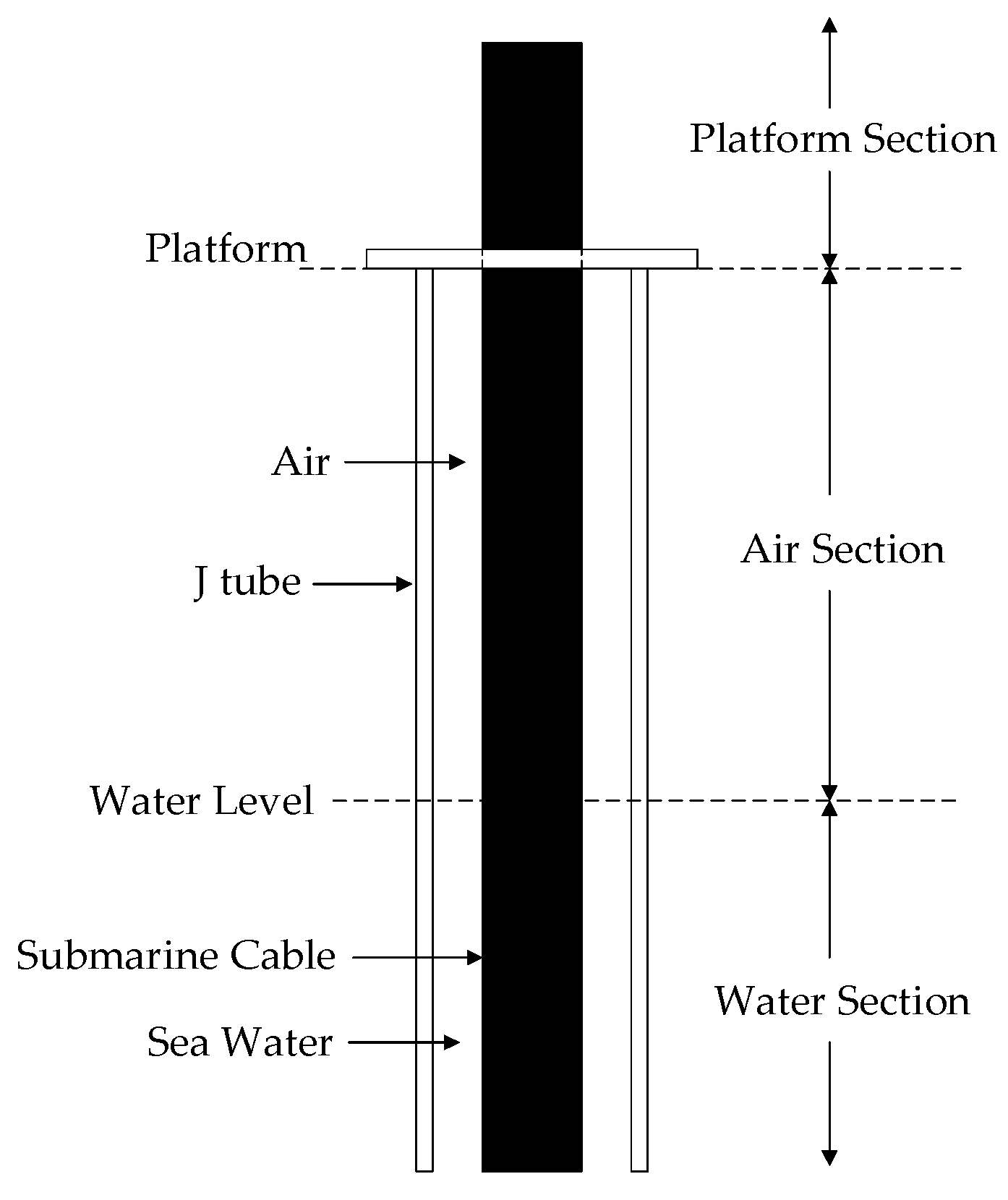
The structure of the J-tube is shown in
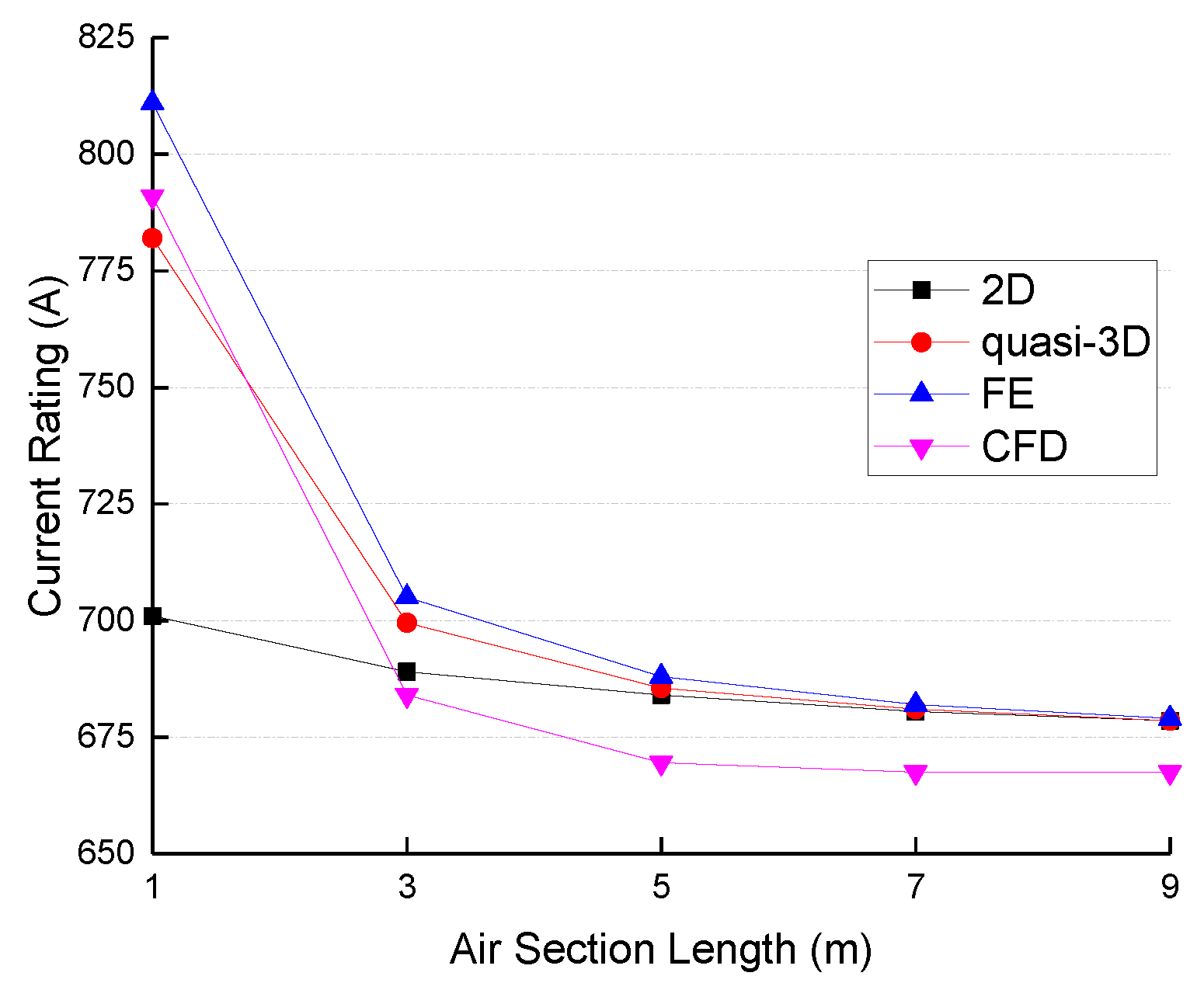
Figure 1. In the models, the length of the air section (Lair) varies from 1 m to 9 m, while the lengths of the water section and the platform section are set at 5 m. The inner radius of the J-tube is twice the outer radius of the cable. The J-tube is of steel construction and is 15 mm thick, with a thermal conductivity of 18 W·m
−1·K
−1, thus the outer diameter of the J-tube (Do) is 261.6 mm. The platform has a short thickness (0.3 m) and large areas for heat dissipation to the ambient air. Thus, it was not modeled in [
4] due to its negligible impact on the overall thermal profile, and it is modeled in this study as a vertical annulus with the same material and outer diameter as the J-tube.
3.2. Enclosed J-Tube Model
The CFD analysis of the enclosed J-tube system needs to consider the thermo-fluid phenomena involving heat conduction, radiation, convection, conjugate heat transfer between the solid and fluid elements, and buoyancy.
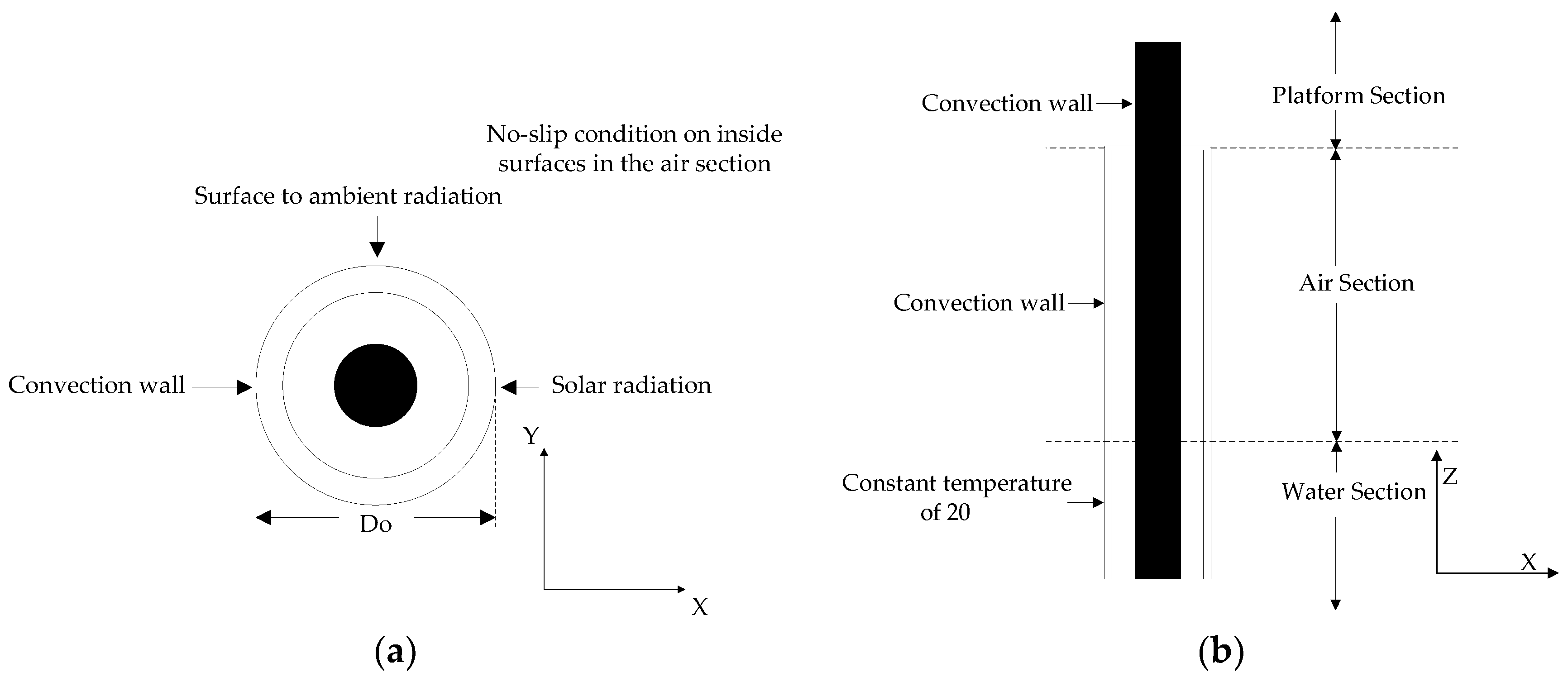
In order to save the computing time that is needed to solve the external flow field, the air outside the J-tube is not included in the computational domain, with the interaction with the external air handled via boundary CHTCs. The computational domain is shown in
Figure 2.
Conduction is assumed to be the only heat transfer mode within the cable and the J-tube. In particular, for the water section (similar to [
4]), the inside seawater is thermally assumed to be a solid, with a thermal conductivity of 0.58 W·m
−1·K
−1, and the J-tube’s external surface is assumed to be at a constant temperature of 293 K (20 °C). Besides, the ambient air temperature (
Tamb, K) is set to be 298 K in winter, 303 K in spring and autumn, and 308 K in summer, respectively.
For the air section, the radiation exchanges between the walls inside the annular enclosure are evaluated by setting up the surface to surface (S2S) radiation model, in which the energy exchange parameters are accounted for by a geometric function, called the “view factor” [
14]. The surface emissivity values are taken to be 0.9 and 0.7 for the cable surface and J-tube, respectively.
The natural flow in the air enclosure is expected to be turbulent, since the Rayleigh number based on the air section length is estimated to be larger than 10
9 [
15]. The inside turbulent flow is modeled by the Reynolds-averaged Navier-Stokes (RANS) equations for conservation of momentum and the continuity equation for conservation of mass [
16]. Although many different turbulence models exist, the standard
k-
ε model [
16] is chosen to predict the turbulent effects. This is because the standard
k-
ε model achieves a good balance between the computing time and accuracy, while many other models, such as the SST-k-omega model, require enormous computer resources. It has also been demonstrated in [
17] that the standard
k-
ε model can predict results with fairly good accuracy in the case of a tall vertical cavity with inside turbulent flow and surface to surface radiation, which is very similar to an enclosed J-tube.
The Boussinesq approximation is applied to model buoyancy effects inside the J-tube. It is valid due to the small temperature difference Δ
T (K) between two vertical walls (less than 35 K in this study) [
18], that is
where
β is the thermal expansion coefficient (K
−1). The buoyancy reference temperature and air properties are evaluated at the mean air temperature, which is obtained iteratively from the CFD solutions with initially estimated values.
In addition, the flow near the solid-fluid interfaces inside the J-tube is modeled using the wall function from [
19,
20], and these surfaces are modeled as no-slip walls, that is
where
u is the velocity in X direction (m/s);
v is the velocity in Y direction (m/s); and,
w is the velocity in Z direction (m/s).
The boundary-layer meshing technique is also used to ensure enough grid density within the boundary layers.
The dimensionless local cable CHTC
hc,loc (W·m
−2·K
−1) and radiative heat transfer coefficient (RHTC)
hr,loc (W·m
−2·K
−1) are defined as
where
T is the fluid temperature (K);
Th is the local cable surface temperature (K);
Tc is the local J-tube inside surface temperature (K); and,
qr is the cable radiative heat flux (W/m
2).
The final step is defining the boundary conditions that are imposed on external surfaces above the sea level.
Modeling of the surface to ambient radiation is also achieved with the S2S radiation model.
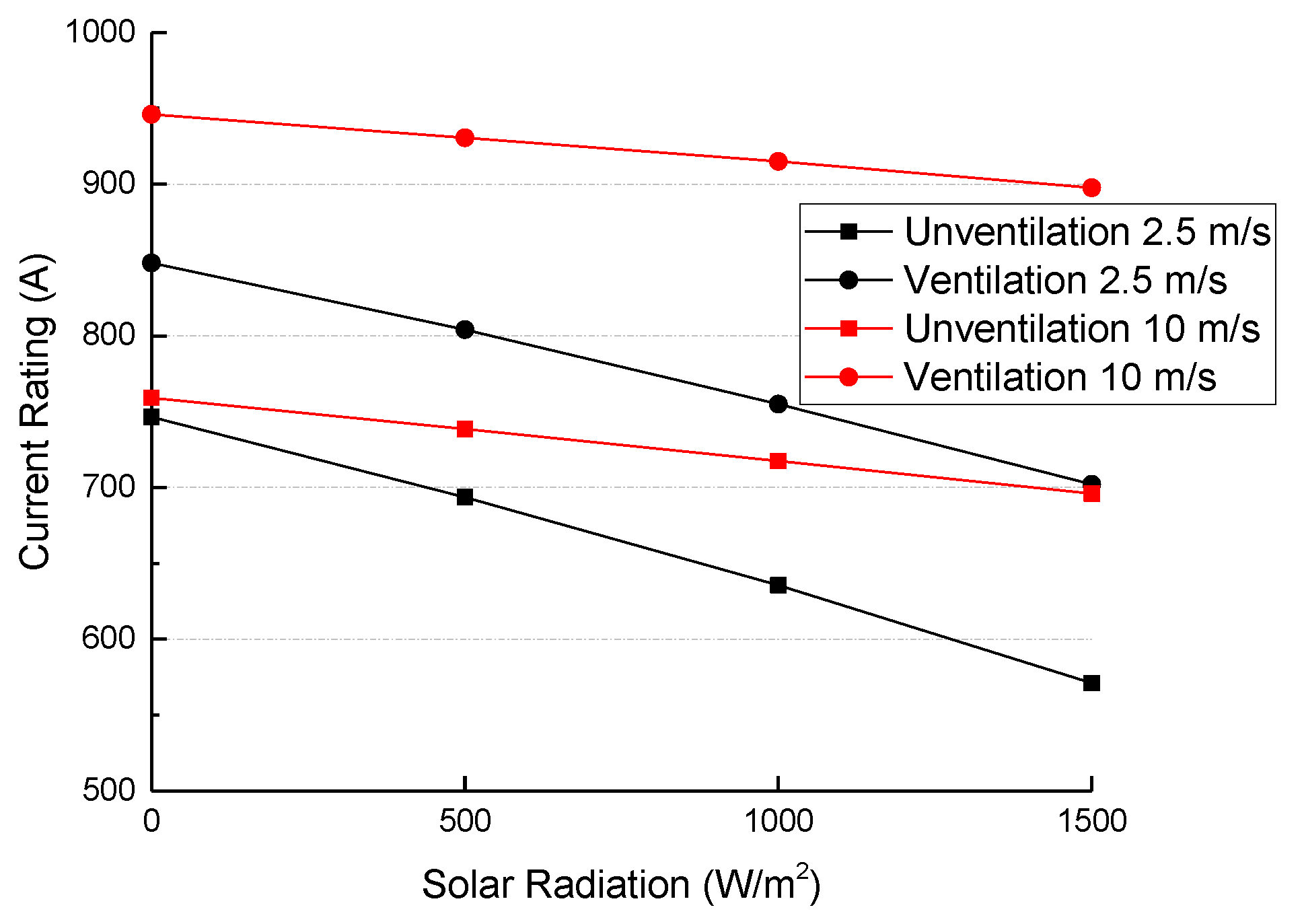
The effect of solar radiation is modeled by boundary heat sources distributed uniformly on the external surfaces, that is,
where
qb is the boundary heat source (W/m
2);
α0 (dimensionless) is the absorptivity to solar radiation, which is assumed to be 0.95 for all external surfaces;
qsun (W/m
2) is the solar flux, which is set to be 1000 W/m
2 according to IEC 60287-2 [
21]; and, the additional 0.5 term is used since the solar flux can only affect half of the surface due to shadow.
Equivalent average CHTCs
hcomb (W·m
−2·K
−1) is applied to external surfaces, that is
where
hnc (W·m
−2·K
−1) and
hfc (W·m
−2·K
−1) are the heat transfer coefficients for natural convection and forced convection, respectively. The calculation methods can be found in [
6].
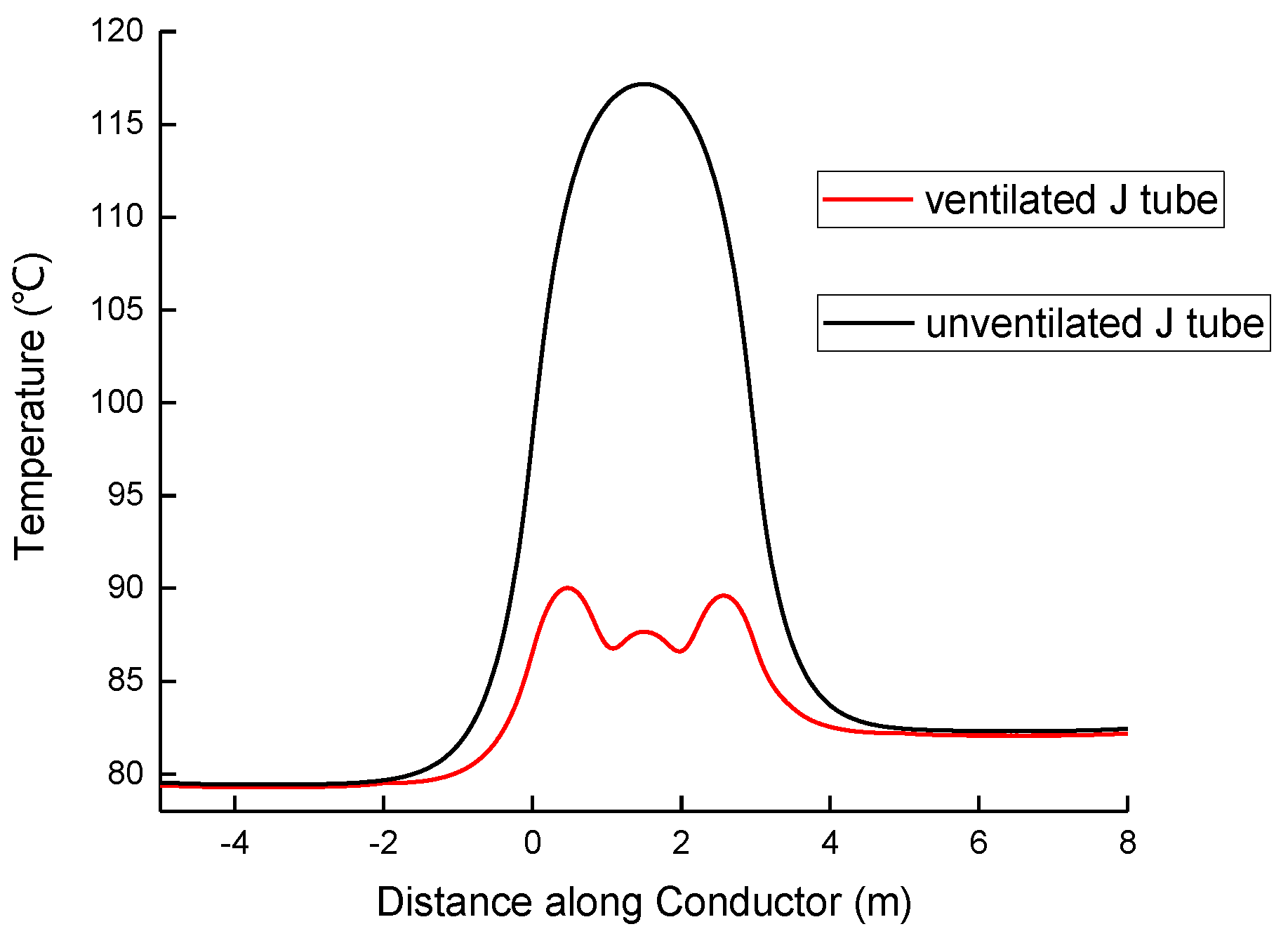
3.3. Ventilated J-Tube Model
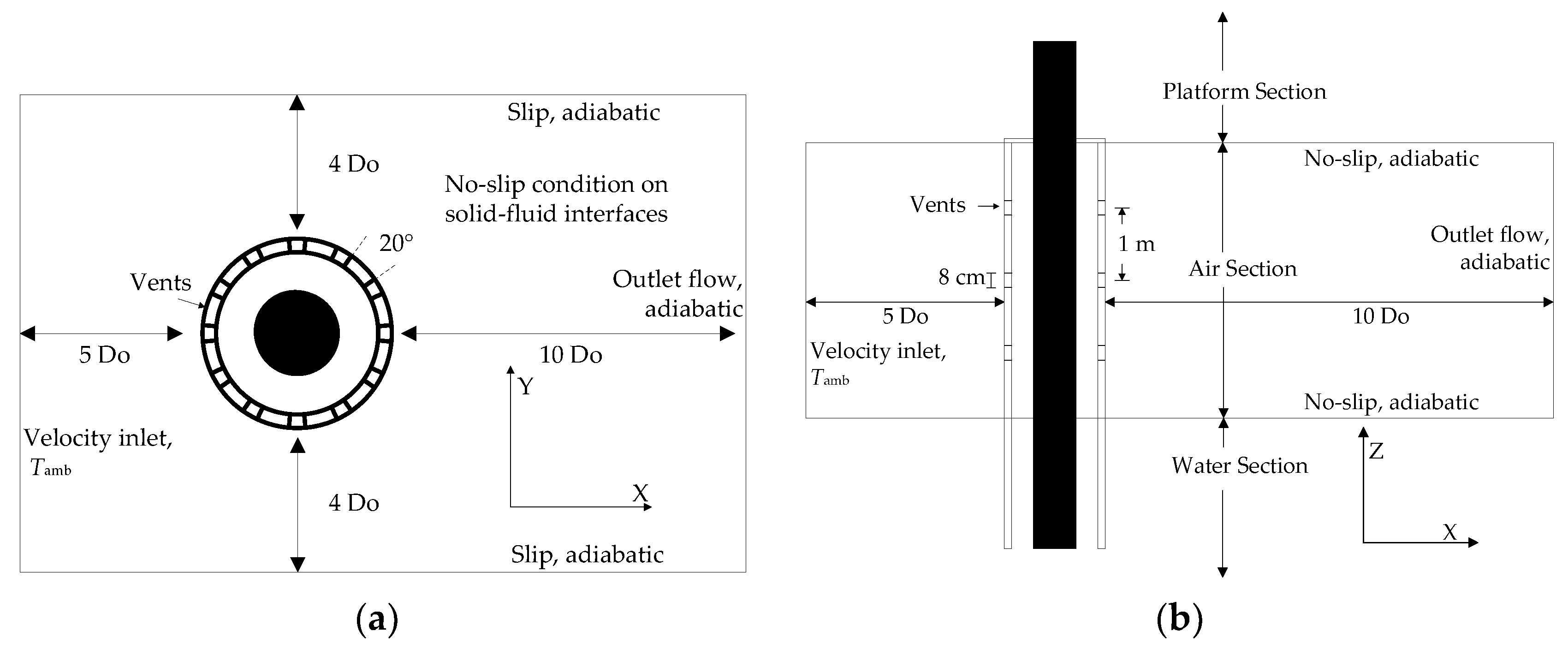
For the ventilated J-tube, the model is built on the basis of the enclosed J-tube model, and much of the design is similar to that of the enclosed case, with the only changes being some air vents on the J-tube, as shown in
Figure 3.
Since the flow field inside the J-tube is closely associated with the external flow filed, the external air needs to be included in the computational domain, as shown in
Figure 3. It should be noted that only the ambient air around the air section is modeled, and the equivalent CHTCs calculated by Equation (7) are applied on the external surfaces in the platform section. Thus, the domain height is equal to the Lair. It is considered that this simplification would have little impact on the rating that was obtained, since the platform section provides much less thermal limitation than the air section, and the rating mainly relies on the thermal environment between the cable and the J-tube in the air section. Therefore, for the air section, in the X and Y directions, −5.5 ≤
x/Do ≤ 10.5 and −4.5 ≤
y/Do ≤ 4.5, and in the Z direction, 0 ≤
z ≤ Lair.
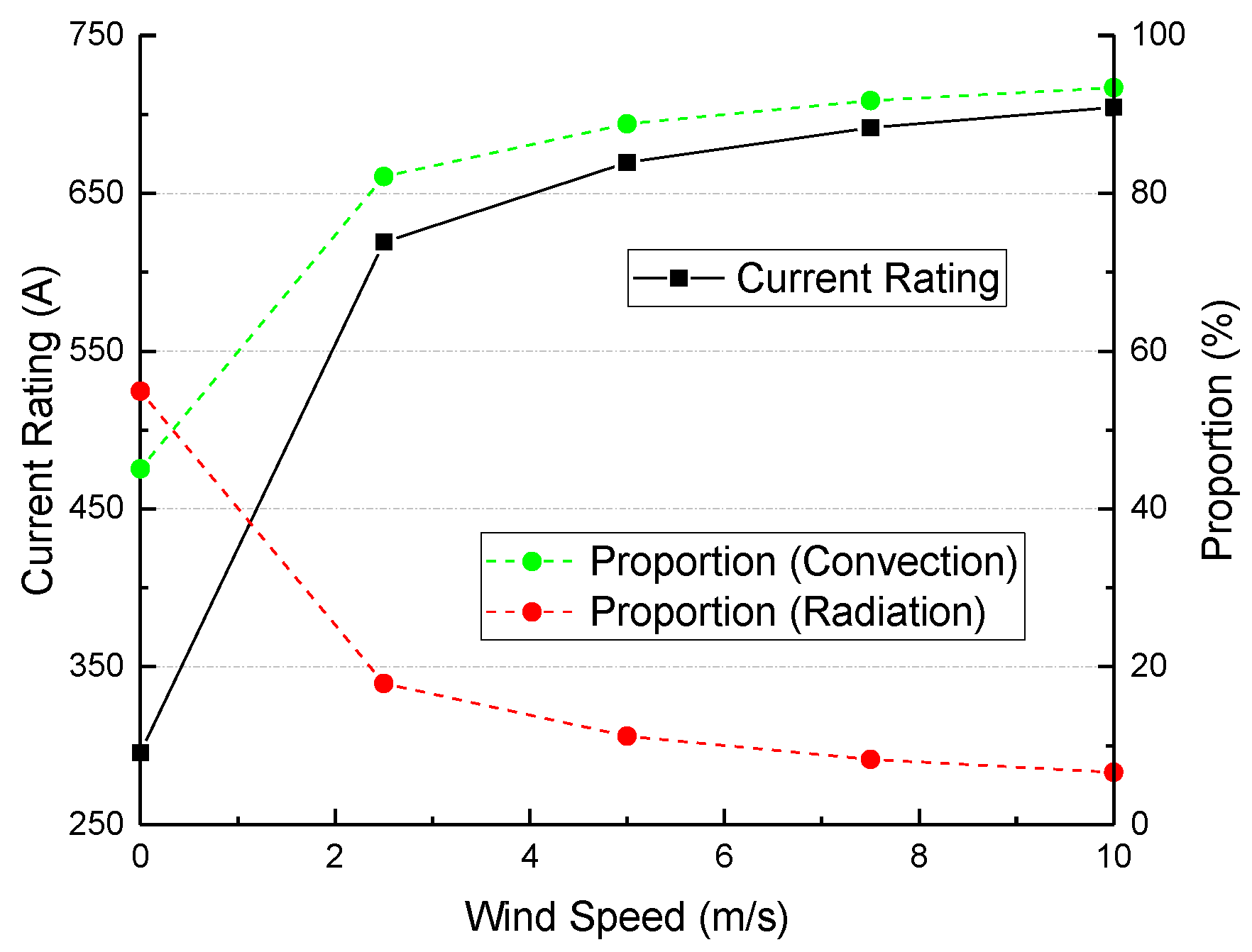
The external flow across the J-tube is often turbulent, since the Reynolds number based on Do is estimated to be from 5 × 10
4 to 2 × 10
5 for wind speeds from 2.5 to 10 m/s [
15]. The flow inside the tube is complicated, but the mean air speed should be much larger than that of the enclosed case due to the forced ventilation, and thus turbulent flow is also expected. The turbulent flow model that is applied in the enclosed case is also used here to solve the whole flow field in the computational domain. Besides, a boundary-layer meshing technique is also used to ensure enough grid density near the fluid-solid interfaces, especially near the vents.
The final step is defining the boundary conditions of the domain, as shown in
Figure 3.
At the inlet of the domain, the mean wind speeds perpendicular to the inlet and uniform ambient air temperature Tamb are specified. Zero static pressure is specified at the outlet. No-slip wall conditions are imposed at the top and ground boundaries when considering the upper platform and the lower seawater (assumed to be solid). The lateral boundaries of the domain are modeled as slip walls, that is
For all the boundaries of the domain except the inlet, adiabatic boundary conditions are assumed. This simplified assumption may affect the temperature and flow fields adjacent to the platform and the sea water, but it should have small impact on the whole temperature and flow fields due to the large volume of the air flowing into the domain.
Other boundary conditions, such as the temperature settings, surface to ambient radiation, and solar radiation, are same with those of the enclosed case.