Modeling of a District Heating System and Optimal Heat-Power Flow
Abstract
:1. Introduction
2. The Steady State Model of DHS
2.1. The SP Model
2.2. The LP Model and Radiator Model
2.2.1. The Tee Pipe Model
2.2.2. The Reducer Union Model and Elbow Pipe Model
2.2.3. The Valve Model
2.2.4. The Radiator Model
2.3. Simplifications of the DHS Model
3. The Optimal Heat-Power Flow Model
3.1. The Connection Matrix of HP
3.2. The OHPF Model
3.2.1. The Objective Function
3.2.2. The Constraints of DHS
3.2.3. The Constraints of PDS
3.2.4. The Constraints of Coupling Devices
4. Case Studies
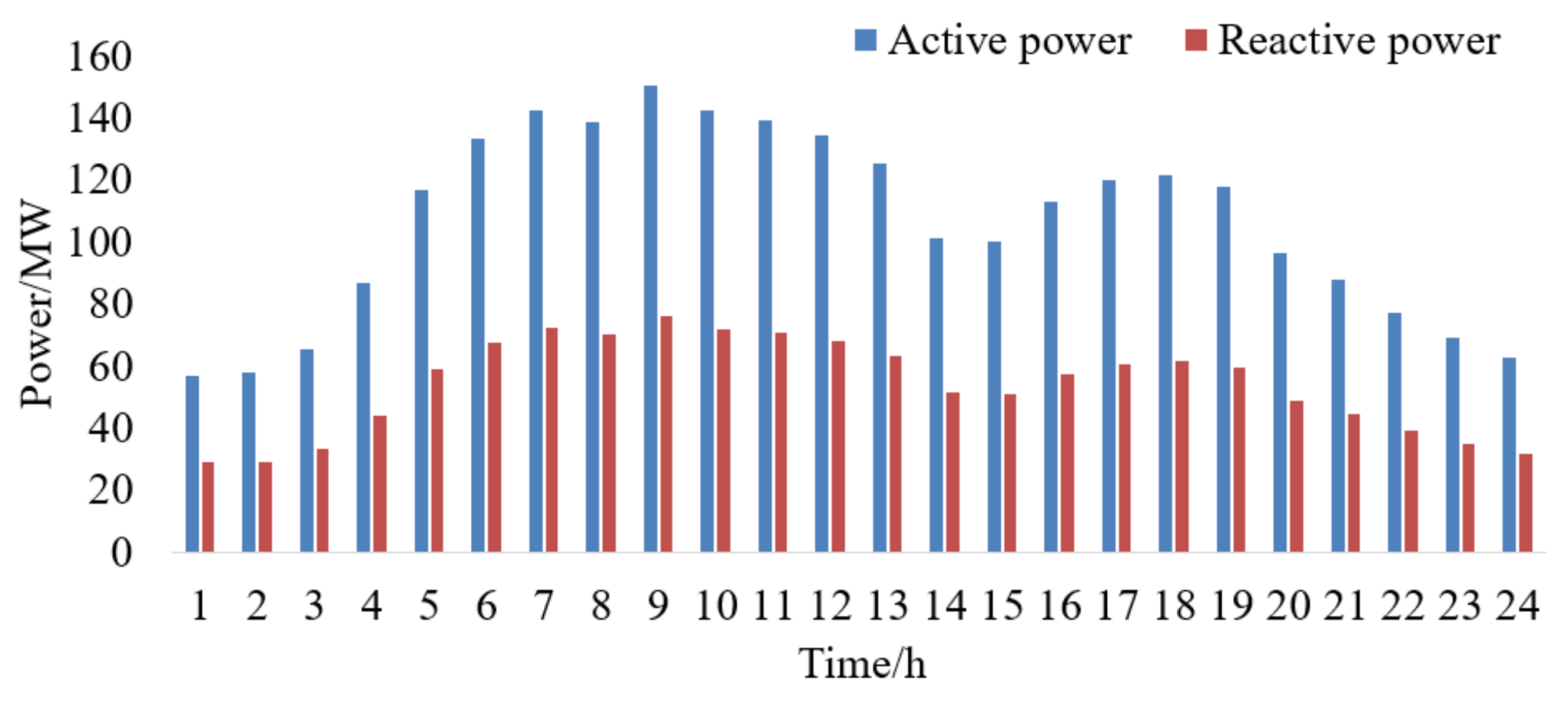
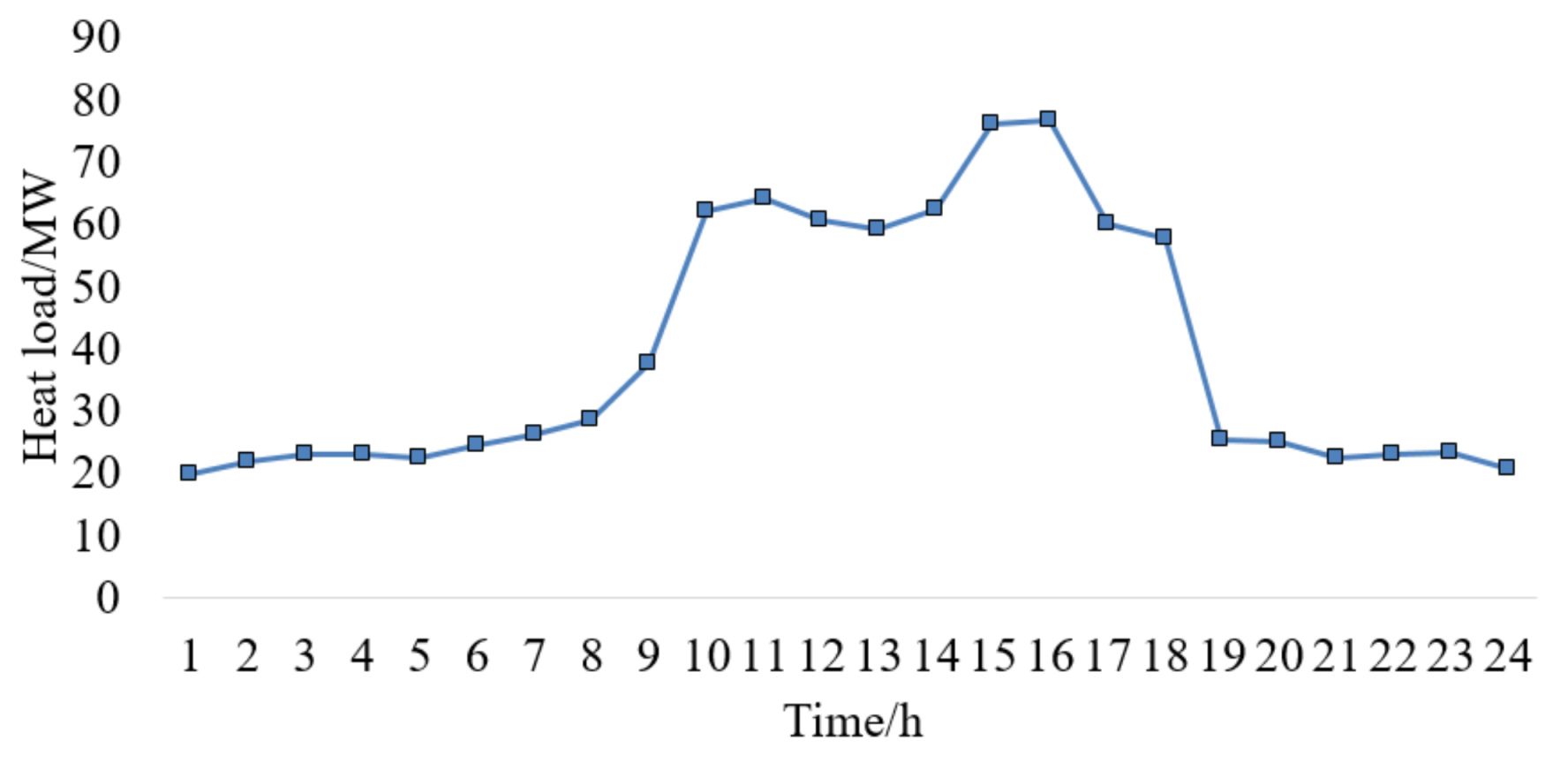
4.1. Sample System 1
4.1.1. Accuracy of the OHPF Model
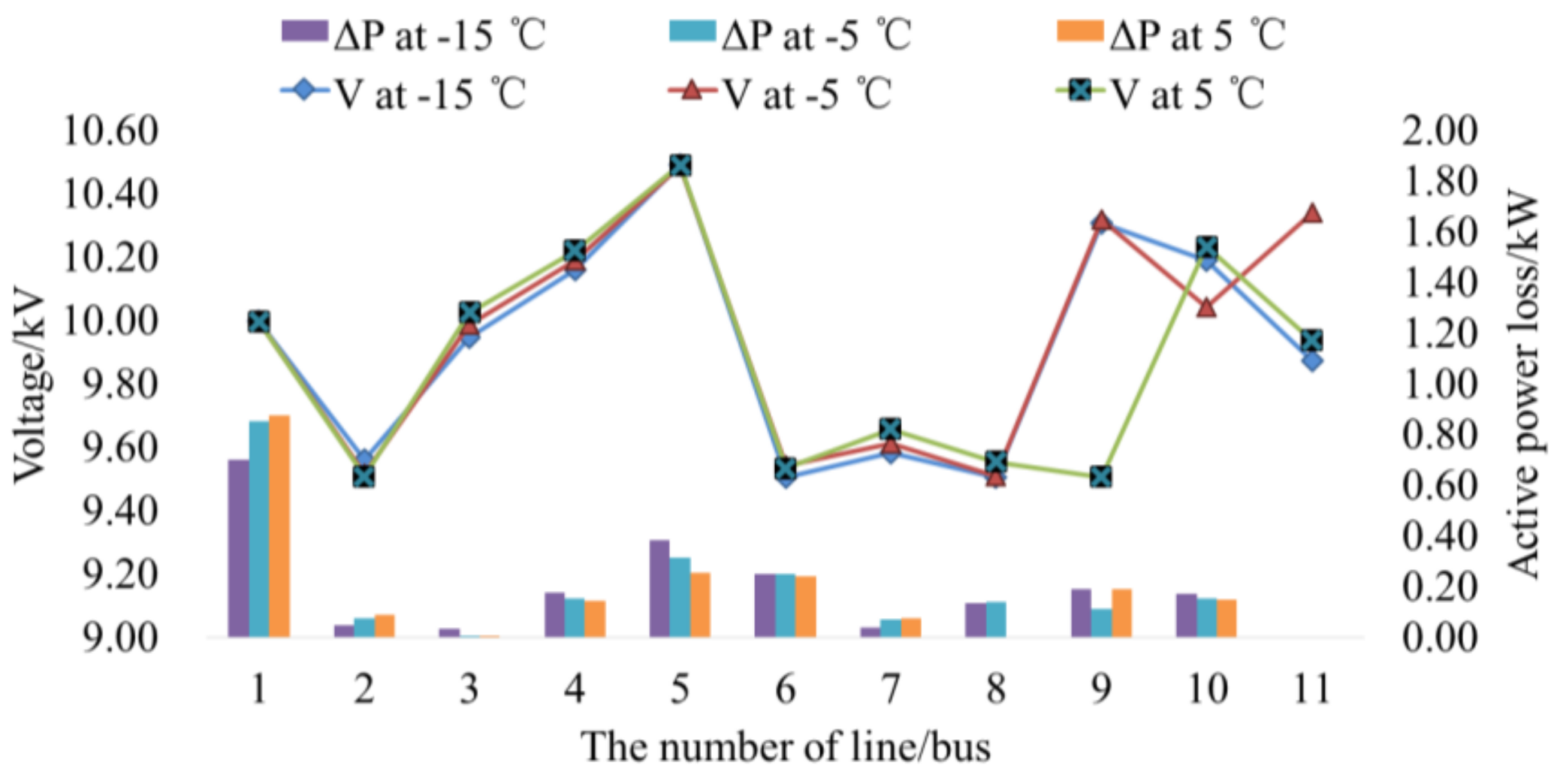
4.1.2. Temperature Sensitivity Analysis based on the OHPF Model
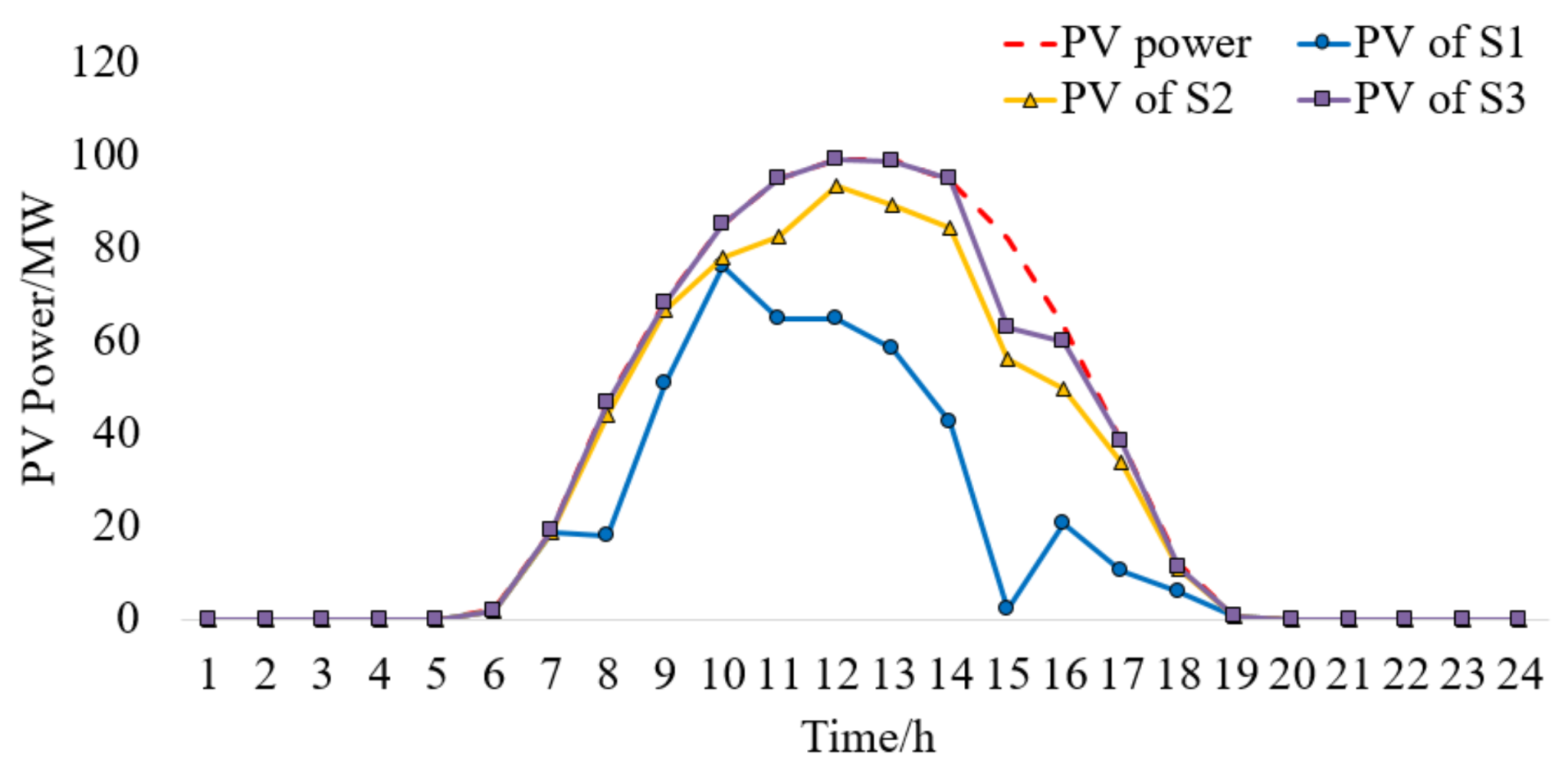
4.2. Sample System 2
- (1)
- S1: No electric heating load;
- (2)
- S2: 50% of the heating load is supplied by EBs; and,
- (3)
- S3: The heating load is fully supplied by EBs.
5. Conclusions
- (1)
- The OHPF model will be employed to optimize the coordinated planning and the operation strategies for integrated heat-gas-power energy systems by including the operation constraints of the nature gas distribution system.
- (2)
- Modeling of heat storage equipment will be addressed to expand the steady state model that is presented in this work, and to include more feasible operation modes of IPHSs.
- (3)
- Intelligent traffic networks with various kinds of electric vehicles will be included in the expansion planning of multi-energy systems and charging infrastructures.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclatures
| PDS | Power distribution system |
| DHS | District heating system |
| OHPF | Optimal heat-power flow |
| CHP | Combined heat and power |
| EBs | Electric boilers |
| IPHS | Integrated power and heating systems |
| HP | Heating pipe |
| SP | Straight pipe |
| LP | Local pipe |
| DPM | Distributed parameter model |
| CP | Circulating pump |
| PV | Photovoltaic |
| ZL | Equivalent pressure resistance of SP [kpa/kW] |
| YL | Equivalent thermal conductance of SP [kW/kpa] |
| Φ | Inlet or outlet heat flow of a HP [kW] |
| p | Pressure of a HP [kpa] |
| D | Mass flow of a HP [kg/s] |
| dL | Inner diameter of SP [m] |
| λ | Friction factor of SP |
| L | Length of SP [m] |
| ρ | Density of hot water [t/m3] |
| c | Specific heat of hot water [kJ/(kg·K)] |
| k | Heat transferring coefficient of the pipe wall [W/(m·K)] |
| T0 | Environment temperature [°C] |
| z0 | Unit pressure resistance of SP [kpa/kW] |
| y0 | Unit thermal conductance of SP [kW/kpa] |
| ZT | Pressure resistances of outlet pipe in the tee pipe [kpa/kW] |
| Kf | Local loss coefficient |
| dT | Inner diameter of the tee pipe [m] |
| Local loss coefficient of the reducer union | |
| ZR | Pressure resistances of the reducer union [kpa/kW] |
| ZE | Pressure resistances of the elbow pipe [kpa/kW] |
| dR1 | Inner diameter of the reducer union [m] |
| dE | Inner diameter of the elbow pipe [m] |
| ZV | Variable pressure resistance of the valve [kpa/kW] |
| dV | Inlet inner diameter of the valve [m] |
| α, β | Fitting coefficient of the valve |
| ΦL | Heat load [kW] |
| YM | Thermal conductance of the radiator [kW/kpa] |
| εRij | Binary variables that indicating whether or not HP contains the reducer union |
| εVij | Binary variables that indicating whether or not HP contains the valve |
| εEij | Binary variables that indicating whether or not HP contains the elbow pipe |
| εMij | Binary variables that indicating whether or not HP contains the radiator |
| C1ij, C2ij, C3ij, Cij | Constants of the representative HP |
| ξi,l | An element of the HP connection matrix |
| ΩH | Set of nodes of the DHS |
| ΔOHPF | Optimization objective of the OHPF model [104 $] |
| Γ | Run time of an IHPS [h] |
| ΩL | Set of HPs in the DHS |
| ΩP | Set of feeders in the PDS |
| ΔΦl | Heat losses of HP l [kW] |
| Δpl | Pressure losses of HP l [kpa] |
| ΔPi | Active power losses of feeder i [MW] |
| ΔQi | Reactive power losses of feeder i [MVar] |
| φH | Unit price of heat power [$/(MW·h)] |
| φP | Unit price of electrical power [$/(MW·h)] |
| Thermal power output of the CHP plant in HP l [kW] | |
| Thermal power output of the EB in HP l [kW] | |
| Pressure compensation of the CP in HP l [kpa] | |
| Elements of the incidence matrixes of the DHS | |
| Elements of the incidence matrixes of the PDS | |
| Upper and heat flow limit of HP l [kW] | |
| Lower heat flow limit of HP l [kW] | |
| Upper limit of the pressure at node i [kpa] | |
| Lower limit of the pressure at node i [kpa] | |
| Pi | Active power in feeder i [MW] |
| Qi | Reactive power in feeder i [MVar] |
| Upper limit of active power in feeder i [MW] | |
| Upper limit of reactive power in feeder i [MVar] | |
| Injection active power at the power-outflow terminal of feeder i [MW] | |
| Injection reactive power at the power-outflow terminal of feeder i [MVar] | |
| Active loads at the power-outflow terminal of feeder i [MW] | |
| Reactive loads at the power-outflow terminal of feeder i [MVar] | |
| Power output of the CHP plant at the power-outflow terminal of feeder i [MW] | |
| Power demand of the CP at the power-outflow terminal of feeder i [MW] | |
| Power demand of the EB at the power-outflow terminal of feeder i [MW] | |
| CCHP | Heat-power ratio of the CHP plants |
| μCP | Efficiency factor of the CPs [kpa/MW] |
| CEB | Heat-power ratio of the EBs |
| Pi | Upper limit of active power in feeder i [MW] |
| Qi | Upper limit of reactive power in feeder i [MVar] |
| Ri | Resistance of feeder i [Ω/km] |
| Xi | Reactance of feeder i [Ω/km] |
| ΔVi | Voltage losses of feeder i [kV] |
| VB | Reference voltage of the PDS [kV] |
| Vi | Voltage at the power-outflow terminal of feeder i [kV] |
| Upper limit of injection active power at the power-outflow terminal of feeder i [MW] | |
| Lower limit of injection active power at the power-outflow terminal of feeder i [MW] | |
| Upper limit of injection reactive power at the power-outflow terminal of feeder i [MVar] | |
| Lower limit of injection reactive power at the power-outflow terminal of feeder i [MVar] | |
| Upper limit of the thermal power output of the CHP plant in HP l [kW] | |
| Lower limit of the thermal power output of the CHP plant in HP l [kW] | |
| Upper limit of the pressure compensation of the CP in HP l [kpa] | |
| Lower limit of the pressure compensation of the CP in HP l [kpa] | |
| Upper limit of the power demand of the EB at the power-outflow terminal of feeder i [MW] | |
| Lower limit of the power demand of the EB at the power-outflow terminal of feeder i [MW] | |
| ΛEB | Location transformation matrixes of the EBs |
| ΛCHP | Location transformation matrixes of the CHP plants |
| ΛCP | Location transformation matrixes of the CPs |
Appendix A
Appendix A.1. The Tee Pipe Model
Appendix A.2. The Reducer Union Model and Elbow Pipe Model
Appendix A.3. The Valve Model
Appendix B
References
- Chen, Y.; Liu, Y.; Hung, S.; Cheng, C. Multi-input inverter for grid-connected hybrid PV/wind power system. IEEE Trans. Power Electron. 2007, 22, 1070–1077. [Google Scholar] [CrossRef]
- Momete, D.C. Measuring renewable energy development in the Eastern Bloc of the European Union. Energies 2017, 10, 2120. [Google Scholar] [CrossRef]
- Raunbak, M.; Zeyer, T.; Zhu, K.; Greiner, M. Principal mismatch patterns across a simplified highly renewable European electricity network. Energies 2017, 10, 1934. [Google Scholar] [CrossRef]
- Gu, Z.; Kang, C.; Chen, X.; Bai, J.; Cheng, L. Operation optimization of integrated power and heat energy systems and the benefit on wind power accommodation considering heating network constraints. Proc. CSEE 2015, 35, 3596–3604. [Google Scholar]
- Wang, J.; Gu, W.; Lu, S.; Zhang, C.; Wang, Z.; Tang, Y. Coordinated planning of multi-district integrated energy system combining heating network model. Autom. Electric Power Syst. 2016, 40, 17–24. [Google Scholar]
- Jia, C.; Wu, C.; Zhang, C.; Zhou, J.; Liu, G.; Bai, M.; Cai, Y.; Tang, W.; Sun, C. Optimum configuration of energy station in urban hybrid area of commerce and residence based on integrated planning of electricity and heat system. Power Syst. Prot. Control 2017, 45, 30–36. [Google Scholar]
- Bakken, B.H.; Dyken, S.V. Integrated planning of electricity, gas and heat supply to municipality. Strojarstvo 2013, 55, 109–126. [Google Scholar]
- Li, J.; Fang, J.; Zeng, Q.; Chen, Z. Optimal operation of the integrated electrical and heating systems to accommodate the intermittent renewable sources. Appl. Energy 2016, 167, 244–254. [Google Scholar] [CrossRef]
- Lyu, Q.; Jiang, H.; Chen, T.; Wang, H.; Lyu, Y. Wind power accommodation by combined heat and power plant with electric boiler and its national economic evaluation. Autom. Electric Power Syst. 2014, 38, 6–12. [Google Scholar]
- Chen, J.; Wu, W.; Zhang, B.; Sun, Y. A rolling generation dispatch strategy for co-generation units accommodating large-scale wind power integration. Autom. Electric Power Syst. 2012, 36, 21–27. [Google Scholar]
- Chen, X.; Kang, C.; O’Malley, M.; Xia, Q.; Bai, J. Increasing the flexibility of combined heat and power for wind power integration in China: Modeling and implications. IEEE Trans. Power Syst. 2015, 30, 1848–1857. [Google Scholar] [CrossRef]
- Jing, Z.; Jiang, X.; Wu, Q.; Tang, W.; Hua, B. Modelling and optimal operation of a small-scale integrated energy based district heating and cooling system. Energy 2014, 73, 399–415. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R. Simultaneous integrated optimal energy flow of electricity, gas, and heat. Energy Convers. Manag. 2015, 101, 579–591. [Google Scholar] [CrossRef]
- Cahill, D.G. Analysis of heat flow in layered structures for time-domain thermoreflectance. Rev. Sci. Instrum. 2004, 75, 5119–5122. [Google Scholar] [CrossRef]
- Liu, X.; Wu, J.; Jenkins, N.; Bagdanavicius, A. Combined analysis of electricity and heat networks. Appl. Energy 2016, 162, 1238–1250. [Google Scholar] [CrossRef]
- Gamberi, M.; Manzini, R.; Regattieri, A. Simulink©, simulator for building hydronic heating systems using the Newton-Raphson algorithm. Energy Build. 2009, 41, 848–855. [Google Scholar] [CrossRef]
- Fedorov, M. Parallel implementation of a steady state thermal and hydraulic analysis of pipe networks in OpenMP. Lect. Notes Comput. Sci. 2009, 17, 360–369. [Google Scholar]
- Kona, A.; Verda, V. Multiobjective optimization applied to district heating network planning. Compet. Intell. Rev. 2011, 5, 64–66. [Google Scholar]
- Wang, H.; Duanmu, L.; Li, X.; Lahdelma, R. Optimizing the district heating primary network from the perspective of economic-specific pressure loss. Energies 2017, 10, 1095. [Google Scholar] [CrossRef]
- Aringhieri, R.; Malucelli, F. Optimal operations management and network planning of a district heating system with a combined heat and power plant. Ann. Oper. Res. 2003, 120, 173–199. [Google Scholar] [CrossRef]
- Obara, S.; Kudo, K. Route planning and estimate of heat loss of hot water transportation piping for fuel cell local energy network. Trans. Jpn. Soc. Refrig. Air Cond. Eng. 2005, 22, 13–24. [Google Scholar]
- Zhang, S.; Jin, Z.; Hao, L.; Wang, X.; Chen, P. An analysis on the safety performance of the combined fittings of straight tees and long radius elbows. Chem. Eng. Mach. 2008, 4, 151–158. [Google Scholar]
- Xu, B.; Fu, L.; Di, H. Dynamic simulation of space heating systems with radiators controlled by TRVs in buildings. Energy Build. 2008, 40, 1755–1764. [Google Scholar] [CrossRef]
- Wang, Y. Research of Modeling and Control Method for District Heating System; Southeast University: Nanjing, China, 2013; pp. 18–44. [Google Scholar]
- Liu, X.; Mancarella, P. Modelling, assessment and Sankey diagrams of integrated electricity-heat-gas networks in multi-vector district energy systems. Appl. Energy 2016, 167, 336–352. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Optimal power flow of multiple energy carriers. IEEE Trans. Power Syst. 2007, 22, 145–155. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, W.; Qi, F.; Wen, F.; Zhao, J.; Dong, Z. A distributed parameter model of heating pipe networks and coordinated planning of electrical and heating coupled systems. Electric Power Constr. 2017, 38, 77–87. [Google Scholar]
- Chen, Q.; Fu, R.; Xu, Y. Electrical circuit analogy for heat transfer analysis and optimization in heat exchanger networks. Appl. Energy 2015, 139, 81–92. [Google Scholar] [CrossRef]
- Bojic, M.; Trifunovic, N. Linear programming optimization of heat distribution in a district-heating system by valve adjustments and substation retrofit. Build. Environ. 2000, 35, 151–159. [Google Scholar] [CrossRef]
- Chotivisarut, N.; Kiatsiriroat, T. Cooling load reduction of building by seasonal nocturnal cooling water from thermosyphon heat pipe radiator. Int. J. Energy Res. 2010, 33, 1089–1098. [Google Scholar] [CrossRef]
- Yeh, H.G.; Gayme, D.F.; Low, S.H. Adaptive VAR control for distribution circuits with photovoltaic generators. IEEE Trans. Power Syst. 2012, 27, 1656–1663. [Google Scholar] [CrossRef]
- Faqiry, M.N.; Edmonds, L.; Zhang, H.; Khodaei, A.; Wu, H. Transactive-market-based operation of distributed electrical energy storage with grid constraints. Energies 2017, 10, 1891. [Google Scholar] [CrossRef]
- Marguc, J.; Truntic, M.; Rodic, M.; Milanovic, M. Modelling of power electronics converters by using the incidence matrix approach. In Proceedings of the IEEE International Symposium on Industrial Electronics, Edinburgh, UK, 19–21 June 2017; pp. 1–6. [Google Scholar]
- Zafra-Cabeza, A.; Ridao, M.A.; Alvarado, I.; Camacho, E.F. Applying risk management to combined heat and power plants. IEEE Trans. Power Syst. 2008, 23, 938–945. [Google Scholar] [CrossRef]
- Liao, Z.; Dexter, A.L. The potential for energy saving in heating systems through improving boiler controls. Energy Build. 2004, 36, 261–271. [Google Scholar] [CrossRef]









| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| λ | 0.326 | -- | T0 | −5.000 | °C |
| k | 1.056 | W/(m·K) | Kf | 1.015 | -- |
| c | 4.186 | kJ/(kg·K) | α | 0.865 | -- |
| ρ | 0.935 | t/m3 | β | 0.563 | -- |
| VB | 10.5 | kV | CEB | 0.15 | -- |
| Γ | 1 | h | CCHP | 0.05 | -- |
| μCP | 25.69 | kpa/MW | φP | 103 | $/(MW·h) |
| φH | 377 | $/(MW·h) | -- | -- | -- |
| No. | HP | ΔΦ (kW) | Δp (kpa) | D (kg/s) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| From | To | −15 °C | −5 °C | 5 °C | −15 °C | −5 °C | 5 °C | −15 °C | −5 °C | 5 °C | |
| 1 | ① | ② | 61.55 | 60.34 | 42.70 | 22.52 | 23.44 | 19.83 | 0.06 | 0.06 | 0.04 |
| 2 | ④ | ① | 34.87 | 34.82 | 24.51 | 22.21 | 23.12 | 19.56 | 0.06 | 0.06 | 0.04 |
| 3 | ② | ③ | 31.57 | 31.08 | 22.91 | 2.77 | 2.89 | 2.44 | 0.03 | 0.03 | 0.02 |
| 4 | ⑤ | ④ | 21.63 | 21.54 | 15.80 | 4.31 | 4.48 | 3.79 | 0.03 | 0.03 | 0.02 |
| 5 | ② | ④ | 21.63 | 21.54 | 15.80 | 13.28 | 13.82 | 11.69 | 0.03 | 0.03 | 0.02 |
| 6 | ③ | ⑤ | 17.85 | 17.79 | 14.60 | 6.20 | 6.45 | 5.46 | 0.02 | 0.02 | 0.01 |
| 7 | ③ | ⑤ | 17.85 | 17.79 | 14.60 | 6.20 | 6.45 | 5.46 | 0.01 | 0.01 | 0.01 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Wen, F.; Wang, K.; Huang, Y.; Salam, M.A. Modeling of a District Heating System and Optimal Heat-Power Flow. Energies 2018, 11, 929. https://doi.org/10.3390/en11040929
Yang W, Wen F, Wang K, Huang Y, Salam MA. Modeling of a District Heating System and Optimal Heat-Power Flow. Energies. 2018; 11(4):929. https://doi.org/10.3390/en11040929
Chicago/Turabian StyleYang, Wentao, Fushuan Wen, Ke Wang, Yuchun Huang, and Md. Abdus Salam. 2018. "Modeling of a District Heating System and Optimal Heat-Power Flow" Energies 11, no. 4: 929. https://doi.org/10.3390/en11040929
APA StyleYang, W., Wen, F., Wang, K., Huang, Y., & Salam, M. A. (2018). Modeling of a District Heating System and Optimal Heat-Power Flow. Energies, 11(4), 929. https://doi.org/10.3390/en11040929





