X-Pinch Plasma Generation Testing for Neutron Source Development and Nuclear Fusion

Abstract

Nuclear fusion is a sought-out technology in which two light elements are fused together to create a heavier element and releases energy. Two primary nuclear fusion technologies are being researched today: magnetic and inertial confinement. However, a new type of nuclear fusion technology is currently being research: multi-pinch plasma beams. At the University of Ontario Institute of Technology, there is research on multi-pinch plasma beam technology as an alternative to nuclear fusion. The objective is to intersect two plasma arcs at the center of the chamber. This is a precursor of nuclear fusion using multi-pinch. The innovation portion of the students’ work is the miniaturization of this concept using high energy electrical DC pulses. The experiment achieved the temperature of 2300 K at the intersection. In comparison to the simulation data, the temperature from the simulation is 7000 K at the intersection. Additionally, energy harvesting devices, both photovoltaics and a thermoelectric generator, were placed in the chamber to observe the viable energy extraction.

1. Introduction

Transmutation is a method of converting one element to another element via neutron bombardment. By bombarding an element using neutrons, the element undergoes radioactive decay, normally beta-negative decay. Transmutation is an important aspect of nuclear physics in order to convert depleted uranium rods into viable fuel sources.

Canadian Deuterium-Uranium (CANDU) reactors use natural uranium (0.72% U-235) with heavy water (D₂O) to produce heat for nuclear fission. The uranium rods are spent over time and end up going to waste. This waste has a lower fissile percentage than the natural uranium. However, it does contain fertile uranium-238. This element can be converted to plutonium-239 to be a viable nuclear fuel source via transmutation.

$${}_{92}{}^{238}\mathrm{U}{+}_0^1\mathrm{n}\to {}_{92}{}^{239}\mathrm{U}\stackrel{{\mathsf{\beta }}^{-}}{\to }{}_{93}{}^{239}\mathrm{N}\mathrm{p}\stackrel{{\mathsf{\beta }}^{-}}{\to }{}_{94}{}^{239}\mathrm{P}\mathrm{u}$$

(1)

Since this research focuses on the development of the X-pinch plasma generator, an in-depth description of transmutation is not presented. The reader should refer to References [1,2] for further details.

A novel concept from the University of Ontario Institute of Technology and HOPE Innovations is to use intersecting beams to produce neutrons for fuel conversion. Subsequently, this also is a nuclear fusion source by using deuterium-tritium fuel,

$$\begin{array}{cc}\left\{1\right\}& {}_1{}^2\mathrm{H}+{}_1{}^2\mathrm{H}\to {}_2{}^3\mathrm{H}\mathrm{e}+{}_0{}^1\mathrm{n}+3.27\mathrm{MeV}\\ \left\{2\right\}& {}_1{}^2\mathrm{H}+{}_1{}^2\mathrm{H}\to {}_1{}^3\mathrm{H}+{}_1{}^1\mathrm{H}+4.03\mathrm{MeV}\\ \left\{3\right\}& {}_1{}^2\mathrm{H}+{}_1{}^3\mathrm{H}\to {}_2{}^4\mathrm{H}\mathrm{e}+{}_0{}^1\mathrm{n}+17.6\mathrm{MeV}\\ \left\{4\right\}& {}_1{}^2\mathrm{H}+{}_2{}^3\mathrm{H}\mathrm{e}\to {}_2{}^4\mathrm{H}\mathrm{e}+{}_1{}^1\mathrm{H}+18.3\mathrm{MeV}\end{array}$$

(2)

This research focuses on the X-pinch plasma technology for nuclear fusion and fuel conversion applications [3]. The technology readiness level is one during the time when this paper is written. This chamber houses the intersecting plasma beam pinching at the center of the chamber. Miao and Feng have released a couple of papers discussing the concept of the multi-beam pinch plasma. Figure 1 illustrates the full concept [4,5]. The chamber that was built is tested under benign conditions. The benign conditions are no nuclear fuels are presents, the gas is approximately 80% nitrogen and 20% oxygen (air); the ambient pressure is 0.1 atm.

With reference to Figure 1, the plasma beam density proposed to be 0.2724 kg/m³ or 2.46 × 10²⁴ m⁻³ of the deuterium-tritium mixture, according to Miao et al. [4,5]. Ultimately, the input energy per plasma channel under the design from Miao is 50 MW with the current of 100 kA in the axial direction. The volume of the intersecting region is 78.5 mm³, where plasma bombardment interaction occurs [4]. During the plasma transport, the beam passes through the region once; however, the fluid is recycled throughout the system, making multiple passes. The time of the plasma confinement is defined using the Lawson Criterion [6],

$${\tau }_{D-D}=\frac{5\times {10}^{15}}{n},$$

(3)

$${\tau }_{D-T}=\frac{2\times {10}^{14}}{n},$$

(4)

where ${\tau }_{D-D}$ and ${\tau }_{D-T}$ are the confinement times of deuterium–deuterium and deuterium–tritium reactions, respectively. The confinement times of the D−D and D−T under the configuration are 203 ps and 8.13 ps, respectively. This is a fast reaction under the right condition.

This paper discusses the design and findings of the chamber used for the multi-beam pinch. The paper first discusses the engineering design of the chamber; this includes the geometry and dimensions and the structural analysis under static load. Dynamic loading is not included in the research as the chamber does not undergo external vibrations and the chamber is stabilized on a large surface. Then, the paper discusses a methodology explaining how the chamber was constructed and set-up for the test. This includes the electronics used to produce the plasma and a brief description of the diagnostics used to measure the plasma. The results display the findings from the diagnostics and energy harvesting, including the electron temperature and density, the temperature, the pressure, and the power generated. A discussion is included to deliberate on the findings and determine how it is extrapolated for fusion and nuclear fuel conversion.

2. Engineering Design and Theory

2.1. Chamber

In order to evaluate the effectiveness of the chamber design, a 3D model must be made and subjected to the maximum possible stress for the chamber. The stress analysis is evaluated from the NX’s finite element analysis. In the case of this analysis, the model is assigned to be made out of a standard acrylic that can be used as a benchmark and has 12.5 mm (0.5 inches) meshes. The reason for this mesh size is for performance purposes and limited computing power. Therefore, a compromise had to be made in order to gain reliable outputs and a 12.5 mm mesh size gives a reasonable level of accuracy to the requirements of this experiment.

The material used in the finite element model is standard acrylic. The primary reason for choosing acrylic as the material for the chamber is for ease of manufacturing. This is a pre-alpha prototype and the input power is scaled small enough such that the radiative heat expelled from the plasma would not cause thermal damage. With the use of this acrylic, the stress acting on the chamber can be compared directly with the yield or tensile strengths of the potential material and used to determine if the steel in question is potentially capable of handling the stresses. The yield strength of this material is 70 MPa, or 10.15 kilopound-force per square inch (ksi), which is lower than any other material being considered. With this baseline, any stresses shown acting on the model from the finite element method (FEM) analysis would be further reduced when compared to much stronger materials.

2.1.1. Geometry and Dimensions

Figure 2 illustrates the 3D model of the chamber. The chamber was designed as is as it was the most efficient design with high strength, high shock tolerance, and large enough to fit a large number of sensors or plasma generators. The design of the chamber chosen is a cubic chamber with a 5-inch outer length, 4.5 inch inner length, 0.5 inch thick walls, seven standard ports 0.75 inches in diameter for electrodes and sensors. It is sealed together with epoxy and form a gas-tight seal. The pieces are designed to be machined out of a single piece of acrylic plate material which is designed to make manufacturing simpler by eliminate the need for welding and increase strength.

Furthermore, all channels can be machined in maintaining strength and simplicity. This design includes having the channels on both the horizontal and vertical planes; with the viewing ports being capable of being used as electrodes or instrumentations ports. The channels are machined at specific angles for increased flexibility in plasma geometries. Having a chamber with an internal diameter of 4.5 inches across is useful as the large internal volume allows for geometries such as those proposed by HOPE Innovation to be formed in small scale.

The use of 0.5 inch thick walls is required to withstand 1.45 ksi of internal pressure. In order to ensure a gas-tight seal, the faces of the base and chamber that make contact with each other must undergo a special finish in order to assist in the gas seal. The finish chamber has a surface roughness of 0.2 micrometers and is considered to be effective for electrical components.

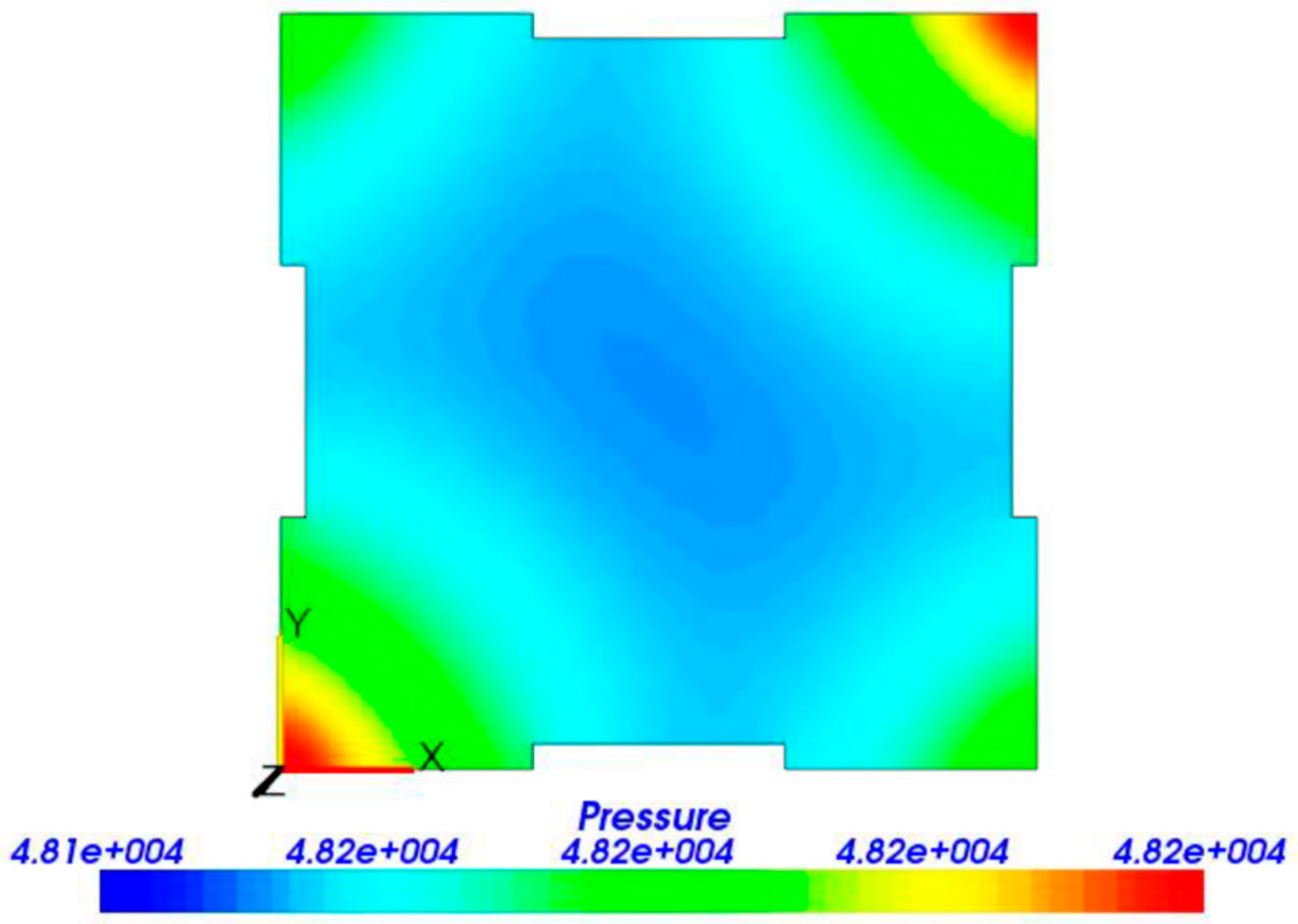
2.1.2. Finite Element Analysis

As shown by the FEM models in Figure 3 and Figure 4, the chamber has 10 mm meshes and has undergone the internal 1.45 ksi pressure. In order to properly test the chamber, each section must be fitted with a fixed constraint. In this case, the fixed constraint represents the anchor points of the chamber. For the chamber base, the anchor points are taken on the bottom of the chamber where it is anchored to either a table or a stabilizing mass. It is anchored at the top. A 1.45 ksi stress is applied to the inside of the chamber, excluding the grove cut at the top of the chamber. The top of the chamber is designed for the rubber casket.

The simulation shows a maximum Von Mises stress of 237.62 psi concentrated mainly on the sections around the fixed constraints. The overall deformation of the base is 4.8 thousandth of an inch (thou); it is located at the center of the chamber. This deformation is mainly negligible as it is small, relative to the chamber.

2.2. Electronics

The circuit in Figure 5 used to generate the necessary high voltage employed a simple setup in which 120 V, 60 Hz AC input was stepped up to approximately 30,000 V pulsed DC using a flyback transformer and regulated with a 555 timer. The circuit was initially simulated to confirm the output square waveform at the base of the output transistor and the results of its success can be seen in Figure 6. It should be noted that although the user does not have the ability to vary the output voltage in the presented circuit, a simple change can be done to the overall setup in order to have that freedom by adding a potentiometer in parallel with R1 to vary the voltage feeding the primary of the flyback [7,8]. The design requirements are the following:

• The circuit must be able to discharge at 1200 V and 5 mA so that the lower end of the high voltage plasma experiments can be operated and conducted. The ideal discharge voltage is 9000 V and 30 mA.
• The circuit must operate in such a manner that the user can control the rate of discharge, including frequencies at least in the 20 kHz range.
• The user must have the capacity to trigger an event manually using a button and a mechanical switch to turn off the whole experiment in case of an emergency. It must be mechanical because the chances of digital failure are mitigated.
• Discharge circuit must be entirely isolated from the manual trigger and control circuit using relays. The switch, in particular, will be designed so that its activation will allow for the relays to convey the necessary signal to initiate the power supply dumping its energy into the discharge circuit.
• The circuit must be able to modify the pulsed discharge parameters such as pulse width, amplitude, waveform, and frequency, using a set of 555 timer circuits which work in harmony.

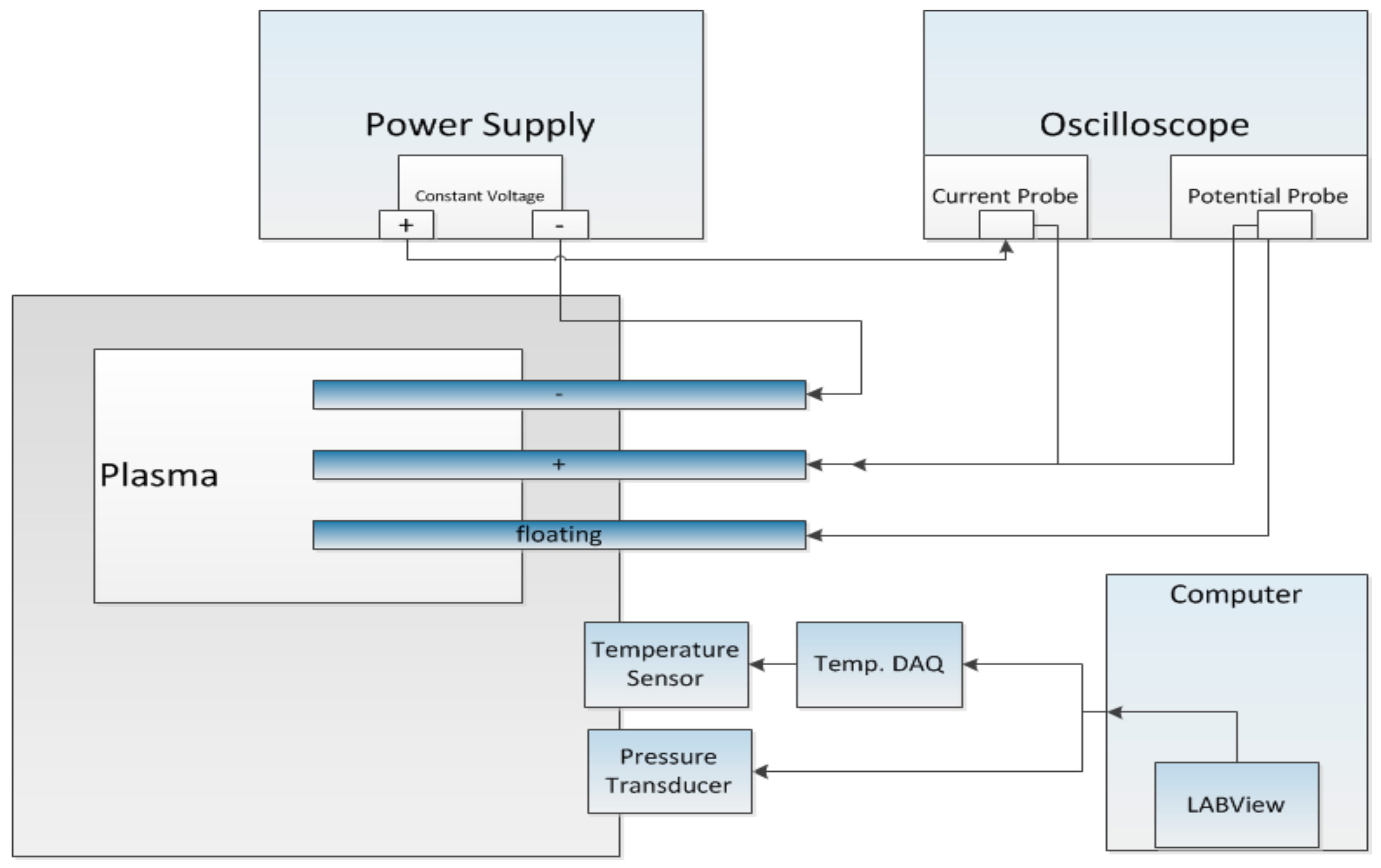
2.3. Instruments

The goal of the instrumentation system is to measure and record meaningful parameters for the analysis of the experiment and testing of the simulation model. The objective is to understand what components are necessary and how to achieve the given goal as part of the client requirements [9,10].

Figure 7 shows the setup of the triple Langmuir probe. The triple Langmuir probe consists of three durable leads interconnected with instrumentation to measure the voltage and current, and a ground and biasing potential source. The voltage and current measurement instruments that can be used include oscilloscopes, which have provide greater accuracy than handheld voltmeters and can output measured data. The use of the Langmuir probe is as follows: the potential difference measured between V₊ and V_fl is used to calculate the electron temperature using a simple relation for hot diffuse plasmas and the electron density is found similarly by analyzing the current flow between V₋ and V₊/V_fl, shown in Figure 8, depending on the biasing source at the current measurement device. The probe also has a ground leg which is grounded by connection to the reaction vessel walls.

Figure 8 shows the electrical circuit diagram of the triple Langmuir probe. The Langmuir probe will measure the temperature of the plasma and the density while the previously mentioned pressure and temperature transducers will be used to measure the conditions inside the chamber but not of the plasma itself.

$$T_e\left[\mathrm{eV}\right]=\frac{V_{+}-V_{fl}}{\ln \left(2\right)}.$$

(5)

The Langmuir probe can also be used to measures the current of the plasma. The current yields the current density and the ion density of the plasma [11],

$$J=\frac{I_{-+}}{A_{active}}·\frac{1}{\exp \left(-\frac{V_{+-}-V_{+fl}}{T_e\left(\mathrm{eV}\right)}\right)-1}.$$

(6)

With the current density, the ion density is [11] shown below:

$$n_i=\frac{J·\exp \left(\frac{1}{2}\right)}{e\sqrt{e·\frac{T_e\left(\mathrm{eV}\right)}{m_i}}}.$$

(7)

2.4. Energy Harvesting

2.4.1. Photovoltaics

The secondary energy harvester in the research is the photovoltaics. Photovoltaics is the use semiconducting materials in order to convert solar energy into direct current electricity. Photovoltaics have a similar structure to thermoelectric generators such that there are two semiconductor types, N-type and P-type. The semiconductors are assembled together and the layer of transmittable material is placed on top. The top surface of the material is transmittable and the bottom is reflective to keep the photons from escaping. The energy from the photons activates the semi-conductors. The holes and electrons migrate, conducting electricity. Figure 9 illustrates the photovoltaic theory.

2.4.2. Thermoelectric Generation

Thermoelectric generators function by converting the difference in temperature between two bodies into electric current. The Seebeck effect occurs where two dissimilar metals have different temperatures. In between the dissimilar metals, there are p and n junction semi-conductors which function as a barrier. Figure 10 illustrates this phenomenon.

The electromotive force in the Seebeck effect is the product of the Seebeck coefficient (S_Seebeck) and the temperature gradient, T,

$$E_{emf}=-S_{Seebeck}·\nabla T$$

(8)

The Seebeck coefficient, also known as the thermopower coefficient, is material dependent.

3. Methodology

3.1. Simulation

Specifically, for Plasma parameters, the analytical modeling will use magnetohydrodynamics (MHD) governing equations. Plasma is modeled as a fluid where the magnetic field around the fluid is created under a specific temperature and pressure combination which gives the fluid the ability to drive the current in a specific direction [14]. The ideal MHD equations are

$$\begin{gathered} \frac{\partial \mathit{\rho }}{\partial t}+\nabla ·\mathit{\rho }\mathit{u}=0, \\ \frac{\partial B}{\partial t}=\nabla \times \left(\mathit{u}\times B\right), \\ \rho \left(\frac{\partial \mathit{u}}{\partial t}+\mathit{u}·\nabla \mathit{u}\right)+\nabla \mathit{p}=J\times B, \\ \frac{\partial \mathit{p}}{\partial t}+\mathit{u}·\nabla \mathit{p}+\gamma \mathit{p}\nabla ·\mathit{u}=0, \\ \nabla \times B={\mu }_{0}J. \end{gathered}$$

(9)

Mathematical modeling component of the ElmerGUI solver includes setting up the geometry (both 2D and 3D) in the solver environment and applying mathematical properties and setting up governing equations in order for the geometry to be simulated under certain conditions.

In the initial setup menu, the coordinate system and the simulation type is determined. The coordinate system was kept to be Cartesian and the steady-state simulation type was used. The setup menu also helps set the maximum output level of the results and the steady state maximum iterations, as well as the time stepping controls. Moreover, constants such as gravity, Boltzmann, vacuum permittivity, and Stefan Boltzmann are set to match the relevant criteria.

The geometry and boundary conditions are shown in Figure 11. The boundary conditions are the following:

• The terminal and ground are assigned opposite to the electrodes.

  ○

  The electrodes potential difference is 9000 V (+9000 V–0 V).

• The middle is an open gap in which the MHD equations are acted upon.
• No-slip boundary conditions are set for the entire geometry.

3.2. Diagnostics

The design of the plasma instrumentation aims to meet the primary requirement of accurate measuring and recording plasma properties for the further understanding of the behavior and characteristics of the interaction of plasma beams. The qualitative property table shows that the triple Langmuir probe does not require complex timing electronics as no voltage sweeps are required to produce current–voltage curves [15].

3.3. Energy Harvesting

The photovoltaic test was conducted with a flat-ended solar panel, a single beam, and a double beam electrode connected through the inside of the plasma chamber. The photovoltaic material is made up of a crystalline silicon and predominantly commercial photovoltaic material. The solar panel includes PV materials such as polysilicon and monocrystalline silicon.

Three separate voltages, as well as currents, for each electrode type, were recorded. The tests were conducted under single and double beam plasma generation. The poses of the solar panels were arbitrarily selected. The orientation was relative to the X-pinch configuration.

Table 1. The positions and orientations of the solar panel.

Test Run	Position from Plasma Center (inches)	Orientation
1	2.5	Horizontal
2	1.5	Horizontal
3	2.5	Vertical
4	1.9	Vertical

shows the positions and orientations of the solar panel in the experiment.

The thermoelectric generator lab involved a 2.48 square-centimeter, high voltage thermoelectric generator connected to the plasma chamber. Its position and orientation are proximate to the plasma horizontally. The surface of the thermoelectric generator was blackened to increase its emissivity. The experiment involved both single and double transformers. The current, voltage, and power were recorded for both.

4. Results

4.1. Simulation

For the potential distribution, the steady state versus transient simulations had a significant impact. In the steady state results in Figure 12, the plasma does not form between two beams electrodes. It can be seen in Figure 12 that the voltage in the middle is 4500 V.

Figure 13 shows how joule heat is simulated in the transient simulation. It initially started by providing 1.18 × 10⁸ W to heat the gas in order to achieve ionization. With further time iterations, the amount of power needed to heat the air decreased to a very low number. This could possibly have been due to the fact that this was inside the vacuum and once the initial ionization occurred, the amount of power needed to sustain the plasma (in a transient frame) was very low inside the chamber.

Furthermore, Figure 14 shows how the temperature increases in the middle region. The first iteration shows the temperature increase building up at the anode and the nearest cathode instead of forming a straight beam with the cathode in front of it. This is potentially the main reason why the beams never collide as they were supposed to. This shows, that with the time steps in simulation, the middle region of the CAD model (prototype of two pairs of electrodes) can get as high as 7000 K. In addition to the temperature profile, Figure 15 represents the change in pressure when plasma is formed virtually. The pressure increases to as much as 48,200 Pa before settling to roughly 48,100 Pa. Figure 15 shows the pressure profile when the pressure decreases after the peak increase and settles down to 48,100 Pa as mentioned above. Finally, the velocity profile is represented in Figure 16 below. This shows how the particles tend to move to the nearest electrode as opposed to going straight to the cathode electrode.

4.2. Plasma Diagnostics

In the first trial, the plasma temperature was calculated using the data gathered from the triple Langmuir probe. The initial experiment conditions were a voltage source of 9 kV at 30 mA for the generation of plasma at a chamber pressure of 10.1 kPa. The resulting plasma temperature calculated from the average of the sample data was approximately 5200 Kelvin. The electron density calculated was 1.44 × 10²⁰ electrons per unit space using the formula based on the current and voltage.

In the second trial, the plasma temperature was calculated using the data gathered from the triple Langmuir probe. The initial experiment conditions were a voltage source of 4.5 kV at 30 mA for the generation of the plasma beam at a chamber pressure of 10.1 kPa. The resulting plasma temperature calculated from the average of the sample data was approximately 2300 Kelvin. The plasma density calculated was 2.7 × 10¹⁹ electrons per unit space using the formula based on the current and voltage. Figure 17 shows the three-dimensional plot of the absorption power versus potential difference and electron temperature.

4.3. Energy Harvesting

Table 2. The results of power and efficiency from the single and double beams.

Orientation–Position (inches)	Pinch Type	Voltage (mV)	Current (µA)	Power (µW)	Efficiency (%)
Horizontal–2.50	Z	53	6	0.318	1.17 × 10−7
Horizontal–2.50	X	80	10	0.800	2.96 × 10−7
Horizontal–1.25	Z	120	20	2.400	8.88 × 10−7
Horizontal–1.25	X	131	30	3.930	1.45 × 10−7
Vertical–2.50	Z	43	8	0.344	1.27 × 10−7
Vertical–2.50	X	65	14	0.910	3.37 × 10−7
Vertical–1.90	Z	80	11	0.880	3.25 × 10−7
Vertical–1.90	X	100	16.5	1.650	6.11 × 10−7

shows the results of the photovoltaics experiment. The results showed that the double beam electrode produced more power than the single beam electrode. The maximum power produced by the solar panel is by using the double beam electrode while the flat ended solar panel is vertically orientated and closer by 0.6 inches from the surface of the plasma chamber. This is due to more photons coming in contact with the solar panel in this orientation. The maximum power produced by the photovoltaic experiment was 6.11 × 10⁻⁷ W.

Table 3. The results of the power and efficiency for both the single and double beam plasmas.

Beam Type	Voltage (mV)	Current (µA)	Power (mW)	Efficiency (%)
Single Beam–Z-Pinch	215	156	33.54	0.0124
Double Beam–X-Pinch	209	64.1	13.38	0.0049

shows the results of the thermoelectric generation experiments. The results show the thermoelectric generator produces more power than the solar panel. The use of the single transformer in the thermoelectric generator produces more power than the double transformer. The maximum power produced is 0.03354 W from the thermoelectric generator using a single transformer. The amount of power in the plasma is 270 W. The efficiency of producing power from the solar panel and the thermoelectric generator is, hence, very low. The maximum efficiency was 0.0124%. However, to produce electrical power, the thermoelectric generator is relatively much more efficient when compared to the solar panel. The maximum efficiency of the solar panel was only 6.11 × 10⁻⁷%. However, for fusion reactors, the thermoelectric generator efficiency is still very low when compared to the 270 W of energy available from the plasma.

5. Discussion

5.1. Plasma Characteristics

Based on the electron density and temperature of the plasma in the first trial, there are three major properties that can be inferred from those measurements. The plasma is weakly coupled, densely populated, and energetically cold [10]. Weakly coupled means that the interaction within the small local regions of the plasma does not have an effect on other local regions beyond the initial region where the interaction occurred. Densely populated refers to the electron density, which is assumed to be equivalent to the ion density based on the assumption of quasi-neutrality [16]. Due to the density and temperature, the plasma is energetically cold, although, at a temperature above the room temperature relative to the plasmas temperatures, it is not energetic as the plasmas for the density measured have much higher temperatures. In the second trial, there are three major properties that were inferred from the measurements of the electron temperature and density. The plasma is weakly coupled, densely populated, and energetically cold. Weakly coupled means that the interaction within the small local regions of the plasma does not have an effect on the other local regions beyond the initial region where the interaction occurred. Densely populated refers to the electron density which is assumed to be equivalent to the ion density based on the assumption of quasi-neutrality. At the electron density measured, the electron temperature is low, meaning that the plasma is energetically cold in comparison to what is referred to as hot plasmas where the electrons are at a higher temperature.

The electron temperature calculated in each of the experiments was compared to the results of the simulation module. The electron density was excluded because the electron density was calculated in such a manner as to be based on the electron temperature. For the first experiment, the electron temperature differed by 34% in the experimental results from the simulation results. From the second experiment, the difference was 56% between the electron temperature measured experimentally and the simulation result. These are acceptable results as plasma temperature can vary greatly by several magnitudes. Even a difference of 56%, which is less than one magnitude of variation, suggests that further work is required in both aspects to further reduce the difference. Design improvements are necessary for the experimental measurement of electron temperature.

The density and the shape of the plasma are not affected by the solar panel as the solar panel is passive. The plasma is also not affected by the thermoelectric generator as the thermoelectric generator is also passive and the proximity of it is not close to the plasma. The current and voltage also do not affect the density and shape of the plasma. The Z-pinch instability is a sausage and kink instability. It affects the fusion process, as well as the solar panel and the thermoelectric generator receiving energy output from the plasma. However, it does not affect the plasma directly.

5.2. Extrapolation of the Data

Based on the experimental and simulation data, the results can be extrapolated to predict the required power input to create fusion under the X-Pinch plasma. It requires 270 W of electrical power to produce the temperature of 5200 K with an efficiency of 46%, averaging from the results from the simulation comparison. Joule heating under capacitive, or DC, discharge is ${\sigma }_{dc}{E}^2$, and assuming that the plasma conductivity changes slower than the electric field, the projection of the plasma temperature is calculated to be around 3.13 × 10⁶ K.

The power required to have sustainable fusion is 25 MW. This is assuming the ionization energy is taken from the air and not hydrogen and its isotopes. With the implemented power input from the plasma beam, the pressure inside the chamber reaches up to 35 MPa. At that pressure, the original design of the chamber would not withstand the internal pressure. To remedy the situation, a magnetic bottle has to be implemented to keep the plasma located away from the walls.

The main benefit of the research is the miniaturization of the sustainable plasma generation for nuclear fusion and neutron production. Most nuclear fusion power plants are the size of three football fields (300 m long) and cannot be compacted any further due to physical constraints. The use of plasma beam intersection would produce neutrons and fusion at a smaller size. In addition to the smaller size, replacing by the standard Brayton cycle power generation, the X-pinch plasma can use thermophotovoltaics, as demonstrated in the results. An application of miniaturization is in astronautics. Having a reliable source of energy from hydrogen and its isotopes to produce nuclear fusion rather than the use of nuclear fissile material, such as uranium or plutonium, would allow renewability in space, based on the Bussard ramjet concept.

6. Conclusions

Overall, this research is still in the stage of basic principles (TRL 1) for future development in X-pinch and multi-pinch plasma. The research was based on the proof-of-concept from Miao, Zheng, and Deng [4,5]. Further development of the research is in development from HOPE Innovations.