Research into an Online Calibration System for the Errors of Voltage Transformers Based on Open–Closed Capacitor
Abstract
:1. Introduction
2. Overall Structure of the Online Calibration System
3. Performance Analysis of Standard Voltage Sensor
4. Research on High Accuracy Data Processing Algorithm
4.1. Principle of Hybrid Convolution Window Algorithm
4.2. Characteristic of the Algorithm
- (1)
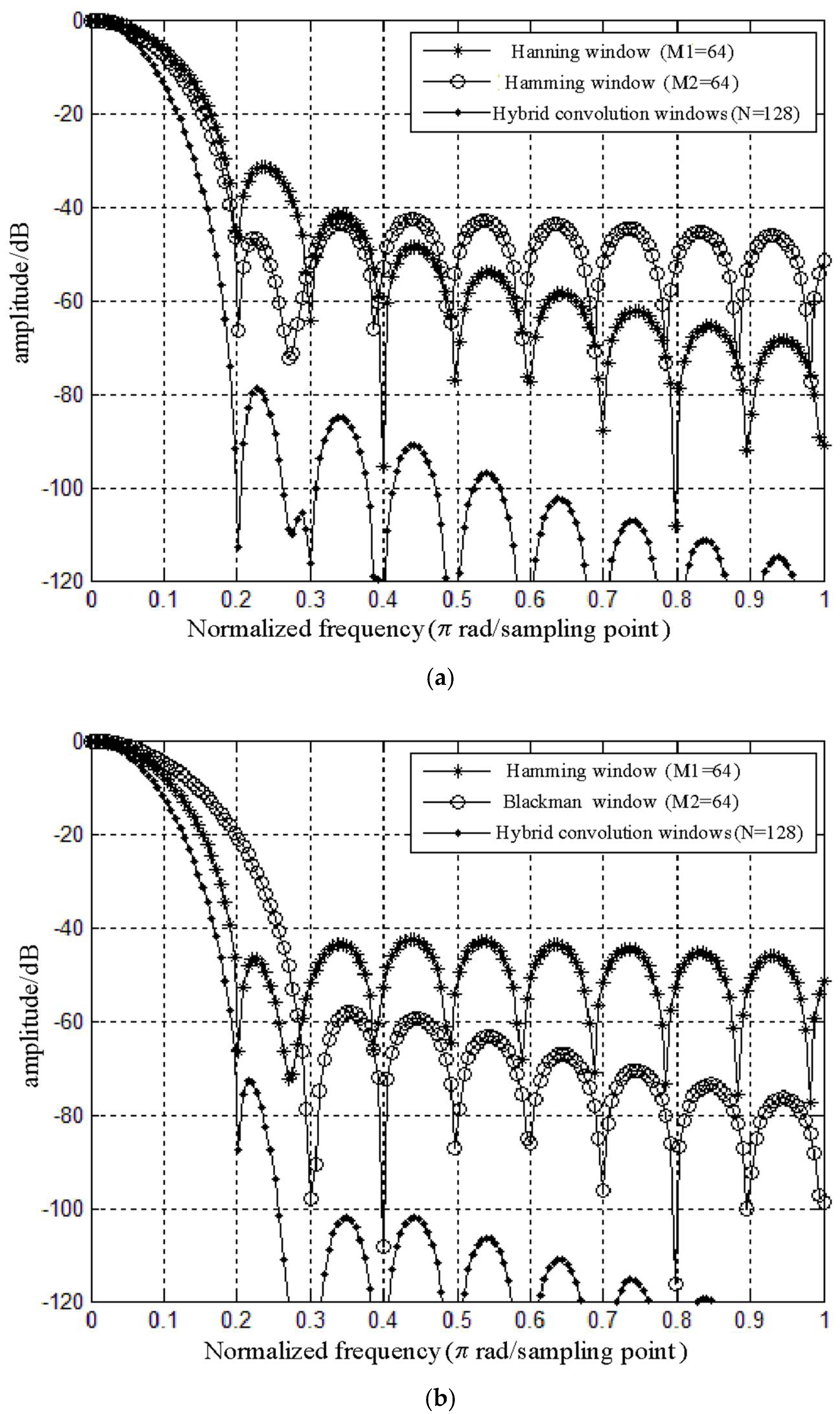
- Figure 4a is the amplitude-frequency response diagram of the hybrid convolution window that is calculated by the convolution of a Hanning window (M1 = 64) and a Hamming window (M2 = 64). From the figure we can see that the main lobe width of is the same as that of Hanning window and Hamming window with a value of . The side lobe attenuation rate is approximately 24 dB/oct, and is the sum of the other two window functions (Hanning window is 18 dB/oct and Hamming window is 6 dB/oct). The side lobe peak level is −113 dB when , and is the sum of Hanning window (−48 dB) and Hamming window (−65 dB).
- (2)
- Figure 4b is the amplitude-frequency response diagram of the hybrid convolution window that is calculated by the convolution of a Hamming window (M1 = 64) and a Blackman window (M2 = 64). From the figure we can see that the main lobe width of is the same as that of Hamming window and Blackman window with a value of . The side lobe attenuation rate is approximately 24 dB/oct, and is the sum of the other two window functions (Hamming window is 6 dB/oct and Blackman window is 6 dB/oct). The side lobe peak level is −88 dB when , and is the sum of Hamming window (−66 dB) and Blackman window (−22 dB).
- (3)
- Figure 4c is the amplitude-frequency response diagram of the hybrid convolution window that is calculated by the convolution of a Hanning window (M1 = 64) and a Hamming window (M2 = 128). From the figure we can see that the main lobe width of is the same as that of Hamming window with a value of . The side lobe attenuation rate is approximately 24 dB/oct, and is the sum of the other two window functions (Hanning window is 18 dB/oct and Hamming window is 6 dB/oct). The side lobe peak level is −113 dB when , and is the sum of Hanning window (−48 dB) and Hamming window (−65 dB).
4.3. Harmonic Accuracy Test of the Algorithm
4.4. Frequency Fluctuation Test
5. System Test
5.1. Basic Accuracy Test
5.2. Test of Temperature Compensation Effect
6. Conclusions
- (1)
- Two open–closed capacitors and other auxiliary devices are used as a standard voltage sensor, which can calibrate the transformer without power off, effectively reduce the calibration cost, and save on the calibration time.
- (2)
- A high accuracy data processing algorithm based on a hybrid convolution window is used to extract the components of the signal. The improved FFT algorithm based on the hybrid convolution window can effectively reduce the calculation error of harmonics and improve the measurement accuracy of the system.
- (3)
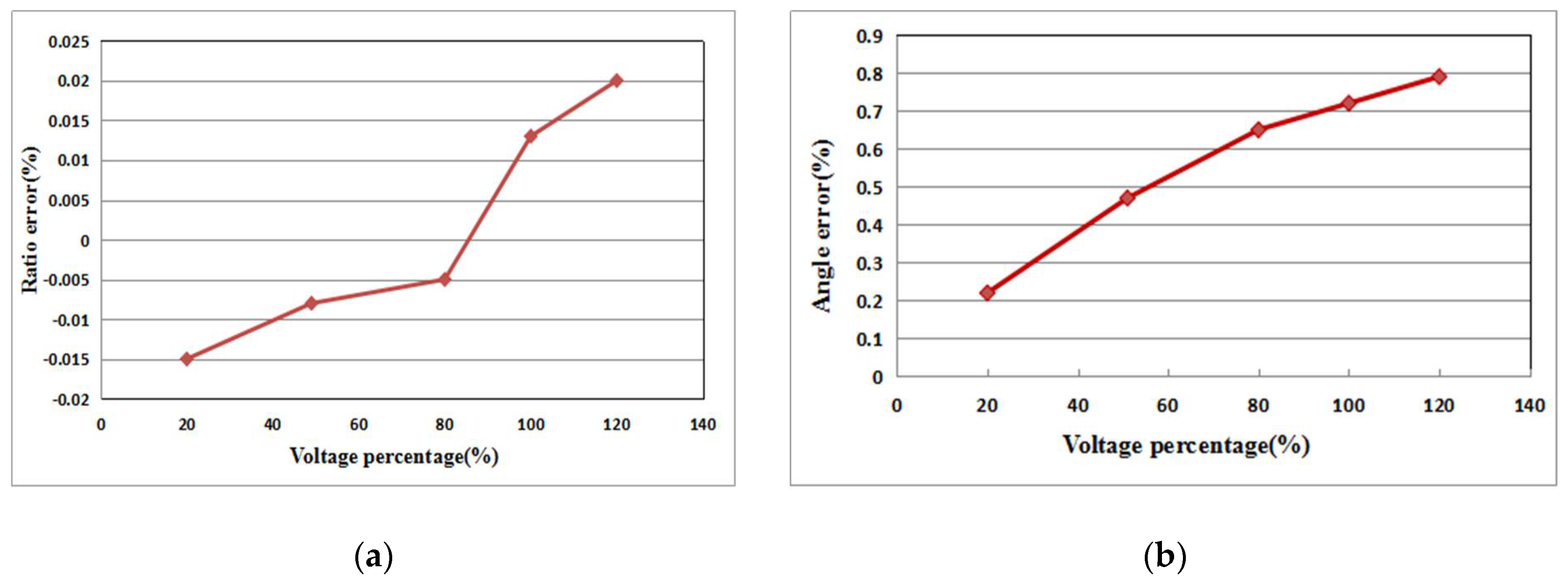
- According to a basic accuracy test, the variation of the ratio error is less than 0.037%, and the variation of the angle error is less than 0.45%. In the range of −20–50 °C, the variation of the ratio error is less than 0.05% and the variation of the angle error is less than 1.2′. The test results show that accuracy of the system can be achieved to 0.05 accuracy class, with high accuracy and convenience of operation.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Martínez, J.; Babic, S.; Akyel, C. On Evaluation of Inductance, DC Resistance, and Capacitance of Coaxial Inductors at Low Frequencies. IEEE Trans. Magn. 2014, 50. [Google Scholar] [CrossRef]
- Tajdinian, M.; Allahbakhshi, M.; Seifi, A.R.; Bagheri, A. Analytical discrete Fourier transformer based phasor estimation method for reducing transient impact of capacitor voltage transformer. IEE J. Mag. 2017, 11, 2324–2332. [Google Scholar] [CrossRef]
- Wu, W.; Xu, Y.; Xiao, X.; Hu, H. Research on Proximity Effect in Measuring Error of Active Electronic Voltage Transformers. IEEE Trans. Instrum. 2016, 65, 78–87. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Xiao, X.; Xu, Z.; Hu, H. Monitoring and analysis of electronic current transformer’s field operating errors. Measurement 2017, 112, 117–124. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Tang, D.; Hu, C.; Jiao, Y. Monitoring the metering performance of an electronic voltage transformer on-line based on cyber-physics correlation analysis. Meas. Sci. Technol. 2017, 28. [Google Scholar] [CrossRef]
- Pal, A.; Chatterjee, P.; Thorp, J.S.; Centeno, V.A. Online Calibration of Voltage Transformers Using Synchrophasor Measurements. IEEE Trans. Power Deliv. 2016, 31, 370–380. [Google Scholar] [CrossRef]
- Arnaldo, B.; Marco, F.; Roberto, O. A Simple Method for the Calibration of Traditional and Electronic Measurement Current and Voltage Transformers. IEEE Tradit. Trans. Instrum. Meas. 2009, 58, 1345–1353. [Google Scholar]
- Li, Z.; Li, H.; Zhang, Z. An accurate online calibration system based on combined clamp-shape coil for high voltage electronic current transformers. Rev. Sci. Instrum. 2013, 84, 075113. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, H.; Zhang, Z.; Luo, P. An Online Calibration Method for Electronic Voltage Transformers Based on IEC 61850-9-2. MAPAN 2014, 29, 97–105. [Google Scholar] [CrossRef]
- Li, Z.; Yan, S.; Hu, W.; Li, Z.; Xu, Y. High Accuracy On-Line Calibration System for Current Transformers Based on Clamp-Shape Rogowski Coil and Improved Digital Integrator. MAPAN 2016, 31, 119–127. [Google Scholar] [CrossRef]
- Xiao, Y.; Pan, F.; Sun, W. A method for calibration of electronic voltage transformer. Eng. J. Wuhan Univ. 2014, 47, 350–353. [Google Scholar]
- Li, Z.; Li, H.; Zhang, Z.; Luo, P.; Li, H.; Zhang, W. High-accuracy online calibration system for electronic voltage transformers with digital output. Trans. Inst. Meas. Control 2014, 36, 734–742. [Google Scholar] [CrossRef]
- Wang, L.; Du, Z. Double Air-gap Current Transformer Applied to High Voltage Transmission Line On-site Mobile Comparison System. High Volt. Eng. 2015, 41, 106–114. [Google Scholar]
- Liang, C.; Chen, K.; Tsai, Y.; Chen, N. New Electronic Current Transformer with a Self-Contained Power Supply. IEEE Trans. Power Deliv. 2015, 30, 184–192. [Google Scholar] [CrossRef]
- Liu, K.; Fu, R.; Gao, Y.; Sun, Y.; Yan, P. High-Voltage Repetition-Frequency Charging Power Supply for Pulsed Laser. IEEE Trans. Plasma Sci. 2015, 43, 1387–1392. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, X.; Tian, W.; Wang, X. Analysis of power supply from high-voltage side for electronic Current Transformer. In Proceedings of the International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Shanghai, China, 27–29 June 2017; pp. 1–6. [Google Scholar]
- Zotov, L.G.; Razinkin, V.P.; Atuchin, V.V. Controllable electronic transformer based on the resonance structure with switching capacitor forlow-rise buildings residential area power supply stabilization systems. Int. J. Electr. Power Energy Syst. 2017, 91, 117–120. [Google Scholar] [CrossRef]
- Wen, H.; Zhang, J.; Meng, Z.; Guo, S.; Li, F.; Yang, Y. Harmonic Estimation Using Symmetrical Interpolation FFT Based on Triangular Self-Convolution Window. IEEE Trans. Ind. Inform. 2015, 11, 16–26. [Google Scholar] [CrossRef]
- Dong, H.; Wang, C.; Liu, W. A novel interpolated FFT algorithm based on convolution window. In Proceedings of the 2012 IEEE 14th International Conference on Communication Technology (ICCT), Chengdu, China, 9–11 November 2012; pp. 1139–1142. [Google Scholar]
- Xu, Y.; Liu, Y.; Lu, M. Improved harmonic analysis based on quadruple-spectrum-line interpolation FFT with multiple cosine window. In Proceedings of the 2017 First International Conference on Electronics Instrumentation & Information Systems (EIIS), Harbin, China, 3–5 June 2017. [Google Scholar]
- Princy, R.M.; Bella, A.B. Performance analysis of FFT algorithm. In Proceedings of the 2017 IEEE International Conference on Electrical, Instrumentation and Communication Engineering (ICEICE), Karur, India, 27–28 April 2017; pp. 1–5. [Google Scholar]





| Harmonic Order | 1 | 3 | 5 | 7 |
|---|---|---|---|---|
| Amplitude (V) Phase (°) | 100 | 30 | 20 | 10 |
| 0 | 20 | 130 | 150 |
| Window Functions | A1 (%) | A3 (%) | A5 (%) | A7 (%) |
|---|---|---|---|---|
| Blackman | −1.0 × 10−3 | −3.02 × 10−4 | −2.03 × 10−4 | −1.0 × 10−4 |
| Hanning | 1.01 × 10−3 | 13.0 × 10−4 | 2.01 × 10−4 | 1.05 × 10−4 |
| Hamming | −8.0 × 10−4 | −2.10 × 10−4 | −2.03 × 10−4 | −7.01 × 10−5 |
| Hanning–Hamming | −3.13 × 10−6 | −3.45 × 10−5 | −7.32 × 10−5 | −2.17 × 10−5 |
| Hamming–Blackman | −1.08 × 10−6 | −1.14 × 10−5 | −1.92 × 10−6 | 2.78 × 10−5 |
| Window Functions | Φ1 (°) | Φ3 (°) | Φ5 (°) | Φ7 (°) |
|---|---|---|---|---|
| Blackman | 1.99 × 10−4 | −2.10 × 10−4 | −2.03 × 10−3 | −2.10 × 10−3 |
| Hanning | 3.0 × 10−4 | 4.87 × 10−3 | −4.02 × 10−3 | −4.21 × 10−3 |
| Hamming | 1.42 × 10−3 | −1.52 × 10−1 | 4.37 × 10−1 | −1.98 × 10−3 |
| Hanning–Hamming | 9.43 × 10−7 | −3.24 × 10−6 | −5.57 × 10−5 | 4.21 × 10−5 |
| Hamming–Blackman | 1.68 × 10−5 | −2.23 × 10−5 | −8.34 × 10−6 | 5.68 × 10−5 |
| Window Functions | A49.5 (%) | A49.7 (%) | A50 (%) | A50.2 (%) | A50.2 (%) |
| Hanning–Hamming | −0.0094 | −2.10 × 10−4 | −2.03 × 10−3 | −2.10 × 10−3 | −2.10 × 10−3 |
| Hamming–Blackman | −0.0112 | 4.87 × 10−3 | −4.02 × 10−3 | −4.21 × 10−3 | −4.21 × 10−3 |
| Window Functions | Φ49.5 (′) | Φ49.7 (′) | Φ50 (′) | Φ50.2 (′) | Φ50.5 (′) |
| Hanning–Hamming | −0.511 | −0.452 | 0 | −0.405 | −0.425 |
| Hamming–Blackman | −0.504 | −0.487 | 0 | −0.401 | −0.498 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Li, Q.; Wu, Z.; Li, Z. Research into an Online Calibration System for the Errors of Voltage Transformers Based on Open–Closed Capacitor. Energies 2018, 11, 1455. https://doi.org/10.3390/en11061455
Li Z, Li Q, Wu Z, Li Z. Research into an Online Calibration System for the Errors of Voltage Transformers Based on Open–Closed Capacitor. Energies. 2018; 11(6):1455. https://doi.org/10.3390/en11061455
Chicago/Turabian StyleLi, Zhenhua, Qiuhui Li, Zhengtian Wu, and Zhenxing Li. 2018. "Research into an Online Calibration System for the Errors of Voltage Transformers Based on Open–Closed Capacitor" Energies 11, no. 6: 1455. https://doi.org/10.3390/en11061455
APA StyleLi, Z., Li, Q., Wu, Z., & Li, Z. (2018). Research into an Online Calibration System for the Errors of Voltage Transformers Based on Open–Closed Capacitor. Energies, 11(6), 1455. https://doi.org/10.3390/en11061455





