Impact of Component Reliability on Large Scale Photovoltaic Systems’ Performance
Abstract
:1. Introduction
2. Reliability and Availability Modelling
2.1. Risk Assessment
2.2. Fault Tree Analysis
2.3. Reliability
2.4. Failure Rate and Mean Time between Failures
2.5. Failure Rates Used in This Work
2.6. Bathtub Curve
2.7. Availability
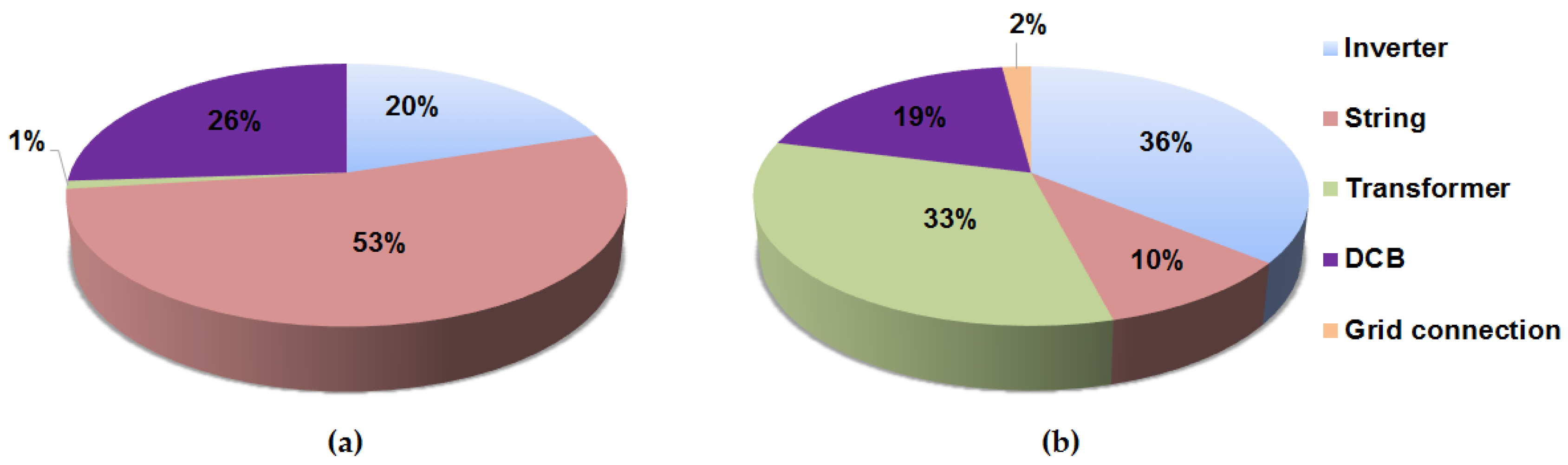
3. Subsystems Reliability
Comparison of Central Inverter vs. Transformerless String Inverter Scheme
- PV string,
- DCB,
- CI,
- transformer,
- grid connection.
- For the SI configuration, the modelled system has a different structure, as fewer PV strings are connected to each inverter. Multiple low voltage (LV) cables are then collected in an AC combiner box (ACB) with a D02 fuse switch disconnector (FSD) on the inverter side and an NH2 FSD on the transformer side. Thicker LV AC main cables connect the terminals with the transformer station. Assuming each ACB collects input from 10 inverters, then nine ACBs can be connected to a 1600 kVA transformer station. A PV plant that uses (transformerless) SI consists of the following subsystems:PV strings,
- string inverters,
- ACBs,
- transformer(s),
- grid connection.
4. Components and Subsystems for Modelling
4.1. PV String Sub-System
4.1.1. Modules
4.1.2. PV Connectors and Terminals
4.1.3. Fuse, Fuse Combinations, Switch Disconnectors and Circuit Breaker
4.1.4. Surge and Lightning Protection
4.1.5. Cables
4.1.6. Overall Failure Model
4.2. DC Combiner Box
4.3. Central Inverter
4.4. Transformer-Switchgear Station
4.5. String Inverter
4.6. AC Combiner Box
4.7. Point of Common Coupling-Grid
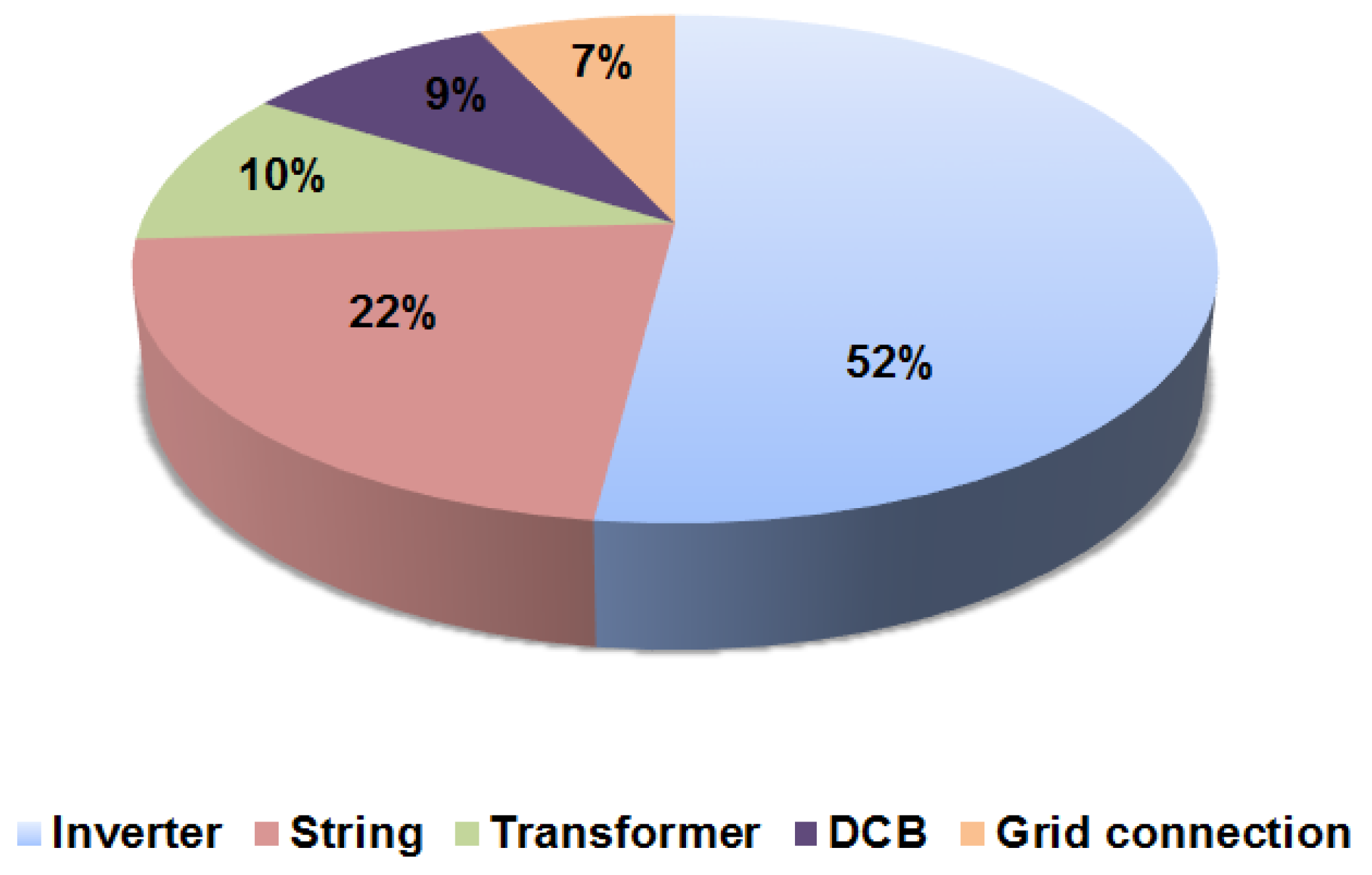
5. Impact of Reliability on System Operation
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| MVSG | MV switchgear |
| MVAC | MV AC cables |
| Tr | Transformer |
| Tl | Terminal lugs |
| BDC | DC breaker |
| BAC | AC breaker |
| IGBT | IGBT switch |
| ACF | AC filter |
| CCB | Control and communication board |
| CF | Cooling fan |
| LVAC | LV AC cables |
| Cap | DC capacitor |
| SMU | String monitoring unit |
| DCMC | DC main cable |
| SD | Switch disconnector |
| Ts | Screw terminal |
| F | Fuse |
| M | (PV) module |
| gPV | DC PV string fuse |
| PVC | PV string cable |
| Tb | Block terminal |
| C | (PV) Connector |
References
- REN 21. Renewables 2017: Global Status Report. Available online: http://www.ren21.net/gsr-2017/ (accessed on 9 August 2017).
- Golnas, A. PV System Reliability: An Operator’s Perspective. IEEE J. Photovolt. 2013, 3, 416–421. [Google Scholar] [CrossRef]
- Vargas, J.P.; Goss, B.; Gottschalg, R. Large scale PV systems under non-uniform and fault conditions. Sol. Energy 2015, 116, 303–313. [Google Scholar] [CrossRef] [Green Version]
- Granata, J.E.; Miller, S.; Stein, J.S. Sandia’s Photovoltaic Reliability and Performance Model; Sandia National Laboratories (SNL-NM): Albuquerque, NM, USA, 2011; p. 6.
- Alonso, R.; Román, E.; Sanz, A.; Martínez Santos, V.E.; Ibáñez, P. Analysis of inverter-voltage influence on distributed MPPT architecture performance. IEEE Trans. Ind. Electron. 2012, 59, 3900–3907. [Google Scholar] [CrossRef]
- Smet, V.; Forest, F.; Huselstein, J.J.; Richardeau, F.; Khatir, Z.; Lefebvre, S.; Berkani, M. Ageing and failure modes of IGBT modules in high-temperature power cycling. IEEE Trans. Ind. Electron. 2011, 58, 4931–4941. [Google Scholar] [CrossRef]
- Wohlgemuth, J.H.; Cunningham, D.W.; Monus, P.; Miller, J.; Nguyen, A. Long term reliability of photovoltaic modules. In Proceedings of the 2006 IEEE 4th World Conference on Photovoltaic Energy Conversion, Waikoloa, HI, USA, 7–12 May 2006; pp. 2050–2053. [Google Scholar]
- Dhere, N.G.; Shiradkar, N.; Schneller, E.; Gade, V. The reliability of bypass diodes in PV modules. In Proceedings of the Reliability of Photovoltaic Cells, Modules, Components, and Systems VI, San Diego, CA, USA, 26–29 August 2013. [Google Scholar]
- Köntges, M.; Kurtz, S.; Packard, C.; Jahn, U.; Berger, K.A.; Kato, K.; Friesen, T.; Liu, H.; Van Iseghem, M. Review of Failures of Photovoltaic Modules; IEA-PVPS T13-01:2014; International Energy Agency: Paris, France, 2014. [Google Scholar]
- Wu, D.; Zhu, J.; Betts, T.R.; Gottschalg, R. Degradation of interfacial adhesion strength within photovoltaic mini-modules during damp-heat exposure. Prog. Photovolt. 2014, 22, 796–809. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Li, W.; Li, S.; Wang, Y.; Xiao, W. Reliability assessment of photovoltaic power systems: Review of current status and future perspectives. Appl. Energy 2013, 104, 822–833. [Google Scholar] [CrossRef]
- Jahn, U.; Nasse, W. Operational performance of grid-connected PV systems on buildings in Germany. Prog. Photovolt. 2004, 12, 441–448. [Google Scholar] [CrossRef]
- Perdue, M.; Gottschalg, R. Energy yields of small grid connected photovoltaic system: Effects of component reliability and maintenance. IET Renew. Power Gener. 2015, 9, 432–437. [Google Scholar] [CrossRef] [Green Version]
- Hamdy, M.A.; Beshir, M.E.; Elmasry, S.E. Reliability analysis of photovoltaic systems. Appl. Energy 1989, 33, 253–263. [Google Scholar] [CrossRef]
- Hu, R.; Mi, J.; Hu, T.; Fu, M.; Yang, P. Reliability research for PV system using BDD-based fault tree analysis. In Proceedings of the 2013 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Chengdu, China, 15–18 July 2013; pp. 359–363. [Google Scholar]
- Zini, G.; Mangeant, C.; Merten, J. Reliability of large-scale grid-connected photovoltaic systems. Renew. Energy 2011, 36, 2334–2340. [Google Scholar] [CrossRef]
- Chiacchio, F.; Famoso, F.; D’Urso, D.; Brusca, S.; Aizpurua, J.I.; Cedola, L. Dynamic performance evaluation of photovoltaic power plant by stochastic hybrid fault tree automaton model. Energies 2018, 11, 306. [Google Scholar] [CrossRef]
- Akhmedjanov, F.M. Reliability Databases: State-of-the-Art and Perspectives; Report R-1235; Risö National Laboratory: Roskilde, Denmark, 2001.
- Olalla, C.; Maksimovic, D.; Deline, C.; Martinez-Salamero, L. Impact of distributed power electronics on the lifetime and reliability of PV systems. Prog. Photovolt. 2017, 25, 821–835. [Google Scholar] [CrossRef]
- Lillo-Bravo, I.; González-Martínez, P.; Larrañeta, M.; Guasumba-Codena, J. Impact of Energy Losses Due to Failures on Photovoltaic Plant Energy Balance. Energies 2018, 11, 363. [Google Scholar] [CrossRef]
- Collins, E.; Dvorack, M.; Mahn, J.; Mundt, M.; Quintana, M. Reliability and availability analysis of a fielded photovoltaic system. In Proceedings of the 2009 34th IEEE Photovoltaic Specialists Conference (PVSC), Philadelphia, PA, USA, 7–12 June 2009. [Google Scholar]
- Ahadi, A.; Ghadimi, N.; Mirabbasi, D. Reliability assessment for components of large scale photovoltaic systems. J. Power Sources 2014, 264, 211–219. [Google Scholar] [CrossRef]
- JUWI—Passion for Renewable Energies. Available online: http://www.juwi.co.uk/ (accessed on 2 August 2017).
- Zhang, P.; Wang, Y.; Xiao, W.; Li, W. Reliability evaluation of grid-connected photovoltaic power systems. IEEE Trans. Sustain. Energy 2012, 3, 379–389. [Google Scholar] [CrossRef]
- Colli, A. Failure mode and effect analysis for photovoltaic systems. Renew. Sustain. Energy Rev. 2015, 50, 804–809. [Google Scholar] [CrossRef]
- Denson, W.; Chandler, G.; Crowell, W.; Wanner, R. Non-Electronic Parts Reliability Data; IIT Research Institute: Chicago, IL, USA, 1991. [Google Scholar]
- Department of Defense of the USA. Reliability Prediction of Electronic Equipment. 1991. Available online: https://snebulos.mit.edu/projects/reference/MIL-STD/MIL-HDBK-217F-Notice2.pdf (accessed on 3 September 2017).
- Koutroulis, E.; Blaabjerg, F. Design optimization of transformerless grid-connected PV inverters including reliability. IEEE Trans. Power Electron. 2013, 28, 325–335. [Google Scholar] [CrossRef]
- Mesić, M.; Plavšić, T. The contribution of failure analyses to transmission network maintenance preferentials. Eng. Fail. Anal. 2013, 35, 262–271. [Google Scholar] [CrossRef]
- Ma, Z.J.; Thomas, S. Reliability and maintainability in photovoltaic inverter design. In Proceedings of the Annual Reliability and Maintainability Symposium, Lake Buena Vista, FL, USA, 24–27 January 2011. [Google Scholar]
- Bahaj, A. Predicting photovoltaic connector lifetime. In Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003; pp. 2833–2836. [Google Scholar]
- Zehner, M.; Hartmann, M.; Weizenbeck, J.; Gratzl, T.; Weigl, T.; Mayer, B.; Wirth, G.; Krawczynski, M.; Betts, T.; Gottschalg, R.; et al. Systematic analysis of meteorological irradiation effects. In Proceedings of the 25th European Photovoltaic Solar Energy Conference Exhibition, Valencia, Spain, 6–9 September 2010; pp. 4545–4548. [Google Scholar]
- BS 5760-2:1994. Reliability of Systems, Equipment and Components. Guide to the Assessment of Reliability; British Standards Institution: London, UK, 1994. [Google Scholar]
- Charki, A.; Bigaud, D. Availability estimation of a photovoltaic system. In Proceedings of the Annual Reliability and Maintainability Symposium, Orlando, FL, USA, 28–31 January 2013; pp. 4–8. [Google Scholar]








| Component | Λ | MTBF | R (20y) | Ref |
|---|---|---|---|---|
| PV module | 0.0152 | 16,386 | 99.80% | [16] |
| 1.14 | 218 | 91.20% | [24] | |
| 0.025 | 9963 | 99.80% | - | |
| 0.035 | 7116 | 99.70% | - | |
| 0.04 | 6227 | 99.60% | - | |
| (Thin film) | 0.137 | 1818 | 98.90% | - |
| PV Connector | 0.00024 | 1 Mio | 100.00% | [16] |
| 0.0056 | 44,476 | 99.90% | - | |
| PV string cable | 0.002 | 124,533 | 99.60% | - |
| Terminal (lug) | 0.001 | 249,066 | 99.90% | [26] |
| -(metal sleeve) | 0.0007 | 355,809 | 99.90% | [26] |
| -(screw) | 0.603 | 413 | 95.20% | [26] |
| -(stud) | 0.0007 | 355,809 | 99.90% | [26] |
| -(block) | 0.124 | 2009 | 99.00% | [27] |
| -(block) | 0.0146 | 17,059 | 99.80% | [26] |
| -(strip) | 0.0022 | 113,212 | 99.90% | [26] |
| Fuses | 0.02 | 12,453 | 99.80% | [27] |
| String Fuse | 5.71 | 43.6 | 63.20% | [24] |
| 0.065 | 3831.8 | 99.40% | - | |
| 0.063 | 3953.4 | 99.50% | - | |
| SMU | 4.9 | 50.8 | 67.40% | - |
| 1.65 | 150.9 | 87.50% | - | |
| DC switch | 0.2 | 1245 | 98.40% | [16] |
| DC main cable | 0.0483 | 5157 | 99.60% | [28] |
| AC cable | 0.013 | 19,160 | 99.90% | [28] |
| Disconnector | 0.1 | 3558.1 | 99.40% | [29] |
| String Inverter | 18.4 | 13.5 | 22.80% | [28] |
| 12.6 | 19.8 | 36.30% | [15] | |
| 15.1 | 16.5 | 29.80% | - | |
| CI | 40.29 | 8 | 3.93% | [16] |
| 74 | 3.4 | 0.26% | - | |
| 130 | 1.9 | 0.00% | - | |
| DC Capacitor | 10.1 | 24.7 | 44.40% | [30] |
| 17.8 | 14 | 23.90% | - | |
| 41.5 | 6 | 3.57% | - | |
| DC main breaker | 8.9 | 28 | 48.90% | - |
| 6.075 | 41 | 51.10% | [30] | |
| IGBT module | 11.4 | 21.9 | 40.10% | [30] |
| 8.9 | 28 | 48.90% | - | |
| AC filter caps | 2 | 124.5 | 85.10% | [30] |
| AC circuit breaker | 5.712 | 43.6 | 63.20% | [16] |
| 2.6 | 96.2 | 81.20% | [29] | |
| 8.9 | 28 | 1.00% | ||
| 6.075 | 41 | 51.10% | - | |
| CCB | 24.9 | 10 | 13.50% | [30] |
| 26.7 | 9.3 | 11.70% | - | |
| 18.3 | 13.6 | 23.00% | [15] | |
| Cooling fan | 26.7 | 9.3 | 11.70% | - |
| Transformer | 27.4 | 9.1 | 11.10% | [30] |
| 17.8 | 14 | 23.90% | - | |
| Power switch gear | 2.01 | 123.9 | 85.00% | [29] |
| 4 | 62.3 | 72.50% | [30] |
| Topology | Cable type | Length (m) |
|---|---|---|
| CI | Solar cables | 100 |
| DC main cables | 75 | |
| Inverter to transformer | 5 | |
| Transformer to PCC * | 100 | |
| SI | String | 70 |
| Inverter to ACB | 75 | |
| ACB to transformer | 100 | |
| Transformer to PCC | 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baschel, S.; Koubli, E.; Roy, J.; Gottschalg, R. Impact of Component Reliability on Large Scale Photovoltaic Systems’ Performance. Energies 2018, 11, 1579. https://doi.org/10.3390/en11061579
Baschel S, Koubli E, Roy J, Gottschalg R. Impact of Component Reliability on Large Scale Photovoltaic Systems’ Performance. Energies. 2018; 11(6):1579. https://doi.org/10.3390/en11061579
Chicago/Turabian StyleBaschel, Stefan, Elena Koubli, Jyotirmoy Roy, and Ralph Gottschalg. 2018. "Impact of Component Reliability on Large Scale Photovoltaic Systems’ Performance" Energies 11, no. 6: 1579. https://doi.org/10.3390/en11061579
APA StyleBaschel, S., Koubli, E., Roy, J., & Gottschalg, R. (2018). Impact of Component Reliability on Large Scale Photovoltaic Systems’ Performance. Energies, 11(6), 1579. https://doi.org/10.3390/en11061579





