Strategic Behavior of Retailers for Risk Reduction and Profit Increment via Distributed Generators and Demand Response Programs
Abstract
:1. Introduction
- Providing a detailed mathematical formulation for retailers’ decision-making problem, considering the possibility of the retailer to provide energy from forward contracts, spot electricity market, distributed generators, and demand response program;
- Modeling dynamic pricing approach by retailers as a demand-side management technique to modify customers’ load profile;
- Considering the customers’ welfare within the retailer’s decision-making problem through bi-level programming in which the first level is the retailer’s profit maximization, including the risk factor in the objective function, and the second level is customers’ cost minimization.
- Performing the proposed decision–making model on a test-case, considering the uncertainty of spot electricity prices and electricity demand, for a 1-week (168 h) period to show the effectiveness of the demand response program on the retailer’s profitability and risk;
2. Modeling the Retailer’s Decision-Making Problem
2.1. Uncertainty Modeling
2.2. Risk Aversion of Retailer
2.3. Problem Formulation
2.3.1. First-Level Problem
Profit Function
Risk Model
Constraints
2.3.2. Second-Level Problem
2.3.3. The Proposed Modeling Approach
3. Numerical Simulation and Case Study
3.1. Input Data of the Case Study
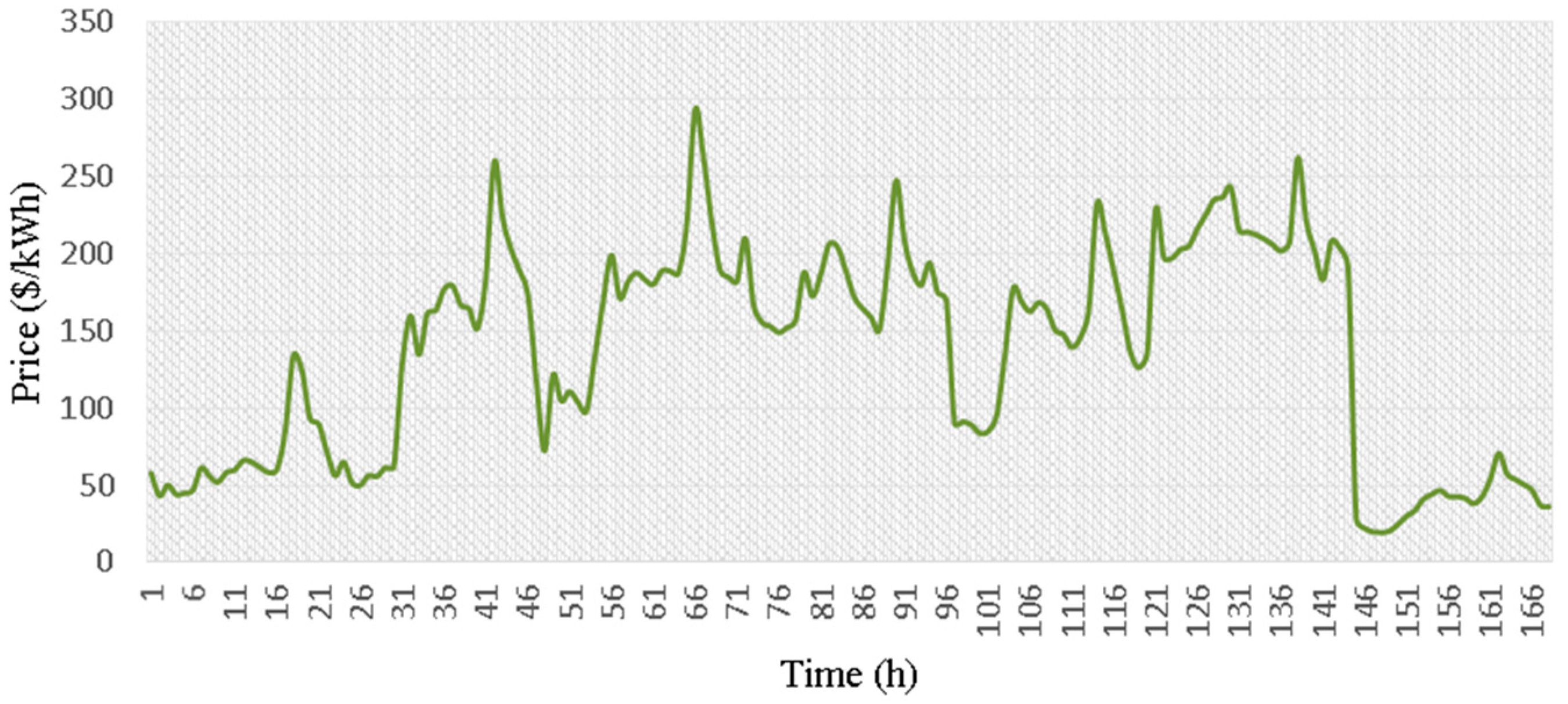
3.1.1. Spot Market Data
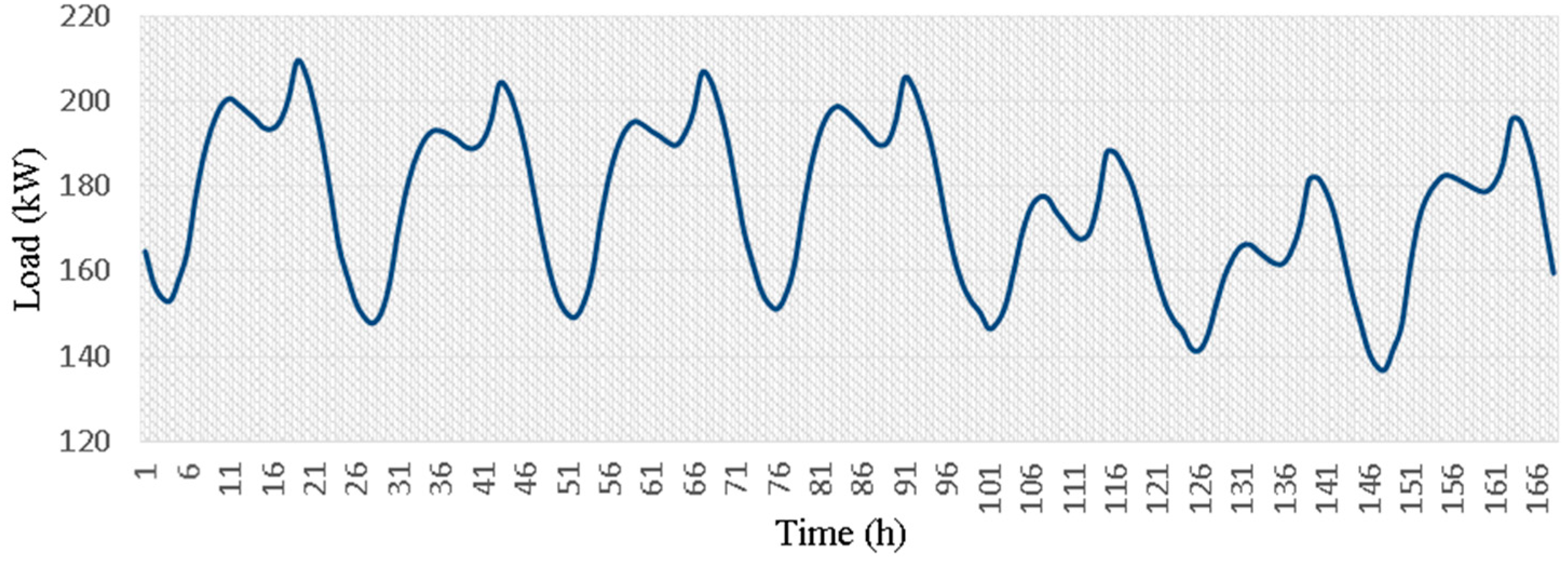
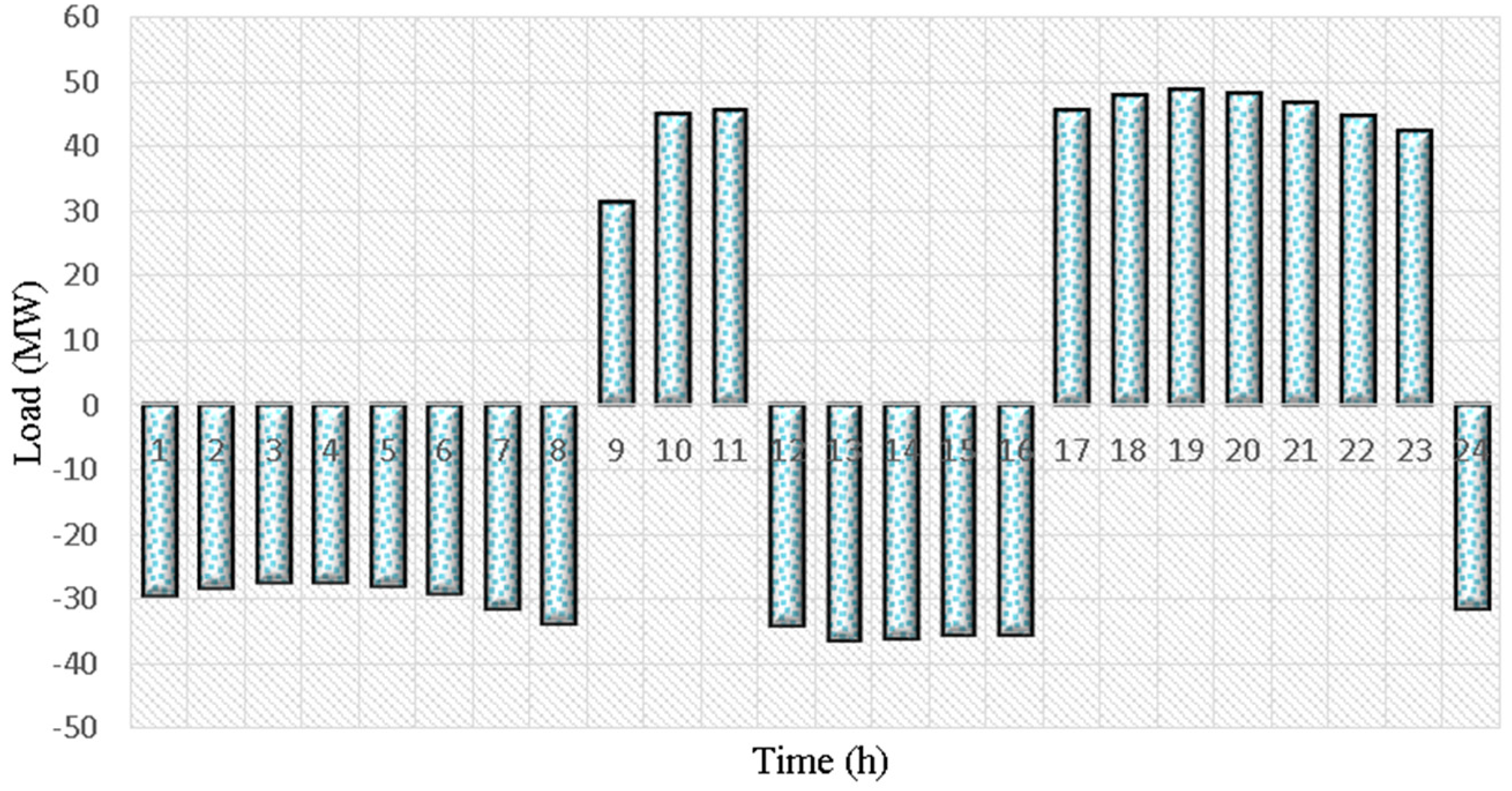
3.1.2. Load Data
3.1.3. Distributed Generators’ Data
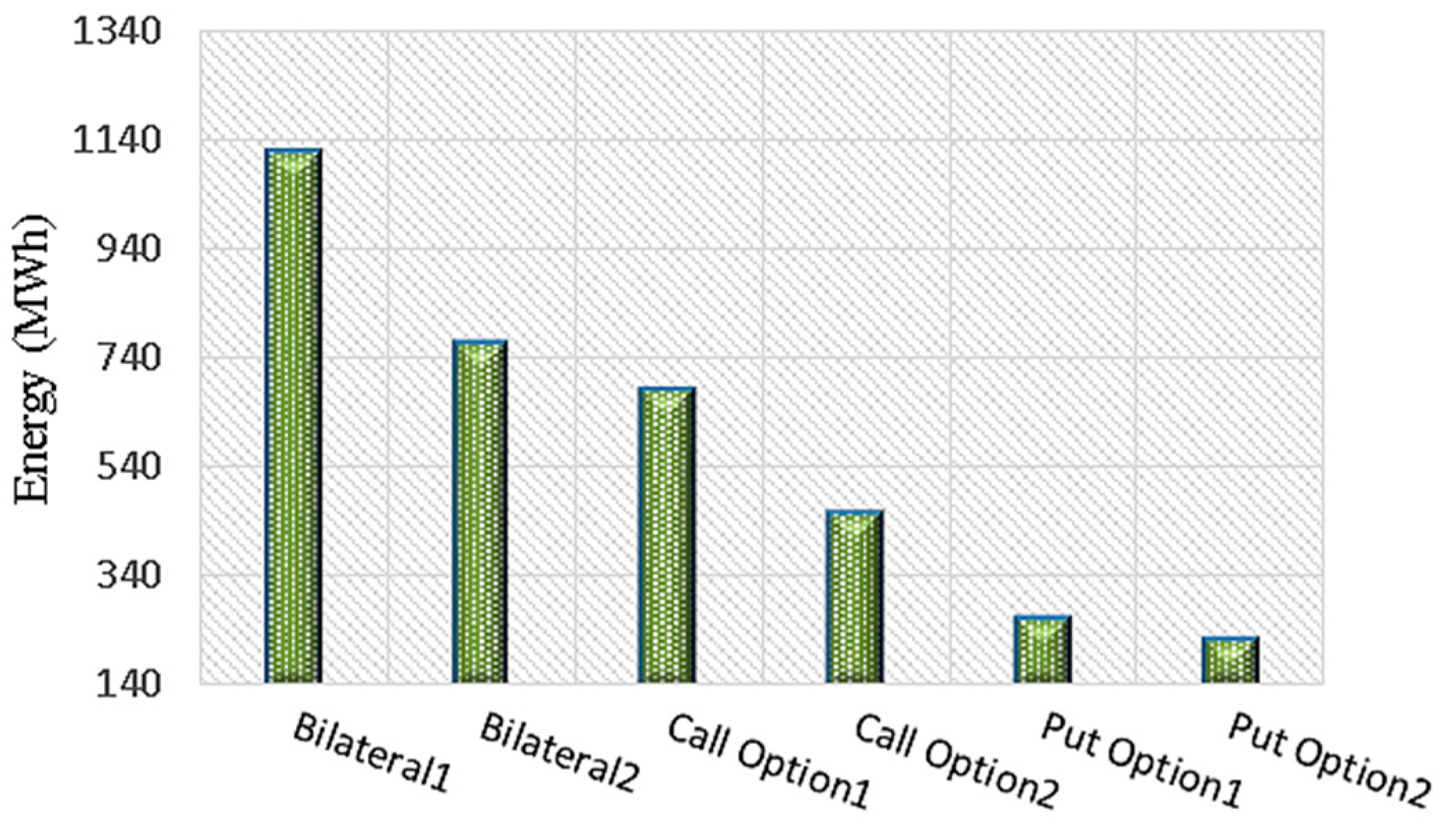
3.1.4. Contracts’ Data
3.1.5. Other Required Input Data
3.2. Results and Discussion
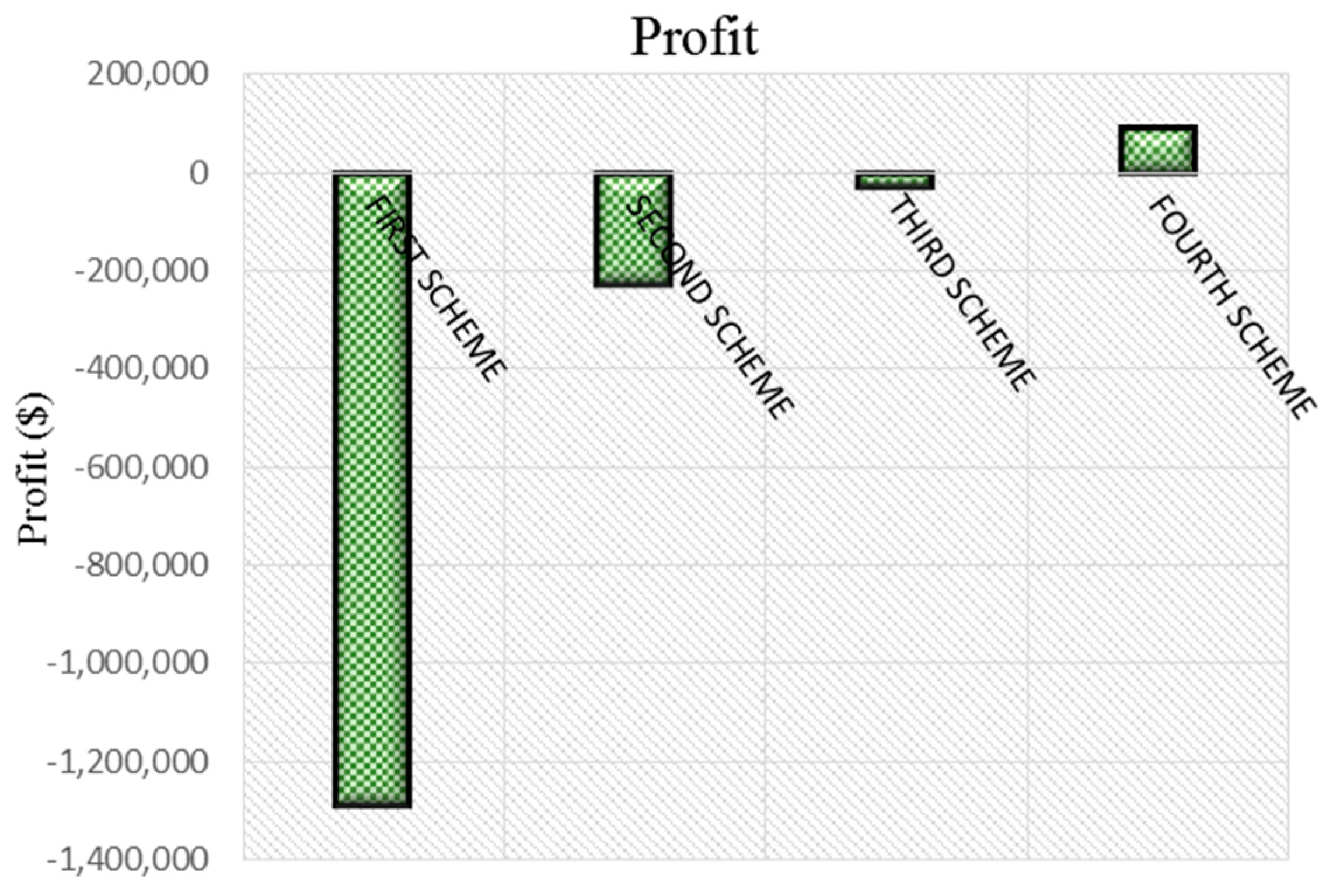
3.2.1. First Scheme: Without Forward Contracts, DGs, and DRP
3.2.2. Second Scheme: With DGs but without Forward Contracts and DRP
3.2.3. Third Scheme: With DGs and Forward Contracts but without DRP
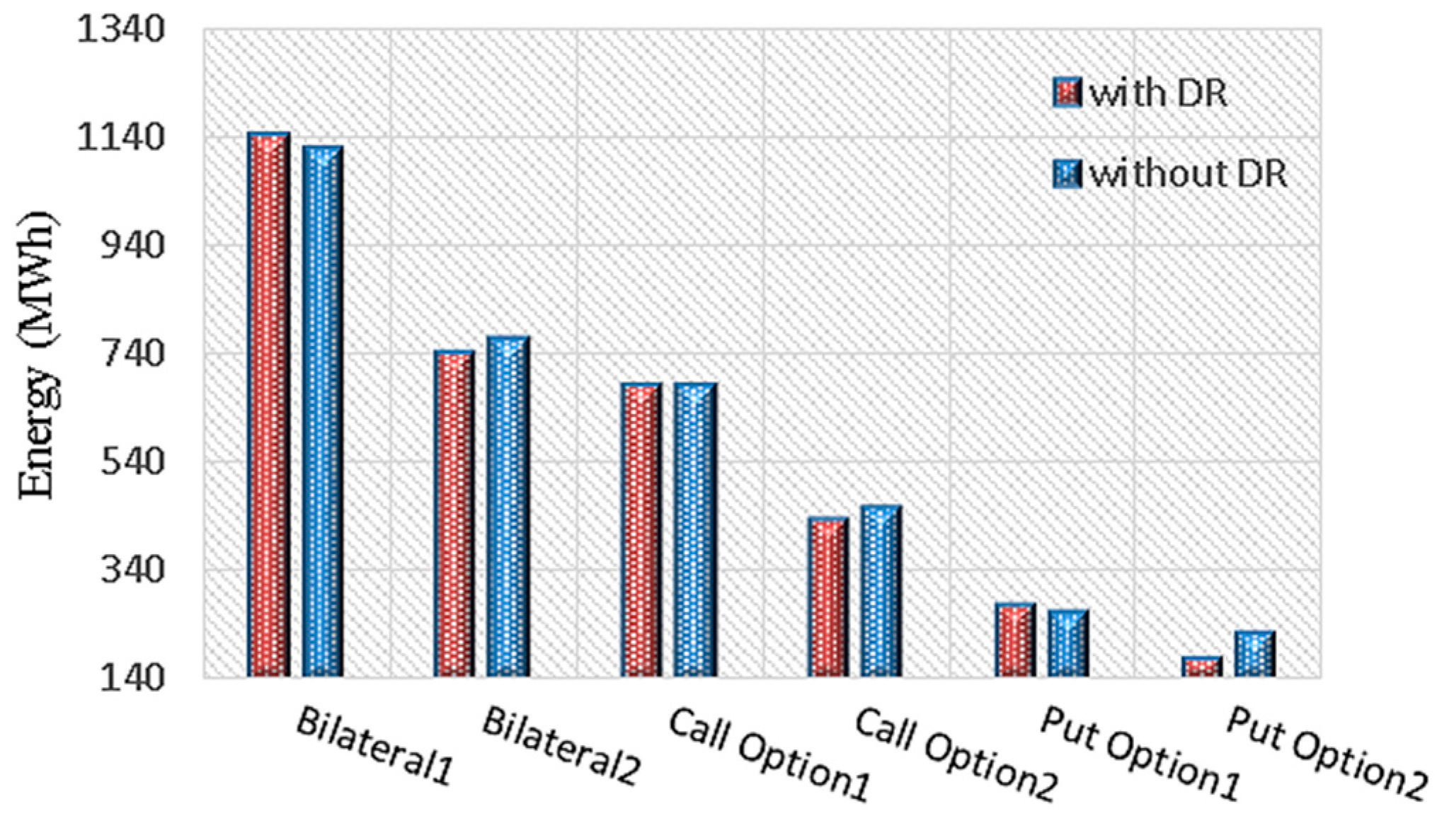
3.2.4. Fourth Scheme: With DGs, forward Contracts, and DRP
4. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| A Indices | |
| Index of uncertainty scenarios | |
| Index of scheduling time | |
| Index of customers | |
| Index of Bilateral Contracts | |
| Index of Put Options | |
| Index of Call Options | |
| Index of DGs | |
| B Parameters | |
| Number of scheduling time periods | |
| Number of spot electricity market price scenarios | |
| Number of customer’s load scenarios | |
| Total number of uncertainty scenarios | |
| Total number of Bilateral Contracts | |
| Total number of Put Options | |
| Total number of Call Options | |
| Total number of retailer’s customers | |
| Total number of DGs | |
| Probability of the spot market price scenarios | |
| Probability of the customer’s load scenarios | |
| Probability of uncertainty scenario | |
| Constant costs of the retailer | |
| Retailer’s selling price of reactive power to its customers () | |
| Contracted energy price of Bilateral Contract | |
| Minimum energy purchase limit of Bilateral Contract () | |
| Number of offer blocks of Bilateral Contract | |
| Size of each offered power block of Bilateral Contract | |
| Fixed contract price of Put Option for the retailer | |
| Contracted energy price of Put Option for the retailer | |
| Minimum energy purchase limit of Put Option | |
| Number of offer blocks of Put Option | |
| Size of each offered power block of Put Option | |
| Fixed contract price of Call Option for the retailer | |
| Contracted energy price of Call Option for the retailer | |
| Size of each offered power block of Call Option | |
| Minimum energy purchase limit of Call Option | |
| Number of offer blocks of Call Option | |
| Price of active power generation by DG unit | |
| Price of reactive power generation by DG unit | |
| Price of active energy in spot market at time | |
| Price of reactive energy in spot market at time | |
| Weighting factor of scheduling time period for risk measurement | |
| Confidence level | |
| Minimum active power generation limit of DG unit under network connection status () | |
| Maximum active power generation limit of DG unit under network connection status | |
| Minimum reactive power generation limit of DG unit under network connection status () | |
| Maximum reactive power generation limit of DG unit under network connection status () | |
| Maximum contracted power limit of Bilateral Contract | |
| Minimum contracted power limit of Bilateral Contract | |
| Minimum selling price of energy by retailer to its customers | |
| Maximum selling price of energy by retailer to its customers | |
| Average selling price of energy by retailer to its customers | |
| Energy consumption of customer at time period without implementing demand response | |
| Coefficient of maximum load reduction of each customer under demand response programs during one hour | |
| Coefficient of maximum load increment of each customer under demand response programs during one hour | |
| C Variables | |
| Profit of the retailer | |
| Revenue of the retailer | |
| Cost of buying electrical energy through Bilateral contracts | |
| Cost of buying electrical energy through Put Options | |
| Cost of buying electrical energy through Call Options | |
| Cost of providing electrical energy from DGs | |
| Energy purchased from Bilateral Contract () | |
| Energy purchased from Put Option () | |
| Binary variable indicating ratification of Bilateral Contract by the retailer | |
| Binary variable indicating ratification of Put Option by the retailer | |
| Binary variable indication execution of the Put Option by the retailer at time under scenario () | |
| Energy purchased from Call Option () | |
| Binary variable indicating ratification of Call Option by the retailer | |
| Binary variable indication execution of the Call Option by the retailer at time under scenario () | |
| Active energy generated by DG unit at time under scenario () | |
| Reactive energy generated by DG unit at time under scenario () | |
| Binary variable indicating network connection of DG unit at time under scenario | |
| Retailer’s selling price of active power to its customers at time (dynamic price) () | |
| Risk measure of the objective function | |
References
- Kirschen, D.S.; Strbac, G. Fundamentals of Power System Economics; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Nojavan, S.; Zare, K.; Mohammadi-Ivatloo, B. Risk-based framework for supplying electricity from renewable generation-owning retailers to price-sensitive customers using information gap decision theory. Int. J. Electr. Power Energy Syst. 2017, 93, 156–170. [Google Scholar] [CrossRef]
- Carrion, M.; Conejo, A.J.; Arroyo, J.M. Forward contracting and selling price determination for a retailer. IEEE Trans. Power Syst. 2007, 22, 2105–2114. [Google Scholar] [CrossRef]
- Shahidehpour, M.; Yamin, H.; Li, Z. Market Overview in Electric Power Systems. Market Operations in Electric Power Systems: Forecasting, Scheduling, and Risk Management; John Wiley & Sons: New York, NY, USA, 2002; pp. 1–20. [Google Scholar]
- Gabash, A.; Li, P.U. Reverse active-reactive optimal power flow in ADNs: Technical and economical aspects. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Dubrovnik, Croatia, 13–16 May 2014. [Google Scholar]
- Gabash, A.; Li, P.U. On variable reverse power flow-part I: Active-Reactive optimal power flow with reactive power of wind stations. Energies 2016, 9, 121. [Google Scholar] [CrossRef]
- Gabash, A.; Li, P.U. Variable reverse power flow-part II: Electricity market model and results. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015. [Google Scholar]
- Gabash, A.; Li, P.U. Active-reactive optimal power flow for low-voltage networks with photovoltaic distributed generation. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012. [Google Scholar]
- Gabash, A.; Li, P.U. Active-reactive optimal power flow in distribution networks with embedded generation and battery storage. IEEE Trans. Power Syst. 2012, 27, 2026–2035. [Google Scholar] [CrossRef]
- Gabash, A.; Li, P.U. Flexible optimal operation of battery storage systems for energy supply networks. IEEE Trans. Power Syst. 2013, 28, 2788–2797. [Google Scholar] [CrossRef]
- Kirzner, I.M. Competition and Entrepreneurship; University of Chicago Press: Chicago, IL, USA, 2015. [Google Scholar]
- Kirzner, I.M. Entrepreneurial discovery and the competitive market process: An Austrian approach. J. Econ. Lit. 1997, 35, 60–85. [Google Scholar]
- Khojasteh, M.; Jadid, S. Decision-making framework for supplying electricity from distributed generation-owning retailers to price-sensitive customers. Util. Policy 2015, 37, 1–12. [Google Scholar] [CrossRef]
- Kirschen, D.S. Demand-side view of electricity markets. IEEE Trans. Power Syst. 2003, 18, 520–527. [Google Scholar] [CrossRef]
- Marzband, M.; Fouladfar, M.H.; Akorede, M.F.; Lightbody, G.; Pouresmaeil, E. Framework for smart transactive energy in home-microgrids considering coalition formation and demand side management. Sustain. Cities Soc. 2018, 40, 136–154. [Google Scholar] [CrossRef]
- Nojavan, S.; Zare, K.; Mohammadi-Ivatloo, B. Optimal stochastic energy management of retailer based on selling price determination under smart grid environment in the presence of demand response program. Appl. Energy 2017, 187, 449–464. [Google Scholar] [CrossRef]
- Ayón, X.; Moreno, M.Á.; Usaola, J. Aggregators’ Optimal Bidding Strategy in Sequential Day-Ahead and Intraday Electricity Spot Markets. Energies 2017, 10, 450. [Google Scholar] [CrossRef]
- Eydeland, A.; Wolyniec, K. Energy and Power Risk Management: New Developments in Modeling, Pricing, and Hedging; John Wiley & Sons: New York, NY, USA, 2003; Volume 206. [Google Scholar]
- Sheikhahmadi, P.; Mafakheri, R.; Bahramara, S.; Damavandi, M.Y.; Catalão, J.P. Risk-Based Two-Stage Stochastic Optimization Problem of Micro-Grid Operation with Renewables and Incentive-Based Demand Response Programs. Energies 2018, 11, 610. [Google Scholar] [CrossRef]
- Li, Y.-P.; Li, X.-G. Power supplier’s risk types and optimal asset management reckon in biding failure. In Proceedings of the Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 557–560. [Google Scholar]
- Yu, Q.; Zhang, L. Research in bidding strategies under different price mechanisms in generation-right trading. In Proceedings of the 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC), Zhengzhou, China, 8–10 August 2011; pp. 4197–4200. [Google Scholar]
- Hatami, A.; Seifi, H.; Sheikh-El-Eslami, M.K. A stochastic-based decision-making framework for an electricity retailer: Time-of-use pricing and electricity portfolio optimization. IEEE Trans. Power Syst. 2011, 26, 1808–1816. [Google Scholar] [CrossRef]
- Tavakoli, M.; Shokridehaki, F.; Akorede, M.F.; Marzband, M.; Vechiu, I.; Pouresmaeil, E. CVaR-based energy management scheme for optimal resilience and operational cost in commercial building microgrids. Int. J. Electr. Power Energy Syst. 2018, 100, 1–9. [Google Scholar] [CrossRef]
- Tanlapco, E.; Lawarrée, J.; Liu, C.-C. Hedging with futures contracts in a deregulated electricity industry. IEEE Trans. Power Syst. 2002, 17, 577–582. [Google Scholar] [CrossRef]
- Imani, M.H.; Niknejad, P.; Barzegaran, M. The impact of customers’ participation level and various incentive values on implementing emergency demand response program in microgrid operation. Int. J. Electr. Power Energy Syst. 2018, 96, 114–125. [Google Scholar] [CrossRef]
- Act, E.P. Energy Policy Act of 2005; US Congress: Washington, DC, USA, 2005.
- Valero, S.; Ortiz, M.; Senabre, C.; Alvarez, C.; Franco, F.; Gabaldon, A. Methods for customer and demand response policies selection in new electricity markets. IET Gener. Transm. Distrib. 2007, 1, 104–110. [Google Scholar] [CrossRef]
- Ma, Z.; Billanes, J.D.; Jørgensen, B.N. Aggregation Potentials for Buildings—Business Models of Demand Response and Virtual Power Plants. Energies 2017, 10, 1646. [Google Scholar]
- Abrishambaf, O.; Ghazvini, M.A.F.; Gomes, L.; Faria, P.; Vale, Z.; Corchado, J.M. Application of a home energy management system for incentive-based demand response program implementation. In Proceedings of the 2016 27th International Workshop on Database and Expert Systems Applications (DEXA), Porto, Portugal, 5–8 September 2016; pp. 153–157. [Google Scholar]
- Yousefi, S.; Moghaddam, M.P.; Majd, V.J. Optimal real time pricing in an agent-based retail market using a comprehensive demand response model. Energy 2011, 36, 5716–5727. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Xia, X. Optimal dispatch for a microgrid incorporating renewables and demand response. Renew. Energy 2017, 101, 16–28. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Dong, Z.Y.; Wong, K.P. Robust coordination of distributed generation and price-based demand response in microgrids. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Bompard, E.; Ma, Y.; Napoli, R.; Abrate, G. The demand elasticity impacts on the strategic bidding behavior of the electricity producers. IEEE Trans. Power Syst. 2007, 22, 188–197. [Google Scholar] [CrossRef]
- Aghaei, J.; Alizadeh, M.-I.; Siano, P.; Heidari, A. Contribution of emergency demand response programs in power system reliability. Energy 2016, 103, 688–696. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Negnevitsky, M.; De Groot, M. Pool-based demand response exchange—Concept and modeling. IEEE Trans. Power Syst. 2011, 26, 1677–1685. [Google Scholar] [CrossRef]
- Marzband, M.; Azarinejadian, F.; Savaghebi, M.; Pouresmaeil, E.; Guerrero, J.M.; Lightbody, G. Smart transactive energy framework in grid-connected multiple home microgrids under independent and coalition operations. Renew. Energy 2018, 126, 95–106. [Google Scholar] [CrossRef]
- Wei, W.; Liu, F.; Mei, S. Energy pricing and dispatch for smart grid retailers under demand response and market price uncertainty. IEEE Trans. Smart Grid 2015, 6, 1364–1374. [Google Scholar] [CrossRef]
- Mahmoudi, N.; Eghbal, M.; Saha, T.K. Employing demand response in energy procurement plans of electricity retailers. Int. J. Electr. Power Energy Syst. 2014, 63, 455–460. [Google Scholar] [CrossRef]
- Dutta, G.; Mitra, K. A literature review on dynamic pricing of electricity. J. Oper. Res. Soc. 2017, 68, 1131–1145. [Google Scholar] [CrossRef]
- Karandikar, R.; Khaparde, S.; Kulkarni, S. Strategic evaluation of bilateral contract for electricity retailer in restructured power market. Int. J. Electr. Power Energy Syst. 2010, 32, 457–463. [Google Scholar] [CrossRef]
- Fotouhi Ghazvini, M.A.; Soares, J.; Morais, H.; Castro, R.; Vale, Z. Dynamic Pricing for Demand Response Considering Market Price Uncertainty. Energies 2017, 10, 1245. [Google Scholar] [CrossRef]
- Sheybani, H.R.; Buygi, M.O. Put Option Pricing and Its Effects on Day-Ahead Electricity Markets. IEEE Syst. J. 2017. [Google Scholar] [CrossRef]
- Barroso, L.A.; Rosenblatt, J.; Guimarães, A.; Bezerra, B.; Pereira, M.V. Auctions of contracts and energy call options to ensure supply adequacy in the second stage of the Brazilian power sector reform. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar]
- Rockafellar, R.T.; Uryasev, S. Conditional value-at-risk for general loss distributions. J. Bank. Financ. 2002, 26, 1443–1471. [Google Scholar] [CrossRef] [Green Version]
- Valinejad, J.; Marzband, M.; Akorede, M.F.; Barforoshi, T.; Jovanović, M. Generation expansion planning in electricity market considering uncertainty in load demand and presence of strategic GENCOs. Electr. Power Syst. Res. 2017, 15, 92–104. [Google Scholar] [CrossRef]
- Available online: http://www.gams.com (accessed on 24 April 2018).
- Available online: http://www.nyiso.com (accessed on 24 April 2018).






| DGs | Min Uptime (h) | Min Down Time (h) | Pmax (MW) | Pmin (MW) |
|---|---|---|---|---|
| DG 1 | 1 | 1 | 15 | 0 |
| DG 2 | 1 | 1 | 25 | 4 |
| DG 3 | 1 | 1 | 30 | 10 |
| DG 4 | 1 | 1 | 40 | 15 |
| DG 5 | 1 | 1 | 25 | 0 |
| Peak Load Offered Price ($/kWh) | Mid Load Offered Price ($/kWh) | Low Load Offered Price ($/kWh) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blocks | B 1 | B 2 | B 3 | B 4 | B 5 | B 1 | B 2 | B 3 | B 4 | B 5 | B 1 | B 2 | B 3 | B 4 | B 5 |
| DG 1 | 9.3 | 18.7 | 26.15 | 29.33 | 36.27 | 3.25 | 7 | 13.25 | 18.42 | 21.18 | 2.83 | 6.57 | 9.80 | 11.16 | 16.72 |
| DG 2 | 6.73 | 12.43 | 14.95 | 21.51 | 25.77 | 3.5 | 4.85 | 9.47 | 10.64 | 15.41 | 4.41 | 8.18 | 15.38 | 16.05 | 18.86 |
| DG 3 | 9.83 | 15.52 | 19.38 | 20.3 | 22.63 | 2.45 | 7.15 | 13 | 13.54 | 15.82 | 2.40 | 2.24 | 6.94 | 8.34 | 12.45 |
| DG 4 | 5.53 | 9.11 | 12.77 | 17.68 | 19.92 | 1.65 | 4.02 | 7.3 | 9.31 | 14.62 | 1.19 | 3.49 | 7.04 | 7.59 | 9.16 |
| DG 5 | 5 | 10.04 | 11.36 | 13.98 | 18.33 | 1.45 | 3.84 | 7.54 | 8.11 | 9.74 | 2.68 | 6.52 | 9.51 | 11.34 | 15.41 |
| Peak Load Offered Power (kWh) | Mid Load Offered Power (kWh) | Low Load Offered Power (kWh) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blocks | B 1 | B 2 | B 3 | B 4 | B 5 | B 1 | B 2 | B 3 | B 4 | B 5 | B 1 | B 2 | B 3 | B 4 | B 5 |
| DG 1 | 3 | 4 | 4 | 2 | 2 | 3 | 4 | 4 | 2 | 2 | 5 | 6 | 2 | 1 | 1 |
| DG 2 | 4 | 3 | 6 | 7 | 5 | 5 | 5 | 5 | 5 | 5 | 8 | 6 | 3 | 5 | 3 |
| DG 3 | 10 | 3 | 5 | 5 | 7 | 12 | 4 | 8 | 2 | 4 | 15 | 8 | 5 | 1 | 1 |
| DG 4 | 15 | 5 | 3 | 8 | 9 | 15 | 5 | 8 | 5 | 7 | 15 | 8 | 8 | 5 | 4 |
| DG 5 | 3 | 3 | 5 | 6 | 8 | 5 | 4 | 6 | 3 | 7 | 9 | 8 | 6 | 1 | 1 |
| Peak Load Offered Price ($/KVArh) | Mid Load Offered Price ($/KVArh) | Low Load Offered Price ($/KVArh) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blocks | B 1 | B 2 | B 3 | B 4 | B 5 | B 1 | B 2 | B 3 | B 4 | B 5 | B 1 | B 2 | B 3 | B 4 | B 5 |
| DG 1 | 0.33 | 0.67 | 0.93 | 1.05 | 1.13 | 0.10 | 0.22 | 0.41 | 0.58 | 0.66 | 0.12 | 0.15 | 0.25 | 0.28 | 0.42 |
| DG 2 | 0.24 | 0.44 | 0.53 | 0.77 | 0.81 | 0.11 | 0.15 | 0.30 | 0.33 | 0.48 | 0.10 | 0.18 | 0.39 | 0.40 | 0.47 |
| DG 3 | 0.35 | 0.55 | 0.69 | 0.63 | 0.71 | 0.18 | 0.22 | 0.41 | 0.37 | 0.44 | 0.11 | 0.13 | 0.15 | 0.18 | 0.31 |
| DG 4 | 0.20 | 0.28 | 0.40 | 0.55 | 0.62 | 0.15 | 0.19 | 0.23 | 0.29 | 0.40 | 0.13 | 0.15 | 0.16 | 0.17 | 0.22 |
| DG 5 | 0.18 | 0.36 | 0.36 | 0.44 | 0.57 | 0.15 | 0.17 | 0.24 | 0.25 | 0.27 | 0.12 | 0.14 | 0.21 | 0.28 | 0.38 |
| Peak Load Offered Power (KVArh) | Mid Load Offered Power (KVArh) | Low Load Offered Power (KVArh) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Blocks | B 1 | B 2 | B 3 | B 4 | B 5 | B 1 | B 2 | B 3 | B 4 | B 5 | B 1 | B 2 | B 3 | B 4 | B 5 |
| DG 1 | 2 | 2 | 2 | 1 | 1 | 1.5 | 2 | 2 | 1 | 1 | 3 | 3.5 | 1 | 0.5 | 0.5 |
| DG 2 | 2 | 1.5 | 3 | 4 | 2 | 3 | 2 | 2 | 2 | 2 | 4.5 | 2.5 | 1.5 | 2 | 1.5 |
| DG 3 | 5 | 2 | 2 | 2 | 3 | 7 | 2 | 6 | 1 | 2 | 8 | 4 | 2 | 1 | 0.5 |
| DG 4 | 10 | 2 | 1 | 3 | 4 | 10 | 2 | 3 | 2 | 4 | 9 | 4 | 4 | 2 | 2.5 |
| DG 5 | 1.5 | 1 | 2 | 3 | 5 | 2 | 1.5 | 2 | 2 | 3 | 5 | 4 | 3.5 | 0.5 | 0.5 |
| Contracts | Prepayment ($/MW) | Minimum Power (MW) | Maximum Power (MW) |
|---|---|---|---|
| Bilateral 1 | 0 | 1.5 | 12 |
| Bilateral 2 | 0 | 0.5 | 10 |
| Call option 1 | 25 | 0 | 8 |
| Call option 2 | 30 | 0 | 9 |
| Put option 1 | 10 | 0.25 | 5 |
| Put option 2 | 12 | 0.2 | 6 |
| Peak Load Price | Mid Load Price | Low Load Price | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ($/kWh) | ($/kWh) | ($/kWh) | |||||||
| Step | S 1 | S 2 | S 3 | S 1 | S 2 | S 3 | S 1 | S 2 | S 3 |
| Bilateral 1 | 62 | 81 | 106 | 50 | 75 | 95 | 80 | 95 | 125 |
| Bilateral 2 | 68 | 106 | 146 | 56 | 80 | 102 | 88 | 116 | 150 |
| Call option 1 | 80 | 82.5 | 85 | 80 | 82.5 | 85 | 95 | 115 | 143 |
| Call option 2 | 112 | 126 | 151 | 90 | 95 | 100 | 120 | 145 | 169 |
| Put option 1 | 110 | 125 | 136 | 90 | 105 | 115 | 115 | 120 | 140 |
| Put option 2 | 124 | 139 | 156 | 110 | 132 | 140 | 124 | 139 | 156 |
| Peak Load Power | Mid Load Power | Low Load Power | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (kWh) | (kWh) | (kWh) | |||||||
| Step | S 1 | S 2 | S 3 | S 1 | S 2 | S 3 | S 1 | S 2 | S 3 |
| Bilateral 1 | 3 | 4 | 5 | 4 | 4 | 4 | 3 | 2 | 7 |
| Bilateral 2 | 3 | 3 | 4 | 3.3 | 3.3 | 3.4 | 3 | 4 | 3 |
| Call option 1 | 1 | 3 | 4 | 2 | 2 | 4 | 2 | 3 | 2 |
| Call option 2 | 2 | 2 | 5 | 3 | 3 | 3 | 2 | 4 | 3 |
| Put option 1 | 1 | 2 | 2 | 2 | 1 | 2 | 0 | 3 | 2 |
| Put option 2 | 2 | 2 | 2 | 2 | 1 | 3 | 1 | 3 | 2 |
| Risk aversion factor | 0.5 | |
| Confidence level | 95% | |
| Weighting factor | 1 | |
| Maximum selling price | 90 ($/MWh) | |
| Average selling price | 63 ($/MWh) | |
| Minimum selling price | 54 ($/MWh) | |
| Retailer’s constant costs | 35,000$ |
| For 63 ($/MWh) | For 72 ($/MWh) | |
|---|---|---|
| Net profit | −226,035 | 19,236.97 |
| Payment to spot market | 1,115,485 | 1,158,658 |
| Payment to DGs | 846,242 | 849,171.7 |
| For 63($/MWh) | For 65($/MWh) | |
|---|---|---|
| Net profit | −29,790 | 11,630 |
| Payment to spot market | 626,425 | 596,420 |
| Payment to DGs | 791,614 | 792,744 |
| Payment to contracts | 347,442 | 370,194 |
| For 60 ($/MWh) | For 63 ($/MWh) | |
|---|---|---|
| Net profit | 238 | 94,043 |
| Payment to spot market | 566,805 | 612,408 |
| Payment to DGs | 717,642 | 699,785 |
| Payment to contracts | 348,357 | 329,780 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini Imani, M.; Zalzar, S.; Mosavi, A.; Shamshirband, S. Strategic Behavior of Retailers for Risk Reduction and Profit Increment via Distributed Generators and Demand Response Programs. Energies 2018, 11, 1602. https://doi.org/10.3390/en11061602
Hosseini Imani M, Zalzar S, Mosavi A, Shamshirband S. Strategic Behavior of Retailers for Risk Reduction and Profit Increment via Distributed Generators and Demand Response Programs. Energies. 2018; 11(6):1602. https://doi.org/10.3390/en11061602
Chicago/Turabian StyleHosseini Imani, Mahmood, Shaghayegh Zalzar, Amir Mosavi, and Shahaboddin Shamshirband. 2018. "Strategic Behavior of Retailers for Risk Reduction and Profit Increment via Distributed Generators and Demand Response Programs" Energies 11, no. 6: 1602. https://doi.org/10.3390/en11061602
APA StyleHosseini Imani, M., Zalzar, S., Mosavi, A., & Shamshirband, S. (2018). Strategic Behavior of Retailers for Risk Reduction and Profit Increment via Distributed Generators and Demand Response Programs. Energies, 11(6), 1602. https://doi.org/10.3390/en11061602






