RANS and Hybrid RANS-LES Simulations of an H-Type Darrieus Vertical Axis Water Turbine
Abstract
:1. Introduction
2. Reference Experimental Set Up
3. Methodology
3.1. Computational Domain
3.2. Mesh Generation
3.3. URANS k-ω SST Simulation Set-Up
4. URANS Model Convergence
5. DES Model Adaptation
6. Results
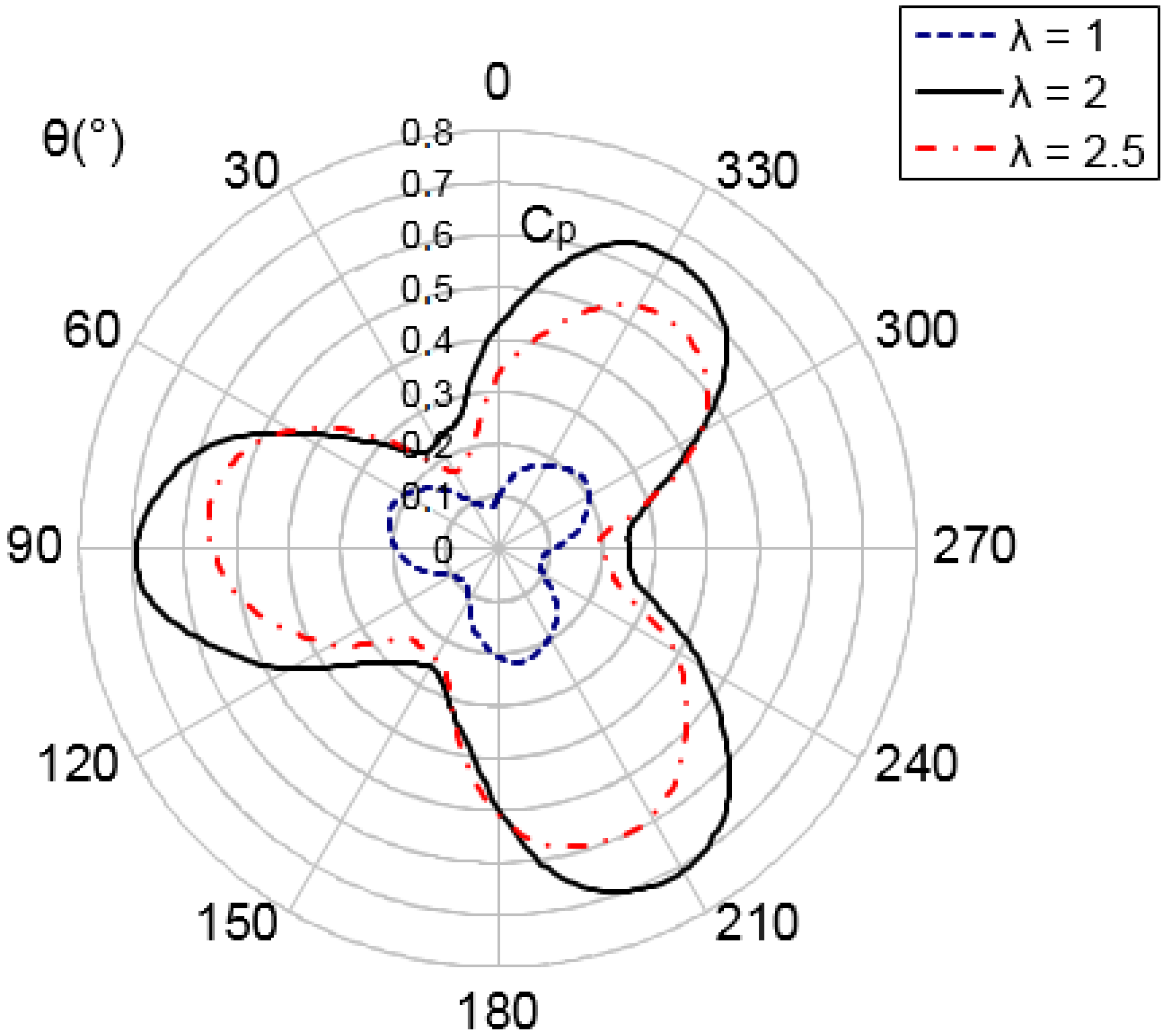
6.1. Power Coefficient
6.2. Turbulent Viscosity Ratio (TVR)
6.3. Vorticity Field
6.4. 3D Visualization of Vortex Structures Using Q-Criterion
6.5. Computational Costs
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hall, T.J. Numerical Simulation of a Cross Flow Marine Hydrokinetic Turbine. Master’s Thesis, University of Washigton, Seattle, WA, USA, 2012. [Google Scholar]
- Antheaume, S.; Maitre, T.; Achard, J. Hydraulic darrieus turbines efficiency for free fluid flow conditions versus power farms conditions. Renew. Energies 2008, 33, 2186–2198. [Google Scholar] [CrossRef]
- Dai, Y.M.; Lam, W. Numerical Study of Straight-bladed Darrieus-type Tidal Turbine. ICE Energy 2009, 162, 67–76. [Google Scholar] [CrossRef]
- Lain, S.; Osorio, C. Simulation and Evaluation of a Straight-bladed Darrieus-type Cross Flow Marine Turbine. J. Sci. Ind. Res. (JSIR) 2010, 69, 906–912. [Google Scholar]
- Nabavi, Y. Numerical Study of the Ducted Shape Effect on the Performance of a Ducted Vertical Axis Tidal Turbine. Master’s Thesis, The University of British Columbia, Vancouver, BC, Canada, 2008. [Google Scholar]
- Rawlings, G.W. Parametric Characterization of an Experimental Vertical Axis Hydro Turbine. Master’s Thesis, The University of British Columbia, Vancouver, BC, Canada, 2008. [Google Scholar]
- Ferreira, C.J.; Bijl, H.; van Bussel, G.; van Kuik, G. Simulating Dynamic Stall in a 2D VAWT: Modeling Strategy, Verification and Validation with Particle Image Velocimetry Data. J. Phys. Conf. Ser. 2007, 75, 012023. [Google Scholar] [CrossRef]
- Lei, H.; Zhou, D.; Bao, Y.; Li, Y.; Han, Z. Three-dimensional Improved Delayed Detached Eddy Simulation of a two-bladed vertical axis wind turbine. Energy Convers. Manag. 2017, 133, 235–248. [Google Scholar] [CrossRef]
- Maître, T.; Amet, E.; Pellone, C. Modeling of the Flow in a Darrieus Water Turbine: Wall Grid Refinement Analysis and Comparison with Experiments. Renew. Energy 2013, 51, 497–512. [Google Scholar] [CrossRef]
- Marsh, P.; Ranmuthugala, D.; Penesis, I.; Thomas, G. Three Dimensional Numerical Simulations of a Straight-Bladed Vertical Axis Tidal Turbine. In Proceedings of the 18th Australasian Fluid Mechanics Conference, Launceston, Australia, 3–7 December 2012. [Google Scholar]
- Pellone, C.; Maître, T.; Amet, E. 3D RANS Modeling of a Cross Flow Water Turbine. In Proceedings of the SimHydro: New Trends in Simulation Hydroinformatics and 3D modeling, Nice, France, 12–14 September 2012. [Google Scholar]
- Amet, E. Simulation Numerique d’une Hydrolienne à Axe Vertical de Type Darrieus. Ph.D. Thesis, Institut Polytechnique Grenoble, Grenoble, France, 2009. [Google Scholar]
- Eca, L.; Hoekstra, M. A Verification Exercise for Two 2-D Steady Incompressible Turbulent Flows. In Proceedings of the ECCOMAS European Congress on Computational Methods in Applied Sciences and Engineering, Jyväskylä, Finland, 24–28 July 2004. [Google Scholar]
- Spalart, P.R.; Jou, W.-H.; Strelets, M.; Allmaras, S. Comments on the Feasibility of LES for Wings, and on a Hybrid RANS/LES Approach. In Proceedings of the Advances in DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Shur, M.; Spalart, P.R.; Strelets, M.; Travin, A. Detached-eddy simulation of an airfoil at high angle of attack. In Proceedings of the Engineering Turbulence Modelling and Experiments-4, Corsica, France, 24–26 May 1999. [Google Scholar]
- Spalart, P.R. Young-Person’s Guide to Detached-Eddy Simulation Grids; NASA/CR-2001-211032; NASA Langley Research Center: Hampton, VA, USA, 2001.
- Bussiere, M. The Experimental Investigation of Vortex Wakes from Oscillating Airfoils. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2012. [Google Scholar]
- Gorle, J.M.; Chatellier, L.; Pons, F.; Ba, M. Flow and Performance analysis of H-Darrieus hydro turbine in a confined flow: A computational and experimental study. J. Fluids Struct. 2016, 66, 382–402. [Google Scholar] [CrossRef]
- Marsh, P.; Ranmuthugala, D.; Penesis, I.; Thomas, G. Three-dimensional Numerical Simulations of a Straight-Bladed Vertical Axis Tidal Turbine Investigating Power Output, Torque Ripple and Mounting Forces. Renew. Energy 2015, 83, 67–77. [Google Scholar] [CrossRef]














| Mesh Size | First Row Thickness (mm) | Growth Rate | Number of Layers | Number of Elements | Average Y+ at the Blades | Average Power Coefficient |
|---|---|---|---|---|---|---|
| Coarse (M4) | 0.106 | 1.1 | 17 | 514,741 | 16.12 | 0.412 |
| Medium (M3) | 0.015 | 1.1 | 40 | 3,954,000 | 2.15 | 0.440 |
| Fine (M2) | 0.005 | 1.12 | 45 | 8,016,441 | 0.73 | 0.457 |
| Extrafine (M1) | 0.003 | 1.12 | 50 | 11,355,960 | 0.43 | 0.463 |
| Mesh Sizes | Calculated Order of Accuracy (p) | Apparent Convergence Condition | Grid Convergence Index | |
|---|---|---|---|---|
| M3 M2 M1 | 1.87 | 0.353 | 0.487 | 0.031 |
| λ | Exp | Num 3D [11] | Num 3D |
|---|---|---|---|
| 1 | 0.127 | 0.055 | 0.153 |
| 2 | 0.345 | 0.460 | 0.457 |
| 2.5 | 0.282 | - | 0.393 |
| Turbulence Model | Number of Time Steps | Number of Iterations | Total Number of Iterations | Iteration Time (s) | Simulation Time (days) |
|---|---|---|---|---|---|
| URANS | 1800 | 75 | 135000 | 6.4 | ~10 |
| DES | 2060 | 75 | 154500 | 16.4 | ~30 |
| DDES | 2060 | 75 | 154500 | 16.4 | ~30 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mejia, O.D.L.; Quiñones, J.J.; Laín, S. RANS and Hybrid RANS-LES Simulations of an H-Type Darrieus Vertical Axis Water Turbine. Energies 2018, 11, 2348. https://doi.org/10.3390/en11092348
Mejia ODL, Quiñones JJ, Laín S. RANS and Hybrid RANS-LES Simulations of an H-Type Darrieus Vertical Axis Water Turbine. Energies. 2018; 11(9):2348. https://doi.org/10.3390/en11092348
Chicago/Turabian StyleMejia, Omar D. Lopez, Jhon J. Quiñones, and Santiago Laín. 2018. "RANS and Hybrid RANS-LES Simulations of an H-Type Darrieus Vertical Axis Water Turbine" Energies 11, no. 9: 2348. https://doi.org/10.3390/en11092348
APA StyleMejia, O. D. L., Quiñones, J. J., & Laín, S. (2018). RANS and Hybrid RANS-LES Simulations of an H-Type Darrieus Vertical Axis Water Turbine. Energies, 11(9), 2348. https://doi.org/10.3390/en11092348







