Crack Patterns in Heterogenous Rocks Using a Combined Phase Field-Cohesive Interface Modeling Approach: A Numerical Study
Abstract
:1. Introduction
1.1. Experimental Investigations
1.2. Numerical Investigations
- Methods based on continuum damage mechanics (CDM) encompass the stiffness degradation, by defining a set of internal-damage variables [21]. In their local forms, CDM models suffer from well-known pathological sensitivity of the corresponding estimations on the spatial discretization (finite element mesh) due to the loss of ellipticity of the corresponding governing equations. To mitigate such deficiency, integral regularization schemes and gradient-enhanced formulations have been proposed [22,23,24,25,26], apart from the alternative procedures introduced by Areias and coauthors [27] by combining the local damage formulation with local re-meshing techniques.
- Explicit crack tools can be employed to envisage a strong discontinuity in the displacement field. They rely on either the enrichment of the nodal displacement field at the element level using the partition of unity methods (PUM) [28,29,30], or the enrichment of the strain field (enhanced FEM, E-FEM) [31,32,33,34].
1.3. Objectives and Organization
2. Fundamentals of the Phase Field Approach for Brittle Fracture
2.1. Basic Concepts
2.2. Numerical Implementation
3. Bulk Failure Predictions
3.1. Validation of the Developed PF Approach for Fracture Using the Brazilian Splitting Test
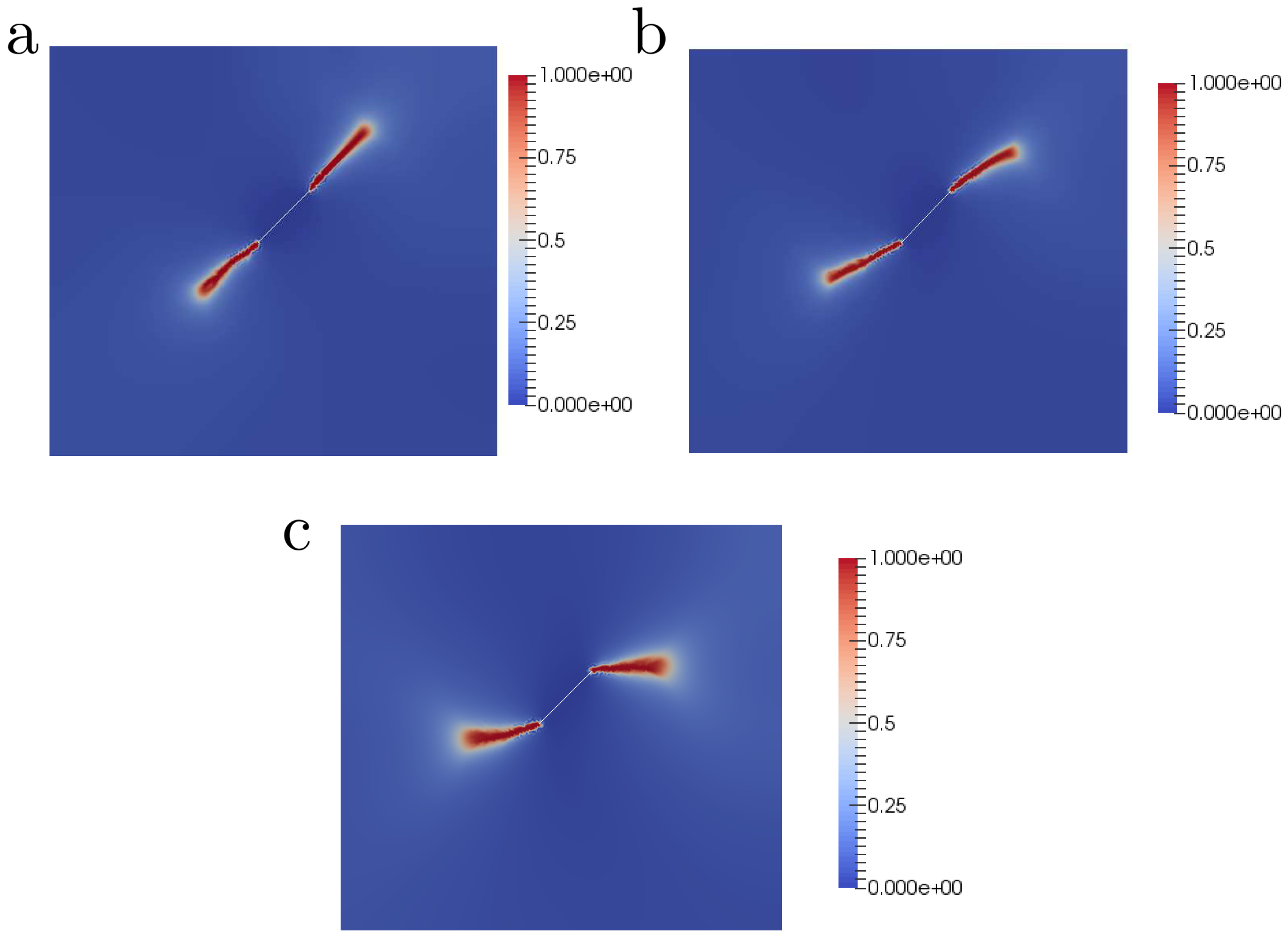
3.2. Numerical Predictions of Rock Fracture: Estimation of Damage Patterns Various Load Cases for Specimens with Multiple Flaws
3.2.1. Uniaxial Compression Test
3.2.2. Uniaxial Tensile Test
3.2.3. Compressive-Traction and Traction-Traction Tests
4. Coupling the PF Approach for Rock Fracture and the Interface Cohesive Zone Model: Application to Heterogeneous Media
4.1. General Aspects
4.2. Variational Form and Finite Element Formulation
5. Fracture Analysis in Heterogeneous Rock Masses Using the PF-CZM Approach
5.1. General Considerations
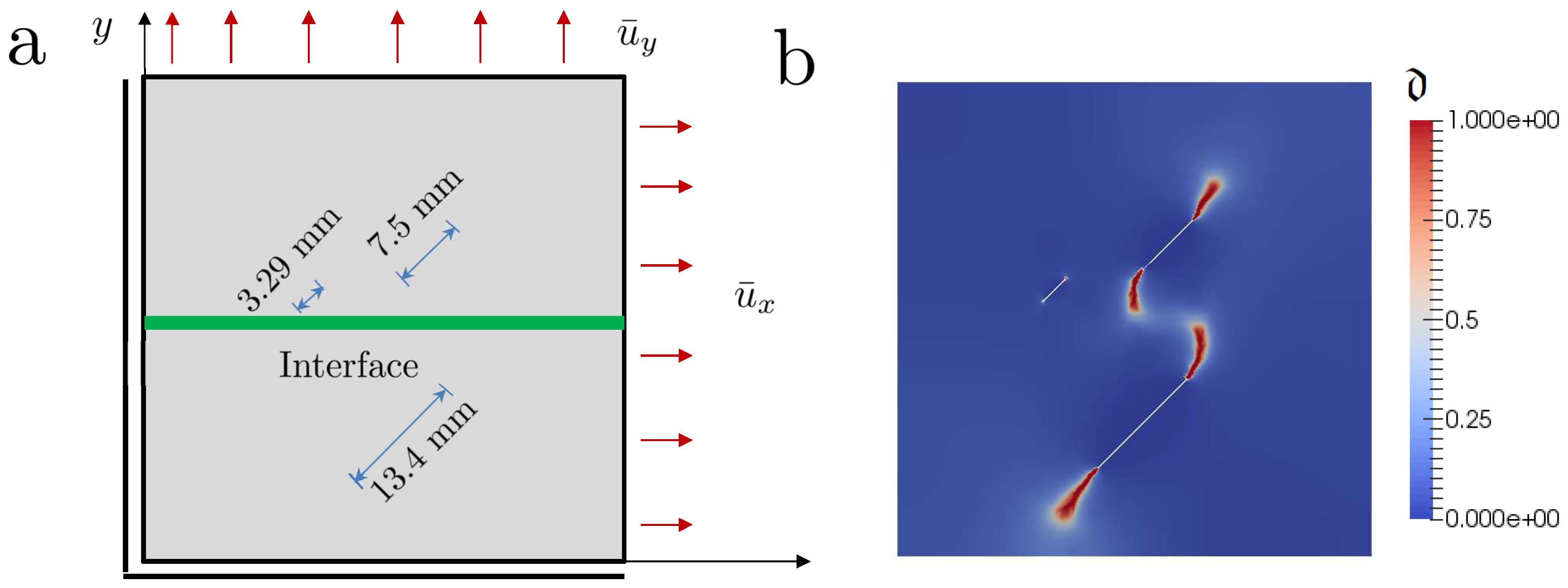
5.2. Application to Rock Salt Fracture with Inclined Interfaces
5.3. Numerical Investigation: Specimen with Multiple Flaws and Presence of Interfaces
5.3.1. Specimen with Two Inclined Flaws and a Horizontal Joint
5.3.2. Specimen with Three Inclined Flaws
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hoek, E.; Bieniawski, Z.T. Brittle Fracture Propagation in Rock under Compression. Int. J. Fract. 1984, 26, 276–294. [Google Scholar] [CrossRef]
- Hoek, E. Brittle failure of rocks in rock mechanics in engineering practice. In Rock Mechanics in Engineering Practice; Stagg, K.G., Zienkiewicz, O.C., Eds.; Wiley: New York, NY, USA, 1968; pp. 99–124. [Google Scholar]
- Lajtai, E.Z. Brittle Fracture in Compression. Int. J. Fract. 1974, 10, 525–536. [Google Scholar] [CrossRef]
- Ingraffea, A.R.; Heuze, F.E. An Analysis of Discrete Fracture Propagation in Rock Loaded in Compression. In Proceedings of the 18th U.S. Symposium on Rock Mechanics, Keystone, Colorado, CO, USA, 22–24 June 1977. [Google Scholar]
- Suits, L.D.; Sheahan, T.C.; Wong, L.N.Y.; Einstein, H.H. Using high speed video imaging in the study of cracking processes in rock. Geotech. Test. J. 2009, 32, 164–180. [Google Scholar] [CrossRef]
- Bobet, A. Numerical simulation of initiation of tensile and shear cracks. In Proceedings of the DC Rocks (2001) the 38th US Symposium on Rock Mechanics (USRMS), Washington, DC, USA, 7–10 July 2011. [Google Scholar]
- Yang, S.Q.; Yang, D.S.; Jing, H.W.; Li, Y.H.; Wang, S.Y. An experimental study of the fracture coalescence behaviour of brittle sandstone specimens containing three fissures. Rock Mech. Rock Eng. 2012, 45, 563–582. [Google Scholar] [CrossRef]
- Reyes, O.; Einstein, H.H. Failure mechanisms of fractured rock—A fracture coalescence model. In Proceedings of the 7th International Conference on Rock Mechanics, International Society for Rock Mechanics, Aachen, Germany, 16–20 September 1991. [Google Scholar]
- Wong, L.; Einstein, H. Crack coalescence in molded gypsum and carrara marble: Part 1. Macroscopic observations and interpretation. Rock Mech. Rock Eng. 2009, 42, 475–511. [Google Scholar] [CrossRef]
- Wong, R.; Chau, K.; Tang, C.; Lin, P. Analysis of crack coalescence in rock-like materials containing three flaws—Part I: Experimental approach. Int. J. Rock Mech. 2001, 38, 909–924. [Google Scholar] [CrossRef]
- Sagong, M.; Bobet, A. Coalescence of multiple flaws in a rock-model material in uniaxial compression. Int. J. Rock Mech. Min. Sci. 2002, 39, 229–241. [Google Scholar] [CrossRef]
- Ma, G.W.; Dong, Q.Q.; Fan, L.F.; .Gao, J. An investigation of non-straight fissures cracking under uniaxial compression. Eng. Fracture Mechanics 2018, 15, 300–310. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T. Cracking particles: A simplified meshfree method for arbitrary evolving cracks. Int. J. Numer. Meth. Eng. 2004, 61, 2316–2343. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T. A three-dimensional large deformation meshfree method for arbitrary evolving cracks. Comput. Methods Appl. Mech. Eng. 2007, 196, 2777–2799. [Google Scholar] [CrossRef] [Green Version]
- Rabczuk, T.; Zi, G.; Bordas, S.; Nguyen-Xuan, H. A simple and robust three-dimensional cracking-particle method without enrichment. Comput. Methods Appl. Mech. 2010, 199, 2437–2455. [Google Scholar] [CrossRef]
- Rabczuk, T.; Ren, H. A peridynamics formulation for quasi-static fracture and contact in rock. Eng. Geol. 2017, 225, 42–48. [Google Scholar] [CrossRef]
- Ren, H.; Zhuang, X.; Cai, Y.; Rabczuk, T. Dual-horizon peridynamics. Int. J. Numer. Meth. Eng. 2016, 108, 1451–1476. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.; Zhuang, X.; Rabczuk, T. Dual-horizon peridynamics: A stable solution to varying horizons. Comput. Methods Appl. Mech. Eng. 2017, 318, 762–782. [Google Scholar] [CrossRef] [Green Version]
- Bobet, A.; Einstein, H.H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression. Int. J. Rock Mech. Min. Sci. 1998, 35, 863–888. [Google Scholar] [CrossRef]
- Gonçalves da Silva, B.; Einstein, H.H. Modeling of crack initiation, propagation and coalescence in rocks. Int. J. Fract. 2013, 182, 167–186. [Google Scholar] [CrossRef] [Green Version]
- Lemaitre, J.; Desmorat, R. Engineering Damage Mechanics: Ductile, Creep, Fatigue and Brittle Failures; Springer-Verlag: Berlin, Germany, 2005. [Google Scholar]
- Bažant, Z.P.; Pijaudier-Cabot, T.G.P. Nonlocal continuum damage, localization instability and convergence. J. Appl. Mech. 1988, 55, 287–293. [Google Scholar] [CrossRef]
- Jirásek, M. Nonlocal models for damage and fracture: Comparison of approaches. Int. J. Solids Struct. 1988, 35, 4133–4145. [Google Scholar] [CrossRef]
- Forest, S. Micromorphic approach for gradient elasticity, viscoplasticity, and damage. J. Engnr. Mech. 2009, 35, 117–131. [Google Scholar] [CrossRef]
- Dimitrijevic, B.J.; Hackl, K. A regularization framework for damage-plasticity models via gradient enhancement of the free energy. Int. J. Numer. Methods Biomed. Energy 2011, 27, 1199–1210. [Google Scholar] [CrossRef]
- Peerlings, R.; Geers, M.; de Borst, R.; Brekelmans, W. A critical comparison of non local and gradient-enhanced softening continua. Int. J. Solids Struct. 2001, 38, 7723–7746. [Google Scholar] [CrossRef]
- Areias, P.; Msekh, M.A.; Rabczuk, T. Damage and fracture algorithm using the screened Poisson equation and local remeshing. Eng. Fract. Mech. 2016, 158, 116–143. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Dolbow, J.; Moeës, N.; Belytschko, T. An extended finite element method for modeling crack growth with contact. Comput. Meth. Appl. Mech. Eng. 2001, 190, 6825–6846. [Google Scholar] [CrossRef]
- Fries, T.P.; Belytschko, T. The extended/generalized finite element method: An overview of the method and its applications. Int. J. Numer. Methods Eng. 2010, 84, 253–304. [Google Scholar] [CrossRef]
- Simo, J.C.; Oliver, J.; Armero, F. An analysis of strong discontinuities induced by strainsoftening in rate-independent inelastic solids. Comput. Mech. 1993, 12, 277–296. [Google Scholar] [CrossRef]
- Linder, C.; Armero, F. Finite elements with embedded strong discontinuities for the modeling of failure in solids. Int. J. Numer. Methods Eng. 2007, 72, 1391–1433. [Google Scholar] [CrossRef]
- Oliver, J.; Huespe, A.; Blanco, S.; Linero, D. Stability and robustness issues in numerical modeling of material failure with the strong discontinuity approach. Comput. Methods Appl. Mech. Eng. 2006, 195, 7093–114. [Google Scholar] [CrossRef]
- Armero, F.; Linder, C. New finite elements with embedded strong discontinuities for finite deformations. Comput. Methods Appl. Mech. Eng. 2008, 197, 3138–3170. [Google Scholar] [CrossRef]
- Xu, X.P.; Needleman, A. Numerical simulation of fast crack growth in brittle solids. J. Mech. Phys. Solids 1994, 42, 1397–1434. [Google Scholar] [CrossRef]
- Ortiz, M.; Pandolfi, A. Finite deformation irreversible cohesive elements for three-dimensional crack-propagation analysis. Int. J. Num. Meth. Eng. 1999, 44, 1267–1282. [Google Scholar] [CrossRef]
- Park, K.; Paulino, G.H.; Roesler, J.R. A unified potential-based cohesive model of mixed-mode fracture. J. Mech. Phys. Solids 2009, 57, 891–908. [Google Scholar] [CrossRef]
- Paggi, M.; Wriggers, P. Stiffness and strength of hierarchical polycrystalline materials with imperfect interfaces. J. Mech. Phys. Solids 2012, 60, 557–572. [Google Scholar] [CrossRef]
- Reinoso, J.; Paggi, M. A consistent interface element formulation for geometrical and material nonlinearities. Comput. Mech. 2014, 54, 1569–1581. [Google Scholar] [CrossRef] [Green Version]
- Infuso, A.; Corrado, M.; Paggi, M. Image analysis of polycrystalline solar cells and modelling of intergranular and transgranular cracking. J. Eur. Ceram. Soc. 2015, 34, 2713–2722. [Google Scholar] [CrossRef]
- Paggi, M.; Reinoso, J. An anisotropic large displacement cohesive zone model for fibrillar and crazing of interfaces. Int. J. Solids Struct. 2015, 69, 106–120. [Google Scholar] [CrossRef]
- Francfort, G.A.; Marigo, J.J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomena of rupture and flow in solids. Philos. Trans. Royal Soc. Lond. A 1921, 221, 163–198. [Google Scholar] [CrossRef]
- Ambrosio, L.; Tortorelli, V.M. Approximation of functional depending on jumps by elliptic functional via C-convergence. Commun. Pure Appl. Math. 1990, 43, 999–1036. [Google Scholar] [CrossRef]
- Ambrosio, L.; Tortorelli, V.M. On the approximation of free discontinuity problems. Boll. Union Mat. Ital. 1992, 6, 105–123. [Google Scholar]
- Dal Maso, G. Introduction to Γ-Convergence. Progress in Nonlinear Differential Equations and Their Applications, Birkhäuser. Progress in Nonlinear Differential Equations and Their Applications. Available online: https://link.springer.com/book/10.1007/978-1-4612-0327-8 (accessed on 13 March 2019).
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. The variational approach to fracture. J. Elast. 2008, 91, 145–148. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rateindependent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phasefield models of fracture: Variational principles and multi-field fe-implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Kuhn, C.; Müller, R. A continuum phase field model for fracture. Eng. Fract. Mech. 2010, 77, 3625–3634. [Google Scholar] [CrossRef]
- Borden, M.J.; Hughes, T.J.R.; Landis, C.M.; Verhoosel, C.V. A higher-order phase-field model for brittle fracture: Formulation and analysis within the isogeometric analysis framework. Comput. Methods Appl. Mech. Eng. 2014, 273, 100–118. [Google Scholar] [CrossRef]
- Amiri, F.; Millán, D.; Shen, Y.; Rabczuk, T.; Arroyo, M. Phase-field modeling of fracture in linear thin shells. Theor. Appl. Fract. Mech. 2014, 69, 102–109. [Google Scholar] [CrossRef] [Green Version]
- Areias, P.; Rabczuk, T.; Msekh, M.A. Phase-field analysis of finite-strain plates and shells including element subdivision. Comput. Methods Appl. Mech. Eng. 2016, 312, 322–350. [Google Scholar] [CrossRef]
- Reinoso, J.; Paggi, M.; Linder, C. Phase field modeling of brittle fracture for enhanced assumed strain shells at large deformations: Formulation and finite element implementation. Comp. Mech. 2017. [Google Scholar] [CrossRef]
- Ulmer, H.; Hofacker, M.; Miehe, C. Phase field modeling of brittle and ductile fracture. Proc. Appl. Math. Mech. 2013, 13, 533–536. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; de Lorenzis, L. Phase-field modeling of ductile fracture. Comp. Mech. 2015, 55, 1–24. [Google Scholar] [CrossRef]
- Verhoosel, C.; de Borst, R. A phase-field model for cohesive fracture. Int. J. Numer. Meth. Eng. 2013, 96, 43–62. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.R.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 77–95. [Google Scholar] [CrossRef]
- Hofacker, M.; Miehe, C. A phase field model of dynamic fracture: Robust field updates for the analysis of complex crack patterns. Int. J. Numer. Methods Eng. 2013, 93, 276–301. [Google Scholar] [CrossRef]
- Miehe, C.; Schanzel, L.; Ulmer, H. Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 449–485. [Google Scholar] [CrossRef]
- Miehe, C.; Schanzel, L.; Ulmer, H. Phase field modeling of fracture in multi-physics problems. Part II. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 486–522. [Google Scholar] [CrossRef]
- Martínez-Pañeda, E.; Golahmar, A.; Niordson, C.F. A phase field formulation for hydrogen assisted cracking. Comput. Methods Appl. Mech. Eng. 2018, 342, 742–761. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuang, X.; Zhu, H.; Rabczuk, T. Phase field modelling of crack propagation, branching and coalescence in rocks. Theor. Appl. Fract. Mech. 2018, 96, 174–192. [Google Scholar] [CrossRef]
- Zhang, X.; Sloan, S.W.; Vignes, C.; Sheng, D. A modification of the phase-field model for mixed mode crack propagation in rock-like materials. Comput. Methods Appl. Mech. Eng. 2017, 322, 123–136. [Google Scholar] [CrossRef]
- Bryant, E.C.; Sun, W. A mixed-mode phase field fracture model in anisotropic rocks with consistent kinematics. Comput. Methods Appl. Mech. Eng. 2018, 342, 561–584. [Google Scholar] [CrossRef]
- Li, L.; Xia, Y.; Huang, B.; Zhang, L.; Li, M.; Li, A. The Behaviour of Fracture Growth in Sedimentary Rocks: A Numerical Study Based on Hydraulic Fracturing Processes. Energies 2016, 9, 169. [Google Scholar] [CrossRef]
- Paggi, M.; Reinoso, J. Revisiting the problem of a crack impinging on an interface: A modeling framework for the interaction between the phase field approach for brittle fracture and the interface cohesive zone model. Comput. Methods Appl. Mech. Eng. 2017, 321, 145–172. [Google Scholar] [CrossRef]
- Carpinteri, A.; Paggi, M. Size-scale effects on strength, friction and fracture energy of faults: A unified interpretation according to fractal geometry. Rock Mech. Rock Eng. 2008, 41, 735–746. [Google Scholar] [CrossRef]
- Wu, J.Y. A unified phase-field theory for the mechanics of damage and quasi-brittle failure in solids. J. Mech. Phys. Solids 2017, 103, 72–99. [Google Scholar] [CrossRef]
- Wu, J.Y.; Nguyen, V.P. A length scale insensitive phase-field damage model for brittle fracture. J. Mech. Phys. Solids 2018, 119, 20–42. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Wu, J.Y. Modeling dynamic fracture of solids using a phase-field regularized cohesive zone model. Comput. Methods Appl. Mech. Eng. 2018, 340, 1000–1022. [Google Scholar] [CrossRef]
- Amor, H.; Marigo, J.J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Msekh, M.A.; Sargado, M.; Jamshidian, M.; Areias, P.; Rabczuk, T. Abaqus implementation of phase-field model for brittle fracture. Comput. Mater. Sci. 2015, 96, 472–484. [Google Scholar] [CrossRef]
- Lei, Q.; Latham, J.P.; Xiang, J. Implementation of an emprirical joint constitutive model into finite-discrete element analysis of the geomechanical behavior of fractured rocks. Rock Mech. Rock Eng. 2016, 49, 4799–4816. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Barton, N. Shear strength criteria for rock, rock joints and rock masses: Problems and some solutions. J. Rock Mech. Geotech. Eng. 2013, 5, 249–261. [Google Scholar] [CrossRef]
- Helgeson, D.E.; Aydin, A. Characteristics of joint propagation across layer interfaces in sedimentary rocks. J. Struct. Geol. 1991, 13, 897–911. [Google Scholar] [CrossRef]
- Li, Y.; Liu, W.; Yang, C.; Daemen, J.J.K. Experimental investigation of mechanical behavior of bedded rock salt containing inclined interlayer. Int. J. Rock Mech. Min. Sci. 2014, 69, 39–49. [Google Scholar] [CrossRef]
- Tromans, D.; Meech, J.A. Fracture toughness and surface energies of minerals: Theoretical estimates for oxides, sulphides, silicates and halides. Miner. Eng. 2002, 15, 1027–1041. [Google Scholar] [CrossRef]

















| Material | E (GPa) | (Jm) | |
|---|---|---|---|
| Halite | 36.87 | 0.254 | 1.155 |
| Anhydrite | 74.36 | 0.269 | 1.805 |
| Critical traction Mode I interface | 75 MPa |
| Critical traction Mode II interface | 90 MPa |
| Fracture toughness Mode I | 0.002 N/mm |
| Fracture toughness Mode II | 0.008 N/mm |
| 10 | |
| 0.194 mm | |
| JCS | 169 MPa |
| JRC | 9.7 |
| Friction angle | 32º |
| 0.2 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reinoso, J.; Durand, P.; Budarapu, P.R.; Paggi, M. Crack Patterns in Heterogenous Rocks Using a Combined Phase Field-Cohesive Interface Modeling Approach: A Numerical Study. Energies 2019, 12, 965. https://doi.org/10.3390/en12060965
Reinoso J, Durand P, Budarapu PR, Paggi M. Crack Patterns in Heterogenous Rocks Using a Combined Phase Field-Cohesive Interface Modeling Approach: A Numerical Study. Energies. 2019; 12(6):965. https://doi.org/10.3390/en12060965
Chicago/Turabian StyleReinoso, José, Percy Durand, Pattabhi Ramaiah Budarapu, and Marco Paggi. 2019. "Crack Patterns in Heterogenous Rocks Using a Combined Phase Field-Cohesive Interface Modeling Approach: A Numerical Study" Energies 12, no. 6: 965. https://doi.org/10.3390/en12060965






