Characterizing Flexoelectricity in Composite Material Using the Element-Free Galerkin Method
Abstract
:1. Introduction
2. Simulation Method
3. Numerical Examples
3.1. Cantilever Beam
3.1.1. Mechanical Loading
3.1.2. Electrical Loading
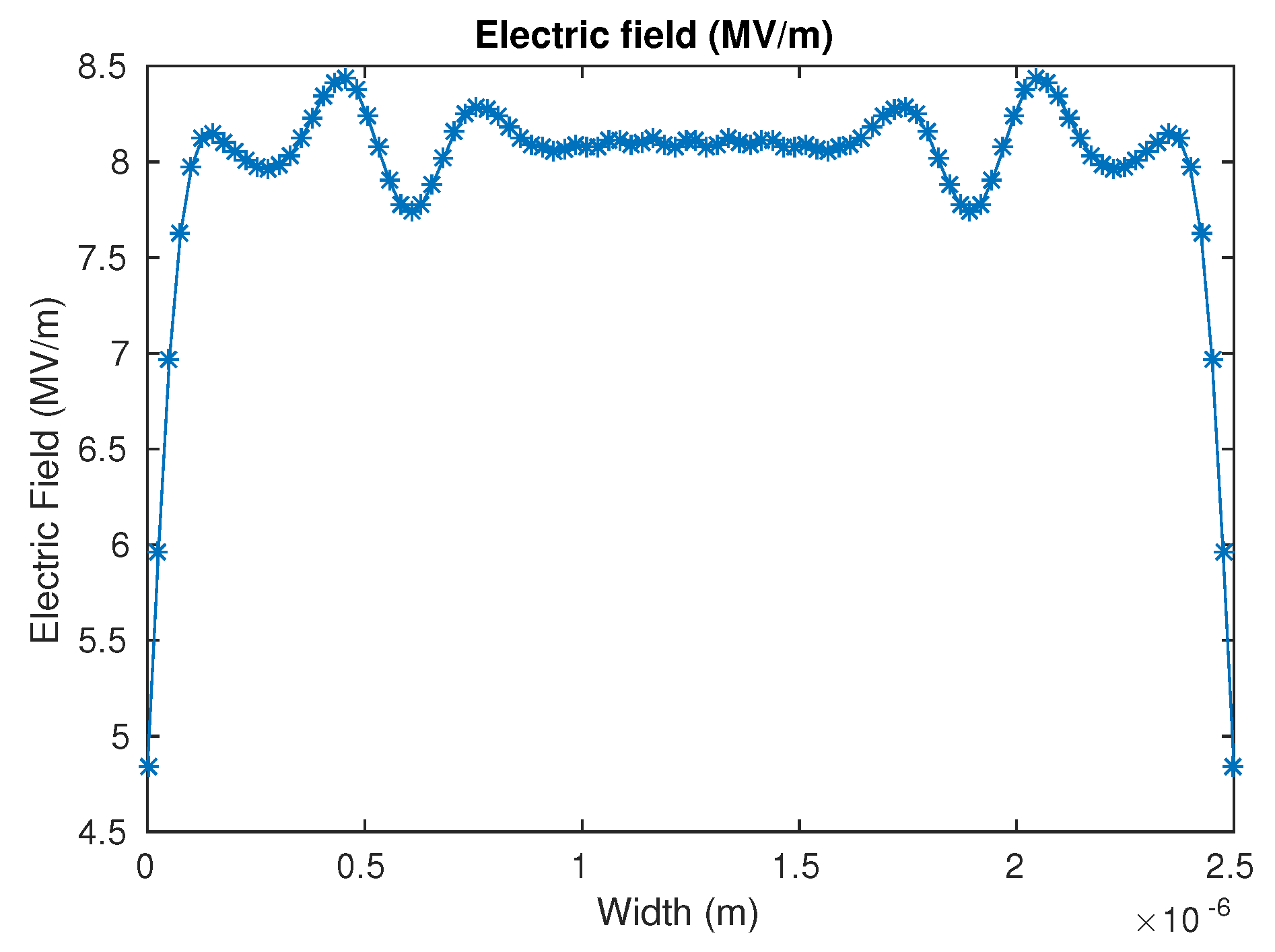
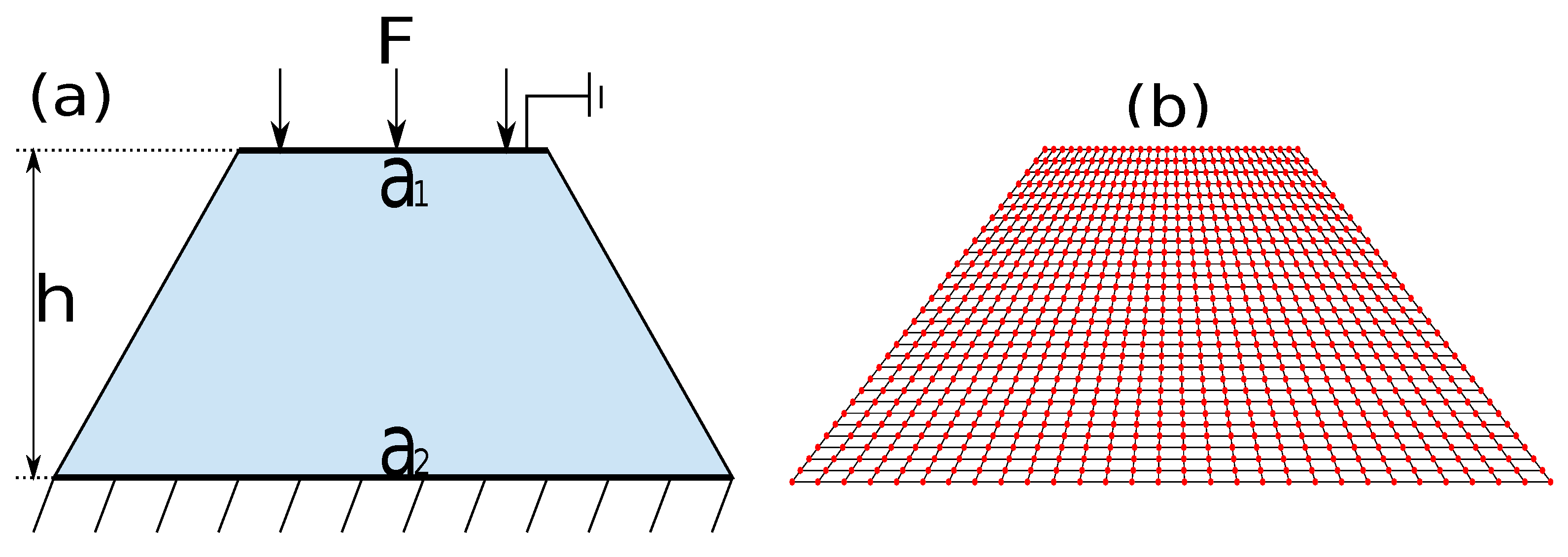
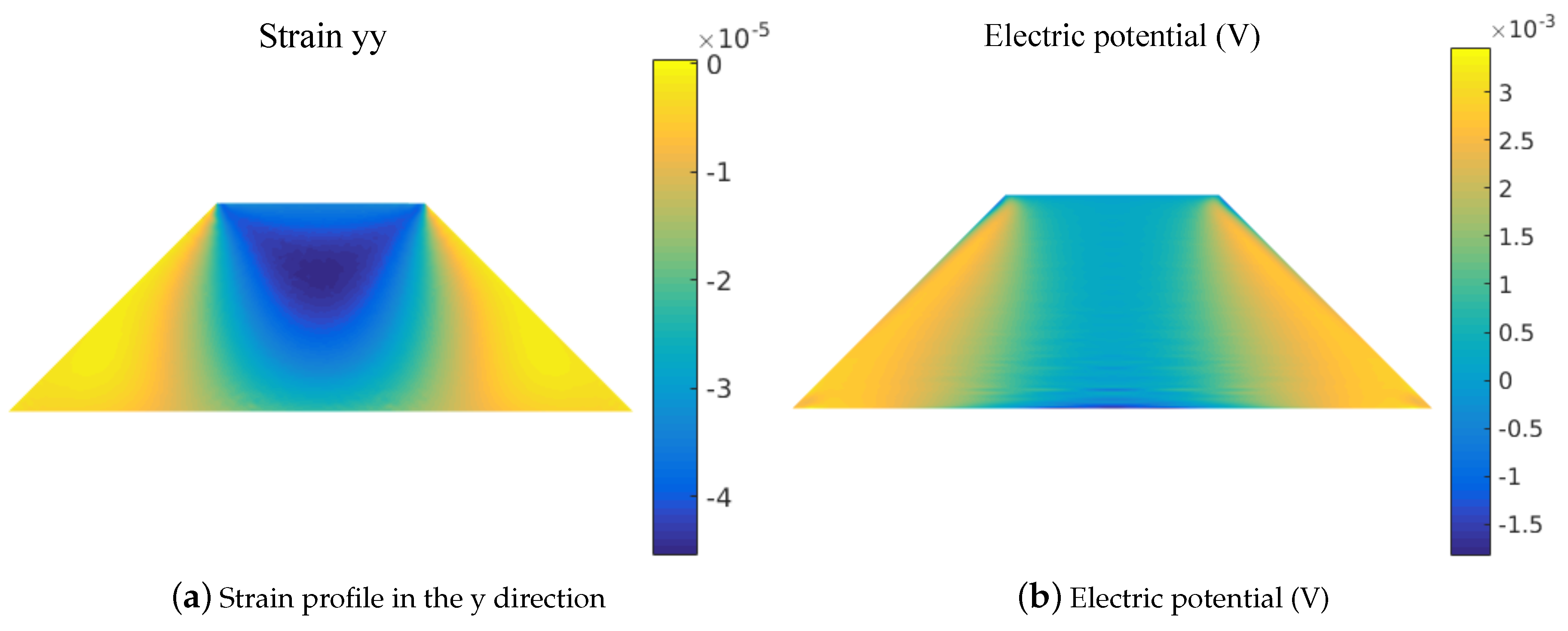
3.2. Compress Truncated Pyramid
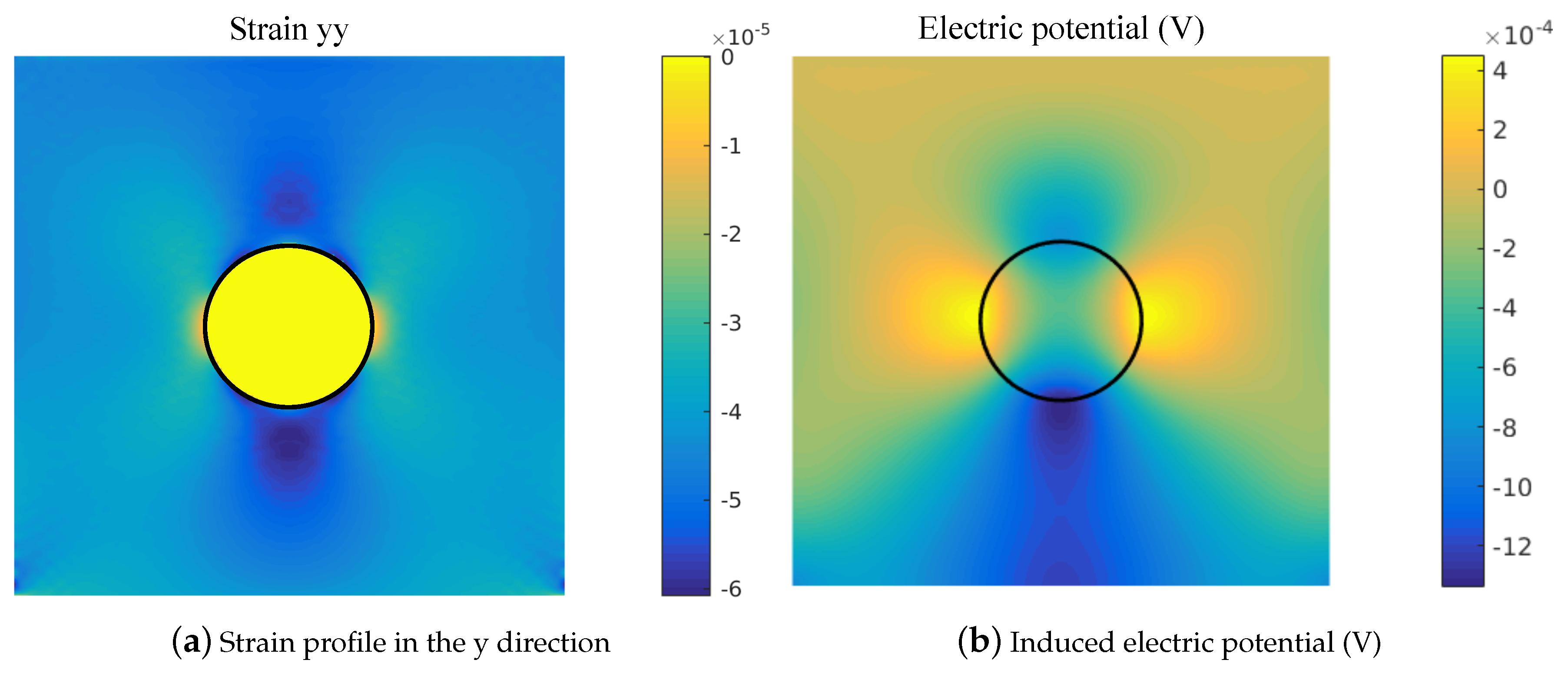
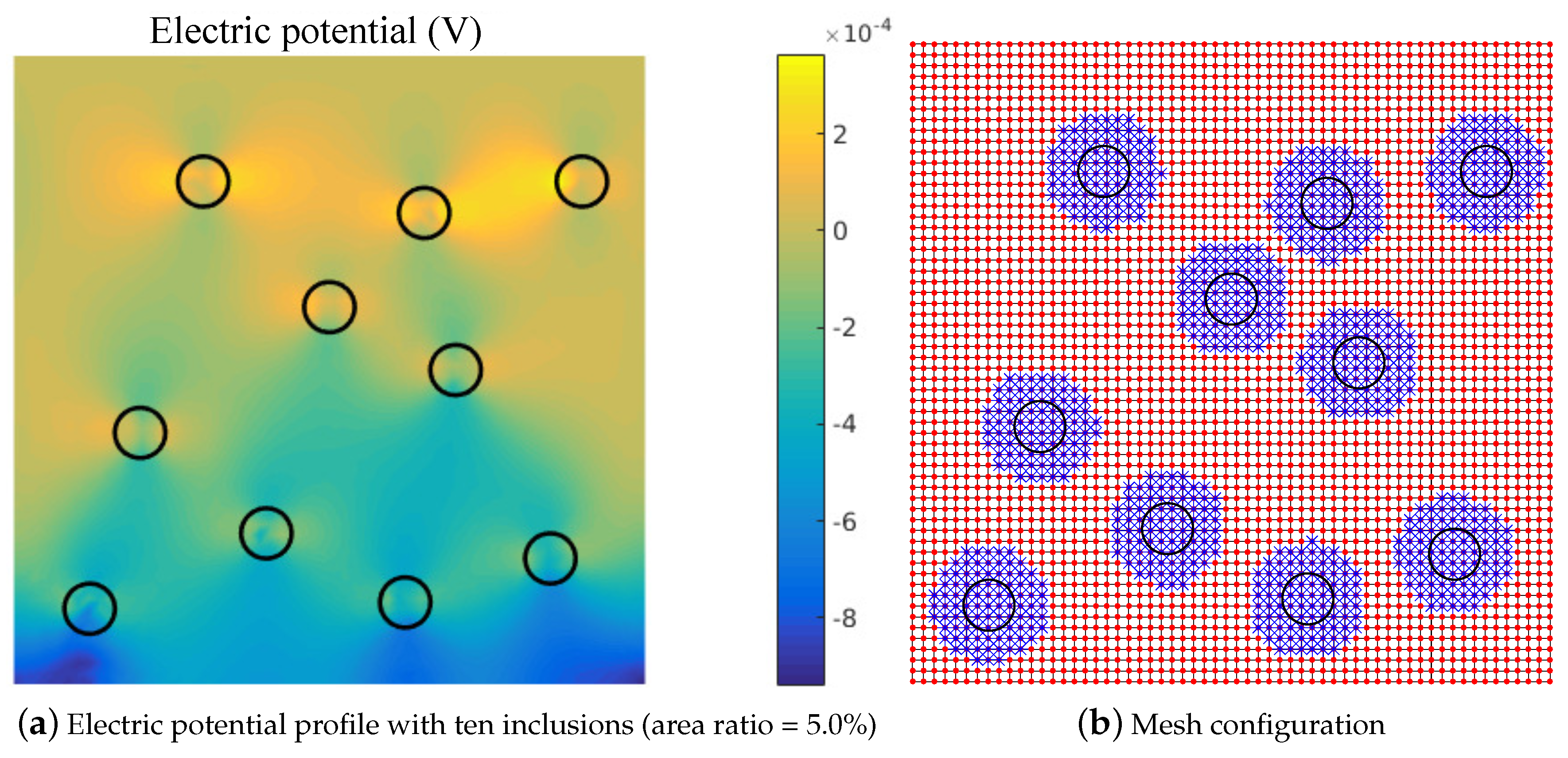
3.3. Flexoelectricity in Composite
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Theory of Flexoelectricity
Appendix B. Details of the Shape Function
Appendix C. Mathematical Expression for the Elements in Equation (4)
References
- Chen, J.; Qiu, Q.; Han, Y.; Lau, D. Piezoelectric materials for sustainable building structures: Fundamentals and applications. Renew. Sustain. Energy Rev. 2019, 101, 14–25. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Barreneche, C.; Miró, L.; Morera, J.M.; Bartolí, E.; Fernández, A.I. Low carbon and low embodied energy materials in buildings: A review. Renew. Sustain. Energy Rev. 2013, 23, 536–542. [Google Scholar] [CrossRef]
- Ramesh, T.; Prakash, R.; Shukla, K. Life cycle energy analysis of buildings: An overview. Energy Build. 2010, 42, 1592–1600. [Google Scholar] [CrossRef]
- Scopelianos, A.G. Piezoelectric Biomedical Device. US Patent 5,522,879, 4 June 1996. [Google Scholar]
- Zhou, Q.; Lau, S.; Wu, D.; Shung, K.K. Piezoelectric films for high frequency ultrasonic transducers in biomedical applications. Prog. Mater. Sci. 2011, 56, 139–174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, X.; Huang, W.; Zhang, S. Flexoelectric nano-generator: Materials, structures and devices. Nano Energy 2013, 2, 1079–1092. [Google Scholar] [CrossRef]
- Zhuang, X.Y.; Huang, R.Q.; Liang, C.; Rabczuk, T. A coupled thermo-hydro-mechanical model of jointed hard rock for compressed air energy storage. Math. Probl. Eng. 2014, 2014, 179169. [Google Scholar] [CrossRef]
- Ahmadpoor, F.; Sharma, P. Flexoelectricity in two-dimensional crystalline and biological membranes. Nanoscale 2015, 7, 16555–16570. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Observation of the flexoelectric effect in relaxor Pb (Mg 1/3 Nb 2/3) O 3 ceramics. Appl. Phys. Lett. 2001, 78, 2920–2921. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Flexoelectricity of barium titanate. Appl. Phys. Lett. 2006, 88, 232902. [Google Scholar] [CrossRef]
- Hong, J.; Catalan, G.; Scott, J.; Artacho, E. The flexoelectricity of barium and strontium titanates from first principles. J. Phys. Condens. Matter 2010, 22, 112201. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Wang, J.; Shimada, T.; Kitamura, T. Direct approach for flexoelectricity from first-principles calculations: Cases for SrTiO3 and BaTiO3. J. Phys. Condens. Matter 2013, 25, 415901. [Google Scholar] [CrossRef] [PubMed]
- Kundalwal, S.; Meguid, S.; Weng, G. Strain gradient polarization in graphene. Carbon 2017, 117, 462–472. [Google Scholar] [CrossRef]
- Javvaji, B.; He, B.; Zhuang, X. The generation of piezoelectricity and flexoelectricity in graphene by breaking the materials symmetries. Nanotechnology 2018, 29, 225702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, B.; Javvaji, B.; Zhuang, X. Size dependent flexoelectric and mechanical properties of barium titanate nanobelt: A molecular dynamics study. Phys. B Condens. Matter 2018, 545, 527–535. [Google Scholar] [CrossRef]
- Zhang, Z.; Geng, D.; Wang, X. Calculation of the piezoelectric and flexoelectric effects in nanowires using a decoupled finite element analysis method. J. Appl. Phys. 2016, 119, 154104. [Google Scholar] [CrossRef] [Green Version]
- Nanthakumar, S.; Zhuang, X.; Park, H.S.; Rabczuk, T. Topology optimization of flexoelectric structures. J. Mech. Phys. Solids 2017, 105, 217–234. [Google Scholar] [CrossRef]
- Nanthakumar, S.S.; Lahmer, T.; Zhuang, X.Y.; Zi, G.; Rabczuk, T. Detection of material interfaces using a regularized level set method in piezoelectric structures. Inverse Probl. Sci. Eng. 2016, 24, 153–176. [Google Scholar] [CrossRef]
- Deng, F.; Deng, Q.; Yu, W.; Shen, S. Mixed Finite Elements for Flexoelectric Solids. J. Appl. Mech. 2017, 84, 081004. [Google Scholar] [CrossRef]
- Mao, S.; Purohit, P.K.; Aravas, N. Mixed finite-element formulations in piezoelectricity and flexoelectricity. Proc. R. Soc. A 2016, 472, 20150879. [Google Scholar] [CrossRef] [Green Version]
- Ghasemi, H.; Park, H.S.; Rabczuk, T. A level-set based IGA formulation for topology optimization of flexoelectric materials. Comput. Methods Appl. Mech. Eng. 2017, 313, 239–258. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Ghasemi, H.; Zhuang, X.Y.; Alajlan, N.; Rabczuk, T. Sensitivity and uncertainty analysis for flexoelectric nanostructures. Comput. Methods Appl. Mech. Eng. 2018, 337, 95–109. [Google Scholar] [CrossRef]
- Nguyen-Thanh, N.; Valizadeh, N.; Nguyen, M.N.; Nguyen-Xuan, H.; Zhuang, X.Y.; Areias, P.; Zi, G.; Bazilevs, Y.; De Lorenzis, L.; Rabczuk, T. An extended isogeometric thin shell analysis based on Kirchhoff–Love theory. Comput. Methods Appl. Mech. Eng. 2015, 284, 265–291. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Anitescu, C.; Bordas, S.P.; Rabczuk, T. Isogeometric analysis: An overview and computer implementation aspects. Math. Comput. Simul. 2015, 117, 89–116. [Google Scholar] [CrossRef] [Green Version]
- Hughes, T.J.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Abdollahi, A.; Peco, C.; Millán, D.; Arroyo, M.; Arias, I. Computational evaluation of the flexoelectric effect in dielectric solids. J. Appl. Phys. 2014, 116, 093502. [Google Scholar] [CrossRef]
- Abdollahi, A.; Millán, D.; Peco, C.; Arroyo, M.; Arias, I. Revisiting pyramid compression to quantify flexoelectricity: A three-dimensional simulation study. Phys. Rev. B 2015, 91, 104103. [Google Scholar] [CrossRef]
- Bernholc, J.; Nakhmanson, S.M.; Nardelli, M.B.; Meunier, V. Understanding and enhancing polarization in complex materials. Comput. Sci. Eng. 2004, 6, 12–21. [Google Scholar] [CrossRef] [Green Version]
- Ghidelli, M.; Sebastiani, M.; Collet, C.; Guillemet, R. Determination of the elastic moduli and residual stresses of freestanding Au-TiW bilayer thin films by nanoindentation. Mater. Des. 2016, 106, 436–445. [Google Scholar] [CrossRef]
- Msekh, M.A.; Cuong, N.H.; Zi, G.; Areias, P.; Zhuang, X.Y.; Rabczuk, T. Fracture properties prediction of clay/epoxy nanocomposites with interphase zones using a phase field model. Eng. Fract. Mech. 2018, 188, 287–299. [Google Scholar] [CrossRef]
- Bhavanasi, V.; Kumar, V.; Parida, K.; Wang, J.; Lee, P.S. Enhanced Piezoelectric Energy Harvesting Performance of Flexible PVDF-TrFE Bilayer Films with Graphene Oxide. ACS Appl. Mater. Interfaces 2016, 8, 521–529. [Google Scholar] [CrossRef]
- Biswal, A.K.; Das, S.; Roy, A. Designing and synthesis of a polymer matrix piezoelectric composite for energy harvesting. IOP Conf. Ser. Mater. Sci. Eng. 2017, 178, 012002. [Google Scholar] [CrossRef] [Green Version]
- Sidhardh, S.; Ray, M.C. Effective properties of flexoelectric fiber-reinforced nanocomposite. Mater. Today Commun. 2018, 17, 114–123. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Silani, M.; Zhuang, X.Y.; He, P.F.; Rabczuk, T. Stochastic analysis of the fracture toughness of polymeric nanoparticle composites using polynomial chaos expansions. Int. J. Fract. 2017, 206, 215–227. [Google Scholar] [CrossRef]
- Ghasemi, H.; Park, H.S.; Rabczuk, T. A multi-material level set-based topology optimization of flexoelectric composites. Comput. Methods Appl. Mech. Eng. 2018, 332, 47–62. [Google Scholar] [CrossRef]
- Cordes, L.; Moran, B. Treatment of material discontinuity in the element-free Galerkin method. Comput. Methods Appl. Mech. Eng. 1996, 139, 75–89. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T.; Xiao, S.P. Stable particle methods based on Lagrangian kernels. Comput. Methods Appl. Mech. Eng. 2004, 193, 1035–1063. [Google Scholar] [CrossRef]
- Krongauz, Y.; Belytschko, T. EFG approximation with discontinuous derivatives. Int. J. Numer. Methods Eng. 1998, 41, 1215–1233. [Google Scholar] [CrossRef]
- Rabczuk, T.; Zi, G.; Bordas, S.; Nguyen-Xuan, H. A geometrically non-linear three-dimensional cohesive crack method for reinforced concrete structures. Eng. Fract. Mech. 2008, 75, 4740–4758. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.P.; Rabczuk, T.; Bordas, S.; Duflot, M. Meshless methods: A review and computer implementation aspects. Math. Comput. Simul. 2008, 79, 763–813. [Google Scholar] [CrossRef] [Green Version]
- Budarapu, P.R.; Gracie, R.; Yang, S.W.; Zhuang, X.Y.; Rabczuk, T. Efficient coarse graining in multiscale modeling of fracture. Theor. Appl. Fract. Mech. 2014, 69, 126–143. [Google Scholar] [CrossRef]
- Sukumar, N.; Chopp, D.L.; Moës, N.; Belytschko, T. Modeling holes and inclusions by level sets in the extended finite-element method. Comput. Methods Appl. Mech. Eng. 2001, 190, 6183–6200. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.L.; Zhuang, X.Y.; Rabczuk, T. Dual-horizon peridynamics: A stable solution to varying horizons. Comput. Methods Appl. Mech. Eng. 2017, 318, 762–782. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.L.; Zhuang, X.Y.; Cai, Y.C.; Rabczuk, T. Dual-horizon peridynamics. Int. J. Numer. Methods Eng. 2016, 108, 1451–1476. [Google Scholar] [CrossRef] [Green Version]
- Rabczuk, T.; Bordas, S.; Zi, G. On three-dimensional modelling of crack growth using partition of unity methods. Comput. Struct. 2010, 88, 1391–1411. [Google Scholar] [CrossRef]
- Rabczuk, T.; Areias, P.M.A.; Belytschko, T. A meshfree thin shell method for non-linear dynamic fracture. Int. J. Numer. Methods Eng. 2007, 72, 524–548. [Google Scholar] [CrossRef] [Green Version]
- Rabczuk, T.; Belytschko, T. A three-dimensional large deformation meshfree method for arbitrary evolving cracks. Comput. Methods Appl. Mech. Eng. 2007, 196, 2777–2799. [Google Scholar] [CrossRef] [Green Version]
- Rabczuk, T.; Belytschko, T. Cracking particles: A simplified meshfree method for arbitrary evolving cracks. Int. J. Numer. Methods Eng. 2004, 61, 2316–2343. [Google Scholar] [CrossRef]
- Rabczuk, T.; Bordas, S.; Zi, G. A three-dimensional meshfree method for continuous multiple-crack initiation, propagation and junction in statics and dynamics. Comput. Mech. 2007, 40, 473–495. [Google Scholar] [CrossRef] [Green Version]
- Majdoub, M.; Sharma, P.; Cagin, T. Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B 2008, 77, 125424. [Google Scholar] [CrossRef]
- Majdoub, M.S.; Sharma, P.; Çağin, T. Erratum: Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect [Phys. Rev. B 77, 125424 (2008)]. Phys. Rev. B 2009, 79, 119904. [Google Scholar] [CrossRef]
- Sharma, N.; Landis, C.; Sharma, P. Piezoelectric thin-film superlattices without using piezoelectric materials. J. Appl. Phys. 2010, 108, 024304. [Google Scholar] [CrossRef] [Green Version]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.; Gu, L.; Tabbara, M. Element-free Galerkin methods for static and dynamic fracture. Int. J. Solids Struct. 1995, 32, 2547–2570. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- He, B.; Mortazavi, B.; Zhuang, X.; Rabczuk, T. Modeling Kapitza resistance of two-phase composite material. Compos. Struct. 2016, 152, 939–946. [Google Scholar] [CrossRef]






| Name | Symbol | Value |
|---|---|---|
| Poisson’s ratio | 0.37 | |
| Young’s modulus | E | 100 GPa |
| Piezoelectric constant | −4.4 nC/m | |
| Flexoelectric constant | 1 C/m | |
| Dielectric constant | ; | 11 nC/Vm; 12.48 nC/Vm |
| Electric susceptibility | 1408 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, B.; Javvaji, B.; Zhuang, X. Characterizing Flexoelectricity in Composite Material Using the Element-Free Galerkin Method. Energies 2019, 12, 271. https://doi.org/10.3390/en12020271
He B, Javvaji B, Zhuang X. Characterizing Flexoelectricity in Composite Material Using the Element-Free Galerkin Method. Energies. 2019; 12(2):271. https://doi.org/10.3390/en12020271
Chicago/Turabian StyleHe, Bo, Brahmanandam Javvaji, and Xiaoying Zhuang. 2019. "Characterizing Flexoelectricity in Composite Material Using the Element-Free Galerkin Method" Energies 12, no. 2: 271. https://doi.org/10.3390/en12020271





