A Study of Cloth Seal Leakage Performance Based on Geometry and Pressure Load
Abstract
:1. Introduction
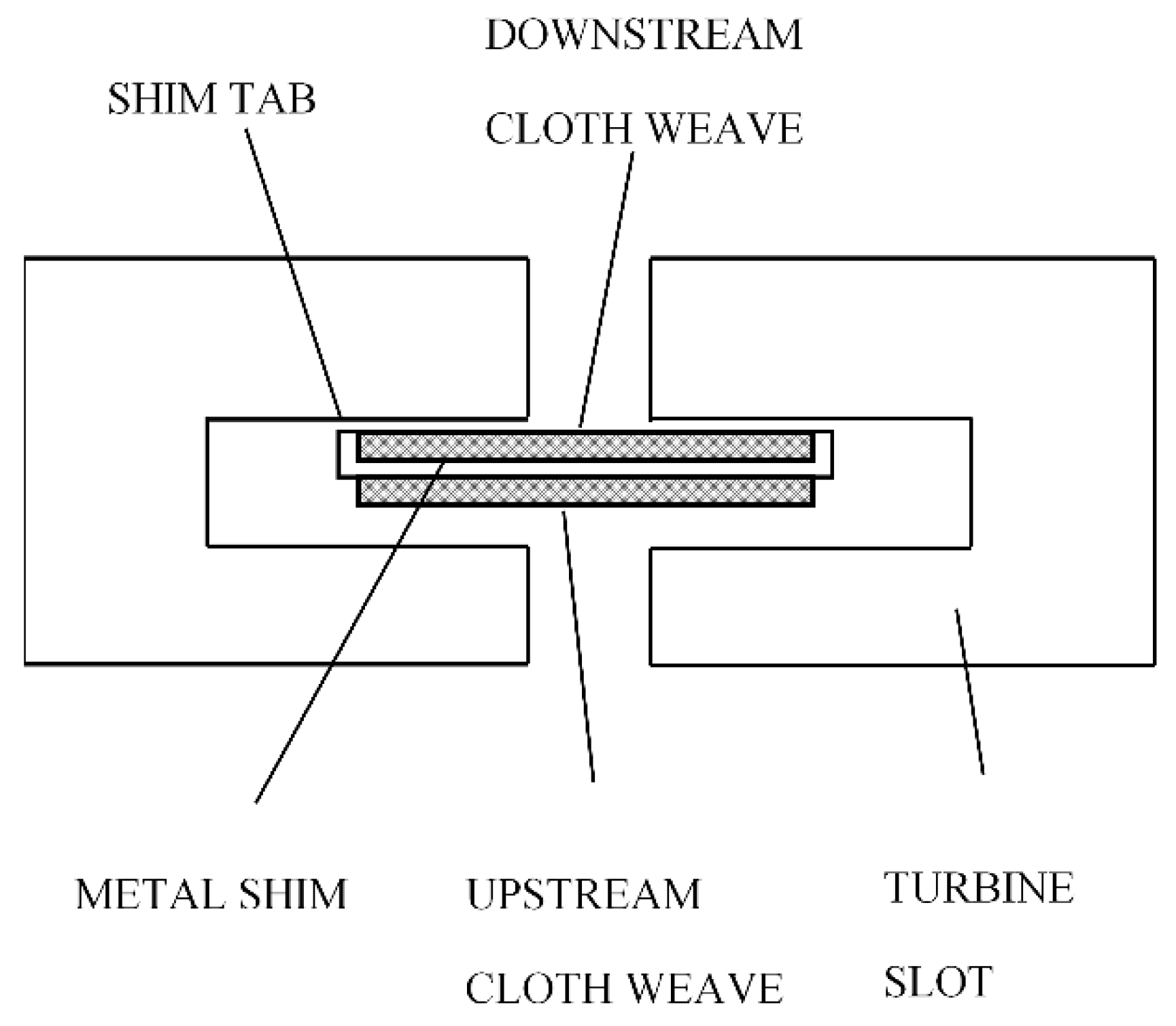
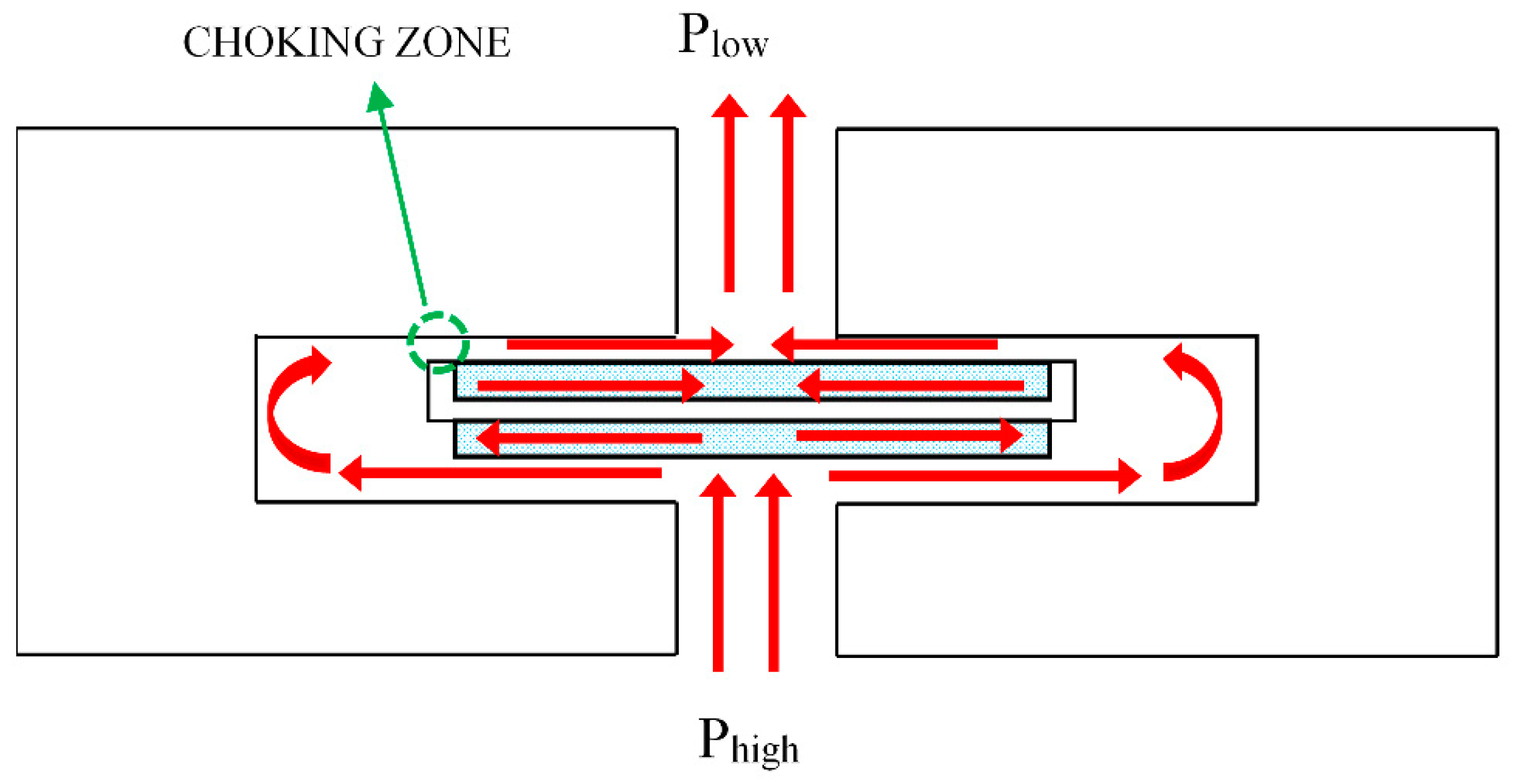
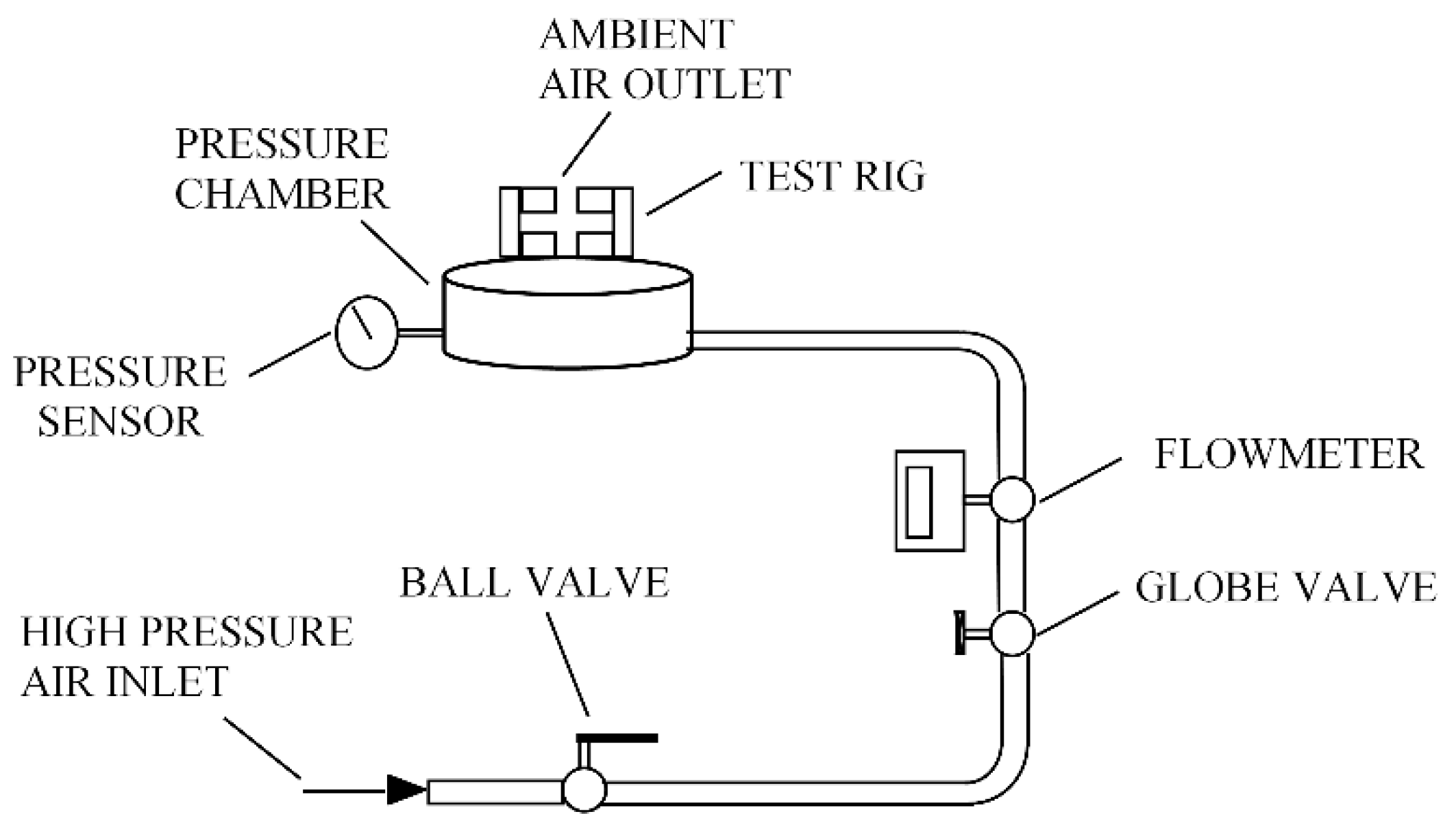
2. Test Setup
3. Experimental Design
- Identification of the parameters affecting the leakage performance
- Selection of the method for screening experiments
- Establishing an experimental design for screening experiments
- Pareto chart and identification of strong parameters
- Comparison test results with the data existing in the literature
- Establishing experimental design for main experiments
- Pareto chart and a closed-form equation for strong parameters
3.1. Screening Experiments
3.2. Main Experiments
4. Results and Discussion
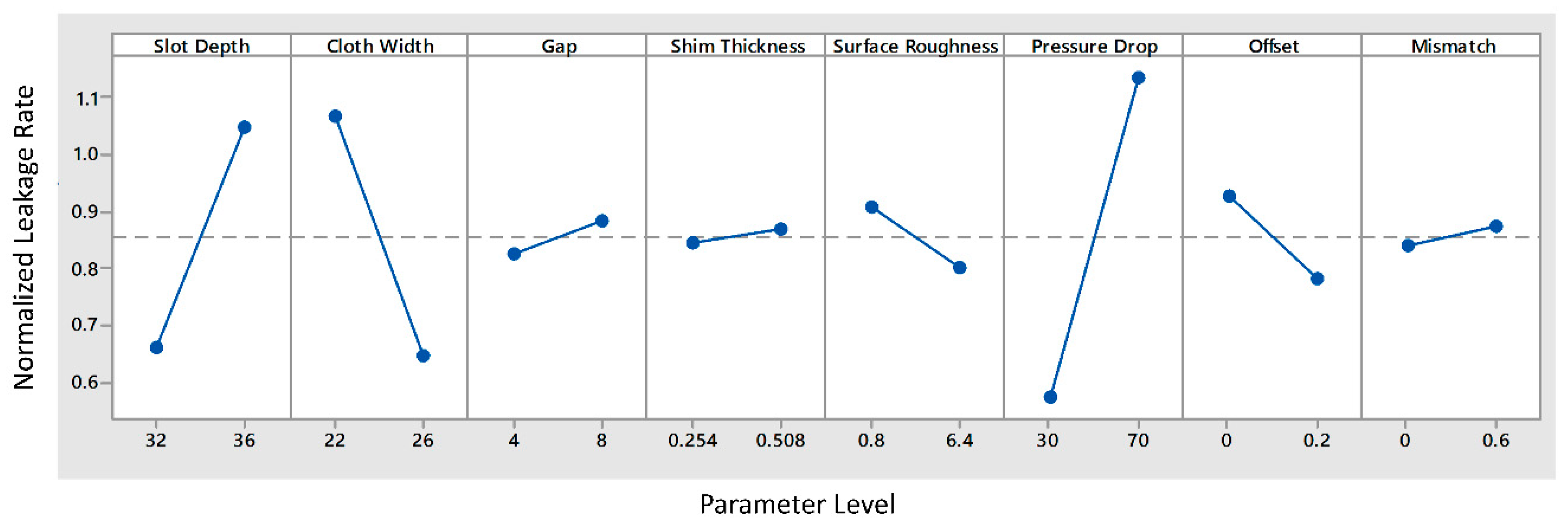
4.1. Screening Experiment Results
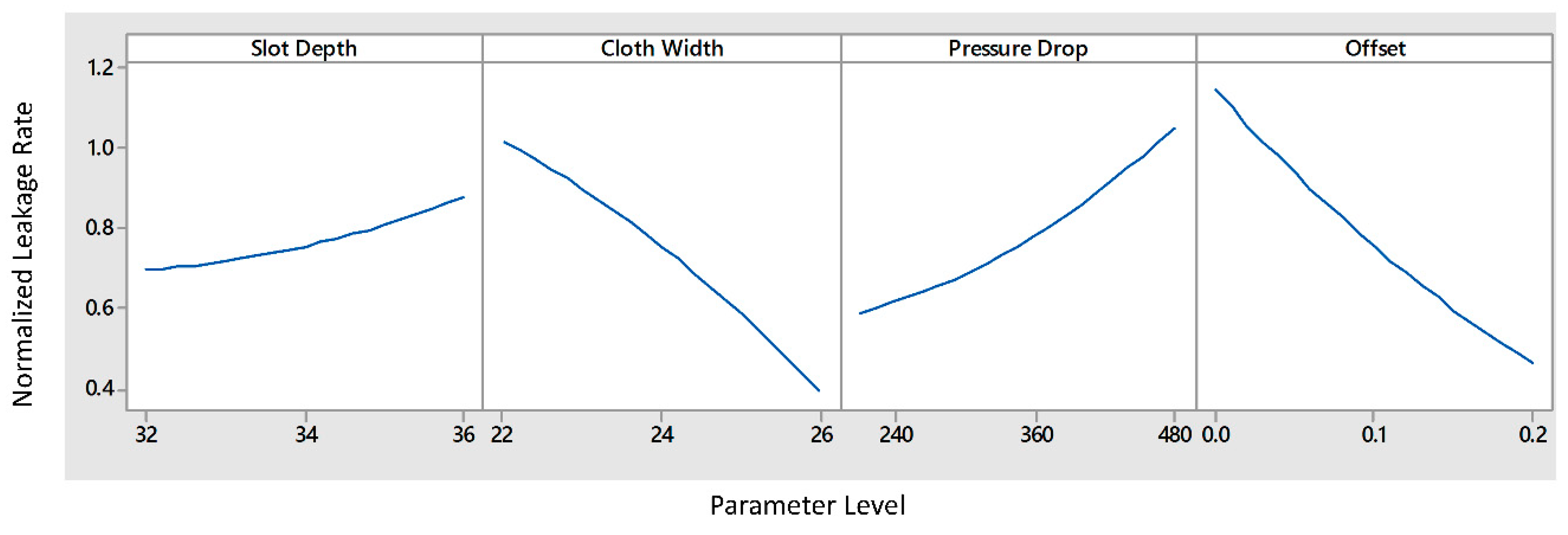
4.2. Main and Confirmation Experiment Results
5. Conclusions
5.1. Screening Experiments
5.2. Main and Confirmation Experiments
Author Contributions
Funding
Conflicts of Interest
Appendix A
Uncertainty Analysis

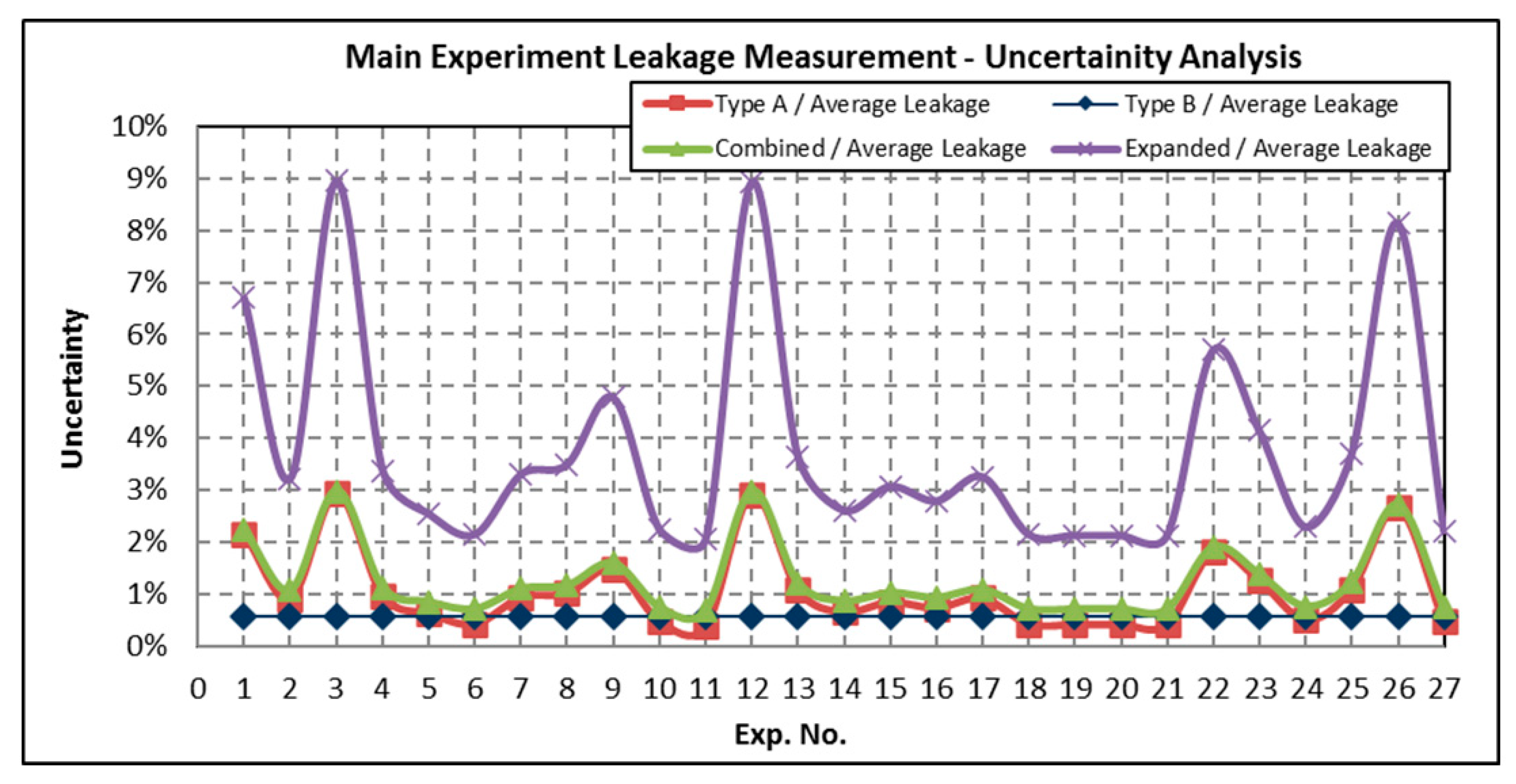
References
- Dogu, Y.; Aksit, M.F.; Bagepalli, B.; Burns, J.; Sexton, B.; Kellock, I. Thermal and flow analysis of cloth-seal in slot for gas turbine shroud applications. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998. [Google Scholar] [CrossRef]
- Aksit, M.F. Seeking design solutions through decoupling problems—A global engineering example. ME Today ASME Int. Online J. Acad. Ind. Perspect. 2010, 11. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.611.9143&rep=rep1&type=pdf (accessed on 1 November 2020).
- Dinc, O.S.; Bagepalli, B.S.; Wolfe, C.; Aksit, M.F.; Calabrese, S. A new metal cloth stationary seal for gas turbine applications. In Proceedings of the 33rd AIAA/ASME/SAE/ ASEE Joint Propulsion Conference, AIAA Paper 97-2732, Seattle, WA, USA, 6–9 July 1997. [Google Scholar] [CrossRef]
- Paprotna, H.E.; Morrision, M.J. Biased Wear Resistant Turbine Seal Assembly. U.S. Patent US6733234B2, 11 May 2004. [Google Scholar]
- McMahan, K.W.; Demiroglu, M.; Repikov, T.R. Spring Loaded Seal Assembly for Turbines. U.S. Patent US8398090B2, 19 March 2013. [Google Scholar]
- Samudrala, O.; Sarawate, N.N. Cloth Seal for Turbo-Machinery. U.S. Patent US8613451B2, 24 December 2013. [Google Scholar]
- Riggi, V.T.; Monshower, B.; Hyslop, J.D. Brazed Turbine Seal. U.S. Patent US8696309B2, 15 April 2014. [Google Scholar]
- Sarawate, N.N.; Morgan, V.J.; Weber, D.W. Layered Seal for Turbomachinery. U.S. Patent US9188228B2, 17 November 2015. [Google Scholar]
- Chupp, R.E.; Hendricks, R.C.; Lattime, S.B.; Steinetz, B.M. Sealing in Turbomachinery; NASA/TM-2006-214341: Cleveland, OH, USA, 2006. [Google Scholar] [CrossRef]
- Johnston, J.R. Performance and Reliability Improvements for Heavy-Duty Gas Turbines; GE Power Systems: Schenectady, NY, USA, 2002. [Google Scholar]
- Aksit, M.F.; Bagepalli, B.S.; Aslam, S. High performance combustor cloth seals. In Proceedings of the 36th AIAA/ASME/SAE/ASEE Joint Cleveland, Ohio Propulsion Conference & Exhibit, Huntsville, AL, USA, 16–19 July 2000. [Google Scholar] [CrossRef]
- Aksit, M.F.; Bagepalli, B.S.; Demiroglu, M.; Dinc, O.S.; Kellock, I.; Farell, T. Advanced flexible seals for gas turbine shroud applications. In Proceedings of the 35th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Los Angeles, CA, USA, 20–24 June1999. [Google Scholar] [CrossRef]
- Amaki, K.; Hasegawa, T.; Narumi, T. Drag Reduction in the Flow of Aqueous Solutions of Detergent Through Mesh Screens. Nihon Reoroji Gakkaishi 2008, 36, 125–131. [Google Scholar] [CrossRef] [Green Version]
- Kolodziej, A.; Lojewska, J. Experimental and Modelling Study on Flow Resistance of Wire Gauzes. Chem. Eng. Process 2009, 48, 816–822. [Google Scholar] [CrossRef]
- Yoshida, Y.; Inoue, Y.; Shimosaka, A.; Shirakawa, Y.; Hidaka, J. Effect of Aperture Structure of Dutch Weave Mesh on Flow Resistivity. J. Chem. Eng. Jpn. 2015, 48, 730–741. [Google Scholar] [CrossRef] [Green Version]
- Ongun, R.; Aksit, M.F.; Goktug, G. A simple model for wear of metal cloth seals. In Proceedings of the 40th AIAA/SAE/ASME/ASEE Joint Propulsion Conference & Exhibit, AIAA-2004-3892, Fort Lauderdale, FL, USA, 11–14 July 2004. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981. [Google Scholar] [CrossRef]
- Archard, J.F.; Hirst, W. The wear of metals under unlubricated conditions. Proc. Roy. Soc. 1956, 236, 397–410. [Google Scholar]
- Dogu, Y.; Bahar, A.S.; Sertcakan, M.C.; Piskin, A.; Arican, E.; Kocagul, M. Computational fluid dynamics investigation of brush seal leakage performance depending on geometric dimensions and operating conditions. J. Eng. Gas. Turbines Power 2016, 138, 032506. [Google Scholar] [CrossRef]
- Li, J.; Qiu, B.; Feng, Z. Experimental and numerical investigations on the leakage flow characteristics of the labyrinth brush seal. J. Eng. Gas Turbines Power 2012, 134, 102509. [Google Scholar] [CrossRef]
- Li, J.; Obi, S.; Feng, Z. The effects of clearance sizes on labyrinth brush seal leakage performance using a Reynolds-averaged Navier-Stokes solver and non-Darcian porous medium model. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 953–964. [Google Scholar] [CrossRef]
- Choi, S.M.; Choi, S.; Cho, H.H. Effect of Various Coolant Mass Flow Rates on Sealing Effectiveness of Turbine Blade Rim Seal at First Stage Gas Turbine Experimental Facility. Energies 2020, 13, 4105. [Google Scholar] [CrossRef]
- Aksit, M.F.; Bagepalli, B.S.; Burns, J.; Stevens, P.; Vehr, J. Parasitic Corner Leakage Reduction in Gas Turbine Nozzle-Shroud Inter-Segment Locations. In Proceedings of the 37th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Salt Lake City, UT, USA, 8–11 July 2001. [Google Scholar] [CrossRef]
- Chupp, R.E.; Hendricks, R.C.; Lattime, S.B.; Steinetz, B.M.; Aksit, M.F. Turbomachinery Clearance Control. Turbine Aerodynamics, Heat Transfer, Materials, and Mechanics; AIAA: Reston, VA, USA, 2007; pp. 61–188. [Google Scholar] [CrossRef] [Green Version]




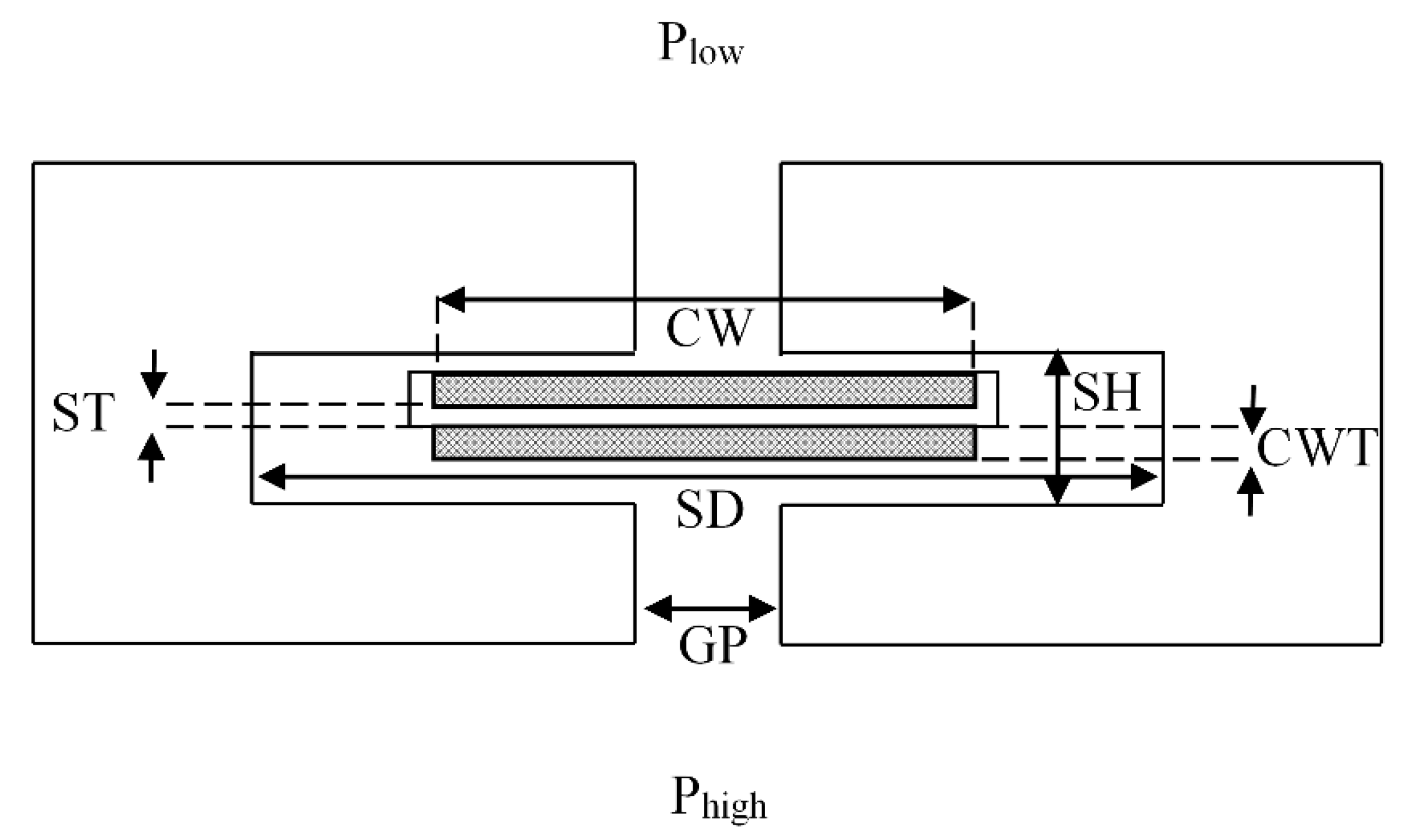





| No | Parameter Name | Abbreviation | No | Parameter Name | Abbreviation |
|---|---|---|---|---|---|
| 1 | Slot depth | SD | 10 | Cloth material | CM |
| 2 | Cloth width | CW | 11 | Cloth weave thickness | CWT |
| 3 | Gap | GP | 12 | Dia. of warp fiber | DW |
| 4 | Shim thickness | ST | 13 | Dia. of shute fiber | DS |
| 5 | Surface roughness | SR | 14 | Weave type | WT |
| 6 | Pressure drop | PD | 15 | Weave density | WD |
| 7 | Offset | OF | 16 | Spot weld dia. | SW |
| 8 | Mismatch | MI | 17 | Slot height | SH |
| 9 | Shim material | SM | 18 | Temperature | TE |
| No | Parameter Name | Unit | Abbreviation | Level |
|---|---|---|---|---|
| 1 | Slot depth | mm | SD | 32–36 |
| 2 | Cloth width | mm | CW | 22–26 |
| 3 | Gap | mm | GP | 4–8 |
| 4 | Shim thickness | mm | ST | 0.254–0.508 |
| 5 | Surface roughness | µm | SR | 0.8–6.4 |
| 6 | Pressure drop | kPad | PD | 206.8–482.6 |
| 7 | Offset | mm | OF | 0–0.2 |
| 8 | Mismatch | ° | MI | 0–0.6 |
| Exp. No. | SD (mm) | CW (mm) | GP (mm) | ST (mm) | SR (µm) | PD (kPad) | OF (mm) | MI (°) |
|---|---|---|---|---|---|---|---|---|
| 1 | 32 | 22 | 4 | 0.254 | 0.8 | 206.8 | 0 | 0 |
| 2 | 36 | 22 | 4 | 0.254 | 0.8 | 482.6 | 0.2 | 0.6 |
| 3 | 32 | 26 | 4 | 0.254 | 6.4 | 206.8 | 0.2 | 0.6 |
| 4 | 36 | 26 | 4 | 0.254 | 6.4 | 482.6 | 0 | 0 |
| 5 | 32 | 22 | 8 | 0.254 | 6.4 | 482.6 | 0.2 | 0 |
| 6 | 36 | 22 | 8 | 0.254 | 6.4 | 206.8 | 0 | 0.6 |
| 7 | 32 | 26 | 8 | 0.254 | 0.8 | 482.6 | 0 | 0.6 |
| 8 | 36 | 26 | 8 | 0.254 | 0.8 | 206.8 | 0.2 | 0 |
| 9 | 32 | 22 | 4 | 0.508 | 6.4 | 482.6 | 0 | 0.6 |
| 10 | 36 | 22 | 4 | 0.508 | 6.4 | 206.8 | 0.2 | 0 |
| 11 | 32 | 26 | 4 | 0.508 | 0.8 | 482.6 | 0.2 | 0 |
| 12 | 36 | 26 | 4 | 0.508 | 0.8 | 206.8 | 0 | 0.6 |
| 13 | 32 | 22 | 8 | 0.508 | 0.8 | 206.8 | 0.2 | 0.6 |
| 14 | 36 | 22 | 8 | 0.508 | 0.8 | 482.6 | 0 | 0 |
| 15 | 32 | 26 | 8 | 0.508 | 6.4 | 206.8 | 0 | 0 |
| 16 | 36 | 26 | 8 | 0.508 | 6.4 | 482.6 | 0.2 | 0.6 |
| No | Parameter Name | Unit | Abbreviation | Level |
|---|---|---|---|---|
| 1 | Slot depth | mm | SD | 32–34–36 |
| 2 | Cloth width | mm | CW | 22–24–26 |
| 3 | Gap | mm | GP | 4 |
| 4 | Shim thickness | mm | ST | 0.254 |
| 5 | Surface roughness | µm | SR | 6.4 |
| 6 | Pressure drop | kPad | PD | 206.8–344.7–482.6 |
| 7 | Offset | mm | OF | 0–0.1–0.2 |
| 8 | Mismatch | ° | MI | 0 |
| Exp. No. | SD (mm) | CW (mm) | GP (mm) | ST (mm) | SR (µm) | PD (kPad) | OF (mm) | MI (°) |
|---|---|---|---|---|---|---|---|---|
| 1 | 32 | 22 | 4 | 0.254 | 6.4 | 344.7 | 0.1 | 0 |
| 2 | 32 | 26 | 4 | 0.254 | 6.4 | 344.7 | 0.1 | 0 |
| 3 | 32 | 24 | 4 | 0.254 | 6.4 | 344.7 | 0 | 0 |
| 4 | 32 | 24 | 4 | 0.254 | 6.4 | 344.7 | 0.2 | 0 |
| 5 | 32 | 24 | 4 | 0.254 | 6.4 | 206.8 | 0.1 | 0 |
| 6 | 32 | 24 | 4 | 0.254 | 6.4 | 482.6 | 0.1 | 0 |
| 7 | 34 | 24 | 4 | 0.254 | 6.4 | 206.8 | 0 | 0 |
| 8 | 34 | 24 | 4 | 0.254 | 6.4 | 482.6 | 0 | 0 |
| 9 | 34 | 24 | 4 | 0.254 | 6.4 | 206.8 | 0.2 | 0 |
| 10 | 34 | 24 | 4 | 0.254 | 6.4 | 482.6 | 0.2 | 0 |
| 11 | 34 | 22 | 4 | 0.254 | 6.4 | 206.8 | 0.1 | 0 |
| 12 | 34 | 26 | 4 | 0.254 | 6.4 | 206.8 | 0.1 | 0 |
| 13 | 34 | 22 | 4 | 0.254 | 6.4 | 482.6 | 0.1 | 0 |
| 14 | 34 | 26 | 4 | 0.254 | 6.4 | 482.6 | 0.1 | 0 |
| 15 | 34 | 22 | 4 | 0.254 | 6.4 | 344.7 | 0 | 0 |
| 16 | 34 | 26 | 4 | 0.254 | 6.4 | 344.7 | 0 | 0 |
| 17 | 34 | 22 | 4 | 0.254 | 6.4 | 344.7 | 0.2 | 0 |
| 18 | 34 | 26 | 4 | 0.254 | 6.4 | 344.7 | 0.2 | 0 |
| 19 | 34 | 24 | 4 | 0.254 | 6.4 | 344.7 | 0.1 | 0 |
| 20 | 34 | 24 | 4 | 0.254 | 6.4 | 344.7 | 0.1 | 0 |
| 21 | 34 | 24 | 4 | 0.254 | 6.4 | 344.7 | 0.1 | 0 |
| 22 | 36 | 22 | 4 | 0.254 | 6.4 | 344.7 | 0.1 | 0 |
| 23 | 36 | 26 | 4 | 0.254 | 6.4 | 344.7 | 0.1 | 0 |
| 24 | 36 | 24 | 4 | 0.254 | 6.4 | 344.7 | 0 | 0 |
| 25 | 36 | 24 | 4 | 0.254 | 6.4 | 344.7 | 0.2 | 0 |
| 26 | 36 | 24 | 4 | 0.254 | 6.4 | 206.8 | 0.1 | 0 |
| 27 | 36 | 24 | 4 | 0.254 | 6.4 | 482.6 | 0.1 | 0 |
| Case | Outlier No(s) (from Main Experiments) | Max Error % (Main Experiments) | Max Error % (Confirmation Experiments) |
|---|---|---|---|
| Without Outlier | - | 53 | 53 |
| One Outlier Excluded | 3 | 56 | 38 |
| 6 | 55 | 49 | |
| 17 | 45 | 41 | |
| 20 | 53 | 53 | |
| Two Outliers Excluded | 3, 6 | 58 | 26 |
| 3, 17 | 33 | 40 | |
| 3, 20 | 43 | 50 | |
| 6, 17 | 35 | 29 | |
| 6, 20 | 30 | 37 | |
| 17, 20 | 47 | 43 | |
| Three Outliers Excluded | 3, 6, 17 | 35 | 33 |
| 3, 6, 20 | 39 | 44 | |
| 3, 17, 20 | 36 | 38 | |
| 6, 17, 20 | 39 | 33 | |
| Four Outliers Excluded | 3, 6, 17, 20 | 20 | 20 |
| Exp. No. | SD (mm) | CW (mm) | GP (mm) | ST (mm) | SR (µm) | PD (kPad) | OF (mm) | MI (°) | Norm. Leak. (Eq.) | Norm. Leak. (Exp.) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 32 | 22 | 4 | 0.254 | 6.4 | 206.8 | 0.1 | 0 | 0.3869 | 0.3306 | 15% |
| 2 | 32 | 24 | 4 | 0.254 | 6.4 | 206.8 | 0.2 | 0 | 0.4155 | 0.3339 | 20% |
| 3 | 32 | 24 | 4 | 0.254 | 6.4 | 344.7 | 0.1 | 0 | 0.7139 | 0.6651 | 7% |
| 4 | 34 | 22 | 4 | 0.254 | 6.4 | 344.7 | 0.1 | 0 | 1.0388 | 1.1325 | 9% |
| 5 | 34 | 26 | 4 | 0.254 | 6.4 | 344.7 | 0.1 | 0 | 0.4042 | 0.4850 | 20% |
| 6 | 34 | 22 | 4 | 0.254 | 6.4 | 206.8 | 0.2 | 0 | 0.6588 | 0.5273 | 20% |
| 7 | 34 | 24 | 4 | 0.254 | 6.4 | 206.8 | 0.1 | 0 | 0.6481 | 0.6007 | 7% |
| 8 | 36 | 24 | 4 | 0.254 | 6.4 | 206.8 | 0 | 0 | 1.1235 | 1.0195 | 9% |
| Exp. No. | SD (mm) | CW (mm) | GP (mm) | ST (mm) | SR (µm) | PD (kPad) | OF (mm) | MI (°) | Norm. Leak. (Eq.) | Norm. Leak. (Exp.) | Error |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 32 | 22 | 4 | 0.254 | 6.4 | 482.6 | 0.1 | 0 | 1.0464 | 1.0196 | 3% |
| 2 | 32 | 24 | 4 | 0.254 | 6.4 | 482.6 | 0.2 | 0 | 0.6285 | 0.6654 | 6% |
| 3 | 34 | 24 | 4 | 0.254 | 6.4 | 344.7 | 0.2 | 0 | 0.4863 | 0.5188 | 7% |
| 4 | 34 | 26 | 4 | 0.254 | 6.4 | 482.6 | 0 | 0 | 1.0652 | 0.9064 | 15% |
| 5 | 34 | 22 | 4 | 0.254 | 6.4 | 482.6 | 0.2 | 0 | 1.0389 | 0.9112 | 12% |
| 6 | 34 | 24 | 4 | 0.254 | 6.4 | 482.6 | 0.1 | 0 | 1.0147 | 0.9193 | 9% |
| 7 | 36 | 24 | 4 | 0.254 | 6.4 | 482.6 | 0 | 0 | 1.6437 | 1.7629 | 7% |
| 8 | 36 | 24 | 4 | 0.254 | 6.4 | 482.6 | 0.2 | 0 | 0.6748 | 0.7511 | 11% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorgun, E.; Aksit, M.F.; Dogu, Y. A Study of Cloth Seal Leakage Performance Based on Geometry and Pressure Load. Energies 2020, 13, 5884. https://doi.org/10.3390/en13225884
Gorgun E, Aksit MF, Dogu Y. A Study of Cloth Seal Leakage Performance Based on Geometry and Pressure Load. Energies. 2020; 13(22):5884. https://doi.org/10.3390/en13225884
Chicago/Turabian StyleGorgun, Erdem, Mahmut Faruk Aksit, and Yahya Dogu. 2020. "A Study of Cloth Seal Leakage Performance Based on Geometry and Pressure Load" Energies 13, no. 22: 5884. https://doi.org/10.3390/en13225884





