A Benders’ Decomposition Approach for Renewable Generation Investment in Distribution Systems
Abstract
:1. Introduction
- The stochastic multi-stage DGP problem is formulated using Benders’ decomposition that decomposes the problem per both scenario and planning period and
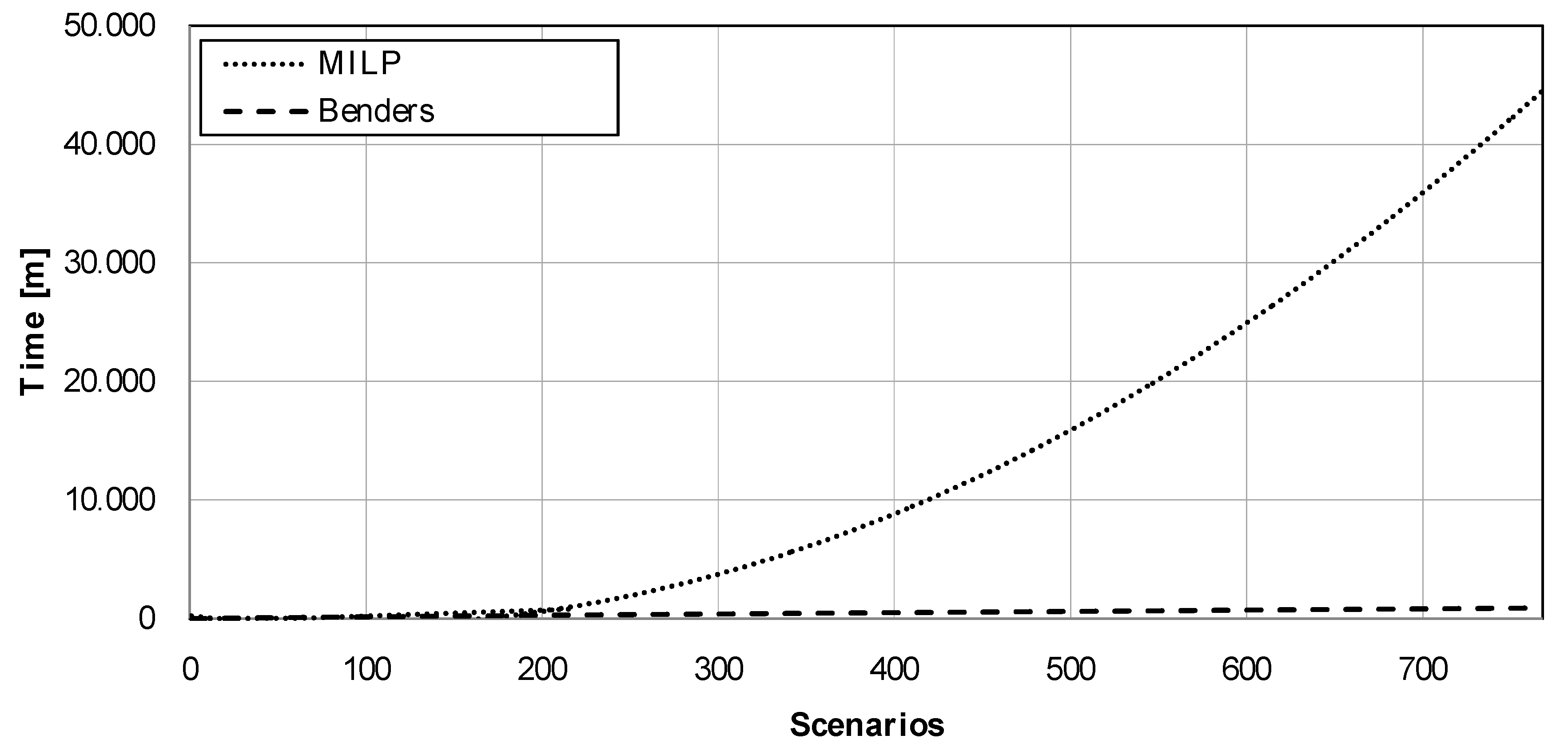
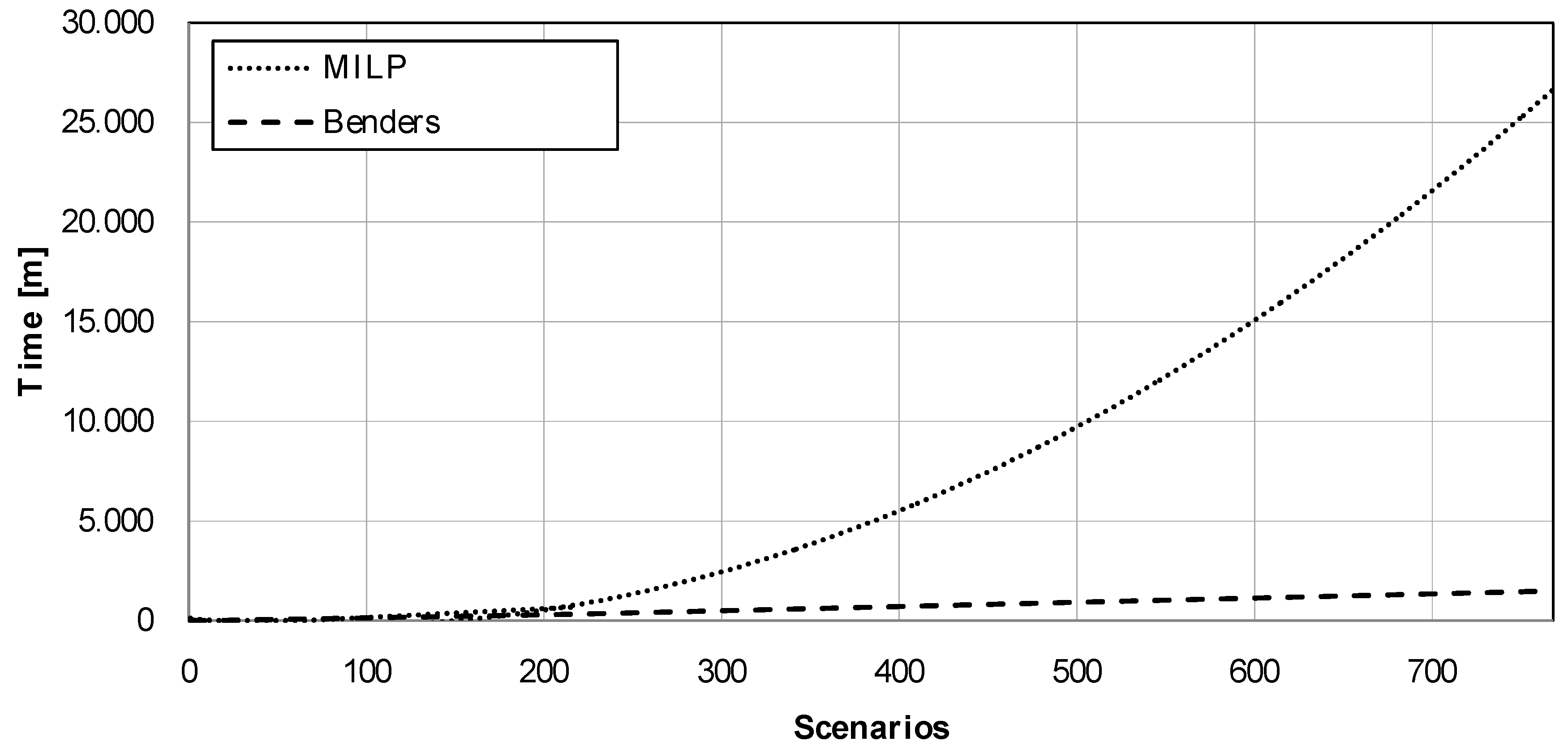
- A comparison with a standard MILP model is provided and results with a 34-bus test case are shown, where the significant computational advantage of using Benders’ decomposition with respect to the MILP model is also shown.
2. Notation
3. Problem Formulation
3.1. Objective Function
3.2. Constraints
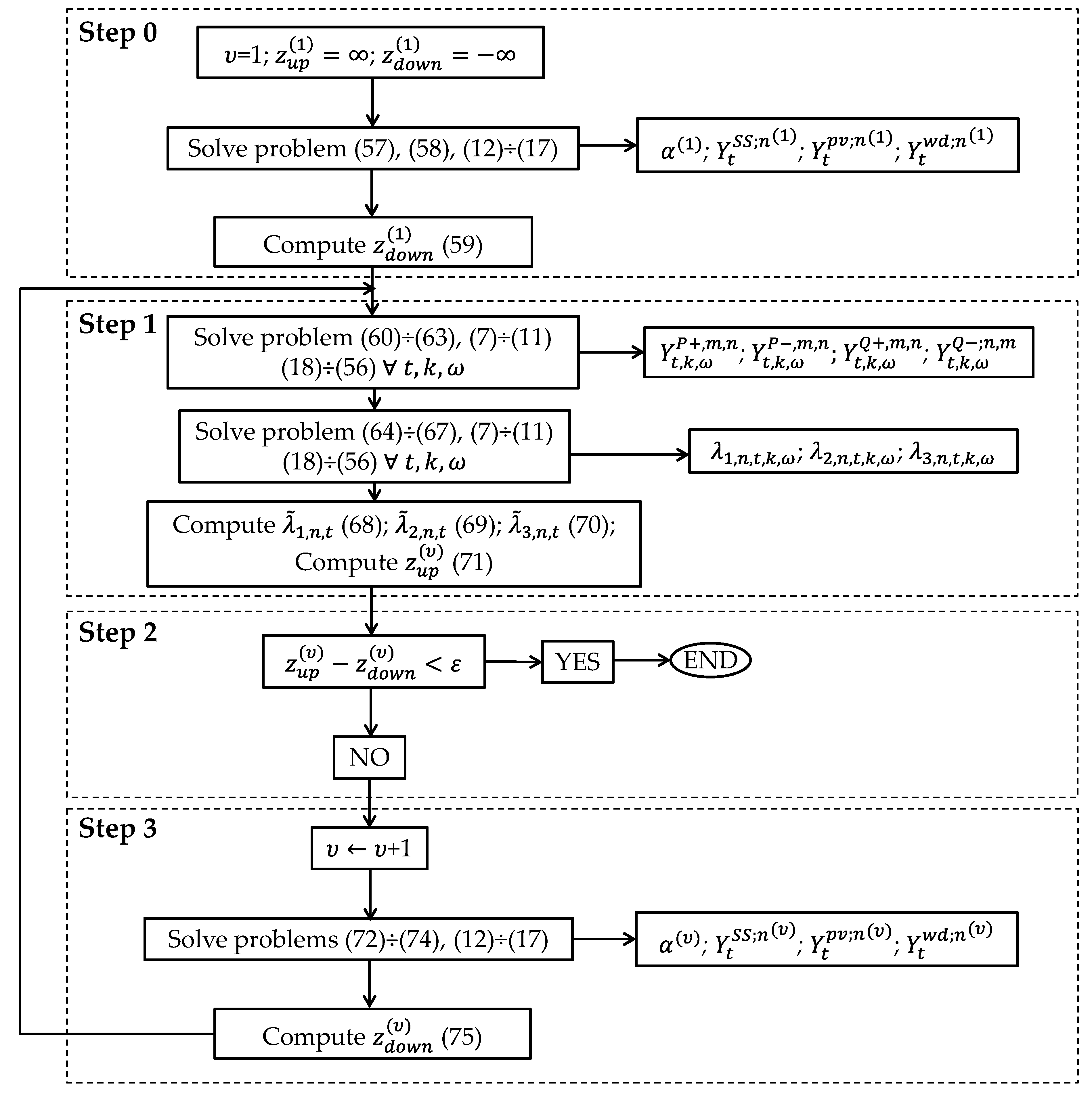
4. Solution Procedure: Benders’ Decomposition
- Step 0. Initialization: Initialize the iteration counter, υ = 1, the upper bound of the objective function, and its lower bound, and solve the following problem:subject to constraints (12)–(17) and
- 2.
- Step 1. Sub-problem solution: The variables , , and are set, to their optimal values from the previous step and solve the following sub-problems, one for each year , time block , and scenario .subject to constraints (7)–(11), (18)–(56) andwhere:
- 3.
- Step 2: Convergence checking: Check if the difference between the upper and the lower bounds, is lower than a predefined tolerance, ε. If so, the algorithm has converged, and the optimal solution consists of variables , , ; as well as the variables in set for iteration . If not, the algorithm proceeds to the next step.
- 4.
- Step 3: Master problem solution: Update the iteration counter,, and solve the following master problem:subject to constraints (12)–(17) andwhere is defined in Equations (5) and (6) and their parameters in Equations (2)–(4).
5. Case Study Data
6. Results Discussion
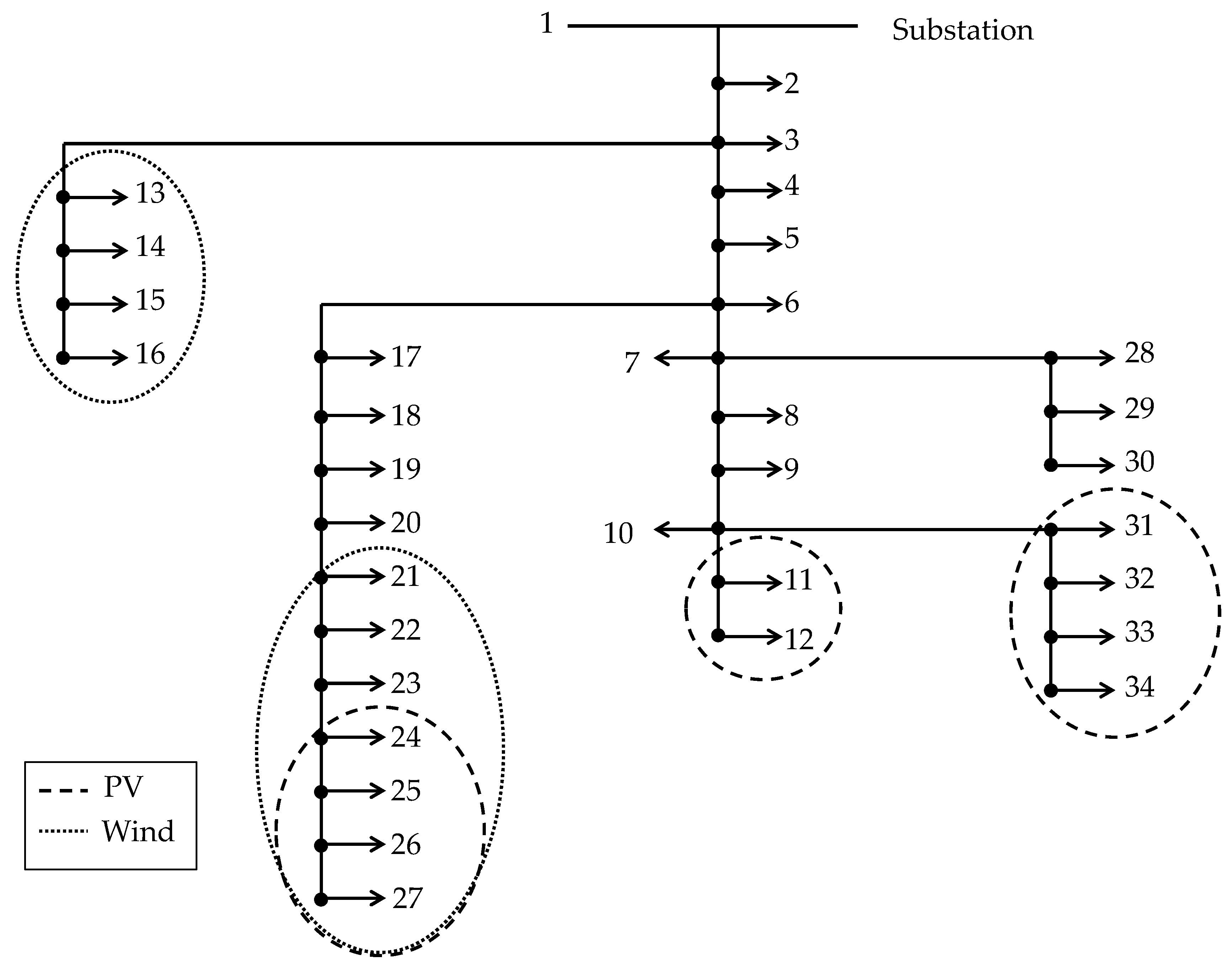
- Case a. Investment limits included: This case represents the most realistic scenario all constraints of the model are taken in account. The first year of the time horizon the renewable technology chosen for investment is photovoltaic (PV), with an installed capacity of 1047.5 kW (see Table 5). The expansion of the substation is carried out in the ninth year, with a new transformer. The new PV devices are installed at the end of the branches because it reduces the costs associated with energies losses. The location of the PV modules within the network is displayed in Table 6. The CPU time decreases by 97.9% when Benders’ decomposition is the method chosen for the simulations.
- Case b. Investment limits not included: in this case, investment constraints (Equations (16) and (17)) are not considered. This new constraint scenario allows the investment in, not only new transformers and PV modules, but also in wind units (see Table 7). Two expansions of the substation are made, in years 9 and 16, PV modules are installed in all candidate nodes, and six wind units, in total, are also installed in the last year. In this case, the new installed capacity is 4725 kW. The location of the PV modules within the network is displayed in Table 8. The CPU time decreases by 94.4% using Benders’ algorithm.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Payasi, R.P.; Singh, A.K.; Singh, D. Review of distributed generation planning: Objectives, constraints and algorithms. Int. J. Eng. Sci. Technol. 2011, 3, 133–153. [Google Scholar] [CrossRef]
- Viral, R.; Khatod, D.K. Optimal planning of distributed generation systems in distribution system: A review. Renew. Sustain. Energy Rev. 2012, 16, 5146–5165. [Google Scholar] [CrossRef]
- Hadjsaid, N.; Canard, J.F.; Dumas, F. Dispersed generation impact on distribution networks. IEEE Comput. Appl. Power 1999, 12, 23–28. [Google Scholar] [CrossRef]
- Barker, P.P.; De Mello, R.W. Determining the impact of distributed generation on power systems: Part I. Radial distribution systems. IEEE Power Eng. Soc. Summer Meet. 2000, 3, 1645–1656. [Google Scholar]
- Dugan, R.C.; McDermott, T.E.; Ball, G.J. Planning for distributed generation. IEEE Ind. Appl. Mag. 2001, 7, 80–88. [Google Scholar] [CrossRef]
- El-Khattam, W.; Hegazy, Y.G.; Salama, M.M.A. An integrated distributed generation optimization model for distribution system planning. IEEE Trans. Power Syst. 2005, 20, 1158–1165. [Google Scholar] [CrossRef]
- Keane, A.; O’Malley, M. Optimal allocation of embedded generation on distribution networks. IEEE Trans. Power Syst. 2005, 20, 1640–1646. [Google Scholar] [CrossRef]
- Zou, K.; Agalgaonkar, A.P.; Muttaqi, K.M.; Perera, S. Multi-objective optimization for distribution system planning with renewable energy resources. In Proceedings of the ENERGYCON 2010: IEEE International Energy Conference, Manama, Bahrain, 18–21 December 2010; pp. 670–675. [Google Scholar]
- Kagan, N.; Adams, R.N. A Benders’ decomposition approach to the multi-objective distribution planning problem. Int. J. Electr. Power Energy Syst. 1993, 15, 259–271. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Jadid, S.; Siano, P. Economic-environmental energy and reserve scheduling of smart distribution systems: A multiobjective mathematical programming approach. Energy Convers. Manag. 2014, 78, 151–164. [Google Scholar] [CrossRef]
- Ghasemi, A.; Mortazavi, S.S.; Mashhour, E. Integration of nodal hourly pricing in day-ahead SDC (smart distribution company) optimization framework to effectively activate demand response. Energy 2015, 86, 649–660. [Google Scholar] [CrossRef]
- Hytowitz, R.B.; Hedman, K.W. Managing solar uncertainty in microgrid systems with stochastic unit commitment. Electr. Power Syst. Res. 2015, 119, 111–118. [Google Scholar] [CrossRef]
- Bloom, J.A.; Caramanis, M.; Charny, L. Long-range generation planning using generalized Benders’ decomposition: Implementation and experience. Oper. Res. 1984, 32, 290–313. [Google Scholar] [CrossRef]
- Kim, H.; Sohn, H.S.; Bricker, D.L. Generation expansion planning using Benders’ decomposition and generalized networks. Int. J. Ind. Eng. 2011, 18, 25–39. [Google Scholar]
- Wang, J.; Wang, R.; Zeng, P.; You, S.; Li, Y.; Zhang, Y. Flexible transmission expansion planning for integrating wind power based on wind power distribution characteristics. J. Electr. Eng. Technol. 2015, 10, 709–718. [Google Scholar] [CrossRef] [Green Version]
- Kazempour, S.J.; Conejo, A.J. Strategic generation investment under uncertainty via Benders’ decomposition. IEEE Trans. Power Syst. 2012, 27, 424–432. [Google Scholar] [CrossRef]
- Baringo, L.; Conejo, A.J. Wind power investment: A Benders’ decomposition approach. IEEE Trans. Power Syst. 2012, 27, 433–441. [Google Scholar] [CrossRef]
- Montoya-Bueno, S.; Muñoz, J.I.; Contreras, J. A stochastic investment model for renewable generation in distribution systems. IEEE Trans. Sustain. Energy 2015, 6, 1466–1474. [Google Scholar] [CrossRef]
- Meneses de Quevedo, P.; Contreras, J.; Rider, M.J.; Allahdadian, J. Contingency assessment and network reconfiguration in distribution grids including wind power and energy storage. IEEE Trans. Sustain. Energy 2015, 6, 1524–1533. [Google Scholar] [CrossRef]
- Conejo, A.J.; Castillo, E.; Mínguez, R.; García-Bertrand, R. Decomposition Techniques in Mathematical Programming. Engineering and Science Applications; Springer-Verlag: Heidelberg, Germany, 2006. [Google Scholar]
- Kirmani, S.; Jamil, M.; Rizwan, M. Optimal placement of SPV based DG system for loss reduction in radial distribution network using heuristic search strategies. In Proceedings of the 2011 International Conference on Energy Automation, and Signal (ICEAS), Bhubaneswar, India, 28–30 December 2011; pp. 1–4. [Google Scholar]
- Baringo, L.; Conejo, A.J. Correlated wind-power production and electric load scenarios for investment decisions. Appl. Energy 2013, 101, 475–482. [Google Scholar] [CrossRef]
- Brooke, A.; Kendrick, D.; Meeraus, A.; Raman, R. GAMS/CPLEX: A User’s Guide; GAMS: Washington, DC, USA, 2003. [Google Scholar]
| Indices and Sets | |
| Set of indices of time blocks. | |
| Set of indices of load buses. | |
| Set of indices of branches. | |
| Set of indices of blocks used in the piecewise linearization. | |
| Set of indices of substation buses. | |
| Set of indices of years. | |
| Set of indices of scenarios for the k-th block. | |
| k | Index of time blocks. |
| n, m | Indices of buses. |
| r | Index used in the linearization. |
| t | Index of years. |
| ω | Index of scenarios. |
| Constants and Parameters | |
| PV module annualized investment cost []. | |
| Wind turbine annualized investment cost []. | |
| Transformer annualized investment cost []. | |
| PV module investment cost []. | |
| Wind turbine investment cost []. | |
| Transformer investment cost [€]. | |
| Investment budget per year [€]. | |
| Investment budget throughout the life cycle of the new devices [€]. | |
| PV module operation and maintenance costs []. | |
| Wind turbine operation and maintenance costs []. | |
| Loss cost []. | |
| cns | Cost of energy not supplied []. |
| Cpv,n | Vector of candidate buses to install PV modules. |
| Cost of the energy purchased by the substation []. | |
| Vector of candidate buses to install wind turbines. | |
| Discount rate. | |
| Increasing load factor. | |
| Demand factor. | |
| Increasing energy cost factor. | |
| Wind turbine power factor available. | |
| PV module power factor available. | |
| Maximum current through branch []. | |
| Interest rate. | |
| Transformer life cycle []. | |
| PV module life cycle []. | |
| Wind turbine life cycle []. | |
| Slope of the r-th block of the piecewise linearization for branch . | |
| Number of hours in time block []. | |
| Active power load in bus []. | |
| Maximum active power output of PV modules []. | |
| Maximum active power output of wind turbine []. | |
| Maximum active power that can be installed in each bus []. | |
| Reactive power load in bus []. | |
| Resistance of branch []. | |
| Number of blocks used in the piecewise linearization. | |
| Maximum power output of new transformers []. | |
| Maximum new power allowed for installment in the substation in bus []. | |
| Existing power in the substation in bus []. | |
| Power base []. | |
| Tangent angle in substation. | |
| Tangent angle of PV modules. | |
| Tangent angle of wind turbines. | |
| Minimum voltage magnitude []. | |
| Maximum voltage magnitude []. | |
| Nominal voltage of the distribution network []. | |
| Reactance of branch []. | |
| Maximum number of PV modules to be installed in bus . | |
| Maximum number of wind turbines to be installed in bus n. | |
| Zn,m | Impedance of branch []. |
| Weight of scenario in time block . | |
| Upper bound of each r block of the power flow through branch []. | |
| Present worth factor. | |
| Variables | |
| Investment cost []. | |
| Losses cost []. | |
| Penalty for not supplied energy []. | |
| Maintenance and operation costs of DG candidates []. | |
| Maintenance and operation total costs []. | |
| Cost of energy purchased by the substation []. | |
| Square of current flow magnitude of branch n, m []. | |
| Active power of wind turbines to be installed in bus []. | |
| Active power of PV modules to be installed in bus []. | |
| Not supplied active power in bus []. | |
| Active power injected by PV modules in bus []. | |
| Active power injected by wind turbines in bus []. | |
| Active power purchased by the substation in bus []. | |
| Active power flow in branch in the forward direction []. | |
| Active power flow in branch in the backward direction []. | |
| Not supplied reactive power in bus []. | |
| Reactive power injected by PV modules in bus []. | |
| Reactive power injected by wind turbines in bus []. | |
| Reactive power purchased by the substation in bus n []. | |
| Reactive power flow through branch in the forward direction []. | |
| Reactive power flow through branch n, m in the backward direction []. | |
| Total available power in the substation in bus []. | |
| New power installed in the substation in bus []. | |
| Square of voltage magnitude in node []. | |
| Number of PV modules to be installed in bus . | |
| Number of wind turbines to be installed in bus . | |
| Number of transformers to be installed in bus . | |
| Binary variable that defines if the active power flow through branch is in the forward direction. | |
| Binary variable that defines if the active power flow through branch is in the backward direction. | |
| Binary variable that defines if the reactive power flow through branch is in the forward direction. | |
| Binary variable that defines if the reactive power flow through branch is in the backward direction. | |
| Value of the r-th block associated with the active power through branch []. | |
| Value of the r-th block associated with the reactive power through branch []. | |
| Unit | Investment Cost [€] | Life Cycle [years] | Tan (φ) |
|---|---|---|---|
| Transformer | 20,000 | 20 | 0.48 |
| Wind turbines | 125,155 | 20 | 0.48 |
| PV modules | 3445 | 20 | 0.48 |
| Blocks | Hours | Price [€/MWh] | Demand Factors | Wind Speed Factors | Wind Production Factors | Irradiation Factors | PV Production Factors |
|---|---|---|---|---|---|---|---|
| 1 | 144 | 70.99 | 0.92 | 0.45 | 1.00 | 0.78 | 0.76 |
| 62.89 | 0.90 | 0.29 | 0.76 | 0.20 | 0.20 | ||
| 67.36 | 0.88 | 0.17 | 0.37 | 0.00 | 0.00 | ||
| 57.74 | 0.87 | 0.05 | 0.00 | 0.00 | 0.00 | ||
| 2 | 1108 | 53.41 | 0.85 | 0.49 | 1.00 | 0.71 | 0.70 |
| 48.54 | 0.82 | 0.29 | 0.76 | 0.17 | 0.17 | ||
| 42.94 | 0.80 | 0.20 | 0.45 | 0.00 | 0.00 | ||
| 44.85 | 0.78 | 0.08 | 0.08 | 0.00 | 0.00 | ||
| 3 | 960 | 45.59 | 0.77 | 0.47 | 1.00 | 0.76 | 0.74 |
| 41.21 | 0.75 | 0.29 | 0.77 | 0.21 | 0.21 | ||
| 42.09 | 0.72 | 0.19 | 0.42 | 0.00 | 0.00 | ||
| 42.55 | 0.69 | 0.07 | 0.04 | 0.00 | 0.00 | ||
| 4 | 1029 | 41.65 | 0.66 | 0.48 | 1.00 | 0.73 | 0.71 |
| 39.94 | 0.62 | 0.29 | 0.76 | 0.22 | 0.22 | ||
| 37.11 | 0.59 | 0.19 | 0.44 | 0.00 | 0.00 | ||
| 35.13 | 0.55 | 0.08 | 0.07 | 0.00 | 0.00 | ||
| 5 | 1027 | 32.37 | 0.52 | 0.49 | 1.00 | 0.72 | 0.70 |
| 28.50 | 0.50 | 0.28 | 0.73 | 0.16 | 0.16 | ||
| 23.91 | 0.49 | 0.19 | 0.42 | 0.00 | 0.00 | ||
| 25.36 | 0.47 | 0.07 | 0.04 | 0.00 | 0.00 | ||
| 6 | 112 | 18.87 | 0.45 | 0.43 | 1.00 | 0.76 | 0.74 |
| 16.10 | 0.44 | 0.24 | 0.62 | 0.18 | 0.18 | ||
| 18.35 | 0.43 | 0.15 | 0.30 | 0.00 | 0.00 | ||
| 3.19 | 0.40 | 0.05 | 0.00 | 0.00 | 0.00 | ||
| 7 | 46 | 57.38 | 0.97 | 0.47 | 1.00 | 0.76 | 0.74 |
| 55.58 | 0.95 | 0.32 | 0.85 | 0.48 | 0.48 | ||
| 54.79 | 0.94 | 0.19 | 0.45 | 0.08 | 0.08 | ||
| 53.64 | 0.93 | 0.08 | 0.06 | 0.00 | 0.00 | ||
| 8 | 1083 | 53.19 | 0.89 | 0.44 | 1.00 | 0.69 | 0.67 |
| 52.62 | 0.85 | 0.27 | 0.71 | 0.27 | 0.27 | ||
| 49.51 | 0.82 | 0.18 | 0.41 | 0.01 | 0.01 | ||
| 48.08 | 0.80 | 0.07 | 0.04 | 0.00 | 0.00 | ||
| 9 | 1084 | 44.25 | 0.78 | 0.45 | 1.00 | 0.70 | 0.69 |
| 47.11 | 0.76 | 0.28 | 0.73 | 0.31 | 0.31 | ||
| 44.67 | 0.73 | 0.19 | 0.44 | 0.02 | 0.02 | ||
| 46.98 | 0.70 | 0.08 | 0.07 | 0.00 | 0.00 | ||
| 10 | 1028 | 47.89 | 0.67 | 0.46 | 1.00 | 0.71 | 0.70 |
| 47.16 | 0.65 | 0.28 | 0.74 | 0.30 | 0.29 | ||
| 43.81 | 0.62 | 0.19 | 0.43 | 0.01 | 0.01 | ||
| 42.42 | 0.58 | 0.07 | 0.05 | 0.00 | 0.00 | ||
| 11 | 1025 | 41.53 | 0.55 | 0.47 | 1.00 | 0.69 | 0.67 |
| 39.15 | 0.53 | 0.28 | 0.75 | 0.26 | 0.26 | ||
| 38.14 | 0.51 | 0.20 | 0.46 | 0.00 | 0.00 | ||
| 34.68 | 0.49 | 0.08 | 0.09 | 0.00 | 0.00 | ||
| 12 | 114 | 34.74 | 0.47 | 0.45 | 1.00 | 0.64 | 0.63 |
| 36.49 | 0.47 | 0.28 | 0.73 | 0.20 | 0.20 | ||
| 32.55 | 0.46 | 0.19 | 0.44 | 0.00 | 0.00 | ||
| 33.54 | 0.44 | 0.08 | 0.07 | 0.00 | 0.00 |
| Case | a | b | ||
|---|---|---|---|---|
| MILP | Benders | MILP | Benders | |
| Total Costs | 12,330,870 | 12,336,090 | 11,748,580 | 11,758,350 |
| O&M system costs | 11,178,621 | 11,134,070 | 9,308,298 | 9,314,627 |
| Investment costs | 1,152,249 | 1,202,020 | 2,440,282 | 2,443,723 |
| CPU time (hours) | 742 | 15 | 444 | 24.8 |
| Case | a | ||
|---|---|---|---|
| Year | Substation | Wind | PV |
| 1 | - | - | 1047.5 |
| 9 | 1000 | - | - |
| Total | 2047.5 | ||
| Year | Substation | Wind | Photovoltaic | |||
|---|---|---|---|---|---|---|
| Node | No. Units | Node | No. Units | Node | No. Units | |
| 1 | - | - | - | - | 11 24 25 26 27 31 | 77 85 85 85 85 2 |
| 9 | 1 | 1 | - | - | - | - |
| Case | b | ||
|---|---|---|---|
| Year | Substation | Wind | PV |
| 1 | - | - | 2125 |
| 9 | 1000 | - | - |
| 16 | 1000 | - | - |
| 20 | - | 600 | - |
| Total | 4725 | ||
| Year | Substation | Wind | Photovoltaic | |||
|---|---|---|---|---|---|---|
| Node | No. Units | Node | No. Units | Node | No. Units | |
| 1 | - | - | - | - | 11 12 24 25 26 27 31 32 33 34 | 85 85 85 85 85 85 85 85 85 85 |
| 9 | 1 | 1 | - | - | - | - |
| 16 | 1 | 1 | - | - | - | - |
| 20 | - | - | 21 22 23 | 2 2 2 | - | - |
| Case | a | b | a | b |
|---|---|---|---|---|
| MILP | Benders | MILP | Benders | |
| Total O&M Costs | 11,178,621 | 11,134,070 | 9,308,298 | 9,314,627 |
| Losses costs | 701,609 | 694,314 | 598,504 | 597,734 |
| Not supplied energy cost | 13,572 | 54,010 | 361 | 14,866 |
| Purchase energy cost | 10,195,660 | 10,104,480 | 8,138,853 | 8,130,402 |
| DG O&M costs | 267,780 | 281,266 | 570,580 | 571,625 |
| Problem | Case a | Case b | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Scenarios | 1 | 8 | 64 | 216 | 768 | 1 | 8 | 64 | 216 | 768 |
| MILP | 4 s | 1.9 m | 0.7 h | 13 h | 742 h | 1 s | 30 s | 3 m | 11.1 h | 444 h |
| Benders | 36 s | 5.3 m | 1.7 h | 4.9 h | 15 h | 11 s | 90 s | 72 m | 5.1 h | 24.8 h |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montoya-Bueno, S.; Muñoz-Hernandez, J.I.; Contreras, J.; Baringo, L. A Benders’ Decomposition Approach for Renewable Generation Investment in Distribution Systems. Energies 2020, 13, 1225. https://doi.org/10.3390/en13051225
Montoya-Bueno S, Muñoz-Hernandez JI, Contreras J, Baringo L. A Benders’ Decomposition Approach for Renewable Generation Investment in Distribution Systems. Energies. 2020; 13(5):1225. https://doi.org/10.3390/en13051225
Chicago/Turabian StyleMontoya-Bueno, Sergio, Jose Ignacio Muñoz-Hernandez, Javier Contreras, and Luis Baringo. 2020. "A Benders’ Decomposition Approach for Renewable Generation Investment in Distribution Systems" Energies 13, no. 5: 1225. https://doi.org/10.3390/en13051225





