Implementation and Critical Analysis of the Active Phase Jump with Positive Feedback Anti-Islanding Algorithm
Abstract
:1. Introduction
- Mathematical analysis of the APJPF NDZ and the influence of each parameter on its mapping and size;
- Proposal of a new design criterion for the APJPF scheme;
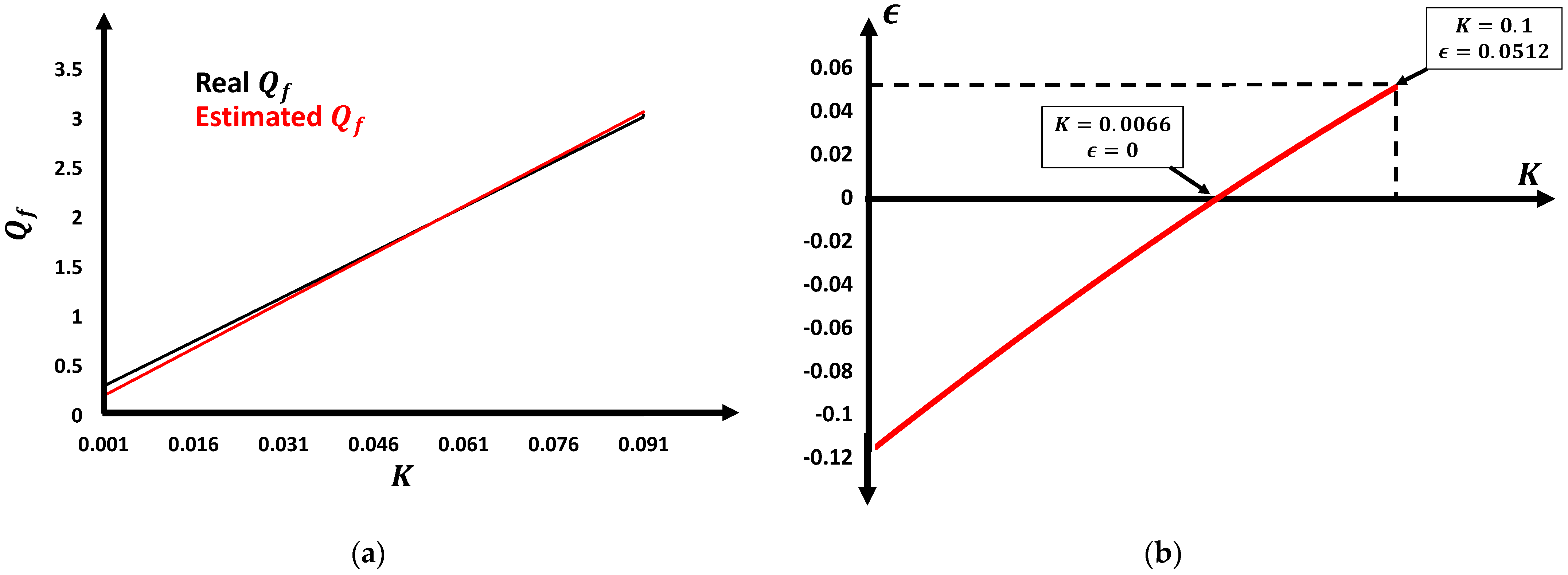
- Determination of a criterion of project for the AFDPCF algorithm;
- Computational and experimental evaluation of the APJPF under different values of capacitance, compared with other AIP: Classic AFD, AFD by [24], SFS, and AFDPCF;
- Computational and experimental analysis of the influence of the parameter in the detection time of the AFDPCF scheme.
2. NDZ Mapping
3. Anti-Islanding Methods
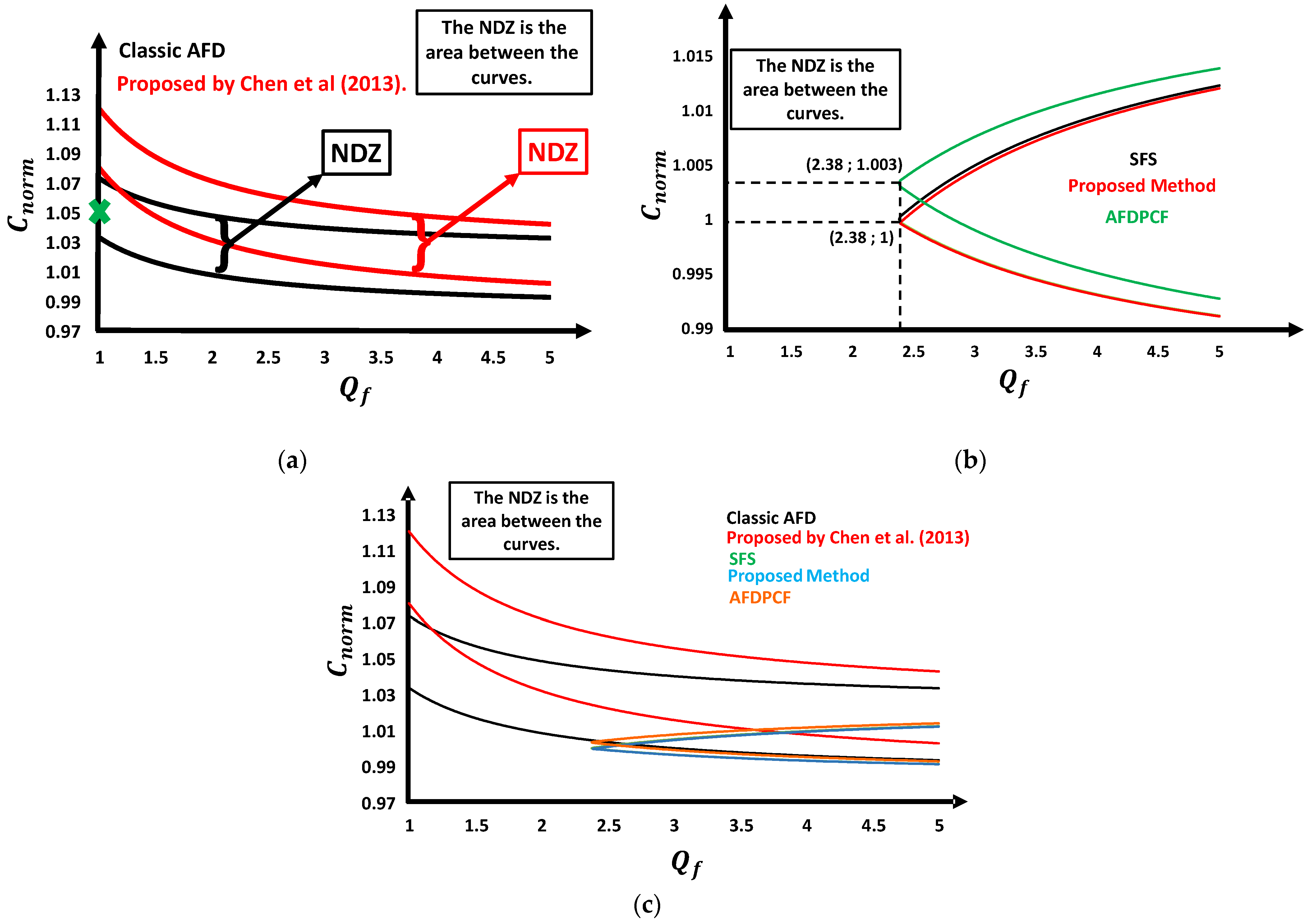
3.1. Active Frequency Drift (AFD)
3.2. Sandia Frequency Shift (SFS)
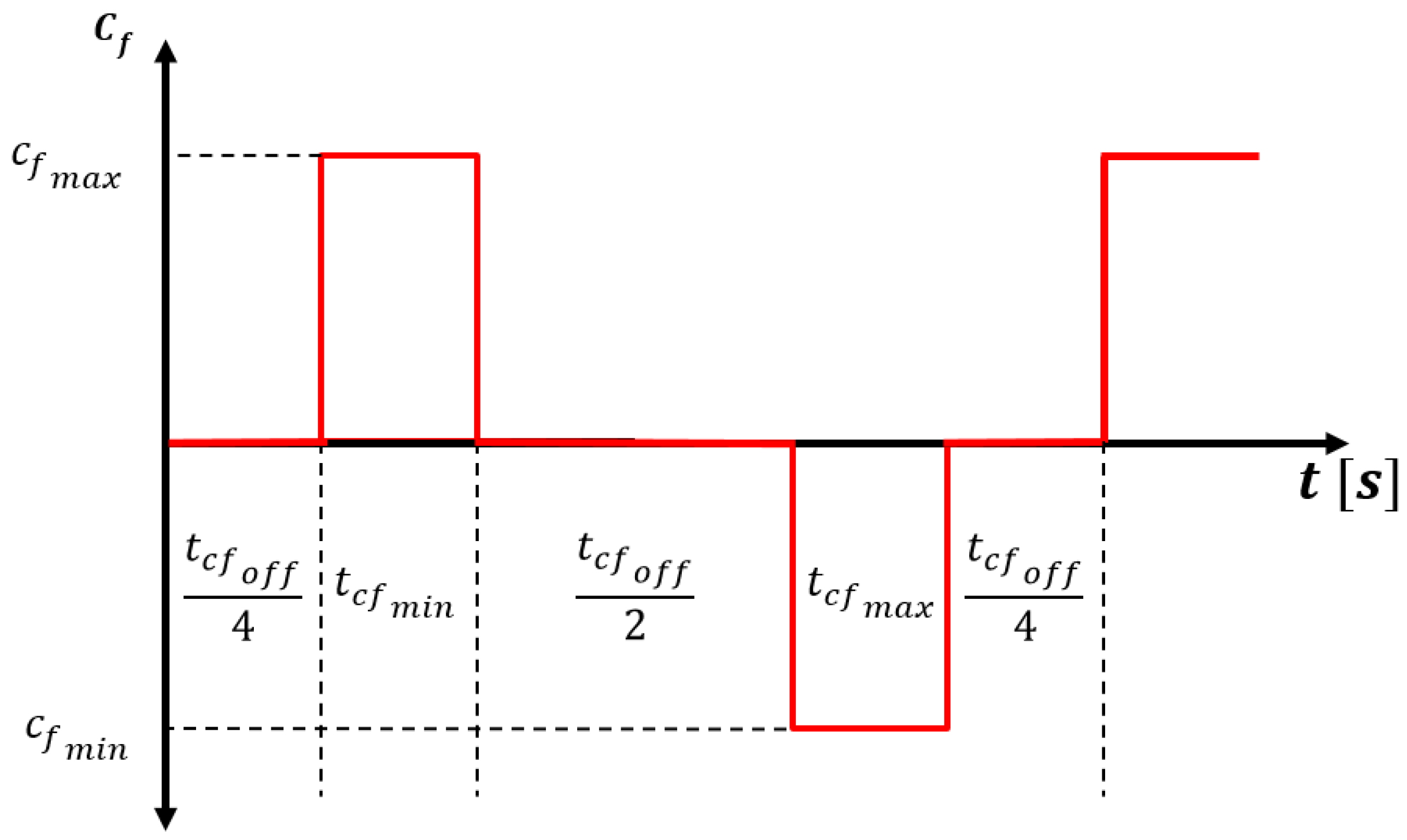
3.3. Active Frequency Drift with Pulsating Chopping Factor (AFDPCF)
3.4. AFD Proposed by Chen et al. (2013)
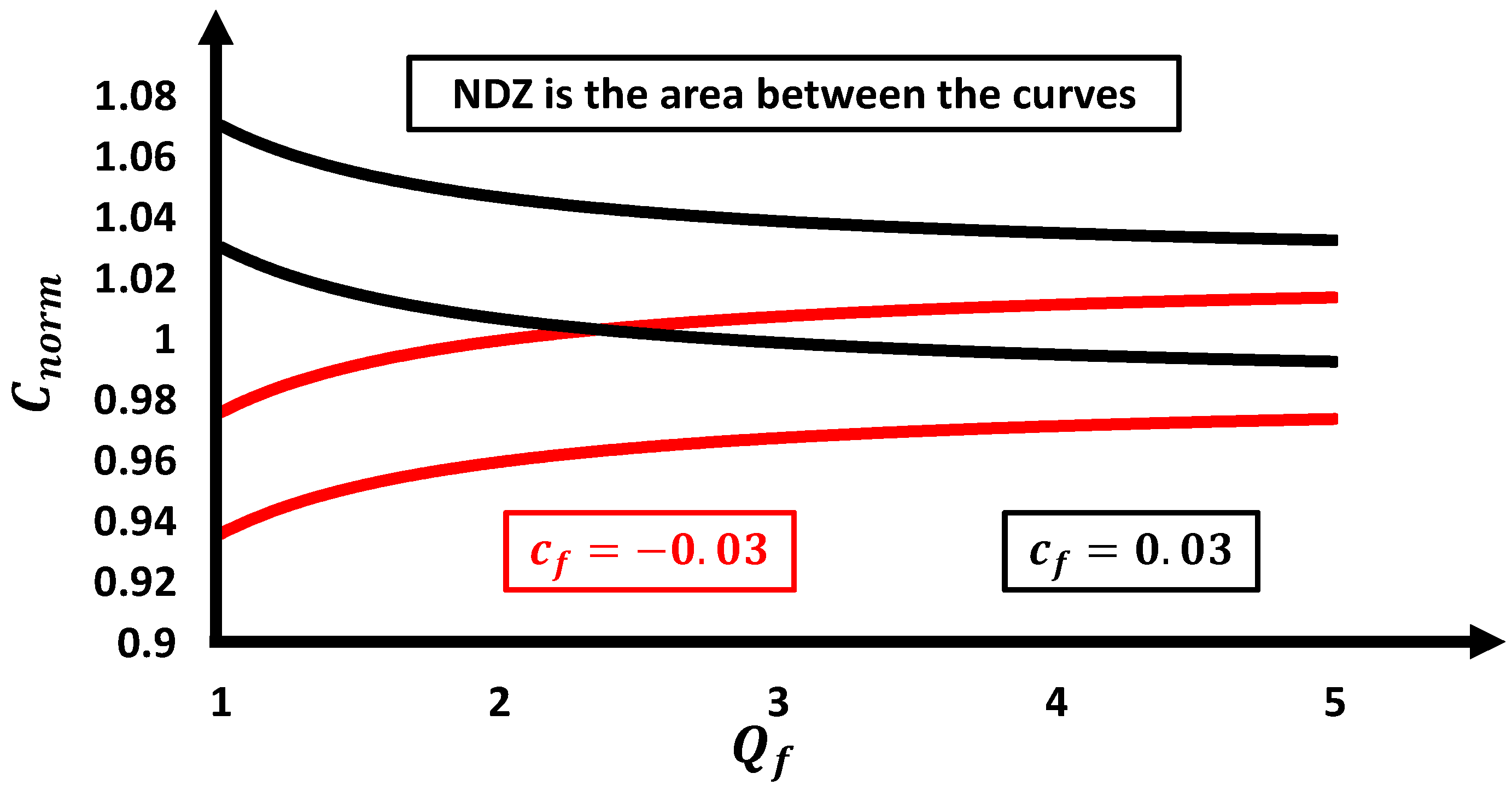
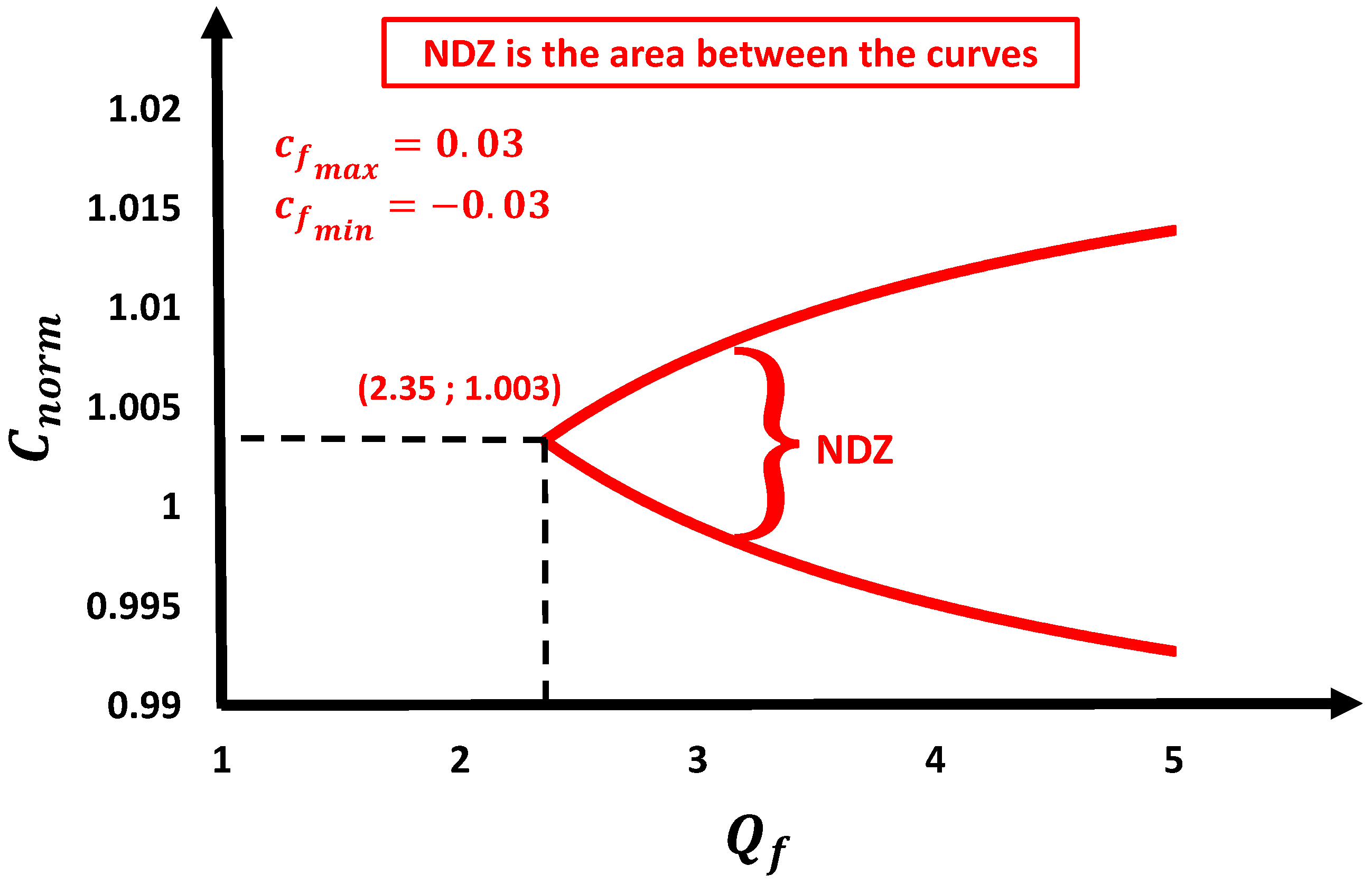
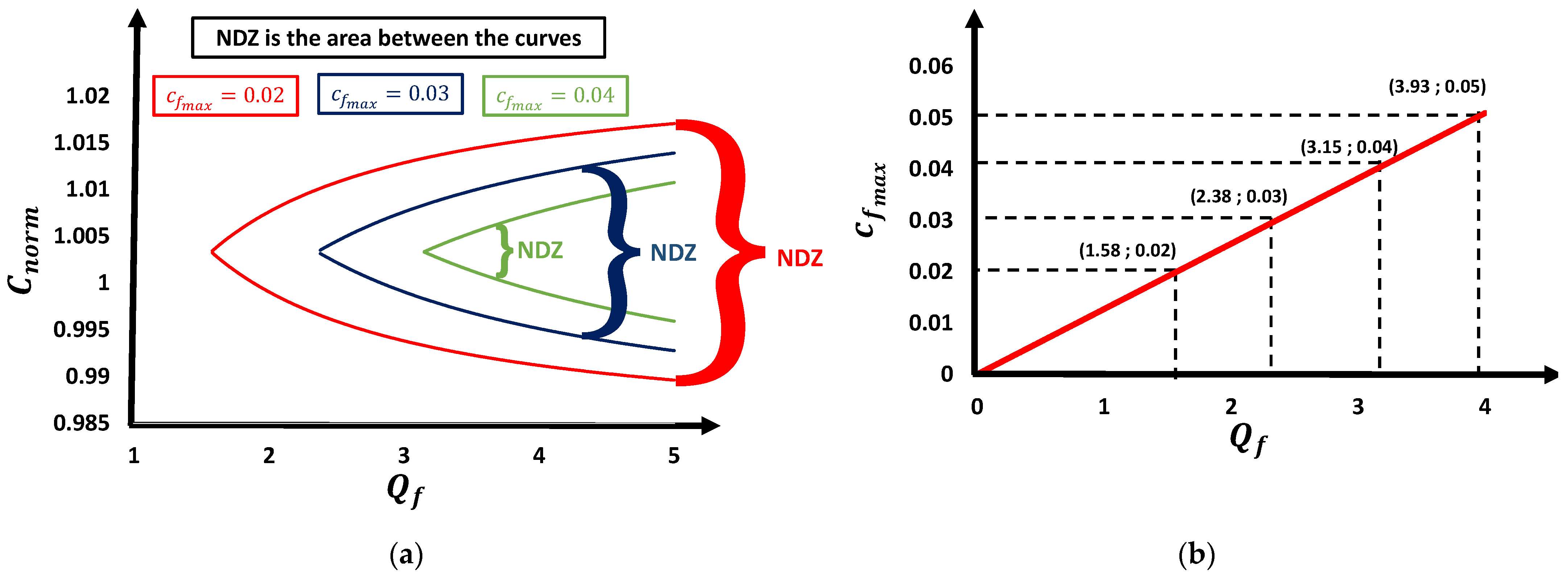
3.5. Active Phase Jump with Positive Feedback (APJPF)
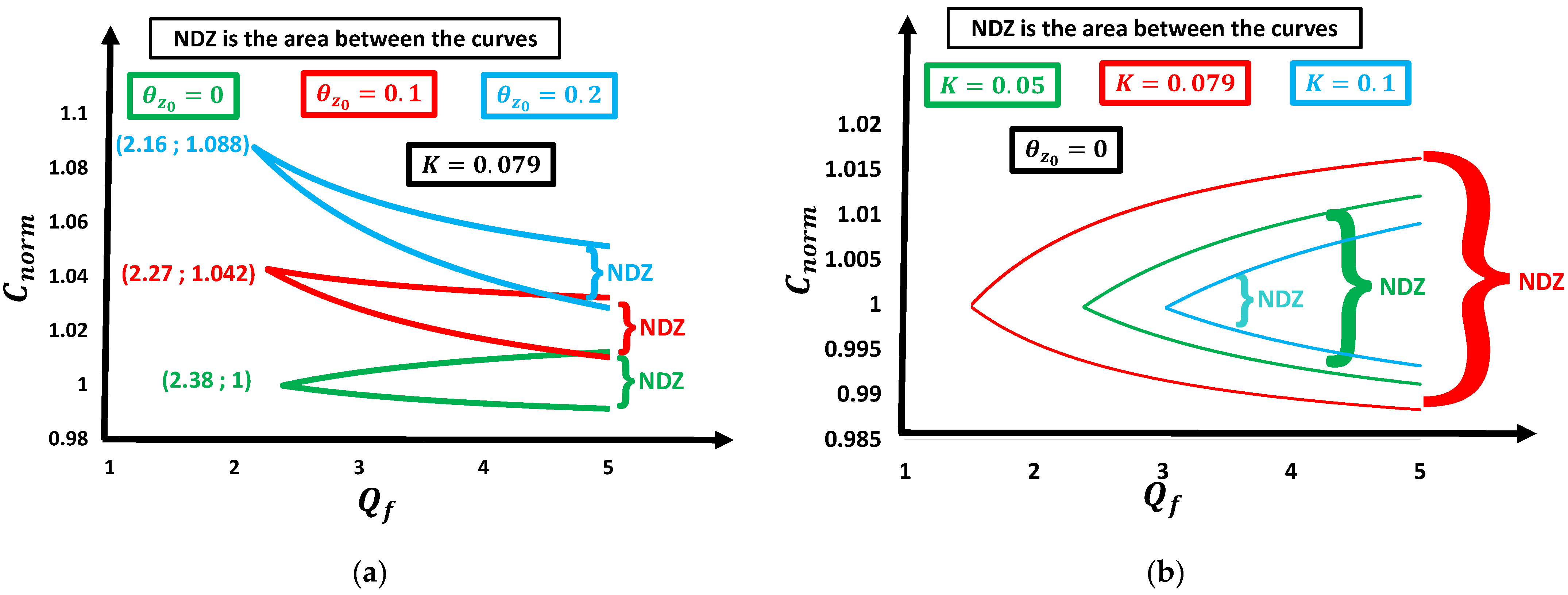
- affects positively the value of and negatively the value of ;
- affects positively the value of , reducing effectively the NDZ and does not impact the value of .
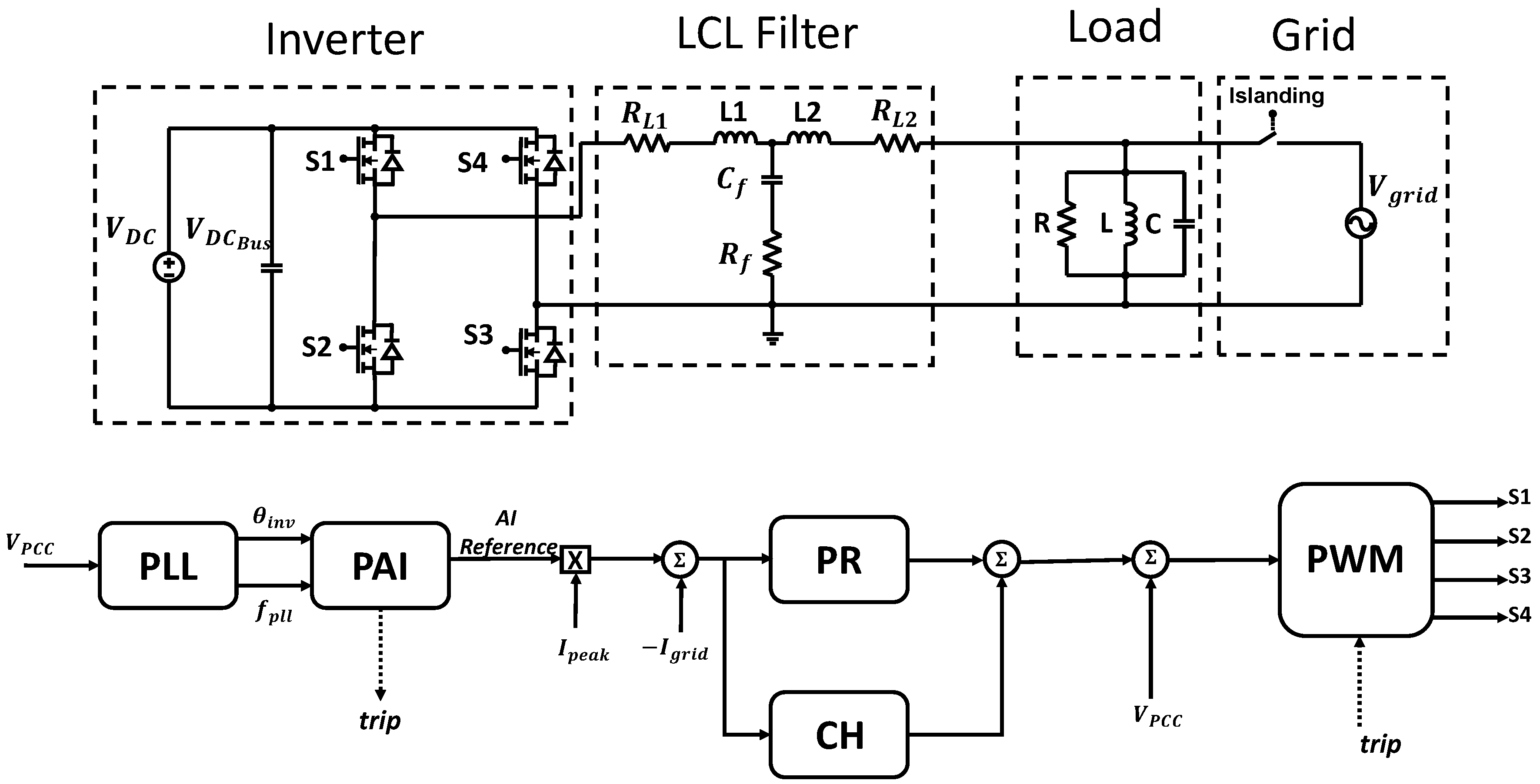
4. System Description
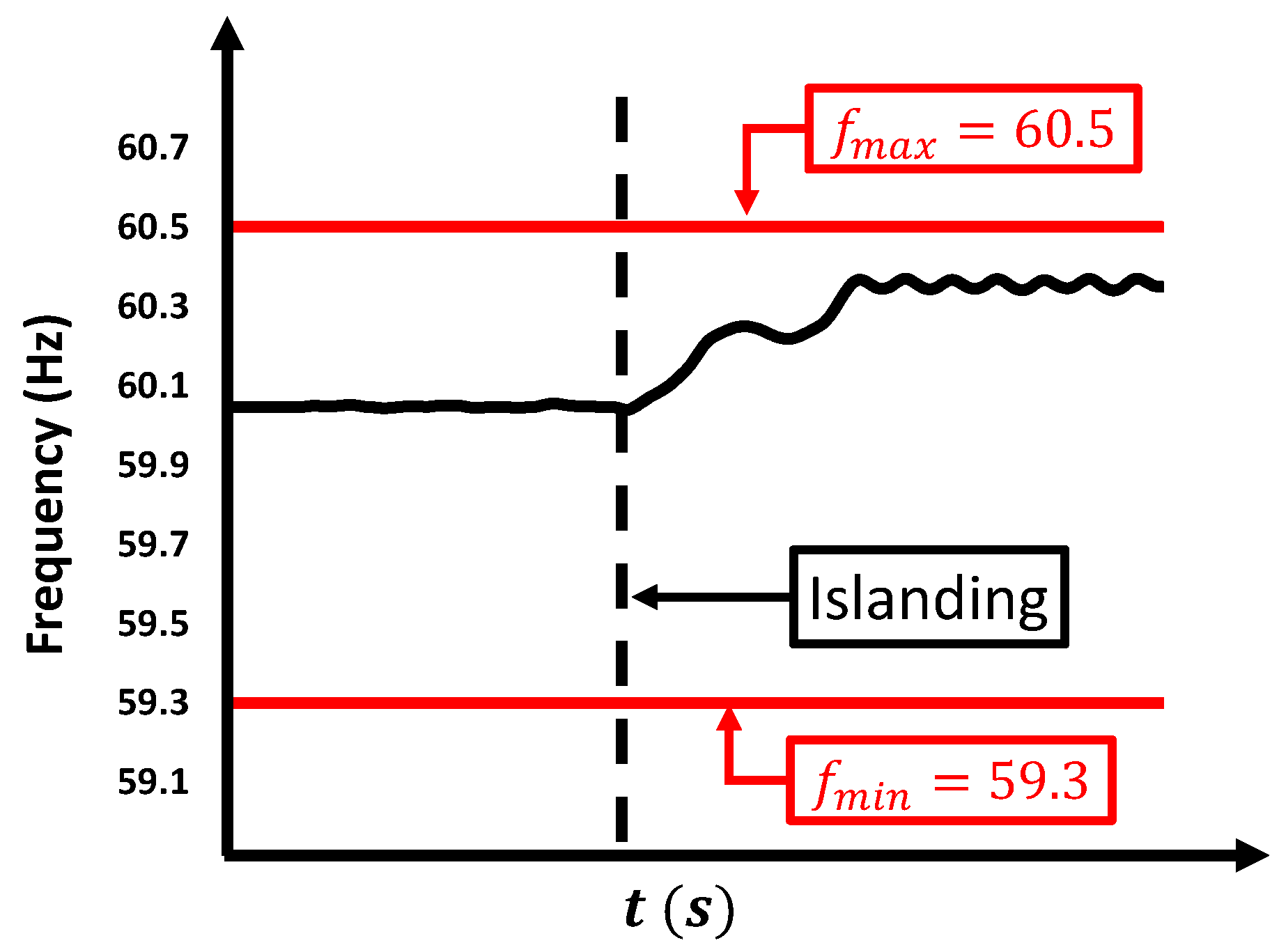
5. Standards Considerations
6. Experimental Validation Methodology
7. Computational Results
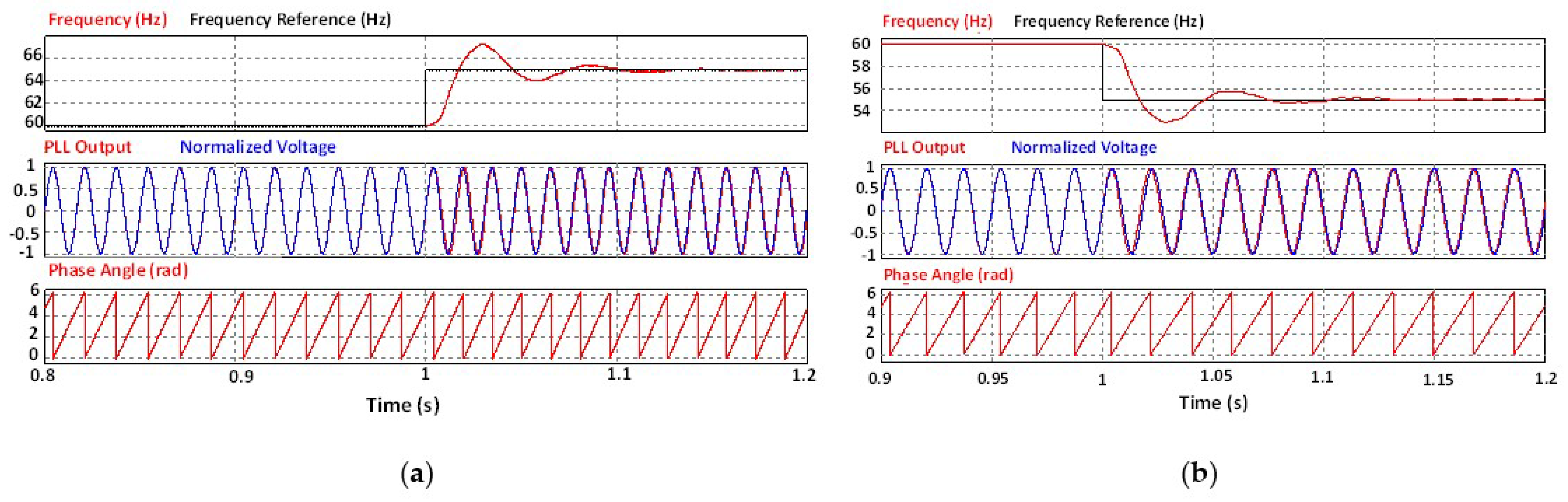
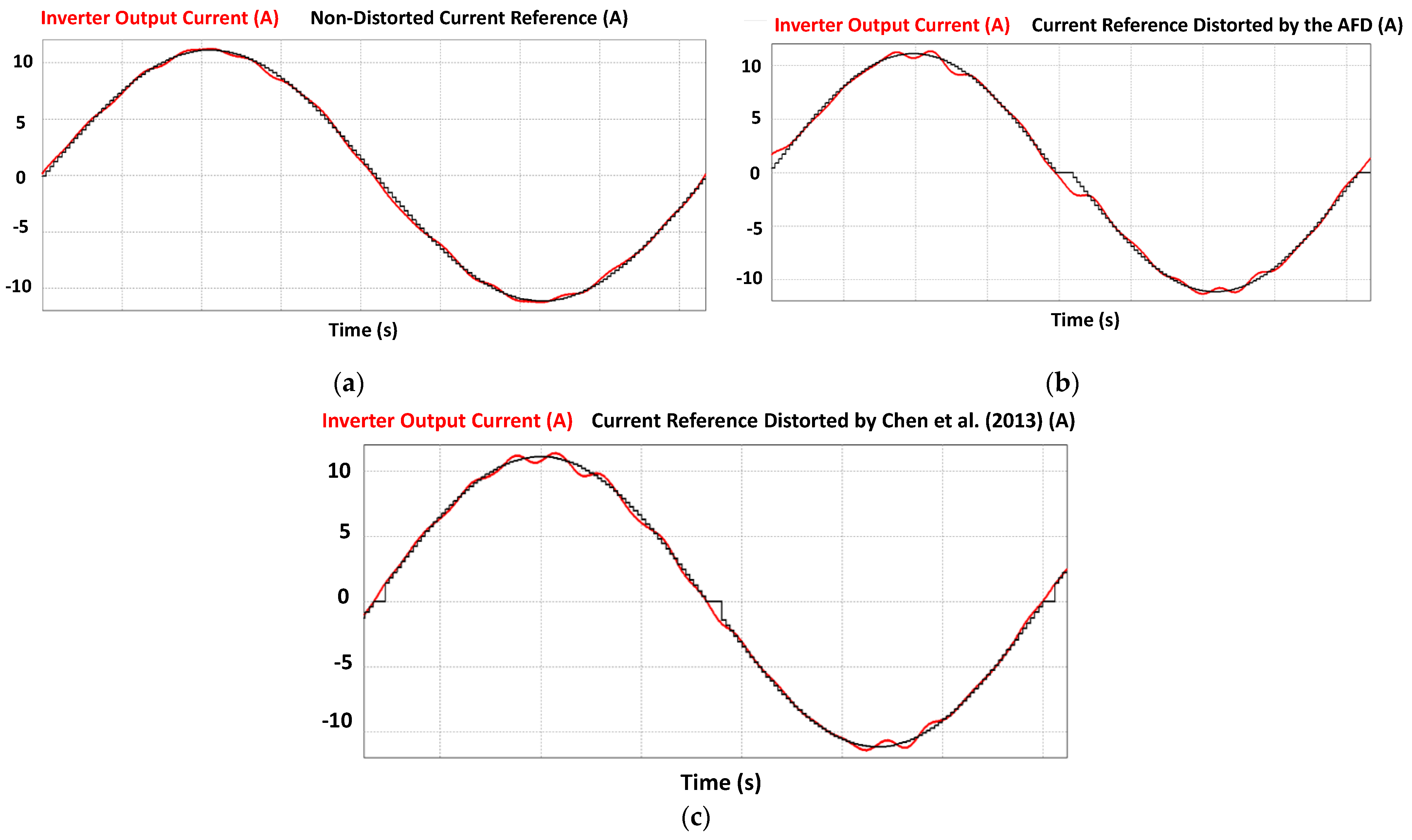
7.1. Active AIP Computational Implementation
7.2. Active AIP Computational Implementation: Group I
7.3. Active AIP Computational Implementation: Group II
7.4. Active AIP Computational Implementation: Final Considerations
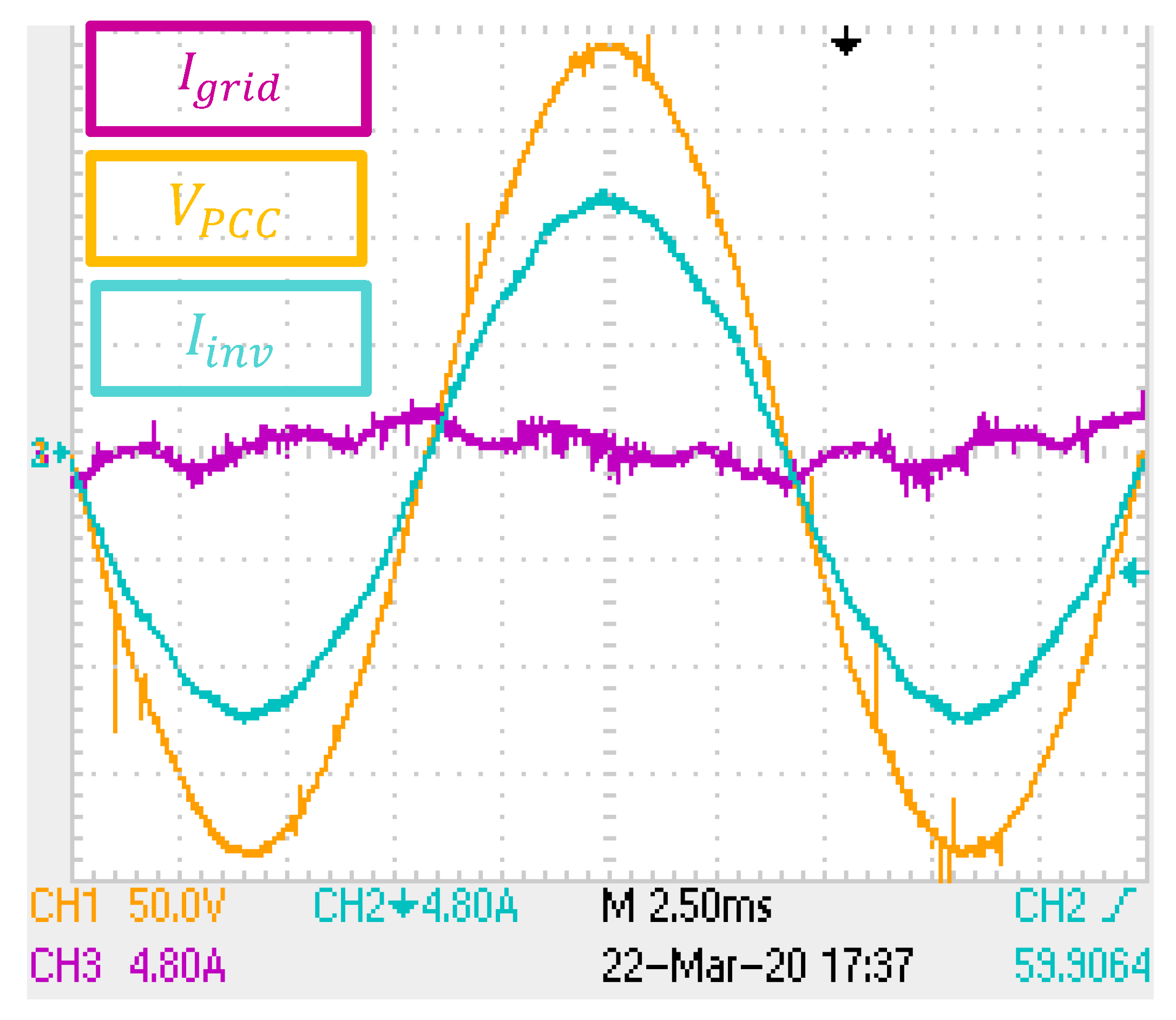
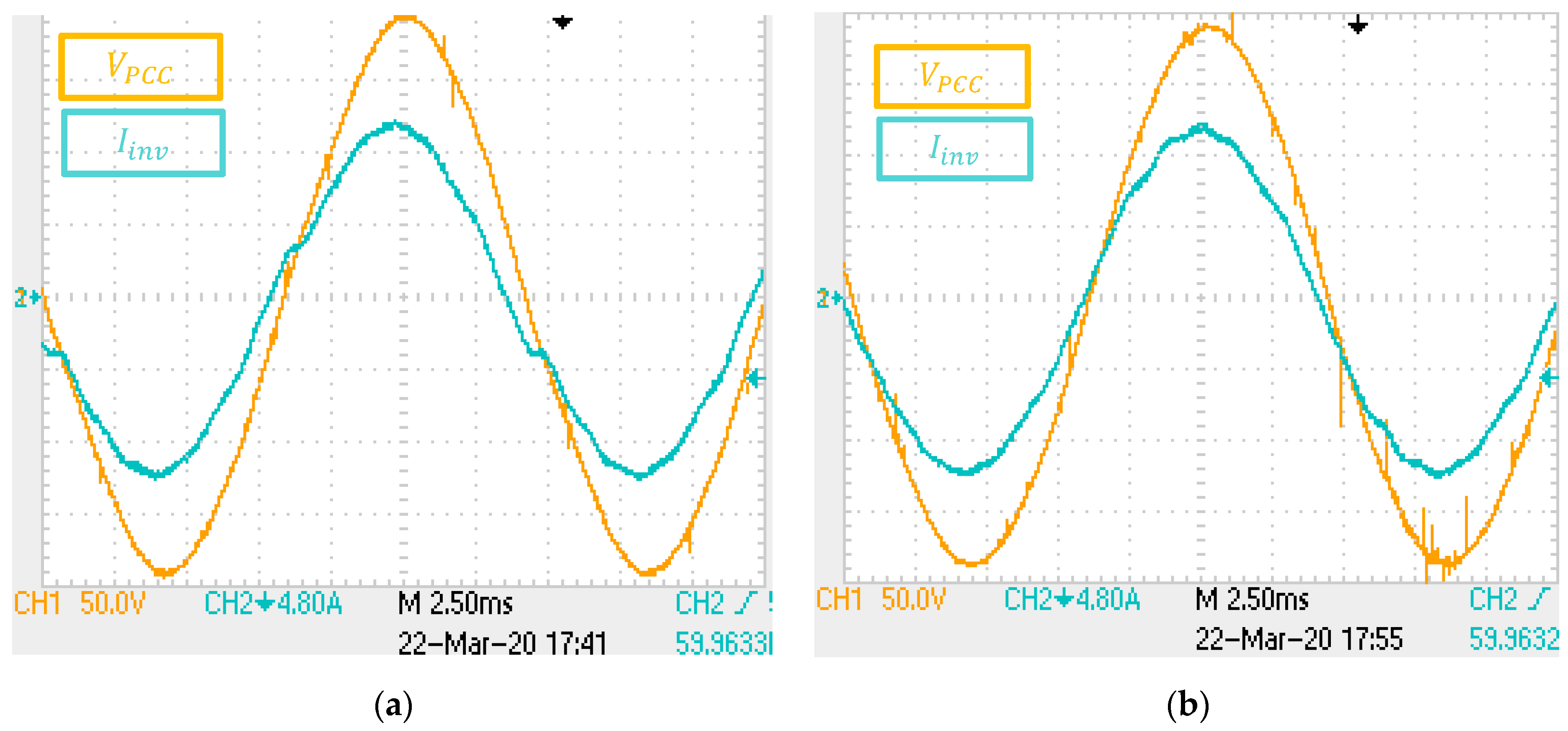
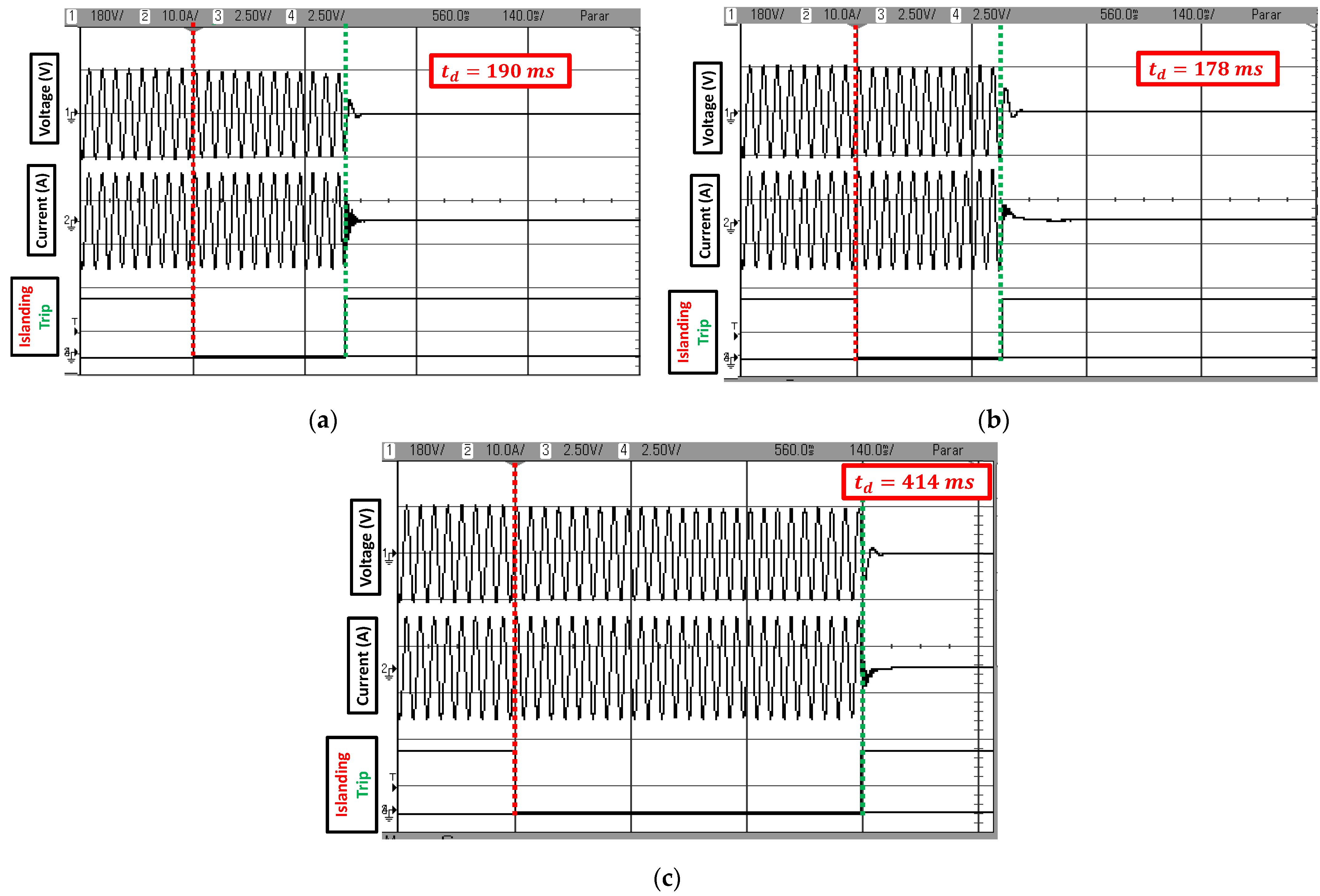
8. Experimental Results
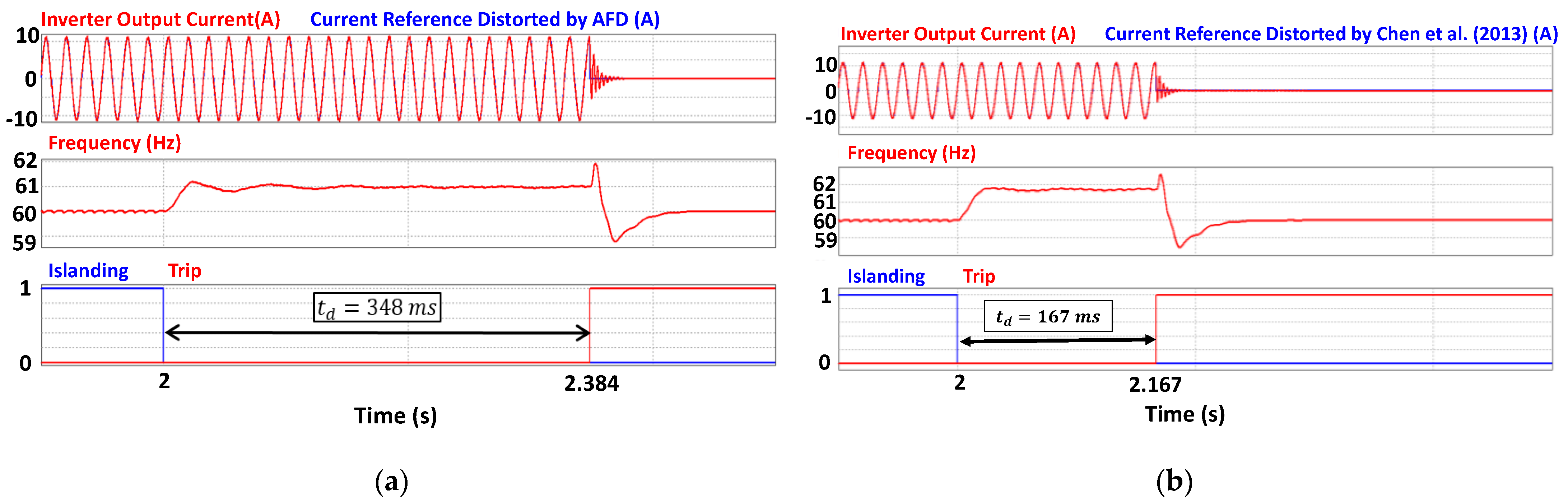
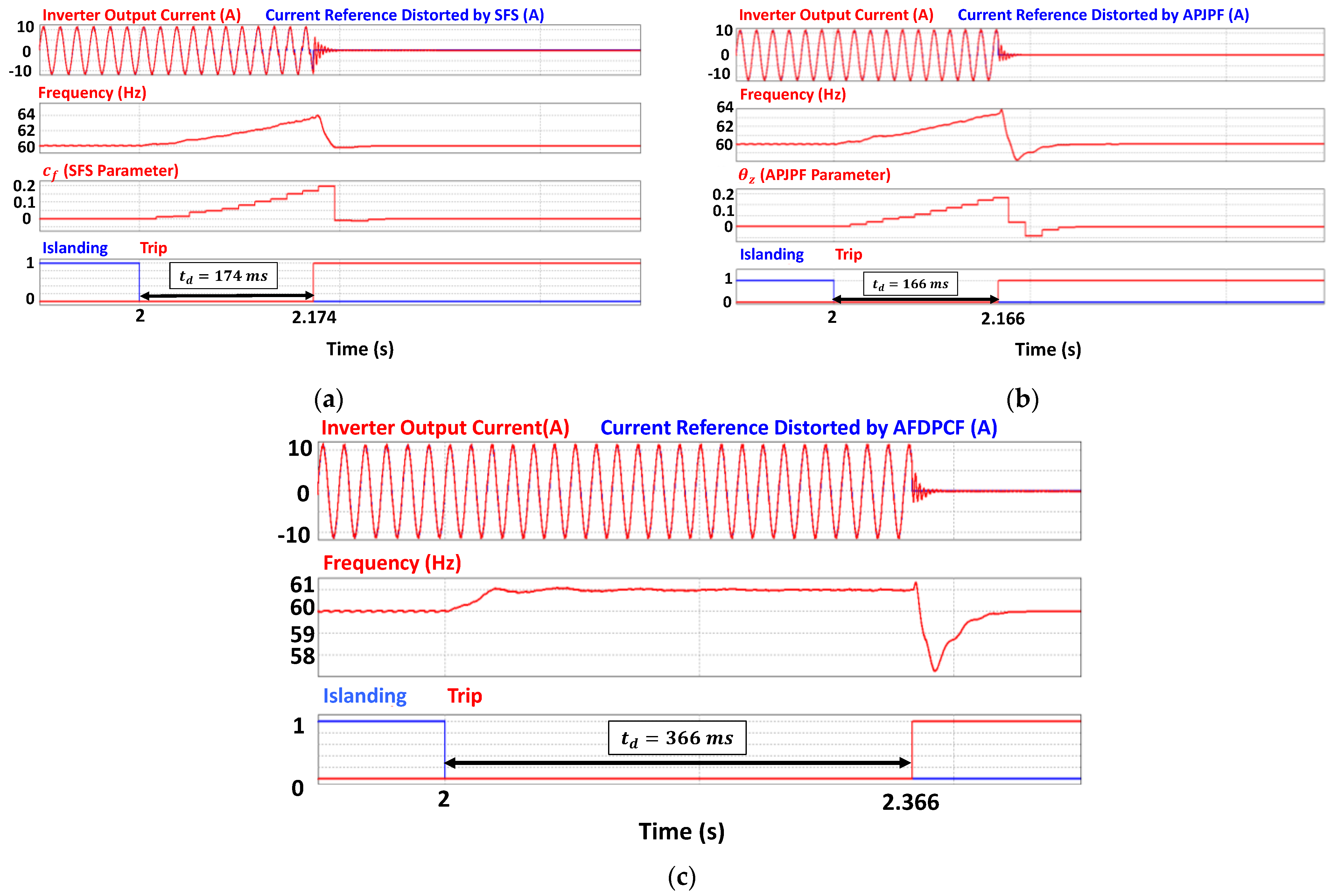
8.1. Experimental Results: Group I
8.2. Experimental Results: Group II
8.3. Experimental Results: Final Considerations
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| C | Load capacitance |
| LCL filter capacitance | |
| cot | Trigonometric operation of cotangent. |
| NDZ boundary curves | |
| Normalized capacitance | |
| Chopping factor and initial chopping factor, respectively | |
| Minimum and maximum AFDPCF chopping factor, respectively | |
| Frequency error | |
| Error between the estimated and the real quality factor | |
| f | Grid frequency |
| f’ | Frequency after the AFD implementation |
| Minimum and maximum Standards frequency thresholds | |
| Resonance frequency | |
| Frequency measured by the PLL | |
| AFD current reference | |
| Inverter current | |
| Current peak | |
| Grid current | |
| K | Accelerating gain |
| Counter gain | |
| Correction factor of the design methodology of the APJPF | |
| Load quality factor | |
| L | Load inductance |
| L1, L2 | First and second LCL filter inductances |
| Load resistance. | |
| LCL filter damping resistor | |
| LCL filter inductors resistances | |
| Time and Dead Time, respectively | |
| Islanding detection time | |
| tg | Trigonometric operation of tangent |
| Time for and for the AFDPCF | |
| Actual and anterior counter state | |
| Time for for the AFDPCF | |
| Period | |
| Sampling period | |
| Phase angle for the inverter current | |
| DC bus voltage | |
| PCC voltage | |
| Minimum and maximum Standards voltage thresholds | |
| Grid voltage | |
| Phase jump and Initial phase jump, respectively | |
| Grid angular frequency | |
| Minimum and maximum Standards angular frequency thresholds |
References
- IEC 62116:2014; Utility-Interconnected Photovoltaic Inverters-Test Procedure of Islanding Prevention Measures. International Electrotechnical Commission: Geneva, Switzerland, 2014.
- IEEE Std 929-2000; IEEE Recommended Practice for Utility Interface of Photovoltaic (PV) Systems, USA, IEEE Std 929-2000 (Revision of IEEE Std 929–1988). IEEE Standards Association: Piscataway, NJ, USA, 2000. Available online: https://standards.ieee.org/standard/929-2000.html (accessed on 2 May 2022).
- IEEE Std 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces (Revision of IEEE Std 1547–2003). IEEE Standards Association: Piscataway, NJ, USA, 2018.
- ABNT NBR Standards 16149-2013; Photovoltaics (FV) Systems—Characteristics of the Utility Interface, BR. ABNT NBR Standards: São Paulo, Brazil, 2013.
- Suman, M.; Kirthiga, M. Chapter 17—Unintentional Islanding Detection. In Distributed Energy Resources in Microgrids, 1st ed.; Chauhan, R., Chauhan, K., Eds.; Chauhan Academic Press: New York, NY, USA, 2019; pp. 419–440. ISBN 978-0-12-817774-7. [Google Scholar] [CrossRef]
- Kim, M.-S.; Haider, R.; Cho, G.-J.; Kim, C.-H.; Won, C.-Y.; Chai, J.-S. Comprehensive Review of Islanding Detection Methods for Distributed Generation Systems. Energies 2019, 12, 837. [Google Scholar] [CrossRef] [Green Version]
- Cebollero, J.A.; Cañete, D.; Martín-Arroyo, S.; García-Gracia, M.; Leite, H. A Survey of Islanding Detection Methods for Microgrids and Assessment of Non-Detection Zones in Comparison with Grid Codes. Energies 2022, 15, 460. [Google Scholar] [CrossRef]
- Ahmad, K.N.E.K.; Rahim, N.A.; Sevaraj, J.; Rivai, A.; Chaniago, K. An effective passive islanding detection method for PV single-phase grid-connected inverter. Sol. Energy 2013, 97, 155–167. [Google Scholar] [CrossRef]
- Abokhalil, A.G.; Awan, A.B.; Qawasmi, A.R.A. Comparative Study of Passive and Active Islanding Detection Methods for PV Grid-Connected Systems. Sustainability 2018, 10, 1798. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.-H.; Tsai, H.-T.; Lee, T.-L. Islanding detection method based on second-order harmonic injection for voltage-controlled inverter. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Khodaparastan, M.; Vahedi, H.; Khazaeli, F.; Oraee, H. A Novel Hybrid Islanding Detection Method for Inverter-Based DGs Using SFS and ROCOF. IEEE Trans. Power Deliv. 2017, 32, 2162–2170. [Google Scholar] [CrossRef]
- Subramanian, K.; Loganathan, A.K. Islanding Detection Using a Micro-Synchrophasor for Distribution Systems with Distributed Generation. Energies 2020, 13, 5180. [Google Scholar] [CrossRef]
- Mango, F.; Liserre, M.; Dell’Aquila, A.; Pigazo, A. Overview of Anti-Islanding Algorithms for PV Systems. Part I: Passive Methods. In Proceedings of the 2006 12th International Power Electronics and Motion Control Conference, Portorož, Slovenia, 30 August–1 September 2006; pp. 1878–1883. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Chapter 5—Islanding Detection. In Grid Converters for Photovoltaic and Wind Power Systems, 2nd ed.; Wiley-IEEE Press: New York, NY, USA, 2019; pp. 81–141. ISBN 9780470667057. [Google Scholar]
- Yu, B.; Matsui, M.; Yu, G. A review of current anti-islanding methods for photovoltaic power system. Sol. Energy 2010, 84, 745–754. [Google Scholar] [CrossRef]
- Voglitsis, D.; Valsamas, F.; Papanikolaou, N.; Tsimtsios, A.; Perpinias, I.; Korkas, C. A Simple Strategy to Reduce the NDZ Caused by the Parallel Operation of DER-Inverters. Clean Technol. 2020, 2, 17–31. [Google Scholar] [CrossRef] [Green Version]
- Ropp, M.; Begovic, M.; Rohatgi, A. Analysis and performance assessment of the active frequency drift method of islanding prevention. IEEE Trans. Energy Convers. 1999, 14, 810–816. [Google Scholar] [CrossRef]
- Reis, M.V.; Barros, T.A.; Moreira, A.B.; Ruppert, E.; Villalva, M.G. Analysis of the Sandia Frequency Shift (SFS) islanding detection method with a single-phase photovoltaic distributed generation system. In Proceedings of the 2015 IEEE PES Innovative Smart Grid Technologies Latin America (ISGT LATAM), Montevideo, Uruguay, 5–7 October 2015. [Google Scholar] [CrossRef]
- Gao, Y.; Ye, J. Improved Slip Mode Frequency-Shift Islanding Detection Method. In Proceedings of the 2019 International Conference on Virtual Reality and Intelligent Systems (ICVRIS), Jishou, China, 14–15 September 2019; pp. 152–155. [Google Scholar] [CrossRef]
- Jung, Y.; Choi, J.; Yu, B.; So, J.; Yu, G.; Choi, J. A Novel Active Frequency Drift Method of Islanding Prevention for the grid-connected Photovoltaic Inverter. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 12–16 June 2005; pp. 1–6. [Google Scholar] [CrossRef]
- Vahedi, H.; Karrari, M. Adaptive Fuzzy Sandia Frequency-Shift Method for Islanding Protection of Inverter-Based Distributed Generation. IEEE Trans. Power Deliv. 2013, 28, 84–92. [Google Scholar] [CrossRef]
- Zeineldin, H.; Salama, M.M.A. Impact of Load Frequency Dependence on the NDZ and Performance of the SFS Islanding Detection Method. IEEE Trans. Ind. Electron. 2011, 58, 139–146. [Google Scholar] [CrossRef]
- Resende, Ê.C.; Carvalho, H.T.M.; Melo, F.C.; Coelho, E.A.A.; de Lima, G.B.; de Freitas, L.C.G. A Performance Analysis of Active Anti-Islanding Methods Based on Frequency Drift. In Proceedings of the 2019 IEEE 15th Brazilian Power Electronics Conference and 5th IEEE Southern Power Electronics Conference (COBEP/SPEC), Santos, Brazil, 1–4 December 2019; pp. 1–6. [Google Scholar]
- Chen, W.; Wang, G.; Zhu, X.; Zhao, B. An improved active frequency drift islanding detection method with lower total harmonic distortion. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 5248–5252. [Google Scholar] [CrossRef]
- Resende, Ê.C.; Carvalho, H.T.M.; Coelho, E.A.A.; de Lima, G.B.; de Freitas, L.C.G. Proposal of a New Active Anti-Islanding Strategy Based on Positive Feedback. Eletrônica Potência 2021, 26, 302–314. [Google Scholar] [CrossRef]
- Messenger, R.; Abtahi, A. Chapter 4—Grid-Connected Utility-Interactive PV Systems. In Photovoltaics System Engineering, 4th ed.; CRC Press: New York, NY, USA, 2017; p. 112. ISBN 1498772773. [Google Scholar]
- Ropp, M.E.; Begovic, M.; Rohatgi, A.; Kern, G.A.; Bonn, R.H.; Gonzalez, S. Determining the relative effectiveness of islanding detection methods using phase criteria and non-detection zones. IEEE Trans. Energy Convers. 2000, 15, 290–296. [Google Scholar] [CrossRef]
- Lopes, L.A.C.; Huili, S. Performance assessment of active frequency drifting islanding detection methods. IEEE Trans. Energy Convers. 2006, 21, 171–180. [Google Scholar] [CrossRef]
- Liu, F.; Kang, Y.; Duan, S. Analysis and optimization of active frequency drift islanding detection method. In Proceedings of the APEC 07—Twenty Second Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 25 February–1 March 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Resende, Ê.C.; Carvalho, H.T.M.; Coelho, E.A.A.; de Lima, G.B.; de Freitas, L.C.G. Computational Implementation of Different Anti-Islanding Techniques Based on Frequency Drift for Distributed Generation Systems. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference—Latin America, Gramado, Brazil, 15–18 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Hong, Y.; Huang, W. Investigation of Frequency drift methods of Islanding Detection with multiple PV inverters. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014; pp. 429–434. [Google Scholar] [CrossRef]
- Wang, X.; Freitas, W. Impact of Positive-Feedback Anti-Islanding Methods on Small-Signal Stability of Inverter-Based Distributed Generation. IEEE Trans. Energy Convers. 2008, 23, 923–931. [Google Scholar] [CrossRef]
- Zeineldin, H.H.; Kennedy, S. Sandia Frequency-Shift Parameter Selection to Eliminate Non detection Zones. IEEE Trans. Power Deliv. 2009, 24, 486–487. [Google Scholar] [CrossRef]
- Hatata, A.Y.; Abd-Raboh, E.-H.; Sedhom, B. Proposed Sandia frequency shift for anti-islanding detection method based on artificial immune system. Alex. Eng. J. 2018, 57, 235–245. [Google Scholar] [CrossRef]
- Vahedi, H.; Karrari, M.; Gharehpetian, G.B. Accurate SFS Parameter Design Criterion for Inverter-Based Distributed Generation. IEEE Trans. Power Deliv. 2016, 31, 1050–1059. [Google Scholar] [CrossRef]
- Yuan, L.; Zhang, X.; Zheng, J.; Mei, J.; Gao, M. An improved islanding detection method for grid-connected photovoltaic inverters. In Proceedings of the 2007 International Power Engineering Conference (IPEC 2007), Singapore, 3–6 December 2007; pp. 538–543. [Google Scholar]
- Al Hosani, M.; Qu, Z.; Zeineldin, H.H. Scheduled Perturbation to Reduce Nondetection Zone for Low Gain Sandia Frequency Shift Method. IEEE Trans. Smart Grid 2015, 6, 3095–3103. [Google Scholar] [CrossRef]
- Wang, X.; Freitas, W.; Xu, W. Dynamic Non-Detection Zones of Positive Feedback Anti-Islanding Methods for Inverter-Based Distributed Generators. IEEE Trans. Power Deliv. 2011, 26, 1145–1155. [Google Scholar] [CrossRef]
- Reznik, A.; Simoes, M.G.; Al-Durra, A.; Muyeen, S.M. LCL Filter Design and Performance Analysis for Grid-Interconnected Systems. IEEE Trans. Ind. Appl. 2014, 50, 1225–1232. [Google Scholar] [CrossRef]
- Xu, J.; Qian, H.; Hu, Y.; Bian, S.; Xie, S. Overview of SOGI-Based Single-Phase Phase-Locked Loops for Grid Synchronization Under Complex Grid Conditions. IEEE Access 2021, 9, 39275–39291. [Google Scholar] [CrossRef]
- Souza, M.E.T.; Resende, Ê.C.; Melo, F.C.; Lima, G.B.; Freitas, L.C.G. Computational Implementation and Comparative Analysis of Phase-Locked Loop (PLL) Methods Under Different Power Quality Disturbances. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference—Latin America, Gramado, Brazil, 15–18 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Cha, H.; Vu, T.; Kim, J. Design and control of Proportional-Resonant controller based Photovoltaic power conditioning system. In Proceedings of the IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 2198–2205. [Google Scholar] [CrossRef]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and control of an LCL-filter-based three-phase active rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]







| Grid | |
|---|---|
| Rated Voltage | 127 Vrms |
| Nominal Frequency | 60 Hz |
| THDv | <2.5% |
| Inverter | |
| Output Voltage | 127 V |
| Output Current | 7.89 A |
| Rated Power | 1000 W |
| First Filter Inductor | 1.5 mH |
| First Inductor Resistance | |
| Second Filter Inductor | 10.5 mH |
| Second Inductor Resistance | 0.05 Ω |
| Dampping Resistor | 2 Ω |
| Filter Capacitor | |
| Switching Frequency | 10 kHz |
| Load | |
| Type | Parallel RLC |
| Total Resistance | 16.129 Ω |
| Total Inductance | 42.48 mH |
| Total Capacitance | |
| Resonance Frequency | 60.05 Hz |
| Quality Factor | 1.01 |
| Electrical Variable | IEEE 929–2000 | IEEE 1547–2003 | ABNT 16149 | |||
|---|---|---|---|---|---|---|
| Voltage | Range (%) | Time (s) | Range (%) | Time (s) | Range (%) | Time (s) |
| V < 50 | 0.1 | V < 50 | 0.16 | - | - | |
| 50 ≤ V ≤ 88 | 2 | 50 ≤ V < 88 | 2 | V < 80 | 0.4 | |
| 88 ≤ V ≤ 110 | 88 ≤ V ≤ 110 | 80 ≤ V ≤ 110 | ||||
| 110 ≤ V ≤ 137 | 2 | 110 ≤ V < 120 | 1 | 110 < V | 0.2 | |
| 137 ≤ V | 0.1 | V ≥ 120 | 0.16 | - | - | |
| Frequency | Range (Hz) | Time (s) | Range (Hz) | Time (s) | Range (Hz) | Time (s) |
| f < 59.5 | 0.1 | f < 59.3 | 0.16 | f < 58.5 | 0.2 | |
| f > 60.5 | 0.1 | f > 60.5 | 0.16 | f > 61.5 | 0.2 | |
| TDHv | Total | 5 % | Total | 5 % | Total | <5% |
| Groups | Methods | THDi | Detection Time | Detection Time | Detection Time |
|---|---|---|---|---|---|
| I | Classic AFD | 4.72% | 166 ms | 348 ms | Not Detected |
| Proposed by [24] | 3.18% | 113 ms | 167 ms | 351 ms | |
| II | SFS | 2.75% | 96 ms | 174 ms | 236 ms |
| AFDPCF1 | 3.15% | 171 ms | 366 ms | 566 ms | |
| AFDPCF2 | 166 ms | 315 ms | 913 ms | ||
| AFDPCF3 | 176 ms | 551 ms | 580 ms | ||
| APJPF | 2.73% | 88 ms | 166 ms | 182ms |
| Groups | Methods | THDi | Detection Time | Detection Time | Detection Time |
|---|---|---|---|---|---|
| I | Classic AFD | 4.57% | 134 ms | 222 ms | Not Detected |
| Proposed in [24] | 2.56% | 100 ms | 140 ms | 264 ms | |
| II | SFS | 2.41% | 110 ms | 190 ms | 194 ms |
| AFDPCF | 3.58% | ||||
| APJPF | 2.34% | 96 ms | 178 ms | 166 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Resende, Ê.C.; de Moura Carvalho, H.T.; Freitas, L.C.G. Implementation and Critical Analysis of the Active Phase Jump with Positive Feedback Anti-Islanding Algorithm. Energies 2022, 15, 4609. https://doi.org/10.3390/en15134609
Resende ÊC, de Moura Carvalho HT, Freitas LCG. Implementation and Critical Analysis of the Active Phase Jump with Positive Feedback Anti-Islanding Algorithm. Energies. 2022; 15(13):4609. https://doi.org/10.3390/en15134609
Chicago/Turabian StyleResende, Ênio Costa, Henrique Tannús de Moura Carvalho, and Luiz Carlos Gomes Freitas. 2022. "Implementation and Critical Analysis of the Active Phase Jump with Positive Feedback Anti-Islanding Algorithm" Energies 15, no. 13: 4609. https://doi.org/10.3390/en15134609







