Combustion Stability Control Based on Cylinder Pressure for High Efficiency Gasoline Engines
Abstract
:1. Introduction
2. Engine Stability and Fuel Consumption Compromise
2.1. Stationary Regime
2.2. Standard Engine Calibration
2.3. Benefit from a Closed Loop Controller
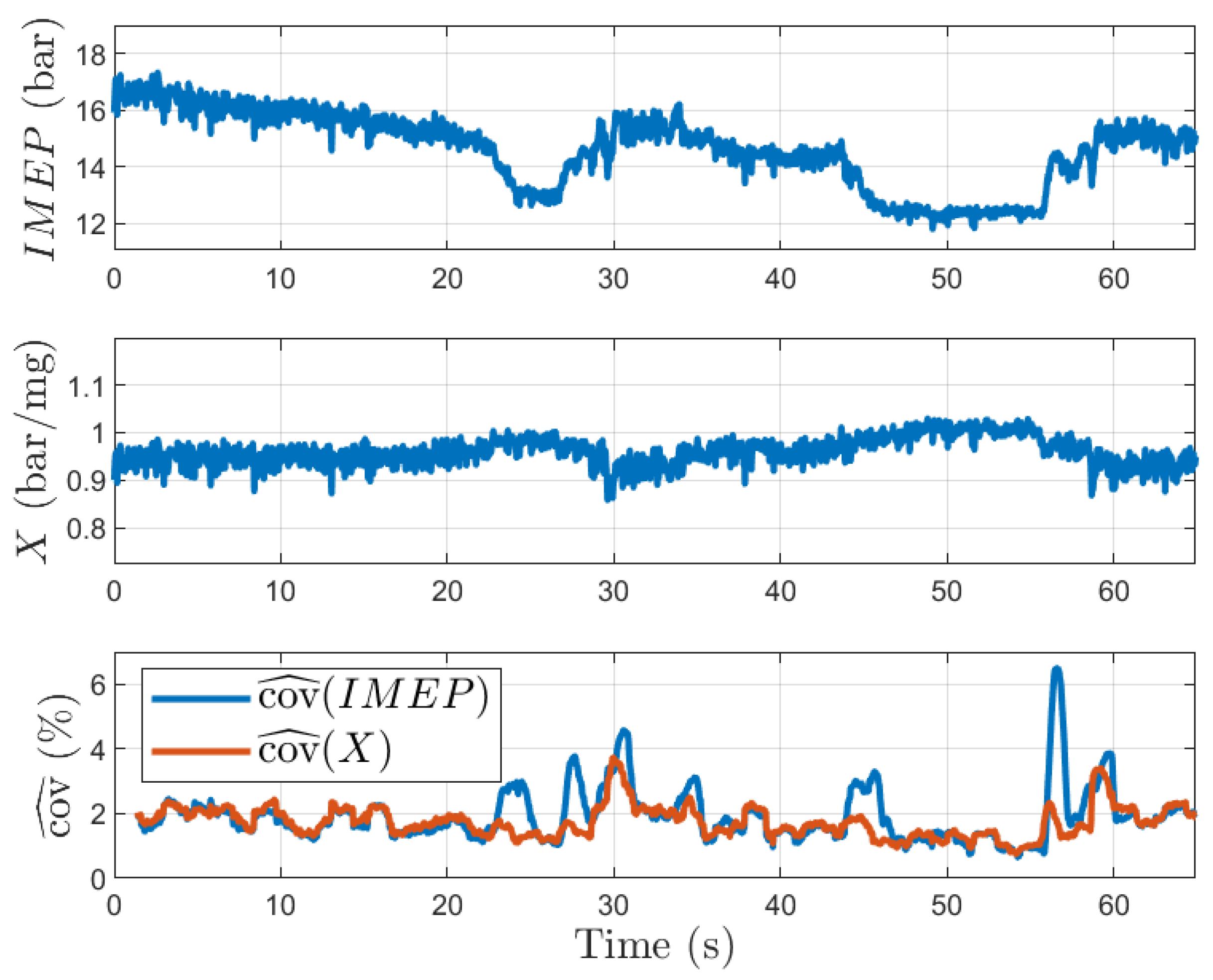
2.4. Estimation Bias in Transient States
3. Proposition
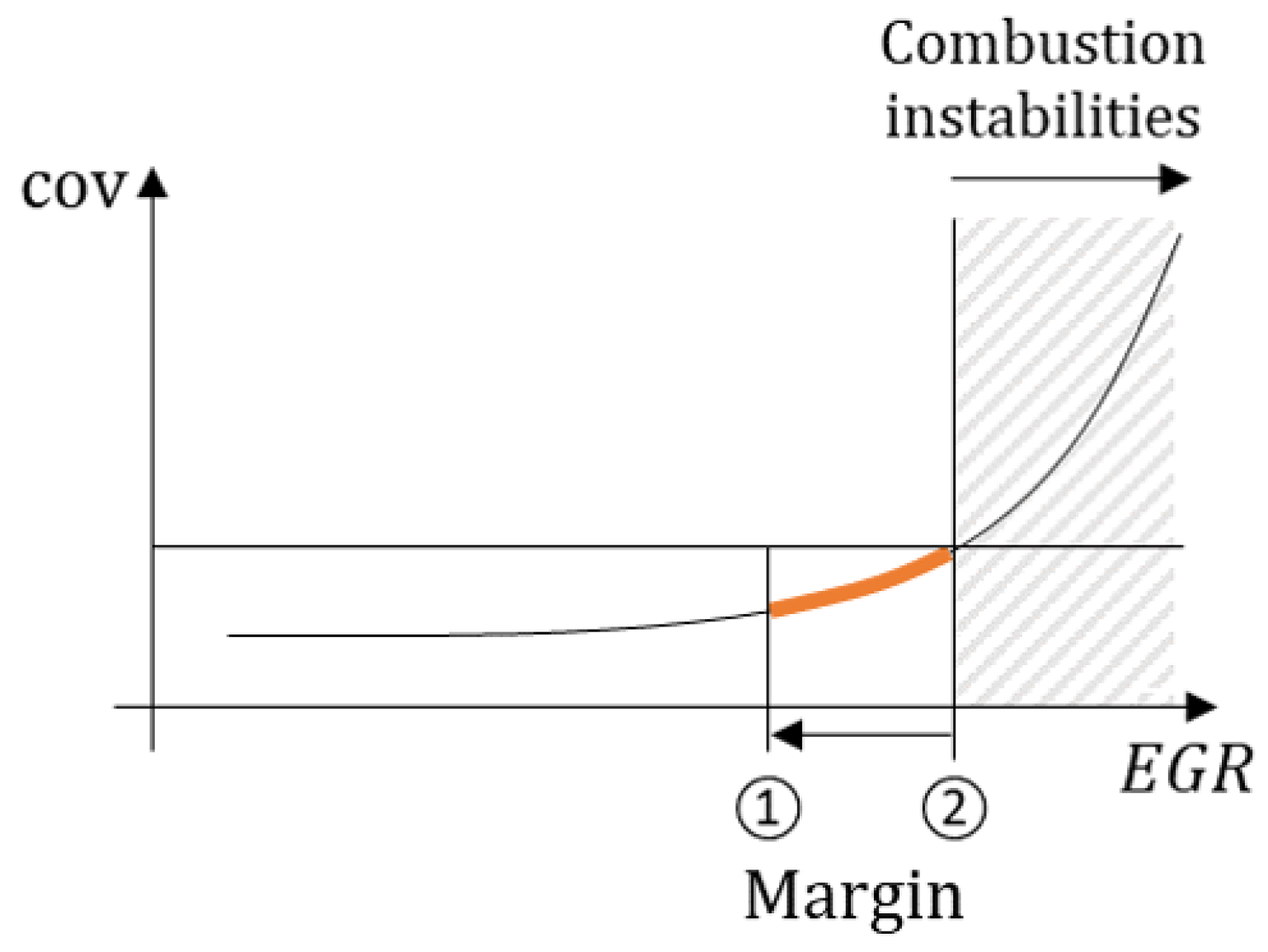
3.1. Combustion Stability Indicator
3.2. Combustion Stability Control
4. Experimental Setup
4.1. Engine Setup
4.2. Test-Bench Setup
4.3. Control Strategy Implementation
5. Experimental Results
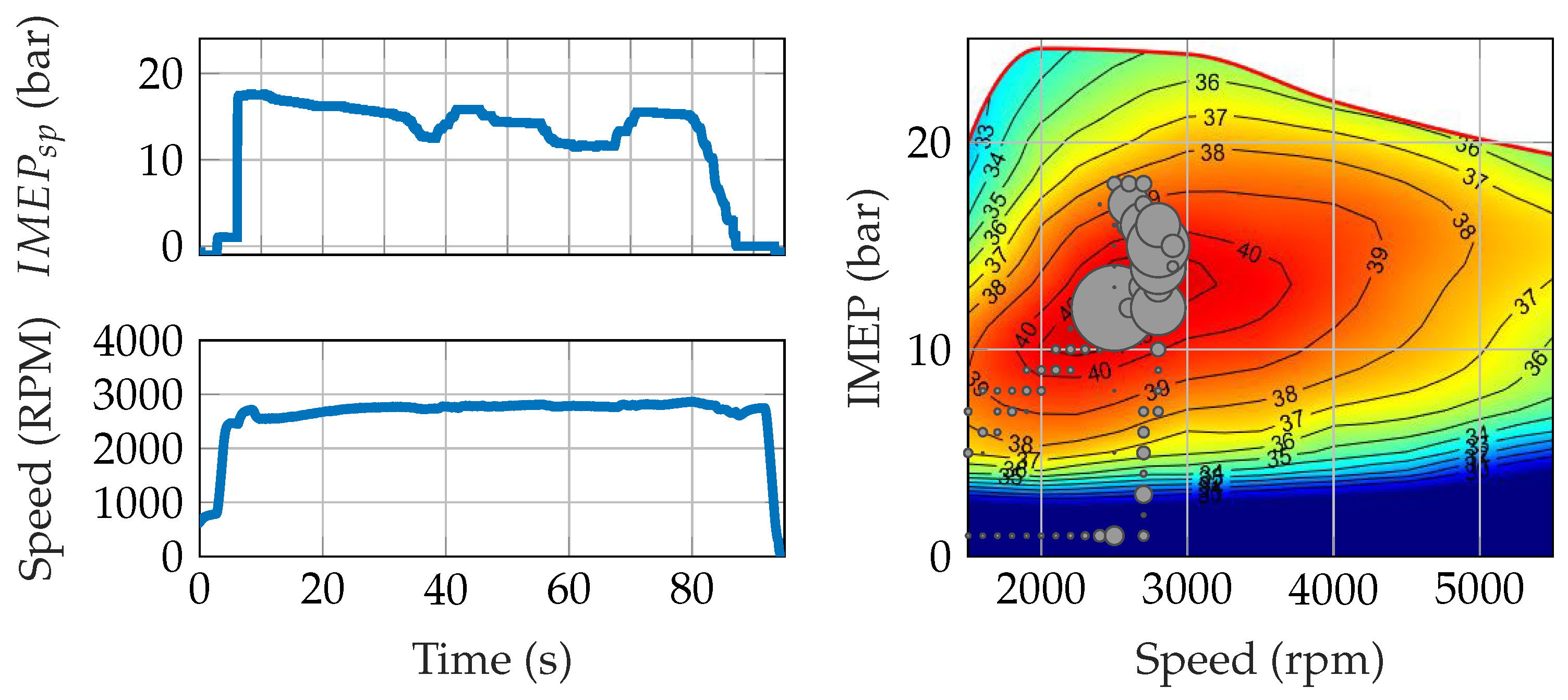
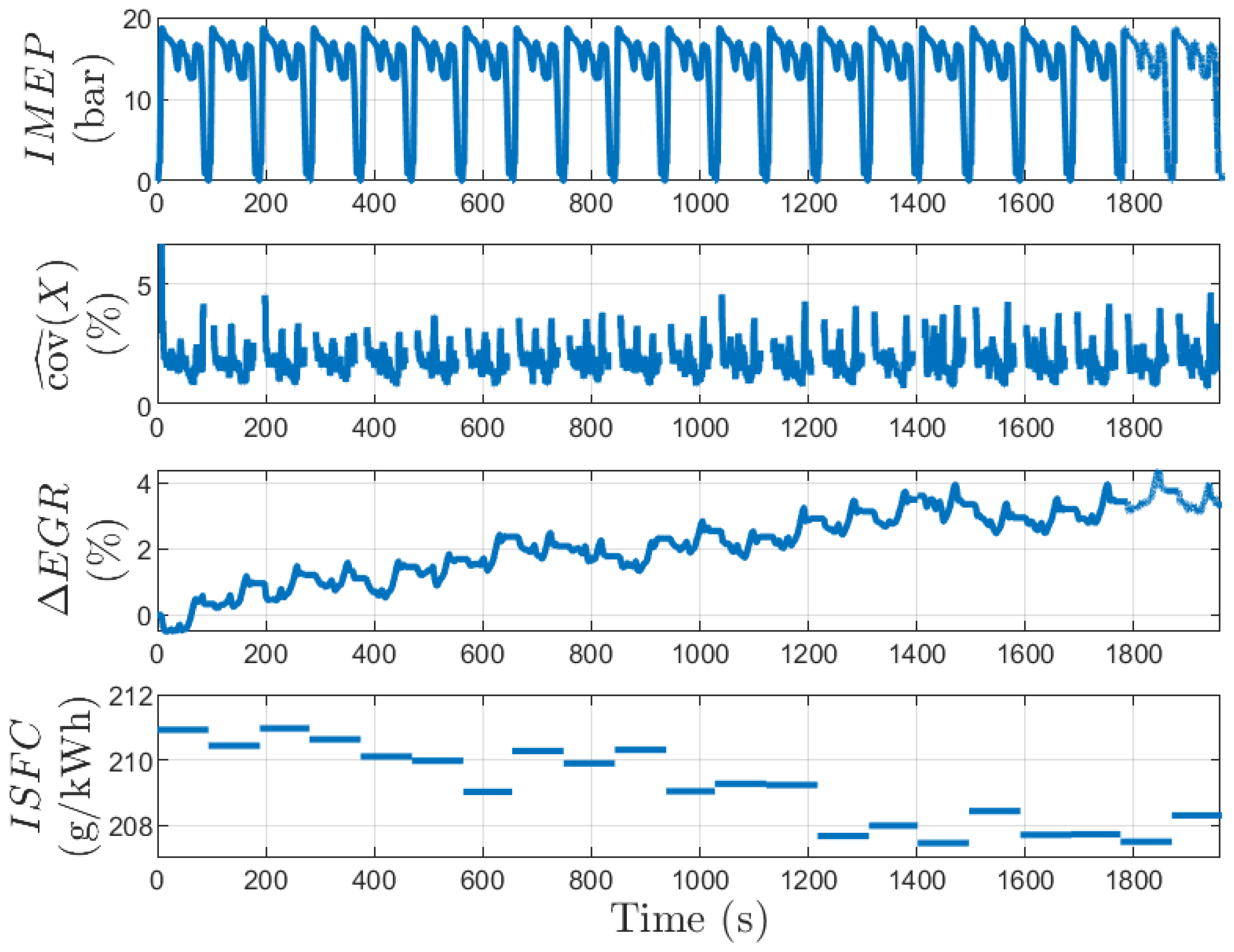
5.1. Torque Trajectory on WTLP Cycle
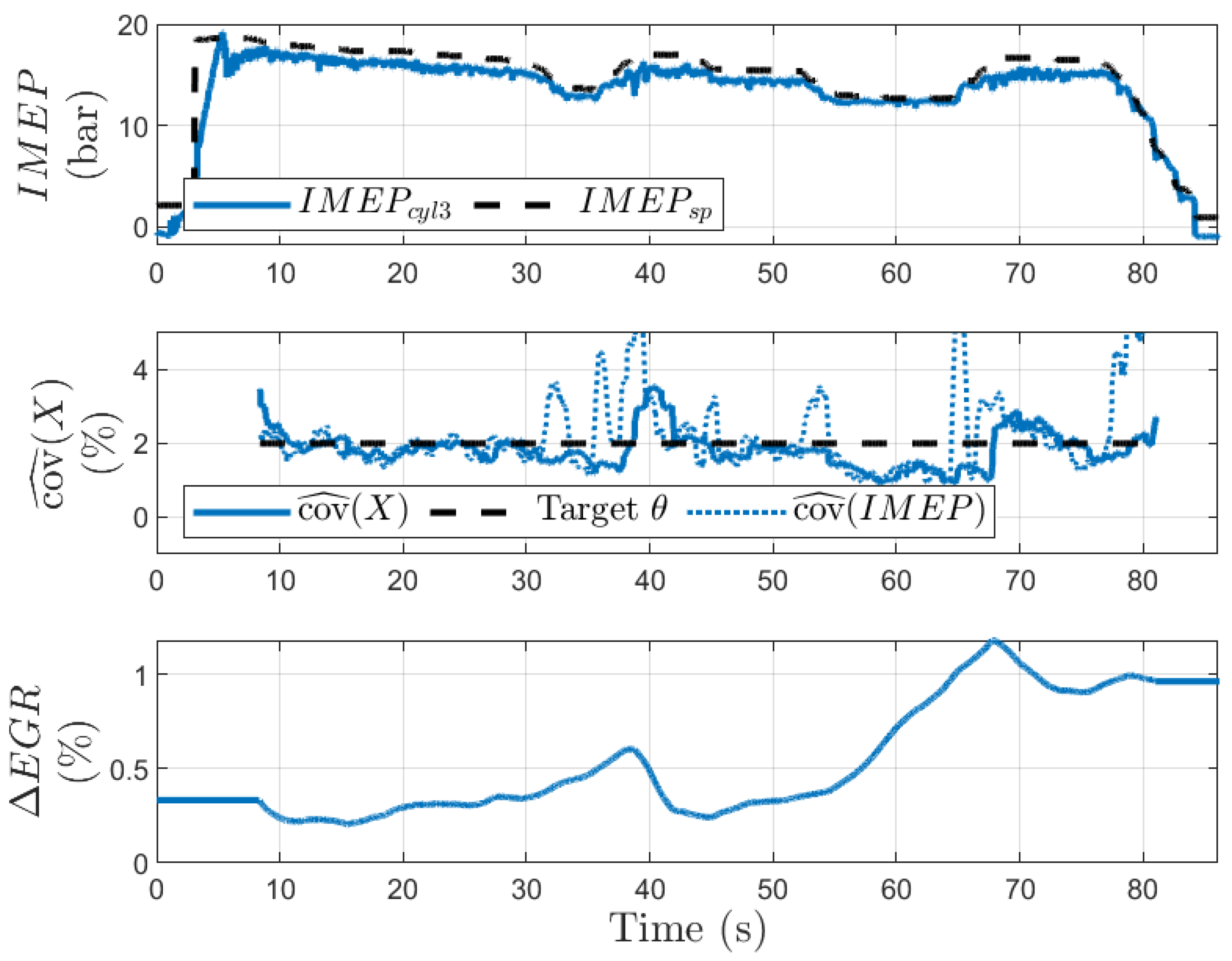
5.2. Strategy Validation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kapus, P.; Ellinger, R.; Bogner, E.; Schrank, G.; Teuschl, G.; Sams, C.; Prochazka, W.; Fraidl, G. Passenger car powertrain 4. x–from vehicle level to a cost optimized powertrain system. In Proceedings of the 41st International Vienna Motor Symposium, Vienna, Austria, 22–24 April 2020; pp. 22–24. [Google Scholar]
- Gautrot, X.; Bardi, M.; Leroy, T.; Luca, P.; Nowak, L.; Reveille, B. Swumble In-Cylinder Fluid Motion for High Efficiency Gasoline SI Engines: Development of the second generation. In Proceedings of the SIA Powertrain and Electronics, Rouen, France, 3–4 June 2020. [Google Scholar]
- Kiwan, R.; Stefanopoulou, A.; Martz, J.; Surnilla, G.; Ali, I.; Styles, D. Effects of differential pressure measurement characteristics on low pressure-EGR estimation error in SI-engines. IFAC 2016, 49, 722–729. [Google Scholar]
- Nyerges, A.; Zoldy, M. Verification and Comparison of Nine Exhaust Gas Recirculation Mass Flow Rate Estimation Methods. Sensors 2020, 20, 7291. [Google Scholar] [CrossRef] [PubMed]
- Booven, B.; Schüle, H.; Walder, T.; Rottengruber, H. Potential of Series-Compatible In-Cylinder Pressure Sensors for Gasoline Engines Using the Example of Ignition Angle Control. In Proceedings of the International Conference on Knocking in Gasoline Engines, Berlin, Germany, 12–13 December 2017; pp. 279–296. [Google Scholar]
- Booven, B.; Schüle, H.; Walder, T.; Casal, K.; Rottengruber, H.; Bargende, M. Real-time assessment of in-cylinder pressure for fresh air mass estimation using the example of modern spark-ignited combustion engines. Int. J. Engine Res. 2018, 19, 250–256. [Google Scholar] [CrossRef]
- Maldonado, B.; Stefanopoulou, A.; Kaul, B. Artificial-intelligence-based prediction and control of combustion instabilities in spark-ignition engines. In Artificial Intelligence and Data Driven Optimization of Internal Combustion Engines; Elsevier: Amsterdam, The Netherlands, 2022; pp. 185–212. [Google Scholar]
- Singh, A.; Vance, J.B.; Kaul, B.; Drallmeier, J.; Jagannathan, S. Neural network control of spark ignition engines with high EGR levels. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network Proceedings, Vancouver, BC, Canada, 16–21 July 2006; pp. 4978–4985. [Google Scholar]
- Norouzi, A.; Heidarifar, H.; Shahbakhti, M.; Koch, C.R.; Borhan, H. Model predictive control of internal combustion engines: A review and future directions. Energies 2021, 14, 6251. [Google Scholar] [CrossRef]
- Yao, C.; Hu, Y.; Zhou, T.; Yang, F.; Ouyang, M.; Huang, H. Combustion Stability Control of Dieseline PPCI Based on In-Cylinder Pressure Signals. IFAC PapersOnLine 2016, 49, 333–339. [Google Scholar] [CrossRef]
- Haertl, S.; Kainz, J.; Schuele, H.; Gaderer, M. Experimental Investigation of a Control Strategy Based on Combustion Stability and Combustion Phasing for a Multi-Cylinder Engine with Fueled Pre-Chambers and Cylinder Pressure Transducers; Technical Report, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2021. [Google Scholar]
- Wei, H.; Zhu, T.; Shu, G.; Tan, L.; Wang, Y. Gasoline engine exhaust gas recirculation—A review. Appl. Energy 2012, 99, 534–544. [Google Scholar] [CrossRef]
- Tornatore, C.; Bozza, F.; De Bellis, V.; Teodosio, L.; Valentino, G.; Marchitto, L. Experimental and numerical study on the influence of cooled EGR on knock tendency, performance and emissions of a downsized spark-ignition engine. Energy 2019, 172, 968–976. [Google Scholar] [CrossRef]
- Randolph, E.; Fieseler, K.; Conway, G.; Alger, T.; Chadwell, C. The Effects of EGR Composition on Combustion Performance and Efficiency. SAE Int. J. Adv. Curr. Pract. Mobil. 2020, 3, 250–261. [Google Scholar] [CrossRef]
- Byttner, S.; Rögnvaldsson, T.; Wickström, N. Estimation of Combustion Variability Using in-Cylinder Ionization Measurements; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2001; pp. 1–3485. [Google Scholar]
- Kaiadi, M.; Tunestål, P.; Johansson, B. Closed-Loop Combustion Control Using Ion-Current Signals in a 6-Cylinder Port-Injected Natural-Gas Engine; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2008; pp. 1–2453. [Google Scholar]
- Byttner, S.; Holmberg, U. Closed-loop control of EGR using ion currents. In Proceedings of the 27th IASTED International Conference on Modelling, Identification, and Control, Innsbruck, Austria, 11–13 February 2008; p. 7. [Google Scholar]
- Leroy, T.; Nowak, L.; Odillard, L.; François, D. New Combustion Process for Higher Efficiency of Gasoline Engines. MTZ Worldw. 2021, 82, 16–25. [Google Scholar] [CrossRef]
- Grondin, O.; Duval, L.; Guillemin, F.; Ker, S.; Corde, G.; Vigild, C. Rapid-prototyping multi-sensors processing platform for real time engine control and diagnosis. IFAC 2007, 40, 555–562. [Google Scholar] [CrossRef]
- Vollberg, D.; Wachter, D.; Kuberczyk, T.; Schultes, G. Cylinder pressure sensors for smart combustion control. J. Sens. Sens. Syst. 2019, 8, 75–85. [Google Scholar] [CrossRef]
- Hellemans, A.; Landrevie, L.; Venzal, S.; Walker, E. In-cylinder pressure sensor. MTZ Worldw. EMag. 2011, 72, 42–48. [Google Scholar] [CrossRef]
- Leroy, T.; Nowak, L.; Gautrot, X.; Alvarado, L.M. Swumble 3-Cylinder High Efficiency Gasoline Engine for Future Electrified Powertrains. In Proceedings of the 42nd International Vienna Motor Symposium, Online, 29–30 April 2021. [Google Scholar]



| Engine displacement [L] | 1.2 |
| Vol. compression ratio [-] | 13.65:1 |
| Bore × Stroke [mm] | 75 × 90.5 |
| Number of intake/exhaust valves | 2/2 |
| Valve lift CA duration, at 1 mm [°C A] | Intake 140, Exhaust 210 |
| Injection system | Central direct injection |
| Injector | Bosch HDEV6, six holes |
| Injection pressure [bar] | 350 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jean, M.; Granier, P.; Leroy, T. Combustion Stability Control Based on Cylinder Pressure for High Efficiency Gasoline Engines. Energies 2022, 15, 2530. https://doi.org/10.3390/en15072530
Jean M, Granier P, Leroy T. Combustion Stability Control Based on Cylinder Pressure for High Efficiency Gasoline Engines. Energies. 2022; 15(7):2530. https://doi.org/10.3390/en15072530
Chicago/Turabian StyleJean, Maxime, Pascal Granier, and Thomas Leroy. 2022. "Combustion Stability Control Based on Cylinder Pressure for High Efficiency Gasoline Engines" Energies 15, no. 7: 2530. https://doi.org/10.3390/en15072530






